1. На главную
  2. Электронные версии
  3. Поверхность. Рентгеновские, синхротронные и нейтронные исследования
  4. № 4, 2021

Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2021, № 4, стр. 108-112

Энергия и ширина донорного уровня вблизи гетерограницы

Т. Т. Муратов *

Ташкентский государственный педагогический университет им. Низами
100185 Ташкент, Узбекистан

* E-mail: temur-muratov@yandex.ru

Поступила в редакцию 07.07.2020
После доработки 25.09.2020
Принята к публикации 30.09.2020

Полный текст (PDF)

Аннотация

Рассмотрено влияние гетерограницы на энергетический спектр мелких и глубоких центров. Получены формулы для уширения энергии примесного центра и времени жизни электрона в квазистационарном состоянии. Проведено уточнение соответствующих аналитических формул, полученных в других работах. Показано, что в данном случае роль эффективного радиуса мелкого центра выполняет не его боровский радиус rB, а величина, равная 2.5rB.

Ключевые слова: мелкие и глубокие центры, гетерограница, ширина квазистационарного уровня, туннельный эффект.

ВВЕДЕНИЕ

Ситуация, когда донорный центр локализован вблизи гетероперехода, довольно часто реализуется в полупроводниковых гетероструктурах. Наличие характерных полос люминесценции в инфракрасной области спектра при очень низких температурах [1, 2] дает основание полагать, что электрон донорного центра, находящегося, например, в широкозонной части гетероперехода, сможет протуннелировать через потенциальный барьер в узкозонную часть гетероперехода с последующей рекомбинацией с дыркой. С учетом разрыва зон электрон, изначально находящийся в квазисвязанном состоянии, переходит в квазисвободное состояние. При этом его энергия не изменяется. Конечное время пребывания в связанном состоянии приводит к энергетическому сдвигу примесного уровня и эффекту перезарядки, заключающемуся в том, что вакантное место будет занято электроном соседнего донора. По сути, время перезарядки равно времени жизни электрона на центре.

В ряде работ [3–5] получены аналитические формулы для расчета различных параметров рассеяния и туннелирования носителя нейтрального центра. Эффект “диагонального туннелирования” носителя оказывается принципиально важным для работы целого ряда полупроводниковых приборов: светодиодов, фотоприемников, биполярных транзисторов и других [1]. Основной практической задачей является стимулирование туннельных эффектов, приводящих к значительному уменьшению концентрации неосновных носителей в указанных приборах. Для этого предлагается, например, на основе теоретических оценок использовать электрические поля с напряженностью E ~ 2 × 106 В · см–1 [3] (в гетероструктуре GaAlAs).

В глубине широкозонной части гетероперехода доминируют процессы рассеяния носителей на нейтральных центрах [4], вблизи гетероперехода – эффекты туннелирования [5]. В [5] рассчитаны ширина квазистационарного уровня и время жизни электрона в квазистационарном состоянии. Однако полученные асимптотические формулы требуют уточнения. Некоторая неточность была допущена при усреднении квазиклассической (отраженной) волновой функции по ее угловой переменной. Как будет показано в настоящей работе, замена синуса и косинуса приосевого угла θ их приближенными значениями приводит к потере важной информации об отраженной волновой функции.

Целью настоящей работы было корректное угловое усреднение отраженной квазиклассической волновой функции с последующим получением исходных “точных” формул для ширины квазистационарного уровня и времени жизни электрона на этом уровне. Для сравнения рассматривается аналогичная процедура расчета для донорного центра, описываемого потенциалом нулевого радиуса (потенциалом Луковского [4, 6]).

МЕТОДИКА РАСЧЕТА

Рассмотрим донорный центр вблизи гетероперехода, моделируемого потенциальным барьером $ \pm {{V}_{0}}$ (рис. 1, 2). Гамильтониан электрона на таком центре имеет вид:

(1)
$\hat {H} = - \frac{{{{\hbar }^{2}}}}{{2m{\kern 1pt} {\text{*}}}}{{\nabla }^{2}} - \frac{{{{e}^{2}}}}{{\varepsilon r}} + V(z),\,\,\,\,V(z) = \left\{ \begin{gathered} 0,\,\,\,\,\,\,z < L \hfill \\ {{V}_{0}},\,\,\,\,z > L. \hfill \\ \end{gathered} \right.$
Здесь $m{\text{*}}$ – эффективная масса электрона, ε – диэлектрическая проницаемость.

Рис. 1.

Переход квазисвязанного электрона в зону проводимости узкозонного полупроводника возможен за счет его перехода в зону проводимости широкозонного материала с последующим термостимулированным просачиванием через барьер.

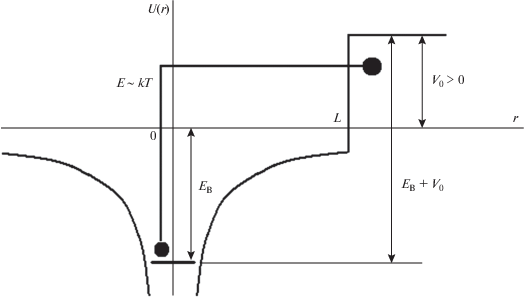
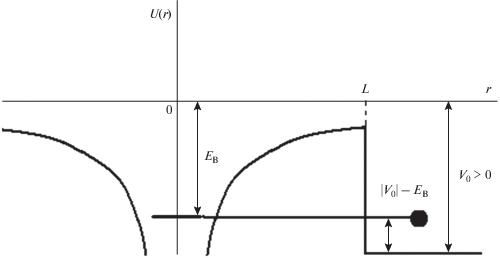
Рис. 2.

Переход квазисвязанного электрона в состояние сплошного спектра за счет туннельного эффекта.

Волновая функция основного состояния при $L \to \infty $ (барьер находится на очень большом расстоянии от центра) имеет вид:

(2)
${{\psi }_{{\text{B}}}}(r) = \frac{1}{{\sqrt {\pi r_{{\text{B}}}^{3}} }}\exp \left( { - \frac{r}{{{{r}_{{\text{B}}}}}}} \right),$
где ${{r}_{{\text{B}}}}$ – боровский радиус основного состояния мелкой примеси (~10 Å) с энергией связи ${{E}_{{\text{B}}}}$ (~10–2 эВ). Наличие барьера на конечном расстоянии от центра приводит к изменению асимптотического поведения волновой функции (2) и, как следствие, к сдвигу энергии основного состояния. Как видно из рис. 2, при EB < –V0 основное состояние примеси квазистационарное и возможен туннельный переход электрона в состояние сплошного спектра.

Решения уравнения Шредингера для областей z < L и z > L выражаются через вырожденные гипергеометрические функции: $F( - n + l + 1,2l + 2;\rho ).$ По разные стороны от барьера решения отличаются только значениями параметров гипергеометрической функции. Вдали от центра можно пренебречь вкладом возбужденных состояний и рассматривать только s-состояния [5], которые мало отличаются от (2), т.е.

(3)
$\begin{gathered} {{\psi }_{s}} = \frac{1}{{\sqrt {\pi r_{{\text{B}}}^{3}} }}\exp ( - {\kern 1pt} \sqrt {1 - \Delta } {\kern 1pt} \rho ) \times \\ \times \,\,F\left( {1 - \frac{1}{{\sqrt {1 - \Delta } }},2;2\sqrt {1 - \Delta } {\kern 1pt} \rho } \right), \\ \end{gathered} $
где введены обозначения: $\rho = {r \mathord{\left/ {\vphantom {r {{{r}_{{\text{B}}}}}}} \right. \kern-0em} {{{r}_{{\text{B}}}}}}$ и $\Delta = {E \mathord{\left/ {\vphantom {E {{{E}_{{\text{B}}}} + 1}}} \right. \kern-0em} {{{E}_{{\text{B}}}} + 1}}.$ При $\rho \gg 1$ и $\left| \Delta \right| \ll 1$ можно воспользоваться асимптотикой F [7 ] :
(4)
${{\psi }_{s}}(\rho )\mathop \approx \limits_{\rho \to \infty } \frac{1}{{\sqrt {\pi r_{{\text{B}}}^{3}} }}\left( {\exp ( - \rho ) + \frac{{{{{(2\rho )}}^{{ - 2}}}}}{{\Gamma ({{ - \Delta } \mathord{\left/ {\vphantom {{ - \Delta } 2}} \right. \kern-0em} 2})}}\exp (\rho )} \right),$
где $\Gamma (x)$ – гамма-функция.

Из квазиклассической волновой функции (4) нетрудно выделить ее падающую и отраженную компоненты: $\psi _{s}^{ - } = {{C}_{1}}\exp ( - \rho ),$ $\psi _{s}^{ + } = {{C}_{2}}\exp (\rho ).$ Множитель перед растущей экспонентой в (4) есть отношение амплитуд “падающей” и “отраженной” s-волн:

(5)
$\frac{{{{{(2\rho )}}^{{ - 2}}}}}{{\Gamma ({{ - \Delta } \mathord{\left/ {\vphantom {{ - \Delta } 2}} \right. \kern-0em} 2})}} \approx - \frac{\Delta }{{8{{\rho }^{2}}}} = \frac{{{{C}_{2}}}}{{{{C}_{1}}}},\,\,\,\,\left| \Delta \right| \ll 1.$
На основе (5) можно найти сдвиг примесного уровня $\Delta {\kern 1pt} .$ Для этого надо сконструировать отраженную от плоскости $z = L$ волну и выделить из нее s-компоненту, т.е. практически определить отношение C2/C1.

Рассмотрим квазиклассические траектории, расположенные под углом θ к оси z (рис. 3). Амплитуда отраженной волны в точке C на сфере r = L отличается от амплитуды падающей волны в точке A фактором $G\exp \left( { - \frac{{{{r}_{{AB}}} + {{r}_{{BC}}}}}{{{{r}_{{\text{B}}}}}}} \right),$ где G – стандартный коэффициент, равный

(6)
$G({{V}_{0}}) = \frac{{\sqrt {{{E}_{{\text{B}}}}} - \sqrt {{{V}_{0}} + {{E}_{{\text{B}}}}} }}{{\sqrt {{{E}_{{\text{B}}}}} + \sqrt {{{V}_{0}} + {{E}_{{\text{B}}}}} }}.$
Для суммы расстояний в экспоненте rAB + $ + \,{{r}_{{BC}}} \approx 2{{r}_{{AB}}}$ = ${{2L(1 - \cos \theta )} \mathord{\left/ {\vphantom {{2L(1 - \cos \theta )} {\cos \theta }}} \right. \kern-0em} {\cos \theta }}.$ В отличие от [5] косинус угла не заменяется на $1 - {{{{\theta }^{2}}} \mathord{\left/ {\vphantom {{{{\theta }^{2}}} 2}} \right. \kern-0em} 2}.$ Следовательно, уравнение отраженной на сфере радиуса r = L волны имеет вид:
(7)
${{\psi }_{ + }}(\theta ,L) = \frac{1}{{\sqrt {\pi r_{{\text{B}}}^{3}} }}G({{V}_{0}})\exp \left( { - \frac{{2L}}{{{{r}_{{\text{B}}}}\cos \theta }}} \right)\exp \left( {\frac{L}{{{{r}_{{\text{B}}}}}}} \right).$
Для того чтобы выделить из ${{\psi }_{ + }}(\theta ,L)$ ее s-компоненту, следует усреднить (7) по полному телесному углу первого октанта:
(8)
$\begin{gathered} {{\left\langle {{{\psi }_{ + }}(\theta ,L)} \right\rangle }_{\Omega }} = {{\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {{{\psi }_{ + }}(\theta ,L)\sin \theta d\theta } } \mathord{\left/ {\vphantom {{\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {{{\psi }_{ + }}(\theta ,L)\sin \theta d\theta } } {\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\sin \theta d\theta } }}} \right. \kern-0em} {\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\sin \theta d\theta } }} = \\ = \frac{1}{{\sqrt {\pi r_{{\text{B}}}^{3}} }}G({{V}_{0}})\exp \left( {\frac{L}{{{{r}_{{\text{B}}}}}}} \right)\int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {\exp \left( { - \frac{{2L}}{{{{r}_{{\text{B}}}}\cos \theta }}} \right)\sin \theta d\theta } = \\ = \frac{1}{{\sqrt {\pi r_{{\text{B}}}^{{\text{3}}}} }}G({{V}_{0}})\exp \left( { - \frac{L}{{{{r}_{{\text{B}}}}}}} \right) \times \\ \times \,\,\left\{ {1 - \frac{{2L}}{{{{r}_{{\text{B}}}}}}\exp \left( {\frac{{2L}}{{{{r}_{{\text{B}}}}}}} \right)\left[ { - Ei\left( { - \frac{{2L}}{{{{r}_{{\text{B}}}}}}} \right)} \right]} \right\}, \\ \end{gathered} $
где $ - Ei( - x)$ – интегральная показательная функция. Так как ${L \mathord{\left/ {\vphantom {L {{{r}_{{\text{B}}}}}}} \right. \kern-0em} {{{r}_{{\text{B}}}}}} \gg 1,$
(9)
${{\left\langle {{{\psi }_{ + }}(\theta ,L)} \right\rangle }_{\Omega }} = \frac{{G({{V}_{0}})}}{{2L\sqrt {\pi {{r}_{{\text{B}}}}} }}\exp \left( { - \frac{L}{{{{r}_{{\text{B}}}}}}} \right).$
Как видно из (9), результирующее значение получилось вдвое больше, чем то, что следует из [5]. Компонента (8) примечательна еще и тем, что при ${{2L} \mathord{\left/ {\vphantom {{2L} {{{r}_{{\text{B}}}}}}} \right. \kern-0em} {{{r}_{{\text{B}}}}}} \geqslant 5$ соответствует минимальному расстоянию от центра, за которым допускается квазиклассическое рассмотрение [8–11]. Параксиальное приближение, используемое в [5], не дает возможности указать критерий перехода от волновой функции (2) к квазиклассической волновой функции (4). Согласно (8) переход начинается примерно с расстояния $L = 2.5{{r}_{{\text{B}}}}.$ На таких расстояниях ($L > 2.5{{r}_{{\text{B}}}}$) отраженная волна (8) почти отсутствует. Подстановка (9) в (5) с учетом ${{C}_{1}} = {1 \mathord{\left/ {\vphantom {1 {\sqrt {\pi r_{{\text{B}}}^{3}} }}} \right. \kern-0em} {\sqrt {\pi r_{{\text{B}}}^{3}} }}$ дает для энергетического сдвига формулу:
(10)
$\delta {{E}_{{\text{B}}}} = {{E}_{{\text{B}}}}\Delta = 4{\kern 1pt} \left( {\frac{L}{{{{r}_{{\text{B}}}}}}} \right){\kern 1pt} \frac{{\sqrt {{{E}_{{\text{B}}}} + {{V}_{0}}} - \sqrt {{{E}_{{\text{B}}}}} }}{{\sqrt {{{E}_{{\text{B}}}} + {{V}_{0}}} + \sqrt {{{E}_{{\text{B}}}}} }}\exp {\kern 1pt} \left( { - {\kern 1pt} \frac{{2L}}{{{{r}_{{\text{B}}}}}}} \right){\kern 1pt} {{E}_{{\text{B}}}}.$
Энергетический сдвиг оказался в два раза больше сдвига, полученного в [5]. При очень низких температурах (~4 К), может реализоваться ситуация, указанная на рис. 2, и $\delta {\kern 1pt} {{E}_{{\text{B}}}}$ становится комплексным. Используя (10), нетрудно найти время жизни частицы на квазистационарном уровне:
(11)
$\begin{gathered} {{\tau }_{{\text{B}}}} = \frac{\hbar }{{2\operatorname{Im} (\delta E)}} = \\ = \frac{\hbar }{{16{{E}_{{\text{B}}}}}}\frac{{\left| {{{V}_{0}}} \right|}}{{\sqrt {{{E}_{{\text{B}}}}(\left| {{{V}_{0}}} \right| - {{E}_{{\text{B}}}})} }}\left( {\frac{{{{r}_{{\text{B}}}}}}{L}} \right)\exp \left( {\frac{{2L}}{{{{r}_{{\text{B}}}}}}} \right). \\ \end{gathered} $
Оценки на основе (11) для параметров мелких примесей (Ge, Si) дают времена жизни порядка 10–11–10–10 с, что находится в разумном согласии с экспериментальными данными [2, 6].

Рис. 3.

Отражение волновой функции связанного на центре электрона от потенциального барьера. На отрезках АВ и ВС используется квазиклассическое описание падающей и отраженной от барьера волн. На сфере r = L квазиклассическое решение сшивается с s-компонентой волновой функции примесного центра. Угол падения θ равен углу отражения в точке B.

В отличие от мелких примесных уровней, потенциал центра с большой энергией ионизации (глубокие центры) нельзя рассматривать как медленно меняющийся [12, 13]. По этой причине его можно смоделировать δ-функцией: $U(r) = - {{U}_{0}}\delta (r)$ [6]. Качественно понятно, что частота изменения потенциала глубокого центра гораздо больше частоты перехода частицы в состояние сплошного спектра, т.е. гетерограница не успевает “следить” за электроном, и его время жизни на глубоком центре существенно возрастает по сравнению со временем жизни на мелком центре (11). Расчеты, аналогичные проведенным выше, дают отличие примерно в $2{{({L \mathord{\left/ {\vphantom {L {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}})}^{2}},$ где r0 – радиус связанного состояния мелкого центра (r0 ~ 10–6 см). Оценки показывают, что τ0 ~ 10–9–10–8 с.

ЗАКЛЮЧЕНИЕ

Основное содержание работы можно резюмировать формулами (9), (10) и (11), уточняющими соответствующие формулы, полученные в [5]. Анализ (8) указывает на наличие определенной границы ($L \leqslant 2.5{{r}_{{\text{B}}}}$), в пределах которой энергетический спектр мелкого центра еще не возмущен. В случае глубоких примесей влияние гетерограницы примерно на два порядка меньше, чем в случае мелких примесей.

Список литературы

  1. Алферов Ж.И. // ФТП. 1998. Т. 32. С. 3.

  2. Бреслер М.С., Гусев О.Б., Михайлова М.П. и др. // ФТП. 1991. Т. 25. С. 298.

  3. Пахомов А.А. // ФТТ. 1992. Т. 34. С. 3417.

  4. Гейлер В.А., Маргулис В.А., Чучаев И.И. // ФТТ. 1995. Т. 37. С. 837.

  5. Иванов М.Г., Меркулов И.А., Эфрос А.Л. // ФТП. 1988. Т. 22. С. 628.

  6. Абакумов В.Н., Перель В.И., Яссиевич И.Н. Безызлучательная рекомбинация в полупроводниках. С.-Пб.: ПИЯФ РАН, 1997. 376 с.

  7. Никифоров А.Ф., Уваров В.Б. Специальные функции математической физики. М.: Наука, 1978. 320 с.

  8. Арфкен Г. Математические методы в физике. М.: Атомиздат, 1970. 712 с.

  9. Федоров М.В. // ЖЭТФ. 2016. Т. 149. С. 522.

  10. Михайлова М.П., Иванов Э.В., Данилов Л.В. и др. // ФТП. 2020. Т. 54. С. 1267.

  11. Торхов Н.А. // ФТП. 2021. Т. 55. С. 16.

  12. Татохин Е.А., Буданов А.В., Бутусов И.Ю. и др. // Вестн. ВГУ. Сер. Физика. Математика. 2008. № 2. С. 60.

  13. Миронов А.Г., Серов А.С. // Вестн. МГУ. Сер. 3. Физика. Астрономия. 2011. № 3. С. 65.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал