Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2021, № 7, стр. 104-107

Зависимость параметров каскадного размножения частиц от вида атомного потенциала

А. И. Толмачев^a, *, Л. Форлано^b, **

^a Российский новый университет
105005 Москва, Россия

^b Университет Калабрии
87036 Козенца, Италия

^* E-mail: tolmachev.alex@rambler.ru
^** E-mail: forlano@vegachess.com

Поступила в редакцию 18.09.2020
После доработки 20.11.2020
Принята к публикации 25.11.2020

DOI: 10.31857/S1028096021060157

Полный текст (PDF)

Аннотация

Теоретически рассмотрено каскадное размножение атомов в твердотельной мишени для различных видов сечения рассеяния. Решение транспортного уравнения в одних случаях найдено в аналитическом виде, в других сводится к численному интегрированию. Получены выражения для энергетического распределения и полного числа каскадных атомов, а также для полной энергии каскада как функций глубины мишени и вида атомного взаимодействия. Результаты теории обобщают теорию каскадных ливней Ландау–Румера на случай произвольных видов атомных потенциалов – от потенциала твердых сфер до кулоновского.

Ключевые слова: теоретический анализ, каскадное размножение, атомный потенциал, сечение рассеяния.

ВВЕДЕНИЕ

Распыление твердых тел под действием ионной бомбардировки представляет собой сложное физическое явление [1, 2]. При столкновении атомов внутри мишени образуются две частицы, каждая со своей энергией и направлением движения, зависящими от закона межатомного взаимодействия. Объяснение наблюдаемых закономерностей распыления возможно в основном только с помощью программ компьютерного моделирования [3, 4].

Для теоретического изучения каскадного размножения в [5, 6] была сделана попытка разделить анализ энергетического и углового распределений: сначала рассмотреть энергетическое распределение каскада частиц, движущихся прямолинейно [5], а затем получить угловое распределение как поправку к прямолинейному решению [6]. Результаты [5, 6] были получены для конкретного вида сечения рассеяния, соответствующего взаимодействию электронов и фотонов. В настоящей работе теория обобщена на случай степенной зависимости сечения рассеяния от переданной энергии. Изменение степенного параметра позволяет рассмотреть широкий класс межатомных взаимодействий – от взаимодействия по закону твердых сфер до резерфордовского взаимодействия, характерного для кулоновского потенциала.

УРАВНЕНИЕ КАСКАДНОГО РАЗМНОЖЕНИЯ

Рассмотрим следующую задачу. Первичный ион с энергией ${{E}_{0}}~$ входит в мишень. В мишени ион испытывает упругие столкновения с неподвижными атомами и выбивает их из положений равновесия. Выбитые атомы, в свою очередь, испытывают столкновения с другими атомами мишени и так далее – возникает каскад. Каскадное размножение атомов продолжается до того момента, когда энергия атома уменьшается до величины ${{E}_{{{\text{min}}}}},$ недостаточной для разрушения атомной связи. Рассчитаем энергетическое распределение и число каскадных атомов в зависимости от глубины мишени для различных видов межатомного взаимодействия. Предполагается, что массы ионов и атомов равны, что соответствует случаю так называемого самораспыления.

Будем измерять энергию атомов $~E$ в относительных единицах $u = {E \mathord{\left/ {\vphantom {E {{{E}_{0}}}}} \right. \kern-0em} {{{E}_{0}}}},$ ${{u}_{{{\text{min}}}}} = {{{{E}_{{{\text{min}}}}}} \mathord{\left/ {\vphantom {{{{E}_{{{\text{min}}}}}} {{{E}_{{0~}}}}}} \right. \kern-0em} {{{E}_{{0~}}}}}$ и обозначим функцией $f\left( {x,u} \right)$ число атомов с энергией $u$ на нормированной глубине x. Транспортное уравнение для функции распределения $f\left( {x,u} \right)$ имеет вид [7–11]:

(1)

$\begin{gathered} \frac{{~\partial f\left( {x,u} \right)~}}{{~\partial x~}} + f\left( {x,u} \right) = \int\limits_u^1 {f\left( {x,u{\kern 1pt} '} \right)} \times ~ \\ \times \,\,\left[ {K\left( {u{\kern 1pt} ',u{\kern 1pt} '\, - u} \right) + K\left( {u{\kern 1pt} ',u} \right)} \right]~du{\kern 1pt} '. \\ \end{gathered} $

Первое слагаемое в левой части уравнения (1) описывает изменение числа атомов между столкновениями. Два слагаемых в правой части уравнения (1) отражают тот факт, что в результате столкновения атома с энергией $u{\kern 1pt} '$ с неподвижным атомом образуются два атома, значения энергии которых $u$ и $u{\kern 1pt} '\, - u.$ Граничное условие к уравнению (1) имеет дельтаобразный вид $f\left( {0,u} \right) = \delta \left( {1 - u} \right)$ и указывает на то, что энергия иона, инициирующего каскад, равна ${{E}_{0}}.$

В качестве сечения рассеяния для столкновения двух атомов выберем сечение, зависящее по степенному закону от переданной энергии T :

(2)

$K\left( {E,T} \right)dT = n{{E}^{{ - n}}}{{T}^{{n - 1}}}dT,$

где E – энергия налетающего атома, $n > 0$ – степенной параметр. В каскадной теории электронных ливней [5] авторы использовали комбинацию из трех сечений рассеяния (2) с тремя различными значениями степенного параметра: $n = 1,2,3.$ В атомных столкновениях степенной параметр меняется в пределах $0 < n \leqslant 1,$ что существенно отличается от случая электронных ливней. При малых значениях энергии ионов имеем $n = 1$ и взаимодействие частиц по закону твердых сфер. При больших значениях энергии ионов степенной параметр мал ($n \ll 1$), что соответствует резерфордовскому рассеянию.

ОБЩЕЕ РЕШЕНИЕ

Подстановка (2) в уравнение (1) дает

(3)

$\begin{gathered} \frac{{~\partial f\left( {x,u} \right)~}}{{~\partial x~}} + f\left( {x,u} \right) = \\ = n\int\limits_u^1 {f\left( {x,u{\kern 1pt} '} \right)} \frac{{~{{u}^{{n\,\, - \,\,1}}} + {{{\left( {u{\kern 1pt} '\, - u} \right)}}^{{n - 1}}}~}}{{{{u}^{{'n}}}}}~du{\kern 1pt} '. \\ \end{gathered} $

Для исследования уравнения вместо переменной $u$ введем новую независимую переменную s, используя преобразование Меллина:

(4)

${{f}_{s}}\left( x \right) = \int\limits_0^1 {{{u}^{{s\,\, - \,\,1}}}f} \left( {x,u} \right)~du,\,\,\,\,\left( {1 \leqslant s < \infty } \right).$

Функция ${{f}_{s}}\left( x \right)$ однозначно выражается через функцию $f\left( {x,u} \right)$ и наоборот. В результате преобразований получаем

(5)

$\frac{{~d{{f}_{s}}\left( x \right)~}}{{~dx~}} + {{f}_{s}}\left( x \right) = {{Q}_{s}}~{{f}_{s}}\left( x \right),$

(6)

$\begin{gathered} {{Q}_{s}} = n\int\limits_0^1 {{{\xi }^{{s\,\, - \,\,1}}}~\left[ {{{\xi }^{{n\,\, - \,\,1}}} + {{{\left( {1 - \xi } \right)}}^{{n\,\, - \,\,1}}}} \right]~d\xi } = \\ = n\left[ {~\frac{1}{{~s + n - 1~}} + {\text{{\rm B}}}\left( {s,n} \right)} \right], \\ \end{gathered} $

где ${\text{{\rm B}\;}}$ обозначает бета-функцию [12]. Решение уравнения (5) имеет вид:

(7)

${{f}_{s}}\left( x \right) = {\text{exp}}\left( {x{{Q}_{s}}} \right){\text{exp}}\left( { - x} \right).$

Таким образом, решение транспортного уравнения (3) сведено к нахождению обратного преобразования Меллина и вычислению интеграла в комплексной плоскости [13, 14]:

(8)

$f\left( {x,t} \right) = \frac{1}{{2\pi i}}\int\limits_{1\,\, - \,\,i\infty }^{1\,\, + \,\,i\infty } {{\text{exp}}\left( {st} \right){{f}_{s}}\left( x \right)~ds} ,\,\,\,\,t = {\text{ln}}\frac{1}{u}.$

Функция $f\left( {x,t} \right)$ представляет собой дифференциальную характеристику – энергетическое распределение каскадных атомов на глубине x. Также представляет интерес интегральная характеристика – число каскадных атомов с энергией в диапазоне ${{u}_{{{\text{min}}}}} \leqslant u \leqslant 1$ на глубине x:

(9)

$F\left( {x,{{t}_{{{\text{max}}}}}} \right) = \int\limits_0^{{{t}_{{{\text{max}}}}}} {f\left( {x,t} \right)~dt} ,\,\,\,\,{{t}_{{{\text{max}}}}} = {\text{ln}}\frac{1}{{{{u}_{{{\text{min}}}}}}}.$

Другой важной интегральной характеристикой является полная энергия каскада на глубине x:

(10)

$\bar {u}\left( x \right) = \int\limits_{{{u}_{{{\text{min}}}}}}^1 {uf\left( {x,u} \right)du} = \int\limits_0^{{{t}_{{{\text{max}}}}}} {{\text{exp}}\left( { - 2t} \right)f} \left( {x,t} \right)~dt.$

РЕШЕНИЕ ДЛЯ ПОТЕНЦИАЛА ТВЕРДЫХ СФЕР

В случае взаимодействия частиц по закону твердых сфер решение может быть представлено в аналитическом виде. Подстановка $~n = 1~$ в уравнение (6) дает ${{Q}_{s}} = {2 \mathord{\left/ {\vphantom {2 {s,}}} \right. \kern-0em} {s,}}$

(11)

${{f}_{s}}\left( x \right) = {\text{exp}}\left( {\frac{{~2x~}}{s}} \right){\text{exp}}\left( { - x} \right),$

и из таблиц [15] находим функцию распределения:

(12)

$f\left( {x,t} \right) = \left[ {\delta \left( t \right) + \sqrt {~\frac{{~2x~}}{t}~} ~{{I}_{1}}\left( {\sqrt {~8xt~} ~} \right)} \right]{\text{exp}}\left( { - x} \right).$

Здесь ${{I}_{1}}$ обозначает модифицированную функцию Бесселя первого порядка [12], первое слагаемое в скобках относится к первичному иону, инициирующему каскад, второе слагаемое относится к собственно каскаду.

Из интеграла (9) вычисляем число каскадных атомов:

(13)

$F\left( {x,{{t}_{{{\text{max}}}}}} \right) = {{I}_{0}}\left( {\sqrt {~8x{{t}_{{{\text{max}}}}}~} ~} \right){\text{exp}}\left( { - x} \right).$

Дифференцирование уравнения (13) по $x$ приводит к трансцендентному уравнению для определения координаты максимума числа каскадных атомов ${{x}_{{{\text{max}}}}}{\text{:}}$

(14)

$\sqrt {\frac{{{{x}_{{{\text{max}}}}}}}{{~2{{t}_{{{\text{max}}}}}~}}} = \frac{{~{{I}_{1}}\left( {\sqrt {~8~{{x}_{{{\text{max}}}}}~{{t}_{{{\text{max}}}}}~} ~} \right)~}}{{{{I}_{0}}\left( {\sqrt {~8~{{x}_{{{\text{max}}~}}}{{t}_{{{\text{max}}}}}~} ~} \right)}}.$

Асимптотическое разложение функций Бесселя в уравнении (14) показывает, что при больших значениях энергии ионов кривая ${{x}_{{{\text{max}}}}}\left( {{{t}_{{{\text{max}}}}}} \right)$ стремится к прямой линии:

(15)

${{x}_{{{\text{max}}}}} = 2{{t}_{{{\text{max}}}}} - \frac{1}{{~2~}}~\,\,\,\,{\text{при}}\,\,\,\,{{t}_{{{\text{max}}}}} \gg 1.$

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Распределение числа каскадных атомов по глубине мишени определяется функцией (9), график которой изображен на рис. 1 для степенного параметра $n = 0.5$ и различной энергии ионов. Видно, что число каскадных частиц на заданной глубине увеличивается с ростом энергии ионов до тех пор, пока не достигнута критическая область, после которой дальнейшее увеличение энергии уменьшает число каскадных частиц. Кривая имеет максимум на глубине, для которой производная $~{{dF} \mathord{\left/ {\vphantom {{dF} {d{{t}_{{{\text{max}}}}}}}} \right. \kern-0em} {d{{t}_{{{\text{max}}}}}}}$ обращается в нуль.

Рис. 1.

Зависимость числа каскадных атомов от глубины мишени для энергии ионов Е₀: 10E_min (1); 100E_min (2); 1000E_min (3). Значение степенного параметра $n = 0.5.$

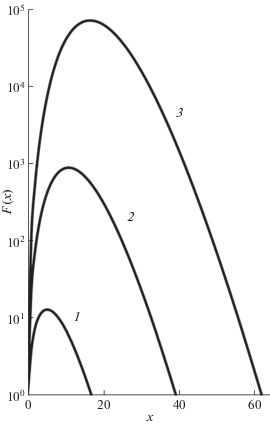
Рис. 2 показывает зависимость положения максимума от энергии ионов и значения степенного параметра. Видно, что при значениях ${{t}_{{{\text{max}}}}} \leqslant 0.5$ распределение монотонно убывает и не имеет максимума. Максимум появляется на распределении при значениях ${{t}_{{{\text{max}}}}} > 0.5,$ и его положение смещается в сторону больших глубин мишени при уменьшении степенного параметра. Это указывает на то, что при больших значениях энергии ионов частицы испытывают резерфордовское рассеяние, характерное для кулоновского потенциала, и проникают на большую глубину по сравнению с ионами малых энергий, рассеивающимися по закону твердых сфер.

Рис. 2.

Зависимость координаты максимума от энергии ионов для значений степенного параметра n: 1 (1); 0.4 (2); 0.2 (3); 0.1 (4).

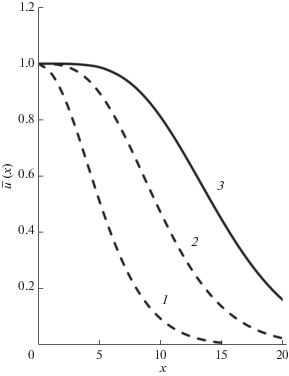
На рис. 3 изображено изменение полной энергии каскада с глубиной мишени, рассчитанное по формуле (10) для взаимодействия по закону твердых сфер. Если бы энергия отсечки была равна нулю, полная энергия каскада на любой глубине была бы равна ${{E}_{0}},$ что соответствует прямой $\bar {u} = 1$ на рис. 3. Начальные участки всех кривых действительно совпадают с прямой $~\bar {u} = 1.$ Учет энергии отсечки приводит к тому, что на некоторой глубине энергия атомов уменьшается настолько, что они выбывают из каскада, что ведет к уменьшению полной энергии. Эффект уменьшения тем сильнее, чем меньше энергия ионов.

Рис. 3.

Зависимость полной энергии каскада от глубины мишени для энергии ионов Е₀: 10E_min (1); 100E_min (2); 1000E_min (3). Значение степенного параметра $n = 1.$

Полученные результаты и приведенные рисунки представляют собой обобщение предыдущих теорий каскадного размножения частиц на случай различных видов межатомного взаимодействия. Изменение степенного параметра в сечении рассеяния позволяет рассматривать атомные потенциалы от потенциала твердых сфер до кулоновского. Самостоятельное значение имеют аналитические формулы (11)–(15), которые могут быть использованы для тестирования программ компьютерного моделирования, а также в учебных целях.

Список литературы

Фундаментальные и прикладные аспекты распыления твердых тел. Сб. статей. / Сост. Машкова Е.С. М.: Мир, 1989. 349 с.
Борисов А.М., Машкова Е.С. Физические основы ионно-лучевых технологий. II. Распыление поверхности твердых тел. М.: МАКС Пресс, 2013. 196 с.
Eckstein W. Computer Simulation of Ion-Solid Interactions. Berlin: Springer, 1991. 296 p.
Behrish R., Eckstein W. Sputtering by Particle Bombardment. Berlin: Springer, 2007. 470 p.
Landau L., Rumer G. // Proceed. Royal Soc. (London). A. 1938. V. 166. № 925. P. 213.
Landau L. // J. Phys. USSR. 1940. V. 3. P. 237.
Sigmund P. // Phys. Rev. 1969. V. 184. № 2. P. 383.
Roosendaal H.E., Sanders J.B. // Rad. Effects. 1980. V. 52. P. 137.
Waldeer K.T., Urbassek H.M. // Appl. Phys. A. 1988. V. 45. P. 207.
Толмачев А.И. // Изв. АН СССР. Сер. физ. 1991. Т. 55. С. 2409.
Tolmachev A.I. // Nucl. Instrum. Methods Phys. Res. B. 1994. V. 93. № 4. P. 415.
Abramowitz M., Stegun I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. N.Y.: Dover, 1972.
Лаврентьев М.А., Шабат Б.В. Методы функций комплексного переменного. М.: Наука, 1973. 736 с.
Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной. М.: Наука, 1974. 320 с.
Bateman H., Erdelyi A. Tables of Integral Transforms. V. 1. N.Y., Toronto, London: McGraw-Hill Book Company, 1954.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал