Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2021, № 7, стр. 84-88

Статистические свойства уровней энергии поперечного движения при каналировании электронов в кристалле кремния в условиях динамического хаоса

В. В. Сыщенко^a, *, А. И. Тарновский^a

^a Белгородский государственный национальный исследовательский университет
308015 Белгород, Россия

Поступила в редакцию 30.12.2020
После доработки 28.01.2021
Принята к публикации 30.01.2021

DOI: 10.31857/S1028096021070207

Аннотация

Движение частиц во внешних полях в классическом пределе зачастую носит хаотический характер, оставаясь при этом строго детерминированным. Исследование квантового поведения таких систем составляет проблематику квантового хаоса. Одним из ярких проявлений квантового хаоса являются статистические свойства массивов уровней энергии таких систем. В большинстве работ, тем не менее, исследуются системы типа бильярдов с жесткими стенками. В настоящей работе рассчитаны уровни энергии поперечного движения релятивистских электронов, движущихся в режиме аксиального каналирования в направлении [110] кристалла кремния, описываемого как движение в плавно меняющемся потенциале. Для области значений параметров, в которой классическом пределе реализуется хаотический режим движения, исследованы распределения расстояний между соседними уровнями, а также спектральная жесткость. Обе эти характеристики демонстрируют согласие с предсказаниями теории квантового хаоса.

Ключевые слова: хаотическая динамика, квантовый хаос, каналирование, уровни энергии, распределение межуровневых расстояний, распределение Вигнера, спектральная жесткость.

ВВЕДЕНИЕ

Сущность проблематики квантового хаоса заключается в поиске отличительных особенностей поведения квантовых систем, обладающих хаотической динамикой в классическом пределе [1–4]. Одной из таких особенностей являются статистические свойства уровней энергии квантовой системы. У систем с регулярной динамикой отсутствуют корреляции между различными уровнями энергии, что приводит к экспоненциальному распределению расстояний s между соседними уровнями с максимумом при s = 0, характерному для пуассоновского потока. В хаотических же системах корреляции между различными уровнями приводят к их взаимному отталкиванию; в этом случае межуровневые расстояния подчиняются распределению Вигнера:

(1)

$p{\kern 1pt} {\text{(}}s{\text{)}} = {\text{(}}{{\pi {{\rho }^{2}}s} \mathord{\left/ {\vphantom {{\pi {{\rho }^{2}}s} 2}} \right. \kern-0em} 2}{\text{)exp(}} - {{\pi {{\rho }^{2}}{{s}^{2}}} \mathord{\left/ {\vphantom {{\pi {{\rho }^{2}}{{s}^{2}}} 4}} \right. \kern-0em} 4}{\text{),}}$

где ρ – средняя плотность уровней на рассматриваемом участке энергетического спектра системы (которая предполагается при этом постоянной на всем участке). Наличие корреляций между уровнями энергии проверяется также с помощью Δ₃-статистики [2–5].

В работе [6] предсказания теории квантового хаоса были проверены для уровней энергии поперечного движения релятивистских электронов, движущихся в режиме аксиального каналирования [7, 8] вблизи направления [110] кристалла кремния. При этом статистика уровней энергии исследовалась в узком интервале вблизи верхнего края потенциальной ямы, образованной непрерывными потенциалами атомных цепочек, в пределах которого среднюю плотность уровней можно считать постоянной.

В настоящей работе найдены все уровни энергии поперечного движения электронов с энергией продольного движения 500 МэВ в такой яме и исследованы их статистические свойства во всем интервале поперечных энергий, в пределах которого классическая динамика носит хаотический характер. При этом исходный набор уровней подвергается процедуре развертывания [2, 4], в результате которой получается новый массив уровней с постоянной на всем интервале средней плотностью.

МЕТОДИКА

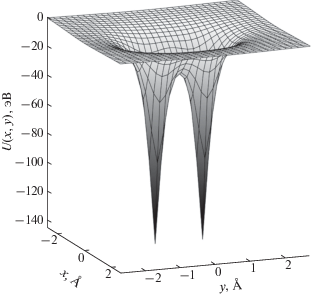
При падении релятивистской заряженной частицы под малым углом к плотно упакованной атомами кристаллографической оси возможно явление аксиального каналирования, когда частица совершает финитное движение в плоскости, перпендикулярной оси цепочки [7, 8]. В этом случае дискретный потенциал цепочки можно заменить непрерывным потенциалом, усредненным вдоль ее длины. В таком потенциале сохраняется компонента импульса частицы p_||, параллельная оси цепочки, что позволяет описывать движение частицы в поперечной плоскости с помощью двумерного уравнения Шредингера:

(2)

$\hat {H}\Psi \left( {x{\text{,}}\,y} \right) = {{E}_{ \bot }}\Psi {\text{(}}x{\text{,}}\,y{\text{),}}$

с оператором Гамильтона

(3)

$\hat {H} = - \frac{{{{\hbar }^{2}}}}{{{{2{{E}_{\parallel }}} \mathord{\left/ {\vphantom {{2{{E}_{\parallel }}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}} \right) + U(x,~y),$

в котором роль массы частицы играет величина ${{{{E}_{\parallel }}} \mathord{\left/ {\vphantom {{{{E}_{\parallel }}} {{{c}^{2}},}}} \right. \kern-0em} {{{c}^{2}},}}$ где ${{E}_{{\parallel ~}}} = {{({{m}^{2}}{{c}^{4}} + {{p}_{\parallel }}{{c}^{2}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ – энергия продольного движения [7].

Непрерывный потенциал отдельной атомной цепочки может быть аппроксимирован формулой [7]:

(4)

${{U}_{1}}\left( {x,~y} \right) = - {{U}_{0}}\ln \left( {1 + \frac{{\beta {{R}^{2}}}}{{{{x}^{2}} + {{y}^{2}} + \alpha {{R}^{2}}}}} \right),$

где для цепочки [110] кристалла кремния ${{U}_{0}} = 60$ эВ, $\alpha = {\text{0}}{\text{.37,}}$ $\beta = {\text{3}}{\text{.5,}}$ $R = {\text{0}}{\text{.194}}\,{\text{{\AA}}}$ (радиус Томаса–Ферми). Расстояние между двумя ближайшими цепочками [110] в кристалле кремния составляет ${a \mathord{\left/ {\vphantom {a 4}} \right. \kern-0em} 4},$ где $a = 5.431\,{\text{{\AA}}}$ – период решетки кристалла. Учитывая это и пренебрегая влиянием удаленных цепочек, непрерывный потенциал будет иметь вид

(5)

$U\left( {x,~y} \right) = {{U}_{1}}(x,~y + {a \mathord{\left/ {\vphantom {a 8}} \right. \kern-0em} 8}) + {{U}_{1}}(x,~y - {a \mathord{\left/ {\vphantom {a 8}} \right. \kern-0em} 8}).$

Симметрия потенциала (5) относительно плоскостей $x = 0$ и $y = 0$ (рис. 1) приводит к наличию четырех классов симметрии волновых функций, описывающей собственное состояние электрона:

(6)

$\left\{ \begin{gathered} {{\Psi }_{{ + + }}}\left( { - x,y} \right) = {{\Psi }_{{ + + }}}\left( {x,~y} \right) \hfill \\ {{\Psi }_{{ + + }}}\left( {x, - y} \right) = {{\Psi }_{{ + + }}}\left( {x,~y} \right), \hfill \\ \end{gathered} \right.$

(7)

$\left\{ \begin{gathered} {{\Psi }_{{ + - }}}\left( { - x,y} \right) = {{\Psi }_{{ + - }}}\left( {x,y} \right) \hfill \\ {{\Psi }_{{ + - }}}\left( {x, - y} \right) = - {{\Psi }_{{ + - }}}\left( {x,y} \right), \hfill \\ \end{gathered} \right.$

(8)

$\left\{ \begin{gathered} {{\Psi }_{{ - + }}}\left( { - x,y} \right) = - {{\Psi }_{{ - + }}}\left( {x,y} \right) \hfill \\ {{\Psi }_{{ - + }}}\left( {x, - y} \right) = {{\Psi }_{{ - + }}}\left( {x,y} \right), \hfill \\ \end{gathered} \right.$

(9)

$\left\{ \begin{gathered} {{\Psi }_{{ - - }}}\left( { - x,y} \right) = - {{\Psi }_{{ - - }}}\left( {x,y} \right) \hfill \\ {{\Psi }_{{ - - }}}\left( {x, - y} \right) = - {{\Psi }_{{ - - }}}\left( {x,y} \right). \hfill \\ \end{gathered} \right.$

Поскольку группа симметрии является абелевой, все четыре типа собственных состояний являются невырожденными [9]. При этом статистические свойства уровней энергии для каждого из этих классов необходимо исследовать независимо [3]. Уровни энергии поперечного движения заряженной частицы ${{E}_{ \bot }}$ в поле (5) находятся численно с помощью спектрального метода [10], успешно использованного в задаче о каналировании в [6, 11–14].

Рис. 1.

Потенциальная энергия (5) электрона в поле двух ближайших цепочек [110] кристалла кремния.

Статистические свойства массивов уровней квантовых систем, приводящие к распределению (1), описывают флуктуации положений уровней относительно их средней плотности, которая, как правило, не постоянна [9]. Для выделения этих флуктуаций из фактического расположения уровней используется процедура, называемая развертыванием (unfolding) [2, 4], состоящая в следующем.

На первом шаге процедуры вводится интегрированная плотность уровней:

(10)

$~N(E) = \int\limits_{{{E}_{{\min }}}~}^E {\rho \left( {E{\kern 1pt} '} \right)~dE{\kern 1pt} '} ,$

где $\rho (E) = \sum\nolimits_{\text{i}} {\delta (E - {{E}_{{\text{i}}}})} $ – фактическая плотность уровней ${{E}_{{\text{i}}}}$ квантовой системы. Ступенчатая функция (10) может быть представлена в виде суммы гладкой и флуктуирующей частей:

(11)

$N(E) = {{N}_{{{\text{av}}}}}\left( E \right) + {{N}_{{{\text{fl}}}}}(E).$

В настоящей работе функция ${{N}_{{{\text{av}}}}}\left( E \right)$ аппроксимируется полиномом пятой степени. На следующем шаге с ее помощью выполняется отображение исходных уровней энергии:

(12)

$\widetilde {{{E}_{{\text{i}}}}} = {{N}_{{{\text{av}}}}}\left( {{{E}_{{\text{i}}}}} \right).$

Полученная в результате новая последовательность уровней $\widetilde {{{E}_{{\text{i}}}}}$ будет обладать постоянной средней плотностью $\rho ,$ равной единице.

Помимо исследования распределения расстояний между соседними уровнями, наличие корреляций проверяется также с помощью вычисления так называемой спектральной жесткости, или ${{\Delta }_{{\text{3}}}}$-статистики [2–5]. Для набора развернутых уровней на некотором интервале

(13)

$\alpha \leqslant \widetilde {{{E}_{{\text{i}}}}} \leqslant \alpha + L$

строится ступенчатая функция $\tilde {N}(\tilde {E}),$ аналогичная (10), и вычисляется дисперсия отклонения этой функции от прямой, подбираемой по методу наименьших квадратов:

(14)

${{\Delta }_{3}}\left( {\alpha ,~L} \right) = \frac{1}{L}~\mathop {\min }\limits_{A,~B} \int\limits_\alpha ^{\alpha ~ + ~L} {{{{\left( {\tilde {N}\left( {\tilde {E}} \right) - A\tilde {E} - B} \right)}}^{2}}d\tilde {E}} .$

Среднее значение этой величины ${{\Delta }_{3}}{\kern 1pt} \left( L \right) = \left\langle {{{\Delta }_{3}}{\kern 1pt} \left( {\alpha ,L} \right)} \right\rangle $ по множеству последовательных неперекрывающихся интервалов служит мерой корреляции уровней в спектре. Для полностью некоррелированных уровней (пуассоновского потока, характерного для регулярных в классическом пределе систем) зависимость величины ${{\Delta }_{{\text{3}}}}$ от числа уровней N в интервале шириной L описывается формулой ${{\Delta }_{3}}\left( N \right) = {N \mathord{\left/ {\vphantom {N {15}}} \right. \kern-0em} {15}}.$ Для хаотической квантовой системы, спектральные свойства которой описываются, как в нашем случае, гауссовым ортогональным ансамблем случайных матриц [2–4], эта величина (называемая также спектральной жесткостью) описывается формулой [4]:

(15)

${{\Delta }_{3}}\left( N \right) = \frac{1}{{{{\pi }^{2}}}}\left( {\ln \left( {2\pi N} \right) + \gamma - \frac{5}{4} - \frac{{{{\pi }^{2}}}}{8}} \right),$

где $\gamma = 0.577216 \ldots $ – постоянная Эйлера.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Полное число уровней энергии поперечного движения в потенциальной яме, образованной непрерывными потенциалами цепочек, растет с увеличением энергии продольного движения ${{E}_{\parallel }}$ [7]; при этом выбор ${{E}_{\parallel }} = 500$ МэВ обеспечивает достаточное количество уровней для исследования их статистических свойств.

Седловая точка потенциала (5) находится на глубине –29.38 эВ. Как показывает построение сечений Пуанкаре [7, 8], на интервале

(16)

$ - 29.38 \leqslant {{E}_{ \bot }} \leqslant - 3\,\,{\text{эВ}}$

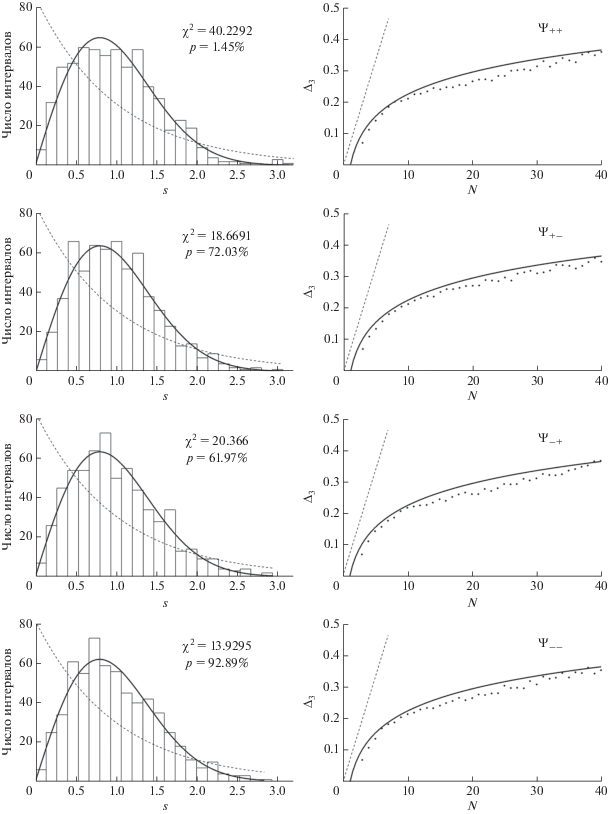
(от седловой точки до верхнего края потенциальной ямы) классическая динамика электрона является хаотической для подавляющего большинства начальных условий (регулярные траектории занимают менее 1% доступной для движения области фазового пространства). Таким образом, можно ожидать, что распределение расстояний между соседними уровнями энергии после процедуры развертывания будет описываться формулой Вигнера (1).

На рис. 2 слева представлены гистограммы распределения межуровневых расстояний на интервале (13) для состояний, принадлежащих каждому из четырех классов симметрии (6)–(9), а также кривые, соответствующие предсказанию (1). Мы видим хорошее согласие полученных распределений с предсказанием теории квантового хаоса, что подтверждается также критерием ${{\chi }^{2}}$ (величины ${{\chi }^{2}}$ и соответствующие им p-значения для 23 степеней свободы указаны на рисунках). Справа представлены результаты вычисления спектральной жесткости, также хорошо согласующиеся с предсказаниями теории для систем, проявляющих в классическом пределе хаотическое поведение.

Рис. 2.

Распределение расстояний между соседними уровнями энергий после процедуры развертывания для интервала (16) значений энергии поперечного движения электрона (гистограммы) для четырех классов симметрии волновой функции (6)–(9); сплошные кривые соответствуют распределению Вигнера (1) – слева. Результаты вычисления спектральной жесткости для тех же массивов развернутых уровней; сплошные кривые соответствуют предсказанию (15). Штриховыми линиями обозначены предсказания теории для регулярных систем – справа.

ЗАКЛЮЧЕНИЕ

В работе численно найдены все уровни энергии поперечного движения электрона с энергией 500 МэВ, движущегося в режиме аксиального каналирования в направлении [110] кристалла кремния. В этом направлении пары ближайших друг к другу параллельных атомных цепочек создают двухъямные потенциалы, выше седловых точек которых классическое движение электрона носит хаотический характер для подавляющего большинства начальных условий. Для уровней энергии, лежащих выше седловой точки, исследованы два статистических свойства: распределение расстояний между ближайшими соседними уровнями и спектральная жесткость (${{\Delta }_{{\text{3}}}}$-статистика Дайсона–Мехты). Обе эти характеристики демонстрируют хорошее согласие с предсказаниями теории квантового хаоса для систем, чья динамика полностью хаотична в классическом пределе.

Список литературы

Berry M.V. // Proceedings of the Royal Society A. 1987. V. 413. P. 183. https://doi.org/10.1098/rspa.1987.0109
Bohigas O., Giannoni M.-J. Chaotic Motion and Random Matrix Theories / Eds. Dehesa J.S., Gomez J.M.G., Polls A. Mathematical and Computational Methods in Nuclear Lecture Physics. Springer, Berlin, Heidelberg, 1984. V. 209. P. 1–99. https://doi.org/10.1007/3-540-13392-5_1
Штокман Х.Ю. Квантовый хаос. М.: ФИЗМАТЛИТ, 2004. 376 с.
Райхл Л.Е. Переход к хаосу в консервативных классических и квантовых системах. М.–Ижевск: РХД, 2008. 756 с.
Dyson F.J., Mehta M.L. // J. Math. Phys. 1963. V. 4. P. 713. https://doi.org/10.1063/1.1704009
Шульга Н.Ф., Сыщенко В.В., Тарновский А.И., Исупов А.Ю. // Поверхность. Рентген., синхротр. и нейтрон. иссслед. 2015. № 7. С. 72. https://doi.org/10.7868/S0207352815070197
Ахиезер А.И., Шульга Н.Ф. Электродинамика высоких энергий в веществе. М.: Наука, 1993. 344 с.
Ахиезер А.И., Шульга Н.Ф., Трутень В.И. Гриненко А.А., Сыщенко В.В. // УФН. 1995. Т. 165. № 10. С. 1165.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. В 10 томах. Том 3. Квантовая механика. Нерелятивистская теория. М.: ФИЗМАТЛИТ, 2016. 800 с.
Feit M.D., Fleck J.A., Jr., Steiger A. // J. Computational Physics. 1982. V. 47. P. 412. https://doi.org/10.1016/0021-9991(82)90091-2
Шульга Н.Ф., Сыщенко В.В., Нерябова В.С. // Поверхность. Рентген., синхротр. и нейтрон. иссслед. 2013. № 3. С. 91. https://doi.org/10.7868/S0207352813030189
Shul’ga N.F., Syshchenko V.V., Neryabova V.S. // Nucl. Instrum. Methods B. 2013. V. 309. P. 153. https://doi.org/10.1016/j.nimb.2013.01.022
Shul’ga N.F., Syshchenko V.V., Neryabova V.S. // Problems of Atomic Science and Technology. 2014. № 5(93). Series: Nuclear Physics Investigations (63). P. 111.
Shul’ga N.F., Syshchenko V.V., Tarnovsky A.I., Isupov A.Yu. // Nucl. Instrum. Methods B. 2016. V. 370. P. 1. https://doi.org/10.1016/j.nimb.2015.12.040

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал