Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2021, № 9, стр. 3-8

Образование узлов из углеродных нанотрубок в матрице изотактического полипропилена по результатам малоуглового рассеяния нейтронов и численного моделирования на решетке

Л. В. Ельникова^a, *, А. Н. Озерин^b, В. Г. Шевченко^b, **, П. М. Недорезова^c, О. М. Палазник^c, А. Т. Пономаренко^b, В. В. Ской^d, e, А. И. Куклин^d, e, ***

^a НИЦ “Курчатовский институт” – ИТЭФ им. А.И. Алиханова
117218 Москва, Россия

^b Институт синтетических полимерных материалов им. Н.С. Ениколопова РАН
117393 Москва, Россия

^c Институт химической физики им. Н.Н. Семенова РАН
119991 Москва, Россия

^d Объединенный институт ядерных исследований
141980 Дубна, Россия

^e Московский физико-технический институт (Национальный исследовательский университет)
141701 Долгопруный, Россия

^* E-mail: elnikova@itep.ru
^** E-mail: shev@ispm.ru
^*** E-mail: kuklin@nf.jinr.ru

Поступила в редакцию 25.12.2020
После доработки 22.02.2021
Принята к публикации 28.02.2021

DOI: 10.31857/S1028096021090041

Полный текст (PDF)

Аннотация

Представлен анализ данных по морфологии наночастиц аллотропов углерода в матрице изотактического полипропилена (ИПП), полученных методом малоуглового рассеяния нейтронов на спектрометре ЮМО на реакторе ИБР2, в ЛНФ им. И.М. Франка ОИЯИ, в г. Дубне Российской Федерации. С помощью пакета программ ATSAS вычислена фрактальная размерность, проведена реконструкция формы и определены геометрические размеры полученных частиц и агрегатов из одностенных углеродных нанотрубок (ОУНТ) в объеме ИПП, взятых в концентрациях 1.2, 2.6 и 8 масс. %. Установлено, что в объеме ИПП нанотрубки формируют фрактальные нанообъекты с грубой шероховатой поверхностью. Композитные системы ИПП/О УНТ являются полидисперсными в значительной степени, нанотрубки скручиваются в витки и узлы и становятся более упакованными, в объеме полимера размеры образовавшихся наночастиц и их агрегатов в несколько раз превышают заложенные при синтезе. Для интерпретации результатов и предсказания возможной морфологии, формирующейся в образцах такого типа, в данной работе применяется модель образования узлов в полимерных материалах, основанная на вычислении асимптотического инварианта Хопфа и фрактальной размерности на решетке. С помощью метода Монте-Карло качественно оценены энергии и вероятности образования узлов.

Ключевые слова: малоугловое рассеяние нейтронов, полимерные нанокомпозиты, изотактический полипропилен, углеродные нанотрубки, фрактальные агрегаты, топологические инварианты узлов, решеточное моделирование Монте-Карло.

ВВЕДЕНИЕ

Полимерные композиты, допированные наночастицами, составленными из аллотропов углерода, например, из углеродных нанотрубок (УНТ), находят широкое применение в народном хозяйстве как элементы наноэлектроники, спинтроники, оптических и радиотехнических устройств, в биомедицинских приложениях, датчиках и пр. [1].

Получение информации о морфологии наполнителей в ангстремных и нанометровых масштабах в объеме полимера имеет большое значение при характеризации перспективных полимерных композитов, так как внесение наночастиц в матрицу полимера изменяет его физико-химические свойства, в частности, электропроводность, упругие модули и др.

Метод малоуглового рассеяния нейтронов (МУРН) является наиболее информативным, так как позволяет обнаруживать размерные эффекты в масштабах порядка Å. По сравнению с другими структурными методами, например, растровой электронной микроскопией (РЭМ), МУРН является неразрушающим методом анализа, исключающим потерю информации из-за механических повреждений внутренней структуры, возникающих при подготовке образца к измерениям.

Изучаемые системы, состоящие из ОУНТ в матрице изотактического полипропилена с высокой степенью кристалличности, уникальны по своему составу и свойствам. Ранее образцы были синтезированы и исследованы в работах [2, 3] методами растровой и просвечивающей электронной микроскопии, дифференциальной сканирующей калориметрии, диэлектрической спектроскопии и рентгеновской дифракции. Привлечение метода МУРН связано с необходимостью установить характер агрегации наночастиц в матрице полимера и их распределение по объему, а далее определить влияние этой морфологии на электрические и механические свойства полимерных нанокомпозитов этого типа.

Вместе с тем, для предсказания геометрических особенностей наноструктур в подобных композиционных материалах требуется развитие различных теоретических моделей, раскрывающих происхождение самоорганизованного поведения наполнителей в матрице полимера и их агрегации в структуры с фрактальной размерностью. Для этих целей к настоящему времени глубоко разработана статистическая теория [4, 5], применяется топологический подход, основанный на теории узлов [6, 7], и методы численного моделирования [8, 9]. Согласно литературным данным топологический анализ таких эффектов, как образование узлов и зацеплений, можно обобщить на многие типы линейных структур и макромолекул, включая ДНК, УНТ и пр.

Данная работа посвящена исследованию нанокомпозитов ИПП с ОУНТ экспериментальным методом малоуглового рассеяния нейтронов и теоретическим моделированием фрактальных размерных особенностей с численным анализом решеточным методом Монте-Карло.

ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ

Объектами исследования являлись образцы ИПП с ОУНТ в различных концентрациях 1.2, 2.6 и 8 масс. % (их производство описано в работах [2, 3]), изначально диаметр ОУНТ составлял 1.4 нм, а длина – более 5 мкм.

Измерения кривых МУРН образцов I(Q) = = dΣ/dΩ(Q) были выполнены на спектрометре ЮМО на реакторе ИБР2 (ЛНФ им. И.М. Франка ОИЯИ, г. Дубна, Россия) (рис. 1) [10]. Длина волны нейтронов λ = 0.7–6 Å, поток нейтронов на образце составлял примерно 10⁷ нейтрон/(c ⋅ см²) [11], диаметр нейтронного пятна на образце был 14 мм. Твердые образцы в форме пленок ИПП и композитов ИПП/ОУНТ были зафиксированы в держателе, который помещался в термобокс. Толщины всех образцов нормировались на толщину пленки ИПП, равную 368 мкм.

Рис. 1.

Экспериментальная интенсивность I(Q) МУРН образцов ОУНТ, масc. %: 1.2 (1), 2.6 (2), 8 (3) в координатах I–Q (а) и lg(I(Q))–lg(Q) (б). Здесь k – значения фрактальной размерности. На графиках lg(I(Q))–lg(Q) 1' – рассеяние от частиц ОУНТ (для простоты указана только одна концентрация ОУНТ 8 масс. %); 2 ' – рассеяние от агрегатов частиц ОУНТ 8 масc. %.

В экспериментах МУРН на ЮМО регистрируется счет частиц в зависимости от времени пролета нейтронов через 16 колец двух детекторов. С помощью программы SAS [12] осуществляется пересчет и нормализация счета с использованием калибровочного стандарта известного сечения в зависимости от времени пролета к дифференциальному сечению рассеяния dΣ/dΩ(Q), а также осуществляется нормализация к толщине образца. Вектор рассеяния Q = 4π sin(θ/2)/λ, λ – волновой вектор нейтронов, θ – угол рассеяния. Предварительно оцененная плотность длины рассеяния для образцов лежит в диапазоне 3.84 × × 10¹⁰–5 × 10¹⁰ см^–1 [13].

Для анализа экспериментальных кривых МУР использовались процедуры программы ATSAS 2.4 [14]. В качестве рассеяния от контрольного образца, которое вычитали из экспериментальной кривой МУР образцов I(Q), использовалось рассеяние на образце матричного ИПП [15]. После учета рассеяния от контрольного образца экспериментальные кривые МУР характеризуются рассеянием только от неоднородных областей (“рассеивающих частиц”) в системе, имеющей длину рассеяния, отличную от длины рассеяния полимерной матрицы. Для расчета регуляризованных кривых рассеяния I_reg(Q), оптимизированных во всем диапазоне углов рассеяния, функции распределения частиц, интегральных значений радиусов инерции частиц рассеивающей фазы и распределения частиц по размерам, использовалась процедура GNOM пакета ATSAS на основе метода регуляризации по Тихонову [16].

Функция Гинье ln(QI(Q))–Q² в обратном пространстве вычислена методом косвенного преобразования [13, 14], примененного ко всему диапазону экспериментальной кривой рассеяния с использованием процедуры GNOM.

В соответствии с методикой [17, 18], для кривых рассеяния образцов ОУНТ (рис. 1) проведено разделение на две регуляризованные составляющие, которые относятся к рассеянию на частицах ОУНТ и рассеянию на агрегатах частиц ОУНТ.

Из наклона линейной части функции Гинье спектров МУРН вычислены радиусы гирации наночастиц и агрегатов наночастиц ОУНТ (табл. 1).

Таблица 1.

Радиусы гирации наночастиц и агрегатов наночастиц из ОУНТ, рассчитанные с помощью процедуры GNOM пакета ATSAS для различных концентраций ОУНТ в ИПП

Образец ИПП/ОУНТ с концентрацией, масс. %	Радиусы гирации ОУНТ, нм	Радиусы гирации агрегатов ОУНТ, нм
1.2	5.6	12.3
2.6	5.1	17.2
8	5.8	18.2

После реконструкции формы агрегатов нанонаполнителей с помощью процедур DAMMIN и DAMMIF [14] обнаружено, что системы являются полидисперсными; ОУНТ объединяются в объеме ИПП в виде фрактальных плотных агрегатов с неровной поверхностью, размеры которых в несколько раз превышают исходные размеры нанотрубок (рис. 2). Рассчитанные значения доли объемного содержания ОУНТ в форме частиц и в форме агрегатов для всех образцов оказались равными друг другу (~0.5).

Рис. 2.

Форма рассеивающих частиц, рассчитанная из кривой рассеяния частиц ОУНТ (а–в) и агрегатов частиц ОУНТ (д–е) образцов ОУНТ 1.2 масc. % (а, г), образцов ОУНТ 2.6 масc. % (б, д), образцов ОУНТ 8 масc. % (в, е). Визуализация моделью объемных виртуальных (“dummy”) атомов и моделью поверхности, доступной растворителю для частиц и агрегатов ОУНТ соответственно.

Реконструкция формы частиц выполнена без каких-либо дополнительных ограничений, наложенных на ожидаемую симметрию и анизометрию частиц.

В объеме ИПП нанотрубки скручиваются в клубки и узлы и становятся более упакованными (рис. 2), форму рассеивающих частиц (агрегатов) проще всего интерпретировать как “переплетения” соседних ОУНТ по аналогии с “переплетениями” макромолекул полимера при более высоких концентрациях, чем концентрация кроссовера.

МОДЕЛЬ ОБРАЗОВАНИЯ УЗЛОВ

Для того, чтобы интерпретировать морфологию обнаруженных наночастиц и агрегатов в объеме ИПП и прогнозировать геометрию поверхности для различных концентраций наполнителей ОУНТ, рассмотрим механизмы скручивания линейных полимеров.

Узлы и зацепления, как топологические дефекты, обусловливают мезоморфизм, подчиняющийся законам сохранения трех топологических инвариантов [19, 20]: инварианту Гаусса, полиному Александера и асимптотическому инварианту Хопфа. Последний аналогичен действующему в магнитной гидродинамике (МГД) [19], описываемой уравнением движения:

(1)

$\frac{{\partial {\mathbf{H}}}}{{\partial t}} = \nabla \times (v \times {\mathbf{H}}) - \nabla \times \nu (\nabla \times {\mathbf{H}}).$

Здесь H – магнитное поле, ν – магнитная вязкость (малая положительная), v – макроскопическая скорость движения плазмы.

В МГД инвариант Хопфа записывается как

(2)

$h = \int\limits_{{\Omega }} {{\mathbf{A}} \cdot {\mathbf{H}}} d{v},$

где Ω – полный объем системы, на границе которой H_n|_∂Ω = 0. A – вектор-потенциал магнитного поля H (${\mathbf{H}} = \nabla \times {\mathbf{A}}$). Доказано [19], что при малых значениях ν h ненулевой, а в асимптотическом приближении является топологическим инвариантом, который единственный сохраняется при перезамыкании.

С другой стороны, используя универсальное определение фрактала:

(3)

$f(R) = \frac{1}{{N(N - 1)}}\sum\limits_{i,j} {{{\theta }}(R - \left| {{{x}_{i}} - {{x}_{j}}} \right|)} ,$

где N – общее число точек, x_i – их координаты, θ – ступенчатая функция, можно сформулировать топологию агрегации в терминах калибровочного монопольного газа [21] со связью фрактала с механизмом конфайнмента. Трубка монопольного тока играет роль струны Дирака, а фрактальная размерность D_f = N₁/N_s служит параметром порядка (N₁ – число ребер, N_s – число узлов, принадлежащих кластерам).

Гамильтониан, связанный с потенциалом A формулы (2), в котором магнитное поле аппроксимируется системой магнитных силовых трубок с внутренним скручиванием, с характеристиками перезамыкания и склеивания, можно записать в виде:

(4)

$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Н} = \sum\limits_{i\, = \,1}^{N - 1} {{{{({{r}_{{i\, + \,1}}} - {{r}_{i}})}}^{2}}} + J\sum\limits_{i\, = \,1}^N {{{{\left( {r_{i}^{2} - {{b}^{2}}} \right)}}^{2}} + {{{{\mu }}}_{i}}} ,$

где r_i – позиция линка на решетке размера N, включающее ориентацию, первое слагаемое имеет смысл взаимодействия ближайших соседей, а второе включает локальные взаимодействия на углах связи [22]; J, b – параметры, химпотенциал μ_i несет смысл среды ИПП, для простоты он выбран постоянным. Выражение (4) сформулировано в духе теории Флори [4]. Монопольные токи в трубке имеют тот же физический смысл, что и в МГД, и протекают по плакетам, натянутым на трилистник (полином Александера 3₁), он выбран при моделировании как простой и ожидаемый в подобных задачах [9]. Статсумма для (4) монопольных токов Z = exp(–Ĥ/β). Здесь β = 1/Tk_B – обратная температура, k_B – постоянная Больцмана, T – абсолютная температура.

Результаты моделирования Монте-Карло на простой кубической решетке размером стороны 96 показаны на рис. 3, 4 .

Рис. 3.

Зависимость энергии конфигураций для “монопольных” токов по трилистнику от обратной температуры, вычисленная методом Монте-Карло с погрешностью 10^–5.

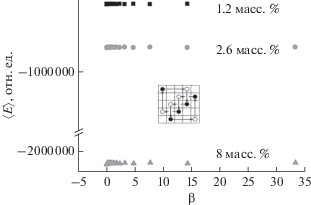
Рис. 4.

Зависимость вероятности образования узлов типа трилистника от обратной температуры, вычисленная методом Монте-Карло с погрешностью 10^–5.

Известно [3, 15], что концентрация ОУНТ порядка 1.68 масс. % соответствует порогу перколяции системы ИПП/ОУНТ, действительно, близкие к порогу концентрации ОУНТ (1.2 и 2.6 масс. %) демонстрируют высокую вероятность скручивания в упорядоченные структуры (узлы) во всем диапазоне температур, при этом структура композита с 1.2 масс. % ОУНТ находится внутри области конфайнмента. Образец с 8 масс. % ОУНТ может демонстрировать скручивание нанотрубок в более сложные узлы.

ЗАКЛЮЧЕНИЕ

Результаты анализа с программой ATSAS спектров МУРН и моделирование в терминах калибровочной теории являются независимыми методами определения морфологических особенностей систем.

В работе качественно продемонстрировано, что наблюдаемые в экспериментах МУРН объекты с поверхностными фракталами могут различаться типами образуемых узлов в зависимости от концентрации наполнителей. Эти оценки могут быть учтены при синтезе материалов с требуемыми свойствами.

Список литературы

Дьячков П.Н. Электронные свойства и применение нанотрубок. М.: БИНОМ, 2015. 491 с.
Polschikov S.V., Nedorezova P.M., Palaznik O.M., Klyamkina A.N., Shashkin D.P., Gorenberg A.Ya., Krasheninnikov V.G., Shevchenko V.G., Arbuzov A.A // Polymer Engineering & Science 2018. V. 58. P. 1461. https://doi.org/10.1002/pen.24644
Palaznik O.M., Nedorezova P.M., Pol’shchikov S.V., Klyamkina A.N., Shevchenko V.G., Krasheninnikov V.G., Monakhova T.V., and Arbuzov A.A. // Polymer Science Series B. 2019. V. 61(2) P. 200. https://doi.org/10.1134/S1560090419020088
Flory P.J. Principles of Polymer Chemistry. N.Y.: Cornell University Press, 1953. 672 p.
Гросберг А.Ю., Хохлов А.Р. Статистическая физика макромолекул. М.: Наука, 1989. 344 с.
Teraoka I. Polymer Solutions. An Introduction to Physical Properties. N.Y.: by John Wiley & Sons, 2002. 332 p.
Франк-Каменецкий M.Д., Вологодский А.В. // УФН. 1981. Т. 134. № 3. С. 641.
Astakhov A.M., Nechaev S.K., Polovnikov K.E. // Polymer Science, Series C. 2018. V. 60. P. S25.
Beaton N.R., Eng J.W., Ishihara K., Shimokawa K., Soteros C.E. // Soft Matter. 2018. V. 28. P. 5775. https://doi.org/10.1039/C8SM00734A
Elnikova L.V., Ozerin A.N., Shevchenko V.G., Nedorezova P.M., Ponomarenko A.T., Skoi V.V., Kuklin A.I. Spatial structure and aggregation of carbon allotrope nanofillers in isotactic polypropylene composites studied by small-angle neutron scattering; http://arxiv.org/ftp/arxiv/papers/2006/2006.07595.pdf.
Kuklin A.I., Rogov A.D., Gorshkova Yu.E., Utrobin P.K., Kovalev Yu.S., Rogachev A.V., Ivankov O.I., Kutuzov S.A., Soloviov D.V., Gordeliy V.I. // Physics of Particles and Nuclei Letters. 2011. V. 8.2. P. 119. https://doi.org/10.1134/S1547477111020075
Soloviev A.G., Solovjeva T.M., Ivankov O.I., Soloviov D.V., Rogachev A.V., and Kuklin A.I. // J. Physics: Conference Series. 2017. V. 848. P. 012020. https://doi.org/10.1088/1742-6596/848/1/012020
Свергун Д.И., Фейгин Л.А. Рентгеновское и нейтронное малоугловое рассеяние. М.: Наука, 1986. 280 с.
Petoukhov M.V., Franke D., Shkumatov A.V., Tria G., Kikhney A.G., Gajda M., Gorba C., Mertens H.D.T., Konarev P.V., Svergun D.I. // J. Appl. Cryst. 2012. V. 45. P. 342. https://doi.org/10.1107/S0021889812007662
Polschikov S.V., Nedorezova P.M., Klyamkina A.N., Kovalchuk A.A., Aladyshev A.M., Shchegolikhin A.N., Shevchenko V.G., Muradyan V.E. // J. Applied Polymer Sci. 2013. V. 127. P. 904. https://doi.org/10.1002/app.37837
Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. M.: Наука, 1979. 284 с.
Ozerin A.N., Kurkin T.S., Ozerina L.A., Dolmatov V.Yu. // Crystallogr. Rep. 2008. V. 53. № 1. P. 60. https://doi.org/10.1134/S1063774508010070
Shtykova E.V. // Nanotechnologies in Russia. 2015. V. 10. № 5–6. P. 408. https://doi.org/10.1134/S1995078015030155
Монастырский М.И., Сасоров П.Н. // Наноструктуры. Математическая физика и моделирование. 2014. Т. 11. № 2. С. 63.
Monastyrsky M., Nechaev S. in Knots’1996. Proceedings of the Fifth International Research Institute of Mathematical Society of Japan. Int. Conf. Center. Tokyo. 22–26 July 1996. Ed. Suzuki. S. Singapore: World Sci. Publisher. 1997. P. 147.
Поликарпов М.И. // УФН. 1995. Т. 165. №. 6. С. 627.
Chernodub M.N., Hu S., Niemi A.J. // Phys. Rev. E. 2010. V. 82. P. 011916.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал