Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 11, стр. 85-94
Нелинейные поверхностные волны вблизи границы градиентного слоя и среды с меняющимся в зависимости от электрического поля знаком керровской нелинейности
a Белгородский государственный технологический университет им. В.Г. Шухова
308012 Белгород, Россия
b Белгородский юридический институт МВД России им. И.Д. Путилина
308024 Белгород, Россия
* E-mail: savotchenkose@mail.ru
Поступила в редакцию 11.02.2022
После доработки 10.03.2022
Принята к публикации 10.03.2022
- EDN: GQKOEN
- DOI: 10.31857/S1028096022110218
Аннотация
Рассмотрен контакт среды, в которой показатель преломления линейно убывает в зависимости от расстояния с нелинейной средой, где знак керровской нелинейности может меняться скачком при достижении напряженности электрического поля порогового значения. Установлено, что вдоль такого контакта могут распространяться поверхностные волны трех типов в зависимости от знака нелинейности и диапазона значений эффективного показателя преломления. Получены явные аналитические выражения для распределения напряженности электрического поля в поперечном относительно плоскости контакта направлении, которые являются точными решениями сформулированных нелинейных уравнений. Показано, что в слое с градиентом показателя преломления возможно формирование соответствующих волноводным модам распределений электрического поля с несколькими максимумами интенсивности.
ВВЕДЕНИЕ
Большой прикладной и теоретический интерес вызывают исследования закономерностей локализации световых полей вдоль границ сред с различными оптическими свойствами [1, 2]. В частности, бурное развитие фотоники привело к возможности использования фотонных кристаллов и оптических волокон для проектирования различных оптоэлектронных устройств и волноводных структур [3, 4].
Волноводные свойства границ разделов оптических сред в первую очередь обусловлены возможностью распространения вдоль них поверхностных электромагнитных волн, в том числе оптического диапазона [5]. Несмотря на то, что свойства нелинейных поверхностных волн исследуют на протяжении многих лет [6–9], остаются малоизученными проблемы, которые связаны с появлением новых материалов, обладающих уникальными оптическими свойствами, а также возможностями сочетаний их различных контактов.
Настоящая работа посвящена теоретическому изучению новых поверхностных волн, распространяющихся вдоль контакта среды с пространственным градиентом показателя преломления, в которой диэлектрическая проницаемость линейно убывает в слое конечной толщины (градиентный слой [10, 11]), с нелинейной средой, в которой диэлектрическая проницаемость, зависящая от квадрата напряженности электрического поля (среда с керровской нелинейностью [12]), может менять знак коэффициента керровской нелинейности с ростом напряженности поля [13–15].
Модели нелинейности со скачкообразным изменением оптических характеристик среды использовали ранее неоднократно для описания самолокализации световых импульсов [16–18], поверхностных волн [19, 20] и эффектов самоотражения в приповерхностных слоях полупроводниковых кристаллов [21]. Локализованные состояния в средах со скачкообразным изменением диэлектрической константы в зависимости от поля изучали в [22–24]. Поверхностные волны в средах со скачкообразным изменением квадратичной зависимости от поля без изменения знака нелинейного отклика рассматривали в [25–27]. Физические основы возможности скачкообразного изменения диэлектрических характеристик полупроводниковых кристаллов в определенном частотном диапазоне изложены в [28–31].
Недавно появилась работа [32], в которой теоретически показана возможность распространения поверхностной волны вдоль градиентного слоя с экспоненциальной зависимостью показателя преломления, покрытого слоем с керровской самофокусирующей нелинейностью. В [33] описано распространение поверхностной волны вдоль градиентного слоя с линейной зависимостью показателя преломления, контактирующего со средой, в которой с ростом напряженности электрического поля появляется самофокусирующий нелинейный отклик керровского типа. В отличие от [33] в настоящей работе будут описаны три новых типа поверхностных волн, возникающих при условии, что покрытие градиентного слоя изначально обладало нелинейным откликом определенного знака, который может меняться скачком с ростом напряженности электрического поля. Сформулированная в рамках предложенной теории модель волноводной структуры позволила получить точные решения нелинейных уравнений и описать их основные свойства в явном аналитическом виде.
ОСНОВНЫЕ УРАВНЕНИЯ
Будем рассматривать поперечные поверхностные волны, распространяющиеся вдоль контакта среды с показателем преломления, линейно убывающим по глубине (градиентный слой) [34, 35], со средой с керровской нелинейностью (нелинейный кристалл), в которой с ростом напряженности электрического поля скачкообразно изменяется знак коэффициента нелинейности на противоположный [13–15].
Выберем координаты так, чтобы плоскость контакта сред находилась в плоскости xy и ось z была ей перпендикулярна. Тогда компонента напряженности электрического поля будет иметь вид: ${{E}_{y}}(x,z) = E(z)\exp \{ i(kx - \omega t)\} $, где k – волновые число, ω – частота волны, а поперечное плоскости контакта распределение поля определяется из уравнения:
(1)
$E{\kern 1pt} ''(z) = ({{k}^{2}} - \varepsilon (z,\left| E \right|){{{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\omega }^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}})E(z),$Пусть градиентный слой располагается в полупространстве z > 0, а нелинейная среда − в z < 0. Тогда диэлектрическую проницаемость ε в (1) можно определить следующим образом:
(2)
$\varepsilon (z,\left| E \right|) = \left\{ \begin{gathered} {{\varepsilon }_{G}}(z),\,\,\,\,\,\,\,z > 0 \hfill \\ {{\varepsilon }_{N}}(\left| E \right|),\,\,\,\,z < 0, \hfill \\ \end{gathered} \right.$(3)
${{\varepsilon }_{G}}(z) = {{\varepsilon }_{0}} - {{\Delta \varepsilon z} \mathord{\left/ {\vphantom {{\Delta \varepsilon z} {a,}}} \right. \kern-0em} {a,}}$(4)
$\varepsilon (\left| E \right|) = \left\{ \begin{gathered} {{\varepsilon }_{1}} - {{\alpha }_{1}}{{\left| E \right|}^{2}},\,\,\,\,\left| E \right| < {{E}_{s}} \hfill \\ {{\varepsilon }_{2}} + {{\alpha }_{2}}{{\left| E \right|}^{2}},\,\,\,\,\left| E \right| > {{E}_{s}}, \hfill \\ \end{gathered} \right.$(5)
$\varepsilon (\left| E \right|) = \left\{ \begin{gathered} {{\varepsilon }_{1}} + {{\alpha }_{1}}{{\left| E \right|}^{2}},\,\,\,\,\left| E \right| < {{E}_{s}} \hfill \\ {{\varepsilon }_{2}} - {{\alpha }_{2}}{{\left| E \right|}^{2}},\,\,\,\,\left| E \right| > {{E}_{s}}. \hfill \\ \end{gathered} \right.$Вблизи контакта в нелинейной среде, где |E| > Es, образуется зона конечной ширины (оптический домен) с оптическими характеристиками, отличающимися от остальной области нелинейной среды. Искомое поле представим в виде:
(6)
$E(z) = \left\{ \begin{gathered} {{E}_{G}}(z),\,\,\,\,\,z > 0 \hfill \\ {{E}_{{N1}}}(z),\,\,\,\,\left| E \right| < {{E}_{s}} \hfill \\ {{E}_{{N2}}}(z),\,\,\,\,\left| E \right| > {{E}_{s}}. \hfill \\ \end{gathered} \right.$(8)
$\frac{{{{d}^{2}}{{E}_{{N1}}}}}{{d{{z}^{2}}}} - q_{1}^{2}{{E}_{{N1}}} \mp {{g}_{1}}E_{{N1}}^{3} = 0,$(9)
$\frac{{{{d}^{2}}{{E}_{{N2}}}}}{{d{{z}^{2}}}} - q_{2}^{2}{{E}_{{N2}}} \pm {{g}_{2}}E_{{N2}}^{3} = 0,$(10)
${{b}^{2}} = ({{\Delta \varepsilon } \mathord{\left/ {\vphantom {{\Delta \varepsilon } {{{z}_{0}}}}} \right. \kern-0em} {{{z}_{0}}}}){{({\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c})}^{2}},$(11)
$p_{0}^{2} = ({{\varepsilon }_{0}} - {{n}^{2}}){{({\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c})}^{2}},$(12)
$q_{{1,2}}^{2} = ({{n}^{2}} - {{\varepsilon }_{{1,2}}}){{({\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c})}^{2}},$(14)
${{E}_{{N1}}}( - {{z}_{s}}) = {{E}_{{N2}}}( - {{z}_{s}}) = {{E}_{s}},\,\,\,\,E_{{N1}}^{'}( - {{z}_{s}}) = E_{{N2}}^{'}( - {{z}_{s}}).$Отметим, что исчезающее при z → +∞ решение уравнения (7) выражается через функцию Эйри Ai(z), исчезающие при z → −∞ решения уравнений (8), (9) солитоноподобной формы выражаются через гиперболические функции в зависимости от знака коэффициента нелинейности.
ПОВЕРХНОСТНЫЕ ВОЛНЫ ВДОЛЬ КОНТАКТА СО СРЕДОЙ С ПЕРЕКЛЮЧЕНИЕМ ДЕФОКУСИРУЮЩЕЙ НЕЛИНЕЙНОСТИ НА ФОКУСИРУЮЩУЮ
Из уравнений (7), (8) следует, что при max{ε1, ε2} < < n2 < ε0 и α1,2 > 0 поверхностная волна в системе с диэлектрической проницаемостью (4) имеет вид:
(15)
${{E}_{G}}(z) = {{E}_{{Gm}}}{\text{Ai(}}{{b}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}z + \delta {\text{),}}$(16)
${{E}_{{N1}}}(z) = - \frac{{{{q}_{1}}}}{{\sqrt {{{g}_{1}}} }}{\text{csch(}}{{q}_{1}}(z - {{z}_{1}})),$(17)
${{E}_{{N2}}}(z) = \frac{{{{q}_{2}}}}{{\sqrt {{{g}_{2}}} }}{\text{sch(}}{{q}_{2}}(z - {{z}_{2}})).$Подставив (15)–(17) в граничные условия (13), (14), можно получить следующие параметры поверхностной волны:
(18)
${{E}_{{Gm}}} = \frac{1}{{{\text{Ai}}\left( \delta \right)}}\sqrt {\frac{{2\left( {{{n}^{2}} - {{\varepsilon }_{2}} - {{\varepsilon }_{{G{\text{eff}}}}}} \right)}}{{{{\alpha }_{2}}}}} ,$(19)
${{z}_{1}} = \frac{c}{{\omega \sqrt {{{n}^{2}} - {{\varepsilon }_{1}}} }}{\text{arsh}}\sqrt {\frac{{{{n}^{2}} - {{\varepsilon }_{1}}}}{{{{\varepsilon }_{1}} - {{\varepsilon }_{2}}}}\frac{{{{\alpha }_{1}} + {{\alpha }_{2}}}}{{{{\alpha }_{1}}}}} - {{z}_{s}},$(20)
${{z}_{2}} = \frac{c}{{\omega \sqrt {{{n}^{2}} - {{\varepsilon }_{2}}} }}{\text{arth}}\sqrt {\frac{{{{\varepsilon }_{{G{\text{eff}}}}}}}{{{{n}^{2}} - {{\varepsilon }_{2}}}}} ,$(21)
${{z}_{s}} = \frac{c}{{\omega \sqrt {{{n}^{2}} - {{\varepsilon }_{2}}} }}{\text{arth}}\sqrt {\frac{{{{\varepsilon }_{1}} - {{\varepsilon }_{2}}}}{{{{n}^{2}} - {{\varepsilon }_{2}}}}\frac{{{{\alpha }_{2}}}}{{{{\alpha }_{1}} + {{\alpha }_{2}}}}} - {{z}_{2}},$(22)
${{E}_{s}} = \sqrt {2\frac{{{{\varepsilon }_{1}} - {{\varepsilon }_{2}}}}{{{{\alpha }_{1}} + {{\alpha }_{2}}}}{\kern 1pt} } .$Проанализируем влияние параметров волноводной системы на профили локализации поля поверхностной волны в поперечном относительно плоскости контакта направлении. Коэффициенты керровской нелинейности и невозмущенные диэлектрические постоянные нелинейного кристалла считаем фиксированными. Основными варьируемыми параметрами рассматриваемой волноводной системы являются характерное расстояние а, на котором убывает показатель преломления в градиентной среде (толщина градиентного слоя), величина убывания Δε, а также эффективный показатель преломления n. Первые два параметра входят во все характеристики волны в виде отношения a/Δε, обозначаемое ξ. Поэтому достаточно проанализировать поведение характеристик волны, например, в зависимости только от а. Увеличение значения a будет эквивалентно уменьшению значения Δε. Данные параметры являются характеристиками среды и не могут варьироваться в ходе эксперимента в отличие от эффективного показателя преломления, значение которого определяется углом падения луча, возбуждающего поверхностную волну.
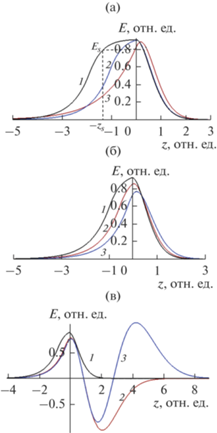
На рис. 1 представлены профили поверхностных волн в зависимости от расстояния от плоскости контакта при различных значениях параметров системы. В рассматриваемой волноводной системе могут существовать волны с одним максимум интенсивности, которые будем называть первой (или основной) волноводной модой, а также с несколькими и максимума и минимумами, которые будем называть модами порядка k, где k – число экстремумов интенсивности. Порядок моды определяется эффективным показателем преломления и характерной шириной градиентного слоя. Наличие многомодовых волноводных состояний является основным отличием от случая поверхностных волн в средах с переключением диэлектрической проницаемости в зависимости от напряженности электрического поля, которые рассматривали в [33].
Рис. 1.
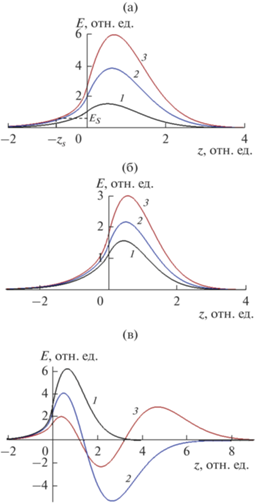
Поверхностная волна (15)–(17) при фиксированных параметрах c = 1, ω = 1, ε0 = 6, Δε = 5, ε1 = 1.1, ε2 = 0.1, α1 = 3.5, α2 = 0.5: a – a = 1, n = 1.3 (1), 2 (2), 4 (3); б – n = 2, a = 0.2 (1), 1 (2), 4 (3); в – n = 1.3, a = 1 (1), 3 (2), 5.47 (3).
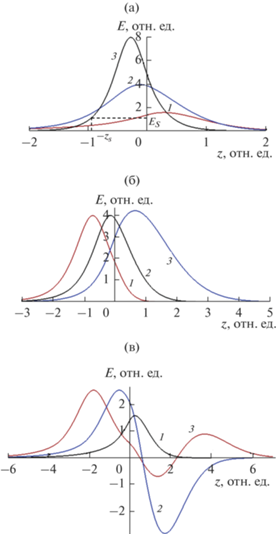
Увеличение эффективного показателя преломления при остальных фиксированных параметрах системы приводит к существенному росту максимума интенсивности электрического поля (рис. 1а). Также наблюдается смещение положения максимума из градиентной среды в нелинейный кристалл.
Увеличение характерной ширины градиентного слоя a при остальных фиксированных параметрах системы приводит к незначительному росту максимума интенсивности электрического поля (рис. 1б). При этом он смещается из нелинейного кристалла в градиентную среду.
На рис. 1в показано формирование двух- (кривая 2) и трехмодовых (кривая 3) волновых состояний при увеличении характерной ширины градиентного слоя a при одном и том же угле падения возбуждающего луча (эффективном показателе преломления). Мода второго порядка (кривая 2) характеризуется резким падением до минимума интенсивности поля в зоне градиента показателя преломления, то время как наибольшая интенсивность поля наблюдается в оптическом домене нелинейного кристалла. Мода третьего порядка (кривая 3) характеризуется одним максимумом интенсивности в нелинейном кристалле, одним максимумом и одним минимумом в зоне градиента показателя преломления. Формирование многомодовых поверхностных состояний обусловлено градиентом показателя преломления и было описано в [33].
Из полученных выражений следует, что поверхностная волна, описываемая (15)–(21), существует при ε1 > ε2. Выражение (21) определяет положение границы оптического домена в зависимости от оптических характеристик нелинейной среды и эффективного показателя преломления. Из (21) следует, что поверхностная волна данного типа существует не при всех значениях эффективного показателя преломления, а только при n > nmin, которое соответствует корням уравнения:
(23)
${{\left( {\frac{{{\text{Ai}}{\kern 1pt} {\text{'}}(\delta {\text{)}}}}{{{\text{Ai}}(\delta {\text{)}}}}} \right)}^{2}} = {{\xi }^{2}}({{\varepsilon }_{1}} - {{\varepsilon }_{2}})\frac{{{{\alpha }_{2}}}}{{{{\alpha }_{1}} + {{\alpha }_{2}}}}.$Рис. 2.
Зависимость минимального значения эффективного показателя преломления, определяемого уравнением (23), от ξ для первой моды при значениях параметров c = 1, ω = 1, ε0 = 6, Δε = 5, ε1 = 1.1, ε2 = 0.1, α1 = 3.5, α2 = 0.5.
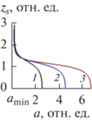
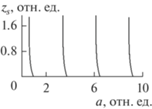
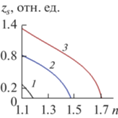
На рис. 3 представлены зависимости ширины оптического домена (21) в нелинейном кристалле от эффективного показателя преломления для первой моды. Положение границы домена в поле переключения, рассчитанном по (22), отмечены на рис. 1а. Только для первой моды отмечается максимум ширины домена.
Рис. 3.
Зависимость ширины домена (21) от эффективного показателя преломления для первой моды при значениях параметров c = 1, ω = 1, ε0 = 6, Δε = 5, ε1 = 1.1, ε2 = 0.1, α1 = 3.5, α2 = 0.5 и а: 1 (1); 2 (2); 4 (3).
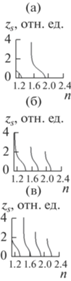
На рис. 4 показана динамика ширины домена при формировании мод второго, третьего и четвертого порядков. Начиная со второго порядка ширина оптического домена монотонно возрастает с увеличением эффективного показателя преломления. Следует отметить наличие запрещенных диапазонов (первый запрещенный диапазон отмечен закрашенной областью на рис. 4а) в интервале значений $n_{{\min }}^{2}$ < n2 < ε0, ширина которых уменьшается с ростом порядка моды, а их количество меньше порядка моды на единицу. С увеличением порядка моды ширина оптического домена растет.
Рис. 4.
Зависимость ширины домена (21) от эффективного показателя преломления при фиксированных параметрах c = 1, ω = 1, ε0 = 6, Δε = 5, ε1 = 1.1, ε2 = 0.1, α1 = 3.5, α2 = 0.5 для мод порядков: а – второго при а = 3; б – третьего при а = 6; в – четвертого при а = 8.
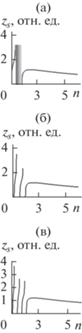
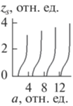
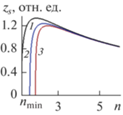
На рис. 5 представлены зависимости ширины оптического домена (21) в нелинейном кристалле от характерной ширины градиентного слоя a для первой моды, а на рис. 6 − для моды четвертого порядка. Для всех порядков мод ширина оптического домена монотонно убывает с ростом характерной ширины градиентного слоя начиная с минимального значения amin, при котором возможно распространение волны данного типа. Запрещенные интервалы (закрашенные области на рис. 6) значений характерной ширины градиентного слоя не меняются с ростом порядка моды.
ПОВЕРХНОСТНЫЕ ВОЛНЫ ВДОЛЬ КОНТАКТА СО СРЕДОЙ С ПЕРЕКЛЮЧЕНИЕМ ФОКУСИРУЮЩЕЙ НЕЛИНЕЙНОСТИ НА ДЕФОКУСИРУЮЩУЮ В ПЕРВОМ ДИАПАЗОНЕ
Далее рассмотрим поверхностные волны в системе с диэлектрической проницаемостью (2), тогда из уравнений (7), (8) следует, что при max{ε1, ε2} < n2 < ε0 и α1,2 > 0 поверхностная волна в слое с градиентом показателя преломления определяется выражением (15), а в нелинейном полупространстве:
(24)
${{E}_{{N1}}}(z) = \frac{{{{q}_{1}}}}{{\sqrt {{{g}_{1}}} }}{\text{sch(}}{{q}_{1}}(z - {{z}_{1}})),$(25)
${{E}_{{N2}}}(z) = - \frac{{{{q}_{2}}}}{{\sqrt {{{g}_{2}}} }}{\text{csch(}}{{q}_{2}}(z - {{z}_{2}})).$(26)
${{E}_{{Gm}}} = \frac{1}{{{\text{Ai}}\left( \delta \right)}}\sqrt {\frac{{2\left( {{{\varepsilon }_{{G{\text{eff}}}}} + {{\varepsilon }_{2}} - {{n}^{2}}} \right)}}{{{{\alpha }_{2}}}}} ,$(27)
${{z}_{1}} = \frac{c}{{\omega \sqrt {{{n}^{2}} - {{\varepsilon }_{1}}} }}{\text{arch}}\sqrt {\frac{{{{n}^{2}} - {{\varepsilon }_{1}}}}{{{{\varepsilon }_{1}} - {{\varepsilon }_{2}}}}\frac{{{{\alpha }_{1}} + {{\alpha }_{2}}}}{{{{\alpha }_{1}}}}} - {{z}_{s}},$(28)
${{z}_{2}} = \frac{c}{{\omega \sqrt {{{n}^{2}} - {{\varepsilon }_{2}}} }}{\text{arsh}}\sqrt {\frac{{{{n}^{2}}~ - {\text{\;}}{{\varepsilon }_{2}}}}{{{{\varepsilon }_{{G{\text{eff}}}}} + {{\varepsilon }_{2}} - {{n}^{2}}}}} {\kern 1pt} {\kern 1pt} ,$(29)
${{z}_{s}} = \frac{c}{{\omega \sqrt {{{n}^{2}} - {{\varepsilon }_{2}}} }}{\text{arsh}}\sqrt {\frac{{{{n}^{2}} - {{\varepsilon }_{2}}}}{{{{\varepsilon }_{1}} - {{\varepsilon }_{2}}}}\frac{{{{\alpha }_{1}} + {{\alpha }_{2}}}}{{{{\alpha }_{2}}}}} - {{z}_{2}},$(30)
${{E}_{s}} = \sqrt {2\frac{{{{\varepsilon }_{2}} - {{\varepsilon }_{1}}}}{{{{\alpha }_{1}} + {{\alpha }_{2}}}}} ,$Так же как для волн, описанных выше, для поверхностных волн данного типа существует ограничение допустимых значений эффективного показателя преломления, которые определяются из условия:
(31)
${{\varepsilon }_{{G{\text{eff}}}}} - {{n}^{2}} \geqslant \left( {{{\varepsilon }_{2}} - {{\varepsilon }_{1}}} \right)\frac{{{{\alpha }_{2}}}}{{{{\alpha }_{1}} + {{\alpha }_{2}}}} - {{\varepsilon }_{2}}.$Динамика изменения профиля поверхностной волны обсуждаемого типа отличается от динамики профиля волны, рассмотренной выше. Для первой моды единственный максимум интенсивности находится в градиентном слое (рис. 7а). Его высота сильно растет при незначительном уменьшении эффективного показателя преломления. Даже незначительное увеличение ширины градиентного слоя приводит теперь к ощутимому росту максимума интенсивности первой моды (рис. 7б). Профили мод первого, второго и третьего порядков приведены на рис. 7в. Максимумы интенсивности снижаются с увеличением порядка моды для данного типа волн.
Рис. 7.
Поверхностная волна (15), (24), (25) при фиксированных параметрах c = 1, ω = 1, ε0 = 6, Δε = 5.5, ε1 = 0.1, ε2 = 1.1, α1 = 0.5, α2 = 3.5: a – a = 2, n = 1.6 (1), 1.5 (2), 1.45 (3); б – n = 1.4, a = 1.5 (1), 1.6 (2), 1.7 (3); в – n = 1.3, a = 1 (1), 3 (2), 5.47 (3).
Оказалось, что в случае волноводной структуры из градиентного слоя, контактирующего с нелинейной фокусирующей средой, в которой с ростом напряженности электрического поля вблизи границы раздела формируется дефокусирующий слой толщиной zs, в нелинейной среде максимум интенсивности не наблюдается ни при каких значениях параметров.
Увеличение эффективного показателя преломления приводит к монотонному убыванию ширины домена (29) (рис. 8). Ни рис. 9 приведена динамика ширины домена (29) при формировании мод второго, третьего и четвертого порядков. Увеличение глубины градиентного слоя a приводит к монотонному росту ширины домена (29) (рис. 10). Можно сказать, что наблюдается тенденция, противоположная динамике ширины домена (21).
Рис. 8.
Зависимость ширины домена (29) от эффективного показателя преломления для первой моды при значениях параметров c = 1, ω = 1, ε0 = 6, Δε = 5.5, ε1 = 0.1, ε2 = 1.1, α1 = 0.5, α2 = 3.5 и а: 1 (1); 1.5 (2); 2.3 (3).
ПОВЕРХНОСТНЫЕ ВОЛНЫ ВДОЛЬ КОНТАКТА СО СРЕДОЙ С ПЕРЕКЛЮЧЕНИЕМ ФОКУСИРУЮЩЕЙ НЕЛИНЕЙНОСТИ НА ДЕФОКУСИРУЮЩУЮ ВО ВТОРОМ ДИАПАЗОНЕ
Теперь рассмотрим поверхностные волны в системе с диэлектрической проницаемостью (2), описываемые уравнениями (7), (8) при ε1 < n2 < < min{ε0, ε2} и α1,2 > 0. Тогда поверхностная волна в слое с градиентом показателя преломления определяется выражением (15), вне оптического домена − выражением (24), а в домене:
(32)
${{E}_{{N2}}}(z) = \frac{{{{q}_{t}}}}{{\sqrt {{{g}_{2}}} }}{\text{th(}}{{q}_{t}}(z - {{z}_{2}})),$Подставив (15), (24), (32) в граничные условия (13), (14), можно получить следующие параметры поверхностной волны:
(34)
${{E}_{{Gm}}} = \frac{{\sqrt {{{\varepsilon }_{{Gt}}} + 2{{\varepsilon }_{t}}} - \sqrt {{{\varepsilon }_{{Gt}}}} }}{{\sqrt {{\text{2}}{{\alpha }_{2}}} {\text{Ai(}}{{\delta }_{t}}{\text{)}}}},$(35)
$\begin{gathered} {{z}_{1}} = \frac{c}{{\omega \sqrt {{{\varepsilon }_{2}} - {{\varepsilon }_{1}} - {{\varepsilon }_{t}}} }} \times \\ \times \,\,{\text{arch}}\left( {\frac{1}{{{{E}_{s}}}}\sqrt {\frac{2}{{{{\alpha }_{1}}}}({{\varepsilon }_{2}} - {{\varepsilon }_{1}} - {{\varepsilon }_{t}})} } \right) - {{z}_{s}}, \\ \end{gathered} $(36)
${{z}_{2}} = - \frac{c}{{\omega \sqrt {{{\varepsilon }_{t}}} }}{\text{arsh}}\sqrt {\frac{{{{\varepsilon }_{t}}}}{{{{\varepsilon }_{{Gt}}}}}} ,$(37)
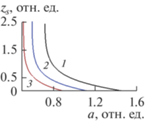
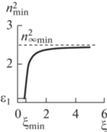
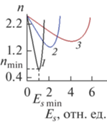
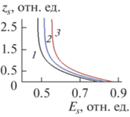
${{z}_{s}} = \frac{c}{\omega }\sqrt {\frac{2}{{{{\varepsilon }_{t}}}}} {\kern 1pt} {\kern 1pt} {\text{arth}}\left( {{{E}_{s}}\sqrt {\frac{{{{\alpha }_{2}}}}{{{{\varepsilon }_{t}}}}} } \right) - {{z}_{2}},$Принципиальное отличие волны данного типа от рассмотренных выше состоит в том, что эффективный показатель преломления не является произвольным, а его значение определятся параметрами среды и полем переключения в соответствии с выражением (33). Кроме того, поле переключения остается варьируемым параметром и не связано с характеристиками нелинейной среды, как это было в случае волн, рассмотренных выше. Такое отличие характерно для волн во втором диапазоне и было отмечено в [13–15]. Зависимость эффективного показателя преломления (33) от поля переключения немонотонная (рис. 11), а ее форма определяется оптическими параметрами нелинейной среды. В частности, возникает запрещенный диапазон напряженности поля переключения, ограниченный значением Esmax, которое совпадает с величиной (30), т.е. поле переключения не должно превышать величину (30). Минимум зависимости (33) наблюдается при Esmin = Esmax/21/2. Отсюда вытекает сужение интервала допустимых значений эффективного показателя преломления: nmin2 < n2 < min{ε0, ε2}, где
(38)
$\begin{gathered} {{n}_{{\min }}} = n({{E}_{s}} = {{E}_{{s\min }}}) = \\ = {{\varepsilon }_{2}} - ({{\varepsilon }_{2}} - {{\varepsilon }_{1}})\sqrt {\frac{{{{\alpha }_{2}}}}{{{{\alpha }_{1}} + {{\alpha }_{2}}}}} {\kern 1pt} {\kern 1pt} . \\ \end{gathered} $Рис. 11.
Зависимость эффективного показателя преломления (33) от поля переключения при: ε1 = 0.1, ε2 = 5.1, α1 = 0.5, α2 = 3.5 (1); α1 = 0.6, α2 = 0.5 (2); α1 = = 0.2, α2 = 0.1 (3).
Форма профиля поля волны, определяемой (15), (24), (32), вблизи границы раздела в данном диапазоне значений эффективного показателя преломления существенно отличается от рассмотренных выше случаев (рис. 12). В случае первой моды глубина проникновения поля в нелинейную среду при определенных значениях параметров системы может быть существенно больше, чем в градиентный слой (рис. 12a, 12б, кривые 1). При этом напряженность поля незначительно снижается по всей ширине приповерхностного оптического домена до значения переключения.
Рис. 12.
Поверхностная волна (15), (24), (32) при фиксированных параметрах c = 1, ω = 1, ε0 = 6, Δε = 5, ε1 = = 0.1, ε2 = 5.1, α1 = 0.5, α2 = 3.5: a – a = 0.7, Es = 0.52 (1), 0.55 (2), 0.85 (3); б – Es = 0.6, a = 0.65 (1), 0.75 (2), 0.95 (3); в – Es = 0.6, a = 0.7 (1), 3.7 (2), 6.5 (3).
Уменьшение напряженности поля переключения приводит к существенному снижению глубины локализации поля в нелинейной среде, однако слабо влияет на глубину локализации поля в градиентном слое (рис. 12а). Максимум интенсивности поля, находящийся в градиентном слое вблизи границы раздела, незначительно смещается. Увеличение ширины градиентного слоя также приводит к существенному снижению глубины локализации поля в нелинейной среде и практически не меняет глубину локализации поля в градиентном слое (рис. 12б). Высота максимума интенсивности поля снижается. Значения максимумов интенсивности возрастают с увеличением порядка моды для данного типа волн (рис. 12в), т.е. интенсивность поля в моде старших порядков может быть в разы выше, чем вблизи границы раздела. Такое формирование профиля поля старших мод отличает данный тип волн от рассмотренных выше.
Увеличение поля переключения приводит к монотонному убыванию ширины домена (37) (рис. 13). Увеличение ширины градиентного слоя a вызывает монотонное уменьшение ширины домена (37) (рис. 14) в отличие от ширины домена (29) при таких же знаках нелинейности, но другом диапазоне значений эффективного показателя преломления. На рис. 15 приведена зависимость ширины домена (37) для мод до четвертого порядка. Так же, как и во всех случаях рассмотренных выше типов волн, образуются запрещенные диапазоны ширин градиентного слоя, при которых данные типы волн не существуют, причем ширина запрещенных диапазонов одинакова при фиксированном порядке моды.
Рис. 13.
Зависимость ширины домена (37) от поля переключения для первой моды при параметрах c = 1, ω = 1, ε0 = 6, Δε = 5, ε1 = 0.1, ε2 = 5.1, α1 = 0.5, α2 = 3.5 и а: 0.75 (1); 0.7 (2); 0.65 (3).
ЗАКЛЮЧЕНИЕ
В работе теоретически описаны новые типы поперечных электрических поверхностных волн, распространяющихся вдоль границы раздела между оптическим слоем с постоянным градиентом показателя преломления и нелинейной средой, в которой с ростом напряженности электрического поля происходит смена знака керровской нелинейности на противоположный. Рассмотрены случай переключения дефокусирующей нелинейности на фокусирующую и два случая переключения фокусирующей нелинейности на дефокусирующую в двух различных диапазонах значений эффективного показателя преломления. Найдены три типа поверхностных волн, представляющих собой точные аналитические решения нелинейных уравнений.
Показано, что формируется оптический домен вблизи границы раздела в нелинейной среде. В градиентной среде возможны случаи немонотонного затухания профиля поля при удалении от границы раздела, соответствующие волноводным модам старших порядков. Отмечено наличие запрещенных диапазонов значений эффективного показателя преломления, а также ширины градиентного слоя, при которых данные типы волн не существуют, причем ширина запрещенных диапазонов одинакова при фиксированном порядке моды для всех полученных типов волн.
Проанализировано влияние параметров системы на распределение профиля волн вблизи границы раздела и максимумы интенсивности напряженности электрического поля в поверхностной волне. В частности, показано, что увеличение характерной ширины градиентного слоя при остальных фиксированных параметрах системы в случае первой моды волн первого типа приводит к незначительному росту максимума интенсивности электрического поля и смещению его положения из нелинейного кристалла в градиентную среду. В случае волн второго типа наблюдается резкий рост высоты максимума интенсивности, а в случае волн третьего типа существенно уменьшается глубина локализации поля в нелинейной среде, причем в градиентном слое она меняется незначительно. Для волн, распространяющихся вдоль контакта со средой с переключением фокусирующей нелинейности на дефокусирующую в обоих диапазонах, максимумы интенсивности поля всегда расположены в градиентном слое, в отличие от волн, распространяющихся с переключением дефокусирующей нелинейности на фокусирующую, когда возможны случаи расположения максимума интенсивности основной моды как в нелинейном оптическом домене, так и в градиентном слое.
Полученные результаты расширяют теоретические представления о локализации световых пучков в средах с распределенными в пространстве показателями преломления и в оптически нелинейных кристаллах, а также могут быть полезными для разработки различных оптических устройств, в том числе волноводных систем.
Конфликт интересов: автор заявляет, что у него нет конфликта интересов.
Список литературы
Surface Waves: New Trends and Developments / Ed. Ebrahimi F. IntechOpen, 2018. 154 p.
Kivshar Yu.S., Agrawal G.P. Optical Solitons: from Fibers to Photonic Crystals. San Diego: Academic Press, 2003. 540 p.
Dragoman D., Dragoman M. Advanced Optoelectronic Devices, Berlin: Springer, 1999. 424 p.
Chen J., Rong K. // Mater. Chem. Front. 2021. V. 5. P. 4502. https://doi.org/10.1039/D0QM01118E
Leble S. Waveguide Propagation of Nonlinear Waves. Berlin: Springer, 2019. 288 p.
Ахмедиев Н.Н., Корнеев В.И., Кузьменко Ю.В. // ЖЭТФ. 1985. Т. 88. С. 107.
Михалаке Д., Назмитдинов Р.Г., Федянин В.К. // Физика элементарных частиц и атомного ядра. 1989. Т. 20. С. 198.
Kartashov Y.V., Malomed B.A., Torner L. // Rev. Modern Phys. 2011. V. 83. P. 247.
Mihalache D. // Romanian Rep. Phys. 2021. V. 73. P. 403.
Touam T., Yergeau F. // Appl. Opt. 1993. V. 32. P. 309.
Chatterjee S., Chaudhuri P.R. // J. Basic Appl. Phys. 2014. V. 3. P. 1.
Čada M., Qasymeh M., Pištora J. // Wave Propagation Theories and Applications. IntechOpen, 2013. P. 175.
Savotchenko S.E. // Romanian Rep. Phys. 2020. V. 72. P. 412.
Savotchenko S.E. // Solid State Commun. 2021. V. 325. P. 114165.
Savotchenko S.E. // Opt. Quantum Electronics. 2021. V. 53. P. 365.
Kaplan A.E. // IEEE J. Quantum Electronics. 1985. V. QE-21. P. 1538.
Enns R.H., Rangnekar S.S., Kaplan A.E. // Phys. Rev. A. 1987. V. 35. P. 466.
Enns R.H., Rangnekar S.S., Kaplan A.E. // Phys. Rev. A. 1987. V. 36. P. 1270.
Хаджи П.И., Федоров Л.В. // ЖТФ. 1991. Т. 61. С. 110.
Белецкий Н.Н., Гасан Е.А. // ФТТ. 1994. Т. 36. С. 647.
Ляхомская К.Д., Хаджи П.И. // ЖТФ. 2000. Т. 70. С. 86.
Savotchenko S.E. // J. Optics. 2020. V. 22. P. 065504.
Савотченко С.Е. // ЖЭТФ. 2020. Т. 158. С. 3.
Савотченко С.Е. // Письма в ЖТФ. 2020. Т. 46. С. 43.
Савотченко С.Е. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2020. № 7. С. 79.
Savotchenko S.E. // Eur. Phys. J. B. 2020. V. 93. P. 182.
Савотченко С.Е. // Оптика и спектроскопия. 2021. Т. 129. С. 201.
Хаджи П.И., Шибаршина Г.Д., Ротару А.Х. Оптическая бистабильность в системе когерентных экситонов и биэкситонов в полупроводниках. Кишинев: Штиинца, 1988. 121 с.
Хаджи П.И., Русанов A.M., Гайван С.Л. // Квантовая электроника. 1999. Т. 27. С. 262.
Коровай А.В., Хаджи П.И. // Квантовая электроника. 2001. Т. 31. С. 937.
Хаджи П.И., Коровай А.В. // Квантовая электроника. 2002. Т. 32. С. 711.
Hussein A.J., Taya S.A., Vigneswaran D., Udiayakumar R., Upadhyay A., Anwar T., Amiri I.S. // Results Phys. 2021. V. 20. P. 103734.
Savotchenko S.E. // Optik. 2022. V. 252. P. 168542.
Adams M.J. An Introduction to Optical Waveguides. Chichester: Wiley, 1981. 401 p.
Chen C.-L. Foundations for Guided-Wave Optics. New Jersey: John Wiley & Sons, 2005. 462 p.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования