Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 4, стр. 39-43
О фазовой диаграмме ферропниктидов
А. Е. Каракозов a, *, М. В. Магницкая a, **
a Институт физики высоких давлений им. Л.Ф. Верещагина РАН
108840 Троицк, Москва, Россия
* E-mail: chkara@rambler.ru
** E-mail: magnma@yandex.ru
Поступила в редакцию 25.05.2021
После доработки 16.06.2021
Принята к публикации 22.06.2021
- EDN: LDNPLL
- DOI: 10.31857/S1028096022010071
Аннотация
Рассмотрен модельный трехзонный сверхпроводник с двумя дырочными зонами, взаимодействующими с электронной зоной посредством спин-флуктуационного межзонного взаимодействия. Для различных заполнений зон и анизотропии спаривания исследована структура сверхпроводящего состояния такого сверхпроводника в зависимости от величины отношения межзонного взаимодействия к внутризонному, рассматриваемому как аналог допинговой зависимости в ферропниктидах. Показано, что такая модель хорошо описывает допинговую эволюцию свойств сверхпроводящих ферропниктидов, в частности, характерную трансформацию электронной теплоемкости при изменении допирования и аномальную температурную зависимость доминирующей сверхпроводящей щели для электронной зоны с наименьшим заполнением и сильной анизотропией внутризонного спаривания. С учетом поправок сильной связи предложенная модель может быть применена для количественной оценки корреляционных эффектов и величины нефононного вклада в сверхпроводимость ферропниктидов.
ВВЕДЕНИЕ
Коррелированные железосодержащие сверхпроводники (далее ферропниктиды) со спин-флуктуационным взаимодействием электронных (e) зон с центрами в точках X = (π, 0) и Y = (0, π) и дырочных (h) зон, центрированных в точке Г, характеризуются универсальной фазовой диаграммой [1]. Область оптимального (с максимальной Tc) допирования x = xopt примерно совпадает с областью антиферромагнитного перехода и наиболее сильных межзонных антиферромагнитных флуктуаций, взаимодействие с которыми в нефононной теории сверхпроводимости считается доминирующим. Плотность доступных для сверхпроводящего спаривания состояний γn(x) и связанное с ней внутризонное (фононное) спаривание также достигает максимума при xopt, поэтому роль фононного и нефононного механизмов в увеличении Tc остается неясной. Построение более полной фазовой диаграммы структуры сверхпроводящего состояния ферропниктидов затрудняется большим разбросом данных вследствие того, что в них щели 4, 5 взаимодействующих сверхпроводящих конденсатов заполняют сравнительно небольшой интервал энергий, сопоставимый с погрешностью большинства экспериментальных методик. По нашему мнению, для построения такой фазовой диаграммы пригодны только три, достоверно установленные универсальные для ферропниктидов, характеристики: а – упомянутая выше допинговая зависимость плотности состояний γn(x); б – характерная трансформация нормированной электронной теплоемкости cs(x, t) (увеличение при промежуточных температурах и соответствующее сохранению энтропии уменьшение вблизи Tc по мере удаления от антиферромагнитного перехода [2–4]); в – сильное отклонение зависимости, доминирующей сверхпроводящей щели ∆L(xopt, t), от универсальной зависимости в модели БКШ в оптимально допированных ферропниктидах [5], которое не объясняется эффектами сильной связи [6]. Нами показано, что отмеченные универсальные свойства имеют место в модели двух h-зон, взаимодействующих с e-зоной с наименьшей плотностью состояний γe посредством спин-флуктуационного взаимодействия λSF(x).
Предложенная нами модель позволяет на основании экспериментальных данных количественно оценить величину корреляционных эффектов и их роль в сверхпроводящих ферропниктидах.
МНОГОЗОННЫЕ МОДЕЛИ СВЕРХПРОВОДЯЩЕГО СОСТОЯНИЯ ФЕРРОПНИКТИДОВ
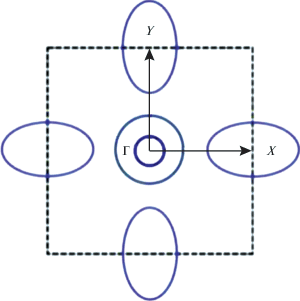
Основные методы исследования структуры сверхпроводящего состояния ферропниктидов – теории Бардина–Купера–Шриффера (БКШ) и Элиашберга [7, 8], которые отличаются моделями электрон-бозонного взаимодействии. В модели БКШ “спаривающее” электрон-бозонное взаимодействие V(k, k', ω) приближенно считается не зависящим от энергии бозонов ω для ω, меньших характерной бозонной частоты Ωc, и равным 0 вне этой области. В ферропниктидах с анизотропной поверхностью Ферми (рис. 1) электрон-бозонное взаимодействие V(k, k') в h-зонах считается постоянным, а в e-зоне для X и Y карманов имеет вид:
(1)
$\begin{gathered} {{V}_{{\text{E}}}}({{\varphi }_{{{X \mathord{\left/ {\vphantom {X Y}} \right. \kern-0em} Y}}}},\varphi _{{{X \mathord{\left/ {\vphantom {X Y}} \right. \kern-0em} Y}}}^{{\text{'}}}) = \\ = {{V}_{{\text{E}}}}(1 \pm d{\text{cos}}2{{\varphi }_{{{X \mathord{\left/ {\vphantom {X Y}} \right. \kern-0em} Y}}}})(1 \pm d{\text{cos}}2\varphi _{{{X \mathord{\left/ {\vphantom {X Y}} \right. \kern-0em} Y}}}^{{\text{'}}}) = \\ = {{V}_{{\text{E}}}}u({{\varphi }_{{{X \mathord{\left/ {\vphantom {X Y}} \right. \kern-0em} Y}}}})u(\varphi _{{{X \mathord{\left/ {\vphantom {X Y}} \right. \kern-0em} Y}}}^{{\text{'}}}), \\ \end{gathered} $Основная трудность исследования структуры сверхпроводящего состояния ферропниктидов заключается в большом количестве параметров теории (функций в теории Элиашберга) и значительном разбросе экспериментальных данных, поэтому возникает необходимость использования упрощенных вариантов теории, позволяющих, тем не менее, описать надежно установленные общие свойства ферропниктидов. В этом смысле преимущество имеют многозонные модели БКШ. Изотропные уравнения БКШ, определяющие сверхпроводящие щели ΔJ(T), имеют вид [14–16]:
(3)
${{I}_{J}}(T) = \int\limits_0^{{{{{\Omega }}}_{c}}} {d\xi {{\operatorname{th} \left( {{{{{E}_{J}}\left( \xi \right)} \mathord{\left/ {\vphantom {{{{E}_{J}}\left( \xi \right)} {2T}}} \right. \kern-0em} {2T}}} \right)} \mathord{\left/ {\vphantom {{\operatorname{th} \left( {{{{{E}_{J}}\left( \xi \right)} \mathord{\left/ {\vphantom {{{{E}_{J}}\left( \xi \right)} {2T}}} \right. \kern-0em} {2T}}} \right)} {{{E}_{J}}\left( \xi \right)}}} \right. \kern-0em} {{{E}_{J}}\left( \xi \right)}}} ,$Для этой цели более пригодна модель двух h-зон, взаимодействующих с e-зоной с константами связи в стандартном БКШ-представлении $\lambda _{{ij}}^{0}$ = = VijNj. С учетом анизотропии внутризонного спаривания в e-зоне (1), e-щель в этой модели для t = T/Tc записывается как ΔE(φ, t) = ΔE(0)δE(t)β(φ, t), β(φ, t) =1 + dR(t) cos 2φ. Трехзонные уравнения для этого случая могут быть получены из изотропной системы (2) в виде:
(5)
$\begin{gathered} D\left( d \right){{I}_{1}}\left( t \right) = {{d}_{{23}}}{{\Delta }_{1}}\left( t \right) - {{\lambda }_{{33}}}{{\lambda }_{{12}}}{{\Delta }_{2}}\left( t \right)\left\langle {u\beta \left( t \right)} \right\rangle + \\ + \,\,{{\lambda }_{{12}}}{{\lambda }_{{23}}}{{\Delta }_{3}}\left( t \right),\,\,\,\,D\left( d \right){{I}_{2}}\left( t \right) = {{\lambda }_{{11}}}{{\lambda }_{{33}}}{{\Delta }_{2}}\left( t \right)\left\langle {u\beta \left( t \right)} \right\rangle - \\ - \,\,{{\lambda }_{{33}}}{{\lambda }_{{21}}}{{\Delta }_{1}}\left( t \right) - {{\lambda }_{{11}}}{{\lambda }_{{23}}}{{\Delta }_{3}}\left( t \right),\,\,\,\,D\left( d \right){{I}_{3}}\left( t \right) = \\ = {{d}_{{12}}}{{\Delta }_{3}}\left( t \right) - {{\lambda }_{{11}}}{{\lambda }_{{32}}}{{\Delta }_{2}}\left( t \right)\left\langle {u\beta \left( t \right)} \right\rangle + {{\lambda }_{{21}}}{{\lambda }_{{32}}}{{\Delta }_{1}}\left( t \right), \\ \end{gathered} $(6)
$\begin{gathered} R(t) = \left\{ {1 - \left( {{{{{\lambda }_{{21}}}} \mathord{\left/ {\vphantom {{{{\lambda }_{{21}}}} {{{\lambda }_{{11}}}}}} \right. \kern-0em} {{{\lambda }_{{11}}}}}} \right){{{{\Delta }_{1}}\left( t \right)} \mathord{\left/ {\vphantom {{{{\Delta }_{1}}\left( t \right)} {{{\Delta }_{2}}\left( t \right)}}} \right. \kern-0em} {{{\Delta }_{2}}\left( t \right)}} - } \right. \\ {{\left. { - \,\,\left( {{{{{\lambda }_{{23}}}} \mathord{\left/ {\vphantom {{{{\lambda }_{{23}}}} {{{\lambda }_{{33}}}}}} \right. \kern-0em} {{{\lambda }_{{33}}}}}} \right){{{{\Delta }_{3}}\left( t \right)} \mathord{\left/ {\vphantom {{{{\Delta }_{3}}\left( t \right)} {{{\Delta }_{2}}\left( t \right)}}} \right. \kern-0em} {{{\Delta }_{2}}\left( t \right)}}} \right\}} \mathord{\left/ {\vphantom {{\left. { - \,\,\left( {{{{{\lambda }_{{23}}}} \mathord{\left/ {\vphantom {{{{\lambda }_{{23}}}} {{{\lambda }_{{33}}}}}} \right. \kern-0em} {{{\lambda }_{{33}}}}}} \right){{{{\Delta }_{3}}\left( t \right)} \mathord{\left/ {\vphantom {{{{\Delta }_{3}}\left( t \right)} {{{\Delta }_{2}}\left( t \right)}}} \right. \kern-0em} {{{\Delta }_{2}}\left( t \right)}}} \right\}} {D(0)}}} \right. \kern-0em} {D(0)}} \\ \end{gathered} $(7)
$\begin{gathered} {{I}_{2}}\left( t \right) = \left\langle {\int\limits_0^{{{{{\Omega }}}_{c}}} {d{{\xi }}u(\varphi {\text{)}}\beta {\text{(}}\varphi ,t){{{\left\langle {u{\kern 1pt} \beta } \right\rangle }}^{{ - 1}}} \times } } \right. \\ \left. {{{_{{_{{_{{}}^{{}}}}^{{}}}}^{{^{{^{{^{{^{{}}}}}}}}}} \times \,\,\operatorname{th} \left( {{{{{E}_{2}}\left( {\xi {\text{,}}\varphi ,t} \right)} \mathord{\left/ {\vphantom {{{{E}_{2}}\left( {\xi {\text{,}}\varphi ,t} \right)} {2t}}} \right. \kern-0em} {2t}}} \right)} \mathord{\left/ {\vphantom {{_{{_{{_{{}}^{{}}}}^{{}}}}^{{^{{^{{^{{^{{}}}}}}}}}} \times \,\,\operatorname{th} \left( {{{{{E}_{2}}\left( {\xi {\text{,}}\varphi ,t} \right)} \mathord{\left/ {\vphantom {{{{E}_{2}}\left( {\xi {\text{,}}\varphi ,t} \right)} {2t}}} \right. \kern-0em} {2t}}} \right)} {{{E}_{2}}\left( {\xi {\text{,}}\varphi ,t} \right)}}} \right. \kern-0em} {{{E}_{2}}\left( {\xi {\text{,}}\varphi ,t} \right)}}} \right\rangle , \\ \end{gathered} $РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Трехзонная система уравнений (5) позволяет рассматривать возможные сценарии фазовой диаграммы, дополнять и уточнять их на основе экспериментальных данных [1] и модели нефононной сверхпроводимости [18]. А также, с учетом поправок сильной связи по предложенному нами способу [19], трехзонная система уравнений (5) может быть применена для анализа экспериментальных характеристик ферропниктидов. Допинговая зависимость Δj(x) и Tc(x) в ферропниктидах связана с изменением внутризонного $\lambda _{{II}}^{0}$ ≈ V(q $ \ll $ Q)γi(x) и межзонного спин-флуктуационного спаривания $\lambda _{{I \ne j}}^{0}$ ≈ V(Q, x)γj(x) на антиферромагнитных векторах Q = (π, 0), (0, π).
В ферропниктидах это электрон-фононное V(q $ \ll $ Q) ≈ u и спин-флуктуационное V(Q, x) ≈ g взаимодействия, одинаковые для всех зон. Для исследования основных особенностей фазовой диаграммы достаточно рассмотреть зависимость структуры сверхпроводящего состояния от величины x = g/u – отношения межзонного взаимодействия g к внутризонному u, рассматриваемому как аналог допинговой зависимости в ферропниктидах, и различных заполнений зон и анизотропии спаривания. В этом случае в системе (5) достаточно ограничиться минимальным набором параметров: $\lambda _{{{\text{11}}}}^{0},$ γ2/γ1, γ3/γ1, d, позволяющим вычислять нормированные физические величины, например, cs(x, t). Качественные особенности допинговой эволюции структуры сверхпроводящего состояния показаны на рис. 2–4. Согласно рис. 2, увеличение спин-флуктуационного взаимодействия увеличивает сверхпроводящей щели и приводит к сближению щелей Δ1(0) и Δ2(0), влияя главным образом на e-щель, как этого можно было ожидать непосредственно из вида системы (5). Анизотропия e-щели dR при увеличении спин-флуктуационного взаимодействия уменьшается (рис. 3). Оба эти обстоятельства (сближение щелей Δ1 и Δ2 и уменьшение анизотропии) приводят к упомянутой во введении характерной трансформации вида cs(x, t) при изменении допирования (как это показано в работе [20]).
Рис. 2.
Зависимость сверхпроводящих щелей Δi (кривые 1, 2, 3), нормированных на максимальную щель в отсутствие межзонного взаимодействия Δ1(0), от отношения межзонного взаимодействия g к внутризонному u, x = g/u, при нулевой температуре.
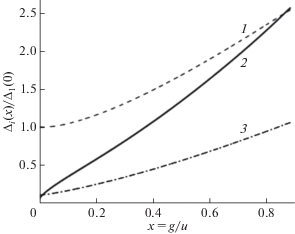
Рис. 3.
Зависимость коэффициента анизотропии электронной щели dR(x) от отношения межзонного взаимодействия g к внутризонному u (x = g/u) при нулевой температуре.
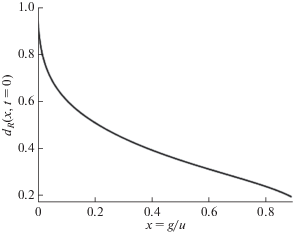
Рис. 4.
Температурная зависимость нормированных сверхпроводящих щелей Δi(t)/Δ1(0) (кривые 1, 2, 3) и максимальной и минимальной электронной щелей Δ2±(t) = Δ2(t)(1 ± dR(t)) (кривые 4 и 5).
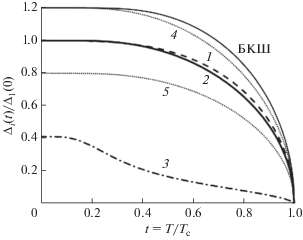
На рис. 4 представлена температурная зависимость сверхпроводящей щелей 1, 2, 3 при γ1 = 0.5, γ2 = 0.2, γ3 = 0.3 и достаточно сильном межзонном взаимодействии (x ≈ 0.9, Δ1(0) = Δ2(0), также рис. 2) и максимальная и минимальная e-щели Δ2±(t) = = Δ2(t)(1 ± dR(t)) (кривые 4, 5). Отметим, что в трехзонном сверхпроводнике при конечных температурах зависимости обеих “больших” щелей Δ1(t) и Δ2(t) расположены ниже кривой ΔБКШ(t) причем, как и можно было ожидать, из-за анизотропии e-щели dR(t) ≈ 20% при конечных температурах Δ2(t > 0) < Δ1(t > 0). В этой работе мы не ставили своей целью количественный анализ экспериментальных данных, так как для этого необходим несколько другой подход [20]. Тем не менее, сравнивая зависимости, показанные на рис. 4, с данными анализа туннельных спектров ферропниктидов (рис. 7 в [17]), можно убедиться, что найденные из эксперимента “аномальные” температурные зависимости сверхпроводящих щелей (с сильным межзонным взаимодействием в зоне с доминирующей щелью и слабым в зоне с малой щелью) могут быть получены в трехзонной модели с реалистичным малым заполнением e-зоны, сильным межзонным спин-флуктуационным взаимодействием, анизотропным спариванием в e-зоне и внутризонными взаимодействиями V(q $ \ll $ Q) ≈ u, одинаковыми для всех зон, как это обычно и предполагается.
ЗАКЛЮЧЕНИЕ
Для теоретического исследования фазовой диаграммы ферропниктидов предложена модель сверхпроводника с двумя дырочными зонами, взаимодействующими с электронной зоной с анизотропным спариванием посредством спин-флуктуационного межзонного взаимодействия. Показано, что такая модель с минимальным набором параметров качественно воспроизводит допинговую эволюцию свойств сверхпроводящих ферропниктидов. В частности, она описывает характерную трансформацию электронной теплоемкости cs(x, t) при изменении допинга и аномальную температурную зависимость доминирующей сверхпроводящей щели в случае электронной зоны с наименьшим заполнением и сильной анизотропией внутризонного спаривания. С учетом поправок сильной связи предложенная модель может быть применена для количественной оценки корреляционных эффектов, величины нефононного вклада и анализа механизма сверхпроводимости ферропниктидов.
Конфликт интересов: Авторы заявляют, что у них нет конфликта интересов.
Список литературы
Lester C., Chu J.-H., Analytis J.G., Capelli S.C., Erickson A.S., Condron C.L., Toney M.F., Fisher I.R., Hayden S.M. // Phys. Rev. B. 2009. V. 79. № 14. P. 144523. https://doi.org/10.1103/PhysRevB.79.144523
Hardy F., Burger P., Wolf T., Fisher R.A., Schweiss P., Adelmann P., Heid R., Fromknecht R., Eder R., Ernst D., Löhneysen H.v., Meingast C. // EPL. 2010. V. 91. № 4. P. 47008. https://doi.org/10.1209/0295-5075/91/47008
Tan G.T., Zheng P., Wang X.C., Chen Y., Zhang X., Luo J., Netherton T., Song Y., Dai P., Zhang C., Li S. // Phys. Rev. B. 2013. V. 87. № 14. P. 144512. https://doi.org/10.1103/PhysRevB.87.144512
Campanini D., Diao Z., Fang L., Kwok W.-K., Welp U., Rydh A. // Phys. Rev. B. 2015. V. 91. № 24. P. 245142. https://doi.org/10.1103/PhysRevB.91.245142
Кузьмичева Т.Е., Муратов А.В., Кузьмичев С.А., Садаков А.В., Алещенко Ю.А., Власенко В.А., Мартовицкий В.П., Перваков К.С., Ельцев Ю.Ф., Пудалов В.М. // УФН. 2017. Т. 187. № 4. С. 450. https://doi.org/10.3367/UFNr.2016.10.038002
Adrian S.D., Wolf S.A., Dolgov O., Shulga S., Kresin V.Z. // Phys. Rev. B. 1997. V. 56. № 13. P. 7878. https://doi.org/10.1103/PhysRevB.56.7878
Элиашберг Г.М. // ЖЭТФ. 1960. Т. 38. № 3. С. 696. http://www.jetp.ac.ru/cgi-bin/dn/e_011_03_0696.pdf
Элиашберг Г.М. // ЖЭТФ. 1961. Т. 39. № 5. С. 1437. http://www.jetp.ac.ru/cgi-bin/dn/e_012_05_1000.pdf
Morel P., Anderson P.W. // Phys. Rev. 1962. V. 125. № 4. P. 1263. https://doi.org/10.1103/PhysRev.125.1263
McMillan W.L. // Phys. Rev. 1968. V. 167. № 2. P. 331. https://doi.org/10.1103/PhysRev.167.331
Chubukov A. // Annu. Rev. Condens. Matter Phys. 2012. V. 3. № 1. P. 55. https://doi.org/10.1146/annurev-conmatphys-020911-125055
Hirschfeld P.J. // C. R. Phys. 2016. V. 17. Iss. 1–2. P. 197. https://doi.org/10.1016/j.crhy.2015.10.002
Проблема высокотемпературной сверхпроводимости / Ред. Гинзбург В.Л., Киржниц Д.А. М.: Наука, 1977.
Москаленко В.А. // ФММ. 1959. Т. 8. № 4. С. 503.
Suhl H., Matthias B.T., Walker L.R. // Phys. Rev. Lett. 1959. V. 3. № 12. P. 552. https://doi.org/10.1103/PhysRevLett.3.552
Москаленко В.А., Палистрант М.Е., Вакалюк В.М. // УФН. 1991. Т. 161. № 8. С. 155. https://doi.org/10.3367/UFNr.0161.199108f.0155
Кузьмичева Т.Е., Кузьмичев С.А., Михеев М.Г., Пономарёв Я.Г., Чесноков С.Н., Пудалов В.М., Хлыбов Е.П., Жигадло Н.Д. // УФН. 2014. Т. 184. № 8. С. 888. https://doi.org/10.3367/UFNr.0184.201408i.0888
Коршунов М.М. // УФН. 2014. Т. 184. № 8. С. 882. https://doi.org/10.3367/UFNr.0184.201408h.0882
Karakozov A.E., Zapf S., Gorshunov B., Ponomarev Ya.G., Magnitskaya M.V., Zhukova E., Prokhorov A.S., Anzin V.B., Haindl S. // Phys. Rev. B. 2014. V. 90. № 1. P. 014506. https://doi.org/10.1103/PhysRevB.90.014506
Karakozov A.E., Magnitskaya M.V., Kadyrov L.S., Gorshunov B.P. // Phys. Rev. B. 2019. V. 99. № 5. P. 054504 https://doi.org/10.1103/PhysRevB.99.054504
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования