Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 7, стр. 27-33

ВВЕДЕНИЕ

Процессы, связанные с электрическими разрядами [1], находят свое применение в современных технологиях, поскольку с их помощью можно создавать наноразмерные элементы. В то же время из-за необходимости создавать объекты еще меньшего размера приходится применять и коронный разряд, так как в этом случае можно получить элементы размерами единиц и долей нанометров [2–4]. Однако до сих пор нет полного понимания того, как именно происходит переход вещества электродов в газообразное состояние [5–7]. Выяснить природу этого явления проще всего на коронном разряде из-за его относительно небольшой энергии.

При протекании коронного разряда атомы и молекулы вещества, из которого изготовлены электроды, оказываются в газовой среде. Это распыление надежно регистрируется спектрометром. Если предположить, что происходит классическое испарение из-за нагревания локальной области контакта плазмы с твердой поверхностью, то из-за теплопроводности материала эта локальная область не сможет достигнуть необходимой для испарения температуры. До сих пор это явление не было описано в литературе, хотя на существование такого испарения указывает появление углубления в месте соприкосновения шнура плазмы с поверхностью электрода. Механизм такого испарения или распыления поверхности остается неизвестным, хотя на его существование уже обращали внимание [8].

В настоящей работе экспериментально исследовано образование и характеристики частиц в коронном разряде при атмосферном давлении. Предложена теоретическая модель испарения или распыления металла. Показано, что причиной аномальной эмиссии атомов могут быть сильные локальные электромагнитные поля поверхностных плазмонов металла, возбуждаемых потоком электронов или ионов коронного разряда.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

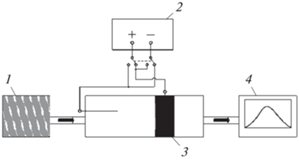
Принципиальная схема установки представлена на рис. 1. В состав экспериментальной установки входит герметизированная стеклянная трубка, в которой помещены два электрода. К электродам прикладывается высокое напряжение – до 10 кВ. Один из электродов (коронирующий или активный) был заострен: он имел выступ с очень малым радиусом кривизны, вокруг которого возникало электрическое поле с высокой напряженностью. Второй электрод, выполненный в форме кольца, материал которого не принимал участия в процессе образования частиц, был изготовлен из произвольного металла. Через трубку был пропущен поток (0.5 л/мин) воздуха, азота или аргона при нормальном давлении. Затем этот поток проходил через диффузионный аэрозольный спектрометр (“ДАС 2702”) [7, 8] для исследования дисперсного состава. “ДАС” позволяет регистрировать размер частиц в диапазоне 3–5 мкм и их концентрацию до 10⁵ см^–3.

Коронный разряд возникает при напряжении 3–10 кВ в зависимости от газа-носителя и материала электрода. При напряжении свыше 10 кВ коронный разряд переходит в искровой, это зависит и от геометрии электродов. При возникновении коронного разряда образуются частицы, размеры которых находятся в пределах 3–100 нм, средний размер частиц 15–20 нм в зависимости от прилагаемого напряжения и возникающего тока. Концентрация и размеры образующихся частиц пропорциональны силе тока в коронном разряде. Ток коронного разряда изменяется в пределах 1–10 мкА. Характерные параметры распределения по размеру образующихся частиц принципиально не изменяются при смене полярности разряда.

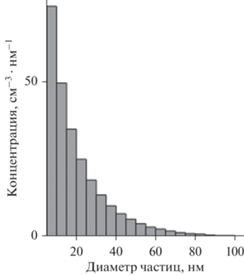
Типичный спектр размеров частиц, возникающих в зоне коронного разряда в экспериментальных условиях, описанных выше, представлено на рис. 2. Подобные распределения были получены для случаев, когда активный электрод был выполнен из серебра, железа, молибдена, вольфрама или графита. Из-за ограниченной чувствительности спектрометра регистрация частиц размером 3 нм была осуществлена с эффективностью 50%, а более мелкие частицы вообще не были зарегистрированы. Поэтому на гистограмме распределения частиц по размеру часть шкалы 0–3 нм в настоящее время недоступна. При увеличении разности напряжений и соответствующем увеличении тока увеличивается размер частиц и их концентрация. Исследования показали, что распределение частиц по размеру не зависит ни от материала электродов, ни от газа-носителя, т.е. оно носит универсальный характер и определяется только напряжением между электродами и силой тока.

По силе тока коронного разряда можно определить верхнюю границу потока атомов металла из кристалла-электрода в объем трубки, где затем из этих атомов и молекул образуются частицы, регистрируемые спектрометром. По концентрации частиц и их распределению по размеру можно найти количество вещества электрода, которое участвовало в образовании частиц. Сопоставление этих величин показывает, что эффективность конденсации составляет 10^–2–10^–3, что означает, что каждый из 100–1000 атомов (или молекул) участвует в образовании частиц или что только небольшая доля ионов и электронов вызывает выбивание атомов или молекул электродов из кристаллической решетки.

ОПИСАНИЕ МОДЕЛИ

Предлагаемая теоретическая модель процессов, происходящих во время коронного разряда, объясняет, почему вырывание иона из вещества электрода происходит при сравнительно невысокой энергии заряженных частиц (порядка нескольких эВ), а также экспериментально наблюдаемую причину независимости явления от знака заряда этих частиц.

Некоторые механизмы потери энергии заряженной частицей, проходящей через конденсированную среду, рассмотрены, например, в [9]. В основе предлагаемой модели лежат особенности взаимодействия падающей заряженной частицы с коллективными электронными возбуждениями в металлическом образце [10–12]. При описании электродинамических свойств металла была использована стандартная модель “желе”, согласно которой ионная решетка заменена однородным положительным “фоном”, а электроны находятся в этом потенциальном поле. Кулоновское взаимодействие электронов проводимости в металле приводит к появлению в нем коллективных возбуждений. В неограниченном металле эти колебания называются объемными плазмонами. Их частота (так называемая классическая плазменная частота неограниченного электронного газа) равна:

где n₀ – плотность электронов проводимости, m и е – масса и заряд электрона. Для реальных металлов ω₀ составила порядка 10¹⁵–10¹⁶ c^–1 (граница видимого и УФ-света). На плоской поверхности идеального металла в вакууме частота колебаний немного меньше: Эти колебания называются поверхностными плазмонами, поскольку колебания электронной плотности локализованы строго на поверхности образца. Обсуждение свойств поверхностных плазмонов можно найти в [13–17].

В случае тонкой металлической пленки толщиной $l$, которая в дальнейшем будет служить моделью поверхностного слоя металла, собственные возбуждения носят характер продольных волн, распространяющихся вдоль поверхности, с законом дисперсии [14]:

где k – волновое число. Знак плюс соответствует асинфазным колебаниям электронной плотности на обеих поверхностях пленки, минус – синфазным. В зависимости от волнового вектора частота плазмона охватывает широкий диапазон вплоть до УФ. При низких частотах плазмон сильно затухает.

На идеально гладкой плоской поверхности металла возбуждение коллективных мод плоской электромагнитной волной запрещено из-за невозможности одновременного выполнения закона сохранения энергии и импульса. В случае шероховатой металлической поверхности при конечном радиусе ее кривизны, а также в тонкой пленке этот запрет снимается, и в этом случае говорят о смешанных продольно-поперечных модах, называемых плазмон-поляритонами. Запрет снимается при возбуждении поверхностных плазмонов заряженными частицами в неупругом канале рассеяния.

В основу рассматриваемой модели положена следующая схема событий. Падающая заряженная частица (ион или электрон) теряет энергию при неупругом рассеянии в электронном газе металла. Потеря энергии происходит как за счет одноэлектронных возбуждений, так и за счет коллективных. В рассматриваемом случае интерес представляют исключительно коллективные возбуждения. Сечение рассеяния резонансно возрастает, если переданная частицей энергия равна энергии возбуждаемого плазмона, которая, в свою очередь, может быть разной в зависимости от длины волны в соответствии с законом дисперсии плазмона. Как показано ниже, кулоновской силы взаимодействия приповерхностного иона решетки с флуктуацией электронной плотности, наведенной плазмоном на поверхности, вполне достаточно для его вырывания из металла. Рассмотрим возбуждение плазмона заряженной частицей при ее неупругом рассеянии.

ВЗАИМОДЕЙСТВИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ С ПОВЕРХНОСТЬЮ МЕТАЛЛА

Вычислим сечение неупругого рассеяния быстрой заряженной частицы на поверхностном слое металла, моделью которого является тонкая металлическая пленка. Предположим, что толщина пленки – это расстояние, на котором плотность электронов изменяется от нулевой (в вакууме) до величины, соответствующей внутренней плотности электронов сплошного металла. Сечение неупругого рассеяния связывается с мнимой частью поляризуемости пленки во внешнем поле специфического вида. Она может быть вычислена вблизи частот поверхностных плазмонов в пленке с использованием стандартных приближений теории многоэлектронных систем.

В первом приближении Борна теории возмущений, где используется система единиц с ћ = 1, вероятность неупругого рассеяния $W$ заряженной частицы [17, 18] имеет вид:

где $U{\kern 1pt} \left( {\mathbf{r}} \right) = {{e}^{2}}\int {d{{{\mathbf{r}}}_{1}}\delta \rho \left( {{{{\mathbf{r}}}_{1}}} \right){\kern 1pt} {{{\left| {{\mathbf{r}} - {{{\mathbf{r}}}_{1}}} \right|}}^{{ - 1}}}} ;$ $\left. {\mathbf{p}} \right\rangle = {{\left( {2\pi \Omega } \right)}^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$ × × ${\text{exp}}\left( {i{\mathbf{pr}}} \right);$ $\delta \rho \left( {\mathbf{r}} \right)$ – электронная плотность; $\Omega $ – нормировочный объем; суммирование ведется по всем возбужденным состояниям электронного газа $\left. s \right\rangle $. Для определенности далее в качестве налетающей частицы использован электрон. Тогда переданная энергия ${{\omega }_{{if}}} = {{\left( {p_{i}^{2} - p_{f}^{2}} \right)} \mathord{\left/ {\vphantom {{\left( {p_{i}^{2} - p_{f}^{2}} \right)} {2m}}} \right. \kern-0em} {2m}}$.

Разделив $W~$ на плотность потока падающих электронов и умножив на плотность конечных состояний ${{\Omega d{{{\mathbf{p}}}_{f}}} \mathord{\left/ {\vphantom {{\Omega d{{{\mathbf{p}}}_{f}}} {{{{\left( {2\pi } \right)}}^{3}}}}} \right. \kern-0em} {{{{\left( {2\pi } \right)}}^{3}}}} = {{\Omega md{{E}_{f}}d{{{\mathbf{n}}}_{f}}} \mathord{\left/ {\vphantom {{\Omega md{{E}_{f}}d{{{\mathbf{n}}}_{f}}} {{{{\left( {2\pi } \right)}}^{3}}}}} \right. \kern-0em} {{{{\left( {2\pi } \right)}}^{3}}}}$, получим для дифференциального сечения рассеяния следующее выражение:

где ${\mathbf{q}}$ – переданный импульс, ${{{\mathbf{n}}}_{f}}$ – единичный вектор в направлении рассеявшегося электрона, ${{\rho }_{q}} = \int {\rho \left( {\mathbf{r}} \right){\text{exp}}\left( {i{\mathbf{qr}}} \right)d{\mathbf{r}}} $.

Как известно, мнимая часть фурье-образа динамической поляризуемости металлического образца имеет следующее спектральное представление лемановского типа [17, 19]:

где $v$ – произвольное внешнее поле, ${{\omega }_{s}} = {{E}_{s}} - {{E}_{0}}$ – энергии возбуждения электронного газа образца и $\delta \to + 0$. Из сравнения выражений (2) и (3) следует, что где ${{\alpha }_{{\mathbf{q}}}}\left( \omega \right)$ – динамическая поляризуемость образца во внешнем поле вида Дифференцирование тождества где θ – угол рассеяния, дает В результате Переданный импульс q меняется от ${{q}_{{{\text{min}}}}} = {{p}_{i}} - {{p}_{f}}$ до ${{q}_{{{\text{max}}}}} = {{p}_{i}} + {{p}_{f}}$. При ${{p}_{i}},{{p}_{f}} \gg {{p}_{i}} - {{p}_{f}}$ ${{q}_{{{\text{min}}}}} \approx {{{{\omega }_{{if}}}} \mathord{\left/ {\vphantom {{{{\omega }_{{if}}}} {{{{v}}_{i}}}}} \right. \kern-0em} {{{{v}}_{i}}}}$ и ${{q}_{{{\text{max}}}}} \approx 2{{p}_{i}}$. В случае ионов характеристики электрона заменяются соответствующими характеристиками ионов, и в выражении (5) появляется множитель ${{Z}^{2}}$, где $Ze$ – заряд иона.

Поляризуемость металлического образца в произвольном внешнем поле ${v}\left( {\mathbf{r}} \right)$ определяется следующим образом:

Как показано в [13, 17], при частотах, много больших частот одноэлектронных переходов в металле, индуцированная электронная плотность $\delta \rho $ выражается через так называемое эффективное поле внутри образца $V\left( {\mathbf{r}} \right)$: Последнее удовлетворяет уравнению где $\eta \left( z \right) = \theta \left( {z + \frac{l}{2}} \right) - \theta \left( {z - \frac{l}{2}} \right)$ – безразмерная плотность электронов поверхностного слоя металла, который моделируется пленкой толщиной $~l$.

После перехода в фурье-представление

где $\mathop {\mathbf{k}}\limits^\prime $ – двумерный вектор в плоскости (x, y), для ${{F}_{k}}\left( z \right)$, связанного с ${{V}_{k}}\left( z \right)$ соотношением получаем следующее уравнение: где $\left( {{{q}_{z}},{\mathbf{k}}} \right)$ – компоненты вектора ${\mathbf{q}}~$ падающего электрона. Из (8) следует, что где ω_± определяются выражением (1). Полюса F_k(z) соответствуют поверхностным плазмонам.

В результате вблизи плазмонных частот для мнимой части поляризуемости, приходящейся на единицу площади пленки, получаем следующее выражение:

Рассмотрим простейший вариант, когда налетающая заряженная частица падает нормально к поверхности пленки. В этом случае из симметрии задачи переданный импульс может иметь только z-составляющую. Приходящееся на единицу площади пленки полное сечение неупругого рассеяния может быть представлено в следующем виде:

где Окончательно: где $\mu = {{{{\varepsilon }_{i}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{i}}} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$, $\xi = {{{{\omega }_{0}}l} \mathord{\left/ {\vphantom {{{{\omega }_{0}}l} c}} \right. \kern-0em} c}$, ${{\xi }^{ \mp }} = {{{{\omega }^{ \mp }}l} \mathord{\left/ {\vphantom {{{{\omega }^{ \mp }}l} c}} \right. \kern-0em} c}$ = ${{\omega }_{s}}l$ × × ${{\sqrt {1 \mp \exp ( - \kappa l)} } \mathord{\left/ {\vphantom {{\sqrt {1 \mp \exp ( - \kappa l)} } c}} \right. \kern-0em} c}$, ${{r}_{e}} = {{{{e}^{2}}} \mathord{\left/ {\vphantom {{{{e}^{2}}} {m{{c}^{2}}}}} \right. \kern-0em} {m{{c}^{2}}}}$ – классический радиус электрона и $ci\left( x \right)$ – интегральный косинус. Таким образом, сечение неупругого рассеяния есть функция параметра kl. При фиксированной величине $l$ оно зависит от длины волны возбуждаемого плазмона, которая в соответствии с (1) может меняться в широких пределах.

ВЗАИМОДЕЙСТВИЕ ИОНА КРИСТАЛЛИЧЕСКОЙ РЕШЕТКИ С ПОЛЕМ ПЛАЗМОНА

Теперь необходимо вычислить силу взаимодействия наведенного плазмоном отрицательного заряда на поверхности с ионом кристаллической решетки, расположенным вблизи поверхности металла. Эта сила равна

где ${{q}_{0}}$ – заряд иона, ${\mathbf{r}}$ – его радиус-вектор и $\delta \rho $ определяется выражением (6). Напомним, что $\delta \rho $ определяется эффективным полем V, удовлетворяющим уравнению (7), где ${v} = {\text{exp}}\left( {i{\mathbf{qr}}} \right)$ и ${\mathbf{q}}$ – импульс, переданный налетающей частицей. Налетающая заряженная частица, подобно камню, падающему в воду, генерирует расходящуюся по поверхности металла цилиндрическую волну электронной плотности, “вырывающую” приповерхностный ион. Это обстоятельство учитывается выбором $v$ в соответствии с выражением (4). Предложенный метод расчета, несмотря на его прозрачность, довольно трудоемок. Упростим задачу.

Как известно [9], в рамках законов электростатики индуцированные ионом с зарядом q₀ = Ze заряды на поверхности металла можно заменить единственным зарядом-изображением:

Тогда сила притяжения иона и заряда-изображения: где $l$ – расстояние от иона до поверхности металла. Как это характерно для классического приближения, формула (10) учитывает многое, в том числе и влияние поверхностного плазмона. Действительно, если воспользоваться выражением для диэлектрической проницаемости металла в высокочастотной области, то увидим, что сила взаимодействия резонансно возрастает вблизи частоты ω_s: С учетом ширины резонанса получим: Как было показано выше, сечение неупругого рассеяния максимальное, если сброшенная частицей энергия ω_if совпадает с частотой поверхностного плазмона. В этом случае сила взаимодействия определяется выражением: Частота ω_s в последней формуле немного отличается от ω_±, но для качественных расчетов это вполне допустимо.

Элементарная трактовка движения свободных электронов дает для безразмерной ширины резонанса g следующую оценку [20]:

где τ – характерное время свободного пробега электрона. Чем меньше τ, тем хуже проявляет себя резонанс.

Рассмотрим самый неблагоприятный сценарий, когда расстояние электрона от поверхности l меньше средней длины свободного пробега электрона в металле λ и ширина резонанса определяется столкновениями электрона с поверхностью. В этом случае

где ${{v}_{{\text{F}}}}$ – скорость Ферми электрона. Электроны, расположенные на расстояниях бóльших $l$ от границы, можно не рассматривать. Это оправдывает используемое моделирование поверхностного слоя с помощью металлической пленки толщины $l$. Сила взаимодействия нечувствительна к знаку бомбардирующих поверхность металла заряженных частиц.

Энергия взаимодействия

вовсе не зависит от $l$. При v_F ~ 10⁶ м/с и вблизи плазмонных частот энергия U порядка десятков эВ. Этого вполне достаточно для вылета иона за пределы металла. Таким образом, достаточно возбудить плазмон за счет неупругого рассеяния налетающей частицы, далее все происходит согласно модели. Энергии взаимодействия иона решетки с флуктуацией электронной плотности на границе металла с избытком хватает для отрыва иона.

Зависимость сечения возбуждения плазмона от параметра kl = 2πl/λ или от обратной длины волны плазмона при μ = 5 для ξ = 0.05, 0.1 и 0.2 представлена на рис. 3. С ростом параметра kl сечение возбуждения плазмона снижается; при kl ~ 1 оно еще довольно велико; при значениях kl $ \ll $ 1 плазмон сильно затухает за счет распада на одночастичные электронно-дырочные возбуждения. Другими словами, существует область частот (или длин волн) плазмона, отвечающая условию kl ≈ 1, при которых и плазмон эффективно возбуждается, и его затухание невелико.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Как можно заметить, сечение рассеяния зависит только от величины заряда падающей частицы и не зависит от ее массы. Параметр ξ при l в диапазоне 0.01–0.1 мкм и ω₀ ≈ 10¹⁶ с^–1 меняется от единицы до десяти. Следовательно, σ/S ~ 10^–1–10^–2. Из определения сечения рассеяния следует, что число N рассеянных электронов или ионов связано с числом падающих N₀ соотношением N = N₀σ/S. Каждый акт рассеяния заряженной частицы с вероятностью, определяемой сечением рассеяния, сопровождается рождением плазмона. В свою очередь, рождение плазмона, как следует из приведенных оценочных выражений, эквивалентно вылету атома из металла. Следовательно, величина N определяет число “испарившихся” атомов. Как нетрудно увидеть, на каждые 10²–10³ налетающих заряженных частиц приходится примерно один вылетающий атом. Таким образом, предложенная модель адекватно описывает представленные в работе экспериментальные результаты.