Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 8, стр. 64-72

Наношероховатость технических поверхностей: статистический анализ

В. В. Измайлов^a, *, М. В. Новоселова^a

^a Тверской государственный технический университет
170026 Тверь, Россия

Поступила в редакцию 20.06.2021
После доработки 25.08.2021
Принята к публикации 29.08.2021

EDN: CRKZKW
DOI: 10.31857/S1028096022050119

Аннотация

Обосновывается применимость модели стационарного случайного процесса к профилю субшероховатости (наношероховатости) технических поверхностей. Проведена проверка нормальности распределения ординат профиля наношероховатости с помощью критериев согласия Пирсона и Лиллиефорса. Рассчитаны автокорреляционные функции и спектральные плотности исследуемых процессов, а также интервал корреляции и эффективная ширина спектра. На примерах показана возможность расчета параметров профиля наношероховатости поверхности на основании автокорреляционной функции. Расчетные значения параметров совпадают с экспериментальными в пределах погрешности.

Ключевые слова: наношероховатость, профиль наношероховатости, случайный процесс, автокорреляционная функция, спектральная плотность, интервал корреляции.

ВВЕДЕНИЕ

В отличие от математической поверхности, которая представляет собой абстрактное понятие и считается абсолютно гладкой, физическая поверхность (поверхность твердого тела) обладает рельефом. Традиционно составляющими рельефа физической поверхности считаются шероховатость и волнистость (ГОСТ Р ИСО 25 178-2-2014). Однако в настоящее время в числе составляющих рельефа поверхности дополнительно выделяют так называемую субшероховатость – совокупность неровностей наномасштабного размера [1–3]. Хотя нормативные документы (например, вышеупомянутый стандарт) не делают различия между шероховатостью и субшероховатостью, к ее выделению в качестве равноправной составляющей рельефа поверхности имеются все основания. Во-первых, субшероховатость (наношероховатость) и традиционная шероховатость (микрошероховатость) отличаются по своей природе. Микрошероховатость является результатом воздействия на поверхность детали обрабатывающего инструмента (резца, абразивного зерна, электрической искры). Наношероховатость в основном обусловлена особенностями строения твердого тела: формой и размерами кристаллитов, островковыми пленками [1]. Во-вторых, для измерения и контроля субшероховатости и микрошероховатости используют разные технические средства. Наиболее распространенными средствами измерения микрошероховатости являются оптические и стилусные электромеханические устройства (профилографы и профилометры). Разрешающая способность оптических средств по амплитуде – порядка 10 нм, стилусных электромеханических – несколько десятков нанометров [1, 2, 4]. Для измерения субшероховатости используют сканирующую туннельную микроскопию и атомную силовую микроскопию с разрешающей способностью на порядок выше.

Следуя [1, 2], будем считать субшероховатостью элементы рельефа поверхности высотой от 1–2 до 25–30 нм. Верхний предел соответствует минимальным размерам неровностей поверхностей, на которые распространяются стандарты на параметры шероховатости [1, 2, 5]. В масштабах менее 1 нм начинает проявляться дискретность строения твердого тела (для сравнения: постоянная кристаллической решетки металлов – десятые доли нанометра), поэтому многие постулаты и модели механики сплошных сред утрачивают силу.

Одним из плодотворных и перспективных подходов к описанию микрошероховатости является статистический, согласно которому поверхность детали рассматривается как случайное поле, а профиль поверхности – как реализация стационарного нормального случайного процесса [6–8].

Цель настоящей работы – обосновать применимость статистической модели профиля технической поверхности как случайного процесса к гораздо менее изученной субшероховатости и на примерах проиллюстрировать возможности этой модели для оценки параметров субшероховатости.

ОБРАЗЦЫ И МЕТОДИКА ИССЛЕДОВАНИЯ

В качестве объектов исследования были выбраны поверхности плоских металлических образцов, изготовленных из циркония и легированной хромистой стали. При выборе материалов учитывали их высокую коррозионную стойкость. Так, на поверхности циркония образуется оксидная пленка толщиной несколько нанометров, которая надежно защищает поверхность от дальнейшего взаимодействия с атмосферой. На поверхности коррозионностойкой хромистой стали аналогичную функцию выполняет тонкая пленка оксида хрома. Вследствие малой толщины такие поверхностные пленки минимально искажают исходную топографию поверхности.

Непосредственным объектом исследования являлись профилограммы исследуемых поверхностей, полученные с помощью атомного силового микроскопа фирмы NT-MDT. Профилограмму рассматривают как реализацию случайного процесса z(x), где z – ордината профиля, отсчитанная от его средней линии; x – координата, направленная вдоль средней линии профиля. Некоторые точечные параметры субшероховатости по ГОСТ 25 142-82 (в редакции 2017 г.) приведены в табл. 1.

Таблица 1.

Некоторые параметры субшероховатости исследованных поверхностей

Параметр	Материал образца
Параметр	Сталь	Цирконий
Среднее арифметическое отклонение профиля R_a, нм	2.2	1.7
Среднеквадратичное отклонение профиля R_q, нм	2.9	2.1
Средний шаг неровностей профиля S_m, мкм	0.18	0.28

При цифровой обработке профилограмм непрерывную функцию z(x) представляют конечным набором N дискретных значений ординаты профиля, соответствующих значениям аргумента x = 0, Δx, 2Δx, … NΔx, где Δx – шаг дискретизации. Чтобы при дискретизации непрерывной функции z(x) не терять информацию о ее спектральном составе, спектры исходной функции и ее дискретного представления должны содержать одинаковый набор частот. Для этого шаг дискретизации должен соответствовать условию:

(1)

$\Delta x \leqslant \frac{1}{{2{{f}_{{{\text{max}}}}}}},$

где f_max – максимальная частота в спектре [9]. Согласно [1, 4] нижняя граница шагов (длин волн) наношероховатости – порядка 0.1 мкм, что соответствует максимальной пространственной частоте 10 мкм^–1. При f_max = 10 мкм^–1 шаг дискретизации Δx согласно уравнению (1) не должен превышать 0.05 мкм. При обработке профилограмм наношероховатости в настоящей работе использовали шаг дискретизации Δx = 0.035 мкм.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Как отмечалось выше, модель профиля шероховатой поверхности в виде реализации случайного процесса основана на определенных предпосылках. В первую очередь это стационарность и нормальность процесса. Во многих случаях полезным является такое свойство случайного процесса, как эргодичность. Приводимые ниже результаты подтверждают справедливость указанных предпосылок для профилограмм субшероховатости поверхностей.

Стационарность процесса

Любой реальный процесс, строго говоря, не стационарен из-за своей конечной длительности. Поэтому говорить о стационарности такого процесса можно только приближенно. Фактически стационарность процесса (в данном случае профиля поверхности на наномасштабном уровне) на некотором его ограниченном участке принимается как постулат, базирующийся на информации о физической природе поверхности и условиях ее формирования [9, 10]. Успешный опыт применения корреляционно-спектрального анализа к самым разным по физической природе случайным процессам, в том числе к микрогеометрии поверхностей, дает основания распространить этот постулат и на профиль субшероховатости.

Для стационарных процессов в широком смысле [9, 11] математическое ожидание и дисперсия постоянны (точнее, не зависят от момента начала отсчета времени или координаты x в случае профилограммы поверхности). Постоянство математического ожидания профиля субшероховатости обеспечивается автоматически, поскольку профиль является центрированным случайным процессом (математическое ожидание равно нулю). Проверка дисперсии исследованных профилограмм на наличие тренда [9] показала отсутствие его статистически значимых значений. Еще одно требование, которому должен удовлетворять стационарный случайный процесс, касается его автокорреляционной функции.

Проверка нормальности процесса

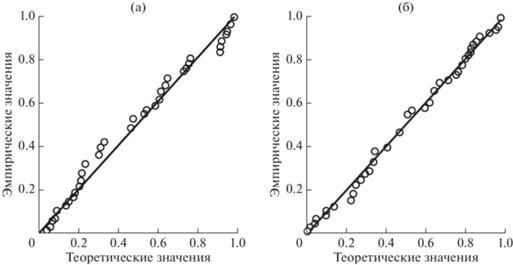
Проверка состоит в оценке достоверности гипотезы о нормальном распределении ординат профиля z_i. Быстрая и наглядная проверка осуществляется с помощью графического сравнения теоретической и эмпирической функций распределения (рис. 1). Процедура построения графиков, следующая [12]. Сначала все элементы выборки z_i ранжируются. Для каждого j-го ранга вычисляются значения

${{z}_{j}} = \sigma {{F}^{{ - 1}}}\left( {\frac{{3j - 1}}{{3N + 1}}} \right),$

где σ ≡ R_q – среднеквадратичное отклонение ординат профиля, F ^–1 – обратная функция стандартного нормального распределения, N – общее число элементов выборки. Ранжированные наблюдаемые (эмпирические) значения z_i отложены по оси ординат, соответствующие расчетные (теоретические) значения z_j – по оси абсцисс. Точки на графике достаточно хорошо ложатся на прямую линию с незначительными отклонениями, носящими случайный характер. Это дает основание считать распределение ординат профиля близким к нормальному.

Рис. 1.

Эмпирическая и теоретическая функции распределения ординат профиля поверхности образцов: циркония (а); стали (б).

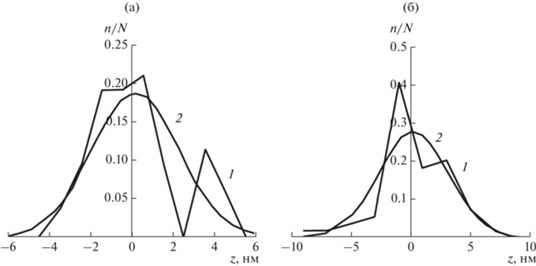
Еще один наглядный способ проверки соответствия теоретического и эмпирического распределения ординат профиля состоит в сравнении полигонов частот случайной величины z_i с графиком плотности нормального распределения при математическом ожидании, равном нулю и соответствующем среднеквадратичном отклонении (табл. 1). Такое сравнение приведено на рис. 2.

Рис. 2.

Полигоны частот (1) и теоретические функции плотности нормального распределения (2) для образцов: циркония (а); стали (б). n/N – частность.

Более строгая проверка соответствия распределения случайной величины z_i нормальному закону выполнена с помощью критериев согласия. В работе использовали критерий χ² Пирсона и критерий Лиллиефорса [13]. Критерий Лиллиефорса – это не что иное, как скорректированный критерий Колмогорова–Смирнова. Оба критерия используют одну и ту же статистику

$D = \mathop {\sup }\limits_{ - \infty {\kern 1pt} < {\kern 1pt} x{\kern 1pt} < {\kern 1pt} \infty } \left| {{{{\hat {F}}}_{n}}\left( x \right) - F\left( x \right)} \right|~,$

где ${{\hat {F}}_{n}}\left( x \right)$ и F(x) – эмпирическая и теоретическая функции распределения. Различие состоит в том, что Лиллиефорс скорректировал критические значения критерия Колмогорова–Смирнова в сторону ужесточения. Это связано с тем, что критерий Колмогорова–Смирнова применим только в том случае, когда параметры распределения случайной величины известны заранее. На практике чаще всего параметры распределения случайной величины, принадлежащей некоторой выборке, определяются на основе этой же выборки, что увеличивает вероятность ошибки второго рода (принятие неверной нулевой гипотезы). Ужесточение критических значений критерия компенсирует это увеличение. По этой же причине происходит аналогичное ужесточение критических значений критерия Пирсона за счет уменьшения числа степеней свободы на величину, равную количеству вычисляемых параметров распределения [11].

Значения статистик критериев Пирсона и Лиллиефорса для исследованных профилограмм приведены в табл. 2. Там же приведены критические значения критериев ${{\chi }}_{{0.1}}^{2}$ и D_0.1 для уровня значимости p = 0.1 [13, 14]. Нулевая гипотеза (о нормальном распределении ординат профиля субшероховатости) отклоняется, если значения соответствующих статистик превышают их критические значения. Как видно из табл. 2, на уровне значимости p = 0.1 можно считать, что нулевая гипотеза не противоречит экспериментальным данным, и нет оснований отклонить ее.

Таблица 2.

Критерии согласия

Материал образца	Значения статистик
	Пирсона		Лиллиефорса
	χ²	${{\chi }}_{{0.1}}^{2}$	D	D_0.1
Цирконий	2.69	6.25	0.109	0.112
Сталь	1.30	4.60	0.096	0.109

Автокорреляционные функции

Автокорреляционные функции исследуемых профилограмм, представленных после процедуры дискретизации массивом дискретных значений ординат профиля z_i, вычисляли по формуле:

(2)

${{K}_{z}}\left( {i\Delta x} \right) = \frac{1}{{N - i}}\sum\limits_{k\,{\kern 1pt} = \,{\kern 1pt} 1}^{N{\kern 1pt} - {\kern 1pt} i} {{{z}_{k}}{{z}_{{k{\kern 1pt} \, + \,{\kern 1pt} i}}}} ,\,\,\,\,i = 0,1, \ldots m,$

где N – общее число ординат, i – номер шага, m – число шагов [9] (m < N). Очевидно, что K_x(0) есть не что иное, как дисперсия случайного процесса. Более наглядно и удобно для анализа представление автокорреляционной функции в безразмерной (нормированной) форме. Нормированную функцию вычисляли по формуле:

(3)

${{\rho }_{z}}\left( {i\Delta x} \right) = \frac{{{{K}_{z}}\left( {i\Delta x} \right)}}{{{{K}_{z}}\left( 0 \right)}}.$

Как видно из уравнений (2) и (3), автокорреляционная функция профилограмм зависит не от значения координаты х, а от лага (интервала) Δx = = x_i _{+ 1} – x_i. Это обстоятельство является одним из условий стационарности случайного процесса наряду с требованием постоянства математического ожидания. Применяя это уравнение, мы фактически постулируем стационарность профиля субшероховатости как случайного процесса.

Для компенсации погрешности, вносимой в оценку автокорреляционной функции конечной длительностью случайного процесса, используют сглаживание с помощью так называемых оконных функций (или просто окон) [15]. Была использована одна из версий окна Блэкмана–Хэрриса – так называемое окно Наттолла [15, 16]:

(4)

$\begin{gathered} w(i) = {{a}_{0}} + {{a}_{1}}\cos \left( {2\pi \frac{i}{m}} \right) + {{a}_{2}}\cos \left( {4\pi \frac{i}{m}} \right) + \\ + \,\,{{a}_{3}}\cos \left( {6\pi \frac{i}{m}} \right), \\ \end{gathered} $

где a₀, a₁, a₂, a₃ – коэффициенты, i = 0…m/2. В работе брали следующие значения коэффициентов [15]: a₀ = 0.3635819, a₁ = 0.4891775, a₂ = 0.1365995 и a₃ = 0.0106411. С учетом формул (2)–(4) расчетная формула для автокорреляционной функции приобретает вид:

(5)

$\rho _{z}^{*}\left( {i\Delta x} \right) = {{\rho }_{z}}\left( {i\Delta x} \right)w\left( i \right).$

Графики сглаженных автокорреляционных функций профилограмм исследованных поверхностей представлены на рис. 3. Характер графиков функций профилограмм субшероховатости подобен характеру аналогичных графиков для микрошероховатости технических поверхностей [5–7]. Согласно [7] такая автокорреляционная функция может быть аппроксимирована функциями вида

(6)

${{\rho }_{{{\text{теор}}}}} = \frac{{{\text{cos}}\left( {{{\omega }_{0}}x} \right)}}{{1 + \alpha {{x}^{2}}}},$

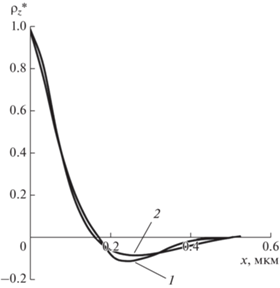
где ω₀ – пространственная циклическая частота, α – коэффициент, характеризующий затухание автокорреляционной функции [7]. Из уравнения (6) видно, что при α → 0 функция имеет вид синусоиды. Это означает, что профиль поверхности также является периодической функцией координаты x. При α → ∞ автокорреляционная функция вырождается в δ-функцию: она отлична от нуля только при x = 0 и равна нулю для всех x > 0, ординаты профиля некоррелированы, т.е. профиль поверхности фактически представляет собой белый шум.

Рис. 3.

Автокорреляционная функция профилограмм субшероховатости поверхности образцов: циркония (а); стали (б).

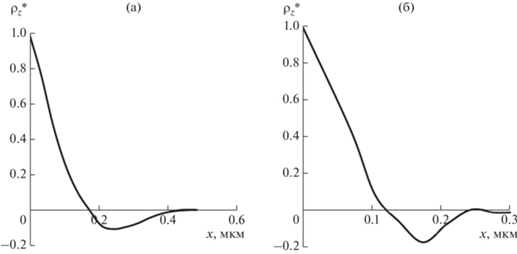
Для нахождения параметров аппроксимации ω₀ и α можно использовать так называемые особые точки профиля: нули (пересечения со средней линией) и максимумы. Важным параметром случайного процесса является величина

$\lambda = \frac{{{{n}_{0}}}}{{{{m}_{S}}}},~$

где n₀ и m_S – соответственно, среднее число нулей и среднее число максимумов на единице длины профилограммы [7]. Этот параметр характеризует степень случайности процесса. Значение λ = 0 соответствует хаотическому, сильно “изрезанному” профилю, для которого при конечном значении n₀ величина m_S → ∞ (множество максимумов между соседними нулями), значение λ = 2 (один максимум между соседними нулями) – гладкому периодическому профилю типа синусоиды. Для исследованных профилограмм в основном значения λ лежат в интервале 0.9 ≤ λ ≤ 1.1, соответственно, 128 ≤ α ≤ 206 и 9.6 ≤ ω₀ ≤ 15.7. Более точно параметры α и ω₀ определяли методом наименьших квадратов. Например, для циркониевых образцов α = 126 мкм^–2, ω₀ = 9.5 мкм^–1. Для сравнения экспериментальная сглаженная и аппроксимированная автокорреляционные функции приведены на рис. 4.

Рис. 4.

Экспериментальная сглаженная автокорреляционная функция (1) и ее аппроксимация (2).

Интервал корреляции

С помощью автокорреляционной функции можно найти важный параметр, характеризующий случайный процесс, – так называемый интервал корреляции x_c. Физический смысл этой величины в том, что при x ≥ x_c ординаты профиля можно считать некоррелированными. К сожалению, не существует единого общепринятого определения интервала корреляции. Соответственно, значения этого параметра могут заметно отличаться в зависимости от способа его определения. Рассмотрим наиболее часто используемые способы определения интервала корреляции [7, 17].

Способ 1. Величина x_c определяется через нормированную автокорреляционную функцию из условия:

(7)

${{x}_{c}} = \int\limits_0^\infty {{{\rho }_{z}}\left( x \right)dx} .$

Подставляя в формулу (7) автокорреляционную функцию в виде аппроксимирующей формулы (6) и выполняя интегрирование, получаем для циркониевого образца при α = 126 мкм^–2 и ω₀ = 9.5 мкм^–1 величину x_c = 0.06 мкм.

Способ 2 аналогичен первому с небольшим изменением условия определения x_c:

(8)

${{x}_{c}} = \int\limits_0^\infty {\left| {{{\rho }_{z}}\left( x \right)} \right|dx} .$

В этом случае для того же образца x_c = 0.1.

Способ 3. Величина x_c определяется из условия |ρ(x)| ≤ ε для всех x ≥ x_c. Здесь ε – некоторая сколь угодно малая положительная величина. Например, при ε = 0.05 для циркониевого образца x_c = = 0.37 мкм. Недостаток этого способа в достаточно произвольном выборе критерия ε, от которого величина x_c зависит существенно.

Способ 4. Интервал корреляции x_c принимают равным расстоянию, на котором нормированная автокорреляционная функция уменьшается в e раз [1]:

$\rho \left( {{{x}_{c}}} \right) = \frac{{\rho \left( 0 \right)}}{e}.$

Рассчитанная этим способом величина x_c ≈ ≈ 0.08 мкм. В данном случае она аналогична по смыслу широко применяемой характеристике затухания самых различных физических процессов, известной под названиями “время релаксации”, “постоянная времени”.

Эргодичность профиля субшероховатости

Многие стационарные случайные процессы обладают свойством эргодичности. Математическое ожидание и автокорреляционную функцию эргодического процесса можно определять по одной достаточно длинной реализации вместо их усреднения по множеству реализаций. Достаточным условием эргодичности случайного процесса по отношению к математическому ожиданию является следующее [6, 9]:

$\mathop {\lim }\limits_{x{\kern 1pt} \to {\kern 1pt} \infty } \rho \left( x \right) = 0.$

Как видно из рис. 3 и уравнения (6), для исследованных поверхностей это условие выполняется.

Очевидно, что для надежного определения характеристик процесса по одной реализации ее длина L должна быть во много раз больше интервала корреляции x_c. Например, для параметра R_a требуемую длину реализации L можно оценить по формуле, полученной на основании обобщения результатов [6, 7, 9, 10]:

$L \geqslant \frac{{{{x}_{c}}}}{{2\varepsilon _{r}^{2}}},$

где x_c – интервал корреляции, рассчитанный способом 1, ε_r – относительная среднеквадратичная погрешность. В качестве примера оценим требуемую длину реализации L для субшероховатости поверхности циркониевого образца. Принимая ε_r = 0.1 и x_c ≈ 0.06 мкм, получаем L ≥ 50x_c ≈ 3 мкм. Следует отметить, что применительно к профилограмме поверхности величина L может быть ограничена возможностями измерительной аппаратуры (профилографа или атомно-силового микроскопа).

Спектральная плотность

Наряду с автокорреляционной функцией спектральная плотность является важным параметром случайного процесса, характеризующим его спектральный состав. Автокорреляционная функция и спектральная плотность однозначно связаны преобразованиями Фурье [9].

Выражение нормированной автокорреляционной функции через аналитическую зависимость (6) позволяет представить нормированную спектральную плотность в виде аналитического выражения [7]:

(8)

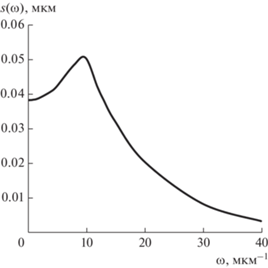
$s\left( \omega \right) = \frac{1}{{2\sqrt \alpha }}\left[ {\exp \left( { - \frac{{\omega + {{\omega }_{0}}}}{{\sqrt \alpha }}} \right) + \exp \left( { - \frac{{\left| {\omega - {{\omega }_{0}}} \right|}}{{\sqrt \alpha }}} \right)} \right]{\kern 1pt} {\kern 1pt} .$

Очевидно, при α → 0 (автокорреляционная функция – периодическая функция с частотой ω₀) спектральная плотность вырождается в δ-функцию при ω = ω₀. При α → ∞ (автокорреляционная функция представляет собой δ-функцию) $s\left( \omega \right) \to \frac{1}{{\sqrt \alpha }},$ т.е. спектральная плотность становится постоянной, что характерно для белого шума.

Нормированная спектральная плотность профиля наношероховатости поверхности циркониевого образца представлена на рис. 5 для приведенных выше значений α и ω₀. Для спектральной плотности существует параметр, связанный с интервалом корреляции для автокорреляционной функции. Это так называемая эффективная ширина спектра. Она определяется следующим выражением [9, 17]:

(9)

$\Delta {{\omega }_{{{\text{эф}}}}} = \frac{1}{{s\left( 0 \right)}}\int\limits_0^\infty {s\left( \omega \right)d\omega {\kern 1pt} {\kern 1pt} } {\text{.}}$

Поскольку для нормированной спектральной плотности интеграл в правой части уравнения (9) равен единице (это площадь под кривой s(ω)), получаем:

$\Delta {{\omega }_{{{\text{эф}}}}} = {1 \mathord{\left/ {\vphantom {1 {s\left( 0 \right)}}} \right. \kern-0em} {s\left( 0 \right)}}.$

При s(0) = 0.038 (рис. 5) имеем Δω_эф = 26.3 мкм^–1.

Рис. 5.

Нормированная спектральная плотность профиля поверхности циркониевого образца.

Связь интервала корреляции x_c, определенного по формуле (7), и эффективной ширины спектра Δω_эф состоит в том, что они подчиняются своеобразному соотношению неопределенностей: x_cΔω_эф = π/2 [17]. Таким образом, чем больше эффективная ширина спектра (больший набор частот присутствует в спектральном составе случайного процесса), тем раньше (при меньших значениях x) ординаты профиля становятся некоррелированными. При x_c = 0.06 мкм и Δω_эф = = 26.3 мкм^–1 произведение x_cΔω_эф = 1.578 ≈ π/2.

Некоторые статистические соотношения для наношероховатости поверхности

Представление профилограммы наношероховатости поверхности в виде нормального стационарного случайного процесса позволяет рассчитывать параметры наношероховатости, определение которых иными способами достаточно трудоемко. Приведем некоторые примеры.

Радиус кривизны вершин неровностей профиля. Моделирование неровностей микро- и наношероховатости сферическими сегментами достаточно распространено в механике контактного взаимодействия и трибологии [2, 18, 19]. Очевидно, что одним из ключевых параметров шероховатости в этом случае становится радиус кривизны вершин неровностей. Определение этого параметра непосредственно с помощью профилограммам по методике [19, 20] трудоемко. На основании рассматриваемого статистического подхода средний радиус кривизны вершин неровностей профиля можно легко рассчитать по формуле [7]:

(10)

$r = \frac{{\lambda \sqrt {2\pi } }}{{4{{\pi }^{2}}{{R}_{q}}n_{0}^{2}}}.$

Все параметры, входящие в формулу (10), определены выше. При λ ≈ 1, n₀ = 2/Sm ≈ 7 мкм^–1 и R_q = = 2.1 нм для наношероховатости поверхности циркониевого образца получаем r ≈ 620 нм. Экспериментально по традиционной методике [19, 20] получено значение r = 590 ± 180 нм. Как видим, в пределах погрешности расчетное и экспериментальное значения среднего радиуса кривизны неровностей наношероховатости совпадают.

Средний угол наклона боковых сторон выступов. Среднее значение тангенса угла наклона боковых сторон выступов можно оценить по формуле [7]:

(11)

${\text{tg}}\theta \approx \frac{4}{3}\sqrt {2\pi } {{R}_{q}}{{n}_{0}}.$

Для наношероховатости поверхности циркониевого образца при R_q = 2.1 нм и n₀ = 7 мкм^–1 расчет по формуле (11) дает величину tg θ = 0.05, что соответствует значению θ = 3°. Экспериментальное значение tg θ = 0.054 ± 0.008. Как видим, в пределах погрешности экспериментальная и теоретическая величины tg θ совпадают.

Максимальная высота пика профиля R_p. Из-за экстремального характера этого параметра точность его определения традиционными методами по профилограммам невысока. На основании статистической модели профиля поверхности как случайного процесса этот параметр можно рассчитать по формуле [7]:

(12)

${{R}_{p}} \approx {{R}_{q}}\sqrt {2\ln \frac{{{{l}_{n}}{{n}_{0}}}}{2}} \left( {1 + \frac{{0.289}}{{\ln \frac{{{{l}_{n}}{{n}_{0}}}}{2}}}} \right),$

где l_n – длина оценки (длина трассы измерения наношероховатости). Для наношероховатости поверхности циркониевого образца при l_n = 2 мкм и n₀ = 7 мкм^–1 расчет по формуле (12) дает величину R_p = 2.26R_q = 4.76 нм. Экспериментальное значение, полученное усреднением по пяти профилограммам, R_p = 4.1 ± 0.8 нм. В пределах погрешности экспериментальная и теоретическая величины R_p совпадают.

ЗАКЛЮЧЕНИЕ

На примере двух технических поверхностей показана применимость модели стационарного случайного процесса к профилю субшероховатости (наношероховатости) этих поверхностей. С помощью критериев согласия показано, что ординаты профиля подчиняются нормальному закону распределения. Полная информация о стационарном нормальном процессе содержится в его автокорреляционной функции и математическом ожидании. Поскольку профиль поверхности является случайным центрированным процессом (математическое ожидание равно нулю), все основные параметры профиля можно рассчитать на основании автокорреляционной функции. Приведены примеры расчета радиуса кривизны вершин неровностей профиля, среднего наклона боковых сторон выступов и максимальной высоты пика профиля. Расчетные значения сопоставлены с экспериментальными, выполненными по традиционным методикам, более трудоемким. В пределах погрешности экспериментальные значения совпадают с расчетными.

Список литературы

Григорьев А.Я. Физика и микрогеометрия технических поверхностей. Минск: Беларуская навука, 2016. 247 с.
Мышкин Н.К., Петроковец М.И. Трение, смазка, износ. Физические основы и технические приложения трибологии. М.: ФИЗМАТЛИТ, 2007. 368 с.
Измайлов В.В., Новоселова М.В. // Физико-химические основы изучения кластеров, наноструктур и наноматериалов. 2018. Вып. 10. С. 313. https://doi.org/10.26456/pcascnn/2018.10.313
Лич Р. Инженерные основы измерений нанометровой точности. Долгопрудный: Издательский Дом “Интеллект”, 2012. 400 с.
Уайтхауз Д. Метрология поверхностей. Принципы, промышленные методы и приборы. Долгопрудный: Издательский Дом “Интеллект”, 2009. 472 с.
Хусу А.П., Витенберг Ю.Р., Пальмов В.А. Шероховатость поверхностей (теоретико-вероятностный подход). М.: Наука, 1975. 344 с.
Рудзит Я.А. Микрогеометрия и контактное взаимодействие поверхностей. Рига: Зинатне, 1975. 210 с.
Thomas T.R. Rough Surfaces. London: Imperial College Press, 1999. 278 p.
Бендат Дж., Пирсол А. Прикладной анализ случайных данных. М.: Мир, 1989. 540 с.
Дунин-Барковский И.В., Карташова А.Н. Измерения и анализ шероховатости, волнистости и некруглости поверхности. М.: Машиностроение, 1978. 232 с.
Вентцель Е.С. Теория вероятностей. М.: Высшая школа, 2006. 575 с.
Боровиков В. STATISTICA: искусство анализа данных на компьютере. СПб.: ПИТЕР, 2001. 656 с.
Lilliefors H.W. // J. Am. Stat. Association. 1967. V. 62. Iss. 318. P. 399.
Gibbons J.D., Chakraborti S. Nonparametric Statistical Inference. Marcel Dekker, 2003. 646 p.
Дворкович В.П., Дворкович А.В. Оконные функции для гармонического анализа сигналов. М.: Техносфера, 2019. 208 с.
Хэррис Ф.Дж. // ТИИЭР. 1978. Т. 66. № 1. С. 60.
Романенко А.Ф., Сергеев Г.А. Вопросы прикладного анализа случайных процессов. М.: Советское радио, 1968. 256 с.
Попов В.Л. Механика контактного взаимодействия и физика трения. От нанотрибологии до динамики землетрясений. М.: ФИЗМАТЛИТ, 2013. 352 с.
Измайлов В.В., Новоселова М.В. Контакт твердых тел и его проводимость: монография. Тверь: ТГТУ, 2010. 112 с.
Измайлов В.В., Новоселова М.В. // Физико-химические основы изучения кластеров, наноструктур и наноматериалов. 2020. Вып. 12. С. 609. https://doi.org/10.26456/pcascnn/2020.12.609

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал