Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 8, стр. 56-63
Статистическая модель дискретных процессов многократного рассеяния заряженных частиц в слое вещества
Н. Н. Михеев *
Институт кристаллографии им. А.В. Шубникова ФНИЦ “Кристаллография и фотоника” РАН
119333 Москва, Россия
* E-mail: kmikran@spark-mail.ru
Поступила в редакцию 26.07.2021
После доработки 29.09.2021
Принята к публикации 07.10.2021
- EDN: BTOJMZ
- DOI: 10.31857/S1028096022060127
Аннотация
Представлены результаты использования принципиально нового подхода для описания дискретных процессов многократного рассеяния направленного пучка протонов в слое вещества. В качестве базового параметра используется среднее число взаимодействий, которые частицы испытали в пленке известной толщины. Это позволяет эффективно рассчитывать энергетические и угловые распределения прошедших пленку быстрых частиц в форме, соответствующей экспериментальным спектрам.
ВВЕДЕНИЕ
Для нанотехнологий и большого числа количественных локальных методов исследования, которые используют направленные электронные и ионные пучки, распределения заряженных частиц по энергии и углу являются важнейшими характеристиками. Именно они определяют возможности как проведения контролируемого технологического воздействия на материал, так и эффективность экспериментальной диагностики свойств материала с высоким пространственным разрешением. В рамках традиционно используемой исследователями базовой концепции непрерывного торможения пучка частиц в веществе [1–4] удовлетворительной теории, позволяющей выполнять расчеты таких распределений, соответствующих экспериментально измеряемым спектрам, не создано. Как правило, используется громоздкий массив табулированных данных, основанный на аппроксимации усредненных, так называемых “наиболее достоверных”, экспериментальных измерений [5–7].
В [8–10] впервые были сформулированы базовые положения новой статистической модели дискретного процесса многократного неупругого рассеяния направленного пучка электронов в веществе. И в дальнейшем они успешно использовались при проведении расчетов информативных сигналов для рентгеноспектрального микроанализа [11–13] и для количественных методов растровой электронной микроскопии [14–16].
В настоящей работе представлены результаты практического применения этой новой модели дискретных процессов многократного рассеяния для решения задач аналитического описания энергетических и угловых спектральных распределений пучков быстрых протонов и альфа-частиц, прошедших пленочную мишень заданной толщины. В двухпотоковом приближении получена формула для расчета наиболее вероятной энергии пучка частиц после прохождения пленки известной толщины, получены формулы для расчета глубины проникновения частиц в вещество при нормальном падении пучка на образец и для расчета транспортной длины в канале неупругого рассеяния. Проведена их проверка на соответствие имеющимся в научных публикациях экспериментальным данным.
ОСНОВНЫЕ ПОЛОЖЕНИЯ СТАТИСТИЧЕСКОЙ МОДЕЛИ ТРАНСПОРТА БЫСТРЫХ ПРОТОНОВ В КОНДЕНСИРОВАННОМ ВЕЩЕСТВЕ ПРИ МНОГОКРАТНОМ РАССЕЯНИИ
Кратко отметим основные положения модели, чтобы учесть те характерные для положительно заряженных и более тяжелых протонов и альфа-частиц особенности, которые существенно отличают их поведение от электронов при транспорте в пленочной мишени.
Неупругое рассеяние – вероятностный процесс. Для протонов и альфа-частиц с кинетической энергией более 1 кэВ на единицу атомной массы доминирующим каналом потерь энергии является неупругое рассеяние на электронах [5]. В статистике многократного рассеяния из числа всех возможных потерь энергии учитывают лишь однократные вероятностные потери энергии εi. Они малы, и величина εi много меньше первичной энергии пучка E0. Для них характерны и наиболее вероятная потеря энергии εp, и максимальная однократная потеря εmax. Ее величина заметно отличается от возможной максимальной потери энергии. Например, быстрый электрон может потерять всю кинетическую энергию в результате однократного акта – торможения в поле ядра атома (тормозное излучение), он может потерять значительную часть своей энергии на ионизацию электронов. Но вероятная однократная потеря энергии, как показано в [10], не превышает всего 0.0625E0 на всех этапах движения частицы в образце. Для протонов при скорости V0 величина однократной потери энергии ограничена сверху значением $2{{m}_{e}}V_{0}^{2},$ что соответствует лобовому столкновению с электроном. Понятно, что это событие возможное, но крайне маловероятное, и поэтому максимальную однократную потерю энергии протонов полагаем далее равной ${{m}_{e}}V_{0}^{2}.$
Всякому многократному рассеянию заряженных частиц в веществе предшествует однократное рассеяние каждой частицы и далее кратное рассеяние. Возможность использования статистической модели для такого рода процессов вытекает из простого соотношения для однократного взаимодействия, которое для быстрого протона принимает следующий вид:
(1)
$\frac{{{{m}_{e}}}}{{{{M}_{p}}}}\left[ {E_{0}^{2} - E_{p}^{2}\left( 1 \right)} \right] = {{J}^{2}},$(2)
$\frac{{{{m}_{e}}}}{{{{M}_{p}}}}\left[ {E_{0}^{2} - E_{p}^{2}\left( n \right)} \right] = {{J}^{2}}\ln \left( {n!} \right).$(3)
$\ln \left( {n!} \right) \approx \left( {n + \frac{1}{2}} \right)\ln n - n + \ln \sqrt {2\pi } ,$(4)
$\frac{{{{m}_{e}}}}{{{{M}_{p}}}}\left[ {E_{0}^{2}\, - E_{p}^{2}} \right] = n{{J}^{2}}\ln \left( {\frac{n}{e}} \right),$Такой подход впервые позволяет однозначно и точно определить среднее число n неупругих взаимодействий, после которых процесс кратного рассеяния для потока заряженных частиц заканчивается. Процесс неупругого рассеяния становится процессом многократного рассеяния, когда составляющая статистической вероятности в виде логарифмического члена формулы (4) становится больше единицы, и это отражает тот факт, что данное состояние (суммарная, наиболее вероятная потеря энергии ∆Ep) может быть реализовано несколькими путями, и поэтому его вероятность ненамного, но возросла. По формуле Стирлинга в (4) это число легко определяется, и оно равно шести.
С увеличением толщины пленки и ростом числа n = εmax/εp наступает момент, когда составляющая статистической вероятности, которая отражена логарифмическим членом в (4), достигает своего максимума при εmax = ${{m}_{e}}V_{0}^{2}.$ Дальнейший рост толщины пленки, числа взаимодействий и суммарных потерь энергии протонами будет связан только с возрастанием члена nJ 2 в (4). Поэтому эту формулу можно записать в виде:
(5)
$\frac{{{{m}_{e}}}}{{{{M}_{p}}}}\left[ {E{}_{0}^{2}\, - E_{p}^{2}} \right] = n{{J}^{2}}\ln \left( {\frac{k}{{{{e}^{{{k \mathord{\left/ {\vphantom {k n}} \right. \kern-0em} n}}}}}}} \right),$Формулы (1)–(5) получены в предположении, что в неупругом рассеянии равновероятно принимают участие все Z электронов вещества мишени. В действительности же необходимо учитывать реальность пространственного распределения электронов внутри атома. Известно, что большая часть электронов атома с номером Z находится на расстояниях от ядра порядка аБZ–1/3 (аБ = 0.529 Å − боровский радиус). Численный расчет показывает, что половина полного электрического заряда атома находится внутри сферы радиуса r0.5 = 1.33аБZ–1/3 [17]. Поэтому в тонких слоях, толщина x которых много меньше транспортного пробега Ltr, неупругое взаимодействие быстрой заряженной частицы с большей вероятностью будет происходить с той половиной полного заряда атома, которая находится вне области радиуса r0.5. Это приводит к формированию двух групп первичных частиц: испытавших неупругое рассеяние только на Z/2 внешних электронах (первая группа), и потока частиц, теряющих энергию с участием всех Z электронов (вторая группа). Возможности такого подхода для описания энергетических спектров пучка быстрых электронов при их транспорте в веществе были показаны в [18]. Но в отличие от электронов, когда обе группы сразу регистрируются в энергетических спектрах самых тонких слоев вещества, для положительно заряженных протонов и альфа-частиц вклад второй группы становится заметным лишь в энергетических спектрах слоев, толщина которых превышает 60% максимального пробега частиц в веществе. В свете сказанного для протонов и альфа-частиц первой группы формулы (1), (2) и (4), (5) примут вид:
(6)
$\frac{{{{m}_{e}}}}{{{{M}_{p}}}}\left[ {E_{0}^{2} - E_{p}^{2}\left( 1 \right)} \right] = \frac{1}{4}{{J}^{2}},$(7)
$\frac{{{{m}_{e}}}}{{{{M}_{p}}}}\left[ {E_{0}^{2} - E_{p}^{2}\left( n \right)} \right] = \frac{1}{4}{{J}^{2}}\ln \left( {n!} \right),$(8)
$\frac{{{{m}_{e}}}}{{{{M}_{p}}}}\left[ {E{}_{0}^{2}\, - E_{p}^{2}} \right] = \frac{1}{4}n{{J}^{2}}\ln \left( {\frac{k}{{{{e}^{{{k \mathord{\left/ {\vphantom {k n}} \right. \kern-0em} n}}}}}}} \right).$(9)
${{n}_{1}} = \frac{{8\pi {{q}^{4}}{{N}_{0}}Z{{z}^{2}}x}}{{{{J}^{2}}\sqrt {1 - {{\beta }^{2}}} }},$(10)
${{n}_{2}} = \frac{{4\pi {{q}^{4}}{{N}_{0}}Z{{z}^{2}}x}}{{{{J}^{2}}\sqrt {1 - {{\beta }^{2}}} }}.$Приведенные выше формулы позволяют надежно проводить расчеты необходимых параметров для энергетического спектра быстрых протонов, которые прошли тонкую пленку вещества. Функция распределения по энергии F(E0, Ep) пучка заряженных частиц, прошедших тонкую пленочную мишень, была получена в [9] как решение одномерного транспортного уравнения. Впервые была учтена зависимость дифференциального сечения многократного неупругого рассеяния от числа испытанных частицей взаимодействий путем простого добавления в классическую формулу кратного рассеяния [17] множителя, равного [ln(∆E/∆Ep) + 2]. В результате удалось, во-первых, устранить извечный расчетный дефицит потерь энергии в толстых пленках [19, 20], и, во-вторых, установить истинную причину неустранимой асимметрии экспериментальных спектров, даже когда среднее число взаимодействий n достигает ≈106. В общем виде функция распределения F(E0, Ep) в статистике многократного рассеяния представима как:
(11)
$\begin{gathered} F\left( {\Delta {{E}_{p}},u} \right) = \\ = \exp \left[ { - \frac{{\Delta {{E}_{p}}}}{{2\Delta {{E}_{{\min }}}}}\exp \left( { - \int\limits_{{{u}_{{\min }}}}^u {\frac{{ds}}{{\frac{1}{2}\ln s + 1 - s}}} } \right)} \right]. \\ \end{gathered} $В отличие от функции распределения Ландау [21] для потерь энергии функция (8) имеет два первых приближенных решения, которые представимы через элементарные функции. Действительно, после разложения ln s в ряд Грегори и последующего учета вклада только первого члена разложения получаем функцию F(ΔEp, ΔE) первого приближения общего решения (8) в достаточно простом аналитическом виде:
(12)
$F\left( {\Delta {{E}_{p}},u} \right) = \exp \left[ { - \frac{{{{{\left( {\Delta E - \Delta {{E}_{p}}} \right)}}^{2}}}}{{2\Delta {{E}_{{\min }}}\Delta E}}} \right].$Из-за наличия в знаменателе показателя экспоненты переменной ∆E асимметрия распределения является ее характерной особенностью при любом среднем числе n взаимодействий частиц в образце. В случае быстрых протонов и альфа-частиц эта асимметрия менее выражена, чем в случае электронов, из-за относительной малости величины εmax (в сравнении с величиной E). Важнейший параметр такого распределения – полная ширина Г на половине высоты:
ТРАНСПОРТНАЯ ДЛИНА И ГЛУБИНА ПРОНИКНОВЕНИЯ ПУЧКА БЫСТРЫХ ПРОТОНОВ И АЛЬФА-ЧАСТИЦ В МИШЕНЬ ПРИ НОРМАЛЬНОМ ПАДЕНИИ ЧАСТИЦ НА ПОВЕРХНОСТЬ ОБРАЗЦА
Во многих практических приложениях теории рассеяния заряженных частиц в веществе исключительное значение имеет интеграл:
который называется транспортным сечением и который представляет собой усредненное по всем возможным угловым отклонениям сечение взаимодействия первичных частиц с веществом. Он определяет величину транспортного пробега Ltr направленного потока частиц в веществе, по достижении которого все направления их движения в мишени становятся равновероятными:(14)
$L_{{{\text{tr}}}}^{{{\text{inel}}}} = \frac{{\frac{{{{m}_{e}}}}{{{{M}_{p}}}}E_{0}^{2}}}{{4\pi {{q}^{4}}{{N}_{0}}Z{{z}^{2}}\frac{1}{{\sqrt {1 - {{\beta }^{2}}} }}\ln \left( {\frac{{2{{m}_{e}}V_{0}^{2}}}{{J\sqrt[4]{{1 - {{\beta }^{2}}}}}}} \right)}}.$Это соотношение, обозначенное в [22] как Rp, было успешно использовано при расчете наиболее вероятного угла рассеяния протонов, прошедших тонкую монокристаллическую пленку кремния в режиме “random”. Более детальная апробация этой формулы будет проведена ниже в разделе, посвященном описанию углового распределения пучка частиц после прохождения ими монокристаллического слоя вещества в режиме каналирования.
Другим параметром, имеющим также большое значение в практических приложениях, является глубина Rx максимального проникновения частиц в бомбардируемый образец. Она определяется толщиной слоя вещества, после прохождения которого средняя кинетическая энергия частиц Em становится равной их тепловой энергии, т.е. практически Em → 0. Для пучка быстрых протонов, прошедших слой вещества, наиболее вероятная энергия Ep из-за малой асимметрии распределений практически равна Em. Как пример, для протонов с начальной энергией 19.68 МэВ, прошедших слой алюминия толщиной 0.0987 см, измеренная величина Ep = 13.60 МэВ [23]. Усреднение по всему энергетическому спектру дает величину Em = 13.5925 МэВ. Поэтому в выражении (4) с полным правом можно заменить Ep на Em. Тогда для протонов второй группы (двухпотокового приближения) в очень тонком слое у поверхности средняя энергия определяется из выражения:
Если провести возможное усреднение этой вероятности как 1/2{ln(n2/e) + 1} = 1/2ln(n2) = = 1/2ln(εmax/εmin) = ${\text{ln}}\left\{ {\left( {{{\left( {{{m}_{e}}V_{0}^{2}} \right)} \mathord{\left/ {\vphantom {{\left( {{{m}_{e}}V_{0}^{2}} \right)} J}} \right. \kern-0em} J}} \right)} \right\}$ и для средней энергии протонов второй группы записать соотношение
(15)
$\frac{{{{m}_{e}}}}{{{{M}_{p}}}}\left( {E_{0}^{2} - E_{m}^{2}} \right) = {{n}_{2}}{{J}^{2}}\ln \left( {\frac{{{{m}_{e}}V_{0}^{2}}}{{J\sqrt[4]{{1 - {{\beta }^{2}}}}}}} \right),$(16)
${{R}_{x}} = \frac{{\frac{{{{m}_{e}}}}{{{{M}_{p}}}}E_{0}^{2}}}{{4\pi {{q}^{4}}{{N}_{0}}Z{{z}^{2}}\frac{1}{{\sqrt {1 - {{\beta }^{2}}} }}\ln \left( {\frac{{{{m}_{e}}V_{0}^{2}}}{{J\sqrt[4]{{1 - {{\beta }^{2}}}}}}} \right)}}.$ФОРМУЛА ДЛЯ РАСЧЕТА НАИБОЛЕЕ ВЕРОЯТНОЙ ЭНЕРГИИ ПУЧКА БЫСТРЫХ ЗАРЯЖЕННЫХ ЧАСТИЦ, ПРОШЕДШИХ СЛОЙ ВЕЩЕСТВА ЗАДАННОЙ ТОЛЩИНЫ
Из-за отмеченной выше близости средней энергии Em наиболее вероятной Ep можно, подставив в формулу (12) выражение для n2формулы (7), получить формулу, которая описывает зависимость Ep2 протонов второй группы от толщины пленки x, когда x → Rx, как
Однако формула (8) для протонов первой группы (двухпотокового приближения), описывающая зависимость Ep1 протонов от толщины мишени, в тонких пленках принимает следующий вид:
Разница между этими двумя выражениями состоит лишь в множителе, равном примерно двум, в логарифмическом члене. Очевидно, что они могут быть объединены в одну формулу, описывающую зависимость Ep всего пучка протонов от толщины пленки во всем диапазоне толщин, если ввести в логарифмический член множитель 2 – x/Rx, величина которого линейно меняется с толщиной мишени. При этом в логарифмическом члене сохраняется начальная скорость V0 частиц, а не текущая средняя V. Получаем:
(17)
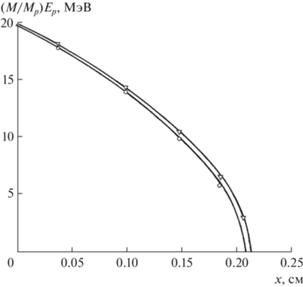
$\frac{{{{m}_{e}}}}{{{{M}_{p}}}}\left( {E_{0}^{2} - E_{p}^{2}} \right) = \frac{{4\pi {{q}^{4}}{{N}_{0}}Z{{z}^{2}}x}}{{\sqrt {1 - {{\beta }^{2}}} }}\ln \left[ {\frac{{\left( {2 - \frac{x}{{{{R}_{x}}}}} \right){{m}_{e}}V_{0}^{2}}}{{J\sqrt[4]{{1 - {{\beta }^{2}}}}}}} \right].$Рис. 1.
Зависимость наиболее вероятной энергии Ep пучка протонов с E0= 19.68 МэВ (кружки) и ионов гелия с E0= 79.8 МэВ (треугольники) от толщины алюминиевой мишени: сплошные кривые – расчет по формуле (14) (М = Mp, Mα для протонов и ионов гелия); символы – экспериментальные результаты [23].
ДВУХПОТОКОВАЯ МОДЕЛЬ ТРАНСПОРТА БЫСТРЫХ ПРОТОНОВ В ВЕЩЕСТВЕ
Для протонов и альфа-частиц совершенно так же, как и для пучка электронов, общий энергетический спектр прошедших пленку частиц представляет собой сумму спектров двух групп частиц:
(18)
$\begin{gathered} {{N}_{T}}\left( {E,{{E}_{{p1}}},{{E}_{{p2}}}} \right) = {{A}_{1}}\exp \left[ { - \frac{{{{{\left( {{{E}_{{p1}}} - E} \right)}}^{2}}}}{{0.5{{m}_{e}}V_{0}^{2}\left( {{{E}_{0}} - E} \right)}}} \right] + \\ + \,\,{{A}_{2}}\exp \left[ { - \frac{{{{{\left( {{{E}_{{p2}}} - E} \right)}}^{2}}}}{{2{{m}_{e}}V_{0}^{2}\left( {{{E}_{0}} - E} \right)}}} \right], \\ \end{gathered} $Но если для отрицательно заряженных электронов после прохождения ими любой тонкой пленки характерно надежно регистрируемое присутствие сразу двух потоков частиц в общем энергетическом спектре [24], то для положительно заряженных протонов вторая группа частиц становится заметной только после прохождения пленок толщиной более 0.5Rx. Пример использования этой формулы для модельных расчетов, связанных с описанием экспериментальных спектров пучка протонов с E0 = 19.68 МэВ, прошедших алюминиевые пленки различной толщины [23], представлен на рис. 2, 3. Видно, что полученные в рамках статистики многократного рассеяния заряженных частиц формулы для расчета величин εp, n, Ep и Г совместно с функцией распределения частиц по энергии F(ΔEp, ΔE) позволяют достаточно детально и аналитически описать энергетические распределения пучка частиц, соответствующие экспериментально регистрируемым спектрам. Также следует обратить внимание на реальное среднее число неупругих взаимодействий, которые частицы испытывают во время своего движения в пленочной мишени. Оно огромно, и имитировать процесс транспорта частиц современными методами математического моделирования вряд ли имеет смысл, располагая возможностью аналитически описать эти процессы проверенными методами дискретной статистики многократного рассеяния.
Рис. 2.
Энергетическое распределение пучка протонов с начальной энергией E0 = 19.68 МэВ после прострела алюминиевых пленок различной толщины x: 1 – 0.0367 (n = 6 × 105); 2 –0.0990 (n = 1.6 × 106); 3, 4 – 0.1474 см (n = 2.4 × 106), n – среднее число неупругих взаимодействий в мишени. Пунктирные линии – рассчитанные по формуле (18) вклады в спектры первой (1–3) и второй (4) групп частиц, сплошная линия 3 – суммарное энергетическое распределение протонов двух групп, символы – экспериментальные спектры [23].
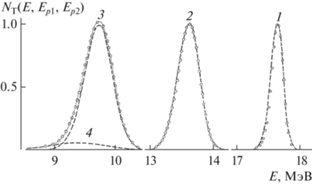
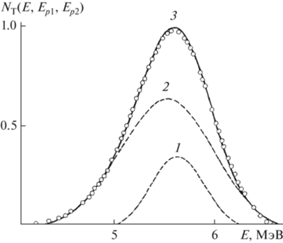
Рис. 3.
Энергетический спектр пучка протонов с начальной энергией E0 = 19.68 МэВ после прохождения алюминиевой пленки толщиной x = 0.1841 см: пунктирные линии – рассчитанные вклады в спектр первой (1) и второй (2) групп протонов; сплошная линия 3 – их суммарное энергетическое распределение; символы – экспериментальный спектр [23].
РАСПРЕДЕЛЕНИЕ ПО УГЛУ НАПРАВЛЕННОГО ПУЧКА ЧАСТИЦ, ПРОШЕДШИХ СЛОЙ ВЕЩЕСТВА, В РЕЖИМАХ “RANDOM” И КАНАЛИРОВАНИЯ
Ранее в [22] функция (9) как решение одномерного транспортного уравнения была успешно использована для описания распределения пучка заряженных частиц по полярному углу θ после их прохождения пленочной мишени известной толщины x при нормальном падении пучка на поверхность образца:
(19)
$\begin{gathered} F\left( {\theta ,{{\theta }_{p}}} \right) = \frac{{dN}}{{d\Omega }} = \frac{{dN}}{{2\pi \theta d\theta }} = \\ = A\exp \left[ { - \frac{{{{\theta }^{2}}}}{{0.75{{\theta }_{p}}\left( {\theta + {{\theta }_{p}}} \right)}}} \right]. \\ \end{gathered} $(20)
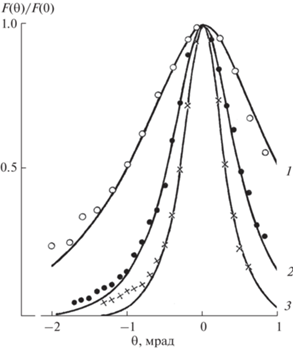
$L_{{{\text{tr}}}}^{{{\text{inel}}}} = \frac{{\frac{{{{m}_{e}}}}{{{{M}_{p}}}}E_{0}^{2}}}{{2\pi {{q}^{4}}{{N}_{0}}Z{{z}^{2}}\frac{1}{{\sqrt {1 - {{\beta }^{2}}} }}\ln \left( {\frac{{\theta _{c}^{2}}}{{\theta _{{\min }}^{2}\sqrt {1 - {{\beta }^{2}}} }}} \right)}}.$Рис. 4.
Спектры угловых отклонений (символы) направленного пучка протонов с начальной энергией E0 = 10.3 МэВ, прошедших тонкую монокристаллическую пленку кремния толщиной x = 0.91 мкм [27] в режимах: “random” (1); аксиального каналирования вдоль оси $\left\langle {111} \right\rangle $ (2); плоскостного каналирования на {100} (3); сплошные кривые – соответствующие этим режимам модельные расчеты.
ЗАКЛЮЧЕНИЕ
В результате проведенных исследований решена задача аналитического описания энергетических и угловых спектральных распределений пучков быстрых протонов и альфа-частиц, прошедших пленочную мишень заданной толщины. В двухпотоковом приближении получена формула для расчета значений наиболее вероятной энергии пучка частиц после прохождения пленки известной толщины, получены формулы для расчета глубины проникновения частиц в вещество при нормальном падении пучка на образец и транспортной длины в канале неупругого рассеяния. Проведена их проверка на соответствие имеющимся в научных публикациях экспериментальным данным.
Список литературы
Bethe H.A. // Ann. Phys. (Leipzig) 1930. B. 5. S. 325.
Bloch F. // Z. Phys. 1933. B. 81. S. 363.
Moliere G. // Z. Naturf. 1947. B. 2a. S. 133.
Штернхеймер Р. Принципы и методы регистрации элементарных частиц / Ред. Арцимович Л.А. М.: Изд-во иностр. лит-ры, 1963. 344 с.
ICRU Report 49. Stopping Powers and Ranges for Protons and Alpha Particles. International Commission on Radiation Units and Measurements. 1993.
Andersen H.H., Ziegler J.F. Hydrogen Stopping Powers and Ranges in All Elements. N.Y.: Pergamon Press, 1977.
ICRU Report 37. Stopping Powers for Electrons and Positrons. International Commission on Radiation Units and Measurements. 1984.
Михеев Н.Н. // Изв. РАН. Сер. физ. 2000. Т. 64. № 11. С. 2137.
Михеев Н.Н., Степович М.А., Юдина С.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2009. № 3. С. 53.
Михеев Н.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2010. № 4. С. 25.
Михеев Н.Н., Степович М.А., Широкова Е.В. // Изв. РАН. Сер. физ. 2010. Т. 74. № 7. С. 1049.
Михеев Н.Н., Степович М.А., Широкова Е.В. // Изв. РАН. Сер. физ. 2012. Т. 76. № 9. С. 1112.
Михеев Н.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2014. № 9. С. 66. https://doi.org./10.7868/S0207352814090133
Михеев Н.Н., Колесник А.С. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2017. № 12. С. 88. https://doi.org/10.7868/S0207352817120083
Михеев Н.Н., Никифорова Н.А., Степович М.А. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2019. № 1. С. 98. https://doi.org/10.1134/S0207352810010141
Михеев Н.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2020. № 12. С. 70. https://doi.org./10.31857/S1028096020120120201
Ландау Л.Д., Лифшиц Е.М. Квантовая механика. Нерелятивистская теория. М.: Физматгиз, 1963. 704 с.
Mikheev N.N., Stepovich M.A. // Mater. Sci. Eng. B. 1995. V. 32. № 1–2. P. 11.
Williams E.J. // Proc. Roy. Soc. 1929. V. 125. S. 420.
Brown D.B., Wittry D.D., Kyzer D.F. // J. Appl. Phys. 1969. V. 40. № 4. P. 1627.
Ландау Л.Д. // Собрание трудов. М.: Наука, 1969. Т. 1. С. 482.
Михеев Н.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2020. № 3. С. 77. https://doi.org./10.31857/S1028096020030127
Tschalär C., Maccabee H.D. // Phys. Rev. B. 1970. 1. P. 2863.
Михеев Н.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2019. № 8. С. 56. https://doi.org/10.1134/S0207352819080109
Линдхард Й. // УФН. 1969. Т. 99. Вып. 2. С. 249.
Оцуки Ё.-Х. Взаимодействие заряженных частиц с твердыми телами. М.: Мир, 1985. 280 с.
Ведьманов Г.Д., Лазарев Ю.Г., Николайчук Л.И., Радченко В.И., Хижняк Н.А. // Изв. РАН. Сер. физ. 1995. Т. 59. № 10. С. 141.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования


