Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 8, стр. 102-107
Квантовый размерный эффект для блоховских волновых функций электронов высокой энергии в тонкой монокристаллической пленке
С. М. Шкорняков *
Институт кристаллографии им. А.В. Шубникова ФНИЦ
“Кристаллография и фотоника” РАН
119333 Москва, Россия
* E-mail: shkornyakov@mail.ru
Поступила в редакцию 07.12.2021
После доработки 22.01.2022
Принята к публикации 25.02.2022
- EDN: HOAMFI
- DOI: 10.31857/S1028096022080143
Аннотация
Произведен расчет коэффициента отражения электронов высокой энергии (25–75 кэВ) при их нормальном падении на тонкую монокристаллическую пленку. Показано, что и при столь высоких энергиях частиц имеет место квантовый размерный эффект для сформировавшихся в пленке блоховских волн. Величина и зависимость коэффициента отражения от энергии электронов, характеризующие этот эффект, легко может быть зарегистрирована экспериментально.
ВВЕДЕНИЕ И ПОСТАНОВКА ЗАДАЧИ
Квантовый размерный эффект электронов в тонких металлических и полупроводниковых пленках хорошо изучен как теоретически, так и экспериментально [1]. Первоначально при моделировании процесса рассеяния частиц электростатический потенциал в пленке выбирали в виде прямоугольной ямы. Так как для экспериментального наблюдения эффекта необходимо, чтобы длина волны электрона была сравнима с неоднородностями на поверхности пленки, энергию частиц следовало выбирать порядка единиц электронвольта. Длина волны электрона при этом была порядка единиц ангстрема, что сравнимо с шероховатостью поверхности.
Ситуация меняется при рассмотрении монокристаллической пленки, так как в ней формируются блоховские волны. Длина волны независимо от энергии электронов изменяется в интервале от периода кристаллической решетки до толщины пленки в каждой разрешенной зоне одномерного кристалла [2]. Поэтому для наблюдения эффекта ограничения на энергию частиц снимаются. Впервые рассеяние волн и частиц на одномерном периодическом потенциале монокристаллической пленки было теоретически и независимо исследовано рядом ученых [2–9]. В работе [10] рассматривали рассеяние с учетом среднего внутреннего потенциала монокристаллической пленки. Было получено компактное аналитическое выражение для коэффициентов прохождения T и отражения R в пленке, используемое для расчетов в настоящей работе. В [10] эта формула была применена для теоретического исследования квантового размерного эффекта при отражении пучка электронов высокой энергии, падающего под малым углом скольжения на тонкую монокристаллическую пленку. В этом случае нормальная составляющая энергии электронов изменяется от единиц до десятков электронвольт, и эффект проявляется сильно.
Формула, полученная в [10], используется для расчета энергетической зависимости коэффициента отражения электронов высокой энергии, падающих нормально на тонкую монокристаллическую пленку. Рассмотрим одномерную модель монокристаллической пленки, в которой потенциальная энергия электрона зависит от координаты вдоль оси x, перпендикулярной поверхности пленки (рис. 1).
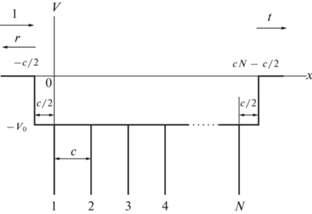
Рис. 1.
Схема потенциала электрона в пленке: V0 – средняя внутренняя энергия; N – число параллельных поверхности монослоев в пленке; c – период одномерной решетки; t – амплитуда прошедшей волны; r – амплитуда отраженной волны.
Насколько известно автору, до настоящего времени квантовый размерный эффект при такой энергии электронов теоретически не исследовали и экспериментально не наблюдали. Только недавно сделаны расчеты эффекта для частиц средней энергии (10–15 кэВ) [11]. Дело в том, что при построении и кинематической, и динамической теории дифракции электронов высокой энергии, падающих нормально на тонкую монокристаллическую пленку, не учитывали отражение частиц от второй поверхности пленки, так как считали, что оно мало [12–15]. Только при рассмотрении динамической дифракции электронов высокой энергии на отражение, когда угол скольжения мал, учитывали отражение от второй границы, поскольку оно в этом случае значительно [16]. Кроме того, для проявления эффекта нужно и в теоретических расчетах, и в эксперименте соблюдать определенные условия [17].
При нормальном падении электронов средней и высокой энергии в монокристаллической пленке формируются, например, в двухволновом приближении блоховские волны большой амплитуды, и отражение от пленки становится заметным, что способствует возникновению квантового размерного эффекта, который проявляется в виде гармонических осцилляций на кривой R(E). Величина этого эффекта вполне достаточна для экспериментального наблюдения. Его теоретическому расчету и посвящена настоящая работа.
ВЫБОР МОДЕЛИ И РАСЧЕТНЫЕ ФОРМУЛЫ
На рис. 1 приведена схема потенциала электрона, падающего нормально на монокристаллическую пленку. Для выявления сути эффекта вполне достаточно одномерной модели. Аналитически вид потенциала, изображенного на рис. 1, задается формулой:
(1)
$\begin{gathered} V\left( x \right) = - {{V}_{0}} + \frac{{{{\hbar }^{2}}}}{{2m}}cU\sum\limits_{n\,\, = \,\,1}^N {~\delta \left( {x - c\left( {n - 1} \right)} \right)} , \\ {\text{для}} - \frac{с}{2} \leqslant x \leqslant cN - \frac{c}{2}~,\,\,\,\,V\left( x \right) = 0, \\ {\text{для}}\,\,\,\,x\left\langle { - \frac{c}{2}~,x} \right\rangle cN - \frac{c}{2}. \\ \end{gathered} $Решая стационарное уравнение Шредингера с этим потенциалом, получаем следующие выражения для коэффициентов прохождения T и отражения R [10]:
(2)
$\begin{gathered} T = tt* = \\ = \,\,\frac{1}{{1 + \frac{1}{4}{{{\left( {\frac{{{\lambda }}}{k}{\text{tg}}\frac{{kc}}{2}{\text{ctg}}\frac{{{{\mu }}c}}{2} - \frac{k}{{{\lambda }}}{\text{ctg}}\frac{{kc}}{2}{\text{tg}}\frac{{{{\mu }}c}}{2}} \right)}}^{2}}{\text{si}}{{{\text{n}}}^{2}}{{\mu }}cN}}~, \\ \end{gathered} $(3)
${\text{cos}}{\kern 1pt} {{\mu }}c = {\text{cos}}{\kern 1pt} kc + \frac{{cU}}{{2k}}{\text{sin}}{\kern 1pt} kc.$РЕЗУЛЬТАТЫ РАСЧЕТОВ И ИХ ОБСУЖДЕНИЕ
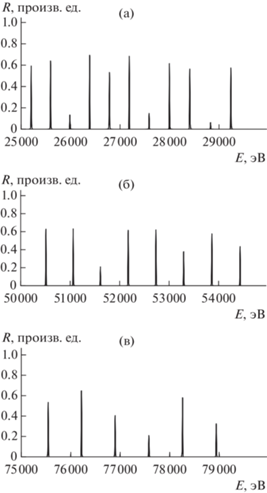
На рис. 2 приведены графики зависимости R(E) для трех диапазонов изменения энергии частиц и для c = 5 Å, y = –2, V0 = 10 эВ. Эти значения выбраны исходя из следующих соображений. Период решетки c = 5 Å соответствует среднему расстоянию между плоскостями с малыми индексами Миллера в большинстве кристаллов. Значение параметра y = –2 приводит к величине запрещенной зоны между валентной зоной и зоной проводимости кристалла порядка единиц электронвольта, что соответствует реальной ситуации. V0 = 10 эВ – это среднее значение внутренней энергии электронов в кристаллах. Толщина пленки соответствует глубине проникновения электронов с данной энергией, обусловленной неупругими процессами. На рис. 2а диапазон значений энергии 25 000–30 000 эВ, количество плоскостей в пленке N = 80, т.е. толщина кристалла 400 Å. На рис. 2б энергия выше – 50 000–55 000 эВ, и N = 100. На рис. 2в энергия еще больше и составляет 75 000–80 000 эВ, а также выбрана и бόльшая толщина образца: Nc = 650 Å. Видно, что брэгговские отражения разделены значительными интервалами энергии, которые увеличиваются с ее ростом по закону ΔЕ ~ Е1/2, что видно из сравнения расстояний между пиками (рис. 2а–2в). Этот закон можно вывести и теоретически. Сделаем это.
Рис. 2.
Коэффициент отражения R падающих электронов при среднем внутреннем потенциале V0 = 10 эВ, отражательной способности одной плоскости, характеризуемой значением параметра y = –2, угле скольжения α = 90° (нормальное падение) и периоде одномерной решетки c = 5 Å: а – E = 25 000–30 000 эВ, N = 80, R = 0–1.0; б – E = 50 000–55 000 эВ, N = 100, R = 0–1.0, в – E = 75 000–80 000 эВ, N = 130, R = 0–1.0. N – количество отражающих плоскостей.
Из (3) следует, что одна из границ запрещенной зоны, а, следовательно, и соответствующего ей брэгговского рефлекса, определяется условием $\frac{{cU}}{{2k}}{\text{sin}}{\kern 1pt} kc = 0,$ т.е. $kc = \pi n,$ где n – целое число. Откуда, поскольку падение нормальное и E1= E, следует $E + {{V}_{0}} = \frac{{{{n}^{2}}}}{{0.0268{{c}^{2}}}}.$ Обозначим энергию E, соответствующую номеру рефлекса n, как En. Тогда
Поскольку при больших n, как в рассматриваемом случае, En $ \gg $ V0, окончательно получаем:
где c – период одномерной решетки [Å], 0.0268, как говорилось выше, – размерный числовой множитель, [Å–2 · эВ–1], что и требовалось доказать.Следует отметить, что появление узких резонансных пиков вовсе не связано с квантовым размерным эффектом, а обусловлено известной формулой Вульфа–Брэгга. Однако при нормальном падении синус угла скольжения равен единице, и параметром в условии резонанса остается длина волны излучения, которая и определяется его энергией. И в случае полубесконечного кристалла эти пики будут присутствовать. Квантовый же размерный эффект проявляется только в пленках конечной толщины в виде гармонических осцилляций интенсивности отраженного пучка.
На рис. 3 приведены результаты расчетов, проведенных для случая, изображенного на рис. 2а, т.е. с теми же значениями параметров соответственно, но с увеличением разрешения, как по энергии, так и по R. Вариант, изображенный на рис. 3а, соответствует диапазонам E = 27 800–8500 эВ и R = 0–0.8. Другие рисунки иллюстрируют, что квантовый размерный эффект проявляется в виде гармонических осцилляций коэффициента отражения R, которые хорошо видны на рис. 3б, где R изменяется в диапазоне 0–0.1, и еще лучше наблюдаются на рис. 3в, где R = 0–0.1, но масштаб по оси энергии укрупнен.
Рис. 3.
Коэффициент отражения R для случая, изображенного на рис. 2а, но с укрупнением масштаба по осям: а – E = 27 800–28 500 эВ, R = 0–0.8; б – E = = 27 800–28 500 эВ, R = 0–0.1; в – Е = 27 950–28 100, R = 0–0.1.
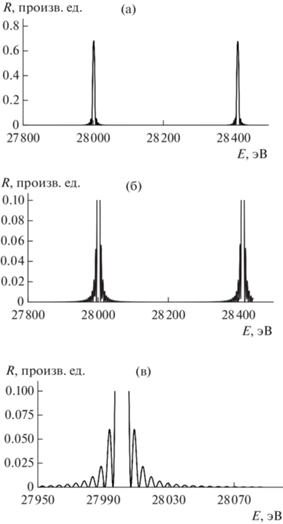
Рис. 4 соответствует рис. 2б, но в увеличенном масштабе. Как и в предыдущем случае, проявляется квантовый размерный эффект, что особенно хорошо видно на рис. 4в. И, наконец, рис. 5 соответствует в увеличенном масштабе рис. 2в. И здесь наблюдается квантовый размерный эффект. Для наглядности на рис. 6 он показан с бóльшим разрешением по энергии. Видны четкие осцилляции интенсивности отраженного пучка, которые можно зарегистрировать экспериментально.
Рис. 4.
Коэффициент отражения R для случая, изображенного на рис. 2б, но с укрупнением масштаба по осям: а – E = 52 000–53 000 эВ, R = 0–0.8; б – E = = 52 000–53 000 эВ, R = 0–0.1; в – E = 27 800–28 500 эВ, R = 0–0.1.
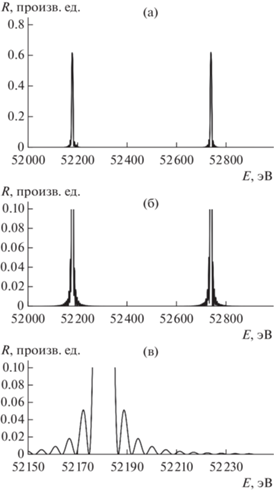
Рис. 5.
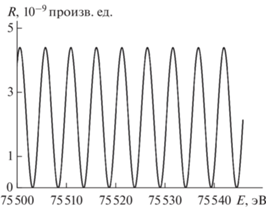
Коэффициент отражения R для случая, изображенного на рис. 2в, но с укрупнением масштаба по осям: а – E = 75 500–76 500 эВ, R = 0–0.8; б – E = = 75 500–76 500 эВ, R = 0–0.1.
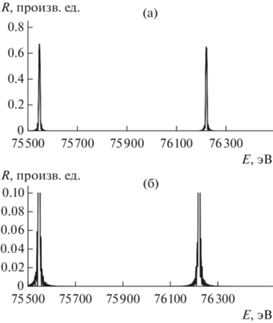
Рис. 6.
Коэффициент отражения R для V0 = 10 эВ, N = = 130, α = 90°, y = –2, E = 75 500–75 700 эВ, R = 0–0.01.
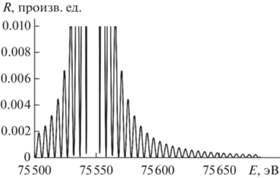
Из рис. 2–6 следует, что гармонические осцилляции, характеризующие квантовый размерный эффект, имеют значительные период и амплитуду и наблюдаются при высоких значениях энергии падающих электронов (25–75 кэВ).
На рис. 7 изображена кривая отражения от прямоугольной потенциальной ямы шириной 650 Å и глубиной 10 эВ. Видим, что интенсивность отраженной волны примерно на семь порядков меньше, чем при отражении электронов с такой же энергией от такой же ямы, но с периодическим потенциалом внутри нее (рис. 6).
Приходим к следующему выводу. При рассмотрении отражения от прямоугольной потенциальной ямы возникает квантовый размерный эффект (рис. 7), но малой амплитуды. Если же добавить к потенциалу ямы периодический потенциал решетки, то амплитуда осцилляций значительно возрастает (рис. 2–6).
ЭКСПЕРИМЕНТАЛЬНЫЕ СПОСОБЫ НАБЛЮДЕНИЯ ЭФФЕКТА
Обсудим возможные методы экспериментального наблюдения предсказанных эффектов. Так как в стандартных электронных приборах не предусмотрена плавная регулировка энергии частиц и потенциал образца обычно находится “на земле”, можно изолировать образец и подавать на него положительное или отрицательное смещение. Варьируя его, получим кривые R(E) или T(E), измеряя соответствующую интенсивность пучка. Пленку не обязательно брать свободную, можно исследовать ее на подложке при измерении отражения R(E).
Методы получения тонких монокристаллических пленок достаточно хорошо разработаны. Материал пленки может быть любым, но лучше брать полупроводник или металл, которые не заряжаются под пучком.
Для проведения экспериментов особенно удобен метод дифракции обратно рассеянных электронов [18]. Дифракционные картины в режиме регистрации обратно рассеянных электронов впервые были зарегистрированы в 1928 г. Нишикавой и Кикучи на том же образце, на котором были получены картины дифракции Кикучи при детектировании прошедших электронов, полученные методом просвечивающей электронной микроскопии [19].
Конечно, расчетная модель не учитывает все экспериментальные факторы. В частности, не рассматривается неупругое рассеяние электронов, которое будет давать фон, а полученные кривые будут его модулировать. Но в целом это не влияет на вывод о том, что квантовый размерный эффект при высоких энергиях частиц может быть зарегистрирован экспериментально.
ЗАКЛЮЧЕНИЕ
Произведен расчет коэффициента отражения электронов, падающих нормально на тонкую монокристаллическую пленку. Показано, что при энергии частиц 25–75 кэВ проявляется квантовый размерный эффект. Ранее этот факт не был известен. Считалось, что этот эффект можно наблюдать только в случае электронов малой энергии, и его действительно наблюдали в экспериментах по туннелированию в тонких твердотельных пленках. В работе же установлены два факта.
Во-первых, в монокристаллических пленках волновые функции электронов представляют собой блоховские волны, длина которых варьируется в интервале от периода решетки до толщины пленки. Это происходит в каждой разрешенной зоне кристалла независимо от энергии электрона. Таким образом, создаются благоприятные условия для наблюдения эффекта, а именно большая длина волны по сравнению с неоднородностями в пленке.
Во-вторых, показано, что учет отражения электронов от второй границы пленки, которым ранее пренебрегали в случае частиц высокой энергии, приводит к заметному проявлению квантового размерного эффекта.
Эти два факта не были раньше учтены ни в теоретических моделях явления, ни при его экспериментальном исследовании. Их учет позволил предсказать возможность наблюдения квантового размерного эффекта при высоких энергиях электронов, что ранее не было известно.
Список литературы
Комник Ю.Ф. Физика металлических пленок. Размерные и структурные эффекты. М.: Атомиздат, 1979. 264 с.
Шкорняков С.М., Сальников М.Л., Семилетов С.А. // ФТТ. 1977. Т. 19. Вып. 3. С. 687.
Пшеничнов Е.А. // ФТТ. 1962. Т. 4. Вып. 5. С. 1113.
Schnupp P. // Phys. Stat. Sol. 1967. V. 21. P. 567.
Schnupp P. // Solid-State Electronics. 1967. V. 10. P. 785.
Cruz E.L., Helman J.S. // Phys. Rev. B. 1974. V. 10. № 4. P. 1751.
Shishido F. // Tech. Rep. ISSP. Ser. A. 1973. № 616. P. 1.
Игнатович В.К. Рассеяние волн и частиц на одномерных периодических потенциалах. Препринт Р4-10778. Дубна: ОИЯИ, 1977. 17 с.
Игнатович В.К. Рассеяние нейтронов на несимметричном одномерном периодическом потенциале. Препринт Р4-11135. Дубна: ОИЯИ, 1978. 23 с.
Шкорняков С.М. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2017. № 6. С. 83. https://doi.org/10.7868/S020735281706018X
Шкорняков С.М. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2022. В печати.
Пинскер З.Г. Дифракция электронов. М.–Л.: Изд-во АН СССР, 1949. 404 с.
Хирш П., Хови А., Николсон Р., Пэшли Д., Уэлан М. Электронная микроскопия тонких кристаллов. М.: Мир, 1968. 574 с.
Каули Дж. Физика дифракции. М.: Мир, 1979. 431 с.
Peng L.-M., Dudarev S.L., Whelan M.J. High-Energy Electron Diffraction and Microscopy. Oxford Science Publications. 2004. 535 p.
Peng L.-M., Whelan M.J. // Surf. Sci. Lett. 1990. V. 238. P. L446.
Шкорняков С.М. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2020. № 5. С. 82. https://doi.org/10.31857/S1028096020050167
Schwartz A. Electron Backscatter Diffraction in Materials Science / Ed. Schwartz A. et al. Springer, 2009. 403 p.
Nishikawa S., Kikuchi S. // Nature. 1928. V. 121. № 3061. P. 1019.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования