1. На главную
  2. Электронные версии
  3. Поверхность. Рентгеновские, синхротронные и нейтронные исследования
  4. № 8, 2022

Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 8, стр. 36-42

Электрическая проводимость тонкого металлического слоя с учетом отклонения от закона Видемана–Франца

Э. В. Завитаев a, *, О. В. Русаков b, Е. П. Чухлеб c

a Мытищинский филиал Московского государственного технического университета им. Н. Э. Баумана
141005 Мытищи, Россия

b Государственный гуманитарно-технологический университет
142611 Орехово-Зуево, Россия

c Муниципальное учреждение дополнительного образования Центр дополнительного образования “Малая академия наук Импульс”
142432 Черноголовка, Россия

* E-mail: eduardzavitaev@yandex.ru

Поступила в редакцию 05.12.2021
После доработки 22.02.2022
Принята к публикации 28.02.2022

Полный текст (PDF)

Аннотация

Впервые аналитически решена задача о влиянии отклонения от закона Видемана–Франца на электрическую проводимость тонкого металлического слоя. Допустимые значения толщины слоя ограничены размерами, при которых не проявляются квантовые и скин-эффекты. Однако отношение толщины слоя к длине свободного пробега электронов может быть произвольным. Решено модифицированное кинетическое уравнение с интегралом столкновений, учитывающим отклонение свойств металлов от закона Видемана–Франца при низких температурах. Учтен тот факт, что для чистых металлов при низких температурах оказываются существенными электрон-электронные столкновения, при которых суммарный импульс электронной подсистемы сохраняется и соответствующее рассеяние электронов не носит изотропный характер. В качестве граничных условий задачи приняты условия зеркально-диффузного отражения электронов от поверхностей слоя. Проведен анализ зависимости электрической проводимости слоя от частоты объемных и поверхностных столкновений электронов, коэффициентов зеркальности его поверхностей и параметра, описывающего отклонение от закона Видемана–Франца. Показано соответствие полученных результатов теоретического расчета электрической проводимости тонкого металлического слоя данным, рассчитанным альтернативным методом при отсутствии поправки к уточняемому экспериментальному закону.

Ключевые слова: тонкий слой, закон Видемана–Франца, локальная проводимость, интегральная проводимость.

ВВЕДЕНИЕ

Появление и востребованность новых технологий в микроэлектронике делает необходимым теоретическое изучение влияния поверхностного рассеяния носителей заряда на электромагнитные свойства малых проводящих объектов [1]. Отличительной чертой таких объектов является то, что средняя длина свободного пробега носителей заряда в них может быть одного порядка с характерным поперечным размером, который, в свою очередь, значительно превосходит длину волны де-Бройля. Это позволяет исключить из рассмотрения квантовые эффекты, но возникает потребность подробного изучения механизма влияния рассеяния носителей заряда.

Все вышесказанное имеет непосредственное отношение, в частности, к исследованию электрических и магнитных свойств тонкого проводящего слоя. Одной из первых работ, которая посвящена решению задачи о статической проводимости тонкой металлической пленки в перпендикулярном магнитном поле с учетом диффузных и зеркально-диффузных граничных условий отражения носителей заряда является работа [2]. Позже по этой же тематике было опубликовано большое количество результатов исследований [3–12]. В современных работах [13–15] впервые построена кинетическая теория высокочастотной электропроводности и постоянной Холла тонкой проводящей пленки с учетом различных коэффициентов зеркальности ее поверхностей. Особенность этих работ заключается в том, что расчеты базируются на применении уравнения Больцмана и с помощью введения соответствующих граничных условий позволяют учесть не только объемное, но и поверхностное рассеяние носителей заряда.

Из вышесказанного следует актуальность применения такого теоретического подхода к проблеме отклонения от закона Видемана–Франца в тонком металлическом слое, когда необходимо ввести в рассмотрение электрон-электронные столкновения. Заметим, что величины отклонения от этого закона при низких температурах могут принимать существенные значения [6, 7]. Поэтому в настоящей работе впервые проведен учет подобного эффекта для тонкого металлического слоя. Следует отметить, что в работе не приняты во внимание квантовые эффекты, учет которых был рассмотрен в [16] в рамках исследования квантовой пленки в диэлектрическом окружении, и не учтено проявление скин-эффекта [17] из предположения, что толщина слоя мала по сравнению с характерной глубиной скин-слоя.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И РАСЧЕТ

Рассмотрим тонкий металлический слой толщиной b, к которому приложено переменное напряжение частоты ω. Электрическое поле параллельно слою и направлено вдоль координатной оси Z, ось X перпендикулярна слою. Напряженность поля Е может быть выражена в зависимости от времени t:

(1)
${\mathbf{E}} = {{{\mathbf{E}}}_{{\text{0}}}}{\text{exp}}( - i\omega t).$

Исходя из того, что неравновесная функция Ферми–Дирака для электронов f(х,v) = f0(ε) + + f1(x,v) удовлетворяет уравнению Больцмана [18], имеем:

(2)
${{v}_{x}}\frac{{\partial {{f}_{1}}}}{{\partial x}} + e{{v}_{z}}E\frac{{\partial {{f}_{0}}}}{{\partial \varepsilon }} - i{{\omega }}{{f}_{1}} = - \frac{{{{f}_{1}}}}{\tau },$
где e – заряд электронов; vz, vx – соответствующие проекции вектора их скорости на координатные оси; τ – время релаксации электронов. Здесь ${{f}_{0}}\left( \varepsilon \right)$ = = – δ(ε – εF), где δ – дельта-функция Дирака; εF – энергия Ферми; ε = mv2/2 – кинетическая энергия электронов; v – модуль вектора скорости электронов v; m – эффективная масса электронов.

Плотность высокочастотного тока j, вызванного приложенным напряжением, может быть рассчитана по формуле:

(3)
${\mathbf{j}} = en{\mathbf{v}} = en{{\left[ {\int {{{f}_{0}}{{d}^{3}}{\mathbf{v}}} } \right]}^{{ - 1}}}\int {{{f}_{1}}{\mathbf{v}}{{d}^{3}}{\mathbf{v}}} .$
Здесь n – концентрация электронов проводимости, определяемая с помощью распределения Ферми–Дирака:
$n = 2{{\left( {\frac{m}{h}} \right)}^{3}}\int {{{f}_{0}}{{d}^{3}}{\mathbf{v}}} = 2{{\left( {\frac{m}{h}} \right)}^{3}}\frac{{4\pi v_{{\text{F}}}^{3}}}{3},$
где h – постоянная Планка, vF – скорость Ферми.

Если кинетическое уравнение Больцмана имеет вид (2), содержание закона Видемана–Франца соответствует времени релаксации порядка τ, когда доминируют объемные и поверхностные столкновения. Такой режим рассеяния электронов реализуется при наличии значительного количества примесей. Когда степень чистоты металла достаточно высока, при низких температурах существенными оказываются электрон-электронные столкновения. Для их учета запишем кинетическое уравнение (2) в следующем виде [19]:

(4)
$\begin{gathered} - i{{\omega }}{{f}_{1}} + {{v}_{x}}\frac{{\partial {{f}_{1}}}}{{\partial x}} + e{{v}_{z}}E\frac{{\partial {{f}_{0}}}}{{\partial \varepsilon }} = \\ = - \frac{1}{{{\tau }}}\left( {{{f}_{1}} - \frac{{3{{g}_{0}}m}}{{4\pi {\mathbf{v}}_{{\text{F}}}^{3}}}{{v}_{z}}\frac{{\partial {{f}_{0}}}}{{\partial \varepsilon }}\int {{{v}_{z}}{{f}_{1}}{{d}^{3}}{\mathbf{v}}} } \right), \\ \end{gathered} $
где g0 – параметр (0 ≤ g0 ≤ 1), характеризующий степень отклонения от закона Видемана–Франца [18]; g0 = 0 соответствует точному выполнению этого закона.

Подставив в уравнение (4) функцию

${{f}_{1}}(x,{\mathbf{v}}) = g(x,{\mathbf{v}})\delta (\varepsilon - {{\varepsilon }_{{\text{F}}}}){\text{exp}}( - i\omega t),$
получим:
(5)
${{\nu }}g + {{v}_{x}}\frac{{\partial g}}{{\partial x}} - e{{v}_{z}}{{E}_{0}} = - \frac{{3{{g}_{0}}m}}{{4\pi v_{{\text{F}}}^{3}\tau }}{{v}_{z}}\int {{{v}_{z}}g\delta \left( {\varepsilon - {{\varepsilon }_{{\text{F}}}}} \right){{d}^{3}}{\mathbf{v}}} ,$
где ν = 1/τ – iω.

Решение уравнения (5) проведем с помощью метода моментов [18]:

(6)
$g = {{a}_{1}}\left( x \right){{v}_{z}} + {{a}_{2}}\left( x \right){{v}_{z}}{\text{sign}}\left( {{{v}_{x}}} \right).$

С учетом (6) уравнение (5) принимает вид:

(7)
$\begin{gathered} \nu \left( {{{a}_{1}}{{v}_{z}} + {{a}_{2}}{{v}_{z}}{\text{sign}}\left( {{{v}_{x}}} \right)} \right) + {{v}_{x}}{{v}_{z}}\frac{{\partial {{a}_{1}}}}{{\partial x}} + \\ + \,\,{{v}_{x}}{{v}_{z}}{\text{sign}}\left( {{{v}_{x}}} \right)\frac{{\partial {{a}_{2}}}}{{\partial x}} - e{{v}_{z}}{{E}_{0}} = ~ \\ = - \frac{{3{{g}_{0}}m}}{{4{{\pi }}v_{{\text{F}}}^{3}\tau }}{{v}_{z}}\int {{{v}_{z}}} \left( {{{a}_{1}}{{v}_{z}} + {{a}_{2}}{{v}_{z}}{\text{sign}}\left( {{{v}_{x}}} \right)} \right)\delta \left( {\varepsilon - {{\varepsilon }_{{\text{F}}}}} \right){{d}^{3}}{\mathbf{v}}. \\ \end{gathered} $

Для вычисления интеграла, стоящего в правой части уравнения (7), удобно перейти к цилиндрической системе координат (${{{\mathbf{v}}}_{ \bot }},$ φ, vz) в пространстве скоростей.

Учитывая свойства дельта-функции Дирака и связи: ${{{\mathbf{v}}}_{x}} = {{{\mathbf{v}}}_{ \bot }}{\text{cos}}{\kern 1pt} {{\varphi }};$ $v_{ \bot }^{2} + v_{z}^{2} = v_{{\text{F}}}^{2},$ имеем

(8)
$\begin{gathered} \left( {{{\nu }} + \frac{{{{g}_{0}}}}{{{\tau }}}} \right){{a}_{1}}{{v}_{z}} + \nu {{a}_{2}}{{v}_{z}}{\text{sign}}\left( {{{v}_{x}}} \right) + {{v}_{x}}{{v}_{z}}\frac{{\partial {{a}_{1}}}}{{\partial x}} + \\ + \,\,{{v}_{x}}{{v}_{z}}{\text{sign}}\left( {{{v}_{x}}} \right)\frac{{\partial {{a}_{2}}}}{{\partial x}} - e{{E}_{0}}{{v}_{z}} = 0. \\ \end{gathered} $

Последовательно умножая равенство (8) сначала на проекцию скорости электронов vz, а затем на vzsign(vx), и, интегрируя по всему пространству скоростей, получим два уравнения:

$\begin{gathered} \left( {\nu + \frac{{{{g}_{0}}}}{{{\tau }}}} \right){{a}_{1}}\int {v_{z}^{2}{{d}^{3}}{\mathbf{v}}} + {{\nu }}{{a}_{2}}\int {v_{z}^{2}{\text{sign}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}}} + \\ + \,\,\frac{{\partial {{a}_{1}}}}{{\partial x}}\int {{{v}_{x}}v_{z}^{2}{{d}^{3}}{\mathbf{v}}} + \frac{{\partial {{a}_{2}}}}{{\partial x}}\int {{{v}_{x}}v_{z}^{2}{\text{sign}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}}} - \\ - \,\,e{{E}_{0}}\int {v_{z}^{2}{{d}^{3}}{\mathbf{v}}} = 0, \\ \left( {\nu + \frac{{{{g}_{0}}}}{{{\tau }}}} \right){{a}_{1}}\int {v_{z}^{2}{\text{sign}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}}} + \nu {{a}_{2}}\int {v_{z}^{2}{\text{sig}}{{{\text{n}}}^{2}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}}} + \\ + \,\,\frac{{\partial {{a}_{1}}}}{{\partial x}}\int {{{v}_{x}}v_{z}^{2}{\text{sign}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}}} + \frac{{\partial {{a}_{2}}}}{{\partial x}}\int {{{v}_{x}}v_{z}^{2}{\text{sig}}{{{\text{n}}}^{2}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}}} - \\ - \,\,e{{E}_{0}}\int {v_{z}^{2}{\text{sign}}\left( {{{v}_{x}}} \right){{d}^{3}}{\mathbf{v}}} = 0. \\ \end{gathered} $

В результате приходим к системе уравнений:

(9)
$\left\{ {\begin{array}{*{20}{c}} {\frac{4}{5}\left( {\nu + \frac{{{{g}_{0}}}}{{{\tau }}}} \right){{a}_{1}} + \frac{{{{v}_{{\text{F}}}}}}{4}\frac{{\partial {{a}_{2}}}}{{\partial x}} = \frac{4}{5}e{{E}_{0}},} \\ {{{a}_{2}} = - \frac{{5{{v}_{{\text{F}}}}}}{{16\nu }}\frac{{\partial {{a}_{1}}}}{{\partial x}}.~~~~~~~~~~~~~~~~} \end{array}~} \right.$

Откуда следует, что

$\frac{{{{\partial }^{2}}{{a}_{1}}}}{{\partial {{x}^{2}}}} - \frac{{{{{16}}^{2}}{{\nu }^{2}}}}{{{{5}^{2}}v_{{\text{F}}}^{2}}}\left( {1 + \frac{{{{g}_{0}}}}{{\nu \tau }}} \right){{a}_{1}} = - \frac{{{{{16}}^{2}}{{\nu }^{2}}}}{{{{5}^{2}}v_{{\text{F}}}^{2}}}\frac{{e{{E}_{0}}}}{\nu },$
или
(10)
$\frac{{{{\partial }^{2}}{{a}_{1}}}}{{\partial {{x}^{2}}}} - {{{{\lambda }}}^{2}}{{a}_{1}} = - {{{{\lambda }}}^{2}}\frac{{e{{E}_{0}}}}{{\nu {{\beta }^{2}}}},$
где ντ = 1 – iωτ = 1 – iτΩvF/b = 1 – iΩ/Δ = Ψ/Δ, Ψ = Δ – iΩ – безразмерная комплексная частота рассеяния электронов; тогда $\beta = \sqrt {1 + {{{{g}_{0}}} \mathord{\left/ {\vphantom {{{{g}_{0}}} {\nu \tau }}} \right. \kern-0em} {\nu \tau }}} = $ $ = \sqrt {1 + {{{{g}_{0}}\Delta } \mathord{\left/ {\vphantom {{{{g}_{0}}\Delta } {{\Psi }}}} \right. \kern-0em} {{\Psi }}}} ;$ λ = 16νβ/5vF.

Моментный коэффициент a1(x) найдем, решая неоднородное дифференциальное уравнение второго порядка (10):

(11)
${{a}_{1}}\left( x \right) = {{A}_{0}} + {{C}_{1}}{\text{exp}}\left( {\lambda x} \right) + {{C}_{2}}{\text{exp}}\left( { - \lambda x} \right),$
где A0 = eE0/νβ2; C1, C2 – константы интегрирования.

Тогда из второго уравнения системы (9) следует, что

(12)
${{a}_{2}}\left( x \right) = {{\beta }}{{C}_{2}}{\text{exp}}\left( { - \lambda x} \right) - \beta {{C}_{1}}{\text{exp}}\left( {\lambda x} \right).$

Подставив (11) и (12) в (6), найдем общий вид решения уравнения (5), т.е.

(13)
$\begin{gathered} g = \left( {{{A}_{0}} + {{C}_{1}}{\text{exp}}\left( {\lambda x} \right) + {{C}_{2}}{\text{exp}}\left( { - \lambda x} \right)} \right){{v}_{z}} + \\ + \,\,\left( {{{\beta }}{{C}_{2}}{\text{exp}}\left( { - \lambda x} \right) - {{\beta }}{{C}_{1}}{\text{exp}}\left( {\lambda x} \right)} \right){{v}_{z}}{\text{sign}}\left( {{{v}_{x}}} \right). \\ \end{gathered} $

Применим граничные условия на верхней и нижней границах слоя для нахождения коэффициентов C1 и C2:

$\left\{ {\begin{array}{*{20}{c}} {g\left( {{{v}_{x}},x} \right) = {{q}_{1}}g\left( { - {{v}_{x}},x} \right),\,\,\,\,{{v}_{x}} < 0,~} \\ {g\left( {{{v}_{x}},x} \right) = {{q}_{2}}g\left( { - {{v}_{x}},x} \right),\,\,\,\,{{v}_{x}} > 0,} \end{array}} \right.$
где q1 и q2 – коэффициенты зеркальности его поверхностей.

С учетом (13), система граничных условий может быть представлена как

$\left\{ {\begin{array}{*{20}{c}} {{{A}_{0}} + {{C}_{1}}{\text{exp}}\left( {\lambda b} \right) + {{C}_{2}}{\text{exp}}\left( { - \lambda b} \right) + \beta {{C}_{1}}{\text{exp}}\left( {\lambda b} \right) - \beta {{C}_{2}}{\text{exp}}\left( { - \lambda b} \right) = ~~~~} \\ { = {{q}_{1}}\left[ {{{A}_{0}} + {{C}_{1}}{\text{exp}}\left( {\lambda b} \right) + {{C}_{2}}{\text{exp}}\left( { - \lambda b} \right) + {{\beta }}{{C}_{2}}{\text{exp}}\left( { - \lambda b} \right) - {{\beta }}{{C}_{1}}{\text{exp}}\left( {\lambda b} \right)} \right],} \\ {{{A}_{0}} + {{C}_{1}} + {{C}_{2}} + \beta {{C}_{2}} - \beta {{C}_{1}} = {{q}_{2}}\left[ {{{A}_{0}} + {{C}_{1}} + {{C}_{2}} + {{\beta }}{{C}_{1}} - {{\beta }}{{C}_{2}}} \right].~~~~~~~~~} \end{array}} \right.$

Откуда

$\left\{ \begin{gathered} {{D}_{1}} = \frac{{\left( {1 - {{q}_{1}}} \right)\left( {{{q}_{2}} - {{\beta }}{{q}_{2}} - {{\beta }} - 1} \right) - {\text{exp}}\left( { - {{\lambda }}b} \right)\left( {1 - {{q}_{2}}} \right)\left( {{{\beta }}{{q}_{1}} + {{q}_{1}} + {{\beta }} - 1} \right)}}{{{\text{exp}}\left( { - {{\lambda }}b} \right)\left( {{{\beta }}{{q}_{1}} + {{q}_{1}} + {{\beta }} - 1} \right)\left( {1 - {{\beta }} - {{q}_{2}} - {{\beta }}{{q}_{2}}} \right) - {\text{exp}}\left( {{{\lambda }}b} \right)\left( {1 + {{\beta }} - {{q}_{1}} + {{\beta }}{{q}_{1}}} \right)\left( {{{q}_{2}} - {{\beta }}{{q}_{2}} - {{\beta }} - 1} \right)}} \hfill \\ {{D}_{2}} = \frac{{\left( {1 - {{q}_{1}}} \right)\left( {1 - {{\beta }} - {{q}_{2}} - {{\beta }}{{q}_{2}}} \right) - {\text{exp}}\left( {{{\lambda }}b} \right)\left( {1 - {{q}_{2}}} \right)\left( {1 + {{\beta }} - {{q}_{1}} + {{\beta }}{{q}_{1}}} \right)}}{{{\text{exp}}\left( { - {{\lambda }}b} \right)\left( {{{\beta }}{{q}_{1}} + {{q}_{1}} + {{\beta }} - 1} \right)\left( {1 - {{\beta }} - {{q}_{2}} - {{\beta }}{{q}_{2}}} \right) - {\text{exp}}\left( {{{\lambda }}b} \right)\left( {1 + {{\beta }} - {{q}_{1}} + {{\beta }}{{q}_{1}}} \right)\left( {{{q}_{2}} - {{\beta }}{{q}_{2}} - {{\beta }} - 1} \right)}}, \hfill \\ \end{gathered} \right.$
где введены новые обозначения D1 = C1/A0, D2 = = C2/A0.

Далее запишем выражения (11) и (13) в следующем виде:

(14)
${{a}_{1}}\left( x \right) = {{A}_{0}}\left( {1 + {{D}_{1}}{\text{exp}}\left( {{{\lambda }}x} \right) + {{D}_{2}}{\text{exp}}\left( { - {{\lambda }}x} \right)} \right),$
(15)
$\begin{gathered} g = {{A}_{0}}\left[ {\left( {1 + {{D}_{1}}{\text{exp}}\left( {{{\lambda }}x} \right) + {{D}_{2}}{\text{exp}}\left( { - {{\lambda }}x} \right)} \right){{v}_{z}} + } \right. \\ \left. { + \,\,\left( {{{\beta }}{{D}_{2}}{\text{exp}}\left( { - {{\lambda }}x} \right) - {{\beta }}{{D}_{1}}{\text{exp}}\left( {{{\lambda }}x} \right)} \right){{v}_{z}}{\text{sign}}\left( {{{v}_{x}}} \right)} \right]. \\ \end{gathered} $

Конкретизировав с помощью (15) вид функции f1(x,v), найдем проекцию плотности тока j внутри слоя на координатную ось Z. Применяя формулу (3), имеем

(16)
${{j}_{z}} = \frac{{ne}}{m}{\text{exp}}\left( { - i{{\omega }}t} \right){{a}_{1}}\left( x \right).$

Выражение для локальной электрической проводимости слоя σ получим как следствие закона Ома в дифференциальной форме:

${{\sigma }} = \frac{{ne{{a}_{1}}\left( x \right)}}{{m{{E}_{0}}}}.$

Учитывая (14), имеем:

(17)
$\sigma = {{\sigma }_{0}}\frac{\Delta }{{{{{{\beta }}}^{2}}{{\Psi }}}}\left( {1 + {{D}_{1}}{\text{exp}}\left( {{{\lambda }}x} \right) + {{D}_{2}}{\text{exp}}\left( { - {{\lambda }}x} \right)} \right),$
где λ = 16νβ/5vF = 16ντβ/5τvF = 16βΨ/5b, σ0 = = ne2τ/m – объемная статическая удельная проводимость металла при отсутствии отклонения от закона Видемана–Франца.

Введя безразмерную координату внутри слоя ξ = x/b, запишем выражения для локальной проводимости (17) и коэффициентов D1, D2 в безразмерной форме:

(18)
$\begin{gathered} \sigma * = \frac{\sigma }{{{{\sigma }_{0}}}} = \frac{\Delta }{{{{{{\beta }}}^{2}}{{\Psi }}}} \times \\ \times \,\,\left( {1 + D_{1}^{*}{\text{exp}}\left( {\frac{{16{{\Psi \beta }}}}{5}{{\xi }}} \right) + D_{2}^{*}{\text{exp}}\left( { - \frac{{16{{\Psi \beta }}}}{5}{{\xi }}} \right)} \right), \\ \end{gathered} $
где

$D_{1}^{*} = \frac{{\left( {1 - {{q}_{1}}} \right)\left( {{{q}_{2}} - {{\beta }}{{q}_{2}} - {{\beta }} - 1} \right) - {\text{exp}}\left( { - \frac{{16{{\Psi \beta }}}}{5}} \right)\left( {1 - {{q}_{2}}} \right)\left( {{{\beta }}{{q}_{1}} + {{q}_{1}} + {{\beta }} - 1} \right)}}{{{\text{exp}}\left( { - \frac{{16{{\Psi \beta }}}}{5}} \right)\left( {{{\beta }}{{q}_{1}} + {{q}_{1}} + {{\beta }} - 1} \right)\left( {1 - {{\beta }} - {{q}_{2}} - {{\beta }}{{q}_{2}}} \right) - {\text{exp}}\left( {\frac{{16{{\Psi \beta }}}}{5}} \right)\left( {1 + {{\beta }} - {{q}_{1}} + {{\beta }}{{q}_{1}}} \right)\left( {{{q}_{2}} - {{\beta }}{{q}_{2}} - {{\beta }} - 1} \right)}},$
$D_{2}^{*} = \frac{{\left( {1 - {{q}_{1}}} \right)\left( {1 - {{\beta }} - {{q}_{2}} - {{\beta }}{{q}_{2}}} \right) - {\text{exp}}\left( {\frac{{16{{\Psi \beta }}}}{5}} \right)\left( {1 - {{q}_{2}}} \right)\left( {1 + {{\beta }} - {{q}_{1}} + {{\beta }}{{q}_{1}}} \right)}}{{{\text{exp}}\left( { - \frac{{16{{\Psi \beta }}}}{5}} \right)\left( {{{\beta }}{{q}_{1}} + {{q}_{1}} + {{\beta }} - 1} \right)\left( {1 - {{\beta }} - {{q}_{2}} - {{\beta }}{{q}_{2}}} \right) - {\text{exp}}\left( {\frac{{16{{\Psi \beta }}}}{5}} \right)\left( {1 + {{\beta }} - {{q}_{1}} + {{\beta }}{{q}_{1}}} \right)\left( {{{q}_{2}} - {{\beta }}{{q}_{2}} - {{\beta }} - 1} \right)}}.$

Проинтегрировав выражение (16), определяем полный ток через поперечное сечение слоя:

(19)
$\begin{gathered} I = \int\limits_0^b {{{j}_{z}}dS} = \frac{{neL}}{m}{\text{\;exp}}\left( { - i{{\omega }}t} \right)\int\limits_0^b {{{a}_{1}}\left( x \right)dx} = \\ = \frac{{n{{e}^{2}}L{{E}_{0}}}}{{m{{\nu }}{{{{\beta }}}^{2}}}}{\text{\;exp}}\left( { - i{{\omega }}t} \right) \times \\ \times \,\,\int\limits_0^b {\left( {1 + {{D}_{1}}{\text{exp}}\left( {{{\lambda }}x} \right) + {{D}_{2}}{\text{exp}}\left( { - {{\lambda }}x} \right)} \right)dx = } \\ = \frac{{{{\sigma }_{0}}Lb{{E}_{0}}{{\Delta }}}}{{{{\Psi }}{{{{\beta }}}^{2}}}}{\text{\;exp}}\left( { - i{{\omega }}t} \right) \times \\ \times \,\,\left( {1 + \frac{{{{D}_{1}}}}{{{{\lambda }}b}}\left( {1 - {\text{exp}}\left( {{{\lambda }}b} \right)} \right) + \frac{{{{D}_{2}}}}{{{{\lambda }}b}}\left( {1 - {\text{exp}}\left( { - {{\lambda }}b} \right)} \right)} \right). \\ \end{gathered} $

Формально, из (19) с помощью закона Ома в виде I = GU, где U – напряжение на концах слоя, можно получить формулу для расчета интегральной проводимости слоя G. Электрическое поле внутри слоя считаем однородным, поэтому U = EL, L – длина слоя.

(20)
$\begin{gathered} G = \frac{{{{G}_{0}}{{\Delta }}}}{{{{\Psi }}{{{{\beta }}}^{2}}}} \times \\ \times \,\,\left( {1 + \frac{{{{D}_{1}}}}{{{{\lambda }}b}}\left( {1 - {\text{exp}}\left( {{{\lambda }}b} \right)} \right) + \frac{{{{D}_{2}}}}{{{{\lambda }}b}}\left( {1 - {\text{exp}}\left( { - {{\lambda }}b} \right)} \right)} \right), \\ \end{gathered} $
где G0 = σ0b.

Заметим, что при проведении численных расчетов результаты, полученные после применения формул (17) и (20) в случае отсутствия поправки к закону Видемана–Франца (когда g0 = 0) совпадают с результатами работы [20], в которой использовали другой математический подход к проблеме.

Запишем выражение (20) в безразмерном виде:

(21)
$G* = \frac{G}{{{{G}_{0}}}} = \frac{{{\Delta }}}{{\Psi {{\beta }^{2}}}}\left( {1 + \frac{{5D_{1}^{*}}}{{16\Psi \beta }}\left( {1 - {\text{exp}}\left( {\frac{{16\Psi \beta }}{5}} \right)} \right) + \frac{{5D_{2}^{*}}}{{16\Psi \beta }}\left( {1 - {\text{exp}}\left( { - \frac{{16\Psi \beta }}{5}} \right)} \right)} \right).$

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

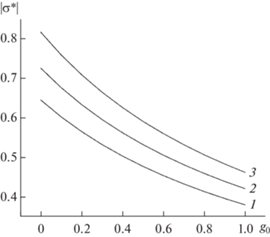
На рис. 1 приведены графики зависимости модуля безразмерной удельной электрической проводимости тонкого металлического слоя σ* (18) от числового параметра g0 который характеризует степень отклонения от закона Видемана–Франца. Все кривые построены при одинаковых значениях безразмерной обратной длины свободного пробега электронов ∆, безразмерной частоты электрического поля Ω и коэффициентов зеркальности q1 и q2 и при различных значениях безразмерной координаты внутри слоя ξ. Из рис. 1 видно, что модуль безразмерной удельной электрической проводимости слоя в значительной степени зависит от параметра g0.

Рис. 1.

Зависимость модуля безразмерной удельной электрической проводимости тонкого металлического слоя от числового параметра g0 при различных значениях безразмерной координаты внутри слоя ξ = 0.1 (1); 0.2 (2); 0.5 (3). Для всех кривых ∆ = 1; Ω = 0.1; q1 = = q2 = 0.1.

На рис. 2 и 3 построены графики зависимостей модуля и аргумента безразмерной удельной электрической проводимости σ* от безразмерной координаты внутри слоя ξ. Числовой параметр g0 варьируется для каждой кривой в соответствующих физическому смыслу пределах. На рис. 2 видно, что при одинаковых коэффициентах зеркальности поверхностей слоя модуль безразмерной удельной электрической проводимости имеет выраженный максимум, величина которого определяется конкретным значением параметра g0. Как следует из рис. 3, зависимость аргумента безразмерной удельной электрической проводимости от безразмерной координаты, установленная в аналогичных условиях, имеет обратную тенденцию с выраженным минимумом.

Рис. 2.

Зависимость модуля безразмерной удельной электрической проводимости тонкого металлического слоя от безразмерной координаты внутри слоя ξ при различных значениях параметра g0 = 0.01 (1); 0.5 (2);1 (3). Для всех кривых ∆ = 0.1; Ω = 0.5; q1 = q2 = 0.5.

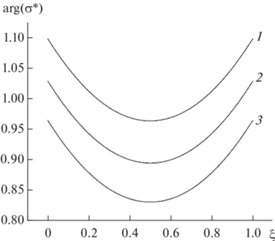
Рис. 3.

Зависимость аргумента безразмерной удельной электрической проводимости тонкого металлического слоя от безразмерной координаты внутри слоя ξ при различных значениях параметра g0 = 0.01 (1); 0.5 (2); 1 (3). Для всех кривых ∆ = 0.1; Ω = 0.5; q1 = = q2 = 0.5.

На рис. 4 представлен график зависимости модуля безразмерной удельной электрической проводимости σ* от безразмерной обратной длины свободного пробега электронов ∆ при варьировании числового параметра g0 для каждой кривой. Из анализа зависимостей можно сделать вывод, что выход модуля безразмерной удельной электрической проводимости на свои асимптотические значения определяется величиной параметра g0.

Рис. 4.

Зависимость модуля безразмерной удельной электрической проводимости тонкого металлического слоя от безразмерной обратной длины свободного пробега электронов ∆ при различных значениях параметра g0 = 0.01 (1); 0.5 (2); 1 (3). Для всех кривых ξ = = 0.5; Ω = 0.5; q1 = q2 = 0.5.

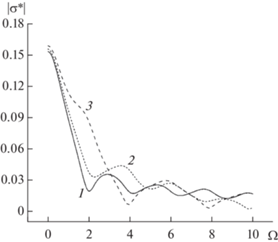
При построении графиков безразмерной удельной электрической проводимости слоя σ* особое внимание следует уделить зависимости ее модуля от безразмерной частоты электрического поля Ω при различных значениях безразмерной координаты внутри слоя ξ (рис. 5). Такой нетривиальный характер поведения кривых по мере увеличения безразмерной координаты ξ связан, по-видимому, с проявлением резонансных эффектов, наблюдаемых при отражении электронов от нижней и верхней поверхностей слоя металла.

Рис. 5.

Зависимость модуля безразмерной удельной электрической проводимости тонкого металлического слоя от безразмерной частоты электрического поля Ω при различных значениях безразмерной координаты внутри слоя ξ = 0.1 (1); 0.2 (2); 0.5 (3). Для всех кривых ∆ = 0.1; g0 = 0.95; q1 = q2 = 0.15.

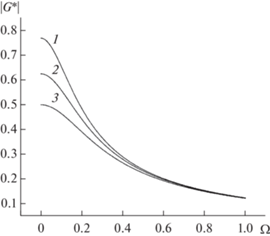
На рис. 6 показана зависимость модуля безразмерной интегральной электрической проводимости G* (21) от безразмерной частоты электрического поля Ω при фиксированных значениях безразмерной обратной длины свободного пробега электронов и коэффициентов зеркальности поверхностей слоя и различных значениях параметра g0. Из хода кривых на рисунке видно, что наибольшее отличие величины модулей интегральной проводимости слоя по мере возрастания отклонения от закона Видемана–Франца наблюдается в статическом случае, тогда как дальнейшее увеличение безразмерной частоты электрического поля приводит к слиянию этих зависимостей.

Рис. 6.

Зависимость модуля безразмерной интегральной электрической проводимости тонкого металлического слоя от безразмерной частоты электрического поля Ω при различных значениях параметра g0 = = 0.3 (1); 0.6 (2); 1 (3). Для всех кривых ∆ = 0.125; q1 = = q2 = 0.25.

Теоретические результаты вычисления электрической проводимости тонкого металлического слоя показывают существенное влияние отклонения от закона Видемана–Франца на рассматриваемую физическую систему. Для малых проводящих объектов это подтверждается сравнением полученных расчетных значений проводимости с экспериментальными данными [21] и позволяет сделать вывод о целесообразности применения такого теоретического подхода к реальным системам.

ЗАКЛЮЧЕНИЕ

В настоящей работе теоретически описано отклонение от закона Видемана–Франца в тонком слое металла без учета квантовых эффектов. Из расчетов следует, что такое отклонение может быть значительным, что подтверждено экспериментальными данными, известными из литературы. Поэтому возникает необходимость применения рассмотренной теории к непосредственному вычислению электрической проводимости тонких слоев из достаточно чистых металлов при низких температурах при практических и технических приложениях, например, при промышленном изготовлении интегральных микросхем.

Список литературы

  1. Петров Ю.И. Физика малых частиц. М.: Наука, 1984. 360 с.

  2. Sondheimer E.H. // Phys. Rev. 1950. V. 80. P. 401.

  3. Булыгин В.С. // Физическое образование в ВУЗах. 2004. Т. 10. № 4. С. 75.

  4. Снарский А.А., Женировский М.И., Безсуднов И.В. // Термоэлектричество. 2006. № 3. С. 59.

  5. Моисеев И.О., Юшканов А.А., Яламов Ю.И. // Оптика и спектроскопия. 2006. Т. 101. № 5. С. 857.

  6. Медведь А.И. // Термоэлектричество. 2006. № 4. С. 19.

  7. Wakeham N., Bangura A.F., Xu X., Mercure J-F., Greenblatt M., Hussey N.E. // Nature Commun. 2011. V. 19. № 2. P. 396. https://doi.org/10.1038/ncomms1406

  8. Gurzhi R.N. // JETP. 1963. V. 17. № 2. P. 521.

  9. Гуржи Р.Н. // Усп. физ. Наук. 1968. Т. 94. Вып. 4. С. 689.

  10. Andreev A.V., Kivelson S., Spivak B. // Phys. Rev. Lett. 2011. V. 106. P. 256804. https://doi.org/10.1103/PhysRevLett.106.256804

  11. Alekseev P. S. // Phys. Rev. Lett. 2016. V. 117. P. 166601. https://doi.org/10.1103/PhysRevLett.117.166601

  12. Levitov L., Falkovich G. // Nature Phys. 2016. V. 12. № 7. P. 672. https://doi.org/10.1038/nphys3667

  13. Савенко О.В. // Вестник МГОУ. Серия: Физика-Математика. 2016. № 4. С. 43. DOI

  14. Кузнецова И.А., Романов Д.Н., Савенко О.В., Юшканов А.А. // Микроэлектроника. 2017. Т. 46. № 4. С. 275. https://doi.org/10.7868/S0544126917040032

  15. Кузнецова И.А., Савенко О.В., Юшканов А.А. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2017. № 11. С. 52. https://doi.org/10.7868/s0207352817110063

  16. Бабич А.В., Погосов В.В. // ФТТ. 2013. Т. 55. Вып. 1. С. 177.

  17. Русаков О.В., Завитаев Э.В., Юшканов А.А. // ФТТ. 2012. Т. 54. Вып. 6. С. 1041.

  18. Завитаев Э.В., Русаков О.В., Юшканов А.А. // Вестник МГОУ. Серия: Физика-Математика. 2012. № 2. С. 122.

  19. De Gennaro S., Rettori A. // J. Phys. F: Metal Phys. 1984. V. 14. P. 237.

  20. Уткин А.И., Завитаев Э.В., Юшканов А.А. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2016. № 9. С. 89. https://doi.org/10.7868/S0207352816090158

  21. Русаков О.В. Отклонение от закона Видемана-Франца и скин-эффект в тонкой цилиндрической проволоке из металла: Дис. … канд. физ.-мат. наук: 01.04.02. М.: МГОУ, 2013. 103 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал