Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2023, № 3, стр. 69-73
Моделирование потенциальной энергии взаимодействия двух атомов с помощью решения системы нелинейных уравнений
В. П. Кощеев a, *, Ю. Н. Штанов b, **
a Московский авиационный институт (национальный исследовательский университет,
филиал “Стрела”
140180 Московская область, Жуковский, Россия
b Тюменский индустриальный университет, филиал ТИУ в г. Сургуте
628404 Сургут, Россия
* E-mail: koshcheev1@yandex.ru
** E-mail: yuran1987@mail.ru
Поступила в редакцию 26.06.2022
После доработки 21.08.2022
Принята к публикации 21.08.2022
- EDN: GKSDEG
- DOI: 10.31857/S1028096023020048
Аннотация
В первом порядке теории возмущений показано, что потенциальная энергия взаимодействия двух атомов может быть вычислена с помощью решения системы нелинейных уравнений. Систему уравнений строили как с учетом, так и без учета принципа Паули, а атомный формфактор вычисляли с использованием волновых функций, которые аппроксимируют решение уравнения Хартри–Фока для изолированных атомов азота. График потенциальной энергии взаимодействия двух атомов азота удовлетворительно согласуется с известными результатами при учете принципа Паули. Показано, что без учета принципа Паули и коллективных колебаний электронов атомов получить согласие с экспериментом не представляется возможным. Показано, что полная энергия двухатомной молекулы является функционалом, который зависит от электронной плотности изолированных атомов.
ВВЕДЕНИЕ
Новый подход к вычислению потенциальной энергии двухатомных молекул [1] получил свое развитие в [2–5], где было построено уравнение полной энергии двухатомной молекулы в первом порядке теории возмущений с учетом принципа Паули и коллективных (плазменных) колебаний электронов атомов. В настоящей работе вычислена потенциальная энергия взаимодействия двух атомов с помощью решения системы нелинейных уравнений.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Двухатомную молекулу будем описывать с помощью стационарного уравнения Шредингера:
Гамильтониан уравнения (1) представим в виде:
(3)
$\begin{gathered} U = \frac{{{{Z}_{1}}{{Z}_{2}}{{e}^{2}}}}{{\left| {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}}} \right|}} + \sum\limits_{{{j}_{1}}{\kern 1pt} \, = \,{\kern 1pt} 1}^{{{Z}_{1}}} {\sum\limits_{{{j}_{2}}{\kern 1pt} \, = {\kern 1pt} \,1}^{{{Z}_{2}}} {\frac{{{{e}^{2}}}}{{\left| {{{{\mathbf{r}}}_{1}} + {{{\mathbf{r}}}_{{1{{j}_{1}}}}} - {{{\mathbf{r}}}_{2}} - {{{\mathbf{r}}}_{{2{{j}_{2}}}}}} \right|}}} } - \\ - \,\,\sum\limits_{{{j}_{1}}{\kern 1pt} \, = \,{\kern 1pt} 1}^{{{Z}_{1}}} {\frac{{{{Z}_{2}}{{e}^{2}}}}{{\left| {{{{\mathbf{r}}}_{1}} + {{{\mathbf{r}}}_{{1{{j}_{1}}}}} - {{{\mathbf{r}}}_{2}}} \right|}}} - \sum\limits_{{{j}_{2}}\, = \,{\kern 1pt} 1}^{{{Z}_{2}}} {\frac{{{{Z}_{1}}{{e}^{2}}}}{{\left| {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}} - {{{\mathbf{r}}}_{{2{{j}_{2}}}}}} \right|}}} , \\ \end{gathered} $Решение уравнения (1) с гамильтонианом (2) будем искать с помощью теории возмущений ψ = = ψ0 + ψ1 +… и E = E0 + E1 +… . Потенциальную энергию (электронные термы) двухатомной молекулы будем искать в первом порядке теории возмущений:
(4)
${{E}^{1}} = \left\langle {\left. {{{\psi }^{0}}} \right|U\left| {{{\psi }^{0}}} \right.} \right\rangle ,$Гамильтониан H 0 представим в виде ${{H}^{0}} = $ $ = H_{1}^{0} + H_{2}^{0},$ где $H_{i}^{0}$ – гамильтониан i-го атома; i = = 1, 2. Решение уравнения Шредингера H 0ψ0 = = E0ψ0, будем искать в виде ${{\psi }^{0}} = \psi _{1}^{0}\psi _{2}^{0}$ и ${{E}^{0}} = E_{1}^{0} + E_{2}^{0},$ уравнение Шредингера для i-го изолированного атома имеет вид:
где $\psi _{i}^{0} = \psi _{i}^{0}\left( {{{{\mathbf{r}}}_{{i1}}},{{{\mathbf{r}}}_{{i2}}},\,\,...\,\,,{{{\mathbf{r}}}_{{i{{Z}_{i}}}}}} \right).$Известно, что волновая функция двухатомной молекулы должна быть антисимметричной относительно перестановки координат, определяющих местоположения электронов. Если она выбрана в виде произведения волновых функций изолированных атомов ${{\psi }^{0}} = \psi _{1}^{0}\psi _{2}^{0},$ то обменные силы будут учитываться отдельно для электронов изолированных атомов и отдельно для электронов, которые принадлежат первому и второму атомам.
Флуктуации потенциальной энергии взаимодействия (3) вызваны квантовыми флуктуациями, которые испытывают электроны. Известно [7], что коллективные колебания атомных ядер в двухатомной молекуле можно описать с помощью уравнения движения для одной частицы с приведенной массой:
где m1 и m2 – массы ядер первого и второго атома соответственно.Коллективные колебания электронов в двухатомной молекуле будем описывать с помощью уравнения движения для одной частицы с приведенной массой:
где me – масса покоя электрона, а χ – варьируемый параметр, который будет определен ниже. Если χ = 0.5, то это задача двух тел, но в коллективных колебаниях участвуют электроны двух атомов.Так как средний квадрат амплитуды ядерных колебаний много меньше среднего квадрата амплитуды электронных колебаний в одной и той же потенциальной яме, при усреднении потенциальной энергии взаимодействия двух атомов учитывали только коллективные колебания электронов. Усреднение по квантовым флуктуациям местоположения электронов будем осуществлять с помощью метода [8], который Бете использовал для вычисления атомного формфактора, а усреднение по коллективным колебаниям электронов выполним по квадрату модуля волновой функции гармонического осциллятора в основном состоянии. Соответствующие средние будем обозначать $\left\langle {\left. {\psi _{1}^{0}} \right|U\left| {\psi _{1}^{0}} \right.} \right\rangle = {{\left\langle {...} \right\rangle }_{{{\text{e}}1}}},$ $\left\langle {\left. {\psi _{2}^{0}} \right|U\left| {\psi _{2}^{0}} \right.} \right\rangle = {{\left\langle {...} \right\rangle }_{{{\text{e}}2}}}$ и ${{\left\langle {\left. {{{\psi }^{0}}} \right|U\left| {{{\psi }^{0}}} \right.} \right\rangle }_{{{\text{pl}}}}}$ = ${{\left\langle {...} \right\rangle }_{{{\text{pl}}}}}.$
Разложим потенциальную энергию взаимодействия (3) в интеграл Фурье:
(6)
$\begin{gathered} U = \int {\frac{{{{d}^{3}}{\mathbf{k}}}}{{{{{\left( {2\pi } \right)}}^{3}}}}} \left( {\frac{{4\pi {{Z}_{1}}{{Z}_{2}}{{e}^{2}}}}{{{{k}^{2}}}}exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}}} \right)} \right) + } \right. \\ + \,\,\frac{{4\pi {{e}^{2}}}}{{{{k}^{2}}}}\sum\limits_{{{j}_{1}}{\kern 1pt} \, = \,{\kern 1pt} 1}^{{{Z}_{1}}} {\sum\limits_{{{j}_{2}}{\kern 1pt} \, = {\kern 1pt} \,1}^{{{Z}_{2}}} {exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{{1{{j}_{1}}}}} - {{{\mathbf{r}}}_{{2{{j}_{2}}}}}} \right)} \right)} } - \\ - \,\,\frac{{4\pi {{Z}_{2}}{{e}^{2}}}}{{{{k}^{2}}}}\sum\limits_{{{j}_{1}}{\kern 1pt} \, = {\kern 1pt} \,1}^{{{Z}_{1}}} {exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{2}} - {{{\mathbf{r}}}_{{1{{j}_{1}}}}}} \right)} \right)} - \\ \left. { - \,\,\frac{{4\pi {{Z}_{1}}{{e}^{2}}}}{{{{k}^{2}}}}\sum\limits_{{{j}_{2}}{\kern 1pt} \, = \,{\kern 1pt} 1}^{{{Z}_{2}}} {exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{{2{{j}_{2}}}}}} \right)} \right)} } \right). \\ \end{gathered} $(7)
$\begin{gathered} {{\left\langle U \right\rangle }_{{e1}}} = \int {\frac{{{{d}^{3}}{\mathbf{k}}}}{{{{{\left( {2\pi } \right)}}^{3}}}}\left( {\frac{{4\pi {{Z}_{1}}{{Z}_{2}}{{e}^{2}}}}{{{{k}^{2}}}}exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}}} \right)} \right) + } \right.} \\ + \,\,\frac{{4\pi {{e}^{2}}}}{{{{k}^{2}}}}{{\left\langle {\sum\limits_{{{j}_{1}}{\kern 1pt} \, = \,{\kern 1pt} 1}^{{{Z}_{1}}} {\sum\limits_{{{j}_{2}}{\kern 1pt} \, = \,{\kern 1pt} 1}^{{{Z}_{2}}} {exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{{1{{j}_{1}}}}} - {{{\mathbf{r}}}_{{2{{j}_{2}}}}}} \right)} \right)} } } \right\rangle }_{{{\text{e}}1}}} - \\ - \,\,\frac{{4\pi {{Z}_{2}}{{e}^{2}}}}{{{{k}^{2}}}}{{\left\langle {\sum\limits_{{{j}_{1}}{\kern 1pt} \, = \,{\kern 1pt} 1}^{{{Z}_{1}}} {exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{2}} - {{{\mathbf{r}}}_{{1{{j}_{1}}}}}} \right)} \right)} } \right\rangle }_{{{\text{e}}1}}} - \\ \left. { - \,\,\frac{{4\pi {{Z}_{1}}{{e}^{2}}}}{{{{k}^{2}}}}\sum\limits_{{{j}_{2}}{\kern 1pt} \, = \,{\kern 1pt} 1}^{{{Z}_{2}}} {exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{{2{{j}_{2}}}}}} \right)} \right)} } \right), \\ {{\left\langle {\sum\limits_{{{j}_{1}}{\kern 1pt} \, = \,{\kern 1pt} 1}^{{{Z}_{1}}} {\sum\limits_{{{j}_{2}}\,{\kern 1pt} = \,{\kern 1pt} 1}^{{{Z}_{2}}} {exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{{1{{j}_{1}}}}} - {{{\mathbf{r}}}_{{2{{j}_{2}}}}}} \right)} \right)} } } \right\rangle }_{{{\text{e}}1}}} = \\ = {{F}_{1}}\left( k \right)\sum\limits_{{{j}_{2}}{\kern 1pt} \, = \,{\kern 1pt} 1}^{{{Z}_{2}}} {exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{{2{{j}_{2}}}}}} \right)} \right)} , \\ {{\left\langle {\sum\limits_{{{j}_{1}}{\kern 1pt} \, = \,{\kern 1pt} 1}^{{{Z}_{1}}} {exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{2}} - {{{\mathbf{r}}}_{{1{{j}_{1}}}}}} \right)} \right)} } \right\rangle }_{{{\text{e}}1}}} = {{F}_{1}}\left( k \right)exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}}} \right)} \right), \\ \end{gathered} $Проведем усреднение ${{\left\langle U \right\rangle }_{{{\text{e}}1}}}$ по квадрату модуля волновой функции электронов второго атома:
(8)
$\begin{gathered} {{\left\langle U \right\rangle }_{{{\text{e}}1,{\text{e}}2}}} = \int {\frac{{{{d}^{3}}{\mathbf{k}}}}{{{{{\left( {2\pi } \right)}}^{3}}}}} \times \\ \times \,\,\left( {\frac{{4\pi {{Z}_{2}}{{e}^{2}}}}{{{{k}^{2}}}}\left( {{{Z}_{1}} - {{F}_{1}}\left( k \right)} \right)exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}}} \right)} \right) - } \right. \\ - \,\,\left. {\frac{{4\pi {{e}^{2}}}}{{{{k}^{2}}}}\left( {{{Z}_{1}} - {{F}_{1}}\left( k \right)} \right){{{\left\langle {\sum\limits_{{{j}_{2}}{\kern 1pt} \, = \,{\kern 1pt} 1}^{{{Z}_{2}}} {exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{{2{{j}_{2}}}}}} \right)} \right)} } \right\rangle }}_{{{\text{e}}2}}}} \right), \\ {{\left\langle {\sum\limits_{{{j}_{2}}\,{\kern 1pt} = \,{\kern 1pt} 1}^{{{Z}_{2}}} {exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{{2{{j}_{2}}}}}} \right)} \right)} } \right\rangle }_{{{\text{e}}2}}} = {{F}_{2}}(k)exp\left( {i{\mathbf{k}}\left( {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}}} \right)} \right). \\ \end{gathered} $Усредним потенциальную энергию взаимодействия двух атомов по квадрату модуля волновой функции гармонического осциллятора в основном состоянии:
(9)
$\begin{gathered} {{\left\langle {U(r)} \right\rangle }_{{e1,e2,pl}}} = \\ = \int {\frac{{{{d}^{3}}{\mathbf{k}}}}{{{{{\left( {2\pi } \right)}}^{3}}}}} \frac{{4\pi {{e}^{2}}}}{{{{k}^{2}}}}\left[ {{{Z}_{1}} - {{F}_{1}}\left( k \right)} \right]\left[ {{{Z}_{2}} - {{F}_{2}}\left( k \right)} \right] \times \\ \times \,\,exp\left[ { - {{k}^{2}}{{\sigma }^{2}}} \right]exp\left( {i{\mathbf{kr}}} \right), \\ \end{gathered} $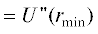 есть значение второй производной в минимуме потенциальной энергии молекулы.
есть значение второй производной в минимуме потенциальной энергии молекулы.
Аналогично тому, как это делается в кинетической теории [9], добавим к выражению для фурье-компоненты потенциальной энергии взаимодействия двух атомов множитель (1 – F(k)/Z), с помощью которого будем учитывать принцип Паули. Величина F(k)/Z является фурье-компонентой плотности распределения электронов, которая нормирована на единицу. Тогда
(10)
$\begin{gathered} {{U}_{4}}\left( {k,\sigma } \right) = \frac{{4\pi {{Z}_{1}}{{Z}_{2}}{{e}^{2}}}}{{{{k}^{2}}}}{{\left[ {1 - \frac{{{{F}_{1}}\left( k \right)}}{{{{Z}_{1}}}}} \right]}^{2}} \times \\ \times \,\,{{\left[ {1 - \frac{{{{F}_{2}}\left( k \right)}}{{{{Z}_{2}}}}} \right]}^{2}}\exp \left[ { - {{k}^{2}}{{\sigma }^{2}}} \right]. \\ \end{gathered} $Выражение для потенциальной энергии взаимодействия двух атомов (электронного терма) имеет вид:
(11)
${{U}_{{2,4}}}\left( r \right) = \int {{{U}_{{2,4}}}\left( {k,\sigma } \right)} \exp \left( {i{\mathbf{kr}}} \right)\frac{{{{d}^{3}}{\mathbf{k}}}}{{{{{\left( {2\pi } \right)}}^{3}}}},$Условие применимости поправки в первом порядке теории возмущений к энергии системы в невозмущенном состоянии имеет вид:
Учет коллективных колебаний электронов приводит к самосогласованной системе уравнений: где U(r) зависит от σ согласно (11).РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Известно [10], что вместо многочастичного уравнения Шредингера (5) строят одночастичные приближения на основе уравнений Хартри–Фока или формализма теории функционала плотности. Например, фурье-компонента плотности распределения электронов атома азота имеет вид:
(13)
$F\left( k \right) = \int {n\left( {\mathbf{r}} \right)exp} \left( { - i{\mathbf{kr}}} \right){{d}^{3}}{\mathbf{r}},$Таким образом, полная энергия двухатомной молекулы в первом порядке теории возмущений является функционалом
(14)
$E = E_{1}^{0}[{{n}_{1}}({\mathbf{r}})] + E_{2}^{0}[{{n}_{2}}({\mathbf{r}})] + U[{{n}_{1}}({\mathbf{r}}),{{n}_{2}}({\mathbf{r}})],$Зависимость полной энергии изолированного атома от его электронной плотности $E_{1}^{0} = E_{1}^{0}[{{n}_{1}}({\mathbf{r}})]$ для уравнений Хартри–Фока и уравнений теории функционала плотности подробно обсуждали в [10]. Волновые функции, которые аппроксимируют решение уравнения Хартри–Фока для изолированных атомов азота, и энергия $E_{i}^{0}$ представлены в [11].
Результаты численного решения системы уравнений (12) показаны на рис. 1 для молекул азота. Имеют место точки пересечения графика гиперболы 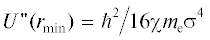 с расчетными значениями второй производной потенциальной энергии U2,4(r) в точке возможного экстремума rmin при различных значениях
с расчетными значениями второй производной потенциальной энергии U2,4(r) в точке возможного экстремума rmin при различных значениях 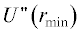 для молекулы азота в зависимости от параметра χ2,4. График потенциальной энергии взаимодействия двух атомов азота в зависимости от расстояния
между ними для двух точек пересечения, которые определяют единственное решение системы
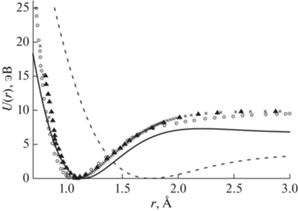
нелинейных уравнений (12), был вычислен с помощью [12, 13] (рис. 2). На рис. 3 представлено сравнение графика на рис. 2а с результатами [14–16]. Видно, что учет принципа Паули приближает результаты к данным [14–16]. Дополнительные материалы размещены в [13].
для молекулы азота в зависимости от параметра χ2,4. График потенциальной энергии взаимодействия двух атомов азота в зависимости от расстояния
между ними для двух точек пересечения, которые определяют единственное решение системы
нелинейных уравнений (12), был вычислен с помощью [12, 13] (рис. 2). На рис. 3 представлено сравнение графика на рис. 2а с результатами [14–16]. Видно, что учет принципа Паули приближает результаты к данным [14–16]. Дополнительные материалы размещены в [13].
Рис. 1.
График второй производной потенциальной энергии 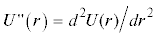 в точке возможного экстремума rmin при различных значениях σ для молекулы азота: U4 (сплошная линия); U2 (пунктир). Гипербола
в точке возможного экстремума rmin при различных значениях σ для молекулы азота: U4 (сплошная линия); U2 (пунктир). Гипербола 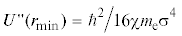 при χ = 0.4792 обозначена кружками, при χ = 0.533 – квадратиками. Точки пересечения
при χ = 0.4792 обозначена кружками, при χ = 0.533 – квадратиками. Точки пересечения
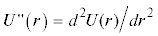 с гиперболой для U4 – ⚫ и U2 – ◼.
с гиперболой для U4 – ⚫ и U2 – ◼.
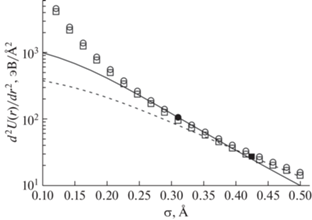
Рис. 2.
Потенциальная энергия взаимодействия двух атомов азота в зависимости от расстояния между ними: a – ${r \mathord{\left/ {\vphantom {r {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}} \in \left[ {0;7} \right];$ б – ${r \mathord{\left/ {\vphantom {r {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}} \in \left[ {5;12} \right].$ Сплошная линия – расчет U4 при χ = 0.4792, пунктир – расчет U2 при χ = 0.533.
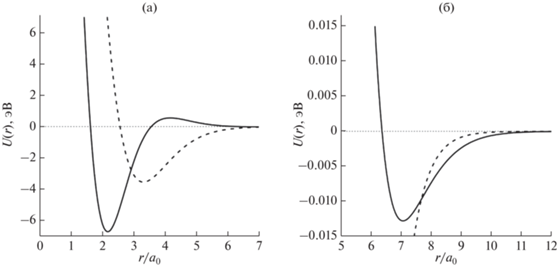
Рис. 3.
Результаты сравнения потенциальной энергии взаимодействия двух атомов азота, полученные по формуле (11) при χ = 0.4792 (U4, сплошная линия) и χ = 0.533 (U2, пунктир), а также расчеты [14] (▲), [15] (ο), [16] (×).
Список литературы
Кощеев В.П., Штанов Ю.Н. // Письма в ЖТФ. 2018. Т. 44. Вып. 13. С. 28. https://doi.org/10.21883/PJTF.2018.13.46324.17133
Кощеев В.П., Штанов Ю.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2019. № 8. С. 53. https://doi.org/10.1134/S0207352819080079
Кощеев В.П., Штанов Ю.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2020. № 8. С. 97. https://doi.org/10.31857/S1028096020080105
Кощеев В.П., Штанов Ю.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2022. № 2. С. 109. https://doi.org/10.31857/S1028096022020066
Кощеев В.П., Штанов Ю.Н. // Письма в ЖТФ. 2022. Т. 48. Вып. 10. С. 28. https://doi.org/10.21883/PJTF.2022.10.52553.19148
Дирак П.А.М. Принципы квантовой механики. М.: Наука, 1979. 479 с.
Ландау Л.Д., Лифшиц Е.М. Квантовая механика (нерелятивистская теория). М.: Наука, 1974. 752 с.
Бете Г. Квантовая механика. М.: Мир, 1965. 333 с.
Лифшиц Е.М., Питаевский Л.П. Физическая кинетика. М.: Физматлит, 2007. 536 с.
Сарры А.М., Сарры М.Ф. // ФТТ. 2012. Т. 54. Вып. 6. С. 1237. https://www.elibrary.ru/rcsqrj
Clementi E., Roetti C. // Atomic Data and Nuclear Data Tables. 1974. V. 14. № 3. P. 177. https://doi.org/10.1016/S0092-640X(74)80016-1
А.с. 2 020 617 054 (РФ). Программа для моделирования потенциальной энергии взаимодействия атомов с водородоподобными волновыми функциями / Роспатент. Штанов Ю.Н., Кощеев В.П. // Б.И. 2020. С. 1.
Штанов Ю.Н., Кощеев В.П., Моргун Д.А. Библиотека программ “JINRLIB”. URL: http://wwwinfo.jinr.ru/programs/jinrlib/tropics/index.html [Электронный ресурс] (дата обращения: 20.05.2022).
Seunghoon L., Huanchen Z., Sandeep S., Umrigar C. J., Kin-Lic Chan G. // J. Chem. Theory Comput. 2021. V. 17. № 6. P. 3414. https://doi.org/10.1021/acs.jctc.1c00205
Bhattacharya D., Shamasundar K.R., Emmanouilidou A. // J. Phys. Chem. A. 2021. V. 125. № 36. P. 7778. https://doi.org/10.1021/acs.jpca.1c04613
Xiangzhu Li, Paldus J. // J. Chem. Phys. 2008. V. 129. P. 054104. https://doi.org/10.1063/1.2961033
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования