Приборы и техника эксперимента, 2019, № 1, стр. 94-98

КОНСТРУКЦИЯ СМЕСИТЕЛЯ

Для безопасного приготовления смесей использовали технологию, в основе которой лежат следующие главные моменты: 1) быстрота смешения реагентов обеспечивается за счет разделения их на множество перемежающихся струй; 2) устраняется возможность образования застойных зон; 3) скорость движения смеси по напускному тракту всюду превышает нормальную скорость горения. Подходящим оказался смеситель на основе структуры из чередующихся отверстий для окислителя и горючего. Характерный размер структуры (расстояние между соседними отверстиями) выбирался достаточно малым, чтобы исключить возможность возникновения застойных зон путем образования отрывного циркуляционного течения, способствующего стабилизации пламени за счет переноса тепла и активных центров к свежей смеси обратными токами.

Изготовленный из нержавеющей стали смеситель содержал 48 капилляров (из нержавеющей стали) с внешним диаметром 0.1 cм и внутренним 0.04 cм, плотно упакованных в цилиндрический канал с внутренним диаметром 0.8 cм. Конструкция смесителя схематически представлена на рис. 1.

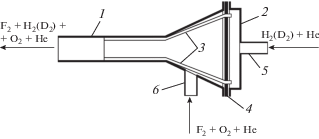
Через капилляры 3 (на рис. 1 показаны 2 капилляра из 48), используя ввод 5, подавали “предсмесь”, содержащую H₂ (или D₂), а через промежутки между капиллярами, используя ввод 6, – “предсмесь”, содержащую F₂. Обычно использовали “предсмеси” с составом 0.1H₂ (или D₂) + 0.9He и 0.3F₂ + 0.06O₂ + 0.64He, дающие при равном расходе требуемую рабочую смесь 0.15F₂ + 0.05H₂ + + 0.03O₂. Кислород добавляется для стабилизации смесей.

Концы капилляров впаивались с помощью свинцово-оловянного припоя в круглую латунную пластину 4 с 48 отверстиями. Пластина вакуумно плотно устанавливалась между корпусом 1 и фланцем 2. Эта пластина разделяла полости, через которые подавались “предсмеси” в смеситель.

Конструкция смесителя обеспечивала в экспериментах суммарную пропускную способность до 2 л · атм/с. Для обычных химических HF(DF)-лазеров с энергией в импульсе 100–150 Дж и рабочим объемом 5–10 л, используемых в наших экспериментах, время готовности лазера к работе при этом составляло 3–5 с. Наибольший габаритный размер смесителя не превышал 10 см.

ТЕОРЕТИЧЕСКАЯ МОДЕЛЬ РАБОТЫ КАПИЛЛЯРНОГО СМЕСИТЕЛЯ

Рассмотрим случай истечения газа через капилляр в среду с возрастающим по мере напуска газа давлением. При движении сжимаемого газа в капилляре с трением связь между безразмерными скоростями потока во входном 1 и выходном 2 сечениях задается соотношением [2, с. 249]:

где ${\chi } = \frac{{2{\zeta }}}{{k + 1}}\frac{L}{d}$; λ₁, λ₂ – безразмерные скорости движения газа во входном 1 и выходном 2 сечениях капилляра в долях критической скорости c* (критическая скорость потока c* равна местной скорости звука); ζ – коэффициент сопротивления капилляра; k – показатель изоэнтропы; L, d – длина и внутренний диаметр капилляра соответственно.

Для капилляра с круглым сечением при сравнительно небольших числах Рейнольдса (Re < 2300), когда течение носит ламинарный характер, коэффициент ζ = 64/Re. Число Рейнольдса записывается как Re = сd/ν, где с – средняя расходная скорость движения газа, ν – кинематическая вязкость газа. Перепишем число Рейнольдса в следующем виде: Re = cdρf/(νρf), где ρ – плотность газа, f = πd²/4 – площадь сечения капилляра. Учитывая, что массовый расход газа через капилляр m = cρf = M/N (M – массовый расход газа через N капилляров), νρ = η (η – динамическая вязкость газа), для числа Рейнольдса получим выражение Re = 4M/πηdN. Тогда

Массовые расходы газа в сечениях 1 и 2 с учетом всех капилляров записываются M₁ = c₁ρ₁F и M₂ = c₂ρ₂F, где F = fN – сумма площадей отверстий всех капилляров. Представим выражения для массовых расходов в виде $({{c}_{1}}{\text{/}}с _{1}^{*})с _{1}^{*}({{\rho }_{1}}{\text{/}}{{\rho }_{{01}}}){{\rho }_{{01}}}F$ и $({{c}_{2}}{\text{/}}с _{2}^{*})с _{2}^{*}({{\rho }_{2}}{\text{/}}{{\rho }_{{02}}}){{\rho }_{{02}}}F$. Здесь и далее индекс “0” будем относить к параметрам заторможенного газа. По определению ${{c}_{1}}{\text{/}}с _{1}^{*} = {{\lambda }_{1}}$, ${{c}_{2}}{\text{/}}с _{2}^{*} = {{\lambda }_{2}}$. Из [2, с. 58–59] $\frac{{{{{\rho }}_{1}}}}{{{{{\rho }}_{{01}}}}} = {{\left( {1 - \frac{{k - 1}}{{k + 1}}{\lambda }_{1}^{2}} \right)}^{{\frac{1}{{k - 1}}}}}$, $\frac{{{{{\rho }}_{2}}}}{{{{{\rho }}_{{02}}}}} = {{\left( {1 - \frac{{k - 1}}{{k + 1}}{\lambda }_{2}^{2}} \right)}^{{\frac{1}{{k - 1}}}}}$, $c_{1}^{*}$ = = $\sqrt {\frac{{2k}}{{k\, + \,1}}\frac{{R{{T}_{{01}}}}}{{\mu }}} $, $c_{2}^{*} = \sqrt {\frac{{2k}}{{k + 1}}\frac{{R{{T}_{{02}}}}}{{\mu }}} $.

Из уравнения состояния ρ₀₁ = P₀₁μ/RT₀₁, ρ₀₂ = = P₀₂μ/RT₀₂, где μ – молекулярный вес газа, P₀₁, P₀₂ и T₀₁, T₀₂ – давление и температура торможения в сечениях 1 и 2 соответственно. При течении без энергообмена (изоэнтропийное течение) T₀₁ = = T₀₂ = T₀. С учетом сказанного можно получить:

Статическое давление P₂ в сечении 2, выраженное в долях давления полного торможения P₀₂, записывается [2, с. 59] в виде

С учетом (6) соотношение (5) перепишется как

При истечении через капилляр скорость газа не может быть больше местной скорости звука, следовательно, расширение в капилляре осуществляется до давлений, не меньших критического давления $Р _{2}^{*}$. При Р₂ = $Р _{2}^{*}$ скорость λ₂ = 1. Если давление газа в реакторе P₃ меньше критического, то расход газа через капилляр определяется величиной $Р _{2}^{*}$ и не зависит от давления в реакторе. Если давление в реакторе становится больше критического, скорость истечения становится дозвуковой и давление P₂ на срезе капилляра сравнивается с давлением в реакторе P₃.

Подставив в формулу (1) выражение для χ(3), можем получить

Массовые расходы газа M₁ и M₂ в сечениях 1 и 2 в силу неразрывности течения равны между собой. При выполнении равенства M₁ = M₂ = M система уравнений (4), (7), (8) дает связь между пятью параметрами – P₀₁, Р₂, λ₁, λ₂, M, и если задать два из них, то остальные три однозначно определяются этой системой. Удобно вместо массового расхода газа M [г/c] использовать объемный расход газа Q [л · атм/с]. Связь между ними дается соотношением Q = (M/μ)V₀, где V₀ – объем идеального газа, равный при стандартных условиях 22.4 л · атм/моль. На рис. 2 приведены зависимости объемного расхода “предсмеси”, содержащей водород, от давления в реакторе P₃ при различных величинах давления на входе капилляров. Использованные в расчетах значения параметров:

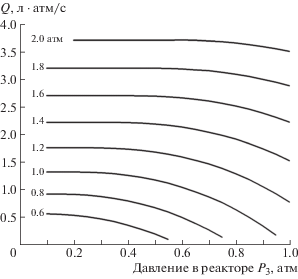
По расчетам при Q = 3.73 л · атм/с (соответствует значению P₀₁ = 2 атм на рис. 2) число Рейнольдса Re = 2100 и при дальнейшем увеличении давления P₀₁ газовый поток перестает быть ламинарным. Горизонтальные участки кривых на рис. 2 отвечают ситуации, когда давление в реакторе P₃ меньше критического давления $Р _{2}^{*}$. При P₃ > $Р _{2}^{*}$ наблюдается падение расхода газа через капилляры с увеличением давления в реакторе для всех значений P₀₁, причем относительная величина падения растет с уменьшением давления на входе капилляров.

ТЕХНОЛОГИЯ ПРИГОТОВЛЕНИЯ РАБОЧЕЙ СМЕСИ

На практике желательно иметь постоянную скорость напуска газа в реактор вне зависимости от возрастающего по мере напуска давления в нем. Для решения этой задачи в напускной тракт перед капиллярами помещали шайбу с отверстием, работающим в критическом режиме. Шайбу изготавливали из алюминиевой фольги толщиной 0.5 мм. Отверстие в фольге пробивали стальной конической иглой. Размер отверстия контролировали с помощью микроскопа отсчетного типа с увеличением 24^×.

Уравнение расхода газа через критическое сечение записывается в виде M^* = ρ*c*F* = (ρ*/ρ₀)c*F*ρ₀.

Учитывая, что $\frac{{{\rho *}}}{{{{{\rho }}_{0}}}} = {{\left( {\frac{2}{{k + 1}}} \right)}^{{\frac{1}{{k - 1}}}}}$ [2, с. 62], ρ₀ = = P₀μ/RT₀, ${{c}^{*}} = \sqrt {\frac{{2k}}{{k + 1}}\frac{{R{{T}_{0}}}}{{\mu }}} $, получаем

где ρ₀, P₀, T₀ – параметры полностью заторможенного газа. Критический расход прямо пропорционален начальному давлению Р₀, площади отверстия F* и не зависит от противодавления. Критический режим для отверстия возможен, если выполняется неравенство P* ≥ $P_{{01}}^{{\max }}$, где P* = = ${{\left( {\frac{2}{{k + 1}}} \right)}^{{\frac{k}{{k - 1}}}}}{{P}_{0}}$ – критическое давление, $P_{{01}}^{{\max }}$ – максимальное давление перед капиллярами, достигаемое в конце напуска газа в реактор. Следовательно, должно выполняться условие P₀ ≥ ${{\left( {\frac{{k + 1}}{2}} \right)}^{{\frac{k}{{k - 1}}}}}P_{{01}}^{{\max }}$. Для рассматриваемого газа это отвечает с хорошей точностью требованию Р₀ ≥ $2P_{{01}}^{{\max }}$. Если считать, что давление в реакторе в конце напуска составляет P₃ = 1 атм, то, согласно рис. 2, $P_{{01}}^{{\max }}$ = = 1.125, 1.25, 1.38 атм для расходов Q = 0.5, 1, 1.5 л · атм/с соответственно, и значит в этих случаях Р₀ = 2.25, 2.5, 2.76 атм. При выполнении условия Р₀ ≥ 2$P_{{01}}^{{\max }}$ отверстие обеспечивает заданный значениями P₀ и F* расход M*. В силу неразрывности течения при этом должно выполняться равенство M* = M. Постоянство расхода в ходе напуска газа в реактор обеспечивается автоматической подстройкой давления P₀₁. Проведенное рассмотрение приводит к практически важному результату: расход газа через систему капилляров можно задать критическим расходом газа через отверстие при надлежащем выборе начального давления P₀ и площади отверстия F*. Правильный подбор значений P₀ и F* обеспечивает как заданный расход газа, так и его постоянство в ходе напуска в реактор.

Отметим, что проведенный расчет касался изоэнтропийного течения. Реально картина течения газа сложнее. Изоэнтропийным можно считать течение до и после капилляра, течение газа в капилляре происходит с энергообменом в силу малости поперечного размера капилляра. В предельном случае бесконечно быстрого энергообмена течение в капилляре будет изотермическим с температурой газа, равной температуре стенки. Можно показать, что в этом случае уравнение (1) преобразуется в уравнение

Отличие в результатах расчетов при замене уравнения (1) на уравнение (10) не превышает нескольких процентов.

В описываемом смесителе, как указывалось, 48 капилляров с внешним диаметром 0.1 см упакованы в цилиндр с внутренним диаметром 0.8 см. Между капиллярами при их упаковке образуются каналы, отличающиеся, вообще говоря, как поперечными размерами, так и формой вследствие неидеальности упаковки. В каналы с наибольшими размерами вставляли проволоку подходящего диаметра. Общее число каналов в конечном итоге составило 64. Через эти каналы подавали “предсмесь” с фтором. Из-за неодинаковости каналов строгий расчет для “предсмеси” с фтором затруднителен. Однако с учетом вышеизложенного можно обойтись вообще без расчета: при заданном Q л · атм/с нужно просто подобрать начальное давление P₀ и площадь отверстия F* такими, чтобы они обеспечивали нужный расход и его постоянство в течение напуска, что нетрудно.

Объемные расходы Q обеих “предсмесей” выбирали одинаковыми. В этом случае суммарный расход газа через смеситель равен 2Q и средняя скорость в соединительной трубке с внутренним диаметром D = 0.8 см составляет с = (2Q/P₃)/(πD²/4). Скорость потока минимальна в конце напуска, когда P₃ = 1 атм, и при Q = 1 л · атм/с, например, она составит 40 м/с, что больше скорости распространения пламени [3].

В напускной тракт созданной установки помимо смесителя и шайб с отверстиями, задающими критический расход “предсмесей”, входили быстродействующие электроклапаны для включения и отключения газовых потоков и резервуары с “предсмесями”. Давление газа в резервуаре задает начальное давлению P₀ перед соответствующим отверстием. Объем резервуара выбирался таким, чтобы в ходе напуска величина P₀ падала несильно.

Обычно падение давления не превышало 10–15%. Соответственно скорости напуска смеси в начале и в конце отличались на 10–15%, что допустимо. При необходимости эту разницу можно уменьшить, например, увеличив объем расходных резервуаров или используя устройства, поддерживающие в них постоянное давление. После напуска давление в резервуарах восстанавливалось до требуемой величины за счет “предсмесей”, заранее приготовленных и хранимых в стальных баллонах объемом 10 л при давлении 15–25 атм. Эксплуатационные параметры созданной установки сохраняли стабильность в течение длительного времени работы, обеспечивая воспроизводимость характеристик лазера от опыта к опыту.

ЗАКЛЮЧЕНИЕ

Подытожим сказанное. Разработана конструкция компактного смесителя, обеспечивающего эффективное смешение газов, с суммарной производительностью до 2 л · атм/с. Смеситель обеспечивает готовность лазера к работе в течение нескольких секунд. При разработке смесителя особое внимание уделено проблеме безопасного смешения высокореакционных газов. Предложена схема напуска газов с использованием расходных шайб с отверстиями, работающими в критическом режиме, которая обеспечивает постоянство расхода смешиваемых газов в течение всего напуска.

Работа выполнена при финансовой поддержке госзадания 01201361840.