Приборы и техника эксперимента, 2021, № 5, стр. 84-89
СРАВНИТЕЛЬНЫЙ АНАЛИЗ ТОЧНОСТИ ОПРЕДЕЛЕНИЯ СДВИГА БРИЛЛЮЭНОВСКОЙ ЧАСТОТЫ В ЭКСТРЕМАЛЬНО ЗАШУМЛЕННЫХ СПЕКТРАХ РАЗЛИЧНЫМИ КОРРЕЛЯЦИОННЫМИ МЕТОДАМИ
А. И. Кривошеев a, *, Ю. А. Константинов a, Ф. Л. Барков c, В. П. Первадчук b
a Пермский федеральный исследовательский центр УрО РАН
614990 Пермь, ул. Ленина, 13а, Россия
b Пермский национальный исследовательский политехнический университет
614990 Пермь, Комсомольский просп., 29, Россия
c Программный комитет международной конференции “Оптическая рефлектометрия, метрология и сенсорика”
614990 Пермь, ул. Ленина, 13а, Россия
* E-mail: antokri@ya.ru
Поступила в редакцию 24.03.2021
После доработки 23.04.2021
Принята к публикации 26.04.2021
Аннотация
С использованием одних и тех же экстремально зашумленных данных сравниваются два корреляционных метода поиска максимумов бриллюэновских спектров. Первый метод представляет собой известный способ корреляции полученного сигнала с идеальной функцией Лоренца. Во втором методе, разработанном авторами ранее, вместо функции Лоренца используется этот же исследуемый спектр, но инвертированный по оси частот. Помимо оценки точности обоих методов, проведено их сравнение с классическим методом аппроксимации лоренцевой функцией. Дана оценка точности рассмотренных методов в зависимости от вероятности появления артефактов в спектрах бриллюэновского рассеяния. Показано, что при превышении 9%-ной вероятности появления артефакта разработанный ранее авторами метод показывает лучшие результаты, чем остальные рассмотренные методы.
ВВЕДЕНИЕ
Распределенные волоконно-оптические датчики нашли свое применение при решении широкого круга научно-технических задач. В общих чертах, их принцип работы основан на регистрации различных компонент обратного рассеяния в каждой точке оптического волокна и изучении его спектральных, фазовых, поляризационных и иных свойств с использованием математической обработки сигнала. В последнее время широкое распространение получили распределенные датчики на основе вынужденного и спонтанного рассеяния Мандельштама–Бриллюэна, работающие по принципу рассеяния света на акустическом фононе, присутствующем в среде распространения, т.е. в оптическом волокне. Температурные и деформационные воздействия изменяют скорость звука в кварцевом стекле, из которого изготовлено волокно, что приводит к частотному смещению сверхслабых спектральных компонент обратного рассеяния. В этом случае главной искомой величиной становится частота максимума спектральной компоненты (BFS – Brillouin Frequency Shift). После первичного аналого-цифрового преобразования регистрируемые спектры представляют собой дискретные функции, содержащие цифровой электрический шум, в которых зачастую скрыта искомая спектральная компонента, представляющая собой функцию Лоренца. Простое нахождение локального максимума в экстремально зашумленных сигналах приводит к появлению погрешностей измерений, по величине сравнимых с исследуемым сигналом.
Современным научным “золотым стандартом” для решения данной задачи стала аппроксимация лоренцевой функцией (Lorentzian Curve Fitting – LCF) [1, 2]. В простейшем случае этот метод основан на итерационном подборе аналитической функции Лоренца и ее количественном сравнении с полученным сигналом. После этого находится максимум уже идеально отмасштабированной и смещенной функции. В настоящее время эта задача решается не так прямолинейно – LCF имеет много новых оптимизированных способов расчета. К алгоритмам аппроксимации функцией Лоренца можно отнести такие, как линейный метод наименьших квадратов, детально описанный в [3, 4], а также нелинейный метод, основанный на алгоритме Левенберга–Марквардта [5, 6]. Многие из данных методов позволили существенно увеличить точность измерений, однако и они оказались не лишенными некоторых недостатков. Главный из них – достаточно высокие требования к вычислительным ресурсам.
В этом плане серьезную конкуренцию LCF стали составлять недавно представленные в литературе корреляционные методы, простые в программной и аппаратной реализации, а следовательно, выигрывающие в быстродействии. Отдельные попытки сравнения точностных параметров разных методов предприняты в работах [7, 8], однако исчерпывающий анализ этой проблемы на данный момент отсутствует. Вдобавок, эксперименты по сравнению методов проведены для разных сигналов, и, как методы поведут себя в одинаковых и при этом не самых “комфортных” условиях, пока неясно. Таким образом, задача настоящей работы – сравнить точности метода обратной корреляции и его классического аналога в условиях экстремального оптоэлектронного и цифрового зашумления.
ПОСТАНОВКА ЧИСЛЕННОГО ЭКСПЕРИМЕНТА
Для проведения эксперимента был сгенерирован набор спектров, содержащих дефекты двух видов. Первые имитируют шум регистраторов и приводят к случайной вариации от спектра к спектру отношения сигнал/шум в диапазоне от 2 до 20 дБ. Вторые представляют собой сбои оцифровки, приводящие к появлению случайных по локации и продолжительности провалов дискретной функции до нулевого значения. Такая дискретная функция может быть выражена следующим образом:
(1)
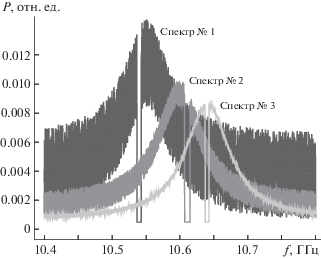
$P(f) = \left( {{{P}_{N}} + \frac{W}{\pi }\left[ {\frac{1}{{{{W}^{2}} + {{f}^{2}}}}} \right]} \right)\left[ {1 + \frac{{(f - \mu ){\text{|}}f - \nu {\text{|}}}}{{(f - \nu ){\text{|}}f - \mu {\text{|}}}}} \right],~$Центральная частота спектральной компоненты также задавалась случайным образом в диапазоне 10.55–10.65 ГГц. На рис. 1 представлены три случайных спектра из полученной выборки.
Далее осуществлялась математическая обработка. Метод LCF достаточно широко представлен в литературе, реализуется по различным алгоритмам, детально описанным в [9]. Традиционный корреляционный метод также хорошо исследован различными авторами [10, 11]. Получаемая с его помощью взаимно-корреляционная функция в непрерывном виде представлена ниже:
где $P$ – функция, описывающая заданный спектр; $L$ – функция, описывающая идеальный спектр Лоренца; $k$ – значение сдвига спектра.Разработанный авторами ранее метод обратной корреляции может быть представлен в виде:
где $P{\kern 1pt} {\text{'}}$ – инвертированный по оси частот исходный спектр, сдвинутый на k точек.Очевидно, что интегрирование функций (2) и (3) методом вычетов в обоих случаях также даст функции Лоренца, имеющие идентифицируемый и однозначно связанный с искомой величиной максимум.
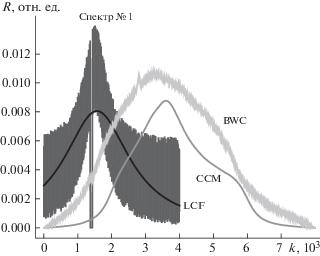
На рис. 2 представлен результат обработки спектра № 1. Приведены результирующие спектры для взаимной корреляции с идеальной кривой Лоренца (CCM – Cross-Correlation Method), а также для обратной корреляции (BWC – Backward Correlation) и LCF. Максимумы BWC и CCМ смещены вправо ввиду своей алгоритмической особенности.
В результате обработки спектра методом обратной корреляции можно заметить дефект, возникающий в том месте, где у исходного спектра наблюдается падение функции до нулевого значения. Этот всплеск связан с тем, что при сдвиге спектров относительно друг друга в момент наложения провалов происходит уменьшение количества нулевых элементов, суммирующихся в результирующей функции, что приводит к всплеску величины корреляционной функции.
Артефакт, описанный в данной работе и представленный как локальное обращение исследуемой функции в ноль, может быть обусловлен не только дефектами оцифровки, но и некорректной работой алгоритма сканирования по спектру. Его протяженность и локация в спектре могут быть совершенно различными. Ниже рассмотрено два случая: первый описывает появление такого дефекта в спектральных областях, не содержащих искомый максимум; второй же, напротив, предполагает, что максимальная частота спектра всегда находится в границах провала.
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ
Для каждого описанного случая возникновения артефактов в спектре было сгенерировано по одной тысяче спектров.
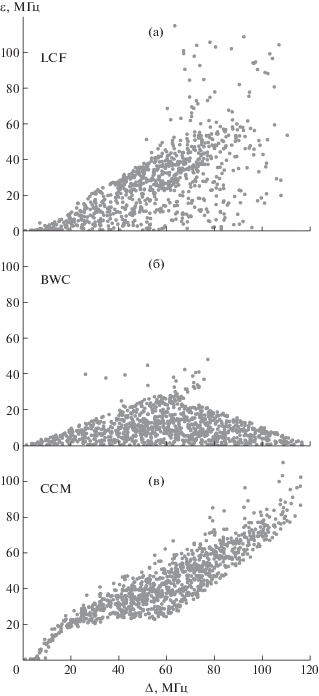
Для оценки влияния артефакта на ошибку нахождения максимума спектра тремя методами были построены зависимости ошибки определения спектра от ширины артефакта. На рис. 3 представлены полученные зависимости для трех методов: LCF, BWC, CCM.
Рис. 3.
Распределение ошибок нахождения максимума бриллюэновского спектра для случая № 1; Δ определяется как ν – μ. А и B – соответственно более и менее “плотные” области.
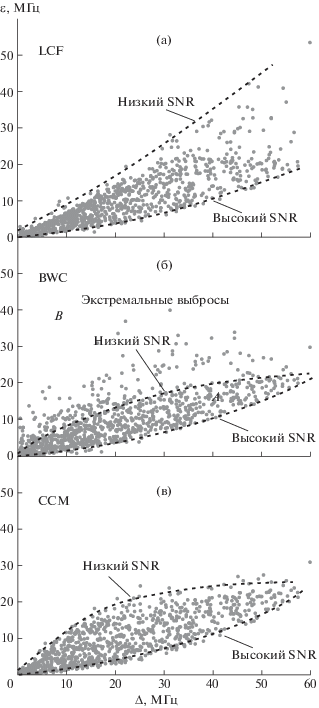
Столь существенный разброс данных на полученных зависимостях обусловлен вариациями отношения сигнал/шум (SNR). При большом количестве экспериментальных данных на графиках можно достаточно четко выделить линиями область, характеризующую точность (здесь – стандартное отклонение) определения искомой величины от самых низких отношений сигнал/шум до самых высоких.
Для метода аппроксимации лоренцевой функцией (рис. 3а) эти линии свидетельствуют о плавном росте ошибки детектирования при увеличении провала во всех случаях. При этом во всей исследованной области стабильно увеличивается и разность стандартных отклонений при экстремально низких отношениях сигнал/шум и практически незашумленном сигнале, что выглядит довольно логично и говорит об эффективности метода лоренцевой аппроксимации при высоких отношениях сигнал/шум и сравнительно небольших размерах провала.
Оба корреляционных метода (рис. 3б, 3в), как несложно заметить, выдают данные, напоминающие форму гистерезиса. При этом в случае метода обратной корреляции (рис. 3б) образованный им (гистерезисом) объект можно условно разделить на две части: более и менее “плотную”.
В более “плотной” части, обозначенной буквой А, сосредоточено больше точек, а значит, больше измерений с соответствующими более высокими точностями. Область В имеет одиночные, но более крупные выбросы, нехарактерные для классического метода взаимной корреляции. На основании этого можно заключить, что метод обратной корреляции здесь более предпочтителен при условии дополнительных средств страховки от крупных отклонений, которые могут отсекаться пороговым алгоритмом.
Данные, полученные для второго случая (рис. 4), когда провал находится в области искомого максимума, во многом схожи с ситуацией, уже описанной выше, за исключением некоторых изгибов и локальных выбросов. Метод обратной корреляции выявил следующие интересные особенности (рис. 4б). Во-первых, наблюдается соразмерное предшествующему росту убывание стандартного отклонения, начинающееся после ширины спектрального провала в 60 МГц. Эта особенность говорит о возможности применения метода для обработки спектров, практически полностью искаженных как шумами, так и частичной потерей информации. Во-вторых, нижняя часть гистерезиса на рис. 4б практически “лежит” на оси частот, что говорит о более высокой вероятности получения точного результата во всей исследованной области.
Рис. 4.
Распределение ошибок нахождения максимума бриллюэновского спектра для случая № 2; Δ определяется как ν – μ.
В табл. 1 приведена информация об эффективности всех трех методов при разных отношениях сигнал/шум (SNR). В каждом случае спектры были поделены на три группы по соотношению сигнал/шум. В первую группу вошли спектры с низким SNR (до 5 дБ), во вторую – со средним SNR (5–10 дБ), а в третью – с высоким SNR (>10 дБ).
Таблица 1.
Эффективность нахождения максимума бриллюэновского спектра
| Метод | SNR, дБ | Стандартное отклонение BFS, МГц | ||
|---|---|---|---|---|
| Без артефакта | Случай 1 | Случай 2 | ||
| LCF | < 5 | 1.12 | 10.68 | 7893.28 |
| 5–10 | 0.24 | 7.55 | 4076.74 | |
| > 10 | 0.04 | 6.19 | 316.42 | |
| BWC | < 5 | 2.17 | 9.12 | 9.69 |
| 5–10 | 0.74 | 6.18 | 7.53 | |
| > 10 | 0.14 | 5.83 | 7.68 | |
| CCM | < 5 | 0.46 | 7.61 | 20.39 |
| 5–10 | 0.19 | 6.54 | 19.51 | |
| > 10 | 0.09 | 6.37 | 16.13 | |
Как уже отмечалось выше, традиционный метод аппроксимации лоренцевой функцией относительно эффективен при высоких отношениях сигнал/шум в случае, если провал не попадает на искомую центральную область спектра. В остальных случаях более эффективны корреляционные методы. Тогда же когда провал находится в области пика, самым эффективным становится метод обратной корреляции; классический корреляционный метод демонстрирует чуть меньшую точность; в то время как метод аппроксимации лоренцевой функцией полностью теряет свою актуальность в столь экстремальных условиях.
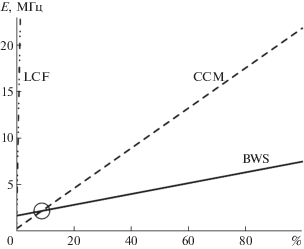
Стоит отметить, что в реальных системах мониторинга, основанных на использовании рассеяния Мандельштама–Бриллюэна, артефакты, о которых говорилось выше, встречаются достаточно редко в коммерческом оборудовании, но могут обнаруживаться при экспериментах на макетных установках. Несомненно, стоит рассмотреть случаи, когда артефакт проявляется в спектре с некоторой долей вероятности. Прогнозируемое стандартное отклонение E измерения BFS в условиях возникновения артефакта с вероятностью P можно оценить приближенно следующим образом:
где ${{E}_{0}}$ – стандартное отклонение в условиях отсутствия артефактов; ${{E}_{a}}$ – стандартное отклонение в условиях наличия артефакта.В результате расчета точности системы были получены графики, представленные на рис. 5. Согласно этим графикам, начиная с 9%-ной вероятности возникновения артефакта (выделенная кружком область), метод BWC показывает лучшие результаты по точности определения максимума бриллюэновского спектра в сравнении с методом CCM. Также для качественной оценки эффективности определения максимума бриллюэновского спектра на рис. 5 представлена аналогичная зависимость для метода LCF.
ЗАКЛЮЧЕНИЕ
Проведено сравнение точностных параметров современных методов детектирования пика рассеяния Мандельштама–Бриллюэна в оптических волокнах. Для всех существующих отношений сигнал/шум метод LCF демонстрирует менее высокую точность, чем оба корреляционных метода. Показано, что метод обратной корреляции опережает по точности классический корреляционный метод в подавляющем большинстве случаев.
Дана оценка точности рассмотренных методов в зависимости от вероятности появления артефактов в спектрах бриллюэновского рассеяния. Показано, что при превышении 9%-ной вероятности появления артефакта метод BWC показывает лучшие результаты, чем остальные рассмотренные методы.
Метод BWC может быть потенциально применим в таких приложениях, как разделение температур и деформаций в волокнах, сохраняющих поляризацию излучения [12], где требуется с высокой точностью разделить бриллюэновские спектры двух поляризационных осей оптического волокна; распределенное измерение двулучепреломления в волокнах, сохраняющих состояние поляризации [7]. Кроме того, потенциальные преимущества данный метод может иметь при рефлектометрическом исследовании нестандартных оптических волокон с высокими потерями (например, активных волоконных световодов [13]).
Список литературы
Madsen K., Nielsen H.B., Tingleff O. Methods for non-linear least squares problems. 2nd ed. London, U.K.: Informatics and Mathematical Modeling Technical University of Denmark, 2004.
Seber G., Wild C.J. Nonlinear Regression. NY, USA: Wiley, 2003.
Dhliwayo J., Webb D.J., Pannell C.N. // Proc. SPIE. 1996. V. 2838. P. 276. https://doi.org/10.1117/12.259808
DeMerchant M., Brown A.W., Bao X., Bremner T.W. // Proc. SPIE. 1998. V. 3330. P. 315. https://doi.org/10.1117/12.316987
Levenberg K. // Quart. Appl. Math. 1944. V. 2. № 2. P. 164. https://doi.org/10.1090/QAM/10666
Fletcher R. A modified Marquardt subroutine for nonlinear least squares. Tech. Rep. AERE-R 6799. Harwell, England: Oxford Univ. Dept. Theoretical Phys. Division, 1971.
Barkov F.L., Konstantinov Yu.A., Krivosheev A.I. // Fibers. 2020. V. 8(9). P. 60. https://doi.org/10.3390/fib8090060
Shahna M. Haneef, Zhisheng Yang, Luc Thévenaz, Deepa Venkitesh, Balaji Srinivasan // Opt. Express. 2018. V. 26(11). P. 14661. https://doi.org/10.1364/OE.26.014661
Cheng Feng, Xin Lu, Preussler S., Schneider T. // Journal of Lightwave Technology. 2019. V. 37. P. 5231. https://doi.org/10.1109/JLT.2019.2930919
Farahani M.A., Castillo-Guerra E., Colpitts B.G. // IEEE Sensors Journal. 2013. V. 13(12). P. 4589. https://doi.org/10.1109/JSEN.2013.2271254
Farahani M.A., Castillo Guerra E., Colpitts B.G. // Optics Letters. 2011. V. 36(21). P. 4275. https://doi.org/10.1364/OL.36.004275
Барков Ф.Л., Константинов Ю.А., Бурдин В.В., Кривошеев А.И. // ПТЭ. 2020. № 4. С. 51. https://doi.org/10.31857/S0032816220040229
Белокрылов М.Е., Константинов Ю.А., Латкин К.П., Клод Д., Селезнев Д.А., Степин А.А., Конин Ю.А., Щербакова В.А., Кашина Р.Р. // ПТЭ. 2020. № 4. С. 45. https://doi.org/10.31857/S0032816220050018
Дополнительные материалы отсутствуют.
Инструменты
Приборы и техника эксперимента