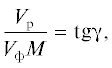Приборы и техника эксперимента, 2022, № 1, стр. 106-119
ИСПОЛЬЗОВАНИЕ МЕТОДА ОПТИЧЕСКОГО РЫЧАГА ДЛЯ ПОЛУЧЕНИЯ УДАРНЫХ АДИАБАТ МАТЕРИАЛОВ
В. И. Таржанов *
Российский федеральный ядерный центр –
Всероссийский научно-исследовательский институт технической физики имени академика Е.И. Забабахина
456770 Снежинск, Челябинской обл., ул. Васильева, 13, Россия
* E-mail: v.i.tarzhanov@vniitf.ru
Поступила в редакцию 12.04.2021
После доработки 28.04.2021
Принята к публикации 01.07.2021
- EDN: ECPSGU
- DOI: 10.31857/S0032816221060112
Аннотация
Рассматривается метод оптического рычага, используемый для получения ударных адиабат материалов. Представлен анализ волновых процессов в исследуемых клиновых образцах с выводом расчетных формул для случаев регистрации одной ударной волны и двухволновых упругопластических конфигураций при нагружении образцов нормально падающей ударной или детонационной волной. Применительно к регистрации одиночных ударных волн построен векторный аналог правила удвоения, позволяющий в гидродинамическом приближении корректно вычислять массовую скорость и другие параметры состояния сжатого материала по измеряемым нормальной компоненте скорости свободной поверхности образца WN и волновой скорости. Для двухволновых конфигураций разработана вычислительная процедура перехода от WN к массовой скорости с использованием модели идеального упругопластического поведения исследуемого материала. Приведены погрешности метода.
ВВЕДЕНИЕ
Высокоскоростная фотографическая регистрация является одним из наиболее эффективных методов исследования быстропротекающих процессов. Непрерывную фотографическую регистрацию изображения объекта, вырезанного узкой щелью, называют фотохронографией. Применением фоторегистратора СФР, созданного в Институте химической физики в 1949 году и используемого во многих научных центрах России до настоящего времени, обеспечивается щелевая регистрация ударно-волновых и детонационных процессов в широком диапазоне скоростей развертки изображений от 0.15 до 3.75 мм/мкс при достаточно высоком пространственном и временном разрешении – 20 линий/мм и 20 нс соответственно [1].
Среди большого количества разработанных методов фотохронографической регистрации особое место занимает метод оптического рычага. Метод оптического рычага (о.р.) был впервые развит Оуэном и Дэйвисом в университете Уэльса (Aberystwyth, Великобритания). Первая публикация о методе [2] относится к 1949 году. Это был однотрековый метод с фотохронографической разверткой во времени узкого пучка одного “светового карандаша”. У Аллена и МакКлери [3] метод стал многотрековым. В работах Катса, Дорана, Куррана [4], Фаулеса [5], Пьерэ, Пуола, Тувенина [6] метод приобрел современный облик. Есть и его вариант – метод погруженной фольги [7, 8].
Метод о.р. широко применяется в РФЯЦ–ВНИИТФ [8–16]. Так, используется вариант метода для исследования откольных явлений при разгрузке ударно-нагруженных образцов [11]. Отработано применение защитных металлических покрытий на диагностируемых поверхностях клиновых образцов для изучения слабоотражающих материалов, таких как взрывчатые вещества (в.в.) [8, 12] или быстро окисляющиеся металлы [13, 14]. Создана модификация метода для исследования материалов во взрывозащитных гермоконтейнерах с несколькими стеклами в иллюминаторе. Разработан двухрастровый метод о.р., позволяющий одновременно с хорошим разрешением регистрировать и слабую, и сильную волну в двухволновых конфигурациях. Метод модифицирован [15, 16] для регистрации дисперсии скорости свободной поверхности образцов, связанной со структурной неоднородностью деформации материалов при ударно-волновом нагружении [17]. Приведенные выше значения временного и пространственного разрешения обеспечиваются в методе о.р. минимизацией вплоть до 0.1 мм ширины щелей фоторегистратора и применяемого растра, а скорость развертки изображения выбирается максимальной – 3.75 мм/мкс. Для повышения точности измерений применяется программа оцифровки треков хронограммы. Двумерное сканирование фотохронограммы с разрешением 2400 линий/дюйм, автоматическое построение программой поперечного фотометрического профиля каждого трека с выделением максимума на каждом временном шаге 3 нс позволили в 3–5 раз улучшить временное и пространственное разрешение метода в зависимости от степени размытия треков из-за дисперсии регистрируемой скорости, характерной для каждого исследуемого материала.
Используемые во ВНИИТФ типовые постановки взрывных экспериментов с диагностикой методом о.р. показаны схематически на рис. 1. Исследуемый образец (50 × 30 × 12 мм с углом при вершине 12°), располагаемый на экране взрывного нагружающего устройства, выполняется в виде клина, свободная поверхность которого полируется и способна служить зеркалом. На известном расстоянии d (длине оптического рычага) от полированной поверхности образца параллельно ей располагается растр с системой щелей.
Рис. 1.
Типовые схемы постановки экспериментов: а, б – нагружение скользящей и нормальной детонацией соответственно (вид сбоку); в – оптическая схема (вид сверху). 1 – исследуемый клинообразный образец; 2 – полированная свободная поверхность образца; 3 – растр; 4 – листовой заряд в.в.; 5 – линейный генератор детонационной волны; 6 – подставка; 7 – цилиндрический заряд в.в.; 8 – направление инициирования в.в. генератором плоской волны; 9 – экран; 10 – взрывная аргоновая подсветка; 11 – изображение светящихся щелей растра в полированной поверхности образца; 12 – поворотные зеркала; d – оптический рычаг.

Фотохронограф фокусируется на изображение светящихся щелей растра в отполированной поверхности образца. Щель фотохронографа ортогональна линиям растра и вырезает систему точечных источников света. Смещения изображений этих источников света по пленке регистрируются непрерывно во времени. Величина d выбирается в диапазоне 20–120 мм в зависимости от решаемой задачи.
Достоинством метода является возможность 10–20-трековой регистрации на разных толщинах образца временных профилей многоволновых конфигураций, связанных с проявлением материалом упругости и пластических свойств, а также с протеканием в нем полиморфных превращений. Пример такой регистрации приведен на рис. 2.
Рис. 2.
Фотохронограмма с регистрацией трехволновой конфигурации в стали 30ХГСА (фотохронограф СФР2М [18]). Нагружение – нормальная детонация слоя октогенсодержащего в.в. через экран из стали 12Х18Н10Т. Скорость развертки по пленке 3.75 мм/мкс. Оптический рычаг – 44 мм. Выходы: 1 – упругого предвестника, 2 – фазового предвестника, 3–5 – основной пластической волны, 6 – волны сжатия от поверхности откольного разрушения.

Следует отметить отсутствие на сегодня общепринятой системы расчетных формул метода. В разных работах используются свои варианты набора формул. Связано, это, во-первых, с разной степенью приближенности рассмотрения течения исследуемого материала в клиновом образце при взаимодействии многих косых волн, во-вторых, с различием способов взрывного нагружения образца, в-третьих, с поведением изучаемого материала (гидродинамическим или упругопластическим с полиморфными превращениями или без них).
Целью данной работы является анализ волновых процессов с выводом расчетных формул метода о.р. для случаев регистрации одной ударной волны и двухволновых упругопластических конфигураций при нагружении образцов нормально падающей ударной или детонационной волной.
РЕГИСТРАЦИЯ ОДНОЙ И ДВУХ УДАРНЫХ ВОЛН
Для упрощения анализа проведем рассмотрение нагружения клинового образца стационарными ударными волнами, т.е. волнами со столообразным профилем. Для случая нестационарных волн проведенное рассмотрение и полученные расчетные формулы будут справедливы в окрестностях каждой фиксируемой на хронограмме растровой линии.
На рис. 3 показана схема регистрации одной ударной волны.
Рис. 3.
Схема расположения в образце ударного фронта и смещенной свободной поверхности в фиксированный момент времени (вид сбоку). ECG – образец; DH – фронт ударной волны; DF – повернутая на угол β свободная поверхность образца; IK – растр; OO' – плоскость изображения растра; A – точечный источник света в плоскости растра; A' – изображение источника А в невозмущенном зеркале CD; A'' – то же в зеркале, повернутом на угол β; A'A'' ≡ a' – смещение изображения источника А при выходе ударной волны в точку D; d – оптический рычаг; z – расстояние от вершины образца до точки М, расположенной на расстоянии х от поверхности нагружения образца, связанной с отражением точечного источника Аn на растре.

Нагружение образца осуществляется с тыльной поверхности образца ударной волной, выходящей из экрана нагружающего устройства.
Видно, что до прихода на диагностируемую поверхность образца ударного фронта в плоскости ОО' наблюдаются мнимые изображения светящихся растровых щелей A'. При отражении фронта ударной волны от поверхности образца появляется повернутый на угол β участок зеркала. Это приводит к возникновению вторых мнимых изображений А'' каждой растровой щели. Для показанной на рисунке одной щели А впервые это изображение появляется на фотопленке, когда ударный фронт приходит в точку D пересечения повернутой поверхности с перпендикуляром к ней из точки А''. Это изображение существует до конца регистрации. При проходе ударным фронтом участка DB клиновой поверхности регистрируются оба мнимых изображения A' и А''. В точке B существовавшее от начала регистрации начальное изображение светящейся растровой щели A' исчезает (срывается).
Регистрируемыми на хронограмме (рис. 4) величинами являются:
Рис. 4.
Схема фотохронограммы с регистрацией методом о.р. выхода двухволновой конфигурации на свободную поверхность образца: a1 и a2 – смещения растровых линий за 1-м и 2-м фронтами; γ1 и γ2 – углы наклона линий срыва растровых линий для 1-й и 2-й волн; 1–14 – номера растровых линий.
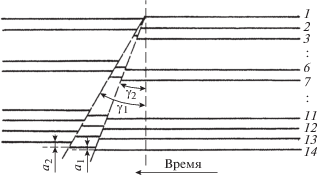
– углы γ1 и γ2 линий срыва исходных растровых линий при выходе на поверхность образца 1‑го и 2-го фронтов;
– смещения a1 и a2 каждой растровой линии после выхода на поверхность образца соответственно 1-го и 2-го волновых фронтов.
Известны три метода получения ударных адиабат материалов – методы “откола”, “торможения” и “отражения” [19]. Метод о.р. очень похож на метод “откола”. В нем также регистрируются волновая скорость и скорость свободной поверхности W после выхода на нее фронта волны. Существенное отличие метода о.р. состоит в использовании клиновой геометрии образца и в выходе фронта ударной волны на его свободную поверхность под углом. В связи с этим первая особенность метода о.р. состоит в том, что в нем регистрируются нормальная компонента WN вектора скорости свободной поверхности, не совпадающая по направлению с вектором массовой скорости u. Поэтому не может непосредственно использоваться правило удвоения скоростей. Должна быть получена специальная функциональная зависимость u = = f(WN) – векторный аналог правила удвоения.
Метод о.р., как и метод откола, не является абсолютно точным. Он может применяться для давлений, при которых не значимы отклонения от правила удвоения. Однако эти давления не так малы. В [20] показано, что правило удвоения выполняется для свинца до 15 ГПа, для алюминия до 60 ГПа, для железа и меди до 80 ГПа, для молибдена до 210 ГПа.
Метод о.р. является аналоговым методом регистрации профилей волн сжатия-разгрузки. Однако, как видно из рис. 5, в случае регистрации нестационарных ударных волн (со снижением параметров за фронтом) текущие значения смещений а(t) растровой линии и, следовательно, текущие значения WN(t) записываются разными участками зеркальной свободной поверхности образца (с разными значениями z). Это означает, что эти текущие WN(t) относятся к разным толщинам х, пройденным волной по образцу.
Рис. 5.
Фрагмент одного трека хронограммы. К объяснению привязки волновой скорости D(t), определяемой по углу γ(t), к WN(t), вычисляемой по a(t) в точке ε.

Таким образом, второй особенностью метода о.р. является получение аналоговой непрерывной во времени записи двумерной зависимости WN(t, х) вместо одномерной W(t), свойственной одномерным методам.
Важно еще отметить в связи со сказанным о записи аi(t) разными участками поверхности образца, что для вычисления всех параметров ударно-волнового состояния в материале на фронте волны по WN(t) значения волновой скорости D(t) надо брать не в точке срыва рассматриваемой растровой линии С (рис. 5), а в начальной точке ε смещенной линии, т.е. именно при тех значениях z и х, которым соответствует запись WN(t). Это значение берется в точке ε из аппроксимирующей зависимости D(z) для всей хронограммы. Можно было бы, наоборот, привязывать WN(z) к D(z) на начальном положении растровой линии, но в этом случае требовалось бы вводить некую “градиентную” поправку в WN(z), отражающую изменение нормальной компоненты скорости свободной поверхности вдоль поверхности образца по координате z. Такой подход с градиентной поправкой использовался в [5].
АНАЛИЗ ЯВЛЕНИЙ ПРИ ВЫХОДЕ НА СВОБОДНУЮ ПОВЕРХНОСТЬ КЛИНОВОГО ОБРАЗЦА ОДНОЙ УДАРНОЙ ВОЛНЫ
Фронт ударной волны, распространяющийся в образце от его тыльной поверхности GE, выходит на свободную зеркальную поверхность клина под углом α (рис. 3). В рассматриваемом случае отсутствия перекоса ударного фронта относительно поверхности нагружения угол выхода фронта на поверхность клинового образца просто равен углу α при его вершине. За единицу времени фронт, перемещающийся со скоростью D, пройдет некоторое расстояние и займет положение DH. Точка наблюдения G на поверхности у вершины клина за эту же единицу времени займет положение F на конце вектора W, расположенного перпендикулярно начальному положению зеркальной поверхности клина. WN– это регистрируемая нормальная компонента вектора скорости свободной поверхности W. Выше точки D свободная поверхность образца повернута на угол β.
Связь угла β с регистрируемым на фотопленке смещением а изображения растровой линии определяется из треугольника AA'A'' (рис. 3):
откуда где d – длина оптического рычага, $a{\kern 1pt} '$ – смещение растровой линии в плоскости OO', M – масштаб съемки фотохронографом плоскости наблюдения OO'.Если tgγ – тангенс угла наклона линии срыва растровых линий на фотохронограмме (рис. 4), а Vp – скорость щелевой развертки фотохронографа, то
где Vф– фазовая скорость пересечения фронтом волны свободной поверхности образца.Из треугольника GLD (рис. 3) для скорости ударного фронта D следует:
Абсолютная величина нормальной компоненты скорости свободной поверхности WN вычисляется из треугольника DGF с использованием (1):
Эта формула является точной для любых β.
Разгрузка ударно-нагруженного образца на свободной поверхности
При выходе ударной волны на поверхность образца под углом α из точки D выходит косая волна разрежения DG с веером (С+)-характеристик, переводящих материал образца из состояния 1 в состояние 2 (рис. 6а). Точка пересечения ударного фронта со свободной поверхностью клина, распространяясь вдоль поверхности с фазовой скоростью Vф, прошла к рассматриваемому моменту времени расстояние от точки О до точки D.
Рис. 6.
Векторная диаграмма поворота потока материала образца в отраженной от свободной поверхности образца волне разрежения: DG – последняя (C+)-характеристика веера волны разрежения, возникающего в точке D; точка A – произвольная точка на (C+)-характеристике; а – полная схема, б – фрагмент к определению WN.

Строя векторную диаграмму поворота потока в волне разрежения, найдем искомую связь WN = = f(u) – векторный аналог правила удвоения.
Известно [19, 20], что скорость свободной поверхности W всегда складывается из двух компонент – инерционной и разгрузочной. Инерционная компонента – это массовая скорость u. Показано, что в одномерном случае в гидродинамическом приближении, когда прочность ударно-сжатого материала несущественна, разгрузочная компонента W – u равна массовой скорости u, откуда следует правило удвоения W = 2u.
При разгрузке образца, нагруженного ударной волной, выходящей под углом относительно его свободной поверхности, направление вектора разгрузочной компоненты изменяется. Абсолютная величина его равна |uразгр| = |W – u|одномерн = |u| (рис. 6), а измененное направление перпендикулярно к последней (C+)-характеристике волны разрежения, на которой заканчивается поворот потока материала образца при разгрузке. Таким образом, вектор скорости свободной поверхности W при разгрузке материала, нагруженного ударной волной, выходящей под углом к поверхности образца, является векторной суммой инерционного вектора массовой скорости u и вектора разгрузки uразгр.
Из уравнений сохранения массы, импульса и энергии вещества на фронте косой волны (см., например, [21]) следует, что при переходе через волну разрежения тангенциальные составляющие векторов потока сохраняются, а нормальная компонента вектора W должна быть равна сумме нормальных компонент векторов u и uразгр. Пренебрегая шириной веера характеристик волны разрежения, будем относить все изменения потока вещества к последней (С+)-характеристике. Из векторной диаграммы скоростей (рис. 6) следует:
Здесь и далее абсолютные величины векторов жирным шрифтом не выделяются.
Формула (4) является связью абсолютной величины вектора скорости свободной поверхности с массовой скоростью u за фронтом ударной волны, если известна зависимость $\delta = f(\alpha ,D,u)$ – угла наклона последней (С+)-характеристики веера волны разрежения к исходному положению свободной поверхности.
Поскольку регистрируемые на хронограммах скачки ${{a}_{{ij}}}$ (рис. 4) определяют собой нормальную (к исходной поверхности клина) составляющую WN скорости свободной поверхности W, то логично связать искомую массовую скорость u с этой нормальной составляющей.
Из рис. 6б видно, что
тогда для u получим:Интересно рассмотреть предельные случаи для формулы (6). Известно, что для слабых волн (в акустическом приближении) $\delta = \alpha $. Для этого случая (6) преобразуется так:
(7)
$u = \frac{{{{W}_{N}}}}{{\cos \alpha + \cos \delta {{{\text{|}}}_{{\delta \to \alpha }}}}} = \frac{{{{W}_{N}}}}{{2\cos \alpha }}.$Такой формулой малоуглового приближения широко пользуются исследователи при нагружении образцов скользящей детонацией, когда продольные напряжения, например, в железе ≤10 ГПа [9–11].
При уменьшении угла выхода ударной волны на свободную поверхность клина α, т.е. при приближении к случаю одномерного нагружения (при α → 0) uN → WN /2.
Вектор W расположен под углом ξ к нормали исходной поверхности клина (рис. 6б).
Используя (4) и (5), получим
В итоге
Видно, что для слабых волн (при α = δ) ξ = 0, т.е. вектор W нормален к исходной поверхности образца. Для умеренно сильных волн и, например, при α ≈12° δ будет лежать в диапазоне 14°–4°, а ξ составит 1°–4°. Это дает отличие модулей векторов |WN| и |W|, равное 2 ⋅ 10–4–2 ⋅ 10–3, т.е. 0.02–0.2%.
Угол δ расположения последней (С+)-характеристики веера центрированной волны разрежения находится с использованием векторной диаграммы, аналогичной применявшейся в методе боковой разгрузки [22]. Эта характеристика строится как касательная к звуковой окружности, расширяющейся внутрь клина со скоростью звука с и смещающейся к диагностируемой поверхности с массовой скоростью u. Тригонометрическое рассмотрение такой диаграммы дает выражение
(9)
$\sin \delta = \frac{{\frac{c}{D} - \frac{u}{D}\frac{{\cos \alpha }}{{\cos \delta }}}}{{\frac{1}{{\sin \alpha }} - \frac{u}{D}\frac{{\sin (\alpha + \delta )}}{{\cos \delta }}}}.$Из (9) следует, что угол δ является функцией и угла α, и параметров ударно-волнового состояния (u, D), и скорости звука с. Формула (9) преобразуется к виду с выделенным частным $\frac{u}{D}$:
(10)
$\frac{u}{D}\frac{{[\sin \delta \sin (\alpha + \delta ) - \cos \alpha ]}}{{\cos \delta }} = \frac{c}{D} + \frac{{\sin \delta }}{{\sin \alpha }}.$Проверка формулы (9) на предельные переходы дает для слабых волн, когда c = D и u → 0:
Результат логичен и подтверждает (9).
Угол δ по (9) или (10) легко определяется численно для выбранных значений с и u.
Представление о влиянии угла δ дают оценки, проведенные для стали 12Х18Н10Т. Минимальный в области существования упруго-пластической конфигурации (u ≤ 0.85 км/с [9]) угол δ равен 7.5° при α = 12°. Для слабых пластических волн, чуть выше предела упругости Гюгонио, при δ = α = 12° $\frac{u}{{{{W}_{N}}}}$ составляет 0.5110, а для более сильных пластических волн, вблизи точки закрытия упругого предвестника, при δmin = 7.5° и α = 12° отношение $\frac{u}{{{{W}_{N}}}}$ = 0.5064. Различие составляет только 0.9%. При выборе образцов с меньшими углами при реализации меньших углов между фронтом ударной волны и поверхностью рассматриваемое различие заметно снижается. Так, для α = 5° при δ = α = 5° отношение $\frac{u}{{{{W}_{N}}}}$ = 0.50191, а при минимальном δmin = = 1.71° – $\frac{u}{{{{W}_{N}}}}$ = 0.50106. Различие составляет всего 0.2%.
Приведенные оценки иллюстрируют величину погрешности в определении u по измеренным WN без знания с в предположении δ = α, т.е. по формуле малоуглового приближения (7).
Несмотря на слабую чувствительность u к углу δ, корректное установление положения волны разрежения в образце необходимо. Оно важно при рассмотрении взаимодействия с ней второй ударной волны в случае регистрации двухволновой конфигурации.
Итак, в итоге – совокупность уравнений (6) и (9) или (6) и (10), в которых две неизвестные величины u и δ и один задаваемый параметр с0, позволяет определять массовую скорость u по первичным параметрам D и WN для одной ударной волны в гидродинамическом приближении. Однако проведенный анализ справедлив и для чисто упругого поведения исследуемого материала. Все полученные соотношения применимы к упругим предвестникам двухволновых структур, реализующихся в упругопластической области. В упругой области сжатия надо использовать продольную нулевую скорость звука cl0, а в пластической области – объемную нулевую cB0.
Вычисление параметров ударно-волнового состояния
В гидродинамическом приближении давление р, сжатие $\frac{\rho }{{{{\rho }_{0}}}}$ и относительная деформация εxx определяются по формулам
Как указано выше, данные формулы справедливы и при чисто упругом сжатии материалов, т.е. для упругих предвестников двухволновых структур, реализующихся при ударном сжатии. При этом первая формула переписывается для продольного напряжения σхх в материале в виде σхх= ρ0Du.
ЯВЛЕНИЯ ПРИ ВЫХОДЕ ВТОРОЙ УДАРНОЙ ВОЛНЫ НА СВОБОДНУЮ ПОВЕРХНОСТЬ КЛИНОВОГО ОБРАЗЦА
Будем рассматривать двухволновую конфигурацию, оба фронта которой рождаются одновременно на поверхности нагружения образца. Такая конфигурация реализуется в веществах с упругопластическим поведением. Кинетикой деформации будем пренебрегать. Обе волны будем считать стационарными, т.е. имеющими столообразные профили. Данное допущение не ограничивает применимости получаемых формул для нестационарных волн в малой окрестности точки пересечения свободной поверхности образца ударным фронтом, если размер этой окрестности значимо меньше характерного размера спада параметров на профиле ударной волны.
Взаимодействие второй ударной волны с волной разгрузки материала, нагруженного первой ударной волной
Рассмотрим сначала, что происходит при выходе двухволновой конфигурации на свободную поверхность образца в одномерном случае (рис. 7). Упругий предвестник переводит материал образца в состояние 1. При выходе его на свободную поверхность образца материал разгружается в первой упругой волне разрежения, распространяющейся навстречу пластическому фронту, переводящему материал в состояние 2. В результате взаимодействия упругой волны разрежения и пластического фронта в материале образца реализуются новый второй упругий предвестник, движущийся к свободной поверхности с состоянием за фронтом 1', и преобразованная пластическая волна, переводящая материал в состояние 2'. После отражения второго упругого предвестника от свободной поверхности с формированием состояния 100 он реверберирует и далее между поверхностью и пластическим фронтом на очень малом расстоянии за все более короткие промежутки времени. При отражении пластического фронта от поверхности реализуется состояние 2'''' со скоростью разгруженного материала образца W2.
Рис. 7.
Двухволновое упругопластическое нагружение материала и его упругопластическая разгрузка в σxx – u-координатах при α = 0.

В интересующей нас клиновой геометрии образца при выходе на его диагностируемую свободную поверхность второй волны под углом реализуются все названные выше волновые взаимодействия. Для их описания мы будем пользоваться одномерной σхх–и-диаграммой (рис. 7), помня, что “разлетные” компоненты массовых скоростей будут неколлинеарны инерционным компонентам и должны складываться с ними векторно.
Из рис. 8 видно, что в результате взаимодействия второго ударного фронта с волной упругой разгрузки в клиновом образце формируется новая упругопластическая конфигурация. За новым упругим предвестником НK формируется состояние 1' с массовой скоростью ${\mathbf{u}}_{1}^{'}$, являющейся суммой векторов W1 и u1. “Представитель” второй ударной волны HS ' вынужден распространяться по состоянию 1', обеспечивая за своим фронтом состояние 2'. “Представитель” – это новая ударная волна, возникающая при распаде второй ударной волны в точке Н на волне разрежения. Из точки K на повернутой свободной поверхности образца, в которой второй упругий предвестник разгружается, выходит вторая волна упругой разгрузки KМ. “Представитель” второй ударной волны взаимодействует с этой второй волной разгрузки в области вблизи точки S ', реализуя за фронтом на участке SS ' состояние 2''. Ниже и левее точки K свободная поверхность образца доворачивается на угол δβ1 прежде, чем на нее выйдет фронт “представителя” SS ' второй волны. Угол δβ1 примерно вдвое меньше, чем β1. При встрече волны разрежения KМ и фронта “представителя” второй волны в точке S ', в принципе, должен сформироваться еще один, третий упругий предвестник (у.п.). Этот предвестник, отразившись от свободной поверхности, сформирует третью волну упругой разгрузки, которая будет еще взаимодействовать с фронтом “представителя” второй волны. Однако это и еще последующие переотражения у.п. в угле KSS ' проходят за весьма короткое время.
Рис. 8.
Результаты взаимодействия 2-й ударной волны с волной разгрузки материала образца за упругим предвестником: А – векторная диаграмма потоков при формировании состояния 1' в произвольной точке Q линии HK в области HKS '; Б – то же при упругой разгрузке из состояния 1' в области KSS '; В – то же при формировании состояния 2" за ударным фронтом SS '.

В связи с тем, что при реально используемых углах α ≤ 12° точка K расположена очень близко к точке S, и второй у.п. обнаруживает себя на очень короткое время (∼0.1 мкс), а также с тем, что состояния 2' и 2'' лежат на единой изэнтропе упругой разгрузки (рис. 7), далее не будем учитывать существование второго у.п. и его волны разгрузки. Будем рассматривать упрощенную картину выхода на свободную поверхность образца только “представителя” второй волны.
Вообще говоря, вторая ударная волна должна преломиться в т. Н (рис. 8) на некий угол φ на первой волне разрежения, а сама волна разрежения – преломиться на ударной волне.
Поскольку разгрузка материала образца из состояния 2 в состояние 2' упругая (рис. 7), то последней (С+)-характеристике волны разрежения, прошедшей “сквозь” второй ударный фронт, соответствует продольная скорость звука сl, характерная для состояния 2'. Распространяется звуковая окружность против вектора массовой скорости u2. Сопоставление на рисунке волн разрежения до и после взаимодействия со второй волной в стали 12Х18Н10Т с использованием данных по скоростям звука из [23] показывает, что угол $\delta {\kern 1pt} '$ отличается от угла δ на 0.9° (при α = 12°) во всем диапазоне существования упругопластической конфигурации.
Так как угол $\delta {\kern 1pt} '$, хоть и немного, но отличается от угла δ, то возникает и небольшой перекос на угол φ “представителя” второго фронта относительно самого фронта.
Проведенная оценка угла перекоса “представителя” второй волны относительно самой второй волны для середины диапазона существования двухволновой конфигурации (u2 = 8u1) в стали 12Х18Н10Т [9] дала значение φmax = 0.3°. Такой перекос фронтов приводит к ошибке в вычислении D2 по Vф2, равной 0.01%. Аналогичный анализ для других металлов дает такие же результаты.
Таким образом, показано, что взаимодействие второй ударной волны с волной разгрузки упругого предвестника не приводит к значимому преломлению ни фронта ударной волны, ни характеристик волны разгрузки. Отсюда следует важный вывод о том, что скорость распространения “представителя” второй волны D2Σ равна скорости самой второй волны D2. Это означает, что плоскость “представителя” является продолжением плоскости фронта второй ударной волны.
Массовая скорость $u_{2}^{'}$ за фронтом “представителя” второй волны может быть выражена через параметры рассматриваемых двух волн.
С использованием векторной диаграммы на рис. 8 абсолютная величина вектора u2 записывается через углы α, δ1 и скорости u2, Δu2 следующим образом:
(11)
$u_{2}^{'} = \sqrt {\Delta u_{2}^{2} + u_{2}^{2} + 2\Delta {{u}_{2}}{{u}_{2}}\cos (\alpha + {{\delta }_{1}})} .$Угол наклона χ вектора ${\mathbf{u}}_{2}^{'}$ к вектору u2 записывается так:
Регистрация второй ударной волны
Регистрация второй ударной волны, распространяющейся в образце, осуществляется через ее “представителя” SH (рис. 9). В связи с этим необходимо установить связь параметров “представителя” с параметрами самой ударной волны.
Рис. 9.
Двухволновая конфигурация в образце в два различных момента времени: D11 и D21 – скорости первого и второго фронтов в момент времени t1; D12 и D22 – скорости фронтов в момент времени t2; CS – геометрическое место точек пересечения клиновой поверхности вторым фронтом в моменты времени от 0 до t2.

Рассматривая положение двухволновой конфигурации в клиновом образце в два момента времени (рис. 9), можно увидеть, что точки пересечения “представителя” SH второй ударной волны с поворачиваемой на угол β1 поверхностью клина при отражении первой волны не лежат ни на линии CD (исходное положение поверхности клина), ни на линии FD (развернутая на угол β1 поверхность). Геометрическим местом расположения точек выхода “представителя” второй ударной волны на регистрируемую зеркальную поверхность в разные моменты времени является прямая CS, наклоненная к CD под углом ξ. Эта прямая наблюдается в виде ее проекции CT на плоскость наблюдения, при этом CT = CScosξ или Vф2 = CScosξ. Здесь под фазовой скоростью Vф2 понимаем не истинную скорость пересечения развернутой поверхности клина фронтом “представителя” второй волны, а ее проекцию на плоскость наблюдения, параллельную исходной поверхности образца (Vф2 ≡ СТ). Это целесообразно в связи с тем, что на пленке регистратора фиксируется с масштабом М именно эта проекция.
Принимая в расчет сказанное, можно записать следующее.
Из треугольника CSD по теореме синусов имеем:
(13)
$\frac{{{{V}_{{{\text{ф1}}}}}}}{{\sin CSD}} = \frac{{CS}}{{\sin CDS}} = \frac{{{{V}_{{{\text{ф}}2}}}}}{{\sin CDS\cos \xi }}.$Так как sinCSD = sin(β1 + ξ) и sinCDS = sinβ1, получаем:
(14)
$\xi = {\text{arctg}}\left[ {\left( {\frac{{{{V}_{{{\text{ф}}1}}}}}{{{{V}_{{{\text{ф}}2}}}}} - 1} \right){\text{tg}}{{\beta }_{1}}} \right].$Для скорости “представителя” второй волны D2Σ, равной D2 (в лабораторной системе координат), из треугольника CSV имеем с учетом (13):
С использованием (14) это выражение преобразуется к следующему виду:
(15)
$\begin{gathered} {{D}_{{2\Sigma }}} = {{D}_{2}} = {{V}_{{{\text{ф}}2}}}\frac{{\sin (\alpha - {{\beta }_{1}})}}{{\cos {{\beta }_{1}}}} + {{V}_{{{\text{ф}}1}}}{\text{tg}}{{\beta }_{1}}\cos \alpha = \\ \, = {{V}_{{{\text{ф}}2}}}\frac{{\sin (\alpha - {{\beta }_{1}})}}{{\cos {{\beta }_{1}}}} + {{W}_{{1N}}}\cos \alpha {\text{.}} \\ \end{gathered} $Смысл последнего выражения ясен. Фронт “представителя” пересекает свободную поверхность образца, не просто повернутую на угол β, но еще и “убегающую” от фронта со скоростью W1Ncosα. Это приводит к занижению Vф2 по сравнению со случаем пересечения неподвижной свободной поверхности. Вторым слагаемым в (15) это занижение компенсируется. Формально же получается, что вектор D2Σ является суммой двух векторов – вектора скорости второй волны, прошедшей сквозь волну разрежения, движущейся по неподвижному веществу, и вектора сноса.
Нахождение приращения нормальной компоненты скорости свободной поверхности клинового образца ΔW2N после выхода на нее “представителя” второй волны по смещению a2 растровой линии не представляет трудностей. Из треугольника АА''А'''(рис. 10) следует:
Рис. 10.
Схема расположения двух ударных волн в клиновом образце и повернутой зеркальной поверхности на углы β1 и β2 (вид сбоку): IK – растр; OO' – плоскость изображения растра; A – точечный источник света в плоскости растра; A' – изображение источника А в невозмущенном зеркале CD; A'' – то же в зеркале, повернутом на угол β1; A''' – то же в зеркале, повернутом на угол β2; $a_{2}^{'}$ – смещение изображения источника А относительно изображения A'' при выходе второй волны в точку F.

Тогда ΔW2N = NFtgβ2 = ${{V}_{{{\text{ф}}2}}}\frac{{{\text{tg}}{{{{\beta }}}_{2}}}}{{\cos {{{{\beta }}}_{1}}}}$ = $\frac{{{{V}_{{\text{р}}}}}}{{M{\text{tg}}{{\gamma }_{2}}\cos {{{{\beta }}}_{1}}}}$ × × ${\text{tg}}\left( {{\text{arctg}}\frac{{{{a}_{2}}}}{{2dM}}} \right)$ = $\frac{{{{V}_{{\text{p}}}}{{a}_{2}}}}{{2d{{M}^{2}}{\text{tg}}{{{{\gamma }}}_{2}}\cos {{{{\beta }}}_{1}}}}$.
Итак,
(16)
$\Delta {{W}_{{2N}}} = \frac{{{{V}_{{\text{р}}}}{{a}_{2}}}}{{2d{{M}^{2}}{\text{tg}}{{\gamma }_{2}}\cos {{{{\beta }}}_{1}}}}.$Абсолютное значение нормальной компоненты скорости свободной поверхности образца определяется так:
Разгрузка “представителя” второй ударной волны на свободной поверхности клинового образца
Из рис. 11 видно, что “представитель” второй ударной волны АН, распространяясь за первой волной разрежения по разгруженному (до нулевого продольного напряжения) материалу образца, выходит на свободную поверхность образца, наклоненную на угол β1 относительно ее исходного положения. Из точки А выходит веер (С+)-характеристик второй волны разгрузки.
Рис. 11.
Векторная диаграмма поворота материала образца на второй волне разрежения при разгрузке второй ударной волны.

Перед волной разрежения имеется вектор массовой скорости u2, за волной разрежения – вектор W2. Связь модулей тангенциальных компонент векторов записывается на последней (С+)-характеристике с использованием законов сохранения следующим образом:
Вектор W2 строится как векторная сумма инерционной компоненты ${\mathbf{u}}_{2}^{'}$ и вектора $\Delta {\mathbf{u}}_{2}^{'}$ – разгрузочной компоненты, направленной перпендикулярно (С+)-характеристике, при этом ${\text{|}}\Delta u_{2}^{'}{\text{|}}$ = ${{({{W}_{2}} - u_{2}^{'})}_{{{\text{одномерн}}}}}$.
Интересующая нас компонента вектора W2, нормальная к повернутой на угол β1 свободной поверхности образца, записывается как сумма нормальных компонент составляющих векторов:
(18)
${{W}_{{2N}}}\, = \,u_{{2n}}^{'}\, + \,\Delta u_{{2n}}^{'}\, = \,u_{2}^{'}{\text{cos}}(\alpha - {{\beta }_{{\text{1}}}} - {{\chi }})\, + \,\Delta u_{2}^{'}{\text{cos}}{{\delta }_{2}},$Итак, используя формулы, написанные в данном подразделе, можно связать измеряемую величину W2N и искомую величину u2, если разобраться с разгрузочной составляющей – величиной $\Delta u_{2}^{'}$, определяющей переход материала образца из состояния 2' в состояние 2'''' (рис. 7). Дело в том, что адиабата разгрузки из состояния 2 в состояние 2'''' не является зеркальным отражением ударной адиабаты.
Упругопластическая разгрузка второй волны
Известно (например, [24]), что разгрузка ударно-сжатого вещества может носить чисто упругий или упругопластический характер в зависимости от величины достигнутого при сжатии продольного напряжения σxx. При анализе одномерных процессов сжатия–разгрузки вещества часто используется модель идеального упругопластического поведения – модель Прандтля, неплохо описывающая поведение многих металлов. Применим ее для получения функциональной связи u2 = f(W2N).
При нагружении вещества в двухволновой упругопластической конфигурации за первым ударным фронтом реализуется состояние σхх1, u1, где ${{\sigma }_{{хх}}}_{1} \equiv \sigma _{{хх}}^{{{\text{УПГ}}}}$ – упругий предел Гюгонио (рис. 7). За вторым фронтом достигаются продольное напряжение σхх2 и массовая скорость u2. Упругая разгрузка реализуется, если σхх2 не превышает значения $2{{\sigma }_{{хх}}}_{1} \equiv 2\sigma _{{хх}}^{{{\text{УПГ}}}}$. Из состояний с большими σхх2 вещество разгружается сначала упруго, а потом – пластически.
Граничное значение ${{W}_{2}}_{*}$, соответствующее разгрузке из состояния $2\sigma _{{хх}}^{{{\text{УПГ}}}}$, находится совместным решением уравнений прямых (в квазиакустическом приближении) с наклонами ρ0D1 и ρ1(D2 – u1), D2 – в лабораторной системе координат:
В пределе равенства наклонов волновых лучей ρ0D1 = ρ1D2, что эквивалентно D2 = D1, формула вырождается в ${{W}_{2}}_{*}$ = 4u1, как и должно быть.
При W2 < ${{W}_{*}}$ аналогичное рассмотрение в одномерном случае дает следующую формулу связи u2 и W2:
Для W2 > ${{W}_{*}}$ связь u2 c W2 записывается так:
В пределе D2 → D1 обе формулы дают “правильное” равенство – ${{u}_{2}} = \frac{{{{W}_{2}}}}{2}$.
Разгрузочные компоненты вектора W2 для рассматриваемых двух случаев разгрузки записываются следующим образом:
для W2 < ${{W}_{*}}$ –
Используем полученные разгрузочные “одномерные” компоненты для получения формул связи ${{u}_{2}}$ и ${{W}_{{2N}}}$ при разгрузке двухволновой упругопластической конфигурации в клиновом образце. При этом в (5) вместо α будем брать (α – β1), а под углом δ будем понимать угол δ2 (рис. 11). Как уже указывалось выше, данные компоненты должны быть направлены перпендикулярно последней (С+)-характеристике волны разрежения.
Для случая W2 < ${{W}_{2}}_{*}$ (упругая разгрузка):
(19)
${{u}_{2}} = \frac{{{{W}_{{2N}}} - {{u}_{1}}\left( {\frac{{{{D}_{1}} - {{D}_{2}}}}{{{{D}_{1}} - {{u}_{1}}}}} \right)\cos {{\delta }_{2}}}}{{\cos (\alpha - {{\beta }_{1}}) + \frac{{{{D}_{2}} - {{u}_{1}}}}{{{{D}_{1}} - {{u}_{1}}}}\cos {{\delta }_{2}}}}.$Для случая W2 > ${{W}_{2}}_{*}$ (упругопластическая разгрузка):
(20)
${{u}_{2}} = \frac{{{{W}_{{2N}}} + {{u}_{1}}\frac{{{{D}_{1}} - {{D}_{2}}}}{{{{D}_{1}} - {{u}_{1}}}}\cos {{\delta }_{2}}}}{{\cos (\alpha - {{\beta }_{1}}) + \cos {{\delta }_{2}}}}.$В пределе слабой второй волны, когда D2 → D1 и δ = α, обе полученные формулы дают выражение
Граничное значение ${{W}_{{2N}}}_{*}$, разделяющее два режима разгрузки, записывается так:
(21)
${{W}_{{2N}}}_{*} = {{u}_{1}}\left\{ {\left[ {1 + \frac{{{{D}_{1}} - {{u}_{1}}}}{{{{D}_{2}} - {{u}_{1}}}}} \right]\cos \alpha + 2\cos {{\delta }_{1}}} \right\}.$Естественно, для случая упругой разгрузки угол δ2 надо определять по (9) с использованием продольной скорости звука Cl0, а для упругопластического случая – CB0.
Приведенные формулы связи u2 и W2N при разгрузке двухволновой конфигурации на свободной поверхности клинового образца получены в предположении, что разгрузка проходит в одной (второй) волне разрежения. В действительности волн разрежения – две (рис. 11), однако это оказывается несущественным. Как показал анализ, вклад первой волны разрежения в суммарный поворот потока вещества от u2 до W2 (или до регистрируемой W2N) пренебрежимо мал – всего лишь 0.03%.
Интересно оценить масштаб уточнения u2, достигаемый при использовании приведенных формул (19)–(21), по сравнению с применением векторного правила удвоения (6) в гидродинамическом приближении. Для этого сопоставим u2, получаемые, во-первых, на верхнем пределе чисто упругой разгрузки, во-вторых, посередине диапазона существования двухволновой конфигурации и, в-третьих, в области закрывания двух-волновой конфигурации. Для стали 12Х18Н10Т при u2 = 0.14, 0.425 и 0.85 км/с интересующие погрешности составят 6%, 4% и 2% соответственно. Это значимые величины, и применение формул (19)–(21) целесообразно.
Не следует забывать о сделанном нами допущении о справедливости идеальной упругопластической модели деформирования материала. Известно, что некоторые металлы лучше описываются моделями с упрочнением [24]. Для этих моделей рассмотрение, подобное приведенному, также может быть проведено.
Вычисление параметров состояния вещества за фронтом второй ударной волны
Продольные напряжения ${{\sigma }_{{xx2}}}$, сжатия $\frac{{{{\rho }_{{\text{2}}}}}}{{{{\rho }_{{\text{1}}}}}}$ и относительная деформация ${{\varepsilon }_{{xx2}}}$ определяются по следующим формулам:
Эти соотношения, строго говоря, справедливые для стационарных ударных волн, можно считать справедливыми и вблизи фронтов нестационарных волн – в области незначительности спада параметров.
ПОГРЕШНОСТИ МЕТОДА ОПТИЧЕСКОГО РЫЧАГА
Напомним, что в методе о.р. прямо измеряемыми величинами являются угол наклона линии срыва растровых линий γ и смещение растровых линий a (рис. 4). Косвенно измеряемыми параметрами являются скорость ударного фронта D, обратно пропорциональная tgγ, и нормальная компонента скорости свободной поверхности образца WN, пропорциональная a. Параметры состояния ударно-сжатого материала образца определяются по скорости ударного фронта и нормальной компоненте скорости свободной поверхности образца с использованием формул, в которые кроме этих двух кинематических величин входят физические и геометрические характеристики образца, а также параметры экспериментальной сборки и фоторегистратора. В связи с этим суммарная погрешность вычисления параметров состояния материала будет определяться погрешностями всех перечисленных характеристик. Ниже представлена сводная таблица погрешностей вычисляемых величин в 1σ-представлении:
| $\frac{{\Delta {{D}_{1}}}}{{{{D}_{1}}}}$ | $\frac{{\Delta {{W}_{{1N}}}}}{{{{W}_{{1N}}}}}$ | $\frac{{\Delta {{u}_{1}}}}{{{{u}_{1}}}}$ | $\frac{{\Delta {{\sigma }_{{xx1}}}}}{{{{\sigma }_{{xx1}}}}}$ | $\frac{{\Delta ({{\rho }_{1}}{\text{/}}{{\rho }_{0}})}}{{({{\rho }_{1}}{\text{/}}{{\rho }_{0}})}}$ | $\frac{{\Delta {{\varepsilon }_{{xx1}}}}}{{{{\varepsilon }_{{xx1}}}}}$ |
| 0.9% | 0.6% | 0.6% | 1.1% | 1.3% | 1.1% |
| $\frac{{\Delta {{D}_{2}}}}{{{{D}_{2}}}}$ | $\frac{{\Delta {{W}_{{2N}}}}}{{{{W}_{{2N}}}}}$ | $\frac{{\Delta {{u}_{2}}}}{{{{u}_{2}}}}$ | $\frac{{\Delta {{\sigma }_{{xx2}}}}}{{{{\sigma }_{{xx2}}}}}$ | $\frac{{\Delta ({{\rho }_{2}}{\text{/}}{{\rho }_{1}})}}{{({{\rho }_{2}}{\text{/}}{{\rho }_{1}})}}$ | $\frac{{\Delta {{\varepsilon }_{{xx2}}}}}{{{{\varepsilon }_{{xx2}}}}}$ |
| 0.9% | 0.6% | 1.2% | 1.5% | 1.4% | 1.6% |
Достигнутый уровень погрешностей нахождения u, σxx и других производных величин связан с переходом к инструментальной обработке фотохронограмм с использованием программы трассировки треков.
ЗАКЛЮЧЕНИЕ
Метод оптического рычага является высокоинформативным многоканальным фотохронографическим методом косвенных измерений двух кинематических параметров ударного сжатия конденсированной среды – скорости ударного фронта D и нормальной компоненты скорости свободной поверхности образца WN при его разгрузке. Измерение параметров ведется на 10–20 толщинах материала, при этом регистрация WN является непрерывной во времени, т.е. в каждом канале (треке) записывается временной профиль импульса сжатия разгрузки.
Некоторая усложненность метода связана с неодномерностью постановки измерений, в которой, во-первых, векторы нормальной компоненты скорости свободной поверхности WN и массовой скорости u неколлинеарны, и, во-вторых, реализуются косые взаимодействия ударных фронтов и волн разрежения.
Подробный анализ волновых процессов в клиновых образцах, проведенный применительно к регистрации одиночных ударных волн и двухволновых упругопластических конфигураций, привел к следующим выводам:
1. Для получения точек ударной адиабаты исследуемого вещества вне области существования двухволновых конфигураций метод о.р. применим с той же степенью корректности, что и одномерные методы, при использовании построенного векторного аналога правила удвоения – функциональной связи массовой скорости u и измеряемой нормальной компоненты скорости свободной поверхности WN. Эта функциональная связь учитывает неодномерность регистрации и включает в качестве основного параметра угол α, под которым ударный фронт выходит на свободную поверхность образца. Точность вычисления u по WN не абсолютна, но весьма высока и определяется (как и в методе “откола”) степенью незеркальности изэнтропы разгрузки по отношению к ударной адиабате.
2. Применение метода о.р. для изучения ударной сжимаемости материалов внутри области существования двухволновых упругопластических конфигураций целесообразно. При этом параметры состояния в упругом предвестнике корректно вычисляются по D и u с использованием векторного аналога правила удвоения. Для получения массовой скорости u за пластическим фронтом по измеряемой WN требуется использовать какую-либо модель упругопластического поведения ударно-нагруженного материала при разгрузке. Это связано с незеркальностью изэнтропы разгрузки по отношению к ударной адиабате. В данной статье представлена процедура вычисления u по WN для пластической (второй) ударной волны двухволновой конфигурации с использованием модели идеального упругопластического поведения материала образца. Уточнение u с использованием развитого подхода по отношению к гидродинамическому приближению с векторным аналогом правила удвоения составляет 6%, 4% и 2% для нижнего края, середины и верхнего края диапазона двухволновых конфигураций.
3. Приведенные погрешности вычисляемых параметров ударно-волновых состояний, получаемых при использовании метода о.р., свидетельствуют о приемлемом уровне его точности.
Список литературы
Дубовик А.С. Дисс. … канд. техн. наук. Зеркальная развертка в фоторегистраторах. М.: ИХФ АН CCCР, 1950.
Owen J.D., Davies R.M. // Nature. 1949. V. 164. P. 752.
Allen W.A., McClary C.L. // Rev. Sci. Instrum. 1953. V. 24. P. 165.
Katz S., Doran D.G., Curran D.R. // J. Appl. Phys. 1959. V. 30. P. 568.
Fowles G.R. // J. Appl. Phys. 1961. V. 32. № 8. P. 1475.
Peyre C., Pujol J., Thouvenin J. // Proc. of 4th Intern. Symp. on Detonation. Washington, 1966. P. 5466.
Ahrens T., Ruderman N. // J. Appl. Phys. 1966. V. 37. № 13. P. 4758.
Таржанов В.И. // Физика горения и взрыва. 1977. Т. 13. № 5. С. 760.
Kozlov E.A. // High Pressure Research. 1992. V. 10. P. 541.
Горновой А.А., Козлов Е.А., Музыря А.К., Шорохов Е.В. // Физика горения и взрыва. 1989. Т. 25. № 4. С. 142.
Козлов Е.А., Музыря А.К., Чинкова Р.Х., Шорохов Е.В. // Физика горения и взрыва. 1984. Т. 20. № 4. С. 123.
Шорохов Е.В. // Химическая физика. 2002. Т. 21. № 8. С. 86.
Козлов Е.А., Таржанов В.И., Теличко И.В., Горбачев Д.М., Панкратов Д.Г. // Доклады академии наук. 2006. Т. 408. № 3. С. 1.
Козлов Е.А., Таржанов В.И., Теличко И.В., Панкратов Д.Г., Кучко Д.П., Ральников М.А., Грей Дж. III, Зочер М. // Материалы XIII Международного семинара “Фундаментальные свойства плутония”. 9–13 сентября 2013 г. Саров: РФЯЦ–ВНИИЭФ, 2013. С. 202.
Козлов Е.А., Таржанов В.И., Теличко И.В., Панкратов Д.Г., Воробьев А.В., Горбачев Д.М., Ставрие-цкий В.И. // V Международный семинар “Фундаментальные свойства плутония”. 12–16 сентября 2005 г. Снежинск: РФЯЦ–ВНИИТФ, 2005. С. 155.
Kozlov E.A., Tarzhanov V.I., Telichko I.V., Pankratov D.G., Vorobyov A.V., Gorbachev D.M., Stavrietsky V.I. // VIII International Conference on High Energy Density Physics – “Zababakhin Scientific Talks-2005”. Snezhinsk, Russia 5–10 September 2005. AIP Conference Proceedings / Eds E.N. Avrorin, V.A. Simonenko. 2005. V. 849. P. 393.
Mescheryakov Yu.I. Shock Compression of Condensed Matter – 1999/ Eds M.D. Furnish, Y.M. Gupta, J.W. Forbts. AIP Conference Proceedings. № 505. Melville, NY. 1999. P. 1065.
Шнирман Г.Л., Дубовик А.С., Кевлишвили П.В. // Высокоскоростная фоторегистрирующая установка СФР. М.: ВИНИТИ АН СССР, 1957.
Альтшулер Л.В. // Успехи физических наук. 1965. Т. 85. Вып. 2. С. 197.
Жерноклетов М.В., Симаков Г.В., Сутулов Ю.Н., Трунин Р.Ф. // Теплофизика высоких температур. 1995. Т. 33. № 1. С. 40.
Курант Г., Фридрихс К. Сверхзвуковое течение и ударные волны. М.: Изд-во иностр. лит-ры, 1950.
Альтшулер Л.В., Кормер С.Б., Бражник М.И., Владимиров Л.А., Сперанская М.П., Фунтиков А.И. // ЖЭТФ. 1960. Т. 38. Вып. 4. С. 1061.
Козлов Е.А., Панкратов Д.Г., Ткачев О.В., Якунин А.К. // Сборник трудов Международной конференции “Ударные волны в конденсированном веществе”. 16–21 сентября 2012. Киев: Интерпресс ЛТД, 2012. С. 263–265.
Канель Г.И., Разоренов С.В., Уткин А.В., Фортов В.Е. Ударно-волновые явления в конденсированных средах. М. Янус-К, 1996.
Дополнительные материалы отсутствуют.
Инструменты
Приборы и техника эксперимента