Приборы и техника эксперимента, 2022, № 2, стр. 43-51

1. ВВЕДЕНИЕ

Несовершенство измерительных систем приводит к искажениям экспериментальных данных, избежать которых крайне трудно, так как зачастую они обусловлены функциональными особенностями измерительной аппаратуры или вызваны паразитными параметрами и взаимосвязями ее составляющих. Аппаратные методы повышения точности измерений связаны с решением сложных научно-технических проблем и дорогостоящих конструктивно-технологических задач. Альтернативой аппаратным методам являются методы математической реконструкции внешних воздействий из экспериментальных данных, получаемых в процессе измерений и искаженных измерительными системами.

Большинство задач реконструкции являются некорректно поставленными и плохо обусловленными (см., например, [1, 2]). Возможность реконструкции зависит от множества факторов, что делает разработку различных методов реконструкции, эффективных в том или ином случае, актуальным направлением исследований. В данной работе предлагаются математические методы реконструкции внешних воздействий линейных стационарных измерительных систем (см., например, [3, 4]), основанные на тестовых измерениях. Тестовая реконструкция позволяет избежать трудоемкого анализа измерительных систем и процесса измерений и с этой точки зрения является более универсальным методом реконструкции. Предлагаемые методы также могут быть использованы для моделирования отклика измерительных систем на заданное воздействие.

2. ПОСТАНОВКА ЗАДАЧ РЕКОНСТРУКЦИИ И МОДЕЛИРОВАНИЯ

Отклик $w(x)~$ линейных стационарных измерительных систем представляет собой свертку внешнего воздействия $v(x)$ на них со стороны исследуемого физического объекта или процесса с импульсной характеристикой $~u(x)$ системы, которая полностью определяет ее поведение в области $D~$проведения измерений (см., например, [3, 4]):

Свертка (1) линейна в смысле суперпозиции откликов при наложении внешних воздействий: $\sum {{{w}_{i}}(x) = (u*\sum {{{{v}}_{i}}} )(x)} $; коммутативна: $(u*{v})(x)$ = = $({v}*u)(x)$ и ассоциативна: $(u*({v}*w))(x)$ = = $((u*{v})*w)(x)$; коммутирует с оператором сдвига $w(x - {{x}_{0}}) = u*{v}(x - {{x}_{0}})$, и тождественным оператором для нее является дельта-функция ${{\delta }}(x)$: $({{\delta }}*v)(x) = v(x)$ (см., например, [5, 6]).

Математические методы реконструкции воздействия $v(x)$ из отклика $w(x)$ измерительной системы основаны на использовании уравнения свертки (1). Обычно на практике эта задача является некорректно поставленной и зачастую плохо обусловленной, поэтому, как правило, ищут регуляризированное решение $v(x)$, обеспечивающее минимум функционала (см., например, [1, 7]):

где $~{\text{||}}f{\text{||}}_{2}^{2} = \int_D {{\text{|}}f(x){{{\text{|}}}^{2}}dx} $ – квадрат евклидовой нормы функции $f(x)$; ${{\alpha }}Q[v]$ – неотрицательный стабилизирующий член, зависящий от функции $v(x)$. Функционал вида $Q[v]\, = \,\int_D {\sum\nolimits_{n = 0}^p {{{q}_{n}}(x){{{\left( {\frac{{{{d}^{n}}v}}{{d{{x}^{n}}}}} \right)}}^{2}}dx} } $, где ${{q}_{n}}(x)$ – некоторые заданные неотрицательные функции, “сглаживает” решение $v(x)$ до производных порядка $~p$ и обеспечивает устойчивость решения при варьировании исходных данных $w(x)$ и $u(x)$, а положительный коэффициент $~{{\alpha }}$ определяет степень сглаживания (см., например, [7]). В частности, используемый в дальнейшем стабилизатор нулевого порядка ${{\alpha }}Q[v]$ = ${{\alpha ||}}v{\text{||}}_{2}^{2}$ обеспечивает поиск решения из класса непрерывных функций, “сглаженных” до производных порядка $p = 0$.

Спектр $V({{\omega }})$ регуляризированного решения $v(x)$ уравнения (2) можно выразить в явном виде, используя интегральное преобразование Фурье (см., например, [1, 7]):

где $F({{\omega }}) = FT\{ f(x)\} $ – спектральная плотность функции $f(x)$, а $U{\text{*}}({{\omega }})$ – комплексно-сопряженная (сопряженно-транспонированная в многомерном случае) к $U({{\omega }})$ величина. Функционал $P({{\omega }}) = \sum\nolimits_{n = 0}^p {{{q}_{n}}{{{{\omega }}}^{{2n}}}} $, где ${{q}_{n}}$ – некоторые неотрицательные константы, осуществляет “сглаживание” решения вплоть до производных порядка $p~$ (см., например, [7]). В частности, стабилизирующий член нулевого порядка ($p = 0$) представляет собой константу ${{\beta }}P({{\omega }}) = {{\beta }} \geqslant ~0$, значение которой подбирается для обеспечения наименьшей погрешности реконструкции.

Спектр (3) регуляризированного решения (2) ограничен полосой пропускания измерительной системы, т.е. диапазонами частот, где спектр импульсной характеристики $u(x)$ не равен нулю: $~U({{\omega }}) \ne 0$. Согласно теореме Планшереля, среднеквадратичная ошибка при вырезании спектра воздействия вне полосы пропускания измерительной системы будет равна интегралу $\int_{\{ U({{\omega }}) = 0\} } {V{\text{*}}({{\omega }})V({{\omega }})d{{\omega }}} $. Воздействие можно восстановить, если его спектр лежит внутри полосы пропускания системы, но, даже если это условие не выполняется, ошибка реконструкции может быть мала, если не входящие в полосу пропускания области спектра имеют меру ноль.

Необходимую для реконструкции импульсную характеристику $u(x)$ измерительной системы можно определить с помощью математического моделирования процесса измерений. Для этого требуется детальный анализ измерительной системы с учетом паразитных параметров ее элементов, линий связи и т.п., провести который в случае сложных измерительных систем крайне трудно. Импульсная характеристика равна отклику на воздействие в виде дельта-функции, но сгенерировать на практике такое воздействие с бесконечной амплитудой и нулевой длительностью невозможно.

Предлагаемый метод реконструкции основан на тестовых измерениях и позволяет обойтись без определения импульсной характеристики. Тестовые измерения заключаются в определении отклика ${{w}_{c}}(x)$ измерительной системы на некоторое известное воздействие ${{v}_{c}}(x)$. Свертывая обе части уравнения свертки (1) с тестовым воздействием ${{v}_{c}}(x)$ и учитывая, что ${{w}_{c}}(x) = (u*{{v}_{c}})(x)$, получим уравнение свертки для реконструкции с использованием тестовых сигналов:

Функции $w(x)$, ${{v}_{c}}(x)$ и ${{w}_{c}}(x)$ в уравнении (4) известны, что позволяет сразу из этого уравнения реконструировать воздействие $v(x)$ рассмотренными выше методами (2) и (3). Для этого в формуле (2) необходимо заменить $w(x)$ на $(w*{{v}_{c}})(x)$ и $u(x)$ на ${{w}_{c}}(x)$: ${{\Phi }}[v{\text{|}}w,{{w}_{c}},{{v}_{c}}]$ = ${\text{||}}w*{{v}_{c}} - {{w}_{c}}*v{\text{||}}_{2}^{2}$ + + $\alpha {\text{||}}v{\text{||}}_{2}^{2}$; а в формуле (3) – W(ω) на $W({{\omega }}){{V}_{c}}({{\omega }})$ и U(ω) на ${{W}_{c}}({{\omega }})$: V(ω) = ${{W}_{c}}^{*}({{\omega }})W({{\omega }}){{V}_{c}}({{\omega }}){\text{/}}({{W}_{c}}^{*}({{\omega }}){{W}_{c}}({{\omega }})$ + + β).

Спектр воздействия, реконструируемого из уравнения (4), будет ограничен и полосой пропускания, и спектром тестового отклика: U(ω)V_c(ω) = = ${{W}_{c}}({{\omega }}) \ne 0$. Согласно теореме Планшереля, среднеквадратичная ошибка реконструкции воздействия за счет несовпадения спектров будет равна интегралу $~\int_{\{ {{W}_{c}}({{\omega }}) = 0\} } {V{\text{*}}({{\omega }})V({{\omega }})d{{\omega }}} $. Воздействие можно восстановить, если его спектр лежит внутри спектра тестового отклика, но, даже если это условие не выполняется, ошибка реконструкции может быть мала, если области, не входящие в спектр воздействия, имеют меру ноль.

С помощью уравнения (4) можно также решить задачу моделирования отклика $w(x)$ на заданное воздействие $v(x)$. Уравнение (4) при этом не изменится: $(v*{{w}_{c}})(x) = ({{v}_{c}}*w)(x)$, но заданными в нем будут считаться функции $v(x)$, ${{v}_{c}}(x)$ и ${{w}_{c}}(x)$. Неизвестный отклик $w(x)$ можно реконструировать из функционала ${{\Phi }}[w{\text{|}}v,{{w}_{c}},{{v}_{c}}]$ = = ${\text{||}}v*{{w}_{c}} - {{v}_{c}}*w{\text{||}}_{2}^{2} + {{\alpha ||}}w{\text{||}}_{2}^{2}$, где функция $~w(x)$ из формулы (2) была заменена на $(v*{{w}_{c}})(x)$ и $u(x)$ ‒ на ${{v}_{c}}(x)$, или из спектра W(ω) = = ${{V}_{c}}^{*}({{\omega }})V({{\omega }}){{W}_{c}}({{\omega }}){\text{/}}({{V}_{c}}^{*}({{\omega }}){{V}_{c}}({{\omega }})$ + β), в котором спектр $W({{\omega }})$ из формулы (3) заменен на $V({{\omega }}){{W}_{c}}({{\omega }})$ и $U({{\omega }})$ – на ${{V}_{c}}({{\omega }})$. При этом спектр моделируемого отклика будет ограничен и полосой пропускания $U({{\omega }}) \ne 0$, и спектром тестового воздействия ${{V}_{c}}({{\omega }}) \ne 0$: $U({{\omega }}){{V}_{c}}({{\omega }}) = {{W}_{c}}({{\omega }}) \ne 0$, и среднеквадратичная ошибка моделирования будет равна интегралу $\int_{\{ {{W}_{c}}({{\omega }}) = 0{\text{\;}}\} } {W{\text{*}}({{\omega }})W({{\omega }})d{{\omega }}} $.

Неопределенности в тестовых сигналах ${{w}_{c}}(x)$ и ${{v}_{c}}(x)$ можно снизить статистическими методами, повторяя тестовые измерения необходимое количество раз. Аналогично можно уменьшить погрешности в отклике $w(x)$, если имеется возможность повторить измерения.

3. ЧИСЛЕННЫЕ РАСЧЕТЫ

На практике данные измерений обычно получают или представляют в дискретном виде как наборы или массивы значений функций в некоторых точках разбиения области наблюдений, затем они обрабатываются численными методами. Представим функции $w(x)$, $v(x)$ и $u(x)$ из формулы (1), определенные на действительной оси $x~$ (многомерный случай будет рассмотрен позже), в дискретном виде как наборы значений этих функций: ${\mathbf{w}} = \{ {{w}_{i}}\} $, ${\mathbf{v}} = \{ {{{v}}_{i}}\} $ и ${\mathbf{u}} = \{ {{u}_{i}}\} $ в точках ${{x}_{i}} = i{{\Delta }}$, где $i$ – целое число, $~{{\Delta \;}}$ – шаг разбиения оси $x$, ${{w}_{i}} = w({{x}_{i}}),{{v}_{i}} = v({{x}_{i}})~$ и ${{u}_{i}} = u({{x}_{i}})$. Из формулы (1) для значения ${{w}_{k}} = w({{x}_{k}})$ в точке ${{x}_{k}} = k{{\Delta \;}}$ получим ${{w}_{k}} = w(k{{\Delta }})$ = $\int_{ - \infty }^\infty {u(k{{\Delta }} - \xi )v(\xi )d\xi } $. На введенном разбиении оси $x$ этот интеграл можно представить в виде частичной суммы: w_k ≈ ${{\Delta }}\sum\nolimits_i {u[(k - i){{\Delta }}]v(i{{\Delta }})} $ = = ${{\Delta }}\sum\nolimits_i {{{u}_{{k - i}}}{{v}_{i}}} $. Переопределив дискретную импульсную характеристику как $~~{{u}_{i}} = u(i{{\Delta }}){{\Delta }}$, получим дискретное уравнение свертки

которое фактически является представлением свертки (1) частичной суммой и, следовательно, обеспечивает лишь приближенное соответствие значений функций $w(x)$, $v(x)$ и $u(x)$ в точках ${{x}_{i}}$ = iΔ с точностью до представления интеграла частичной суммой. Неточности при дискретизации непрерывных процессов можно интерпретировать как искажения исходных данных и использовать рассмотренные ранее методы реконструкции некорректно поставленных задач. Уровень искажений при дискретизации можно снизить, уменьшая шаг дискретизации, так как частичная сумма стремится к значению интеграла при ${{\Delta }} \to 0$: ${{w}_{k}} \to \sum\nolimits_i {{{u}_{{k - i}}}{{v}_{i}}} $.

Интерпретируя значения ${{u}_{i}}$, ${{v}_{i}}$ и ${{w}_{i}}$ как компоненты векторов: ${\mathbf{u}} = \{ {{u}_{i}}\} $, ${\mathbf{v}} = \{ {{v}_{i}}\} $ и ${\mathbf{w}} = \{ {{w}_{i}}\} $, дискретные уравнения свертки (5) можно представить в матричном виде:

где ${\mathbf{U}} = \{ {{u}_{{ij}}}\} = \{ {{u}_{{i - j}}}\} $ и ${\mathbf{V}} = \{ {{v}_{{ij}}}\} = \{ {{v}_{{i - j}}}\} $ – матрицы Теплица с производящими векторами ${\mathbf{u}}$ и ${\mathbf{v}}$.

Чтобы решить задачу реконструкции, матричные уравнения (6) надо свести к системам конечного числа линейных алгебраических уравнений, что означает рассмотрение функций $w(x)$, $u(x)$ и $v(x)$ на конечных интервалах. Если функции $v(x)$ и $u(x)$ из формулы (1) определены на конечных интервалах $(a,c)$ и $(b,d)$, то функция $w(x)$ будет определена на интервале $(a + b,~\,c + d)$. В этом случае при равномерном разбиении оси $x~$ размеры $n$, $m$ и $k~$ векторов ${\mathbf{w}}$, $~{\mathbf{v}}$ и ${\mathbf{u}}$ будут связаны соотношением $n = m + k - 1$, а матрицы ${\mathbf{U}}$ и ${\mathbf{V}}~$ в формуле (6) будут иметь размеры $n \times m$ и $n \times k~$ соответственно. Уравнения (6) будут представлять собой переопределенные прямоугольные системы линейных алгебраических уравнений, содержащие все актуальные значения дискретных функций.

Согласно формуле (2), регуляризированное решение ${\mathbf{v}}$ таких систем со стабилизатором нулевого порядка дается выражением (см., например, [2, 7])

где ${{\gamma \;}}$ – неотрицательный стабилизирующий коэффициент; ${\mathbf{I}}$ и ${{(\, \cdot \,)}^{{ - 1}}}$ – единичная и обратная матрицы размера $m \times m$. Поскольку при получении выражений (7) интегральные преобразования не использовались, будем говорить, что они получены прямыми методами.

Прямоугольные переопределенные системы (7) можно свести к квадратным, дополняя нулями векторы $~{\mathbf{u}}$ и ${\mathbf{v}}$ до размера n вектора ${\mathbf{w}}$. В этом случае для векторов ${\mathbf{w}}$, ${\mathbf{v}}$ и ${\mathbf{u}}$ можно применить дискретно-точечные прямое и обратное преобразования Фурье (д.п.Ф.): ${{Z}_{i}} = \frac{1}{{\sqrt n }}\sum\nolimits_{j = 0}^{n - 1} {{{z}_{j}}{{e}^{{ - \frac{{2{{\pi }}I}}{n}ij}}}} $ и z_j = = $\frac{1}{{\sqrt n }}\sum\nolimits_{i = 0}^{n - 1} {{{Z}_{i}}{{e}^{{\frac{{2{{\pi }}I}}{n}ij}}}} $, $i,j = 0,~ \ldots ,n - 1$, $I = \sqrt { - 1} $. Используя в формуле (3) стабилизаторы нулевого порядка, для дискретного спектра $V = \{ {{V}_{i}}\} $, где $i = 0$, ..., n – 1, воздействия ${\mathbf{v}}$ получим

Задачу реконструкции нефинитных функций ${\mathbf{v}}$, ${\mathbf{u}}$ и w можно свести к поиску финитных, если вне некоторых базовых интервалов: $(a,c)$, $(b,d)~$ и $(a + b,~~c + d)$ – значениями этих функций можно пренебречь, т.е. если $\int_{ - \infty }^{ + \infty } {{\text{|}}v(x){\text{|}}dx} $ ≈ $\int_a^c {{\text{|}}v(x){\text{|}}dx} $, $~\int_{ - \infty }^{ + \infty } {{\text{|}}u(x){\text{|}}dx} $ ≈ $~\int_b^d {{\text{|}}u(x){\text{|}}dx} $ и, следовательно, $\int_{ - \infty }^{ + \infty } {{\text{|}}w(x){\text{|}}dx} $ ≈ $~\int_{a + b}^{c + d} {{\text{|}}w(x){\text{|}}dx} $. Отбрасывание данных вне базовых интервалов можно интерпретировать как внесение дополнительных неточностей в исходные данные при некорректной постановке задачи реконструкции.

Прямые методы (7) позволяют осуществить реконструкцию финитных слева и незатухающих справа функций, даже если конечных базовых интервалов для них не существует. Векторы ${\mathbf{u}} = \{ {{u}_{i}}\} $, ${\mathbf{v}} = \{ {{v}_{i}}\} $ и ${\mathbf{w}} = \{ {{w}_{i}}\} $, $i = 0,~1,~ \ldots $, соответствующие функциям $u(x)$, $v(x)$ и $w(x)$, определенным на интервалах $(a,\infty )$, $(b,\infty )$ и $(a + b,\infty )$, также как и матрицы ${\mathbf{U}} = \{ {{u}_{{ij}}}\} = \{ {{u}_{{i - j}}}\} $ и ${\mathbf{V}} = \{ {{v}_{{ij}}}\} = \{ {{v}_{{i - j}}}\} $, где $~i,~j = 0,~1$ ..., из формулы (6), будут иметь бесконечный размер. Однако для любого необходимого количества $n$ элементов векторов ${\mathbf{w}} = \{ {{w}_{i}}\} $, ${\mathbf{v}} = \{ {{v}_{i}}\} $ или ${\mathbf{u}} = \{ {{u}_{i}}\} $, где $~i = 0,{\text{\;\;}}1,{\text{\;}} \ldots ,{\text{\;\;}}n - 1$, из формулы (6) можно сформировать системы из $n~$ линейных алгебраических уравнений и использовать выражения (7) для поиска регуляризированного решения. Таким образом, прямыми методами можно реконструировать произвольное количество элементов финитных слева функций.

При применении прямых методов реализуется поточечная регуляризация на рассматриваемом интервале, что позволяет реконструировать любую начальную часть воздействия $v(x)$, например, только передний фронт воздействия. Примеры подобных реконструкций будут рассмотрены в численном эксперименте в следующем разделе.

В отличие от прямых методов, использование интегральных преобразований в этом случае может привести к неверным результатам. Функции, рассматриваемые на конечном интервале, при интегральных преобразованиях интерпретируются как периодические, и с помощью выражений (8) будет найдено решение, соответствующее установившемуся отклику на периодические воздействия, а не на единичное воздействие. Следовательно, применение интегральных преобразований возможно только в том случае, когда на рассматриваемом интервале установившийся отклик совпадает с откликом на единичное воздействие, что возможно только для финитных или периодических функций.

В случае периодических функций $w(x)$, $u(x)$ и $v(x)$ задачу реконструкции можно свести к поиску финитных функций на интервале периодичности. При этом можно использовать как прямые методы, так и интегральные преобразования, но последние более предпочтительны, так как значительно ускоряют процесс вычислений, что будет использовано в дальнейшем в численном эксперименте по реконструкции изображений.

При тестовой реконструкции вместо уравнения (1) рассматривается уравнение (4). В случае дискретных функций это означает, что в формулы (6) и (7) вместо матрицы ${\mathbf{U}}~$ надо подставить матрицу ${{{\mathbf{W}}}_{c}}$ с производящим вектором ${{{\mathbf{w}}}_{c}}$, а вместо вектора ${\mathbf{w}}~$ – вектор ${{{\mathbf{V}}}_{c}}{\mathbf{w}} = {\mathbf{W}}{{{\mathbf{v}}}_{c}}$, где ${{{\mathbf{V}}}_{c}}$ и ${\mathbf{W}}$ – матрицы с производящими векторами ${{{\mathbf{v}}}_{c}}$ и ${\mathbf{w}}$ соответственно. Таким образом, из формулы (7) для тестовой реконструкции получим регуляризированное решение:

а из формулы (8) – дискретный спектр решения (когда возможно применение интегральных преобразований):

Аналогично при моделировании отклика ${\mathbf{w}}$ на заданное воздействие ${\mathbf{v}}$ получим выражения: $~{\mathbf{w}} = {{({\mathbf{V}}_{c}^{*}{{{\mathbf{V}}}_{c}} + {{\beta }}{\mathbf{I}})}^{{ - 1}}}{\mathbf{V}}_{c}^{*}{{{\mathbf{W}}}_{c}}{\mathbf{v}}$ и ${{W}_{i}}\, = \,V_{i}^{{c*}}W_{i}^{c}{{V}_{i}}{\text{/}}(V_{i}^{{c*}}V_{i}^{c}\, + \,{{\beta }})$.

Прямые методы реконструкции и моделирования (7) и (9) являются более медленными, чем методы д.п.Ф. (8) и (10), но более универсальными.

4. РЕКОНСТРУКЦИЯ СИГНАЛОВ

Рассмотрим численный эксперимент по восстановлению входных сигналов из сигналов на выходе измерительной системы, например емкостного делителя напряжения, который представляет собой пассивную линейную схему, вырабатывающую выходное напряжение, составляющее часть входного напряжения. Принципиальная схема делителя напряжения и сигналы на его входе ($v(t)$ и $V(t)$) и выходе ($w(t)$ и $W(t)$) представлены на рис. 1. Сигналы рассчитывались с использованием программы расчета электрических цепей Micro-Cap 12.2.0.4 Spectrum Software. Принципиальная схема делителя была взята из стандартной библиотеки этой программы. Выходные сигналы $w(t)$ и $W(t)$ показаны на рис. 1 с масштабным коэффициентом, который компенсирует падение напряжения для сравнения форм входных и выходных сигналов.

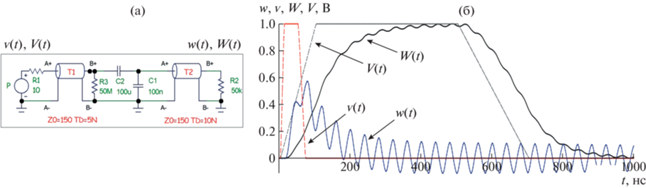
Делитель на основе емкостей ${{C}_{1}}$ = 100 нФ, ${{C}_{2}}$ = = 100 мкФ и сопротивлений ${{R}_{2}}$ = 50 МОм, ${{R}_{3}}$ = = 50 кОм подключен к источнику сигнала $P$ с внутренним сопротивлением ${{R}_{1}}$ = 10 Ом и регистрирующим оборудованием через помехозащищенные линии передачи Т₁ и Т₂ с волновым сопротивлением ${{Z}_{0}}$ = 150 Ом типа витая пара. Линии передачи Т₁ и Т₂ имеют времена задержки распространения сигналов $TD$ = 5, 10 нс соответственно. Частотный анализ показывает, что делитель имеет частоту среза порядка 1 МГц.

Входные сигналы $v(t)$ и $V(t)$ от генератора $P$ на рис. 1 имеют трапециевидную форму. Длительность сигнала $v(t)$ на полувысоте составляет 55 нс, передний и задний фронты – 10 и 20 нс, параметры сигнала $V(t)$ на порядок больше: длительность – 550 нс, фронты – 100 и 200 нс. Спектры входных сигналов (порядка 20 МГц для $v(t)$ и порядка 200 МГц для $V(t)$) значительно превышают частоту среза делителя (порядка 1 МГц), поэтому форма выходных сигналов $w(t)$ и $W(t)$ существенно отличается от формы входных сигналов $v(t)$ и $V(t)$.

При восстановлении входных сигналов из выходных с помощью тестовых сигналов схема измерительного устройства может быть неизвестна. При восстановлении входного сигнала $v(t)$ необходимо знать соответствующий выходной сигнал $w(t)$ и тестовые сигналы $W(t)$ и $V(t)$, а при восстановлении сигнала $V(t)$ известными считаются сигналы $W(t)$, $w(t)$ и $v(t)$.

Сигналы $w(t)$, $v(t)$, $W(t)$ и $V(t)$ на рис. 1 характеризуются временем начала измерений и относятся к финитным слева функциям. Интервал реконструкции $T$ должен включать в себя время начала измерений, и при использовании прямых методов (7) и (9) его длительность может быть выбрана произвольно, а при применении д.п.Ф. (8) и (10) все переходные процессы реконструируемого отклика за пределами интервала реконструкции $T$ должны быть пренебрежимо малы, т.е. интервал должен быть не меньше базового.

Рисунок 2 иллюстрирует процессы дискретизации функций на интервале $T$ = 200 нс (рис. 2а) и реконструкции воздействия $v(t)$ из отклика $w(t)~$ прямыми методами (9) при использовании сигналов ${{w}_{c}}(t) = W(t)$ и ${{v}_{c}}(t) = V(t)$ в качестве тестовых (рис. 2б). Точками показаны дискретные значения функций при шаге дискретизации ${{\Delta }}$ = 2.0 нс. Размерность векторов при этом составила $n$ = 100. Отметим, что шаг дискретизации исходных расчетных данных был в три раза меньше. Погрешность реконструкции воздействия ${{{v}}_{r}}~$ из данных $w$, $W$ и $V$ на рис. 2а составила $\delta {{v}_{r}} = {\text{||}}{{v}_{r}} - v{\text{||/||}}v{\text{||}}$ = = 3.0%.

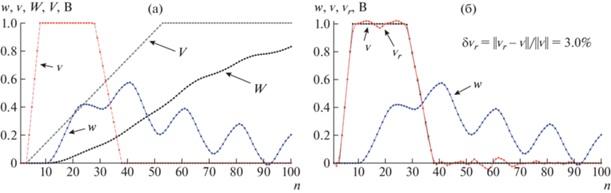
Если, наоборот, в качестве тестовых использовать сигналы ${{w}_{c}}(t) = w(t)$ и ${{v}_{c}}(t) = v(t)$ с более широким спектром и реконструировать на интервале $T$ = 1 мкс (см. рис. 1) воздействие $V(t)$ из отклика $W(t)$ с менее широким спектром, то погрешность реконструкции составит δV_r = ${\text{||}}{{V}_{r}} - V{\text{||/||}}V{\text{||}}$ = 0.1%. Таким образом, погрешность реконструкции ${{\delta }}{{{v}}_{r}}$, равная 3%, на рис. 2б обусловлена в основном несовпадением спектров реконструируемого и тестового сигналов.

При наличии шумов и неопределенностей в исходных данных погрешность реконструкции резко возрастает. Так, при уровне случайных помех в тестовых сигналах ${{\delta }}W\, = \,{\text{||}}\Delta W{\text{||/||}}W{\text{||}}$ = 0.6% и ${{\delta }}V\, = \,{\text{||}}\Delta V{\text{||/||}}V{\text{||}}$ = 0.2% и в отклике δw = ||Δw||/||w|| = = 5.0% погрешность реконструкции составила ${{\delta }}{{{v}}_{r}}\, = \,{\text{||}}{{{v}}_{r}}\, - \,{v}{\text{||/||}}{v}{\text{||}}$ =  9.1%. Однако при дальнейшем увеличении уровня помех в отклике до ${{\delta }}w~$ = 14.6% (почти в 3 раза) (рис. 3а) погрешность реконструкции возросла лишь до ${{\delta }}{{{v}}_{r}}$ = 12.8%, т.е. всего в 1.4 раза, и стала даже меньше уровня помех в исходных данных.

Замедление роста погрешности реконструкции происходит из-за того, что при увеличении амплитуды случайных помех и неизменном шаге дискретизации увеличиваются высокочастотные составляющие спектра помех, которые более эффективно сглаживаются при регуляризации решения. На рис. 3б представлен график зависимости погрешности реконструкции ${{\delta }}{{v}_{r}}[\% ]\, = \,{\text{||}}{{v}_{r}}\, - \,v{\text{||/||}}v{\text{||}}$ внешнего воздействия $v(t)$ от уровня шумов ${{\delta }}w[\% ] = {\text{||}}\Delta w{\text{||/||}}w{\text{||}}$ в отклике $w(t)$ при неизменных уровне и распределении помех в тестовых сигналах ${{\delta }}W = {\text{||}}\Delta W{\text{||/||}}W{\text{||}} = 0.6~\% $ и ${{\delta }}V = {\text{||}}\Delta V{\text{||/||}}V{\text{||}}$ = = 0.2% Здесь также показаны эмпирические границы ${{\delta }}{{{v}}_{{{\text{min}}}}}$ и ${{\delta }}{{{v}}_{{{\text{max}}}}}$ разброса погрешностей реконструкции в проведенных экспериментах. Разброс погрешности реконструкции обусловлен тем, что погрешность зависит не только от уровня помех, но и от случайного распределения этих помех в массиве данных.

Программа реконструкции сигналов была написана на языке Maple 2017.3 Waterloo Maple Inc. и оформлена в виде подпрограммы, входными данными для которой служили векторы ${\mathbf{w}} = \{ {{w}_{i}}\} $, ${{{\mathbf{w}}}_{c}} = \{ w_{i}^{c}\} ~$ и ${{{\mathbf{v}}}_{c}} = \{ v_{i}^{c}\} $, соответствующие исходным искаженному и тестовым данным, и стабилизирующий коэффициент ${{\gamma }}$. Наибольшее время занимал подбор стабилизирующего коэффициента, а время работы подпрограммы при реконструкции сигналов на рис. 3а с выбранным стабилизирующим коэффициентом при расчетах на компьютере HP 255 G7 с процессором AMD Ryzen 3, 2.5 ГГц составило 0.23 с.

Математическая реконструкция входных сигналов из выходных по сути позволяет существенно расширить частотный диапазон емкостного делителя и повысить его точность без внесения изменений в схему или конструкцию устройства. Провести подобную реконструкцию можно для любых измерительных систем, включая устройства с активными элементами, работающими в линейном режиме, или даже для целых измерительных комплексов с многочисленными преобразованиями данных. Необходимыми условиями являются линейность и стационарность измерительной системы в целом в диапазоне реконструкции. При тестовой реконструкции не требуется знать схему измерительного устройства, анализировать процесс измерений или учитывать паразитные взаимосвязи элементов, так как вся эта информация содержится в тестовых сигналах.

Уровень случайных шумов и неопределенностей в тестовых данных можно снизить до приемлемого уровня статистическими методами, проведя тестовые измерения необходимое количество раз. Аналогично можно снизить и уровень шумов в данных измерений, если имеется возможность повторить измерения.

Таким образом, математическая реконструкция позволяет значительно расширить диапазон применения измерительных систем, повысить их точность и разрешающую способность, что является доступной альтернативой трудноразрешимым научно-техническим и дорогостоящим конструктивно-технологическим методам решения задач.

5. РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЙ

Многомерные экспериментальные данные измерительных систем обычно получают в дискретном виде как массивы чисел большого объема. При большом, но конечном объеме данных более эффективно применять методы реконструкции с использованием интегральных преобразований. В случае реконструкции массива дискретных данных $~{\mathbf{V}} = \{ {{v}_{{ij \ldots }}}\} $ из искаженных ${\mathbf{W}} = \{ {{w}_{{ij \ldots }}}\} $ c использованием тестовых данных ${{{\mathbf{V}}}_{c}} = \{ v_{{ij \ldots }}^{c}\} $ и ${{{\mathbf{W}}}_{c}} = \{ w_{{ij \ldots }}^{c}\} ~$ уравнение (10) для спектра регуляризированного решения можно представить в виде

где $V = \{ {{V}_{{ij \ldots }}}\} $, $W = \{ {{W}_{{ij \ldots }}}\} $, ${{V}_{c}} = \{ V_{{ij \ldots }}^{c}\} $ и ${{W}_{c}} = \{ W_{{ij \ldots }}^{c}\} $ – многомерные спектры соответствующих массивов данных $~{\mathbf{V}}$, ${\mathbf{W}}$, ${{{\mathbf{V}}}_{c}}$ и ${{{\mathbf{W}}}_{c}}$, полученные с помощью n-точечного д.п.Ф. Как и в одномерном случае, для применения n-точечного д.п.Ф. размеры массивов должны быть приведены к максимальному значению путем заполнения недостающих элементов массивов нулями. Например, если максимальный размер $n \times m$, $n > m$, имеют двумерные данные ${\mathbf{W}}$, то все массивы, включая ${\mathbf{W}}$, должны быть приведены к размеру $n \times n$.

На рис. 4 представлен пример реконструкции ${{{\mathbf{V}}}_{r}}$ изображения ${\mathbf{V}}$ из искаженного изображения ${\mathbf{W}}$ с использованием тестовых изображений ${{{\mathbf{W}}}_{c}}$ и ${{{\mathbf{V}}}_{c}}$ при ядре искажения ${\mathbf{U}}$. Ядро искажения выбиралось в наиболее общем виде и представляло собой несимметричную прямоугольную матрицу размером $35 \times 55$. Контурный график матрицы ядра искажения на рис. 4 представлен для информации, так как в случае тестовой реконструкции определение ядра искажения не требуется.

Исходные изображения представляли собой однослойные изображения (оттенки серого) в формате .jpeg, которые для проведения расчетов преобразовывались в матрицы. Тестовое изображение ${{{\mathbf{V}}}_{c}}$ имело размер $80 \times 80$ пикселей, а искаженное тестовое ${{{\mathbf{W}}}_{c}}$, увеличенное при размытии, – $114 \times 134~$ пикселя. Размер реконструируемого изображения ${\mathbf{V}}$ составлял $500 \times 700$ пикселей, размытого изображения ${\mathbf{W}}~~--~~534 \times 754$ пикселя. Все изображения ${\mathbf{W}}$, ${{{\mathbf{V}}}_{c}}$ и ${{{\mathbf{W}}}_{c}}$ дополнялись нулями до размера $754 \times 754$ пикселя, и с помощью n‑точечного д.п.Ф. определялись двумерные спектры $W$, ${{V}_{c}}$ и ${{W}_{c}}$ этих изображений размером $754 \times 754~$ пикселя. Далее, согласно формуле (11), был найден спектр ${{V}_{r}},~$ и с помощью обратного д.п.Ф. осуществлена реконструкция ${{{\mathbf{V}}}_{r}}$ изображения ${\mathbf{V}}$ до исходного размера $500 \times 700$ пикселей, который определялся из разницы размеров тестовых изображений.

Программа расчета была написана на языке Maple 2017.3 Waterloo Maple Inc. в виде подпрограммы, входными данными для которой служили исходные изображения ${\mathbf{W}}$, ${{{\mathbf{W}}}_{c}}$ и ${{{\mathbf{V}}}_{c}}$ и стабилизирующий коэффициент ${{\beta }}$. Погрешность реконструкции δV_r = = $\max {\text{|}}{{{\mathbf{V}}}_{r}} - {\mathbf{V}}{\text{|/}}\max {\text{|}}{\mathbf{V}}{\text{|}}$ без дополнительных помех и неопределенностей в данных составила 0.07%, и стабилизирующий коэффициент выбирался равным нулю. Время реконструкции изображения $500 \times 700$ пикселей при расчетах на компьютере HP 255 G7 с процессором AMD Ryzen 3, 2.5 ГГц составило 36.3 с. При уменьшении объема данных оно сокращается. Так, время реконструкции изображения размером $200 \times 200~$ пикселей составляет 2.8 с, а размером $80 \times 80~$ пикселей – 0.7 с.

Аналогичным образом с помощью выражений (11) можно реконструировать и цветные изображения, обрабатывая каждый слой отдельно. При этом время реконструкции увеличится пропорционально количеству обрабатываемых слоев.

6. ЗАКЛЮЧЕНИЕ

Предложено решение задачи восстановления параметров исследуемых физических процессов из данных измерений линейных стационарных систем с помощью тестовых сигналов, использование которых позволяет обойтись без анализа измерительных систем и моделирования процесса измерений, что особенно важно в случае сложных систем, когда провести такой анализ крайне трудно. Предложенные методы позволяют осуществить реконструкцию за один этап без промежуточного определения переходной характеристики системы. Они также могут быть использованы для моделирования отклика измерительных систем на заданное воздействие.

Рассмотрены случаи непрерывных и дискретных данных, проведены оценки погрешности при представлении данных линейных стационарных систем в дискретном виде. Проведен анализ зависимости погрешности реконструкции от спектров измерительных систем, воздействий и тестовых сигналов, от уровней шумов и неопределенностей в них. Предложены методы реконструкции на основе прямых преобразований и с использованием интегральных преобразований Фурье, проведен сравнительный анализ возможностей методов и областей их применения. Представлены расчетные выражения для реконструкции данных в виде финитных и нефинитных функций, а также соответствующих им дискретных данных. Предложенные методы реконструкции используют регуляризацию решений и применимы в случае плохо обусловленных и некорректно поставленных задач.

Проведены численные эксперименты реконструкции одномерных данных и двумерных изображений, подробно описаны процедуры проведения тестовых измерений и представлены графики зависимостей погрешности реконструкции от уровня шумов и неопределенностей в данных.

Разрабатываемые математические методы позволяют повысить точность и разрешающую способность измерительной аппаратуры, значительно расширить диапазон ее применения. Математические методы являются доступной альтернативой аппаратным методам, которые сопряжены с трудноразрешимыми научно-техническими проблемами и дорогостоящими конструктивно-технологическими задачами. Математические методы обработки данных измерений, в отличие от аппаратных, не ограничены условиями физической реализуемости устройств, что значительно расширяет их возможности и области применения.