Прикладная математика и механика, 2019, T. 83, № 1, стр. 3-15
ЭВОЛЮЦИЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ДИНАМИЧЕСКИ СИММЕТРИЧНОГО СПУТНИКА С ВНУТРЕННИМ ДЕМПФИРОВАНИЕМ НА КРУГОВОЙ ОРБИТЕ
Н. И. Амелькин *, В. В. Холощак **
Московский физико-технический институт
Долгопрудный, Россия
* E-mail: namelkin@mail.ru
** E-mail: khoviktoriya@yandex.ru
Поступила в редакцию 20.04.2018
Аннотация
В рамках модели М.А. Лаврентьева изучается влияние внутренней диссипации на вращательное движение спутника в центральном гравитационном поле. Выведены эволюционные уравнения и представлены результаты анализа эволюции вращательного движения динамически симметричного спутника, движущегося по кеплеровой круговой орбите, в зависимости от значений параметров и начальных условий.
Задача о влиянии внутренних диссипативных сил на вращательное движение спутника рассматривалась в разных постановках многими авторами. В большинстве работ для моделирования внутренней диссипации использовалась одна из трех моделей спутника: 1) твердое тело с полостью, заполненной вязкой жидкостью [1–3], 2) твердое тело с шаровым демпфером (модель М.А. Лаврентьева) [4–6], 3) вязкоупругое тело [7, 8]. Для динамически симметричного спутника на круговой орбите эволюция вращательного движения исследовалась ранее [3] в рамках модели 1 для случая сильно вязкой жидкости и больших значений приведенной угловой скорости спутника. Ниже эволюция вращений спутника исследуется в рамках модели М.А. Лаврентьева, причем в существенно более широком по сравнению с предыдущим исследованием [3] диапазоне значений параметров и угловых скоростей спутника.
1. Анализ устойчивости стационарных вращений спутника, близкого к сферически симметричному. Вращательное движение спутника с шаровым демпфером в центральном гравитационном поле на круговой орбите может быть описано системой уравнений [6]
(1.1)
$\begin{gathered} ({\mathbf{J}} - I{\mathbf{E}}){\mathbf{\dot {U}}} + {\mathbf{U}} \times {\mathbf{JU}} = 3{\mathbf{r}} \times {\mathbf{Jr}} + \mu I({\mathbf{V}} - {\mathbf{U}}) \\ {\mathbf{\dot {V}}} + {\mathbf{U}} \times {\mathbf{V}} = - \mu ({\mathbf{V}} - {\mathbf{U}}) \\ 2{\mathbf{\dot {\Lambda }}} = {\mathbf{\Lambda }} \circ {\mathbf{U}} \\ \end{gathered} $Здесь ${\mathbf{J}}$ – центральный тензор инерции всего спутника, $I$ – момент инерции демпфера относительно его центральной оси, E – единичная матрица, ${\mathbf{r}} = {{\mathbf{R}} \mathord{\left/ {\vphantom {{\mathbf{R}} R}} \right. \kern-0em} R}$ – единичный вектор, сонаправленный с радиус-вектором центра масс спутника, ${\mathbf{U}} = {{\mathbf{\omega }} \mathord{\left/ {\vphantom {{\mathbf{\omega }} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$, V = ${\mathbf{\Omega }}{\text{/}}{{\omega }_{0}}$, где ${\mathbf{\omega }}$ – абсолютная угловая скорость оболочки, ${\mathbf{\Omega }}$ – абсолютная угловая скорость демпфера, ${{\omega }_{0}}$ – угловая скорость орбитального базиса, направленная по нормали ${\mathbf{n}}$ к плоскости орбиты, $\mu $ – безразмерный коэффициент демпфирования, ${\mathbf{\Lambda }}$ – кватернион единичной нормы, задающий положение связанного с оболочкой базиса главных осей инерции спутника ${{{\mathbf{e}}}_{1}},{{{\mathbf{e}}}_{2}}$, e3 относительно базиса Кëнига ${{{\mathbf{i}}}_{1}},{{{\mathbf{i}}}_{2}}$, i3. Точкой обозначена производная по безразмерному времени $\tau = {{\omega }_{0}}t$. В уравнениях (1.1) все векторы задаются своими компонентами в базисе ${{{\mathbf{e}}}_{1}},{{{\mathbf{e}}}_{2}}$, e3.
Для динамически симметричного спутника движение относительно орбитального базиса, образованного векторами ${\mathbf{r}}$, ${\mathbf{\tau }} = {\mathbf{n}} \times {\mathbf{r}}$ и ${\mathbf{n}}$, описывается следующей автономной системой уравнений [6]:
(1.2)
$\begin{gathered} {\mathbf{\dot {e}}} = {\mathbf{u}} \times {\mathbf{e}} \\ (A - I)({\mathbf{n}} \times {\mathbf{u}} + {\mathbf{\dot {u}}}) + (C - A)[(({\mathbf{n}} \times {\mathbf{u}} + {\mathbf{\dot {u}}}) \cdot {\mathbf{e}}){\mathbf{e}} + (({\mathbf{n}} + {\mathbf{u}}) \cdot {\mathbf{e}})({\mathbf{n}} + {\mathbf{u}}) \times {\mathbf{e}}] = \\ = \mu I({\mathbf{v}} - {\mathbf{u}}) + 3(C - A)({\mathbf{r}} \cdot {\mathbf{e}})({\mathbf{r}} \times {\mathbf{e}}) \\ {\mathbf{n}} \times {\mathbf{v}} + {\mathbf{\dot {v}}} = - \mu ({\mathbf{v}} - {\mathbf{u}}) \\ \end{gathered} $Здесь через ${\mathbf{u}} = {{({\mathbf{\omega }} - {{{\mathbf{\omega }}}_{0}})} \mathord{\left/ {\vphantom {{({\mathbf{\omega }} - {{{\mathbf{\omega }}}_{0}})} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$ и ${\mathbf{v}} = {{({\mathbf{\Omega }} - {{{\mathbf{\omega }}}_{0}})} \mathord{\left/ {\vphantom {{({\mathbf{\Omega }} - {{{\mathbf{\omega }}}_{0}})} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$ обозначены приведенная угловая скорость несущего тела (оболочки) и приведенная угловая скорость демпфера относительно орбитального базиса, ${\mathbf{e}}$ – ось симметрии спутника, $C$ и $A$ – осевой и экваториальный моменты инерции спутника.
Было показано [6], что предельными движениями спутника являются только положения равновесия относительно орбитального базиса и стационарные вращения вокруг оси симметрии, сонаправленной с нормалью к плоскости орбиты (цилиндрические регулярные прецессии)
(1.3)
${\mathbf{e}}* = {\mathbf{n}},\quad {\mathbf{v}}* = {\mathbf{u}}* = u{\mathbf{n}};\quad u \in ( - \infty , + \infty )$Задача об устойчивости движений (1.3) сводится к исследованию устойчивости характеристического полинома системы, получаемой линеаризацией уравнений (1.2) в окрестности решений (1.3). Этот полином имеет вид [6]
(1.4)
$P(\lambda ) = {{a}_{0}}{{\lambda }^{6}} + {{a}_{1}}{{\lambda }^{5}} + {{a}_{2}}{{\lambda }^{4}} + {{a}_{3}}{{\lambda }^{3}} + {{a}_{4}}{{\lambda }^{2}} + {{a}_{5}}\lambda + {{a}_{6}}$(1.5)
${{a}_{4}} = [{{k}^{2}} + ({{m}^{2}} + 1)(1 + {{k}^{2}})] + \varepsilon [3({{m}^{2}} + 1) - 3k + \mu \gamma m(2\beta k - 3)] + {{\varepsilon }^{2}}{{\beta }^{2}}{{(\mu \gamma )}^{2}}$(1.6)
$\begin{gathered} \alpha = {{(С - I)} \mathord{\left/ {\vphantom {{(С - I)} {(A}}} \right. \kern-0em} {(A}} - I),\quad \gamma = {I \mathord{\left/ {\vphantom {I {(A - I}}} \right. \kern-0em} {(A - I}}),\quad \beta = u + 1 \\ m = \mu (1 + \gamma ),\quad k = 1 - \beta (1 + \varepsilon ),\quad \varepsilon = \alpha - 1;\quad \varepsilon \in [ - 1,1] \\ \end{gathered} $Здесь $\alpha \in [0,2]$ – коэффициент “сплюснутости” вспомогательного тела, образованного оболочкой и точечной массой, равной массе демпфера и расположенной в его центре, $\gamma \in [0,\infty )$ – отношение момента инерции демпфера к экваториальному моменту инерции вспомогательного тела, $\beta $ – отношение абсолютной угловой скорости стационарного вращения спутника к угловой скорости орбитального базиса.
Заметим, что коэффициент сплюснутости всего спутника определяется выражением
(1.7)
$\alpha {\text{*}} = {C \mathord{\left/ {\vphantom {C A}} \right. \kern-0em} A} = {{(\alpha + \gamma )} \mathord{\left/ {\vphantom {{(\alpha + \gamma )} {(1 + \gamma )}}} \right. \kern-0em} {(1 + \gamma )}}$Если $\alpha > 1$, то и $\alpha * > 1$ (сплюснутый спутник), причем $\alpha * < \alpha $. Если $\alpha < 1$, то и $\alpha * < 1$ (вытянутый спутник), причем $\alpha * > \alpha $.
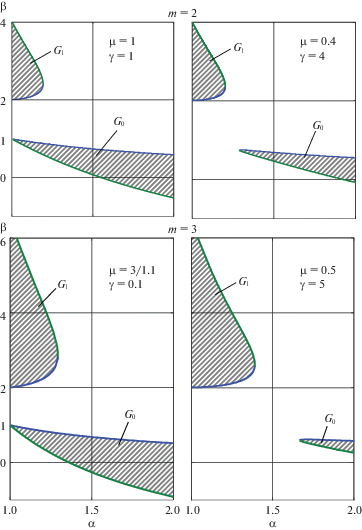
Аналитическое исследование условий устойчивости полинома (1.4) было проведено ранее [6] для значений $\mu \ll 1$ и $\mu \gg 1$. Для остальных значений параметра $\mu $ проводился численный анализ корней полинома (1.4) при значениях $\gamma $, сравнимых по величине с единицей.
В данном разделе проводится аналитическое исследование условий устойчивости стационарных вращений (1.3) во всем диапазоне значений параметров $\mu $ и $\gamma $ для сплюснутого спутника, близкого к сферически симметричному:
По критерию Рауса–Гурвица в форме Льенара–Шипара условия устойчивости описываются системой неравенств
где ${{\Delta }_{3}}$ и ${{\Delta }_{5}}$ – миноры третьего и пятого порядка матрицы Гурвица. Из формул (1.5) и (1.6) следует, что для любых значений $m > 0$ и $\beta $ при достаточно малых значениях $\varepsilon $ коэффициенты ${{a}_{1}},{{a}_{2}},{{a}_{3}}$, a4 будут положительными. Коэффициент a5 при учете соотношений (1.6) записывается в виде полинома второй степени относительно k следующим образом:(1.10)
${{a}_{5}} = {{\mu [2(1 + \gamma + \varepsilon ){{k}^{2}} - 6\varepsilon (1 + \varepsilon )k + \varepsilon \gamma (5 + 3\varepsilon )]} \mathord{\left/ {\vphantom {{\mu [2(1 + \gamma + \varepsilon ){{k}^{2}} - 6\varepsilon (1 + \varepsilon )k + \varepsilon \gamma (5 + 3\varepsilon )]} {(1 + \varepsilon )}}} \right. \kern-0em} {(1 + \varepsilon )}}$При $k = 0$ и $\varepsilon > 0$ имеем ${{a}_{5}} > 0$, а при достаточно малых значениях $\varepsilon $ полином, как нетрудно видеть, не имеет вещественных корней. Поэтому и ${{a}_{5}} > 0$ при $\varepsilon \ll 1$.
Коэффициент ${{a}_{6}}$ тоже выражается полиномом второй степени относительно k. Оставляя в коэффициентах этого полинома только главные члены, получим
(1.11)
${{a}_{6}} = ({{m}^{2}} + 1){{k}^{2}} - \varepsilon (3 - 2{{m}^{2}} + 5\mu m)k + {{\varepsilon }^{2}}(m - \mu )[(m - 4\mu )]$Дискриминант полинома записывается в виде
Если выполняется условие
то полином имеет два вещественных корня которым соответствуют в плоскости $\varepsilon $, $\beta $ две кривыеЕсли неравенство (1.12) имеет обратный знак, что имеет место при одновременном выполнении условий
то ${{a}_{6}} > 0$ при $\varepsilon \ll 1$. В этом случае область неустойчивости ${{G}_{0}}$ “отрывается” от оси $\varepsilon = 0$ и имеет вид, изображенный на фиг. 1 справа.Минор ${{\Delta }_{3}}$ определяется выражением
(1.14)
${{\Delta }_{3}} = 2\mu \gamma m[3 + 2{{(1 - k)}^{2}}][{{(1 + k)}^{2}} + {{m}^{2}}]\varepsilon + O({{\varepsilon }^{2}})$Минор ${{\Delta }_{5}}$ записывается в виде
(1.15)
${{\Delta }_{5}} = 18{{\mu }^{3}}{{\gamma }^{2}}[3 + 2{{(1 - k)}^{2}}][{{(1 + k)}^{2}} + {{m}^{2}}]({{m}^{2}} + 2 + 2k)(1 + k){{\varepsilon }^{3}} + O({{\varepsilon }^{4}})$При $\varepsilon \ll 1$ он принимает положительные значения, если $\beta < 2$, или $\beta > {{({{m}^{2}} + 4)} \mathord{\left/ {\vphantom {{({{m}^{2}} + 4)} 2}} \right. \kern-0em} 2}$. В диапазоне
(1.16)
$2 < \beta < {{({{m}^{2}} + 4)} \mathord{\left/ {\vphantom {{({{m}^{2}} + 4)} 2}} \right. \kern-0em} 2} = \beta {\text{*}}$Таким образом, для сплюснутого динамически симметричного спутника, близкого к сферически симметричному, условия устойчивости стационарных вращений определяются значением одного параметра $m = \mu (\gamma + 1)$. Исключение составляет только узкий диапазон вращений с угловой скоростью, близкой к угловой скорости орбитального базиса, для которых характер устойчивости определяется конкретной комбинаций двух параметров $\mu $ и $\gamma $.
На фиг. 1 представлены полученные численным исследованием корней характеристического уравнения системы диаграммы областей асимптотической устойчивости (не заштрихованы) и неустойчивости (заштрихованы) на интервале $1 < \alpha < 2$ в плоскости параметров α, β при $m = 2$ и $m = 3$, где каждому из указанных значений $m$ соответствуют две разные комбинации параметров μ и $\gamma $. Эти диаграммы, а также результаты других расчетов [6], полностью подтверждают сделанные выше выводы о характере устойчивости стационарных вращений спутника, близкого к сферически симметричному. Линейные размеры области ${{G}_{1}}$ пропорциональны ${{m}^{2}}$, причем, как следует из диаграмм, размер области ${{G}_{1}}$ по оси α слабо зависит от конкретной комбинации параметров $\mu $ и $\gamma $. Установлено также, что при $\mu < {\text{4/3}}$ (1.13) существует такое значение $\gamma {\text{*}}$, что при $\gamma > \gamma {\text{*}}$ область неустойчивости ${{G}_{0}}$ совсем исчезает из интервала $1\, < \alpha < 2$.
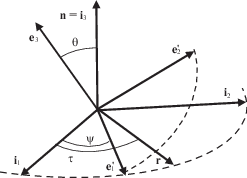
2. Эволюционные уравнения. Для целей аналитического исследования эволюции вращательного движения динамически симметричного спутника запишем уравнения движения в проекциях на оси базиса Резаля ${\mathbf{e}}_{1}^{'},{\mathbf{e}}_{2}^{'}$, e3 (${{{\mathbf{e}}}_{3}}$ – ось симметрии спутника), задаваемого углами $\psi $ и $\theta $ (фиг. 2). Обозначив через ${\mathbf{W}} = {\mathbf{V}} - {\mathbf{U}}$ вектор относительной угловой скорости демпфера, получим уравнения
(2.1)
$\begin{gathered} ({\mathbf{J}} - I{\mathbf{E}}){\mathbf{\dot {U}}} + {\mathbf{u}}{\text{'}} \times ({\mathbf{J}} - I{\mathbf{E}}){\mathbf{U}} = 3{\mathbf{r}} \times {\mathbf{Jr}} + \mu I{\mathbf{W}} \\ {\mathbf{\dot {U}}} + {\mathbf{\dot {W}}} + {\mathbf{u}}{\text{'}} \times ({\mathbf{U}} + {\mathbf{W}}) = - \mu {\mathbf{W}}, \\ \end{gathered} $(2.2)
${\mathbf{u}}{\text{'}} = {\mathbf{e}}_{1}^{'}\dot {\theta } + \dot {\psi }({\mathbf{e}}_{2}^{'}\sin \theta + {{{\mathbf{e}}}_{3}}\cos \theta ) = {\mathbf{U}} - \dot {\phi }{{{\mathbf{e}}}_{3}},$(2.3)
$\dot {\theta } = {{U}_{1}},\quad \dot {\psi }\sin \theta = {{U}_{2}},\quad \dot {\phi } = {{U}_{3}} - {{U}_{2}}\operatorname{ctg} \theta $(2.4)
${\mathbf{u}}{\text{'}} = {{U}_{1}}{\mathbf{e}}_{1}^{'} + {{U}_{2}}{\mathbf{e}}_{2}^{'} + {{U}_{2}}\operatorname{ctg} {\theta }{{{\mathbf{e}}}_{3}}$Действующий на спутник гравитационный момент определяется выражением
(2.5)
${{{\mathbf{m}}}_{g}} = 3{\mathbf{r}} \times {\mathbf{Jr}} = \frac{3}{2}(C - A)\sin \theta {\text{[}}{\mathbf{e}}_{2}^{'}\sin 2(\tau - \psi ) + {\mathbf{e}}_{1}^{'}\cos \theta {\text{(}}\cos 2(\tau - \psi ) - 1)]$Проецируя уравнения (2.1) на оси базиса Резаля, получим при учете соотношений (2.3), (2.4) и (1.6) следующую замкнутую систему из восьми уравнений:
(2.6)
$\begin{gathered} {{{\dot {W}}}_{1}} = \varepsilon {{U}_{2}}{{U}_{3}} + {{U}_{2}}{{W}_{2}}\operatorname{ctg} \theta - {{U}_{2}}{{W}_{3}} - \mu (1 + \gamma ){{W}_{1}} - {{F}_{1}}[\cos 2(\tau - \psi ) - 1] \\ {{{\dot {W}}}_{2}} = - \varepsilon {{U}_{1}}{{U}_{3}} + {{U}_{1}}{{W}_{3}} - {{U}_{2}}{{W}_{1}}\operatorname{ctg} \theta - \mu (1 + \gamma ){{W}_{2}} - {{F}_{2}}\sin 2(\tau - \psi ) \\ \end{gathered} $Функции ${{F}_{1}}$ и ${{F}_{2}}$ определяются формулами
(2.7)
${{F}_{1}} = \frac{{3\varepsilon \sin 2\theta }}{4},\quad {{F}_{2}} = \frac{{3\varepsilon \sin \theta }}{2} = \frac{{{{F}_{1}}}}{{\cos \theta }}$Далее будем рассматривать сплюснутый спутник ($\alpha > 1$), близкий к сферически симметричному, т.е. полагать, что $\varepsilon \ll 1$ (малый параметр). Анализ уравнений (2.6) и результаты численного интегрирования уравнений (1.1) показали, что при m = $\mu (1 + \gamma ) \geqslant \sqrt \varepsilon $ для разных начальных значений угловой скорости оболочки и демпфера наблюдается сравнительно быстрый переходный процесс (быстрая эволюция), в конце которого устанавливается движение, близкое к вращению спутника, как единого твердого тела, вокруг оси симметрии, сонаправленной с начальным значением вектора кинетического момента спутника. Затем происходит медленная эволюция за счет действия гравитационного и диссипативного моментов. При этом переменные ${{U}_{k}}$, Wk и $\theta $ в режиме медленной эволюции в среднем меняются медленно и имеют гармонические составляющие, частота которых близка к значению 2, причем средние значения переменных ${{U}_{1}},{{U}_{2}},{{W}_{1}},{{W}_{2}}$, W3 и их гармонические составляющие являются ограниченными функциями $\varepsilon $.
В задаче об эволюции вращательного движения спутника основной интерес представляет поведение оси вращения спутника и величины угловой скорости. В предположении, что в режиме медленной эволюции движение сплюснутого спутника близко к вращению вокруг оси симметрии, анализ эволюции сводится к изучению поведения фазовых переменных ${{U}_{3}}$, θ и $\psi $.
Наличие малого параметра в уравнениях (2.6) дает основания применить для получения эволюционных уравнений метод осреднения. Но “классическая” схема метода осреднения [9, 10] для системы (2.6) не может быть непосредственно использована, поскольку приведение системы (2.6) к стандартной форме проблематично. Ниже для рассматриваемой задачи применяется вариант метода осреднения без приведения системы (2.6) к стандартной форме.
Введем следующие обозначения для фазовых переменных:
(2.8)
${\mathbf{x}}{\text{:}}\;{{{\mathbf{x}}}^{T}} = ({{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}},{{x}_{5}},{{x}_{6}},{{x}_{7}},{{x}_{8}}) = ({{U}_{1}},{{U}_{2}},{{W}_{1}},{{W}_{2}},{{U}_{3}},{{W}_{3}},\theta ,\psi )$Систему (2.6) перепишем в виде
(2.9)
${\mathbf{\dot {x}}} = {\mathbf{X}}({\mathbf{x}},\tau ) = {\mathbf{L}}({\mathbf{x}}) + {\mathbf{G}}({\mathbf{x}}) + {\mathbf{\tilde {X}}}({\mathbf{x}},\tau ),$Решение будем искать в виде
где компоненты функции ${\mathbf{S}}({\mathbf{y}},\tau )$ выбираются из следующих условий: если ${{\tilde {X}}_{j}} = 0$, то ${{S}_{j}} = 0$, а если ${{\tilde {X}}_{k}} \ne 0$, то ${{S}_{k}}$ удовлетворяет уравнению(2.11)
$\frac{{\partial {{S}_{k}}}}{{\partial \tau }} = {{L}_{k}}({\mathbf{S}}) + {{\tilde {X}}_{k}}({\mathbf{y}},\tau )$(2.12)
$\begin{gathered} {{{\dot {y}}}_{k}} + \frac{{\partial {{S}_{k}}}}{{\partial {{{\mathbf{y}}}^{T}}}}{\mathbf{\dot {y}}} = {{L}_{k}}({\mathbf{y}}) + {{G}_{k}}({\mathbf{y}} + {\mathbf{S}}) + {{{\tilde {X}}}_{k}}({\mathbf{y}} + {\mathbf{S}},\tau ) - {{{\tilde {X}}}_{k}}({\mathbf{y}},\tau );\quad k = 1,2,3,4 \\ {{{\dot {y}}}_{j}} = {{{\dot {x}}}_{j}} = {{X}_{j}}({\mathbf{y}} + {\mathbf{S}});\quad j = 5,6,7,8 \\ \end{gathered} $Найдем компоненты функции ${\mathbf{S}}({\mathbf{y}},\tau )$. Имеем
(2.13)
${{S}_{5}} = {{S}_{6}} = {{S}_{7}} = {{S}_{8}} = 0 \Rightarrow {{y}_{5}} = {{U}_{3}},\quad {{y}_{6}} = {{W}_{3}},\quad {{y}_{7}} = \theta ,\quad {{y}_{8}} = \psi $Остальные компоненты находятся из системы (здесь и далее $U = {{U}_{3}}$, $m = \mu (1 + \gamma )$)
(2.14)
$\begin{gathered} \frac{{\partial {{S}_{1}}}}{{\partial \tau }} = - (1 + \varepsilon )U{{S}_{2}} + \mu \gamma {{S}_{3}} + {{F}_{1}}\cos 2(\tau - \psi ) \\ \frac{{\partial {{S}_{2}}}}{{\partial \tau }} = (1 + \varepsilon )U{{S}_{1}} + \mu \gamma {{S}_{4}} + {{F}_{2}}\sin 2(\tau - \psi ) \\ \frac{{\partial {{S}_{3}}}}{{\partial \tau }} = \varepsilon U{{S}_{2}} - m{{S}_{3}} - {{F}_{1}}\cos 2(\tau - \psi ) \\ \frac{{\partial {{S}_{4}}}}{{\partial \tau }} = - \varepsilon U{{S}_{1}} - m{{S}_{4}} - {{F}_{2}}\sin 2(\tau - \psi ) \\ \end{gathered} $Решение этой системы записывается через гармонические по времени функции
Коэффициенты определяются с точностью до $O({{\varepsilon }^{2}})$ формулами
(2.16)
$\begin{gathered} {{p}_{1}} = (4 + \mu m){{f}_{{12}}},\quad {{q}_{1}} = 2\mu \gamma {\kern 1pt} {{f}_{{12}}},\quad {{p}_{2}} = 2\mu \gamma {\kern 1pt} {{f}_{{21}}},\quad {{q}_{2}} = - (4 + \mu m){{f}_{{21}}}; \\ {{f}_{{ij}}} = \frac{{2{{F}_{i}} + U{{F}_{j}}}}{{(4 + {{m}^{2}})(4 - {{U}^{2}})}} \\ {{p}_{3}} = \frac{{ - 2{{F}_{1}}}}{{4 + {{m}^{2}}}},\quad {{q}_{3}} = \frac{{ - m{{F}_{1}}}}{{4 + {{m}^{2}}}},\quad {{p}_{4}} = \frac{{ - m{{F}_{2}}}}{{4 + {{m}^{2}}}},\quad {{q}_{4}} = \frac{{2{{F}_{2}}}}{{4 + {{m}^{2}}}} \\ \end{gathered} $Функция ${\mathbf{S}}$ зависит только от переменных $\psi $, θ и $U$, поэтому уравнения (2.12) принимают вид
(2.17)
$\begin{gathered} {{{\dot {y}}}_{k}} = - \frac{{\partial {{S}_{k}}}}{{\partial \theta }}({{y}_{1}} + {{S}_{1}}) - \frac{{\partial {{S}_{k}}}}{{\partial \psi }}\frac{{{{y}_{2}} + {{S}_{2}}}}{{\sin \theta }} - \frac{{\partial {{S}_{k}}}}{{\partial U}}\frac{{\mu \gamma }}{{(1 + \varepsilon )}}{{W}_{3}} + {{L}_{k}}({\mathbf{y}}) + {{G}_{k}}({\mathbf{y}} + {\mathbf{S}});\quad k = 1,2,3,4 \\ {{{\dot {W}}}_{3}} = ({{y}_{2}} + {{S}_{2}})({{y}_{3}} + {{S}_{3}}) - ({{y}_{1}} + {{S}_{1}})({{y}_{4}} + {{S}_{4}}) - \frac{{\mu (1 + \gamma + \varepsilon )}}{{1 + \varepsilon }}{{W}_{3}} \\ \dot {U} = \frac{{\mu \gamma }}{{1 + \varepsilon }}{{W}_{3}},\quad \dot {\theta } = {{y}_{1}} + {{S}_{1}},\quad \dot {\psi } = \frac{{{{y}_{2}} + {{S}_{2}}}}{{\sin \theta }} \\ \end{gathered} $Подробный анализ полученной системы показал, что в режиме медленной эволюции переменные ${{y}_{2}}$ и ${{y}_{3}}$ – ограниченные функции $\varepsilon $, а переменные ${{y}_{1}}$, y4 и ${{W}_{3}}$ – ограниченные функции ${{\varepsilon }^{2}}$. При этом для первых пяти уравнений средние значения правых частей, вычисленные в силу уравнений движения, с точностью до $O({{\varepsilon }^{3}})$ совпадают со средними по явно входящему времени. Учитывая это, а также вытекающие из выражений (2.15) формулы (среднее по времени обозначается угловыми скобками, штрихом – производные по переменной $\theta $)
(2.18)
$\left\langle {\frac{{\partial {{S}_{k}}}}{{\partial \theta }}{{S}_{1}}} \right\rangle = \frac{{p_{k}^{'}{{p}_{1}} + k_{k}^{'}{{q}_{1}}}}{2} + O({{\varepsilon }^{3}}),\quad \left\langle {\frac{{\partial {{S}_{k}}}}{{\partial \psi }}{{S}_{2}}} \right\rangle = {{p}_{2}}{{q}_{k}} - {{q}_{2}}{{p}_{k}} + O({{\varepsilon }^{3}})$(2.19)
$\begin{gathered} {{{\dot {\bar {y}}}}_{1}} = - (1 + \varepsilon )U{{{\bar {y}}}_{2}} + \mu \gamma {{{\bar {y}}}_{3}} - {{F}_{1}} + O({{\varepsilon }^{2}}),\quad {{{\dot {\bar {y}}}}_{3}} = \varepsilon U{{{\bar {y}}}_{2}} - m{{{\bar {y}}}_{3}} + {{F}_{1}} + O({{\varepsilon }^{2}}) \\ {{{\dot {\bar {y}}}}_{2}} = U{{{\bar {y}}}_{1}} + \mu \gamma {{{\bar {y}}}_{4}} - \operatorname{ctg} \theta {{({{p}_{2}}{{p}_{1}} + {{q}_{2}}{{q}_{1}})} \mathord{\left/ {\vphantom {{({{p}_{2}}{{p}_{1}} + {{q}_{2}}{{q}_{1}})} 2}} \right. \kern-0em} 2} - {{(p_{2}^{'}{{p}_{1}} + q_{2}^{'}{{q}_{1}})} \mathord{\left/ {\vphantom {{(p_{2}^{'}{{p}_{1}} + q_{2}^{'}{{q}_{1}})} 2}} \right. \kern-0em} 2} \\ {{{\dot {\bar {y}}}}_{4}} = - m{{{\bar {y}}}_{4}} - \operatorname{ctg} {\theta }{{(2{{{\bar {y}}}_{2}}{{{\bar {y}}}_{3}} + {{p}_{2}}{{p}_{3}} + {{q}_{2}}{{q}_{3}})} \mathord{\left/ {\vphantom {{(2{{{\bar {y}}}_{2}}{{{\bar {y}}}_{3}} + {{p}_{2}}{{p}_{3}} + {{q}_{2}}{{q}_{3}})} 2}} \right. \kern-0em} 2} - {{(p_{4}^{'}{{p}_{1}} + q_{4}^{'}{{q}_{1}})} \mathord{\left/ {\vphantom {{(p_{4}^{'}{{p}_{1}} + q_{4}^{'}{{q}_{1}})} 2}} \right. \kern-0em} 2} - {{({{p}_{2}}{{q}_{4}} - {{q}_{2}}{{p}_{4}})} \mathord{\left/ {\vphantom {{({{p}_{2}}{{q}_{4}} - {{q}_{2}}{{p}_{4}})} {\sin \theta }}} \right. \kern-0em} {\sin \theta }} \\ {{{\dot {\bar {W}}}}_{3}} = - m{{{\bar {W}}}_{3}} + {{{\bar {y}}}_{2}}{{{\bar {y}}}_{3}} + {{({{p}_{2}}{{p}_{3}} + {{q}_{2}}{{q}_{3}} - {{p}_{1}}{{p}_{4}} - {{q}_{1}}{{q}_{4}})} \mathord{\left/ {\vphantom {{({{p}_{2}}{{p}_{3}} + {{q}_{2}}{{q}_{3}} - {{p}_{1}}{{p}_{4}} - {{q}_{1}}{{q}_{4}})} 2}} \right. \kern-0em} 2} \\ \end{gathered} $В последних трех уравнениях системы (2.19) правые части выписаны с точностью до $O({{\varepsilon }^{3}})$.
Из уравнений (2.19) найдем значения переменных ${{\bar {y}}_{1}},{{\bar {y}}_{2}},{{\bar {y}}_{3}},{{\bar {y}}_{4}}$, ${{\bar {W}}_{3}}$ в режиме медленной эволюции, полагая производные по времени от этих переменных равными нулю. При учете соотношений (2.7), (2.15) и (2.16) средние значения переменных ${{y}_{2}}$, ${{y}_{3}}$ определятся с точностью до $O({{\varepsilon }^{2}})$ из первых двух уравнений системы следующими формулами:
(2.20)
${{\bar {y}}_{2}} = \frac{{ - {{F}_{1}}}}{{(1 + \gamma + \varepsilon )U}} + O({{\varepsilon }^{2}}),\quad {{\bar {y}}_{3}} = \frac{{{{F}_{1}}}}{{\mu (1 + \gamma + \varepsilon )}} + O({{\varepsilon }^{2}})$Средние значения переменных ${{y}_{1}}$ и ${{y}_{4}}$ находятся из третьего и четвертого уравнений системы (2.19). На основании формул (2.16) и (2.20) с точностью до $O({{\varepsilon }^{3}})$ получим
(2.21)
$\begin{gathered} p_{2}^{'}{{p}_{1}} + q_{2}^{'}{{q}_{1}} = 0,\quad {{p}_{2}}{{p}_{1}} + {{q}_{2}}{{q}_{1}} = 0,\quad {{{\bar {y}}}_{2}}{{{\bar {y}}}_{3}} = - \mu F_{1}^{2}{\text{/}}({{m}^{2}}U),\quad {{p}_{2}}{{p}_{3}} + {{q}_{2}}{{q}_{3}} = \mu {{f}_{{21}}}{{F}_{1}} \\ p_{4}^{'}{{p}_{1}} + q_{4}^{'}{{q}_{1}} = - \mu {{f}_{{12}}}{{F}_{{\text{2}}}}\operatorname{ctg} \theta ,\quad {{p}_{1}}{{p}_{4}} + {{q}_{1}}{{q}_{4}} = - \mu {{f}_{{12}}}{{F}_{{\text{2}}}},\quad {{p}_{2}}{{q}_{4}} - {{q}_{2}}{{p}_{4}} = - \mu {{f}_{{21}}}{{F}_{2}} \\ \end{gathered} $При учете соотношений (2.21) и (2.7) среднее значение переменной ${{y}_{1}}$ выражается в виде
(2.22)
${{\bar {y}}_{1}} = \frac{{\mu \gamma F_{2}^{2}}}{{2(1 + \gamma )U\sin \theta }}\left( {\frac{{U({{{\cos }}^{2}}\theta - 1)\cos \theta - 2(2 + U\cos \theta )}}{{(4 + {{m}^{2}})(4 - {{U}^{2}})}} - \frac{{2{{{\cos }}^{3}}\theta }}{{{{m}^{2}}U}}} \right) + O({{\varepsilon }^{3}})$Значение ${{\bar {W}}_{3}}$ находится из пятого уравнения системы (2.19). Учитывая формулы (2.20), (2.21), (2.22) и (2.7), получим
(2.23)
${{\bar {W}}_{3}} = \frac{{F_{2}^{2}}}{{2(1 + \gamma )}}\left( {\frac{{U(1 + {{{\cos }}^{2}}\theta ) + 4\cos \theta }}{{(4 + {{m}^{2}})(4 - {{U}^{2}})}} - \frac{{2{{{\cos }}^{2}}\theta }}{{{{m}^{2}}U}}} \right) + O({{\varepsilon }^{3}})$Из восьмого уравнения системы (2.17) при учете соотношений (2.20) определяется с точностью до $O({{\varepsilon }^{2}})$ значение средней скорости прецессии спутника формулой
(2.24)
$\dot {\bar {\psi }} = \frac{{{{{\bar {y}}}_{2}}}}{{\sin \theta }} = - \frac{{{{F}_{1}}}}{{(\alpha + \gamma )U\sin \theta }} = - \frac{{3\varepsilon \cos \theta }}{{2(\alpha + \gamma )U}} = \frac{{3(A - C)\cos \theta }}{{2CU}},$Из шестого и седьмого уравнений системы (2.17) определяются средние значения производных по времени от угла нутации и величины угловой скорости спутника формулами
Можно показать (соответствующие выкладки ввиду громоздкости не приводятся), что вычисленное в силу уравнений движения среднее значение функции ${{S}_{1}}$ на периоде выражается членами третьего порядка относительно $\varepsilon $, т.е. ${{\bar {S}}_{1}} = O({{\varepsilon }^{3}})$. Поэтому при учете соотношений (2.22) и (2.23) получим с точностью до $O({{\varepsilon }^{3}})$ следующие выражения для средних значений $\dot {\theta }$ и $\dot {U}$:
(2.25)
$\begin{gathered} \dot {\theta } = \frac{{\mu \gamma F_{2}^{2}}}{{2(1 + \gamma )U\sin \theta }}\left( {\frac{{U({{{\cos }}^{2}}\theta - 3)\cos \theta - 4}}{{(4 + {{m}^{2}})(4 - {{U}^{2}})}} - \frac{{2{{{\cos }}^{3}}\theta }}{{{{m}^{2}}U}}} \right) \\ \dot {U} = \frac{{\mu \gamma F_{2}^{2}}}{{2(1 + \gamma )}}\left( {\frac{{U(1 + {{{\cos }}^{2}}\theta ) + 4\cos \theta }}{{(4 + {{m}^{2}})(4 - {{U}^{2}})}} - \frac{{2{{{\cos }}^{2}}\theta }}{{{{m}^{2}}U}}} \right) \\ \end{gathered} $Полученные уравнения образуют замкнутую систему эволюционных уравнений вращательного движения спутника относительно переменных $\theta $ и $U$. Из этих уравнений следует, что скорость эволюции по переменным $\theta $ и $U$ пропорциональна ${{\varepsilon }^{2}}$, в то время как скорость прецессии спутника (2.24) пропорциональна $\varepsilon $.
Из второго уравнения (2.25) следует, что производная $\dot {U}$ меняет знак в точках $U = 2$ и точках, удовлетворяющих уравнению
(2.26)
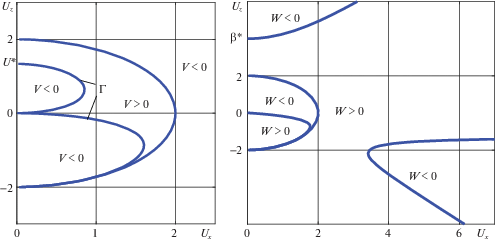
${{U}^{2}}[(2 + M){{\cos }^{2}}\theta + M] + 4MU\cos \theta - 8{{\cos }^{2}}\theta = 0;\quad M = {{{{m}^{2}}} \mathord{\left/ {\vphantom {{{{m}^{2}}} {(4 + {{m}^{2}})}}} \right. \kern-0em} {(4 + {{m}^{2}})}}$На фиг. 3 слева изображена кривая Γ, определяемая этим уравнением и показаны области положительных и отрицательных значений производной $V = \dot {U}$ в плоскости переменных ${{U}_{x}}$, ${{U}_{z}}$, где ${{U}_{x}} = U\sin \theta $ и ${{U}_{z}} = U\cos \theta $ – проекции угловой скорости на плоскость орбиты и на нормаль к плоскости орбиты. При $U > 2$, а также внутри круга $U < 2$ в двух областях, ограниченных кривой Γ, угловая скорость спутника уменьшается, а в остальной области увеличивается. Значение $U{\text{*}}$ определяется формулой
На фиг. 3 справа показаны определяемые из первого уравнения (2.25) области положительных и отрицательных значений производной $W = \dot {\theta }$. Здесь
Эволюционные уравнения (2.25) имеют те же стационарные решения $\theta = 0$, π, $U = \beta = {\text{const}}$, что и точные уравнения (1.2). Условия устойчивости/неустойчивости этих решений для эволюционных уравнений определяются знаком производной $\dot {\theta }$ в окрестности “прямых” ($\theta = 0$) и “обратных” ($\theta = \pi $) стационарных вращений. Как следует из представленных на фиг. 3 результатов анализа этой производной, “прямые” стационарные вращения (${{U}_{x}} = 0$, ${{U}_{z}} > 0$) асимптотически устойчивы в диапазонах $U \in (0,2)$ и $U \in (\beta *,\infty )$, и неустойчивы в диапазоне $U \in (2,\beta *)$. Все “обратные” стационарные вращения (${{U}_{x}} = 0$, ${{U}_{z}} < 0$) кроме, быть может, точки $U = 2$, асимптотически устойчивы. Эти выводы полностью совпадают с полученными в разд. 1 результатами анализа устойчивости стационарных вращений спутника, близкого к сферически симметричному.
Из уравнений (2.25) можно исключить время и получить одно уравнение
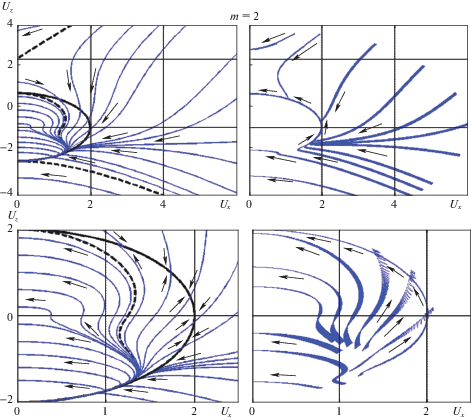
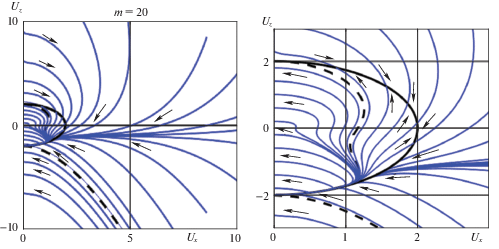
(2.29)
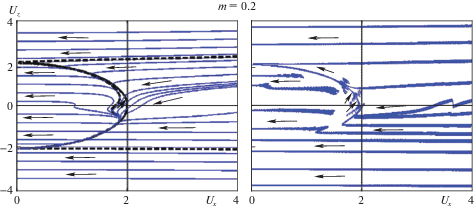
$\frac{{d\theta }}{{dU}} = \frac{{{{U}^{2}}\cos \theta [(2 + M){{{\cos }}^{2}}\theta - 3M] - 4MU - 8{{{\cos }}^{3}}\theta }}{{\{ {{U}^{2}}[(2 + M){{{\cos }}^{2}}\theta + M] + 4MU\cos \theta - 8{{{\cos }}^{2}}\theta \} U\sin \theta }},$Ниже приведены результаты анализа фазовых траекторий (ФТ) эволюции вращательного движения спутника в переменных ${{U}_{x}}$, ${{U}_{z}}$ для разных значений параметра $m$ и разных начальных условий. В левых частях фиг. 4 и 5 изображены ФТ, получаемые из эволюционного уравнения (2.29), а в правых частях – ФТ, полученные численным интегрированием точных уравнений (1.1) для динамически симметричного спутника со значением параметра $\alpha = 1.1$. Стрелками показано направление эволюции. Штриховые линии – сепаратрисы, отделяющие ФТ, попадающие на окружность $U = 2$, от других ФТ. Верхняя сепаратриса начинается в точке ${{U}_{x}} = 0$, ${{U}_{z}} = \beta {\text{*}}$, где величина $\beta {\text{*}}$ определяется формулой (2.28), а нижняя сепаратриса – в точке ${{U}_{x}} = 0$, ${{U}_{z}} = - 2$.
Представленные фазовые портреты свидетельствуют о полном совпадении ФТ эволюции спутника, полученных из эволюционного уравнения (2.29), с одной стороны, и точных уравнений (1.1), с другой стороны.
Как видно из представленных фигур, имеется ограниченная сепаратрисами область начальных условий (обозначим ее через ${{G}_{2}}$), для которой любая ФТ со временем попадает на окружность $U = 2$. При этом для большинства таких ФТ дальнейший (финальный) этап эволюции представляет собой движение по дуге окружности $U = 2$ против часовой стрелки – резонансное вращение 2 : 1 (угловая скорость спутника в два раза больше угловой скорости орбитального базиса), при котором угловая скорость спутника по величине остается постоянной, а ось вращения поворачивается в сторону нормали к плоскости орбиты. В финале таких движений устанавливается стационарное вращение вокруг нормали к плоскости орбиты с угловой скоростью, равной удвоенной угловой скорости орбитального базиса.
При малых по сравнению с единицей значениях $m$ (фиг. 4) асимптоты сепаратрис расположены под малым углом к оси ${{U}_{x}}$ и область ${{G}_{2}}$ занимает сравнительно небольшую часть полуплоскости возможных начальных данных. Поэтому только для небольшой доли начальных данных на финальном этапе реализуется резонансный режим 2 : 1. Для остальных начальных данных ФТ близки к горизонтальным прямым (${{U}_{z}}$ убывает гораздо медленнее, чем ${{U}_{x}}$).
Для значений $m$, сравнимых по величине с единицей (фиг. 5), размеры области ${{G}_{2}}$ сопоставимы с размерами области остальных начальных данных и доля ФТ, финальный этап которых – резонансный режим 2 : 1, сопоставима с долей всех остальных ФТ.
При $m \gg 1$ (фиг. 6) для подавляющего большинства начальных данных из области $U > 2$ финальным этапом будет резонансный режим 2 : 1.
ФТ, стартующие выше верхней сепаратрисы, характеризуются монотонным уменьшением угла $\theta $ до нуля, а ФТ ниже нижней сепаратрисы – монотонным увеличением угла $\theta $ до $\pi $. Такое поведение ФТ подтверждает сделанные ранее выводы о характере устойчивости соответствующих “прямых” и “обратных” стационарных вращений спутника.
На ФТ из области ${{G}_{2}}$ угол $\theta $ меняется немонотонно. При этом часть ФТ, начинающихся в верхней полуплоскости (${{U}_{z}}(0) > 0$), пересекают ось ${{U}_{z}} = 0$, но все они заканчиваются дугой окружности $U = 2$ (резонансным режимом 2 : 1). Таким образом, финалом эволюционного процесса с начальными ФТ из верхней полуплоскости области ${{G}_{2}}$ являются “прямые” стационарные вращения с угловой скоростью, равной удвоенной угловой скорости орбитального базиса. Таким же финалом характеризуется и большая часть ФТ из нижней полуплоскости области ${{G}_{2}}$. В резонансный режим 2 : 1 не захватываются только ФТ, близкие к нижней сепаратрисе; они “прошивают” резонансную окружность $U = 2$ и заканчиваются “обратными” стационарными вращениями с угловой скоростью $U < 2$.
Отметим, что область ${{G}_{2}}$ включает и часть круга $U < 2$. На ФТ из этой части круга угловая скорость спутника увеличивается.
Список литературы
Моисеев Н.Н., Румянцев В.В. Динамика тела с полостями, содержащими жидкость. М.: Наука, 1965. 439 с.
Черноусько Ф.Л. Движение твердого тела с полостями, содержащими вязкую жидкость. М.: Вычисл. центр АН СССР, 1968. 232 с.
Сидоренко В.В. Эволюция вращательного движения планеты с жидким ядром // Астроном. вестник. 1993. Т. 27. № 2. С. 119–127.
Черноусько Ф.Л. О движении твердого тела, содержащего сферический демпфер // ПМТФ. 1968. № 1. С. 73–79.
Амелькин Н.И. Об асимптотических свойствах движений спутников в центральном поле, обусловленных внутренней диссипацией // ПММ. 2011. Т. 75. № 2. С. 204–223.
Амелькин Н.И., Холощак В.В. Об устойчивости стационарных вращений спутника с внутренним демпфированием в центральном гравитационном поле // ПММ. 2017. Т. 81. Вып. 2. С. 123–136.
Вильке В.Г., Копылов С.А., Марков Ю.Г. Эволюция вращательного движения вязкоупругого шара в центральном ньютоновском поле сил // ПММ. 1985. Т. 49. № 1. С 25–34.
Маркеев А.П. К динамике упругого тела в гравитационном поле // Космич. исследования. 1989. Т. 27. Вып. 2. С. 163–175.
Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1974. 503 с.
Журавлев В.Ф., Климов Д.М. Прикладные методы в теории колебаний. М.: Наука, 1988. 326 с.
Белецкий В.В. Движение спутника относительно центра масс в гравитационном поле. М.: Изд-во МГУ, 1975. 308 с.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика