Прикладная математика и механика, 2019, T. 83, № 1, стр. 16-31

Ранее [1, 2] исследованы стационарные вращения и эволюция вращательного движения динамически симметричного спутника с демпфером на круговой орбите. Ниже задача об эволюции вращательного движения решается для несимметричного спутника.

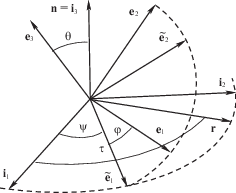
1. Постановка задачи. Уравнения движения. Рассматривается спутник, состоящий из твердой оболочки и шарового демпфера (модель М.А. Лаврентьева) [3, 4]. Обозначим через ${\mathbf{J}} = {\text{diag}}(A,B,C)$ центральный тензор инерции всего спутника (оболочки вместе с демпфером) в главных осях ${{{\mathbf{e}}}_{1}},{{{\mathbf{e}}}_{2}}$, e₃ (фиг. 1), а через $I$ – момент инерции демпфера относительно его центральной оси. Значения моментов инерции спутника ограничены неравенствами треугольника [1]

Для определенности положим, что главные центральные моменты инерции спутника подчиняются условиям

Введем безразмерные параметры, характеризующие геометрию масс спутника:

В качестве независимых параметров выберем следующие:

Тогда получим

Из соотношений (1.1)–(1.4) следует

Значение $\delta = 0$ соответствует динамически симметричному спутнику, сплюснутому вдоль оси симметрии ${{{\mathbf{e}}}_{3}}$, а значение $\delta = \varepsilon $ – динамически симметричному спутнику, вытянутому вдоль оси симметрии ${{{\mathbf{e}}}_{1}}$.

При $\varepsilon \ll 1$ (для спутника, близкого к сферически симметричному) будем иметь

Динамические уравнения вращательного движения спутника с шаровым демпфером в центральном гравитационном поле на круговой орбите записываются в виде [1, 2]

Здесь E – единичная матрица, ${\mathbf{r}} = {{\mathbf{R}} \mathord{\left/ {\vphantom {{\mathbf{R}} R}} \right. \kern-0em} R}$ – единичный вектор, сонаправленный с радиус-вектором центра масс спутника, ${\mathbf{u}} = {{\mathbf{\omega }} \mathord{\left/ {\vphantom {{\mathbf{\omega }} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$ и ${\mathbf{w}} = {{({\mathbf{\Omega }} - {\mathbf{\omega }})} \mathord{\left/ {\vphantom {{({\mathbf{\Omega }} - {\mathbf{\omega }})} {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}$ – безразмерные переменные (приведенная угловая скорость оболочки и приведенная относительная угловая скорость демпфера), где ${\mathbf{\omega }}$ и ${\mathbf{\Omega }}$ – абсолютные угловые скорости оболочки и демпфера, ${{\omega }_{0}}$ – угловая скорость орбитального базиса, направленная по нормали ${\mathbf{n}}$ к плоскости орбиты, $\mu $ – безразмерный коэффициент демпфирования. Точкой обозначена производная по безразмерному времени $\tau = {{\omega }_{0}}t$. В уравнениях (1.8) все векторы задаются своими компонентами в связанном с оболочкой базисе ${{{\mathbf{e}}}_{1}},{{{\mathbf{e}}}_{2}}$, e₃.

В рамках рассматриваемой модели, как и в рамках некоторых других моделей [5–7], предельными движениями несимметричного спутника являются только положения равновесия относительно орбитального базиса (главные оси инерции спутника ${{{\mathbf{e}}}_{1}},{{{\mathbf{e}}}_{2}}$, e₃ параллельны осям орбитального базиса ${\mathbf{r}}$, ${\mathbf{n}}$, ${\mathbf{\tau }} = {\mathbf{n}} \times {\mathbf{r}}$). При этом положения, для которых ось ${{{\mathbf{e}}}_{3}}$ наибольшего момента инерции параллельна нормали ${\mathbf{n}}$ к плоскости орбиты, а ось ${{{\mathbf{e}}}_{1}}$ наименьшего момента инерции параллельна радиус-вектору ${\mathbf{r}}$, асимптотически устойчивы, а все остальные положения равновесия неустойчивы. Таким образом, для любых начальных условий финалом эволюции вращательного движения спутника будут указанные выше асимптотически устойчивые положения равновесия.

Исследуется эволюция вращательного движения спутника в зависимости от значений параметров и начальных условий. Основной интерес представляет поведение оси вращения спутника и величины угловой скорости.

Картину эволюционного процесса можно получить на основе результатов численного интегрирования уравнений (1.8), дополненных кинематическими уравнениями Пуассона

где ${\mathbf{\Lambda }}$ – кватернион единичной нормы, задающий положение связанного с оболочкой базиса главных осей инерции спутника ${{{\mathbf{e}}}_{1}},{{{\mathbf{e}}}_{2}}$, e₃ относительно базиса Кенига ${{{\mathbf{i}}}_{1}},{{{\mathbf{i}}}_{2}}$, i₃. По результатам этого интегрирования находится кватернион ${\mathbf{\Lambda }}(\tau )$ и проекции вектора ${\mathbf{u}}$ на оси ${{{\mathbf{e}}}_{k}}$, а положение осей ${{{\mathbf{e}}}_{k}}$ и компоненты вектора ${\mathbf{u}}$ в базисе Кенига определяются формулами где ${\mathbf{\bar {\Lambda }}}$ – сопряженный кватернион.

Однако подробный анализ эволюции вращательного движения спутника по результатам численного интегрирования уравнений (1.8) – весьма трудоемкая операция, реально осуществимая лишь в малой области значений параметров и фазовых переменных, что обусловлено большой размерностью системы и большим числом параметров (в рассматриваемой модели четыре параметра: ε, δ, γ, μ). Для получения подробной картины эволюции необходимо рассмотреть большое число разных комбинаций значений этих параметров и для каждой из них провести интегрирование уравнений (1.8) на двумерном множестве начальных условий (заданные начальные значения величины $u$ приведенной угловой скорости спутника и угла между осью вращения и нормалью к плоскости орбиты). Кроме того, как будет показано ниже, скорость эволюции так зависит от значений параметров и величины $u$, что во многих случаях для получения только одной полной траектории эволюции требуется неприемлемо большое время работы программы численного интегрирования уравнений (1.8).

Ниже для исследования эволюции вращательного движения спутника во всей области возможных значений параметров и начальных условий будут выведены приближенные (эволюционные) уравнения. Точные уравнения (1.8) будут играть вспомогательную роль. Их численные решения для отдельных значений параметров и начальных данных будут сопоставляться с решениями приближенных уравнений для подтверждения того, что приближенные уравнения адекватно описывают эволюцию вращательного движения спутника. Кроме того, точные уравнения (1.8) будут использоваться для анализа этой эволюции в окрестности тех (резонансных) значений фазовых переменных, где эволюционные уравнения неприменимы из-за наличия в них особенностей.

Обозначим через ${{r}_{k}}$ проекцию вектора ${\mathbf{r}}$ на ось ${{{\mathbf{e}}}_{k}}$. Тогда для компонент приведенного гравитационного момента в осях ${{{\mathbf{e}}}_{k}}$ получим выражение

а уравнения (1.8) в покоординатной форме, дополненные кинематическими уравнениями в углах Эйлера (фиг. 1), запишутся в виде

Здесь

где

Обозначим через ${{U}_{1}},{{U}_{2}}$, U₃ и ${{W}_{1}},{{W}_{2}}$, W₃ проекции векторов ${\mathbf{u}}$ и ${\mathbf{w}}$ на оси базиса Резаля ${{{\mathbf{\tilde {e}}}}_{1}},{{{\mathbf{\tilde {e}}}}_{2}}$, e₃ (фиг. 1):

В этих переменных уравнения (1.11) перепишутся в виде

Здесь

2. Эволюционные уравнения. В этом разделе выводятся эволюционные уравнения для спутника, близкого к сферически симметричному, т.е. при $\varepsilon \ll 1$. При выводе этих уравнений будем учитывать следующие свойства решений уравнений (1.8) и (1.14). При отсутствии гравитационного момента вектор K суммарного кинетического момента спутника остается неизменным и для разных начальных значений угловой скорости оболочки и угловой скорости демпфера движение спутника экпоненциально стремится к вращению вокруг оси ${{{\mathbf{e}}}_{3}}$ наибольшего момента инерции, сонаправленной с вектором K. Это предельное вращение характеризуется нулевыми значениями всех фазовых переменных ${{U}_{k}}$, ${{W}_{k}}$, кроме переменной ${{U}_{3}}$, значение которой определяется формулой $\,{{U}_{3}} = {K \mathord{\left/ {\vphantom {K {(C}}} \right. \kern-0em} {(C}}{{\omega }_{0}})$. При $\varepsilon \ll 1$ (гравитационный момент мал) первая фаза эволюции (быстрая эволюция) представляет собой сравнительно быстрый переходной процесс, в конце которого устанавливается вращение, близкое к вращению вокруг оси ${{{\mathbf{e}}}_{3}}$, с кинетическим моментом, близким к начальному. Далее наступает существенно более длительный режим медленной эволюции, которая и представляет предмет нашего анализа. В этом режиме все переменные ${{U}_{k}}$, ${{W}_{k}}$, кроме переменной ${{U}_{3}}$, будут ограниченными функциями малого параметра $\varepsilon $, вследствие чего и все правые части системы (1.14) тоже будут ограниченными функциями $\varepsilon $. Это свойство решений системы (1.14) дает возможность применить метод осреднения [8, 9] для получения эволюционных уравнений вращательного движения спутника.

Введем следующие обозначения для фазовых переменных:

Систему (1.14) перепишем в виде

Здесь

Функция ${{\Phi }_{1}}$ определяется формулой (1.16), а ${{\tilde {f}}_{1}}\,,\,\,{{\tilde {f}}_{2}}$ и ${{f}_{3}}$ – формулами (1.16) и (1.12), ${\mathbf{D}}({\mathbf{Z}})$ – остальные члены в правой части системы (1.14).

Решение системы (1.14) будем искать в виде

Положим

а остальные компоненты вектор-функции ${\mathbf{S}}$ определим из условия, чтобы уравнение удовлетворялось с точностью до $O({{\varepsilon }^{2}})$.

Выражения для производных ${{\dot {\sigma }}_{k}}$ представим в виде суммы двух слагаемых:

где через ${{v}_{k}}$ обозначено значение производной, вычисленное с точностью до $O(\varepsilon )$, а слагаемое ${{\lambda }_{k}}$ – ограниченная функция $\varepsilon $. Тогда, учитывая, что в режиме медленной эволюции переменные ${{U}_{1}},{{U}_{2}},{{W}_{1}},{{W}_{2}}$, ${{W}_{3}}$ – ограниченные функции $\varepsilon $, из кинематических уравнений системы (1.14) получим

Здесь и всюду далее $U = {{V}_{3}}$.

Отбрасывая в уравнении (2.5) члены выше первого порядка малости по $\varepsilon $, получим уравнение

где через ${\mathbf{L}}({\mathbf{S}})$ обозначены линейные по $\varepsilon $ члены функции ${\mathbf{D}}({\mathbf{S}})$ с компонентами

Решение уравнения (2.8) записывается гармоническими по переменным ${{\sigma }_{k}}$ функциями вида

Коэффициенты при гармониках определяются следующими формулами:

Для k = 1, 2, 3 получим

После подстановки решения (2.10) в уравнения (1.14) получим систему

Здесь компоненты вектор-функции ${\mathbf{L}}({\mathbf{V}})$ определяются аналогичными (2.9) формулами при замене в них ${{S}_{1}}$, ${{S}_{2}}$, ${{S}_{3}}$, ${{S}_{4}}$, ${{S}_{5}}$, ${{S}_{6}}$ соответственно на ${{V}_{1}}$, ${{V}_{2}}$, ${{V}_{3}}$, ${{V}_{4}}$, ${{V}_{5}}$, ${{V}_{6}}$, и введены обозначения

а ${{R}_{j}}$ – ограниченные функции ${{\varepsilon }^{2}}$, определяемые при учете формул (1.5) и (1.7) с точностью до $O({{\varepsilon }^{3}})$ выражениями

Подробный анализ системы (2.13) показал, что в режиме медленной эволюции переменные ${{V}_{2}}$ и ${{V}_{4}}$ будут ограниченными функциями $\varepsilon $, а переменные ${{V}_{1}},{{V}_{5}}$, ${{V}_{6}}$, а также производная $\dot {U}$ – ограниченными функциями ${{\varepsilon }^{2}}$. Обозначим через ${{\bar {V}}_{k}}$ средние значения указанных переменных, а сами эти значения найдем исходя из условия равенства нулю производных ${{\dot {\bar {V}}}_{1}},{{\dot {\bar {V}}}_{2}},{{\dot {\bar {V}}}_{4}},{{\dot {\bar {V}}}_{5}}$, ${{\dot {\bar {V}}}_{6}}$ в режиме медленной эволюции.

Полагая ${{\dot {\bar {V}}}_{1}} = 0$ и $\,{{\dot {\bar {V}}}_{4}} = 0$, из первого и четвертого уравнений системы (2.13) после осреднения по переменным ${{\sigma }_{0}},{{\sigma }_{1}},{{\sigma }_{2}}$, ${{\sigma }_{3}}$ найдем

Из шестого уравнения системы (2.13), полагая ${{\dot {\bar {V}}}_{6}} = 0$ и ограничиваясь членами не выше второго порядка малости по $\varepsilon $, получим (среднее обозначается угловыми скобками)

Отсюда после учета соотношений (1.13), (1.16) и (2.10)–(2.14) и проведения весьма громоздких и трудоемких выкладок величина ${{\bar {V}}_{6}}$ определяется с точностью до $O({{\varepsilon }^{3}})$ выражением

Здесь использованы обозначения

Аналогичной процедурой, полагая ${{\dot {\bar {V}}}_{5}} = 0$, из пятого уравнения системы (2.13) после осреднения по переменным ${{\sigma }_{k}}$ получим с точностью до $O({{\varepsilon }^{3}})$

Для $\,j = 2$ и $\,j = 3$ получим

Поэтому из второго уравнения системы (2.13), полагая ${{\dot {\bar {V}}}_{2}} = 0$, будем иметь

На основании формул (2.15)–(2.20) определяются все основные характеристики эволюции вращательного движения спутника. Из восьмого уравнения системы (2.13) при учете соотношений (2.15) для средней угловой скорости прецессии спутника получим с точностью до $O({{\varepsilon }^{2}})$ выражение

Таким образом, средняя скорость прецессии спутника описывается линейными по $\varepsilon $ членами.

Из третьего и седьмого уравнений системы (2.13), учитывая соотношения (2.19) и (2.20), для средней угловой скорости спутника и угла нутации получим с точностью до $O({{\varepsilon }^{3}})$ следующие уравнения:

Здесь и всюду далее вместо $\bar {U}$ и $\bar {\theta }$ используются обозначения $U$ и $\theta $.

Уравнения (2.22) образуют замкнутую систему относительно переменных $U$ и $\theta $. Они описывают поведение величины угловой скорости спутника и угла между осью вращения ${{{\mathbf{e}}}_{3}}$ и нормалью ${\mathbf{n}}$ к плоскости орбиты в зависимости от безразмерного времени $\tau = {{\omega }_{0}}t$. Для получения полной картины эволюции вращательного движения спутника в плоскости переменных $U$ и $\theta $ достаточно исследовать решения системы (2.22) для значений $U > 0$, $\theta \in [0,\,\pi ]$. Указанные уравнения имеют особенность в точках $U = 2$, $U = 1$ и $U = 0$.

Если определять скорость эволюции значением производной $\dot {U}$, то из первого уравнения (2.22) следует, что для пространственных вращений ($\sin \theta \ne 0$) эта скорость пропорциональна ${{\varepsilon }^{2}}$. Скорость эволюции сложным образом зависит от значений параметров $\mu $ и $\gamma $. При $\mu \ll 1$ она пропорциональна $\mu $, а при $\mu \gg 1$ – обратно пропорциональна $\mu $. В свою очередь, при $\gamma \ll 1$ скорость эволюции пропорциональна $\gamma $, а при $\gamma \gg 1$ – обратно пропорциональна ${{\gamma }^{2}}$. При $U \gg 1$ скорость эволюции обратно пропорциональна $U$. Для плоских вращений спутника вокруг нормали к плоскости орбиты ($\sin \theta = 0$) скорость эволюции пропорциональна ${{\delta }^{2}}$ и обратно пропорциональна ${{U}^{3}}$.

Полученные оценки для скорости эволюции вращательного движения спутника свидетельствуют о том, что для большого множества значений параметров и фазовых переменных эта скорость весьма мала и поэтому получить с должной точностью полную картину эволюционного процесса численным интегрированием точных уравнений (1.8) затруднительно.

Исключая из уравнений (2.22) время, получим одно уравнение

описывающее зависимость угла $\theta $ от величины $U$ приведенной угловой скорости спутника. Как следует из первого уравнения (2.22), $\dot {U} < 0$ при $U > 2$ и $\delta > 0$. Поэтому, если $\delta > 0$, то в области $U > 2$ угловая скорость $U$ будет монотонно убывающей функций времени, уравнение (2.23) в этой области не имеет особенностей и по его решениям можно построить фазовый портрет эволюции спутника в плоскости переменных $U$, $\theta $.

В уравнении (2.23) фигурируют только два параметра: “агрегированный” параметр $m$ (1.15) и параметр $\alpha $, определяемый формулой

Ввиду того, что в уравнении (2.23) $U$ – независимая переменная, для построения фазовых портретов эволюции вращательного движения спутника с помощью этого уравнения потребное время работы программы численного интегрирования оказывается на много порядков меньше, чем при использовании точных уравнений (1.8), причем это время практически не зависит от значений $m$ и $\alpha $.

3. Плоские вращения спутника с демпфером на круговой орбите. Уравнения движения спутника допускают решения, соответствующие плоским вращениям вокруг оси наибольшего момента инерции, сонаправленной с нормалью к плоскости орбиты. Этим решениям соответствуют значения угла $\theta = 0$ (прямые вращения) и $\theta = \pi $ (обратные вращения). Но в отличие от случая динамически симметричного спутника ($\delta = 0$), где эти вращения стационарные, для несимметричного спутника с демпфером угловая скорость $U$ на указанных плоских вращениях меняется с течением времени и в финале эволюции становится равной единице (спутник приходит в положение равновесия относительно орбитального базиса).

Плоские вращения спутника с демпфером на круговой орбите описываются системой из трех уравнений

Здесь $\varphi $ – угол поворота спутника вокруг нормали к плоскости орбиты, $U$ – угловая скорость оболочки, $\,W$ – относительная угловая скорость демпфера.

На основании первого уравнения (2.22) при учете формул (1.3), (1.7) и (2.16) получим для средней угловой скорости спутника уравнение

Его решение записывается в виде

где ${{\bar {U}}_{0}}$ – начальное значение угловой скорости спутника. Решение (3.3) определено до тех значений $\tau $, пока его левая часть не обращается в нуль (спутник приходит в положение относительного равновесия). Время, за которое спутник приходит в положение равновесия, определятся формулой

4. Анализ устойчивости плоских вращений спутника. Для исследования устойчивости плоских вращений спутника используем эволюционные уравнения (2.22). Обозначим через ${{U}_{X}} = U\sin \theta $ и ${{U}_{Z}} = U\cos \theta $ проекции угловой скорости на плоскость орбиты и на нормаль к плоскости орбиты, соответственно. Для плоских вращений ${{U}_{X}} = 0$, а значение ${{U}_{Z}}$ меняется в процессе эволюции от начального значения $U(0)$ до единицы, т.е. фазовые траектории в трехмерном пространстве вектора ${\mathbf{U}}$ представляют собой отрезки прямой линии, параллельной нормали к плоскости орбиты.

Вопрос об устойчивости плоских вращений сводится к исследованию устойчивости решений эволюционных уравнений по отношению к переменной ${{U}_{X}}$. Полагая, как и ранее, $U \geqslant 0$, $0 \leqslant \theta \leqslant \pi $, получим, что если при достаточно малом ${{U}_{X}} > 0$ значение ${{\dot {U}}_{X}} < 0$, то плоское вращение асимптотически устойчиво по переменной ${{U}_{X}}$ (возмущенные траектории “прижимаются” к траекториям плоских вращений), а если ${{\dot {U}}_{X}} > 0$, то неустойчиво.

Как будет показано ниже, характер устойчивости плоского вращения зависит не только от значений параметров, но и от величины угловой скорости. Поэтому за счет изменения угловой скорости в процессе эволюции знак производной ${{\dot {U}}_{X}}$ может меняться, вследствие чего траектории плоских вращений делятся на интервалы асимптотически устойчивых и неустойчивых вращений.

При учете формулы

условие асимптотической устойчивости плоского вращения записывается в виде

Для “прямых” вращений, полагая $0 < \theta \ll 1$ и пренебрегая членами выше первого порядка малости по $\theta $, получим условие асимптотической устойчивости в виде неравенства

Аналогичным образом, полагая $\theta = \pi - \xi $, где $0 < \xi \ll 1$, получим условие асимптотической устойчивости для обратных вращений

Неравенство (4.4) выполняется для всех значений $U > 0$, кроме $U = 1$ и $U = 2$. Поэтому все обратные плоские вращения спутника, за исключением, быть может, точек $U = 1$, $\theta = \pi $ и $U = 2$, $\theta = \pi $, асимптотически устойчивы.

Определим интервалы асимптотической устойчивости и неустойчивости прямых плоских вращений. Предварительно отметим [2], что при $\alpha = 0$ (для динамически симметричного спутника) все плоские вращения являются стационарными. При этом прямые стационарные вращения неустойчивы в интервале

а за пределами этого интервала они асимптотически устойчивы. Для несимметричного спутника, как следует из неравенства (4.3), точные границы интервалов асимптотической устойчивости и неустойчивости определяются вещественными корнями полинома шестой степени, коэффициенты которого сложным образом зависят от параметров $m$ и $\alpha $.

Из неравенства (4.3) следует, что в интервале $1 < U < 2$ прямые вращения асимптотически устойчивы. Для остальных значений $U > 0$ сделаем оценки границ интервалов асимптотической устойчивости и неустойчивости.

При $U > 2$ условие (4.3) можно переписать в виде

где $U_{0}^{*}$ определяется формулой (4.5). Учитывая, что при $U > 2$ выполняется неравенство ${{Z}_{1}} < 4{{Z}_{2}}$, будем иметь

Если предположить, что левая граница интервала асимптотической устойчивости лежит правее точки $U_{0}^{*}$, т.е. рассматривать значения $U > U_{0}^{*}$, то при учете неравенств ${{Z}_{2}} > 4 + {{m}^{2}}$ и $U < 2(U - 1)$ получим

Отсюда следует, что в интервале

прямые плоские вращения асимптотически устойчивы. Но эта оценка верна только при $m < 4$. При $m > 4$ значение $U_{1}^{*}$ лежит левее точки $U_{0}^{*}$ и предположение, при котором получено неравенство (4.7), не выполняется. Поэтому для $m > 4$ в качестве $U_{1}^{*}$ следует брать значение $U_{0}^{*}$, т.е.

Из формулы (4.8) следует, что $U_{1}^{*} \to U_{0}^{*}$ при $\alpha \to 0$. Кроме того, $U_{1}^{*} \to U_{0}^{*}$ при $m \to 0$.

Условие неустойчивости прямых плоских вращений спутника при $U > 2$ описывается неравенством

Для значений $2 < U < U_{0}^{*}$ при учете неравенств

будем иметь

В итоге получим, что в интервале

плоское вращение спутника будет неустойчивым.

Как следует из формулы (4.9), $U_{2}^{*} \to U_{0}^{*}$ при $\alpha \to 0$, а также при $m \to 0$. Кроме того, $U_{2}^{*} \to 2$ при $m \to \infty $.

Вопрос о характере устойчивости плоских вращений несимметричного спутника (при $\alpha > 0$) в интервале $U_{2}^{*} < U < U_{1}^{*}$ остается открытым. При больших по сравнению с единицей значениях $m$ и одновременно существенно отличных от нуля значениях $\alpha $ длина этого интервала также будет большой. В этих случаях, как следует из результатов численного анализа, на интервале $(2,U_{0}^{*})$ возможна неоднократная смена знака производной ${{\dot {U}}_{X}}$.

Исследуем интервал $0 < U < 1$. В этом интервале верны неравенства

при учете которых для функции $f$ в левой части неравенства (4.3) получим соотношение

Из него следует, что в интервале

плоские вращения спутника асимптотически устойчивы.

Условие неустойчивости исследуемых вращений описывается неравенством $f < 0$. При учете соотношений (4.10) получим

Отсюда следует, что в интервале

плоские вращения спутника неустойчивы.

Из формул (4.11) и (4.12) следует, что $U_{3}^{*} \to 1$ и $U_{4}^{*} \to 1$ при $\alpha \to 0$. Кроме того, $U_{3}^{*} > {\text{1/2}}$. Длина интервала $(U_{3}^{*},U_{4}^{*})$, где вопрос о характере устойчивости плоских вращений спутника остается открытым, составляет

При этом $U_{4}^{*} - U_{3}^{*} \to 0$ при $\alpha \to 0$, а также при $m \to \infty $. По результатам численного анализа не обнаружено, чтобы для плоских вращений в интервале $0 < U < 1$ характер устойчивости менялся более одного раза.

5. Результаты анализа эволюции вращательного движения спутника. Если основываться на эволюционных уравнениях (2.22) и вытекающего из них уравнения (2.23), то вид фазовых траекторий (ФТ) в плоскости переменных ${{U}_{X}} = U\sin \theta $ и ${{U}_{Z}} = U\cos \theta $ зависит только от значений параметров $m$ и $\alpha $. Пробные численные расчеты показали, что этим свойством обладают и средние линии ФТ, получаемых из точных уравнений (1.8). Например, для существенно разных комбинаций значений параметров $\mu $ и $\gamma $, соответствующих одному и тому же значению $m = \mu (1 + \gamma )$, получаются трудно отличимые друг от друга средние линии ФТ уравнений (1.8). Кроме того, в тех областях значений параметров и фазовых переменных, где это было возможно, проведено сопоставление ФТ эволюционных уравнений и средних линий траекторий точных уравнений и установлено, что эти траектории близки друг к другу на протяжении всего процесса эволюции спутника. Таким образом, есть основания утверждать, что полученные в разд. 2 эволюционные уравнения адекватно описывают эволюцию вращательного движения спутника и могут быть использованы для анализа эволюции в тех областях значений параметров и фазовых переменных, где использование точных уравнений проблематично.

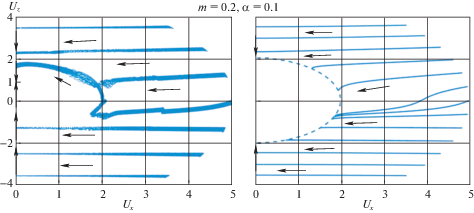
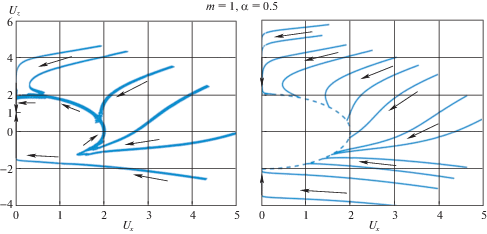
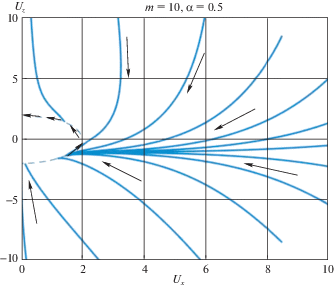
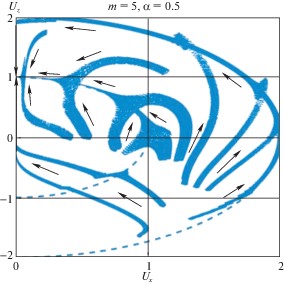
На фиг. 2–5 приведены фазовые портреты эволюции вращательного движения спутника в переменных ${{U}_{X}}$, ${{U}_{Z}}$ для разных значений параметров $m$ и $\alpha $. Стрелками показано направление эволюции. В левых частях фигур 2 и 3 изображены ФТ, полученные численным интегрированием точных уравнений (1.8) для начальных данных из области $U > 2$, а в правых частях фигур 2 и 3, а также на фиг. 4 – траектории, получаемые из эволюционного уравнения (2.23) в области $U > 2$. На фиг. 5 изображены ФТ, полученные численным интегрированием точных уравнений (1.8) для начальных данных из области $U < 2$.

Как видно из представленных фигур, ФТ спутника для начальных данных из области $U > 2$ можно разделить на два класса. К первому классу относятся ФТ, состоящие из двух частей, где первая часть характеризуется монотонным ярко выраженным стремлением к вращению вокруг нормали к плоскости орбиты, а вторая часть близка к отрезку вертикальной прямой, соответствующему плоским вращениям спутника вокруг нормали к плоскости орбиты. Ко второму классу относятся ФТ, состоящие из трех частей. Здесь первая часть заканчивается на окружности радиуса $U = 2$, вторая часть – дуга окружности $U = 2$, а третья часть – линия, близкая к отрезку [1, 2] вертикальной прямой (плоские вращения). Движение по дуге окружности $U = 2$ представляет собой резонансное вращение 2 : 1. Здесь величина угловой скорости остается постоянной, равной удвоенной угловой скорости орбитального базиса, а ось вращения поворачивается против часовой стрелки в сторону нормали к плоскости орбиты.

При малых по сравнению с единицей значениях $m$ (фиг. 2, $m = 0.2$, $\alpha = 0.1$) большинство ФТ в области $U > 2$ относятся к первому классу, причем первые части этих ФТ близки к горизонтальным прямым линиям.

При значениях $m$, сопоставимых с единицей (фиг. 3, $m = 1$, $\alpha = 0.5$), доля начальных данных, для которых ФТ попадают на резонансную окружность $U = 2$, сопоставима с долей всех остальных начальных данных из области $U > 2$.

При $m \gg 1$ (фиг. 4, $m = 10$, $\alpha = 0.5$) большинство ФТ попадают на резонансную окружность $U = 2$.

Приведенные результаты подтверждают сделанные выше выводы о характере устойчивости плоских вращений спутника вокруг нормали к плоскости орбиты. По мере увеличения значений параметра $m$ интервал $(2,U_{2}^{*})$, где прямые плоские вращения неустойчивы, увеличивается и поэтому увеличивается диапазон значений $U$, где близкие к этим вращениям ФТ “уходят” вправо. Подтверждается также и вывод об асимптотической устойчивости обратных плоских вращений спутника. Но с ростом значений $m$ область притяжения для этих движений сужается.

По результатам численного анализа установлено, что значения $\alpha $ несущественно влияют на вид фазового портрета спутника в области $U > 2$. Влияние этого параметра проявляется лишь в том, что по мере уменьшения $\alpha $ ФТ быстрее “прижимаются” к асимптотически устойчивым плоским вращениям вокруг нормали к плоскости орбиты и быстрее отдаляются от неустойчивых.

Сопоставление фазовых портретов несимметричного спутника с полученными ранее [2] фазовыми портретами динамически симметричного спутника показывает, что в области $U > 2$ при одинаковых значениях параметра $m$ их существенное различие состоит только в том, что для симметричного спутника эволюция заканчивается стационарным вращением вокруг нормали к плоскости орбиты, а для несимметричного появляются еще финальные куски ФТ, близкие к нестационарным плоским вращениям вокруг нормали к плоскости орбиты, по которым спутник приходит в положение относительного равновесия.

На фиг. 5 представлен типичный фазовый портрет вращательного движения спутника в области $U \leqslant 2$. Здесь $m = 5$, $\alpha = 0.5$. Видно, что есть область значений фазовых переменных, примыкающая к окружности $U = 2$, движения из которой захватываются в резонансное вращение 2 : 1. Есть также область значений фазовых переменных, примыкающая к окружности $U = 1$, где движения захватываются в резонансное вращение 1 : 1, для которого величина угловой скорости остается постоянной, равной угловой скорости орбитального базиса, а ось вращения поворачивается против часовой стрелки в сторону нормали к плоскости орбиты.

В области $U \leqslant 2$ фазовые портреты динамически симметричного [2] и несимметричного спутников различаются тем, что в последнем случае помимо резонансного вращения 2 : 1 имеется резонансное вращение 1 : 1.

Наличие устойчивых по переменной $U$ резонансных вращений 2 : 1 и 1 : 1 можно объяснить, используя первое уравнение (2.22) при учете формулы (2.16). Отсюда следует, что в точках $U = 2$ и $U = 1$ производная $\dot {U}$ меняет знак, причем так, что в диапазоне $0 < \theta < \pi $ имеются ненулевые окрестности точек $U = 2$ и $U = 1$, в которых $\dot {U} > 0$ при $U < 1$ и $U < 2$, и $\dot {U} < 0$ при $U > 1$ и $U > 2$. Из первого уравнения (2.22) и формулы (2.16) следует также, что при $\theta \to \pi $ уменьшаются до нуля размеры окрестностей внутри кругов $U \leqslant 2$ и $U \leqslant 1$, где производная $\dot {U} > 0$. Этим объясняется, что для значений $\theta $, близких к $\pi $, ФТ “прошивают” резонансные окружности и не “захватываются” в резонансное вращение (фиг. 2, 3, 5). Для несимметричного спутника при $\theta \to 0$ уменьшается до нуля размер окрестности внутри круга $U \leqslant 2$, где $\dot {U} > 0$. Вследствие этого ФТ “срываются” с резонансной окружности $U = 2$, когда значение $\theta $ становится близким к нулю (фиг. 2, 3, 5).

Направление эволюции в резонансных режимах 2 : 1 и 1 : 1 можно объяснить, используя теорему об изменении обобщенной энергии. Применительно к рассматриваемой задаче обобщенная энергия $H$ – сумма кинетической энергии движения относительно орбитального базиса, потенциальной энергии переносных сил инерции и потенциальной энергии гравитационного поля. Производная по времени от функции $H$ равна мощности диссипативных сил и поэтому отрицательна. При условии, что угловая скорость спутника направлена по оси наибольшего момента инерции, среднее для функции $H$ выражается с точностью до аддитивной постоянной следующей формулой:

Так как величина $U$ в резонансном режиме не меняется, для производной $\dot {\bar {H}}$ будем иметь

Поскольку $С $ – наибольший момент инерции спутника, то $0 < 2C - A - B < C$ и выражение в квадратных скобках в левой части неравенства (5.2) при любых значениях $\theta $ положительно как для $U = 2$, так и для $U = 1$. Поэтому из неравенства (5.2) следует, что для резонансных вращений из правой полуплоскости $\dot {\theta } < 0$ (ось вращения спутника поворачивается против часовой стрелки), а для резонансных вращений из левой полуплоскости $\dot {\theta } > 0$ (ось вращения спутника поворачивается по часовой стрелке).