Прикладная математика и механика, 2019, T. 83, № 1, стр. 144-157

АНАЛИТИЧЕСКОЕ РЕШЕНИЕ КРАЕВОЙ ЗАДАЧИ УСТАНОВИВШЕЙСЯ ПОЛЗУЧЕСТИ НЕОСЕСИММЕТРИЧНОЙ ТОЛСТОСТЕННОЙ ТРУБЫ ПОД ДЕЙСТВИЕМ ВНУТРЕННЕГО ДАВЛЕНИЯ

А. Д. Москалик^*, В. П. Радченко^**

Самарский государственный технический университет
Самара, Россия

^* E-mail: annmoskalik1@gmail.com
^** E-mail: radch@samgtu.ru

Поступила в редакцию 18.04.2018

DOI: 10.1134/S0032823519010089

Аннотация

Рассматривается краевая задача установившейся ползучести неосесимметричной толстостенной трубы, находящейся под действием внутреннего давления, с использованием гипотезы несжимаемости материала для деформаций ползучести. Приводится приближенное аналитическое решение задачи методом малого параметра до третьего порядка приближения включительно для плоского деформированного состояния. В качестве малого параметра используется величина смещения центров внутреннего и внешнего радиусов трубы. Погрешность решения задачи оценивается на основании сравнения приближенного аналитического решения с численным решением, построенным методом конечных элементов, для некоторых частных случаев. Анализ аналитического и численного решений для напряжений выполнен в зависимости от величины малого параметра и параметра нелинейности установившейся ползучести. Проанализирована величина погрешности приближенного аналитического решения для компонент тензора напряжений в минимальном сечении в соответствии с техническими нормативными требованиями отраслевых стандартов на допустимую разностенность труб при их промышленном изготовлении.

Ключевые слова: неосесимметричная труба, установившаяся ползучесть, метод малого параметра, третий порядок приближения, погрешность аналитического решения

1. Введение. Состояние тонко- и толстостенных труб при упругопластическом деформировании подробно рассмотрено методом малого параметра в работах научной школы Д.Д. Ивлева, в частности в монографии [1], а также в работах его коллег и учеников для разного вида анизотропного состояния материала, при применении различных условий пластичности т.д. Описано состояние толстостенной двухслойной трубы под внутренним давлением при трансляционной анизотропии свойств материалов каждого слоя [2]. Приведено идеальное упругопластическое состояние толстостенной трубы при взаимодействии различного вида пластической анизотропии [3, 4]. Рассмотрена задача, когда в упругопластической области возмущению подвергается предел текучести материала многослойной трубы [5].

Была приведена задача для неосесимметричной трубы при упругопластическом поведении анизотропного материала с учетом его сжимаемости в предположении отсутствия касательных напряжений [6, 7], что противоречит постановке задачи в условиях несоосности трубы.

Для эксцентричной трубы под внутренним давлением из упрочняющегося материала Ишлинского–Прагера в упругопластической области методом возмущений построено решение для первого порядка приближения [8]. Рассмотрена упругопластическая эксцентричная труба под внутренним давлением при учете второго порядка приближения [9].

В применении метода возмущений к рассмотрению задач ползучести выделяют два подхода: в одном случае рассматривается возмущение реологических свойств материала деформируемого тела (внутренние краевые задачи), в другом случае возмущению подвержены геометрические характеристики тела (внешние краевые задачи). Применение метода малого параметра к решению внутренних краевых задач было подробно рассмотрено [10–15].

Так, принимался нормальный закон распределения свойств материала, в том числе и для толстостенной трубы, находящейся под внутренним давлением, на основе степенной зависимости определяющих соотношений установившейся ползучести [10]. При степенной аппроксимации закона установившейся ползучести показатель нелинейности полагался детерминированной величиной, а второй коэффициент – случайным [11]. В стохастической краевой задаче установившейся ползучести построено решение для толстостенной трубы под внутренним давлением методом малого параметра до третьего приближения включительно [12, 13, 15].

Приведено решение задачи установившейся ползучести толстостенного цилиндра под действием внутреннего давления при возрастающем (градиентном) изменении параметров степенного закона установившейся ползучести материала и показано, что введение подобных зависимостей существенно влияет на напряженно-деформированное состояние трубы [14].

Впервые влияние возмущения внешней границы на напряженно-деформированное состояние толстостенной трубы в условиях ползучести описано в монографии Л.М. Качанова [16], в которой приведена общая постановка задачи для первого приближения без детализации полученных результатов расчетов, обсуждения вопросов сходимости и погрешности полученного решения. Приведено приближенное аналитическое решение данной задачи с учетом первого порядка приближения [17], представлено ее решение с учетом второго порядка приближения [18].

Стоит отметить, что в подавляющем количестве исследований приведено решение для первого порядка приближения. Учет же третьего приближения в решении задач вообще не рассматривался. Также не обсуждался вопрос сходимости полученных аналитических решений и нет сравнительного анализа решений на основе метода малого параметра по отношению к решениям, полученным численными методами или другими аналитическими методами.

Цель настоящей работы – построение приближенного аналитического решения двумерной краевой задачи установившейся ползучести неосесимметричной толстостенной трубы на основе метода малого параметра с учетом третьего приближения, анализ погрешности этого решения по отношению к численному решению по методу конечных элементов и его применение к прикладным задачам в соответствии с существующими отраслевыми нормативными документами по допускам на разностенность [19, 20].

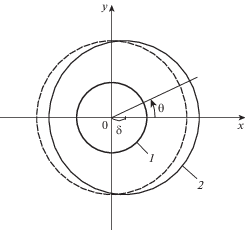
2. Постановка краевой задачи. Рассматривается неосесиметричная толстостенная труба (см. схему на фиг. 1) с внутренним контуром 1 радиуса r = a и смещенным на малую величину δ центром внешнего контура 2 радиуса r = b относительно центра внутренней окружности под действием внутреннего давления q; штрихами показан внешний контур трубы для осесимметричного случая.

Фиг. 1

В дальнейшем величина δ принимается за малый параметр. При получении приближенного аналитического решения предполагается, что упругие деформации малы по сравнению с деформациями ползучести и ими можно пренебречь. С физической точки зрения это означает, что рассматриваются установившиеся поля скоростей деформаций ползучести и напряжений, т.е. деформацией ползучести, накопленной на первой стадии и вызванной перераспределением напряжений от упругого состояния до состояния установившейся ползучести, пренебрегаем.

Разложение тензора напряжений ${{\sigma }_{{ij}}}$, тензора скоростей деформаций ползучести ${{\dot {\varepsilon }}_{{ij}}}$ и вектора скоростей перемещений ${{\dot {u}}_{i}}$ по малому параметру до членов третьего порядка включительно имеют вид

${{\sigma }_{{ij}}} = \sigma _{{ij}}^{{(0)}} + \delta \sigma _{{ij}}^{{(1)}} + {{\delta }^{2}}\sigma _{{ij}}^{{(2)}} + {{\delta }^{3}}\sigma _{{ij}}^{{(3)}} + о ({{\delta }^{4}})$

(2.1)

${{\dot {\varepsilon }}_{{ij}}} = \dot {\varepsilon }_{{ij}}^{{(0)}} + \delta \dot {\varepsilon }_{{ij}}^{{(1)}} + {{\delta }^{2}}\dot {\varepsilon }_{{ij}}^{{(2)}} + {{\delta }^{3}}\dot {\varepsilon }_{{ij}}^{{(3)}} + о ({{\delta }^{4}})$

${{\dot {u}}_{i}} = \dot {u}_{i}^{{(0)}} + \delta \dot {u}_{i}^{{(1)}} + {{\delta }^{2}}\dot {u}_{i}^{{(2)}} + {{\delta }^{3}}\dot {u}_{i}^{{(3)}} + о ({{\delta }^{4}})$

Задача решается в условиях плоского деформированного состояния, т.е. ${{\dot {\varepsilon }}_{{zz}}} = 0$. Используется гипотеза несжимаемости материала для скоростей деформаций ползучести на установившейся стадии:

(2.2)

${{\dot {\varepsilon }}_{{rr}}} + {{\dot {\varepsilon }}_{{\theta \theta }}} = 0,$

что находит экспериментальное обоснование [21, 22].

В монографии Ю.Н. Работнова [23] приведено известное решение задачи в осесимметричной постановке (нулевое приближение):

(2.3)

$\begin{gathered} \sigma _{{rr}}^{{(0)}} = Q[1 - {{(b{\text{/}}r)}^{p}}],\quad \sigma _{{\theta \theta }}^{{(0)}} = Q[1 - (1 - p){{(b{\text{/}}r)}^{p}}],\quad \sigma _{{zz}}^{{(0)}} = Q[1 - (1 + p){{(b{\text{/}}r)}^{p}}] \\ Q = q{\text{/}}[{{(b{\text{/}}a)}^{p}} - 1],\quad p = 2{\text{/}}n \\ \end{gathered} $

Для трубы с возмущенной внешней границей уравнение внешнего контура трубы с учетом возмущения δ имеет вид

(2.4)

${{(r\cos \theta - \delta )}^{2}} + {{r}^{2}}{{\sin }^{2}}\theta = {{b}^{2}}$

Раскладывая последнее соотношение в степенной ряд по параметру δ и оставляя члены до четвертого порядка включительно, получаем

(2.5)

$r = b + \delta \cos \theta + {{\delta }^{2}}(\cos 2\theta - 1){\text{/}}4b - {{\delta }^{4}}{{\sin }^{4}}\theta {\text{/}}8{{b}^{3}}$

Заметим, что это разложение не содержит третьей степени малого параметра.

Постановка задачи включает в себя уравнения равновесия

(2.6)

$\frac{{\partial {{\sigma }_{{rr}}}}}{{\partial r}} = - \frac{1}{r}\frac{{\partial {{\sigma }_{{r\theta }}}}}{{\partial \theta }} - \frac{{{{\sigma }_{{rr}}} - {{\sigma }_{{\theta \theta }}}}}{r},\quad \frac{{\partial {{\sigma }_{{\theta \theta }}}}}{{\partial \theta }} = - r\frac{{\partial {{\sigma }_{{r\theta }}}}}{{\partial r}} - 2{{\sigma }_{{r\theta }}},$

которые линейны относительно компонент напряжений и, следовательно, выполняются для каждого приближения; соотношения Коши

(2.7)

${{\dot {\varepsilon }}_{{rr}}} = \frac{{\partial {{{\dot {u}}}_{r}}}}{{\partial r}};\quad {{\dot {\varepsilon }}_{{\theta \theta }}} = \frac{1}{r}\frac{{\partial {{{\dot {u}}}_{\theta }}}}{{\partial \theta }} + \frac{{{{{\dot {u}}}_{r}}}}{r};\quad {{\dot {\varepsilon }}_{{r\theta }}} = \frac{1}{2}\left( {\frac{1}{r}\frac{{\partial {{{\dot {u}}}_{r}}}}{{\partial \theta }} + \frac{{\partial {{{\dot {u}}}_{\theta }}}}{{\partial r}} - \frac{{{{{\dot {u}}}_{\theta }}}}{r}} \right),$

которые также выполняются для каждого приближения; соотношения теории установившейся ползучести со степенным законом

(2.8)

${{\dot {\varepsilon }}_{{ij}}} = \frac{3}{2}A\sigma _{e}^{{n - 1}}{{S}_{{ij}}};\quad {{S}_{{ij}}} = {{\sigma }_{{ij}}} - \frac{1}{3}{{\sigma }_{{kk}}}{{\delta }_{{ij}}},\quad {{\sigma }_{e}} = \frac{{\sqrt 3 }}{2}{{[{{({{\sigma }_{{rr}}} - {{\sigma }_{{\theta \theta }}})}^{2}} + 4\sigma _{{r\theta }}^{2}]}^{{1/2}}},$

где n и A – постоянные характеристики материала, ${{S}_{{ij}}}$ – девиатор напряжений, ${{\sigma }_{e}}$ – интенсивность напряжений при плоском деформированном состоянии.

Разложение $\sigma _{e}^{{n - 1}}$ в соотношении (2.8) в степенной ряд по малому параметру δ позволяет представить скорости деформаций ползучести (2.8) для каждого приближения в зависимости от компонент тензора напряжений соответствующего и предшествующих приближений:

(2.9)

$\dot {\varepsilon }_{{rr}}^{{(0)}} = \frac{1}{4}L{{r}^{s}}\Delta {{\sigma }^{{(0)}}},\quad \dot {\varepsilon }_{{r\theta }}^{{(0)}} = 0$

(2.10)

$\dot {\varepsilon }_{{rr}}^{{(1)}} = - \dot {\varepsilon }_{{\theta \theta }}^{{(1)}} = \frac{1}{4}L{{r}^{s}}n\Delta {{\sigma }^{{(1)}}},\quad \dot {\varepsilon }_{{r\theta }}^{{(1)}} = \frac{1}{2}L{{r}^{s}}\sigma _{{r\theta }}^{{(1)}}$

(2.11)

$\begin{gathered} \dot {\varepsilon }_{{rr}}^{{(2)}} = - \dot {\varepsilon }_{{\theta \theta }}^{{(2)}} = \frac{1}{4}L{{r}^{s}}\left[ {n\Delta {{\sigma }^{{(2)}}} + \frac{{n - 1}}{2}\frac{{n{{{[\Delta {{\sigma }^{{(1)}}}]}}^{2}} + 4{{{[\sigma _{{r\theta }}^{{(1)}}]}}^{2}}}}{{\Delta {{\sigma }^{{(0)}}}}}} \right] \\ _{{\dot {\varepsilon }_{{r\theta }}^{{(2)}} = \frac{1}{2}L{{r}^{s}}\left[ {\sigma _{{r\theta }}^{{(2)}} + \frac{{(n - 1)\Delta {{\sigma }^{{(1)}}}\sigma _{{r\theta }}^{{(1)}}}}{{\Delta {{\sigma }^{{(0)}}}}}} \right]}} \\ \end{gathered} $

$\dot {\varepsilon }_{{rr}}^{{(3)}} = - \dot {\varepsilon }_{{\theta \theta }}^{{(3)}} = \frac{1}{4}L{{r}^{s}}\left[ {n\Delta {{\sigma }^{{(3)}}} + n(n - 1)\frac{{\Delta {{\sigma }^{{(1)}}}\Delta {{\sigma }^{{(2)}}}}}{{\Delta {{\sigma }^{{(0)}}}}} + } \right.\frac{{n(n - 1)(n - 2)}}{6}\frac{{{{{[\Delta {{\sigma }^{{(1)}}}]}}^{3}}}}{{{{{[\Delta {{\sigma }^{{(0)}}}]}}^{2}}}} + $

(2.12)

$\begin{gathered} + \;2(n - 1)(n - 2)\frac{{\Delta {{\sigma }^{{(1)}}}{{{[\sigma _{{r\theta }}^{{(1)}}]}}^{2}}}}{{{{{[\Delta {{\sigma }^{{(0)}}}]}}^{2}}}} + \left. {4(n - 1)\frac{{\sigma _{{r\theta }}^{{(1)}}\sigma _{{r\theta }}^{{(2)}}}}{{\Delta {{\sigma }^{{(0)}}}}}} \right] \\ \dot {\varepsilon }_{{r\theta }}^{{(3)}} = \frac{1}{2}L{{r}^{s}}\left[ {\sigma _{{r\theta }}^{{(3)}} + \frac{{n - 1}}{{\Delta {{\sigma }^{{(0)}}}}}(\Delta {{\sigma }^{{(1)}}}\sigma _{{r\theta }}^{{(2)}} + \Delta {{\sigma }^{{(2)}}}\sigma _{{r\theta }}^{{(1)}}) + } \right. \\ \end{gathered} $

$\left. { + \;\frac{{(n - 1)\sigma _{{r\theta }}^{{(1)}}}}{{2{{{[\Delta {{\sigma }^{{(0)}}}]}}^{2}}}}((n - 2){{{[\Delta {{\sigma }^{{(1)}}}]}}^{2}} + 4{{{[\sigma _{{r\theta }}^{{(1)}}]}}^{2}})} \right]$

Здесь введены обозначения

(2.13)

$L = 3A{{(\sqrt 3 {{b}^{p}}Q{\text{/}}n)}^{{n - 1}}},\quad s = p - 2,\quad \Delta {{\sigma }^{{(k)}}} = \sigma _{{rr}}^{{(k)}} - \sigma _{{\theta \theta }}^{{(k)}}$

k = 0, 1, 2, 3 – номера приближений.

Поскольку построение третьего приближения основывается на решении задач для предыдущих приближений, приведем решение для первого приближения [17]

(2.14)

$\begin{gathered} \sigma _{{rr}}^{{(1)}}(r,\theta ) = \frac{1}{L}[{{c}_{{11}}} + 4{{c}_{{12}}}{{r}^{{ - p - 1}}} + {{c}_{{13}}}{{p}^{2}}r + {{c}_{{14}}}(4 - {{p}^{2}}){{r}^{{ - 1}}}]\cos \theta = \rho _{{rr}}^{{(1)}}\cos \theta \\ \sigma _{{r\theta }}^{{(1)}}(r,\theta ) = \frac{1}{L}[4{{c}_{{12}}}{{r}^{{ - p - 1}}} + {{c}_{{13}}}{{p}^{2}}r + {{c}_{{14}}}{{(2 - p)}^{2}}{{r}^{{ - 1}}}]\sin \theta = \rho _{{r\theta }}^{{(1)}}\sin \theta \\ \sigma _{{\theta \theta }}^{{(1)}}(r,\theta ) = \frac{1}{L}[{{c}_{{11}}} + {{c}_{{12}}}(4 - 4p){{r}^{{ - p - 1}}} + {{c}_{{13}}}({{p}^{2}} + p)r + \\ + \;{{c}_{{14}}}( - {{p}^{2}} + p + 2){{r}^{{ - 1}}}]\cos \theta = \rho _{{\theta \theta }}^{{(1)}}\cos \theta \\ \end{gathered} $

Здесь c_1i (i = 1, 2, 3, 4) – постоянные интегрирования, определяемые из граничных условий. В дальнейшем также используется обозначение $\Delta {{\rho }^{{(k)}}} = \rho _{{rr}}^{{(k)}} - \rho _{{\theta \theta }}^{{(k)}}$ (k = 1, 2).

Решение во втором приближении [18] основано на предположении, что скорость радиальных перемещений состоит из двух слагаемых, слагаемое $\dot {u}_{r}^{\psi }$ зависит только от радиуса r и определяется прямой подстановкой скоростей перемещений в соотношения Коши (2.7) и затем в условие несжимаемости (2.2): $\dot {u}_{r}^{\psi } = C{\text{/}}r$ (С – постоянная интегрирования), а слагаемое $\dot {u}_{r}^{\rho }$, зависящее и от радиуса r и от угла θ, можно представить с помощью функции перемещений

$\xi _{2}^{{(2)}}(r,\theta ) = {{R}_{2}}(r)\sin 2\theta $

такой, что подстановка этой функции в выражения для скоростей перемещений

(2.15)

$\dot {u}_{r}^{{(2)}}(r,\theta ) = \dot {u}_{r}^{\psi } + \dot {u}_{r}^{\rho } = \frac{C}{r} - \frac{1}{r}\frac{{\partial {{\xi }^{{(2)}}}}}{{\partial \theta }},\quad \dot {u}_{\theta }^{{(2)}}(r,\theta ) = \frac{{\partial {{\xi }^{{(2)}}}}}{{\partial r}} = \dot {u}_{\theta }^{\rho }$

и затем в соотношения Коши позволяет тождественно удовлетворить условие несжимаемости (2.2). Применение представления (2.15) позволяет выразить компоненты напряжения из определяющих соотношений (2.11) в виде

(2.16)

$\begin{gathered} \Delta {{\sigma }^{{(2)}}} = \frac{{2p}}{{L{{r}^{s}}}}(\dot {\varepsilon }_{{rr}}^{\rho }\cos 2\theta + \dot {\varepsilon }_{{rr}}^{\psi }) - B_{2}^{{(2)}}(r)\cos 2\theta - B_{0}^{{(2)}}(r) = \Delta {{\rho }^{{(2)}}}\cos 2\theta + \Delta {{\psi }^{{(2)}}} \\ \sigma _{{r\theta }}^{{(2)}} = \frac{2}{{L{{r}^{s}}}}\dot {\varepsilon }_{{r\theta }}^{\rho }\sin 2\theta - T_{2}^{{(2)}}(r)\sin 2\theta = \rho _{{r\theta }}^{{(2)}}\sin 2\theta , \\ \end{gathered} $

где введены новые обозначения

$B_{{2,0}}^{{(2)}}(r) = \frac{{n - 1}}{{4\Delta {{\sigma }^{{(0)}}}}}({{[\Delta {{\rho }^{{(1)}}}]}^{2}} \mp 2p{{[\rho _{{r\theta }}^{{(1)}}]}^{2}}),\quad T_{2}^{{(2)}}(r) = \frac{{n - 1}}{{2\Delta {{\sigma }^{{(0)}}}}}\Delta {{\rho }^{{(1)}}}\rho _{{r\theta }}^{{(1)}}$

Для определения функции R₂(r) необходимо подставить напряжения (2.16) в уравнения равновесия (2.6) и продифференцировать обе части первого уравнения равновесия по θ, а второго – по r. Разность продифференцированных уравнений равновесия есть вторая смешанная производная по r и θ для выражения $\Delta {{\sigma }^{{(2)}}}$ в первой формуле (2.16). Таким образом, приходим к неоднородному линейному дифференциальному уравнению четвертого порядка для определения функции R₂(r). Используя степенное представление ${{R}_{2}}(r) = {{r}^{\mu }}$, находим величины

(2.17)

$2{{\mu }_{{\overline {1,4} }}}(p) = p \pm \sqrt {{{p}^{2}} + 12p - 8 \pm 4\sqrt {13{{p}^{2}} - 12p - 12} } = p \pm l(p) \pm i2h(p),$

которые при n > 1.31 имеют комплексные значения (l = l(p), h = h(p) – известные величины для конкретного материала). В итоге функцию R₂(r) можно представить в виде

(2.18)

$\begin{gathered} {{R}_{2}}(r) = \sum\limits_{i = 1}^4 {[{{C}_{{2i}}}(r) + {{c}_{{2i}}}]{{m}_{i}}(r)} \\ {{m}_{{1,3}}}(r) = {{r}^{{(p \pm l)/2}}}\cos (h\ln r),\quad {{m}_{{2,4}}}(r) = {{r}^{{(p \pm l)/2}}}\sin (h\ln r) \\ \end{gathered} $

C_2i(r) – известные функции радиуса, определяемые из решения неоднородного дифференциального уравнения четвертого порядка относительно R₂(r), c_2i – постоянные интегрирования.

Второе слагаемое в выражении для скорости радиальных перемещений (2.15) приводит к дополнительному члену в напряжениях для второго приближения:

$\begin{gathered} \psi _{{rr}}^{{(2)}}(r) = - \frac{{2C}}{L}{{r}^{{ - p}}} + \int {\frac{{B_{0}^{{(2)}}(r)}}{r}} dr + {{K}^{\psi }};\quad \Delta {{\psi }^{{(2)}}}(r) = - \frac{{2pC}}{L}{{r}^{{ - p}}} - B_{0}^{{(2)}}(r) \\ \psi _{{\theta \theta }}^{{(2)}}(r) = \frac{{2C}}{L}(p - 1){{r}^{{ - p}}} + B_{0}^{{(2)}}(r) + \int {\frac{{B_{0}^{{(2)}}(r)}}{r}} dr + {{K}^{\psi }} \\ \end{gathered} $

${{K}^{\psi }}$ – постоянная интегрирования. В итоге второе приближение, основанное на нулевом и первом приближениях, имеет вид

(2.19)

$\begin{gathered} \sigma _{{rr}}^{{(2)}}(r,\theta ) = \rho _{{rr}}^{{(2)}}(r)\cos 2\theta + \psi _{{rr}}^{{(2)}}(r),\quad \sigma _{{r\theta }}^{{(2)}}(r,\theta ) = \rho _{{r\theta }}^{{(2)}}(r)\sin 2\theta , \\ \sigma _{{\theta \theta }}^{{(2)}}(r,\theta ) = \rho _{{\theta \theta }}^{{(2)}}(r)\cos 2\theta + \psi _{{\theta \theta }}^{{(2)}}(r) \\ \Delta {{\sigma }^{{(2)}}}(r,\theta ) = \Delta {{\rho }^{{(2)}}}(r)\cos 2\theta + \Delta {{\psi }^{{(2)}}}(r) \\ \end{gathered} $

3. Граничные условия. Рассмотрим граничные условия для третьего приближения. Внутренняя граница не возмущена, следовательно, на внутреннем контуре граничные условия имеют вид

(3.1)

${{\left. {\sigma _{{r\theta }}^{{(3)}}} \right|}_{{r = a}}} = 0,\quad {{\left. {\sigma _{{rr}}^{{(3)}}} \right|}_{{r = a}}} = 0$

Применим метод линеаризации граничных условий ([1], с. 58–62), используя решения для нулевого, первого и второго приближений (2.3), (2.14) и (2.19) [17, 18]. Граничное условие на внешнем возмущенном контуре трубы для третьего приближения содержит функции одинарного и двойного угла θ. Путем элементарных тригонометрических преобразований функций угла θ приходим к граничным условиям для третьего приближения

${{\left. {\sigma _{{r\theta }}^{{(3)}}} \right|}_{{r = b}}} = \left[ {\frac{1}{{8{{b}^{3}}}}\Delta {{\sigma }^{{(0)}}} - \frac{1}{{2{{b}^{2}}}}\rho _{{r\theta }}^{{(1)}} + \frac{1}{{2b}}\Delta {{\rho }^{{(2)}}} - \frac{1}{2}\frac{{d\rho _{{r\theta }}^{{(2)}}}}{{dr}} + \frac{1}{{4b}}\frac{{d\Delta {{\rho }^{{(1)}}}}}{{dr}} - } \right.$

$\left. { - \;\frac{1}{{8b}}\frac{{d\rho _{{r\theta }}^{{(1)}}}}{{dr}} + \frac{1}{{8{{b}^{2}}}}\frac{{d\Delta {{\sigma }^{{(0)}}}}}{{dr}} + \frac{1}{{8b}}\frac{{{{d}^{2}}\Delta {{\sigma }^{{(0)}}}}}{{d{{r}^{2}}}} - \frac{1}{8}\frac{{{{d}^{2}}\rho _{{r\theta }}^{{(1)}}}}{{d{{r}^{2}}}}} \right]\sin 3\theta + $

$ + \;\left[ { - \frac{3}{{8{{b}^{3}}}}\Delta {{\sigma }^{{(0)}}} + \frac{3}{{2{{b}^{2}}}}\rho _{{r\theta }}^{{(1)}} - \frac{1}{{2b}}\Delta {{\rho }^{{(2)}}} - \frac{1}{2}\frac{{d\rho _{{r\theta }}^{{(2)}}}}{{dr}} + \frac{1}{{4b}}\frac{{d\Delta {{\rho }^{{(1)}}}}}{{dr}} + } \right.$

(3.2)

$\begin{gathered} \left. { + \;\frac{3}{{8b}}\frac{{d\rho _{{r\theta }}^{{(1)}}}}{{dr}} - \frac{3}{{8{{b}^{2}}}}\frac{{d\Delta {{\sigma }^{{(0)}}}}}{{dr}} + \frac{1}{{8b}}\frac{{{{d}^{2}}\Delta {{\sigma }^{{(0)}}}}}{{d{{r}^{2}}}} - \frac{1}{8}\frac{{{{d}^{2}}\rho _{{r\theta }}^{{(1)}}}}{{d{{r}^{2}}}} + \frac{1}{b}\Delta {{\psi }^{{(2)}}}} \right]\sin \theta \\ {{\left. {\sigma _{{rr}}^{{(3)}}} \right|}_{{r = b}}} = \left[ {\frac{1}{{4{{b}^{2}}}}\Delta {{\rho }^{{(1)}}} + \frac{1}{{2{{b}^{2}}}}\rho _{{r\theta }}^{{(1)}} + \frac{1}{{2b}}\frac{{d\rho _{{r\theta }}^{{(1)}}}}{{dr}} + \frac{1}{b}\rho _{{r\theta }}^{{(2)}} - \frac{1}{2}\frac{{d\rho _{{rr}}^{{(2)}}}}{{dr}} - } \right. \\ \end{gathered} $

$ - \;\frac{1}{8}\frac{{{{d}^{2}}\rho _{{rr}}^{{(1)}}}}{{d{{r}^{2}}}}\left. { - \frac{1}{{24}}\frac{{{{d}^{3}}\sigma _{{rr}}^{{(0)}}}}{{d{{r}^{3}}}} - \frac{1}{{4{{b}^{2}}}}\frac{{d\Delta {{\sigma }^{{(0)}}}}}{{dr}} - \frac{1}{{8b}}\frac{{d\rho _{{rr}}^{{(1)}}}}{{dr}} - \frac{1}{{8b}}\frac{{{{d}^{2}}\sigma _{{rr}}^{{(0)}}}}{{d{{r}^{2}}}}} \right]\cos 3\theta + $

$ + \;\left[ {\frac{1}{{4{{b}^{2}}}}\Delta {{\rho }^{{(1)}}} + \frac{1}{{4{{b}^{2}}}}\frac{{d\Delta {{\sigma }^{{(0)}}}}}{{dr}} - \frac{1}{{2{{b}^{2}}}}\rho _{{r\theta }}^{{(1)}} + \frac{1}{{8b}}\frac{{d\rho _{{rr}}^{{(1)}}}}{{dr}} + \frac{1}{{8b}}\frac{{{{d}^{2}}\sigma _{{rr}}^{{(0)}}}}{{d{{r}^{2}}}} - } \right.$

$ - \;\frac{1}{{2b}}\frac{{d\rho _{{r\theta }}^{{(1)}}}}{{dr}} - \frac{1}{b}\rho _{{r\theta }}^{{(2)}} - \frac{1}{2}\frac{{d\rho _{{rr}}^{{(2)}}}}{{dr}} - \frac{3}{8}\frac{{{{d}^{2}}\rho _{{rr}}^{{(1)}}}}{{d{{r}^{2}}}} - \frac{{d\psi _{{rr}}^{{(2)}}}}{{dr}}\left. { - \frac{1}{8}\frac{{{{d}^{3}}\sigma _{{rr}}^{{(0)}}}}{{d{{r}^{3}}}}} \right]\cos \theta $

Соотношения (2.2), (2.6), (2.7) и (2.12) с граничными условиями (3.1) и (3.2) образуют краевую задачу для нахождения третьего приближения, которая решается в напряжениях.

4. Метод решения задачи. Метод построения третьего приближения обобщает метод решения для первого и второго приближений задачи.

Сразу сделаем следующее замечание. Ниже будет дана фактически схема решения задачи без детализации многих технических математических (и вполне очевидных) преобразований и явно выписанных выражений для некоторых величин, которые достаточно громоздкие. Но авторами статьи все эти преобразования выполнены.

Граничное условие на внешнем контуре трубы (3.2) содержит две тригонометрические функции угла θ: sin3θ и sinθ. Поэтому задача определения третьего приближения сводится к нахождению суммы двух решений: отдельно для функции, содержащей угол 3θ, отдельно – для функции, содержащей угол θ.

Введем в рассмотрение функцию ${{\xi }^{{(3)}}}(r,\theta )$ и применим метод разделения переменных

(3.3)

${{\xi }^{{(3)}}}(r,\theta ) = \xi _{3}^{{(3)}}(r,\theta ) + \xi _{1}^{{(3)}}(r,\theta ) = {{X}_{3}}(r)\sin 3\theta + {{K}_{3}}(r)\sin \theta $

Функции X₃(r) и K₃(r) подлежат определению при построении решения задачи. Свойства функции ${{\xi }^{{(3)}}}(r,\theta )$ позволяют представить скорости перемещений ползучести для третьего приближения в виде

(3.4)

$\begin{gathered} \dot {u}_{r}^{{(3)}} = - \frac{1}{r}\frac{{\partial {{\xi }^{{(3)}}}}}{{\partial \theta }} = - \frac{1}{r}\frac{{\partial \xi _{3}^{{(3)}}}}{{\partial \theta }} - \frac{1}{r}\frac{{\partial \xi _{1}^{{(3)}}}}{{\partial \theta }} = \dot {u}_{r}^{\chi }(r)\cos 3\theta + \dot {u}_{r}^{\kappa }(r)\cos \theta \\ \dot {u}_{\theta }^{{(3)}} = \frac{{\partial {{\xi }^{{(3)}}}}}{{\partial r}} = \frac{{\partial \xi _{3}^{{(3)}}}}{{\partial r}} + \frac{{\partial \xi _{1}^{{(3)}}}}{{\partial r}} = \dot {u}_{\theta }^{\chi }(r)\sin 3\theta + \dot {u}_{\theta }^{\kappa }(r)\sin \theta \\ \end{gathered} $

Представлением (3.4) можно тождественно удовлетворить условию несжимаемости (2.2), подставив выражения (3.4) в соотношения Коши (2.7). С учетом равенств (3.3) выразим скорости деформаций ползучести, введя обозначения для функций радиуса $\dot {\varepsilon }_{{rr}}^{\chi }$, $\dot {\varepsilon }_{{rr}}^{\kappa }$, $\dot {\varepsilon }_{{r\theta }}^{\chi }$, $\dot {\varepsilon }_{{r\theta }}^{\kappa }$ при функциях угла θ:

(3.5)

$\begin{gathered} \dot {\varepsilon }_{{rr}}^{{(3)}} = 3( - X_{3}^{'}{{r}^{{ - 1}}} + {{X}_{3}}{{r}^{{ - 2}}})\cos 3\theta + ( - K_{3}^{'}{{r}^{{ - 1}}} + {{K}_{3}}{{r}^{{ - 2}}})\cos \theta = \dot {\varepsilon }_{{rr}}^{\chi }(r)\cos 3\theta + \dot {\varepsilon }_{{rr}}^{\kappa }(r)\cos \theta \\ \dot {\varepsilon }_{{r\theta }}^{{(3)}} = \frac{1}{2}(X_{3}^{{''}} - X_{3}^{'}{{r}^{{ - 1}}} + 9{{X}_{3}}{{r}^{{ - 2}}})\sin 3\theta + \frac{1}{2}(K_{3}^{{''}} - K_{3}^{'}{{r}^{{ - 1}}} + {{K}_{3}}{{r}^{{ - 2}}})\sin \theta = \\ = \dot {\varepsilon }_{{r\theta }}^{\chi }(r)\sin 3\theta + \dot {\varepsilon }_{{r\theta }}^{\kappa }(r)\sin \theta \\ \end{gathered} $

Используем эти равенства в определяющих соотношениях (2.12) для третьего приближения, выразив из соотношений (2.12) напряжения $\Delta {{\sigma }^{{(3)}}}$ и $\sigma _{{r\theta }}^{{(3)}}$:

$\Delta {{\sigma }^{{(3)}}} = \frac{{2p}}{{L{{r}^{s}}}}\dot {\varepsilon }_{{rr}}^{{(3)}} - $

$ - \;\frac{{n - 1}}{{2\Delta {{\sigma }^{{(0)}}}}}\left( {\frac{{n - 2}}{{12}}\frac{{{{{[\Delta {{\rho }^{{(1)}}}]}}^{3}}}}{{\Delta {{\sigma }^{{(0)}}}}} + \Delta {{\rho }^{{(1)}}}\Delta {{\rho }^{{(2)}}} - 2p\rho _{{r\theta }}^{{(1)}}\rho _{{r\theta }}^{{(2)}} + (p - 1)\frac{{\Delta {{\rho }^{{(1)}}}{{{[\rho _{{r\theta }}^{{(1)}}]}}^{2}}}}{{\Delta {{\sigma }^{{(0)}}}}}} \right)\cos 3\theta - $

$ - \;\frac{{n - 1}}{{2\Delta {{\sigma }^{{(0)}}}}}\left( {\frac{{n - 2}}{4}\frac{{{{{[\Delta {{\rho }^{{(1)}}}]}}^{3}}}}{{\Delta {{\sigma }^{{(0)}}}}} + 2p\rho _{{r\theta }}^{{(1)}}\rho _{{r\theta }}^{{(2)}} + [\Delta {{\rho }^{{(2)}}} + 2\Delta {{\psi }^{{(2)}}}]\Delta {{\rho }^{{(1)}}} + (1 - p)\frac{{\Delta {{\rho }^{{(1)}}}{{{[\rho _{{r\theta }}^{{(1)}}]}}^{2}}}}{{\Delta {{\sigma }^{{(0)}}}}}} \right)\cos \theta = $

(3.6)

$ = \left[ {\frac{{2p}}{{L{{r}^{s}}}}\dot {\varepsilon }_{{rr}}^{\chi }(r) - B_{3}^{{(3)}}(r)} \right]\cos 3\theta + \left[ {\frac{{2p}}{{L{{r}^{s}}}}\dot {\varepsilon }_{{rr}}^{\kappa }(r) - B_{1}^{{(3)}}(r)} \right]\cos \theta = \Delta {{\chi }^{{(3)}}}\cos 3\theta + \Delta {{\kappa }^{{(3)}}}\cos \theta $

$\sigma _{{r\theta }}^{{(3)}} = \frac{2}{{L{{r}^{s}}}}\dot {\varepsilon }_{{r\theta }}^{{(3)}} - \frac{{n - 1}}{{2\Delta {{\sigma }^{{(0)}}}}}\left( {\frac{{n - 2}}{4}\frac{{\rho _{{r\theta }}^{{(1)}}{{{[\Delta {{\rho }^{{(1)}}}]}}^{2}}}}{{\Delta {{\sigma }^{{(0)}}}}} + \Delta {{\rho }^{{(1)}}}\rho _{{r\theta }}^{{(2)}} + \Delta {{\rho }^{{(2)}}}\rho _{{r\theta }}^{{(1)}} - \frac{{{{{[\rho _{{r\theta }}^{{(1)}}]}}^{3}}}}{{\Delta {{\sigma }^{{(0)}}}}}} \right)\sin 3\theta - $

$ - \;\frac{{n - 1}}{{2\Delta {{\sigma }^{{(0)}}}}}\left( {\Delta {{\rho }^{{(1)}}}\rho _{{r\theta }}^{{(2)}} + \frac{{n - 2}}{4}\frac{{\rho _{{r\theta }}^{{(1)}}{{{[\Delta {{\rho }^{{(1)}}}]}}^{2}}}}{{\Delta {{\sigma }^{{(0)}}}}} + \rho _{{r\theta }}^{{(1)}}(2\Delta {{\psi }^{{(2)}}} - \Delta {{\rho }^{{(2)}}}) + \frac{{3{{{[\rho _{{r\theta }}^{{(1)}}]}}^{3}}}}{{\Delta {{\sigma }^{{(0)}}}}}} \right)\sin \theta = $

$ = \left[ {\frac{2}{{L{{r}^{s}}}}\dot {\varepsilon }_{{r\theta }}^{\chi }(r) - T_{3}^{{(3)}}(r)} \right]\sin 3\theta + \left[ {\frac{2}{{L{{r}^{s}}}}\dot {\varepsilon }_{{r\theta }}^{\kappa }(r) - T_{1}^{{(3)}}(r)} \right]\sin \theta = \chi _{{r\theta }}^{{(3)}}\sin 3\theta + \kappa _{{r\theta }}^{{(3)}}\sin \theta $

Здесь введены новые обозначения $T_{3}^{{(3)}}(r)$, $T_{1}^{{(3)}}(r)$, $B_{3}^{{(3)}}(r)$, $B_{1}^{{(3)}}(r)$ для выражений, содержащих предыдущие приближения, при cos3θ, cosθ, sin 3θ и sinθ; и $\chi _{{rr}}^{{(3)}}$, $\kappa _{{rr}}^{{(3)}}$, $\chi _{{r\theta }}^{{(3)}}$, $\kappa _{{r\theta }}^{{(3)}}$ для функций напряжений третьего приближения при соответствующих функциях угла θ.

Воспользовавшись выражениями (3.6) в уравнениях равновесия (2.6), в итоге приходим к двум неоднородным линейным дифференциальным уравнениям четвертого порядка для определения функций X₃(r) и K₃(r):

(3.7)

$\begin{gathered} X_{3}^{{(IV)}} + 2(3 - p)X_{3}^{{'''}}{{r}^{{ - 1}}} + ({{p}^{2}} - 22p + 21)X_{3}^{{''}}{{r}^{{ - 2}}} + \\ + \;(17{{p}^{2}} - 32p + 15)X_{3}^{'}{{r}^{{ - 3}}} + (81 - {{p}^{2}}){{X}_{3}}{{r}^{{ - 4}}} = L{{r}^{{p - 3}}}Y_{3}^{{(3)}}(r) \\ K_{3}^{{(IV)}} + 2(3 - p)K_{3}^{{'''}}{{r}^{{ - 1}}} + ({{p}^{2}} - 6p + 5)K_{3}^{{''}}{{r}^{{ - 2}}} + \\ + \;({{p}^{2}} - 1)K_{3}^{'}{{r}^{{ - 3}}} + (1 - {{p}^{2}}){{K}_{3}}{{r}^{{ - 4}}} = L{{r}^{{p - 3}}}Y_{1}^{{(3)}}(r) \\ \end{gathered} $

Функции

$Y_{3}^{{(3)}}(r) = r\frac{{{{d}^{2}}T_{3}^{{(3)}}}}{{d{{r}^{2}}}} + 3\frac{{dT_{3}^{{(3)}}}}{{dr}} + 3\frac{{dB_{3}^{{(3)}}}}{{dr}} + 9\frac{{T_{3}^{{(3)}}}}{r} + 3\frac{{B_{3}^{{(3)}}}}{r}$

$Y_{1}^{{(3)}}(r) = r\frac{{{{d}^{2}}T_{1}^{{(3)}}}}{{d{{r}^{2}}}} + 3\frac{{dT_{1}^{{(3)}}}}{{dr}} + \frac{{dB_{1}^{{(3)}}}}{{dr}} + \frac{{T_{1}^{{(3)}} + B_{1}^{{(3)}}}}{r}$

зависят от нулевого, первого и второго приближений. Задача решения уравнений (3.7) аналогична задаче решения неоднородного дифференциального уравнения четвертого порядка для второго приближения (см. (2.17) и (2.18)), и подробности их решения опускаем. После определения функций X₃(r) и K₃(r) находим скорости деформаций ползучести из соотношений (3.5) и затем – напряжения $\sigma _{{r\theta }}^{{(3)}}$ и $\Delta {{\sigma }^{{(3)}}}$ по формулам (3.6). Использование этих напряжений позволяет определить $\sigma _{{rr}}^{{(3)}}$ и $\sigma _{{\theta \theta }}^{{(3)}}$ из уравнений равновесия (2.6) и, следовательно, получить окончательный вид решения задачи в напряжениях для третьего приближения:

(3.8)

$\begin{gathered} \sigma _{{rr}}^{{(3)}}(r,\theta ) = \int {\frac{1}{r}[ - 3\chi _{{r\theta }}^{{(3)}} - \Delta {{\chi }^{{(3)}}} + 3T_{3}^{{(3)}} + B_{3}^{{(3)}}]} dr\cos 3\theta + \\ + \;\int {\frac{1}{r}} [ - \kappa _{{r\theta }}^{{(3)}} - \Delta {{\kappa }^{{(3)}}} + T_{1}^{{(3)}} + B_{1}^{{(3)}}]dr\cos \theta = \chi _{{rr}}^{{(3)}}(r)\cos 3\theta + \kappa _{{rr}}^{{(3)}}(r)\cos \theta \\ \end{gathered} $

(3.9)

$\begin{gathered} \sigma _{{\theta \theta }}^{{(3)}}(r,\theta ) = \sigma _{{rr}}^{{(3)}} - \Delta {{\sigma }^{{(3)}}} = (\chi _{{rr}}^{{(3)}} - \Delta {{\chi }^{{(3)}}})\cos 3\theta + (\kappa _{{rr}}^{{(3)}} - \Delta {{\kappa }^{{(3)}}})\cos \theta = \\ = \chi _{{\theta \theta }}^{{(3)}}(r)\cos 3\theta + \kappa _{{\theta \theta }}^{{(3)}}(r)\cos \theta \\ \end{gathered} $

без приведения алгебраических вычислений ввиду их громоздкости. Выражения (3.6), (3.8) и (3.9) образуют решение третьего приближения в напряжениях.

4. Анализ результатов приближенного аналитического решения. Анализ результатов расчета на основании приближенного аналитического решения до третьего порядка приближения включительно выполнен на модельных примерах для толстостенных труб из различных материалов в широком диапазоне изменения величин малого параметра и показателя нелинейности установившейся ползучести n (см. формулу (2.8)). Рассмотрим подробно выполненное исследование на примере модельных задач для толстостенной трубы с внутренним и внешим радиусами a = 0.115 м и b = 0.15 м под действием внутреннего давления q = 22.07 МПа из углеродистой стали с характеристиками установившейся ползучести n = 3.03, A = 9.04 × 10^–9 МПаⁿ ч^–1 при T = 649°С [24] и из сплава ЭИ698 с характеристиками установившейся ползучести n = 10.96, А = = 4.57 × 10^–33 МПаⁿ ч^–1 при T = 775°С [25].

Наибольший интерес для анализа представляет компонента напряжений ${{\sigma }_{{\theta \theta }}}$. Толщина стенки трубы минимальна при θ = π (см. фиг. 1), поэтому тангенциальные напряжения ${{\sigma }_{{\theta \theta }}}$ = ${{\sigma }_{{\theta \theta }}}(r,\theta )$ максимальны именно в этом сечении. В табл. 1 приведены результаты расчетов на основании построенных аналитических решений значения ${{\sigma }_{{\theta \theta }}}$ на внешнем контуре трубы при θ = π (для обоих материалов результаты практически совпадают, расхождение значений не превышает погрешности вычислений). В дальнейшем напряжения отнесены к безразмерным величинам $\tilde {\delta } = \delta {\text{/}}a$, $\tilde {r} = r{\text{/}}a$. Здесь при θ = π представлены значения: $\sigma _{{\theta \theta }}^{{\text{*}}} = \sigma _{{\theta \theta }}^{{(0 - 1)}}{\text{/}}\sigma _{{\theta \theta }}^{{(0)}}$ – при учете приближения первого порядка на внешней границе трубы при

$r = b + \delta \cos \theta $

$\sigma _{{\theta \theta }}^{{{\text{**}}}} = \sigma _{{\theta \theta }}^{{(0 - 2)}}{\text{/}}\sigma _{{\theta \theta }}^{{(0)}}$ – при учете приближения второго порядка на внешней границе трубы при

$r = b + \delta \cos \theta + {{\delta }^{2}}(\cos 2\theta - 1){\text{/}}(4b)$

$\sigma _{{\theta \theta }}^{{{\text{***}}}} = \sigma _{{\theta \theta }}^{{(0 - 3)}}{\text{/}}\sigma _{{\theta \theta }}^{{(0)}}$ – при учете приближения третьего порядка на внешней границе трубы при

$r = b + \delta \cos \theta + {{\delta }^{2}}(\cos 2\theta - 1){\text{/}}4b - {{\delta }^{4}}{{\sin }^{4}}\theta {\text{/}}(8{{b}^{3}})$

Здесь и в дальнейшем верхний индекс у компонент тензора напряжений означает порядок приближения, используемый для оценки величины.

Таблица 1

$\tilde {\delta } \times {{10}^{2}}$	0	2	4	6	8
$\sigma _{{\theta \theta }}^{{\text{*}}}$	1	1.08	1.17	1.25	1.33
$\sigma _{{\theta \theta }}^{{{\text{**}}}}$	1	1.09	1.18	1.29	1.40
$\sigma _{{\theta \theta }}^{{{\text{***}}}}$	1	1.09	1.19	1.29	1.42

Из данных табл. 1 можно сделать вывод, что приближенное аналитическое решение имеет тенденцию к сходимости в достаточно широком диапазоне изменения величины $\tilde {\delta }$ как при относительно небольшом значении показателя нелинейности установившейся ползучести (n = 3.03, углеродистая сталь), так и для значительно бόльшего значения (n = 10.96, сплав ЭИ698).

5. Численное решение задачи на основе метода конечных элементов. Для оценки погрешности аналитического решения сопоставим данные расчета по предложенному решению с данными численного решения с использованием метода конечных элементов (МКЭ) на примере уже рассмотренного модельного примера трубы из малоуглеродистой стали. Для реализации МКЭ использовался модуль Юнга E = 1.56 × 10⁵ МПа и плотность материала ρ = 7630 кг/м³ при температуре испытаний T = 649°C. Построение конечно-элементной модели проведено в программном комплексе ANSYS. В расчетах использовался плоский восьмиузловой элемент PLANE183, пригодный для моделирования плоского деформированного состояния и позволяющий учитывать большие деформации при установившейся ползучести. В силу симметрии задачи конечно-элементная модель (КЭМ) строилась для половины неосесимметричной трубы.

Решение выполнялось двумя шагами: 1) упругое решение, 2) решение с учетом свойств ползучести материала для трубы из углеродистой стали при давлении 22.07 МПа – за время 100 часов, поскольку за указанное время напряженное состояние практически выходит на стационарный режим, соответствующий стадии установившейся ползучести.

Для оценки адекватности КЭМ на предварительном этапе решалась задача для осесимметричной трубы, находящейся в условиях установившейся ползучести под внутренним давлением q = 22.07 МПа. Полученное численное решение задачи в такой постановке практически соответствует нулевому приближению (2.3) поставленной задачи.

Результаты приближенного аналитического решения сравниваются с результатами численного решения для построенной КЭМ трубы в некоторых частных случаях – в наиболее нагруженной области при θ = π и разных значениях малого параметра δ.

Выполнен анализ оценки погрешности приближенного аналитического решения по отношению к конечно-элементному решению задачи для осесимметричной ($\tilde {\delta } = 0$) и несоосной ($\tilde {\delta } \ne 0$) трубы с учетом третьего порядка приближения (см. табл. 2) на основе значений радиальных ${{\sigma }_{{rr}}}$ и тангенциальных ${{\sigma }_{{\theta \theta }}}$ напряжений в 15 равноотстоящих точках по координате r_i при θ = π

$a \leqslant {{r}_{i}} \leqslant b + \delta \cos \theta + {{\delta }^{2}}(\cos 2\theta - 1){\text{/}}(4b),\quad i = \overline {1,15} $

Таблица 2

$\tilde {\delta } \times {{10}^{2}}$	0	2	4	6	8
Углеродистая сталь
${{\sigma }_{{rr}}}(r,\pi )$	0.12/0.35	0.21/0.41	0.29/0.37	1.64/1.83	1.98/1.96
${{\sigma }_{{\theta \theta }}}(r,\pi )$	0.01/0.02	0.32/0.35	1.24/1.29	1.85/2.08	2.42/2.87
Сплав ЭИ698
${{\sigma }_{{rr}}}(r,\pi )$	0.17/0.39	0.21/0.40	0.40/0.50	1.45/1.76	4.30/4.87
${{\sigma }_{{\theta \theta }}}(r,\pi )$	0.02/0.06	0.32/0.35	1.22/1.24	2.53/3.04	5.59/5.90

Вычисление погрешности проведено по двум нормам

(5.1)

$\begin{gathered} s = \sum\limits_i {\left| {\sigma _{{\omega \omega }}^{{(0 - 3)}}({{r}_{i}},\pi ) - \sigma _{{\omega \omega }}^{{ans}}({{r}_{i}},\pi )} \right|} {{\left( {\sum\limits_i {\left| {\sigma _{{\omega \omega }}^{{ans}}({{r}_{i}},\pi )} \right|} } \right)}^{{ - 1}}} \times 100\% \\ \sigma = {{\left( {\sum\limits_i {{{{[\sigma _{{\omega \omega }}^{{(0 - 3)}}({{r}_{i}},\pi ) - \sigma _{{\omega \omega }}^{{ans}}({{r}_{i}},\pi )]}}^{2}}} {{{\left( {\sum\limits_i {{{{[\sigma _{{\omega \omega }}^{{ans}}({{r}_{i}},\pi )]}}^{2}}} } \right)}}^{{ - 1}}}} \right)}^{{1/2}}} \times 100\% , \\ \end{gathered} $

где ω = r, θ; $\sigma _{{\omega \omega }}^{{(0 - 3)}}({{r}_{i}},\theta )$, $\sigma _{{\omega \omega }}^{{ans}}({{r}_{i}},\theta )$ – расчетные значения для аналитического (с учетом приближений третьего порядка) и численного решений соответственно в точках дискретизации радиуса при θ = π.

В табл. 2 через косую черту представлены погрешности по двум нормам (s/σ) в процентах. По данным табл. 2 можно сделать вывод, что при использовании третьего порядка приближения погрешность приближенного аналитического решения по отношению к численному при величине малого параметра $\tilde {\delta } = 0.04$ и θ = π составляет около 1.3%, а при $\tilde {\delta } = 0.08$ и θ = π не превосходит 3%. Анализ величины погрешности в соответствии с существующими нормативными регламентирующими документами на технологические допуски по разностенности [19, 20] будет выполнен ниже.

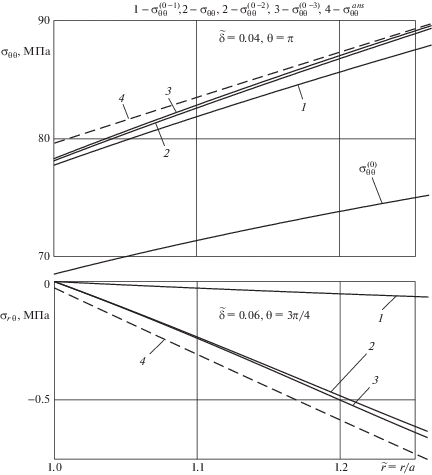
В качестве иллюстрации полученных решений в верхней части фиг. 2 представлен график изменения тангенциальной компоненты тензора напряжений ${{\sigma }_{{\theta \theta }}}$ вдоль радиуса трубы из углеродистой стали (n = 3.03) при величине малого параметра $\tilde {\delta } = 0.04$ при значении угла θ = π, соответствующего максимальным значениям тангенциального напряжения. Поскольку в несимметричных сечениях неосесимметричной трубы возникают и касательные напряжения, то в качестве примера в нижней части фиг. 2 представлен график изменения касательной компоненты тензора напряжений ${{\sigma }_{{r\theta }}}$ вдоль радиуса трубы при величине малого параметра $\tilde {\delta } = 0.06$ при значении угла θ = = 3π/4. Отметим, что для симметричной постановки задачи ${{\sigma }_{{r\theta }}} = 0$.

Фиг. 2

На основании данных, представленных на фиг. 2, можно сделать вывод, что в исследованном диапазоне изменения малого параметра $\tilde {\delta }$ величина возникающих в результате несоосности толстостенной трубы касательных напряжений ${{\sigma }_{{r\theta }}}$ на два порядка меньше величины тангенциальных напряжений ${{\sigma }_{{\theta \theta }}}$.

6. Анализ погрешности приближенного аналитического решения в соответствии с нормативными требованиями ГОСТ по величине несоосности труб. Проанализируем величину погрешности приближенного аналитического решения (до третьего приближения включительно) с учетом существующих нормативных допусков по ГОСТ [19, 20] на разностенность труб при промышленном их изготовлении. Для этой цели предварительно определим степень соответствия величины малого параметра δ, используемого при построении аналитического решения, величине разностенности толстостенной трубы, определенной ГОСТ.

Согласно ГОСТ [19], разностенность труб “не должна выводить размер труб за предельные отклонения по диаметру и толщине стенки”, при этом предельные отклонения по разностенности толстостенных труб составляют не более 10.0% и –12.5% от толщины трубы, а для ГОСТ ISO 9329-4-2013 [20] – не более ±12.5% от толщины трубы.

В качестве примера соотношения малого параметра и допускаемого предельного отклонения по толщине стенки в соответствии с ГОСТ [19, 20] рассмотрим уже рассмотренную ранее модельную трубу с внутренней границей радиуса a = 115 мм и внешней границей радиуса b = 150 мм, следовательно, толщина стенки трубы η = 35 мм. Используя введенное ранее обозначение для безразмерного параметра $\tilde {\delta } = \delta {\text{/}}a$, определим величину разностенности τ как отношение

(6.1)

$\tau = \frac{{\tilde {\delta }a}}{\eta } \times 100\% $

Для модельной трубы ниже представлена связь между геометрическими характеристиками (т.е. величиной малого параметра $\tilde {\delta }$) и разностенностью трубы τ

$\tilde {\delta } \times {{10}^{2}},\;\% $	1	2	3	4	8
τ, %	3.29	6.57	9.86	13.14	26.29

Из ее анализа следует, что значения $\tilde {\delta }$, превышающие уже 3.8%, недопустимы по ГОСТ. Поэтому для целей практического использования полученного приближенного аналитического решения можно ограничиться значением $\tilde {\delta } = 0.04$, при этом (см. табл. 2) максимальная погрешность для напряжения ${{\sigma }_{{rr}}}$ в нормах (5.1) не превышает 0.5%, а для напряжения ${{\sigma }_{{\theta \theta }}}$ – 1.3%, что является приемлемым результатом для теории ползучести с учетом нелинейности краевой задачи. Однако детальный анализ данных табл. 2 и связи (6.1) свидетельствует, что и для величины безразмерного малого параметра $\tilde {\delta }$ до 0.08, соответствующей приблизительно 26% толщины осесимметричной трубы, также наблюдается хорошая согласованность приближенного аналитического решения с численным. Здесь максимальная погрешность для величины ${{\sigma }_{{rr}}}$ составляет не более 5%, а для величины ${{\sigma }_{{\theta \theta }}}$ – не более 6%.

В связи с изложенным предложенное приближенное аналитическое решение (до третьего приближения по малому параметру) можно использовать для расчета напряженного состояния неосесимметричных толстостенных труб в условиях установившейся ползучести, оставаясь в рамках требований по допустимой величине разностенности по ГОСТ, в прикладных задачах оценки прочности различного назначения продуктопроводов.

7. Заключение. Выполненные комплексные исследования позволяют сделать следующие выводы.

1. Построено приближенное аналитическое решение краевой задачи установившейся ползучести неосесимметричной толстостенной трубы под внутренним давлением методом малого параметра до третьего приближения включительно.

2. Исследована апостериорная (практическая) сходимость полученного аналитического решения в зависимости от количества приближений.

3. Проведен сравнительный анализ приближенного аналитического решения с численным решением на основе метода конечных элементов в широком диапазоне изменения величины малого параметра (отношение величины смещения центров внешнего и внутреннего контуров трубы к ее внутреннему радиусу). Установлено, что погрешность аналитического решения по отношению к численному при величине безразмерного малого параметра 0.04 не превосходит 0.5% для ${{\sigma }_{{rr}}}$ и 1.3% для ${{\sigma }_{{\theta \theta }}}$, а величина σ_rθ по модулю на два порядка (и более) меньше величины ${{\sigma }_{{\theta \theta }}}$.

4. Выполнен анализ возможного применения построенного приближенного решения в прикладных задачах в соответствии с требованиями нормативных отраслевых стандартов на допустимую величину разностенности труб при их изготовлении. Установлено, что максимально допустимая величина разностенности соответствует величине безразмерного малого параметра 0.038. Это позволяет рекомендовать аналитическое решение в расчетную практику в прикладных задачах с максимальной погрешностью для компонент тензора напряжений не более 1.3%.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (16-01-00249_а).

Список литературы

Ивлев Д.Д., Ершов Л.В. Метод возмущений в теории упругопластического тела. М.: Наука, 1978. 208 с.
Кержаев А.П. Упругопластическое состояние двухслойной толстостенной трубы, находящейся под действием внутреннего давления, в случае трансляционной анизотропии // Вестн. ЧГПУ им. И.Я. Яковлева. Сер. Мех. пред. сост. 2013. № 2(16). С. 74–81.
Фоминых С.О. Упругоидеальнопластическое состояние анизотропной трубы // Вестн. ЧГПУ им. И.Я. Яковлева. Сер. Мех. пред. сост. 2010. № 2(8). Ч. 2. С. 623–627.
Фоминых С.О. Упругопластическое состояние толстостенной трубы при взаимодействии различных видов пластической анизотропии // Вестн. ЧГПУ им. И.Я. Яковлева. Сер. Мех. пред. сост. 2011. № 1(9). С. 201–216.
Никитин А.В., Миронов Б.Г. Предельное состояние многослойной анизотропной толстостенной трубы // Вестн. ЧГПУ им. И.Я. Яковлева. Сер. Мех. пред. сост. 2014. № 2(22). С. 58–67.
Кульпина Т.А. Напряженное состояние эксцентричной трубы, находящейся под действием внутреннего давления и сдвигающего усилия // Вестн. ЧГПУ им. И.Я. Яковлева. Сер. Естеств. техн. науки. 2007. № 2(66). С. 51–54.
Кульпина Т.А. Анизотропная эксцентричная труба с учетом сжимаемости материала // Вестн. ЧГПУ им. И.Я. Яковлева. Сер. Естеств. техн. науки. 2010. № 1(65). С. 46–51.
Ковалев А.В., Спорыхин А.Н. О нахождении поля напряжений в эксцентричной трубе, подверженной действию внутреннего давления // Вестн. факульт. прикл. матем. механ. Ворон. гос. ун-т. 1997. № 1. С. 85–90.
Ярдыкова Н.А. Упругопластическое состояние пространства, ослабленного цилиндрической полостью, находящегося под действием давления, крутящих и продольных сдвигающих усилий; Дис. … канд. физ.-мат. наук; 01.02.04. ЧГПУ им. И.Я. Яковлева. Чебоксары, 2007. 73 с.
Broberg H., Westlund R. Creep rupture of specimens with random material properties // Int. J. Solids Struct. 1978. V. 14. № 12. P. 959–970.
Broberg H., Westlund R. Properties of a random creep process // Int. J. Solids Struct.1982. V. 18. № 4. P. 275–283.
Должковой А.А., Попов Н.Н., Радченко В.П. Решение стохастической краевой задачи установившейся ползучести для толстостенной трубы методом малого параметра // ПМТФ. 2006. Т. 47. № 1. С. 161–171.
Попов Н.Н., Исуткина В.Н. Построение аналитического решения двумерной стохастической задачи установившейся ползучести для толстостенной трубы // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2007. № 2(15). С. 57–61.
You L.H., Ou H., Zheng Z.Y. Creep deformations and stresses in thick-walled cylindrical vessels of functionally graded materials subjected to internal pressure // Compos. Struct. 2007. V. 78. P. 285–291.
Радченко В.П., Попов Н.Н. Аналитическое решение стохастической краевой задачи установившейся ползучести для толстостенной трубы // ПММ. 2012. Т. 76. Вып. 6. С. 1023–1031.
Качанов Л.М. Теория ползучести. М.: Физматгиз, 1960. 455 с.
Башкинова Е.В. Решение краевой задачи установившейся ползучести для неосесимметричной толстостенной трубы // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2002. № 16. С. 105–110.
Москалик А.Д. Применение метода возмущений к задаче о несоосной трубе в условиях установившейся ползучести // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2013. № 4(33). С. 76–85.
ГОСТ 8732-78 (СТ СЭВ 1481-78). Трубы стальные бесшовные горячедеформированные. М.: ИПК Изд-во Стандартов, 1998. 10 с.
ГОСТ ISO 9329-4-2013. Трубы стальные бесшовные для работы под давлением. Технические условия. Ч. 4. Аустенитные коррозионно-стойкие стали. М.: Стандартинформ, 2014. 32 с.
Никитенко А.Ф. Ползучесть и длительная прочность металлических материалов. Новосибирск: Ин-т гидродинамики СО РАН–НГАСУ, 1997. 280 с.
Работнов Ю.Н. Ползучесть элементов конструкций. М.: Наука, 1966. 752 с.
Работнов Ю.Н. Механика деформируемого твердого тела. М.: Наука, 1979. 744 с.
Малинин Н.Н. Прикладная теория пластичности и ползучести. М.: Машиностр., 1976. 400 с.
Радченко В.П., Саушкин М.Н. Ползучесть и релаксация остаточных напряжений в упрочненных конструкциях. М.: Машиностр. 1, 2005. 226 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал