1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 83, № 1, 2019

Прикладная математика и механика, 2019, T. 83, № 1, стр. 134-143

ОБОБЩЕНИЕ УРАВНЕНИЯ ИЗГИБА ТОНКОЙ ПЛАСТИНЫ ПОД ДЕЙСТВИЕМ ДАВЛЕНИЯ ГАЗА

М. А. Ильгамов 1, 2, *

1 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

2 Институт механики УФИЦ РАН
Уфа, Россия

* E-mail: ilgamov@anrb.ru

Поступила в редакцию 24.10.2017

Полный текст (PDF)

Аннотация

Определяется поперечная распределенная нагрузка на упругую тонкую пластину, находящуюся в газовой среде. Разные значения давления среды на обе поверхности образуют как перепад давления, так и поперечную неуравновешенную силу, зависящую от среднего давления и кривизны срединной поверхности. Показано, что в общем случае обе эти составляющие поперечной силы должны учитываться. При малом отношении среднего давления к модулю упругости материала пластины и при большой относительной толщине влияние второй составляющей нагрузки мало. При малой относительной толщине пластины, большом отношении среднего давления среды к модулю упругости материала влияние второй составляющей поперечной нагрузки на изгиб становится сравнимым с изгибной жесткостью пластины. Рассматривается линейный изгиб и устойчивость пластины.

Ключевые слова: прямоугольная пластина, изгиб, избыточное давление, граничные условия, критическая сжимающая сила, приведенная жесткость

1. Введение. Основными нагрузками, действующими на конструкции, содержащие тонкостенные пластины и оболочки, являются силы веса, силы вдоль срединной поверхности и давление на их поверхности. Первыми двумя видами нагрузок в основном определяется напряженно-деформированное состояние строительных конструкций. В конструкциях оборудования нефтехимии, энергетики, подводных аппаратов, аэрокосмической техники главными нагрузками может быть давление газов и жидкостей на поверхности пластин и оболочек.

Насколько известно, в литературе отсутствует анализ напряженно-деформированного состояния тонкостенных упругих элементов в зависимости от среднего давления окружающей среды pm = (p1 + p2)/2 (p1, p2 – избыточные давления, действующие на поверхности тела). Влияние этого давления представляется пренебрежимо малым. Начиная с работы Лява [1], где систематизированы и обобщены достижения по теории пластин и оболочек к первой четверти двадцатого столетия, фундаментальных трудов И.Г. Бубнова [2], Б.Г. Галеркина [3] и С.П. Тимошенко [4], в последующих публикациях, вплоть до современной монографической, обзорной, справочной и учебной литературы (например, [5–7]) принималось, что поперечная распределенная сила, действующая на тонкую пластину и оболочку, равна q = p1 – p2 – g, где g – сила веса (фиг. 1).

Фиг. 1

Определенное отношение к данному вопросу имеет анализ устойчивости упругой полосы в частном случае давлений p1 = p2 = pm, в условиях малости влияния собственного веса (g = 0) и осевого сжимающего усилия N = pmh, где h – толщина полосы. Возможно, впервые задача об устойчивости прямой формы упругой балки под давлением окружающей среды была рассмотрена в случае колонны под гидростатическим давлением [8] с привлечением элементарной теории изгиба балки и полосы под всесторонним равномерным давлением [9] с использованием соотношений теории упругости. Было показано, что в случае действия на торцевые кромки такого же давления, что на боковые поверхности полосы, не происходит ее изгиба.

Вопросы устойчивости стержней под всесторонним давлением были предметом изучения в публикациях второй половины прошлого века [10–16] и в последующих работах. Были проведены эксперименты [11]. Наиболее подробно задача была рассмотрена также с применением соотношений теории упругости [14]. Задачи изгиба и устойчивости пластин, контактирующих с жидкостью и газом, рассматривались в основном с применением гипотез Кирхгофа для тонкого тела [8, 12, 13, 15–18].

Было показано [18], что поперечная распределенная нагрузка q определяется не только заданным перепадом давлений, но и самой деформацией пластины. В случае статического цилиндрического изгиба свободно опертой по кромкам пластины длиной L и толщиной h из материала с модулем упругости Е и коэффициентом Пуассона ν

(1.1)
$q = {{p}_{{\text{1}}}} - {{p}_{{\text{2}}}} - g - {{p}_{m}}h({{d}^{{\text{2}}}}w{\text{/}}d{{x}^{{\text{2}}}}),$
а прогиб w определяется приведенной жесткостью D(1 + α), где

(1.2)
$D = \frac{{E{{h}^{3}}}}{{12(1 - {{\nu }^{2}})}}{\text{,}}\quad \alpha = \frac{{{{p}_{m}}h{{L}^{2}}}}{{{{\pi }^{2}}D}}$

Этот результат получен для случая, когда давление рm не действует на торцевые кромки пластины и продольная сжимающая сила N отсутствует. Если сжимающая сила появляется в результате действия давления на кромки пластины, то N = рmh. В этом случае прогиб определяется только собственным весом пластины и ее изгибной жесткостью D. Сила N может задаваться независимо от окружающего давления. Для свободно опертой невесомой пластины, на торцевые кромки которой давление не действует, критическое значение сжимающей силы равно

(1.3)
${{N}_{{cr}}} = {{N}_{E}}(1 + \alpha ),\quad {{N}_{E}} = {{\pi }^{2}}{D \mathord{\left/ {\vphantom {D {{{L}^{2}}}}} \right. \kern-0em} {{{L}^{2}}}},$
где NЕ – эйлерово значение критической силы. Таким образом, давление окружающей среды стабилизирует плоское состояние пластины.

Рассмотрено также изменение давлений, связанное с разными удельными весами γ1, γ2 жидкостей снизу и сверху пластины [17]. Тогда в выражении поперечной нагрузки (1.1) появляется член (γ1– γ2)w, где w – функция прогиба. Учет этого фактора приводит к задаче взаимодействия упругой и гидродинамической неустойчивостей. Изучено взаимодействие статической и динамической неустойчивостей при действии сжимающей силы в срединной поверхности пластины и ускорения, направленного по нормали к контактной поверхности жидкостей с разными плотностями. В зависимости от характера действия внешних сил рассмотрены взаимодействия неустойчивостей Эйлера и Релея, Лаврентьева–Ишлинского и Релея–Тейлора, а также Конинга–Тауба и Рихтмайера–Мешкова.

В отличие от предыдущих исследований [17, 18] здесь рассматривается изгиб прямоугольной пластины с конечным отношением сторон, дан вывод уравнения исходя из соотношений теории упругости, изучено влияние переменности кривизны срединной поверхности и разных граничных условий на значение поперечной распределенной силы, прогиба и критических сил.

2. Постановка задачи. Рассматривается статический линейный изгиб прямоугольной пластины размерами Lх × Lу и толщиной h. Отношение сторон находится в пределах 1/2 < Lх/Lу < 2 [3, 5]. На нижнюю и верхнюю поверхности пластины действуют избыточные давления газов р1 и р2. При изгибе пластины давления р1 и р2 остаются неизменными. Не учитывается влияние плотностей газов на изменение давлений (γ1 = γ2 = 0). Рассматриваются случаи, когда давление не действует на кромки пластины и есть такое действие. В отличие от предыдущих постановок задач [17, 18] здесь направление оси z, нагрузки q и прогиба w (x, у) положительно вверх.

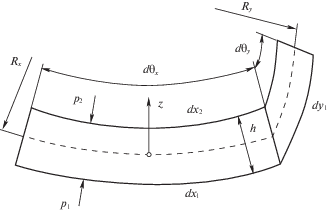
На фиг. 2 представлен элемент срединной поверхности пластины размерами (dx = = Rх dθх) × (dу = Rу dθу). Здесь Rх и Rу – радиусы кривизны, образующейся при изгибе. В соответствии с гипотезами Кирхгофа при изгибе поперечное сечение остается плоским и перпендикулярным к срединной поверхности. Не учитывается также изменение толщины h. Запишем выражения для длины крайних волокон элемента

(2.1)
$d{{x}_{{1,2}}} = ({{R}_{x}} \pm {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2})d{{\theta }_{x}},\quad d{{y}_{{1,2}}} = ({{R}_{y}} \pm {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2})d{{\theta }_{y}}$
Фиг. 2

Поперечная распределенная нагрузка q на пластину определяется по равенству

(2.2)
$qdxdy = {{p}_{1}}d{{x}_{1}}d{{y}_{1}} - {{p}_{2}}d{{x}_{2}}d{{y}_{2}} - \gamma hdxdy$
где γ – удельный вес пластины (собственный вес отнесен к срединной поверхности). Подставляя выражения (2.1) в (2.2) и отбрасывая член (h/2)2(RхRу)–1, малый по сравнению с единицей, и используя равенство суммы главных кривизн лапласиану от функции прогиба w в линейном приближении, получаем

(2.3)
$\begin{gathered} q = {{p}_{e}} + {{p}_{m}}h{{\nabla }^{2}}w;\quad {{p}_{e}} = {{p}_{1}} - {{p}_{2}} - \gamma h, \\ {{p}_{m}} = \frac{{{{p}_{1}} + {{p}_{2}}}}{2},\quad {{\nabla }^{2}} = \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}} \\ \end{gathered} $

Уравнение изгиба пластины [4–6]

$D{{\nabla }^{4}}w + {{N}_{x}}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + {{N}_{y}}\frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} = q,$
где Nx и Ny – сжимающие силы по направлениям осей x и y, с учетом выражения (2.3) приводим к виду

(2.4)
$D{{\nabla }^{4}}w - {{p}_{m}}h{{\nabla }^{2}}w + {{N}_{x}}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + {{N}_{y}}\frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} = {{p}_{e}}$

Выражения (2.1) получены для случая, когда нейтральная поверхность пластины совпадает с ее срединной поверхностью, что не имеет места при действии продольных сил Nx и Ny. Однако учет этого фактора дает незначительную поправку, поэтому она не входит в выражения (2.1) и в линейное уравнение (2.4).

Итак, второй член в левой части уравнения (2.4) появился в результате учета разности площадей выпуклой и вогнутой сторон пластины в соответствии с выражениями (2.1)–(2.3). В этом состоит обобщение классического уравнения изгиба тонкой пластины, основанное на гипотезах Кирхгофа. Первый член в левой части уравнения (2.4), описывающий упругие силы, пропорционален Eh3k4, а второй член – величине pmhk2, где k – волновое число.

3. Вывод обобщенного уравнения изгиба исходя из соотношений теории упругости. Как указывалось во введении, в частном случае Ly = ∞, γ = 0, р1 = р2 = pm уравнение устойчивости полосы под всесторонним давлением (N = рmh) выводилось из линейных [9] и нелинейных [14] соотношений теории упругости, причем сначала определялось обжатие упругого тела, затем рассматривались возмущения этого состояния. При этом не накладывалось ограничение на отношение толщины к длине волны вдоль полосы. Представляется целесообразным вывести обобщенное уравнение изгиба без использования соотношений (2.1) и (2.2) и связи суммы главных кривизн $R_{x}^{{ - 1}}$ и $R_{y}^{{ - 1}}$ с функцией прогиба w(x, y), оставаясь в рамках гипотез Кирхгофа. Для простоты принимаем, что продольные силы в срединной поверхности пластины отсутствуют (Nx = Ny = 0).

В соответствии с гипотезами Кирхгофа деформации εx, εy, γxy выражаются через функции прогиба w формулами [5–7]

(3.1)
${{\varepsilon }_{x}} = - z\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}}\quad (x \leftrightarrow y),\quad {{\gamma }_{{xy}}} = - z\frac{{{{\partial }^{2}}w}}{{\partial x\partial y}}$

Вместо выражения (2.1) можно записать

(3.2)
$d{{x}_{{1,2}}} = (1 + {{\varepsilon }_{x}}( \mp {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}))dx\quad (x \leftrightarrow y)$

Исходя из физических соотношений

${{\sigma }_{x}} = \frac{E}{{1 - {{\nu }^{2}}}}({{\varepsilon }_{x}} + \nu {{\varepsilon }_{y}})\quad (x \leftrightarrow y),\quad {{\tau }_{{xy}}} = \frac{E}{{2(1 + \nu )}}{{\gamma }_{x}}_{y}$
и выражений (3.1) и интегрируя по z первые два уравнения равновесия
$\frac{{\partial {{\sigma }_{x}}}}{{\partial x}} + \frac{{\partial {{\tau }_{{xy}}}}}{{\partial y}} + \frac{{\partial {{\tau }_{{xz}}}}}{{\partial z}} = 0\quad (x \leftrightarrow y)$
получаем [7]

${{\tau }_{{xz}}} = \frac{{E{{z}^{2}}}}{{2(1 - {{\nu }^{2}})}}\frac{\partial }{{\partial x}}{{\nabla }^{2}}w + {{\varphi }_{x}}\quad (x \leftrightarrow y)$

Определяя φx(x, y), φy(x, y) из условий τxz = τyz = 0 (z = ± h/2), имеем

(3.3)
${{\tau }_{{xz}}} = - \frac{{E({{h}^{2}} - 4{{z}^{2}})}}{{8(1 - {{\nu }^{2}})}}\frac{\partial }{{\partial x}}{{\nabla }^{2}}w\quad (x \leftrightarrow y)$

Интегрируя по z третье уравнение равновесия

$\frac{{\partial {{\tau }_{{xz}}}}}{{\partial x}} + \frac{{\partial {{\tau }_{{yz}}}}}{{\partial y}} + \frac{{\partial {{\sigma }_{z}}}}{{\partial z}} = 0$
с учетом равенств (3.3), получаем

(3.4)
${{\sigma }_{z}} = \frac{{Ez({{h}^{2}} - {{4{{z}^{2}}} \mathord{\left/ {\vphantom {{4{{z}^{2}}} 3}} \right. \kern-0em} 3})}}{{8(1 - {{\nu }^{2}})}}{{\nabla }^{4}}w + \psi (x,y)$

Давления р1 и р2 – силы, действующие на единичную площадку поверхностей пластины независимо от ее деформации. А напряжение σz и собственный вес γh определяются в системе координат, деформируемой вместе с пластиной. Иначе говоря, σz по определению приходится на площадку (1 + εх) × (1 + εу), в то время как р1 и р2 определены на площадке 1 × 1. Следовательно, на поверхностях пластины напряжение σz нужно приравнять давлениям р1 и р2, умноженным на соответствующую площадку (1 + εх) × (1 + εу) (отнесем вес γh поровну на обе поверхности), т.е.

(3.5)
${{\sigma }_{z}}( \mp {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}) = \pm {{\gamma h} \mathord{\left/ {\vphantom {{\gamma h} 2}} \right. \kern-0em} 2} - {{p}_{{1,2}}}[1 + {{\varepsilon }_{x}}( \mp {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2})][1 + {{\varepsilon }_{y}}( \mp {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2})]$

Как и выше, не учитывается изменение площадки за счет деформации сдвига γxy.

Подставим в равенства (3.5) выражения (3.1), (3.2) и (3.4). Затем вычитая равенства (3.5) одно от другого и складывая, получаем уравнения

(3.6)
$D{{\nabla }^{4}}w - {{p}_{m}}h{{\nabla }^{2}}w = {{p}_{e}},\quad \psi = - {{p}_{m}} - \left( {{h \mathord{\left/ {\vphantom {h 4}} \right. \kern-0em} 4}} \right)({{p}_{1}} - {{p}_{2}}){{\nabla }^{2}}w$

Первое из них совпадает с уравнением (2.4) (когда Nx = Ny = 0), а второе, согласно равенству (3.4), позволяет получить распределение напряжения σz по толщине пластины. В частности, на срединной поверхности (z = 0)

${{\sigma }_{z}} = - {{p}_{m}} - (h{\text{/2}})({{p}_{1}} - {{p}_{2}}){{\nabla }^{2}}w$

При равенстве давлений на поверхностях (р1 = р2) имеем σz(0) = –рm. В целом второй член мало влияет на распределение напряжения сжатия по толщине пластины. Отметим, что в теории упругости [1, 6, 7] вместо равенств (3.5) принимается σz($ \mp $h/2) = = ±γh/2 – р1, 2. Поэтому в первом уравнении (3.6) отсутствует второй член.

Возникает вопрос, насколько значим последний член в левой части уравнения (2.4) или первого уравнения (3.6) по сравнению с первым членом.

4. Изгиб прямоугольной пластины. Для ответа на поставленный вопрос рассмотрим решение уравнения (2.4) для пластины размерами Lx × Ly, свободно опертой по кромкам, т.е. при условиях

$х = 0,\quad {{L}_{x}}{\text{:}}\;w = {{d}^{{\text{2}}}}w{\text{/}}d{{x}^{{\text{2}}}} = 0;\quad y = 0,\quad {{L}_{y}}{\text{:}}\;w = {{d}^{{\text{2}}}}w{\text{/}}d{{y}^{{\text{2}}}} = 0$

Приближенное решение, удовлетворяющее этим условиям, имеет вид [3–6]

(4.1)
$w = W\sin ax\sin by;\quad a = {\pi \mathord{\left/ {\vphantom {\pi {{{L}_{x}},}}} \right. \kern-0em} {{{L}_{x}},}}\quad b = {\pi \mathord{\left/ {\vphantom {\pi {{{L}_{y}}}}} \right. \kern-0em} {{{L}_{y}}}}$

Подставив выражение (4.1) в уравнение (2.4) и умножив на функцию (4.1), после интегрирования в пределах от 0 до Lx и от 0 до Ly получаем

(4.2)
$W = \frac{{16{{\pi }^{{ - 2}}}{{p}_{e}}}}{{D{{c}^{4}}(1 + \alpha ) - {{N}_{x}}{{a}^{2}} - {{N}_{y}}{{b}^{2}}}}{\text{;}}\quad \alpha = \frac{{{{p}_{m}}h}}{{D{{c}^{2}}}},\quad {{c}^{2}} = {{a}^{2}} + {{b}^{2}}$

Более подробно рассмотрим случай

(4.3)
${{L}_{x}} = {{L}_{y}} = L,\quad {{N}_{x}} = {{N}_{y}} = 0,\quad {{c}^{2}} = 2{{(\pi {\text{/}}L)}^{2}}$

Учет значений D и c по формулам (1.1) и (4.3) и приближение 12π–2(1 – ν2) ≈ 1 приводят к следующему значению безразмерного параметра:

(4.4)
$\alpha \approx ({{p}_{m}}{\text{/}}E){{(L{\text{/}}h)}^{2}}{\text{/}}2$
в два раза меньшему, чем в случае цилиндрического изгиба пластины, когда справедлива оценка (1.1).

Если стальная пластина (E = 2 × 105 МПа) с отношением размеров L/h = 102 находится под избыточным средним давлением pm = 0.4 МПа (4 атм), то по формуле (4.4) α = 10–2. Можно считать, что в этом случае изгиб пластины не зависит от среднего давления окружающей среды. При тех же данных, но отношении L/h = 103, параметр α = 1. Приведенная жесткость D(1 + α) в два раза больше изгибной жесткости D и прогиб в два раза меньше, чем при пренебрежении влиянием среднего давления (при одинаковом перепаде р1– р2). В случае пластикового материала с модулем упругости E = = 104 МПа (L/h = 103) параметр α = 20. Это означает, что основное сопротивление изгибу под действием поперечных сил (например, собственного веса, р1 = р2) оказывает среднее давление окружающей среды.

Итак, при $\alpha \ll {\text{1}}$ изгиб пластины определяется собственной изгибной жесткостью и не зависит от среднего давления окружающей среды. При $\alpha \gg {\text{1}}$ приведенная жесткость и амплитуда прогиба определяются выражениями

(4.5)
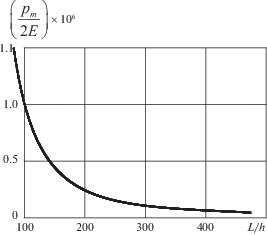
$D(1 + \alpha ) \approx \frac{{{{p}_{m}}h{{L}^{2}}}}{{2{{\pi }^{2}}}},\quad W = \frac{{8{{p}_{e}}{{L}^{2}}}}{{{{\pi }^{4}}{{p}_{m}}h}}$

Отношение прогиба в предельном случае (4.5) к прогибу в случае (4.2)–(4.4), когда в последнем принимаем $\alpha \ll {\text{1}}$, приближенно равно 2(E/pm)(h/L)2. При промежуточных значениях параметра α сопротивление изгибу пластины оказывает и ее собственная изгибная жесткость, и среднее давление окружающей среды. Фиг. 3 построена по формуле (4.4) для α = 10–2. При значениях параметров, дающих область выше кривой, влияние среднего давления pm на изгиб нужно учитывать.

Фиг. 3

Линейное решение (4.2) неограниченно возрастает при приближении знаменателя к нулю. Из этого условия определяется критическая комбинация сжимающих сил

(4.6)
${{({{N}_{x}}{{а }^{{\text{2}}}} + {{N}_{y}}{{b}^{{\text{2}}}})}_{{{\text{cr}}}}} = D{{c}^{{\text{4}}}} + {{p}_{m}}h{{c}^{{\text{2}}}} = D{{c}^{{\text{4}}}}({\text{1}} + \alpha )$

Видно, что для пластины с заданными размерами и свойствами материала эта комбинация сил возрастает с увеличением среднего избыточного давления.

Эти результаты получены в предположении, что давление окружающей среды не действует на кромки пластины. Рассмотрим случай такого действия на кромки при условии равенства давлений p1 = p2 = pm и образования сжимающих сил Nx = Ny = N за счет давления pm. Тогда N = pmh, pe = – γh, и согласно выражению (4.2) прогиб не зависит от давления pm и равен

(4.7)
$W = - 16{{\pi }^{{ - 2}}}\gamma h{\text{/}}({{D}^{2}}{{c}^{4}})$

Имеет место устойчивость изогнутой под собственным весом пластины по отношению к всестороннему давлению. В случае невесомой пластины (γ = 0) из равенства (4.7) следует W ≡ 0, т.е. результат, полученный в предыдущих работах для балки под всесторонним давлением.

5. Зависимость решения от граничных условий. Согласно выражению (2.3), поперечная сила q зависит также от кривизны, образующейся при изгибе. В случае свободного опирания краев пластины знак кривизны не меняется по всей площади, поэтому вклад последнего члена выражения (2.3) в решение является наибольшим. Для оценки этого вклада в случае изменения знака кривизны по площади рассмотрим задачу при условиях защемления краев. Для простоты оценку проведем для случая цилиндрического изгиба под действием давлений p1 и p2 на поверхности пластины и сжимающей силы Nx = N (Nу = 0). Условиям

$х = 0,L\;{\text{:}}\quad w = \partial w{\text{/}}\partial x = 0$
удовлетворяет функция
(5.1)
$w = W{{\sin }^{2}}ax;\quad a = \pi {\text{/}}L$
приближенно описывающая прогиб [4–6]. Из уравнения (2.4) и решения (5.1) методом Бубнова–Галёркина получаем для амплитуды

(5.2)
$W = \frac{{{{\pi }^{{ - 5}}}{{p}_{e}}{{L}^{4}}}}{{D(1 + \alpha - {N \mathord{\left/ {\vphantom {N {{{N}_{E}}}}} \right. \kern-0em} {{{N}_{E}}}})}};\quad \alpha \approx \frac{{{{p}_{m}}}}{E}{{\left( {\frac{L}{{2h}}} \right)}^{2}},\quad {{N}_{E}} = \frac{{4{{\pi }^{2}}D}}{{{{L}^{2}}}}$

Отметим, что в случае свободного опирания краев пластины

$х = 0,L{\text{:}}\quad w = {{\partial }^{{\text{2}}}}w{\text{/}}\partial {{x}^{{\text{2}}}} = 0$
принимая приближенно w = Wsinax, получаем

(5.3)
$W = \frac{{4{{\pi }^{{ - 5}}}{{p}_{e}}{{L}^{4}}}}{{D(1 + \alpha - {N \mathord{\left/ {\vphantom {N {{{N}_{E}}}}} \right. \kern-0em} {{{N}_{E}}}})}};\quad \alpha \approx \frac{{{{p}_{m}}}}{E}{{\left( {\frac{L}{h}} \right)}^{2}},\quad {{N}_{E}} = \frac{{{{\pi }^{2}}D}}{{{{L}^{2}}}}$

Здесь формула для α совпадает с представленными формулами (1.2), если в них принять 12π–2(1 – ν2) ≈ 1. Из выражений (5.2) и (5.3) следует, что параметр α в случае цилиндрического изгиба пластины с защемленными краями в четыре раз меньше, чем в случае ее свободного опирания. Такое уменьшение влияния среднего давления в первом случае объясняется тем, что в центральной части пролета на длине L/2 кривизна положительна, а на прилегающих к опорам участках длиной L/4 – отрицательна (при pe < 0).

Как видно из выражений (5.2) и (5.3), можно судить о продольно-поперечном изгибе как пластины с приведенной жесткостью D(1 + α) под нагрузками pe и N, так и пластины с жесткостью D под поперечной нагрузкой pe и приведенной сжимающей силой N – αNЕ = N – pmh, причем критическое значение сжимающей силы

(5.4)
${{N}_{{{\text{cr}}}}} = {{N}_{E}}({\text{1}} + \alpha )$
выражается через значения NE и α, различающиеся в рассматриваемых случаях в четыре раза.

Если сжимающее усилие N обусловлено действием давления p1 = p2 = pm на кромки пластины, то N = pmh. В обоих случаях закрепления краев пластины в решениях (5.2) и (5.3) исчезает зависимость прогиба от всестороннего давления (в выражениях для NE необходимо принять приближенно 12π–2(1 – ν2) за единицу, либо для α взять точное выражение). Прогиб за счет собственного веса сохраняется неизменным при любом давлении окружающей среды. Если начальное состояние пластины плоское, например, в результате отсутствия гравитационного ускорения, то сохраняется плоская форма пластины.

6. Заключение. Влияние на изгиб среднего избыточного давления pm = (p1 + p2)/2 на поверхности тонкой пластины с изолированными от давления кромками определяется безразмерным параметром α ≈ (κpm/E)(L/h)2, где Е – модуль упругости материала, h и L – толщина и наименьший размер между опорными кромками, κ – коэффициент, зависящий от граничных условий и отношения размеров прямоугольной пластины (при свободном опирании удлиненной пластины κ = 1, квадратной пластины κ = 1/2, при защемлении удлиненной пластины κ = 1/4).

Среднее давление pm окружающей среды приводит к увеличению приведенной изгибной жесткости D(1 + α), где D – собственная изгибная жесткость. Если пластина изогнута, например, под действием только собственного веса (q = –γh, p1 = p2), то при подаче давления pm прогиб ее уменьшается ввиду увеличения приведенной жесткости на величину 1 + α. Физически это объясняется тем, что площадь выпуклой поверхности пластины больше площади ее вогнутой поверхности, что приводит к появлению распределенной силы, которая стремится уменьшить прогиб. Эта сила пропорциональна образующейся при изгибе кривизне срединной поверхности.

При $\alpha \ll {\text{1}}$ справедлива классическая теория изгиба тонких пластин, основанная на гипотезах Кирхгофа. В ней перепадом давлений и собственным весом определяется поперечная распределенная нагрузка (q = p1 – p2 – γh).

При $\alpha \gg {\text{1}}$ решение не зависит от модуля упругости материала (например, приведенная жесткость квадратной пластины равна pmhL2/(2π2)). Это объясняется тем, что собственная жесткость D уменьшается пропорционально кубу толщины, а фактор среднего давления – первой степени толщины. В результате этот предельный случай реализуется в случае тонких пластин и пленок из материалов с малым модулем упругости и при большом среднем давлении окружающих сред. Например, равновесие микро- и нанопленок под собственным весом в газовой среде может быть удовлетворительно определено только с учетом фактора среднего давления.

Критические значения сжимающих сил Ncr в срединной поверхности пластины выше по сравнению с их классическими значениями NЕ ввиду большей приведенной жесткости за счет среднего давления. Например, при сжатии только в одном направлении свободно опертой по всем кромкам квадратной пластины Ncr = NЕ (1 + α), где в выражении для α коэффициент κ = 1/2.

Если давление окружающей среды действует также на опорные кромки пластины, то ее равновесие отличается от изложенного выше. В случае, когда давления на нижнюю и верхнюю поверхности равны (p1 = p2 = pm) и сжимающие силы в срединной поверхности обусловлены их действием на кромки (Nх = Nу = pmh), изгиб пластины не зависит от давления окружающей среды. По отношению к действию всестороннего давления имеет место абсолютная устойчивость изогнутого состояния пластины под действием собственного веса и упругих сил в ней. В частном случае отсутствия собственного веса равновесное состояние является ненапряженным.

Приведенные оценки влияния среднего давления окружающей среды на изгиб указывают на необходимость внесения соответствующих добавлений в теорию изгиба и устойчивости формы тонких пластин и оболочек.

Работа выполнена в рамках государственного задания (проекты № 0120-1359-375, № 0246-2019-0088).

Список литературы

  1. Love A. A Treatise on the Mathematical Theory of Elasticity. Cambridge: Univ. Press, 1927. 643 р. = Ляв А. Математическая теория упругости. М.; Л.: ОНТИ, 1935. 674 с.

  2. Бубнов И.Г. Труды по теории пластин. М.: Гостехиздат, 1953. 423 с.

  3. Галеркин Б.Г. Упругие тонкие плиты. Соб. сочинений. Т. 2. М.: Изд. АН СССР, 1953. 550 с.

  4. Timoshenko S. Theory of Plates and Shells. N.Y.: McGraw–Hill, 1940. 399 р. = Тимошенко С.П. Пластины и оболочки. М.; Л.: Гостехиздат, 1948. 460 с.

  5. Вольмир А.С. Устойчивость упругих систем. М.: Физматгиз, 1963. 880 с.

  6. Прочность, устойчивость, колебания. Справочник. Науч. ред. И.А. Биргер и Я.Г. Пановко. М.: Машиностр., 1968. Т. 1. 831 с.

  7. Безухов Н.И. Теория упругости и пластичности. М.: Высшая шк., 1968. 512 с.

  8. Handelman G.H. Buckling under locally hydrostatic pressure // J. Appl. Mech. 1946. V. 13. P. 198–200.

  9. Ишлинский А.Ю. Исследование устойчивости упругих систем с точки зрения математической теории упругости // Укр. матем. ж. 1954. Т. 6. № 2. С. 140–146.

  10. Nagel F.E. Column instability of pressurized tubes // J. Aerospace Sci. 1956. V. 23. P. 608–609.

  11. Mills B.D., Jr. The fluid column // Am. J. Phys. 1960. V. 28. P. 353–356.

  12. Link H. Über den geraden Druckstab in Flüssigkeit // Ing.-Archiv. 1962. B. 31. P. 149–167.

  13. Peterson J.P. Axially loaded column subjected to lateral pressure // AIAA J. 1963. V. 1. № 6. P. 1458–1459.

  14. Kerr A.D., Tang S. The of lateral hydrostatic pressure on the instability of elastic solids, particularly beams and plates // J. Appl. Mech. 1966. V. 33. P. 617–622.

  15. Newland D.E. Research note: Deflection equation for the buckling of an elastic column subjected to surface pressure // J. Mech. Eng. Sci. 1973. V. 15. № 1. P. 73–75.

  16. Ilgamov M.A. Static Problems of Hydroelasticity M.: Fizmatlit. 1998. 208 p.

  17. Ильгамов М.А. Взаимодействие неустойчивостей в гидроупругой системе // ПММ. 2016. Т. 80. Вып. 5. С. 566–579.

  18. Ильгамов М.А. Влияние давления окружающей среды на изгиб тонкой пластины и пленки // ДАН. 2017. Т. 476. № 4. С. 402–405.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал