Прикладная математика и механика, 2019, T. 83, № 2, стр. 303-313
НЕЛИНЕЙНАЯ МОДЕЛЬ ДЕФОРМИРОВАНИЯ КРИСТАЛЛИЧЕСКИХ СРЕД, ДОПУСКАЮЩИХ МАРТЕНСИТНЫЕ ПРЕВРАЩЕНИЯ: ПЛОСКАЯ ДЕФОРМАЦИЯ
Э. Л. Аэро, А. Н. Булыгин *, Ю. В. Павлов
Институт проблем машиноведения РАН
Санкт-Петербург, Россия
* E-mail: bulygin_an@mail.ru
Поступила в редакцию 12.05.2017
После доработки 13.10.2017
Принята к публикации 27.12.2017
Аннотация
Разрабатываются математические методы решения уравнений статики плоской нелинейной деформации кристаллических сред со сложной решеткой, допускающих мартенситные превращения. Уравнения статики, составляющие систему четырех связанных нелинейных уравнений, сводятся к системе отдельных уравнений. Вектор макросмещений ищется в форме Папковича–Нейбера. Вектор микросмещений находится из уравнения синус-Гордона с переменным коэффициентом (амплитудой) перед синусом и уравнения Пуассона. Для случая постоянной амплитуды найден класс двояко-периодических решений, которые выражаются через эллиптические функции Якоби. Показано, что нелинейная теория приводит к набору решений, описывающих фрагментацию кристаллической среды, появление дефектов структуры разного типа, фазовые превращения и другие особенности деформирования, которые реализуются под действием интенсивных силовых нагрузок и не описываются классической механикой сплошной среды.
Для решения современных проблем получения и изучения новых материалов необходимы аналитические модели, которые могли бы позволять прогнозирование эксплуатационных и прочностных свойств получаемых материалов. Классическая континуальная модель уже не применима к решению новых проблем в области наномасштабов. Была предложена [1, 2] нелинейная модель деформирования кристаллических сред со сложной решеткой, позволяющая описать специфические процессы деформирования, реализуемые в современных технологиях получения новых материалов. Было показано [3], что нелинейная модель может быть использована для описания мартенситных превращений. В последние годы успешно разрабатывается механика многоуровневого деформирования и фазовых переходов, в том числе и мартенситных превращений [4, 5].
1. Нелинейная модель деформирования кристаллических сред со сложной решеткой. Ограничимся рассмотрением двух подрешеток, которые совмещаются сдвигом на постоянный структурный вектор ${\mathbf{u}}$. Введем смещение ${\mathbf{U}}$ центра инерции пары атомов элементарной решетки и относительного их смещения ${\mathbf{u}}$ внутри ячейки следующим образом [6]:
(1.1)
${\mathbf{U}} = \frac{{{{m}_{1}}{{{\mathbf{v}}}_{1}} + {{m}_{2}}{{{\mathbf{v}}}_{2}}}}{{{{m}_{1}} + {{m}_{2}}}},\quad {\mathbf{u}} = {{{\mathbf{v}}}_{1}} - {{{\mathbf{v}}}_{2}}$Уравнения движения, определяющие векторы ${\mathbf{U}}(t,x,y,z)$ (акустическая мода) и ${\mathbf{u}}(t,x,y,z)$ (оптическая мода), получим из вариационного принципа
(1.2)
$J = \int\limits_0^t \int\limits_0^\tau L({{u}_{i}},{{\dot {u}}_{i}},{{u}_{{i,k}}},{{\dot {U}}_{i}},{{U}_{{i,k}}}){\kern 1pt} dtd\tau $Функция Лагранжа $L$ представляет собой разность между плотностью кинетической энергии $Q$ и плотностью энергии деформирования $D$:
(1.4)
$Q = \frac{\rho }{2}{{\dot {U}}_{i}}{{\dot {U}}_{i}} + \frac{\mu }{2}{{\dot {u}}_{i}}{{\dot {u}}_{i}};\quad D = \frac{1}{2}{{\lambda }_{{ilmn}}}{{e}_{{il}}}{{e}_{{mn}}} + \frac{1}{2}{{k}_{{ilmn}}}{{\varepsilon }_{{il}}}{{\varepsilon }_{{mn}}} + \frac{1}{2}{{C}_{{ilmn}}}{{e}_{{il}}}{{\varepsilon }_{{mn}}} + R\Phi ({{u}_{s}})$Запятая в нижнем индексе означает частную производную по координате, индекс которой указан после запятой, а точка сверху означает частную производную по времени. Далее $\rho $ – средняя плотность массы атомов, $\mu $ – приведенная плотность пары атомов:
(1.5)
$\rho = \frac{{{{m}_{1}} + {{m}_{2}}}}{{2V}},\quad \mu = \frac{{{{m}_{1}}{{m}_{2}}}}{{({{m}_{1}} + {{m}_{2}})V}}$(1.6)
${{e}_{{il}}} = \frac{1}{2}({{U}_{{i,l}}} + {{U}_{{l,i}}}),\quad {{\varepsilon }_{{il}}} = \frac{1}{2}({{u}_{{i,l}}} + {{u}_{{l,i}}})$Последнее слагаемое во втором выражении (1.4) отвечает энергии жесткого сдвига подрешеток и позволяет реализовать переходы через точки структурной неустойчивости решетки с образованием, в частности, новых фаз типа мартенситных. Аргумент функции $\Phi $ равен скалярному произведению вектора ${\mathbf{B}}$ обратной решетки [7] на вектор ${\mathbf{u}}$:
Для кристаллов кубической, ромбической и тетрагональной систем векторы ${{{\mathbf{a}}}_{1}}$, ${{{\mathbf{a}}}_{2}}$ и ${{{\mathbf{a}}}_{3}}$ элементарной решетки взаимно ортогональны. Для этих систем взаимно ортогональными будут и векторы обратной решетки. Для кристаллов кубической системы размеры ячейки ${{b}_{1}} = {{b}_{2}} = {{b}_{3}} = b$, а
Определение (1.8) называют физическим, в отличие от кристаллографического определения
которое принимается в настоящей работе, и следовательно, для кристаллов кубической системыПо физическому смыслу функция $\Phi ({{u}_{s}})$ должна быть четной и периодической. В общем случае (при выполнении условий Дирихле) ее можно разложить в ряд Фурье
Здесь учтено, что энергия взаимодействия подрешеток равна нулю, когда ${{u}_{s}} = 0$. В пионерской работе [8] и большинстве современных работ ([9, 10] и др.) принимается, что
Множитель перед функцией $\Phi ({{u}_{s}})$
представляет собой эффективный межатомный барьер – энергию активации связей. Здесь $p$ – половина энергии активации жесткого сдвига решеток, а ${{s}_{{il}}}$ – тензор нелинейной механострикции. Выбор коэффициента $R$ – весьма чувствительный инструмент управления микроструктурой и структурой решетки с помощью макроскопических полей деформаций и напряжений.Отметим, что все материальные тензоры в выражении для плотности энергии деформирования $D$, имеют четный ранг. Это значит, что рассматриваются кристаллические среды, обладающие центром симметрии, для которых тензор нечетного ранга обращается в нуль. Градиентные слагаемые в выражении для плотности энергии $D$ обеспечивают ее инвариантность при микротрансляциях, а выбор функции $\Phi ({{u}_{s}})$ обеспечивает инвариантность $D$ к взаимным трансляциям подрешеток в некотором заданном и фиксированном направлении. Смещение подрешеток на период (или целое число периодов) означает переход подрешеток в новое, но кристаллографически эквивалентное структурное состояние. При таком переходе происходит переключение связей и изменение ближайших соседей каждого атома, т.е. изменение локальной топологии.
Уравнения движения, определяющие векторы ${\mathbf{U}}(t,x,y,z)$ и ${\mathbf{u}}(t,x,y,z)$, находим из вариационного принципа. Их компоненты имеют вид
(1.14)
$\rho {{\ddot {U}}_{i}} = {{\sigma }_{{il,l}}};\quad {{\sigma }_{{il}}} = {{\lambda }_{{ilmn}}}{{e}_{{mn}}} + {{C}_{{ilmn}}}{{\varepsilon }_{{mn}}} - {{s}_{{il}}}\Phi ({{u}_{s}})$(1.15)
$\mu {{\ddot {u}}_{i}} = {{\chi }_{{il,l}}} - R\frac{{\partial \Phi ({{u}_{s}})}}{{\partial {{u}_{i}}}};\quad {{\chi }_{{il}}} = {{k}_{{ilmn}}}{{\varepsilon }_{{mn}}} + {{C}_{{ilmn}}}{{e}_{{mn}}}$Выражение для тензора напряжений ${{\sigma }_{{il}}}$ отличается от классического двумя последними слагаемыми. Первые два слагаемых – упругая составляющая сдвигового напряжения, последнее – неупругая составляющая. Если в плоскости с нормалью n построить вектор силы, соответствующий тензору ${{\sigma }_{{ik}}}$, то этот вектор с компонентами Fi = = ${{s}_{{ik}}}{{n}_{k}}\Phi ({{u}_{s}})$ будет принципиально отличаться от первых двух: он квадратично зависит от компонент вектора микросмещений ${\mathbf{u}}$, а его направление не зависит от направления ${\mathbf{u}}$. Вектор силы с компонентами ${{F}_{i}} = {{s}_{{ik}}}{{n}_{k}}\Phi ({{u}_{s}})$ можно принять за силу трения. Эти компоненты малы при малых микросмещениях и достигают предельно высокого значения $2{{s}_{{il}}}$, когда ${{u}_{s}} = (2n + 1){\pi }$ (предполагается, что функция $\Phi ({{u}_{s}})$ дается формулой (1.12)), т.е. при сдвиге атомов из потенциальных ям на вершины межатомных потенциальных барьеров. Очевидно, что значения компонент материального тензора ${{s}_{{il}}}$ – пределы неупругих напряжений, описывающие потери устойчивости решетки. Далее возможны пластические деформации, фазовые переходы типа аустенитно-мартенситных и другие бифуркационные процессы. Они определяются полем микросмещений ${\mathbf{u}}$, которое является решением уравнений (1.15).
Тензоры ${{\lambda }_{{ilmn}}}$, ${{k}_{{ilmn}}}$, ${{C}_{{ilmn}}}$ симметричны к перестановке пар индексов и индексов пары между собой. Далее, ради определенности, ограничимся рассмотрением кристаллических сред кубической симметрии (КСКС). Для них эти материальные тензоры имеют независимыми лишь три компоненты. Пусть это будут
В дальнейшем от тензорных обозначений перейдем к более простым матричным обозначениям
(1.16)
${{\chi }_{{il}}} = \left\{ {\begin{array}{*{20}{l}} {({{k}_{{11}}} - {{k}_{{12}}}){{\varepsilon }_{{il}}} + ({{C}_{{11}}} - {{C}_{{12}}}){{e}_{{il}}} + ({{k}_{{12}}}\varepsilon + {{C}_{{12}}}e){{\delta }_{{il}}},\quad i = l} \\ {2{{k}_{{44}}}{{\varepsilon }_{{il}}} + 2{{C}_{{44}}}{{e}_{{il}}},\quad i \ne l} \end{array}} \right.$Анизотропию КСКС характеризуют величины
(1.17)
${{a}_{1}} = \frac{{2{{\lambda }_{{44}}}}}{{{{\lambda }_{{11}}} - {{\lambda }_{{12}}}}},\quad {{a}_{2}} = \frac{{2{{k}_{{44}}}}}{{{{k}_{{11}}} - {{k}_{{12}}}}},\quad {{a}_{3}} = \frac{{2{{C}_{{44}}}}}{{{{C}_{{11}}} - {{C}_{{12}}}}}$2. Плоская деформация. Уравнения статики и их общее решение. Деформированное состояние будем называть статически плоским, параллельным оси ${{x}_{3}}$, если
(2.1)
$\begin{gathered} {{U}_{x}} = {{U}_{x}}(x,y),\quad {{U}_{y}} = {{U}_{y}}(x,y),\quad {{U}_{z}} = 0 \\ {{u}_{x}} = {{u}_{x}}(x,y),\quad {{u}_{y}} = {{u}_{y}}(x,y),\quad {{u}_{z}} = 0 \\ \end{gathered} $Тогда уравнения статики в напряжениях, описывающие плоскую деформацию в рамках нелинейной модели, примут вид
(2.2)
${{\sigma }_{{xx,x}}} + {{\sigma }_{{xy,y}}} = 0,\quad {{\sigma }_{{yx,x}}} + {{\sigma }_{{yy,y}}} = 0$(2.3)
${{\chi }_{{xx,x}}} + {{\chi }_{{xy,y}}} - \frac{b}{2}(p - s\operatorname{div} {\mathbf{U}})\sin {{u}_{s}} = 0,\quad {{\chi }_{{yx,x}}} + {{\chi }_{{yy,y}}} - \frac{b}{2}(p - s\operatorname{div} {\mathbf{U}})\sin {{u}_{s}} = 0$Для КСКС
(2.4)
$\begin{gathered} {{\sigma }_{{xx}}} = {{\lambda }_{{11}}}{{e}_{{xx}}} + {{\lambda }_{{12}}}{{e}_{{yy}}} + {{C}_{{11}}}{{\varepsilon }_{{xx}}} + {{C}_{{12}}}{{\varepsilon }_{{yy}}} - s\Phi ({{u}_{s}}),\quad {{\sigma }_{{xy}}} = 2{{\lambda }_{{44}}}{{e}_{{xy}}} + 2{{C}_{{44}}}{{\varepsilon }_{{xy}}}\quad (x \leftrightarrow y) \\ {{\sigma }_{{zz}}} = {{\lambda }_{{12}}}({{e}_{{xx}}} + {{e}_{{yy}}}) + {{C}_{{12}}}({{\varepsilon }_{{xx}}} + {{\varepsilon }_{{yy}}}) - s\Phi ({{u}_{s}}),\quad {{\sigma }_{{xz}}} = {{\sigma }_{{yz}}} = 0 \\ \end{gathered} $В уравнениях (2.3) и соотношениях (2.4) учтено, что для сред кубической системы ${{s}_{{ik}}} = s{{\delta }_{{ik}}}$. Для этих сред
(2.5)
$\begin{gathered} {{\chi }_{{xx}}} = {{k}_{{11}}}{{\varepsilon }_{{xx}}} + {{k}_{{12}}}{{\varepsilon }_{{yy}}} + {{C}_{{11}}}{{e}_{{xx}}} + {{C}_{{12}}}{{e}_{{yy}}},\quad {{\chi }_{{xy}}} = 2{{k}_{{44}}}{{\varepsilon }_{{xy}}} + 2{{C}_{{44}}}{{e}_{{xy}}},\quad (x \leftrightarrow y) \\ {{\chi }_{{zz}}} = {{k}_{{12}}}({{\varepsilon }_{{xx}}} + {{\varepsilon }_{{yy}}}) + {{C}_{{12}}}({{e}_{{xx}}} + {{e}_{{yy}}}),\quad {{\chi }_{{xz}}} = {{\chi }_{{yz}}} = 0 \\ \end{gathered} $Уравнения статики в перемещениях получаются при подстановке выражений (2.4) и (2.5) соответственно в уравнения (2.2) и (2.3):
(2.6)
${{\lambda }_{{44}}}\Delta {\mathbf{U}} + ({{\lambda }_{{12}}} + {{\lambda }_{{44}}})\operatorname{grad} \operatorname{div} {\mathbf{U}} + {{C}_{{44}}}\Delta {\mathbf{u}} + ({{C}_{{12}}} + {{C}_{{44}}})\operatorname{grad} \operatorname{div} {\mathbf{u}} - s\operatorname{grad} \Phi {\text{(}}{{u}_{s}}) = 0$(2.7)
$\begin{gathered} {{k}_{{44}}}\Delta {\mathbf{u}} + ({{k}_{{12}}} + {{k}_{{44}}})\operatorname{grad} \operatorname{div} {\mathbf{u}} + {{C}_{{44}}}\Delta {\mathbf{U}} + ({{C}_{{12}}} + {{C}_{{44}}})\operatorname{grad} \operatorname{div} {\mathbf{U}} - \\ - \;{\mathbf{B}}(p - s\operatorname{div} {\mathbf{U}})\sin {{u}_{s}} = 0 \\ \end{gathered} $Здесь
Уравнения статики (2.6) и (2.7) – это система четырех связанных нелинейных уравнений. Вектор макросмещений ${\mathbf{U}}$ будем искать в виде Папковича–Нейбера
Здесь a, χ и ${\mathbf{A}}$ – произвольная постоянная, скалярная функция $\chi (x,y)$ и векторная функция ${\mathbf{A}}(x,y)$. Если выражение (2.8) подставить в уравнение (2.6), то можно убедиться, что оно будет решено, если векторы ${\mathbf{A}}$ и ${\mathbf{u}}$ удовлетворяют уравнению
а скалярная функция $\chi $ – решение уравнения Пуассона(2.10)
$\Delta \chi = \frac{1}{{{{\lambda }_{{12}}} + 2{{\lambda }_{{44}}}}}\left[ {s\Phi ({{u}_{s}}) - a({{\lambda }_{{12}}} + {{\lambda }_{{44}}})\operatorname{div} {\mathbf{A}} - ({{C}_{{12}}} + {{C}_{{44}}})\operatorname{div} {\mathbf{u}}} \right]$Если выражение (2.8) подставить в уравнение (2.7), то его можно привести к следующему:
(2.11)
$\begin{gathered} {{k}_{{44}}}\Delta {\mathbf{u}} + a{{C}_{{44}}}\Delta {\mathbf{A}} + C\operatorname{grad} \Phi ({{u}_{s}}) - {\mathbf{B}}(p - s\operatorname{div} {\mathbf{U}})\sin {{u}_{s}} + \\ + \;\operatorname{grad} \{ a[{{C}_{{12}}} + {{C}_{{44}}} - C({{\lambda }_{{12}}} + {{\lambda }_{{44}}})]\operatorname{div} {\mathbf{A}} + [{{k}_{{12}}} + {{k}_{{44}}} - C({{C}_{{12}}} + {{C}_{{44}}})]\operatorname{div} {\mathbf{u}}\} = 0 \\ C = \frac{{{{C}_{{12}}} + 2{{C}_{{44}}}}}{{{{\lambda }_{{12}}} + 2{{\lambda }_{{44}}}}} \\ \end{gathered} $Из уравнения (2.11) видно, что уравнение (2.7) будет решено, если принять, что
(2.12)
$\begin{gathered} \operatorname{div} {\mathbf{A}} = \operatorname{div} {\mathbf{u}},\quad a = \frac{{{{k}_{{12}}} + {{k}_{{44}}} - C({{C}_{{12}}} + {{C}_{{44}}})}}{{({{\lambda }_{{12}}} + {{\lambda }_{{44}}})C - ({{C}_{{12}}} + {{C}_{{44}}})}} \\ {{k}_{{44}}}\Delta {\mathbf{u}} + a{{C}_{{44}}}\Delta {\mathbf{A}} + sC\operatorname{grad} \Phi ({{u}_{s}}) - {\mathbf{B}}(p - s\operatorname{div} {\mathbf{U}})\sin {{u}_{s}} = 0 \\ \end{gathered} $Из последнего уравнения (2.12) с помощью уравнения (2.9) можно исключить $\Delta {\mathbf{A}}$ и получить отдельные уравнения для нахождения вектора микросмещений ${\mathbf{u}}$
(2.13)
$K\Delta {{u}_{x}} + sC\frac{{{{b}^{2}}}}{2}\sin {{u}_{s}}\frac{{\partial {{u}_{s}}}}{{\partial x}} - \frac{b}{2}(p - s\operatorname{div} {\mathbf{U}})\sin {{u}_{s}} = 0\quad (x \leftrightarrow y);\quad K = \frac{{{{b}^{2}}}}{2}\left( {{{k}_{{44}}} - \frac{{C_{{44}}^{2}}}{{{{\lambda }_{{44}}}}}} \right)$(2.14)
$\begin{gathered} K\Delta {{u}_{s}} = P\sin {{u}_{s}} \\ P = p - \frac{s}{{{{\lambda }_{{12}}} + 2{{\lambda }_{{44}}}}}[\operatorname{div} {{{\mathbf{u}}}_{ + }} + s\Phi ({{u}_{s}})],\quad {{{\mathbf{u}}}_{ + }} = (a{{\lambda }_{{44}}} - {{C}_{{12}}} - {{C}_{{44}}}){\mathbf{u}} + \frac{{{{b}^{2}}}}{2}({{C}_{{12}}} + 2{{C}_{{44}}}){\mathbf{B}}{{u}_{s}} \\ \end{gathered} $Для определения вектора микросмещений ${\mathbf{u}}$ к уравнению (2.14) нужно добавить уравнения для нахождения компоненты ${{u}_{x}}$ или ${{u}_{y}}$. Они имеют вид
(2.15)
$\Delta \left( {{{u}_{x}} - \frac{b}{2}{{u}_{s}}} \right) = f,\quad \Delta \left( {{{u}_{y}} - \frac{b}{2}{{u}_{s}}} \right) = - f;\quad f = \lambda \left( {\frac{{\partial {{u}_{s}}}}{{\partial y}} - \frac{{\partial {{u}_{s}}}}{{\partial x}}} \right)\sin {{u}_{s}},\quad \lambda = \frac{{sC{{b}^{2}}}}{{4K}}$Таким образом, реализация нелинейной модели сведена к решению уравнения (2.14). Если функция ${{u}_{s}}$ найдена, то компонента ${{u}_{x}}$ или ${{u}_{y}}$, как видно из соотношений (2.15), определяется из решения уравнения Пуассона с известной функцией $f$. К решению уравнения Пуассона приводят и задачи нахождения скалярной функции $\chi $:
(2.16)
$\Delta \chi = \frac{1}{{{{\lambda }_{{12}}} + 2{{\lambda }_{{44}}}}}\{ s\Phi ({{u}_{s}}) - [({{C}_{{12}}} + {{C}_{{44}}}) + a({{\lambda }_{{12}}} + {{\lambda }_{{44}}})]\operatorname{div} {\mathbf{u}}\} $3. Решения уравнений оптической моды и соответствующие им структуры микродеформаций. В литературе отсутствуют аналитические методы решения уравнения СГ с переменной амплитудой. Были построены [14] функционально-инвариантные решения (2 + 1)- и (3 + 1)-мерных уравнений СГ для частного вида амплитуд. Уравнение (2.14) можно привести к хорошо изученным случаям постоянной амплитуды [15–18], если наложить некоторые ограничения на модель или на поле микродеформаций. Так, если не учитывать зависимость потенциала взаимодействия подрешеток от деформации среды, т.е. принять $s = 0$, то уравнение (2.14) становится уравнением СГ с постоянными коэффициентами $K$ и $p$:
Оно же получится, если допустить, что
В случае, когда поле микросмещений удовлетворяет уравнению
уравнение (2.14) станет двойным уравнением СГ с постоянными ${{P}_{1}}$ и ${{P}_{2}}$ коэффициентами:(3.4)
${{l}^{2}}\Delta {{u}_{s}} = {{P}_{1}}\sin {{u}_{s}} + {{P}_{2}}\sin 2{{u}_{s}};\quad {{P}_{1}} = 1 - 2{{P}_{2}},\quad {{P}_{2}} = \frac{{{{s}^{2}}}}{{2p({{\lambda }_{{12}}} + 2{{\lambda }_{{44}}})}}$Как было показано выше, функция ${{u}_{s}}(x,y)$ позволяет рассчитать макроскопические (${{U}_{x}}$, ${{U}_{y}}$) и микроскопические (${{u}_{x}}$, ${{u}_{y}}$) смещения. Для этого нужно поставить и решить соответствующую краевую задачу. Решению краевых задач должно предшествовать построение общего решения уравнений нелинейной модели, что является основным содержанием настоящей работы. Авторы ограничились нахождением частного вида функции ${{u}_{s}}(x,y)$. Функция ${{u}_{s}}(x,y)$ имеет простой механический смысл – это микросмещение вдоль вектора обратной решетки. Она описывает перестройку кристаллической решетки в поле внешних напряжений. На простых решениях уравнений (3.1) и (3.2) рассмотрим примеры образующихся структур.
В литературе широко известен метод решения уравнения СГ (3.1), основанный на подстановке
(3.6)
${{\left( {\frac{{d{{\Phi }_{1}}}}{{dx}}} \right)}^{2}} = \frac{{a + b\Phi _{1}^{2} + c\Phi _{1}^{4}}}{K},\quad {{\left( {\frac{{d{{\Phi }_{2}}}}{{dy}}} \right)}^{2}} = \frac{{c + d\Phi _{2}^{2} + a\Phi _{2}^{4}}}{K}$Здесь a, b, c, d – произвольные постоянные, причем $b + d = p$. Решение (3.5) основано на предположении, что $K > 0$. Если $K < 0$, то решением уравнения (3.1) будет
Подстановку (3.5) связывают с Лэмом (G.L. Lamb Jr.) [19], хотя первым ее использовал Steuerwald [20].
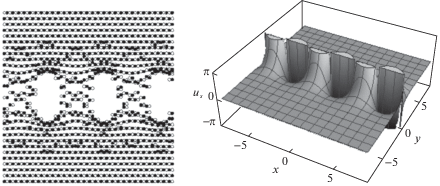
Функции ${{\Phi }_{1}}(x)$ и ${{\Phi }_{2}}(y)$ находятся из соотношений (3.6) обращением соответствующих эллиптических интегралов методом Лежандра. Способ Лежандра достаточно сложный. Был предложен [21] метод нахождения функций ${{\Phi }_{1}}(x)$ и ${{\Phi }_{2}}(y)$, основанный на дифференциальных уравнениях, которым удовлетворяют эллиптические функции Якоби (модифицированный метод Лэма). Предложенный подход позволяет получить широкий класс двоякопериодических решений СГ уравнения. Ниже приведены примеры решений из этого класса и представлены их графические изображения. На левых фрагментах фигур микросмещение ${{u}_{s}}(x,y)$ лежит в плоскости OXY в направлении вертикальной оси, а на правых фрагментах микросмещение перпендикулярно плоскости OX 'Y ', для которой вектор ${\mathbf{B}}$ – нормаль.
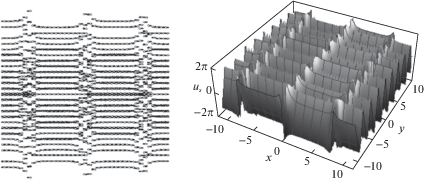
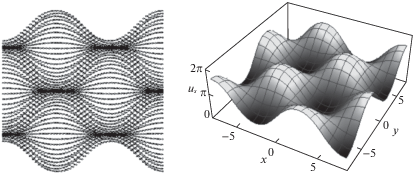
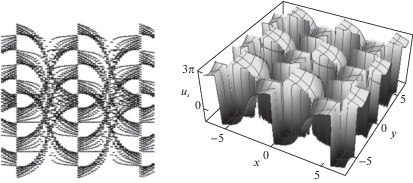
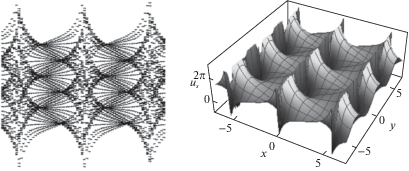
На фиг. 1–4 показаны микросмещения, которые описываются соответствующим решением, согласно данным, указанным в таблице 1 и содержащим полный эллиптический интеграл первого рода ${\kern 1pt} {\text{K}}(\nu )$ и эллиптические функции Якоби.
Таблица 1.
| Фиг. | $\frac{{{{A}^{2}}{{H}^{2}}}}{{{{{\text{K}}}^{2}}({{\nu }_{1}})}}$ | $\frac{{{{A}^{2}}{{B}^{2}}}}{{{{{\text{K}}}^{2}}({{\nu }_{2}})}}$ | ${{A}^{2}}$ | ${{\nu }_{1}}$ | ${{\nu }_{2}}$ |
|---|---|---|---|---|---|
| 1 | ${{u}_{s}} = 4\operatorname{arctg} \left[ {A\frac{{{\text{tn}}(y{\text{/}}B,{{\nu }_{2}})}}{{{\text{sn}}(x{\text{/}}H,{{\nu }_{1}})}}} \right]$ | ||||
| $({{A}^{2}} - 1)({{A}^{2}}\nu _{1}^{2} - 1)$ | $({{A}^{2}} - 1)({{A}^{2}}\nu _{1}^{2} - 1)$ | $\sqrt {1 - \nu _{2}^{2}} {{\nu }^{{ - 1}}}$ | 0.999 | 0.9 | |
| 2 | ${{u}_{s}} = \pi + 4\operatorname{arctg} [A\operatorname{sn} (x{\text{/}}H,{{\nu }_{1}})\operatorname{sn} (y{\text{/}}B,{{\nu }_{2}})]$ | ||||
| $(1 + {{A}^{2}})({{A}^{2}} + \nu _{1}^{2})$ | $(1 + {{A}^{2}})({{A}^{2}} + \nu _{2}^{2})$ | ${{\nu }_{1}}{{\nu }_{2}}$ | 0.5 | 0.5 | |
| 3 | ${{u}_{s}} = \pi + 4\operatorname{arctg} \left[ {\frac{A}{{{\text{tn}}(x{\text{/}}H,{{\nu }_{1}})\operatorname{sn} (y{\text{/}}B,{{\nu }_{2}})}}} \right]$ | ||||
| $(1 - {{A}^{2}})(1 - {{A}^{2}}(1 - \nu _{1}^{2}))$ | $(1 - {{A}^{2}})({{A}^{2}}\nu _{2}^{2} - 1)$ | $\frac{1}{{\nu _{2}^{{}}\sqrt {1 - \nu _{1}^{2}} }}$ | 0.4 | 0.2 | |
| 4 | ${{u}_{s}} = \pi + 4\operatorname{arctg} \left[ {\frac{{A\operatorname{cn} (y{\text{/}}B,{{\nu }_{2}})}}{{{\text{tn}}(x{\text{/}}H,{{\nu }_{1}})\operatorname{dn} (y{\text{/}}B,{{\nu }_{2}})}}} \right]$ | ||||
| $(1 - {{A}^{2}})(1 - {{A}^{2}}(1 - \nu _{1}^{2}))$ | ${{A}^{2}}(1 - {{A}^{2}})(1 - {{A}^{2}}(1 - \nu _{1}^{2}))$ | $\frac{{{{\nu }_{2}}}}{{\sqrt {1 - \nu _{1}^{2}} }}$ | 0.4 | 0.2 | |
На фиг. 1 видно, что в среде возникают дефекты типа микропор. В случаях, представленных на фиг. 2–4, возникает сверхрешетка. На фиг. 2 среда внутри фрагмента деформирована неоднородно, верхние и нижние плоскости фрагментов сильно сжаты. На фиг. 3 и 4 фрагменты деформированы резко неоднородно, нарушается сплошность среды, причем на фиг. 3 видны возникающие дефекты типа микропор сложной формы, а на фиг. 4 внутри фрагментов микропоры не образуются.
Модифицированный метод позволяет из решений, которые выражаются через эллиптические функции Якоби, построить решения, которые выражаются через круговые или гиперболические функции. Это можно сделать, если воспользоваться известными предельными соотношениями
(3.8)
$\begin{array}{*{20}{c}} {\nu \to {\text{0:}}\;\;{\text{sn}}(u,\nu ) \to \sin u,\quad {\text{cn}}(u,\nu ) \to \cos u,\quad {\text{dn}}(u,\nu ) \to 1} \\ {\nu \to {\text{1:}}\;\;\operatorname{sn} (u,\nu ) \to \operatorname{th} u,\quad {\text{cn}}(u,\nu ) \to \frac{1}{{\operatorname{ch} u}},\quad {\text{dn}}(u,\nu ) \to \frac{1}{{\operatorname{ch} u}}} \end{array}$(3.9)
$G = \left\{ {\begin{array}{*{20}{l}} {{\text{ch}}\psi \frac{{\sin (x{\text{/sh}}\psi )}}{{{\text{sh}}(y{\text{/th}}\psi )}}} \\ {{\text{sh}}\psi \frac{{{\text{ch}}(x{\text{/ch}}\psi )}}{{{\text{ch}}(y{\text{/cth}}\psi )}}} \\ {\cos \psi \frac{{{\text{sh}}(y{\text{/sin}}\psi )}}{{\cos (x{\text{/}}{\kern 1pt} \operatorname{tg} \psi )}}} \end{array}} \right.$На фиг. 5 изображено микросмещение, которое описывает первое решение (3.9), при $\psi = \pi {\text{/}}4$. Видно, что в плоскости $y = 0$ возникают регулярно расположенные поры. Объем кристалла практически недеформирован.
Приведенные примеры показывают, что построенная нелинейная теория кристаллических сред описывает структуры, которые реализуются в современных технологиях получения материалов с наноструктурой под действием интенсивных внешних воздействий.
4. Заключение. Найдены точные аналитические решения уравнений нелинейной модели деформирования кристаллических сред со сложной решеткой для случая плоской деформации. Решение системы четырех связанных нелинейных уравнений, из которых определяются макроскопические ${{U}_{x}}$, ${{U}_{y}}$ и микроскопические ${{u}_{x}}$, ${{u}_{y}}$ смещения, сведено к решению уравнения СГ с переменным коэффициентом (амплитудой) перед синусом. Из него находится функция ${{u}_{s}}$ – микросмещение вдоль вектора обратной решетки. Макро- и микросмещения находятся из решений соответствующих уравнений Пуассона, правые части которых однозначно определяются функцией ${{u}_{s}}$. Полученные общие решения позволяют на основе уравнений нелинейной модели проводить конкретные инженерные расчеты современных технологий получения новых материалов и режимов их эксплуатации.
Авторы благодарят А.Л. Корженевского за обсуждения.
Работа поддержана Российским фондом фундаментальных исследований (16-01-00068-а, 17-01-00230-а).
Список литературы
Аэро Э.Л. Микромасштабные деформации в двумерной решетке – структурные переходы и бифуркации при критическом сдвиге // Физ. тверд. тела. 2000. Т. 42. Вып. 6. С. 1113–1119.
Аэро Э.Л. Существенно нелинейная микромеханика среды с изменяемой периодической структурой // Успехи механ. 2002. Т. 1. № 1. С.130–176.
Корженевский А.Л., Аэро Э.Л., Булыгин А.Н. Микроскопическая теория образования мартенситных фаз // Изв. РАН. Сер. физич. 2005. Т. 69. № 9. С. 1271–1281.
Исупова И.Л., Трусов П.В. Математическое моделирование бездиффузионных фазовых превращений в сталях // Вестник Пермск. ун-та. Сер. Физика. 2012. Вып. 4(22). С. 73–78.
Няшина Н.Д., Трусов П.В. Моделирование мартенситных превращений в сталях: кинематика мезоуровня // Вестник ПНИПУ. Механика. 2014. № 4. С. 118–151.
Born M., Huang K. Dynamical Theory of Crystal Lattices. Oxford: Clarendon, 1954 = Борн М., Хуан Кунь. Динамическая теория кристаллических решеток. М.: Изд-во иностр. лит-ры, 1958.
Шаскольская М.П. Кристаллография. М.: Высшая школа, 1984.
Конторова Т.А., Френкель Я.И. К теории пластической деформации и двойникования. I // ЖЭТФ. 1938. Т. 8. Вып. 1. С. 89–95.
Braun O.M., Kivshar Y.S. The Frenkel–Kontorova Model. Concepts, Methods, and Applications. N. Y.: Springer, 2004.
Porubov A.V., Aero E.L., Maugin G.A. Two approaches to study essentially nonlinear and dispersive properties of the internal structure of materials // Phys. Rev. E. 2009. V. 79. No. 4. 046608.
Voigt W. Lehrbuch der Kristalphysik. Leipzig: Teubner, 1910.
Kittel C. Introduction to Solid State Physics. N. Y.: Wiley, 1956 = Киттель Ч. Введение в физику твердого тела. М.: ГИФМЛ, 1963.
Лехницкий С.Г. Теория упругости анизотропного тела. М.: Наука, 1977.
Аэро Э.Л., Булыгин А.Н., Павлов Ю.В. Решения уравнения синус-Гордон с переменной амплитудой // Теор. мат. физ. 2015. Т. 184. № 1. С. 79–91.
Аэро Э.Л., Булыгин А.Н., Павлов Ю.В. Решения трехмерного уравнения синус-Гордона // Теор. мат. физ. 2009. Т. 158. № 3. С. 370–377.
Аэро Э.Л., Булыгин А.Н., Павлов Ю.В. Новый подход к решению классического синус-Гордона уравнения и его обобщений // Диффер. уравн. 2011. Т. 47. № 10. С. 1428–1438.
Aero E.L., Bulygin A.N., Pavlov Yu.V. Functionally invariant solutions of nonlinear Klein-Fock-Gordon equation // Appl. Math. Comput. 2013. V. 223. No. 1. P. 160–166.
Aero E.L., Bulygin A.N., Pavlov Yu.V. Nonlinear model of deformation of crystal media with complex lattice: Mathematical methods of model implementation // Math. Mech. Solids. 2016. V. 21. № 1. P. 19–36.
Lamb G.L., Jr. Analytical Descriptions of Ultrashort Optical Pulse Propagation in a Resonant Medium // Rev. Modern Phys. 1971. V. 43. No. 2. P. 99–124.
Steuerwald R. Uber Enneper’sche Flachen und Backlund’sche Transformationen // Abhandl. Bayerischen Akad. Wissensch. Neue Folge. 1936. Bd. 40. No. 1. S. 1–105.
Aero E.L., Bulygin A.N., Pavlov Yu.V. Mathematical methods for solution of nonlinear model of deformation of crystal media with complex lattice // Proc. Int. Conf. “Days on Diffraction 2015”. St. Petersburg: LGU, 2015. P. 8–13.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика