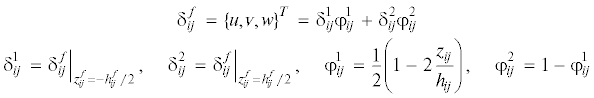Прикладная математика и механика, 2019, T. 83, № 2, стр. 282-294

1. Введение. Оболочки конической формы – распространенные элементы конструкций ракетно-космической, авиационной и др. современной техники [1, 2]. Трехслойные оболочки обеспечивают сочетание высокой несущей способности и живучести с малой массой, а также позволяют достигнуть необходимых тепло-, звуко-, виброизоляционных и многих других важных характеристик. Применение их сдерживается, в частности, недостаточным совершенством моделей при анализе сложных воздействий, поэтому построение адекватных моделей для анализа оболочек слоисто-неоднородной структуры – актуальная научная проблема, имеющая и важное прикладное значение.

Среди работ, посвященных моделям для расчета слоистых оболочек, следует выделить труды С.А. Амбарцумяна, В.В. Болотина, В.В. Васильева, Н.К. Галимова, Э.И. Григолюка, Я.М. Григоренко, М.А. Ильгамова, С.А. Лурье, Х.М. Муштари, И.Ф. Образцова, В.Н. Паймушина, С.Н. Сухинина, Э. Рейсснера, Л. Хэбипа и др.

Рассматривалось построение моделей и выполнение расчетов методом конечных элементов многослойных пластин и оболочек из композиционных материалов [3, 4], причем для слоистых оболочек главным образом – на основе гипотез Тимошенко для пакета слоев, а также трехслойных цилиндрических оболочек c применением гипотезы ломаной линии [5], неоднородных пологих оболочек и пластин – [6] и слоистых оболочек [7–15].

Обычно при расчете как однородных, так и неоднородных оболочек используют элементы с базисными функциями на основе аппроксимации полей перемещений полиномами первого и второго порядков [3, 4]. Применение таких аппроксимаций во многих случаях вынуждает строить весьма громоздкие конечно-элементные модели для достижения приемлемой точности. В связи с этим актуально построение моделей, которые позволяли бы получать необходимую точность численного решения при разумных затратах вычислительных ресурсов. Становится распространенным мнение, высказанное более 40 лет назад [16]: “…конечные элементы стали наиболее употребительным средством вычислительной математики во всем мире, но будет еще лучше, если мы научимся решать те же задачи с меньшими затратами”, это же мнение разделял и И.Ф. Образцов [17].

Проведенные исследования показали, что наиболее эффективными, т.е. приводящими к высокой скорости сходимости численных результатов, являются функции формы, построенные на основе аналитических решений задач теории оболочек [13, 18–21]. Но разработать такой подход удалось только для осесимметричных трехслойных цилиндрических оболочек.

Эффективные функции формы получаются также при аппроксимации обобщенных деформаций с последующим удовлетворением уравнениям совместности деформаций [5, 22–26]. Применение для расчета конечных элементов с такими эффективными функциями формы позволяет увеличить скорость сходимости результатов, а следовательно, приводит к уменьшению порядка систем уравнений по сравнению с общепринятым подходом (аппроксимация перемещений). Этот подход разработан для решения не осесимметричных задач по расчету трехслойных цилиндрических оболочек [5, 22–27]. Для оболочек другой геометрической формы применить такой подход не удалось из-за трудностей, связанных с получением аппроксимирующих функций деформаций и перемещений при удовлетворении уравнениям совместности деформаций.

Проведя анализ перечисленных и многих других работ, следует отметить, что в основном рассмотрены модели на основе гипотез для пакета слоев, когда выбирается одна поверхность приведения и строятся аппроксимации полей перемещений. При этом число степеней свободы конечно-элементной модели (КЭМ) не зависит от числа слоев. Однако такой подход ограничивает круг видов нагружения и условий закрепления слоев, а также приводит к упрощенным моделям или моделям для узкого класса задач, часто не удовлетворяющим требованиям точности расчетов поведения несущих слоев и слоя заполнителя.

Из обзора и анализа большого числа работ можно сделать вывод, что вопросы послойного анализа слоисто-неоднородных оболочек для многих важных задач недостаточно изучены. Это вызвано трудностями при построении соответствующих моделей и необходимостью учета изменения геометрических и физико-механических характеристик слоев и параметров напряженно-деформированного состояния (НДС) по координатам, в том числе по толщине оболочки и слоя заполнителя. Цель работы – построение на основе подхода послойного анализа КЭМ для уточненного исследования НДС трехслойных конических, в общем случае нерегулярных оболочек при наличии неоднородностей, в том числе на уровне слоя заполнителя, приложения нагрузок к несущим слоям и разных условий их закрепления, поперечных деформаций и напряжений, моментного состояния несущих слоев, трехмерного напряженного состояния в слое заполнителя. Построенные модели позволят провести расчет НДС трехслойных конических оболочек с переменными геометрическими и физико-механическими характеристиками и учесть изменения этих характеристик и параметров НДС не только по меридиональной и окружной координатам, но и по толщине слоя заполнителя, которые учитываются в настоящее время недостаточно точно, а некоторые из особенностей вообще не учитываются.

Подход послойного анализа [26, 28–31] заключается в том, что при необходимости стенка оболочки вместе с заполнителем разбивается по толщине на слои, которые затем стыкуются между собой. При таком подходе можно в зависимости от геометрических и физико-механических характеристик слоев и условий задач создавать и применять разные модели для расчета слоев, используя аналитические и численные методы.

Ниже этот подход реализуется с помощью КЭМ естественной кривизны, точно представляющих геометрическую форму исследуемых слоисто-неоднородных оболочек. Рассматриваются тонкие и жесткие несущие слои, которые моделируются конечными элементами (КЭ), построенными на основе моментной теории оболочек, а заполнитель – трехмерными КЭ толстостенной конической оболочки. Геометрические и физико-механические характеристики заполнителя могут варьироваться в широких пределах.

2. Постановка задачи. Рассматриваемая модель послойного анализа для решения задач расчета НДС трехслойных конических нерегулярных оболочек основана на построении и последующем объединении двух типов КЭ естественной кривизны: двумерного КЭ моментных несущих слоев и трехмерного КЭ слоя заполнителя.

Чтобы избежать погрешностей, вызванных разрывом обобщенных перемещений на поверхностях стыковки КЭ несущих слоев и заполнителя, для КЭ заполнителя на конических поверхностях выбирается столько же узлов, сколько их у КЭ несущих слоев. В качестве узловых неизвестных и аппроксимирующих функций используются те же обобщенные перемещения и аппроксимирующие функции, что и у КЭ несущих слоев. Такой алгоритм построения модели для уточненного анализа НДС трехслойных оболочек позволяет более адекватно учесть неоднородность структуры, моментное состояние несущих слоев, трехмерное напряженное состояние в слое заполнителя, а также различные условия закрепления и нагружения слоев. Но при таком подходе значительно растет число степеней свободы КЭМ (которое зависит от числа слоев слоистой оболочки; числа КЭ, которыми моделируются слои, в том числе по толщине, и числа степеней свободы КЭ), а, следовательно, растут погрешности вычислений, необходимые ресурсы ЭВМ и время расчета. Это значительно затрудняет, а нередко делает невозможным проведение исследований таких конструкций с надлежащей точностью, в связи с чем возникает проблема снижения размерности КЭМ слоисто-неоднородных, в общем случае нерегулярных оболочек.

Важное требование к функциям перемещений оболочечных КЭ – учет перемещений как твердых тел [5, 22–26, 32, 33]. Задача построения таких аппроксимирующих функций не нова и она решена в том или ином виде в теории метода конечных элементов (МКЭ) и реализована в некоторых пакетах прикладных программ для расчета изотропных однородных оболочек. К сожалению, в большинстве моделей для расчета оболочек слоисто-неоднородной структуры МКЭ в варианте метода перемещений не учитываются перемещения как твердых тел. Учет таких перемещений позволяет повысить скорость сходимости численной процедуры, а, следовательно, уменьшить требуемое для решения задач число КЭ, что особенно актуально при применении моделей послойного анализа слоистых оболочек.

3. Модель для анализа НДС в тонких моментных несущих слоях трехслойной конической, в общем случае нерегулярной оболочки вращения. Основные соотношения. Если несущие слои рассматриваемой трехслойной конической оболочки достаточно тонкие и жесткие, то для моделирования НДС в них будем применять двумерные КЭ естественной кривизны, разработанные на основе моментной теории оболочек, построенной на гипотезах Кирхгофа–Лява. Пронумеруем слои, начиная с внутренней поверхности оболочки: i = 1, 2, 3. Несущим слоям присвоим индекс с, слоям заполнителя – индекс  f. Расположим системы координат на срединных поверхностях КЭ слоев.

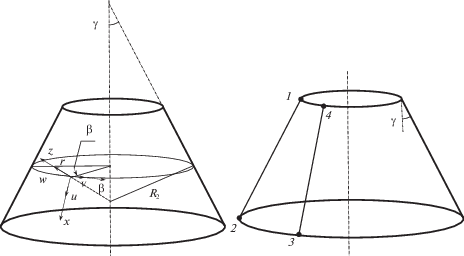
Перемещения точек несущих слоев оболочки определяются перемещениями точек срединной поверхности $\delta _{i}^{c}$ = ${{\{ u,v,w\} }^{T}}$ и углами поворота нормали к срединной поверхности относительно осей x, β (левая часть фиг. 1):

где γ – угол конусности, х – линейная координата, отсчитываемая вдоль меридиана на срединной поверхности каждого несущего слоя (левая часть фиг. 1), β – угловая координата в плоскости, перпендикулярной оси оболочки (левая часть фиг. 1), z – линейная координата, отсчитываемая по нормали к срединной поверхности каждого несущего слоя (левая часть фиг. 1), u, $v$ и w – перемещения точек на срединной поверхности каждого несущего слоя (левая часть фиг. 1), r = R₂cosγ (левая часть фиг. 1).

В дальнейшем индексы, соответствующие номеру слоя, у коэффициентов векторов и матриц указывать не будем.

Компоненты линейной составляющей вектора обобщенных деформаций $\varepsilon _{i}^{c}$ = = ${{\{ {{\varepsilon }_{1}},{{\varepsilon }_{2}},\gamma ,{{\kappa }_{1}},{{\kappa }_{2}},\chi \} }^{T}}$ связаны с перемещениями соотношениями [34]

Функции перемещений как твердого тела $\delta _{c}^{O} = {{\{ {{u}^{O}},{{v}^{O}},{{w}^{O}}\} }^{T}}$ для несущего слоя, представляющего собой тонкую моментную незамкнутую коническую оболочку, определяются интегрированием соотношений (3.2) при нулевых значениях деформаций аналогично принятому ранее подходу [22–26, 32] и имеют вид

где α₁, …, α₆ – постоянные интегрирования, используемые здесь как неопределенные коэффициенты, с помощью которых записываются функции, аппроксимирующие перемещения как твердого тела, $T_{c}^{O}$ – матрица коэффициентов при α₁, …, α₆.

Конечный элемент несущих слоев трехслойной в общем случае нерегулярной конической оболочки. Рассматриваемый КЭ (правая часть фиг. 1) образован сечением конической оболочки двумя плоскостями, перпендикулярными оси вращения, и двумя плоскостями, проходящими через ось оболочки. Узлы расположены в угловых точках КЭ (показаны темными точками) и имеют номера 1–4 (правая часть фиг. 1).

Три линейных перемещения u, $v$, w и углы поворота нормали вокруг координатных осей x и β в каждом из четырех узлов – степени свободы КЭ. Таким образом, КЭ несущих слоев трехслойной, в общем случае нерегулярной конической оболочки имеет двадцать степеней свободы, из которых шесть отвечают за перемещения как твердого тела, а оставшиеся четырнадцать – за перемещения, вызванные деформированием оболочки. Выбор аппроксимирующих функций взаимосвязан с выбором узловых перемещений и числом узлов КЭ.

Вектор перемещений $\delta _{i}^{c}$ КЭ несущих слоев оболочки складывается из жестких $\delta _{c}^{O}$ и деформационных $\delta _{c}^{d}$ смещений $\delta _{c}^{d}$ = ${{\{ {{u}_{d}},{{v}_{d}},{{w}_{d}}\} }^{T}}$ [22–26, 29–31, 35, 36]. Таким образом, будем иметь [29, 30, 35–37]

где $T_{i}^{c}$(3 $ \times $ 20) – матрица аппроксимирующих функций перемещений КЭ несущих слоев при записи которой приняты следующие обозначения: c₁= cosβ, s₁= sinβ, с₂ = cosγ, s₂ = sinγ, r = r₀+ xsinγ, r₀ – радиус окружности в плоскости, перпендикулярной оси вращения и проходящей через начало местной системы координат КЭ, находящейся на пересечении линий, одна из которых проходит на одинаковом расстоянии от криволинейных границ КЭ, а другая от прямолинейных, х – линейная координата вдоль меридиана КЭ, β – угловая координата в плоскости, перпендикулярной оси оболочки (обе координаты отсчитываются от начала местной системы координат КЭ и находятся на его срединной поверхности); ${\alpha }_{i}^{c}$ – вектор неопределенных коэффициентов α₁, …, α₂₀, с помощью которых записываются функции, аппроксимирующие перемещения КЭ.

Подставив координаты узловых точек в зависимости (3.4) и в выражения для углов поворота нормали вокруг координатных осей x и β, записанные через неопределенные коэффициенты с учетом зависимостей (3.4), получим соотношения, связывающие вектор $\alpha _{i}^{c}$ с вектором узловых перемещений $q_{i}^{c}$ КЭ:

где $C_{i}^{c}$(20 $ \times $ 20) – матрица связи вектора $\alpha _{i}^{c}$ с вектором $q_{i}^{c}$.

Из выражения (3.5) определим вектор

Переписав выражения (3.4) с учетом соотношений (3.6), получим функции формы КЭ несущих слоев трехслойной конической оболочки

Подставляя выражения (3.3) в соотношения Коши (3.2), получим

где $\Omega _{i}^{c}$(6 $ \times $ 20) – матрица аппроксимирующих функций обобщенных деформаций.

Получив выражения для обобщенных деформаций, а также усилий и моментов (напряжений), вычисляем матрицу жесткости конечно-элементную по алгоритмам, аналогичным рассмотренным ранее [21], и строим конечно-элементную модель несущих слоев. Была показана сходимость численных решений на основе этой модели [26, 29].

4. Модель для анализа НДС в слое заполнителя трехслойной конической нерегулярной оболочки. КЭ для моделирования НДС в слое заполнителя. Применение двумерных и трехмерных оболочечных КЭ для моделирования соответственно моментных несущих слоев и слоя заполнителя приведет к разрыву обобщенных перемещений на поверхностях контакта этих КЭ, если они построены с использованием различных аппроксимирующих функций перемещений.

Чтобы избежать погрешностей, вызванных таким разрывом обобщенных перемещений, для КЭ слоя заполнителя на конических поверхностях выбирается столько же узлов, сколько их у КЭ несущих слоев, и в качестве узловых неизвестных и аппроксимирующих функций используются те же обобщенные перемещения и аппроксимирующие функции, что и у КЭ несущих слоев.

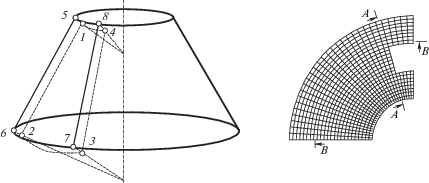
Рассматриваемый КЭ слоя заполнителя показан в левой части фиг. 2. Узлы КЭ расположены в угловых точках (показаны в отличии от узлов КЭ несущих слоев светлыми точками) – по четыре узла на внутренней (номера узлов 1–4, линии их соединяющие показаны пунктиром) и внешней (номера узлов 5–8) конических поверхностях, при этом узлы находятся на нормалях к этим поверхностям КЭ слоя заполнителя. Линии, соединяющие узлы, образованы сечением внутренней и внешней конических поверхностей КЭ слоя заполнителя двумя плоскостями, проходящими через ось оболочки (показана штрих-пунктиром) и двумя коническими поверхностями, образованными вращением вокруг оси оболочки нормалей в узловых точках к внутренней и внешней поверхностям КЭ слоя заполнителя. Таким образом, КЭ получается сечением слоя заполнителя двумя плоскостями, проходящими через ось оболочки, и двумя коническими поверхностями, на которых расположены соответственно узлы 1, 4, 5, 8 и 2, 3, 6, 7.

Степенями свободы в узле КЭ слоя заполнителя, который сопрягается по внутренней и внешней коническим поверхностям с КЭ несущих слоев, являются три линейных перемещения u, $v$, w и углы поворота нормали вокруг координатных осей x и β (у). Таким образом, КЭ слоя заполнителя в общем случае имеет сорок степеней свободы.

Когда конечные элементы слоя заполнителя по толщине оболочки располагаются цепочкой, учет углов поворота нормали теряет смысл. В этом случае соответствующие обобщенные перемещения ликвидируются вычислительной программой, проводящей учет граничных условий.

Уменьшая число степеней свободы КЭ слоя заполнителя, можно переходить от одной модели заполнителя к другой. Если, например, параметры слоистой оболочки и условия задачи таковы, что нет необходимости учитывать поперечные нормальные деформации (обжатие заполнителя по нормали), то уравниваются соответствующие нормальные перемещения в узлах на внутренней и внешней конических поверхностях и число степеней свободы при этом уменьшается с сорока до тридцати шести. Подобным же образом поступаем и в других случаях, если, например, нет необходимости учитывать поперечные сдвиговые деформации в одном или обоих направлениях.

Моделируя по меридиональной, окружной и нормальной к поверхности оболочки координатам слой заполнителя необходимым числом элементов, находим зависимость изменения перемещений, деформаций и напряжений по этим направлениям, в том числе по нормальной к срединной поверхности координате.

Аппроксимирующие функции перемещений конечного элемента слоя заполнителя. Местная система координат у КЭ слоя заполнителя находится на срединной поверхности КЭ с началом координат, расположенном на пересечении двух линий, одна из которых проходит на одинаковом расстоянии от криволинейных границ КЭ, а другая – на одинаковом расстоянии от прямолинейных границ КЭ.

Так как обобщенные перемещения КЭ несущих слоев задавались на срединной поверхности, то при стыковке КЭ несущих слоев и заполнителя, переходим в несущих слоях от срединной поверхности, относительно которой получалась матрица жесткости КЭ этого слоя, к поверхности раздела с заполнителем с помощью матриц перехода, подобно тому, как это описано ранее [4, 38].

Как отмечалось выше, аппроксимирующие функции полей перемещений КЭ слоя заполнителя строятся на внутренней и внешней конических поверхностях этих КЭ. При этом используются функции, полученные для несущих слоев.

Так как разрабатывается КЭМ, позволяющая при необходимости слой заполнителя разбивать и по толщине на требуемое число КЭ, то в этих КЭ можно применять линейную аппроксимацию перемещений по радиальной координате, а закон изменения параметров НДС воспроизводить моделированием по толщине необходимым числом КЭ. Тогда выражение для вектора перемещений j-го КЭ i-го слоя (слоя заполнителя) $\delta _{{ij}}^{f}$ = ${{\{ u,v,w\} }^{T}}$ (u, $v$, w – перемещения точек на срединной поверхности j-го КЭ слоя заполнителя трехслойной конической оболочки) будет иметь вид

Индекс f соответствует слою заполнителя, i – номеру слоя, считая от внутренней поверхности оболочки (для слоя заполнителя i = 2), j – номеру КЭ слоя заполнителя ( j = = 1, …, m); m – число КЭ, которыми моделируется по толщине НДС слоя заполнителя, $\delta _{{ij}}^{1}$ и $\delta _{{ij}}^{2}$ – векторы перемещений точек на внутренней и внешней конических поверхностях j-го КЭ слоя заполнителя.

При разбиении по толщине слоев заполнителя нумерация КЭ проводится от внутренней поверхности заполнителя.

Если слой заполнителя моделируется по толщине одним КЭ ( j = j_max = 1), его конические поверхности будут поверхностями раздела с несущими слоями. Для этого случая запишем выражения для перемещений на внутренней и внешней поверхностях этого КЭ заполнителя

и тогда где $\bar {u}_{{i - 1\left( {i + 1} \right)}}^{c}$, $\bar {v}_{{i - 1\left( {i + 1} \right)}}^{c}$, $\bar {w}_{{i - 1\left( {i + 1} \right)}}^{c}$ – перемещения несущих слоев на поверхностях раздела со слоем заполнителя. В этих выражениях верхние индексы 1 и 2 соответствуют внутренней и внешней коническим поверхностям КЭ слоя заполнителя.

При моделировании слоя заполнителя по толщине несколькими КЭ j = 1, …, m

Зная аппроксимирующие функции несущих слоев, записанные через вектора неопределенных коэффициентов $\alpha _{i}^{c}$ (3.3), с помощью зависимостей (4.1)–(4.3) получим выражения для перемещений в КЭ слоя заполнителя, записанные через вектор неопределенных коэффициентов $\alpha _{{ij}}^{f}$:

где $T_{{ij}}^{f}$ – матрица аппроксимирующих функций перемещений КЭ заполнителя, она имеет максимальную размерность (3 $ \times $ 40). Максимальное число столбцов матрицы $T_{{ij}}^{f}$, равное 40, будет в случае, когда в КЭ слоя заполнителя учитываются в узле все 5 обобщенных перемещений, т.е. когда слой заполнителя моделируется по толщине одним КЭ.

Подставляя в полученные зависимости (4.4) и в выражения для углов поворота нормали вокруг координатных осей x и β (для КЭ слоя заполнителя, граничащих с несущими слоями), записанные через неопределенные коэффициенты $\alpha _{{ij}}^{f}$ с учетом зависимостей (4.4), координаты узлов, определим связь вектора узловых перемещений $q_{{ij}}^{f}$ и вектора $a_{{ij}}^{f}$ для КЭ слоя заполнителя, осуществляемую через матрицу связи $C_{{ij}}^{f}$

$C_{{ij}}^{f}$ – матрица с максимальной размерностью 40 × 40 для случая, когда слой заполнителя моделируется по толщине одним конечным элементом.

Формируя вектор $q_{{ij}}^{f}$ так, чтобы первая половина узловых перемещений относилась к внутренней конической поверхности, а вторая половина к внешней конической поверхности КЭ слоя заполнителя $q_{{ij}}^{f}$ = {$q_{{ij}}^{1}$, $q_{{ij}}^{2}{{\} }^{T}}$, заключаем, что вектор $\alpha _{{ij}}^{f}$ будет иметь следующий вид $\alpha _{{ij}}^{f}$ = {$\alpha _{{ij}}^{1}$, $\alpha _{{ij}}^{2}{{\} }^{T}}$, а матрица перехода от $\alpha _{{ij}}^{f}$ к $q_{{ij}}^{f}$ будет диагональной и состоять из двух блоков $C_{{ij}}^{f}$ = $\left| {\begin{array}{*{20}{c}} {C_{{ij}}^{1}}&0 \\ 0&{C_{{ij}}^{2}} \end{array}} \right|$. Указанное обстоятельство позволяет заменить матрицу $C_{{ij}}^{f}$ матрицами $C_{{ij}}^{1}$ и $C_{{ij}}^{2}$, размеры которых в два раза меньше размеров первоначальной матрицы $C_{{ij}}^{f}$. Использование вместо матрицы $C_{{ij}}^{f}$матриц $C_{{ij}}^{1}$, $C_{{ij}}^{2}$ существенно сказывается на уменьшении времени, необходимом объеме памяти, увеличении точности при выполнении операций с матрицами $C_{{ij}}^{f}$, особенно при их обращении.

Были приведены [39] соотношения Коши, связывающие деформации с перемещениями, для трехмерного тела в криволинейных координатах. Применим эти соотношения для слоя заполнителя, представляющего собой толстостенную коническую оболочку. Имеем равенства

где верхние индексы 1 и 2 соответствуют внутренней и внешней коническим поверхностям КЭ слоя заполнителя.

Подставляя выражения (4.4) в равенства (4.5), получим зависимости для обобщенных деформаций, записанные через вектор неопределенных коэффициентов $\alpha _{{ij}}^{f}$.

С помощью полученных зависимостей для обобщенных деформаций записываем выражения для напряжений на основе физического закона.

Получив выражения для деформаций и напряжений, вычисляем матрицу жесткости КЭ по алгоритмам, аналогичным рассмотренным ранее [21, 38, 40], и строим конечно-элементную модель слоя заполнителя.

Если слои оболочки имеют переменные геометрические и физико-механические свойства по координатам, то задавая для каждого КЭ слоев свои (разные) характеристики, реализуем необходимый закон изменения этих свойств, в том числе по толщине заполнителя.

5. Численный пример. Анализ НДС трехслойной конической оболочки с несквозными вырезами во внутреннем несущем слое. Разрабатываемые на основе подхода послойного анализа модели для уточненного исследования НДС в слоях трехслойных конических, в общем случае нерегулярных оболочек позволяют учесть особенности слоисто-неоднородного строения, например, наличие несквозных вырезов.

В качестве примера решена задача об определении параметров НДС трехслойной конической оболочки с двумя диаметрально противоположными прямоугольными несквозными вырезами во внутреннем несущем слое; при этом внешний несущий слой и слой заполнителя остаются сплошными. Вырезы с углом раствора 30° располагаются на равном расстоянии от торцов оболочки, длина вырезов составляет 1/3 от длины образующей. Оболочка нагружена равномерно распределенным внутренним давлением. Несущие слои оболочки выполнены из стеклопластика, а заполнитель – – из пенопласта. Считается, что граничные условия на торцах оболочки соответствуют случаю жесткой заделки (на торце меньшего диаметра разрешено осевое перемещение). Геометрические параметры оболочки следующие:

R – внутренний радиус большего основания оболочки, L – ее длина, h₁ и h₂ – толщина внутреннего и наружного несущих слоев, H – толщина трехслойного пакета.

Физико-механические характеристики оболочки следующие:

для внутреннего несущего слоя

для наружного несущего слоя

для заполнителя:

Вследствие симметрии в окружном направлении при расчете рассматривается четвертая часть симметричной оболочки, сетка разбиений на КЭ которой приведена в правой части фиг. 2.

Анализ результатов расчета показывает, что НДС оболочки с вырезами, характеризуется ярко выраженным краевым эффектом в окрестности вырезов и особенно вблизи угловых точек вырезов. Наибольшими по абсолютной величине в несущих слоях являются мембранные усилия Т_х и Т_у в окрестности угловой точки выреза во внутреннем несущем слое и в окрестности середины прямолинейного края выреза во внешнем несущем слое. Значения сдвиговых усилий более чем в пять раз меньше максимальных значений усилий Т_х и Т_у.

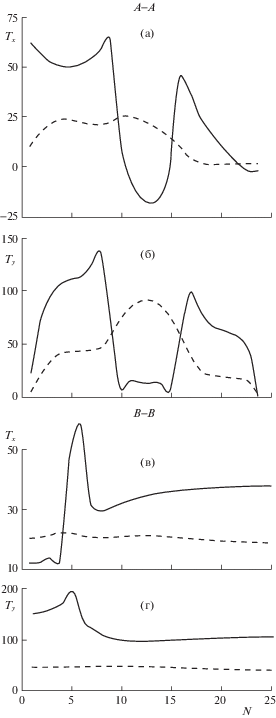
На фиг. 3 представлены графики изменения погонных усилий Т_х (кг/см) и Т_у (кг/см) в несущих слоях в двух сечениях оболочки по линиям А–А и В–В, показанным в правой части фиг. 2. На верхних двух фрагментах фиг. 3 – изменение погонных усилий Т_х и Т_у в сечении плоскостью, проходящей через ось оболочки и меридиональную линию, находящуюся на расстоянии половины размера КЭ в окружном направлении от прямолинейного края выреза (обозначим эту линию А–А). По оси N отложены номера КЭ по линии А–А, отсчет ведется от основания конуса с большим диаметром.

На нижних двух фрагментах фиг. 3 – изменение погонных усилий Т_х и Т_у в сечении плоскостью, перпендикулярной оси оболочки и проходящей через линию, параллельную криволинейному краю выреза и находящуюся на расстоянии половины длины КЭ от этого края выреза (обозначим эту линию В–В). По оси N отложены номера КЭ по линии В–В, отсчет ведется от плоскости симметрии, проходящей через середины криволинейных краев выреза.

Сплошными кривыми показаны графики изменения погонных усилий Т_х и Т_у во внутреннем несущем слое, штриховыми – во внешнем несущем слое.

Следует отметить, что в заполнителе максимальные значения напряжений σ₁ и σ₂, которыми в большинстве случаев пренебрегают, сопоставимы с максимальными значениями напряжений σ₃, τ₂₃ и τ₃₁. Это подтверждает необходимость учета в КЭ заполнителя всех шести компонент вектора напряжений. Для напряжений τ₁₂ максимальные значения в несколько раз ниже, чем для остальных компонент напряженного состояния заполнителя.

Автор благодарит В.В. Репинского за помощь в проведении расчетов.

Работа выполнена в рамках государственного задания, номер государственной регистрации темы АААА-А19-119012290177-0.