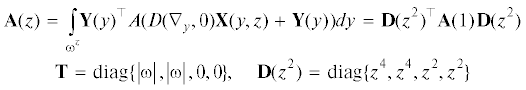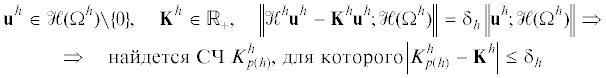Прикладная математика и механика, 2019, T. 83, № 2, стр. 265-281

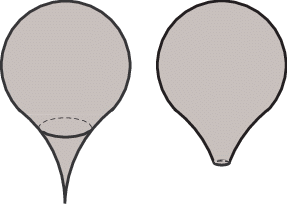
1. Тело с пиком. Деформируемое тело $\Omega \subset {{\mathbb{R}}^{3}}$ ограничено поверхностью $\partial \Omega $, гладкой (класса ${{C}^{\infty }}$ для простоты) всюду кроме точки $\mathcal{O}$, начала декартовых координат x = $({{x}_{1}},{{x}_{2}},{{x}_{3}})$. В окрестности этой точки тело имеет форму пика (левая часть фигуры 1)

Здесь $d > 0$ – длина пика (1.1), $m \geqslant 1$ – показатель заострения, а $\omega $ – эталонное сечение, ограниченное простым замкнутым гладким контуром $\partial \omega $. Масштабированием сведем характерный размер области $\omega $ к единице и сделаем декартовы координаты и геометрические параметры безразмерными.

Рассмотрим задачу о гармонических во времени упругих колебаниях анизотропного и однородного тела, записанную в краткой форме

При этом $u$ – вектор смещений, $\Lambda = \rho {{\gamma }^{2}}$ – спектральный параметр, $\gamma \geqslant 0$ – частота колебаний, $\rho > 0$ – плотность материала, $n = ({{n}_{1}},{{n}_{2}},{{n}_{3}})$ – единичный вектор внешней нормали, а дифференциальные операторы $L$ и $B$ второго и первого порядков соответственно выражаются через декартовы компоненты ${{\sigma }_{{jk}}}$ тензора напряжений

Установлено [1–3], что при $m \in \left[ {1,2} \right)$ спектр задачи (1.2) дискретный, т.е. состоит из нормальных собственных чисел (СЧ) конечных кратностей с единственной точкой сгущения на бесконечности, однако при $m \geqslant 2$ спектр приобретает непрерывную компоненту $[{{\Lambda }^{\dag }}, + \infty )$. В рассматриваемом далее случае

точка отсечки ${{\Lambda }^{\dag }}$ положительна, но ${{\Lambda }^{\dag }} = 0$ при $m > 2$. Непрерывный спектр порождает волновые процессы в конечном объеме (1.1), известные [4–6] в инженерной практике как “черные дыры” для упругих и акустических волн. Вместе с тем, в реальности идеальное острие недостижимо, и далее изучается задача о колебаниях тела с затупленным пиком (правая часть фигуры 1)

Поверхность $\partial {{\Omega }^{h}}$ липшицева, а значит, у задачи (1.3) при $h > 0$ формируется полностью дискретный спектр

Шесть нулевых СЧ отвечают смещениям тела (1.4) как жесткого целого.

Далее исследуется асимптотика при $h \to + 0$ положительных членов последовательности (1.5), среди которых выявлены “малоподвижные”, “планирующие” и “блуждающие” СЧ (разд. 5, 8 и 9 соответственно). Кроме того, описан (разд. 8) новый способ формирования непрерывного спектра $[{{\Lambda }^{\dag }}, + \infty )$ из семейства дискретных спектров (1.5): всякая точка $\Lambda > {{\Lambda }^{\dag }}$ становится СЧ задачи (1.4) для почти периодической в логарифмическом масштабе $\left| {lnh} \right|$ бесконечно малой последовательности $\left\{ {{{h}_{n}}(\Lambda )} \right\}_{{n = 1}}^{\infty }$, однако обычно лежит вне спектра (1.5) в промежутках между критическими длинами ${{h}_{n}}(\Lambda )$ и ${{h}_{{n + 1}}}(\Lambda )$. Иными словами, выше порога ${{\Lambda }^{\dag }}$ непрерывного спектра наблюдается эффект “мигания” СЧ при уменьшении длины обломка ${{\Pi }^{h}}$ и восстановлении идеального острия (разд. 7).

2. Асимптотическое поведение упругих полей в пике. Поскольку диаметр $O({{\zeta }^{2}})$ сечения

много меньше расстояния $\zeta \ll d$ до вершины $\mathcal{O}$, применим процедуру понижения размерности [1–7], в которой удобно использовать матричную форму [8–10] записи определяющих соотношений теории упругости. Вектор смещений $u$ представим как столбец ${{({{u}_{1}},{{u}_{2}},{{u}_{3}})}^{ \top }}$ в фиксированной системе координат $x$; здесь $ \top $ – знак транспонирования и ${{u}_{j}}$ – проекция вектора на ось ${{x}_{j}}$, $j = 1,2,3$. Закон Гука включает симметричную положительно определенную постоянную (6 × 6) -матрицу $A$ упругих модулей и связывает столбец напряжений со столбцом деформаций такого же строения

Множители ${{2}^{{1/2}}}$ и ${{2}^{{ - 1/2}}}$ введены в определения (2.2) и (2.3) для того, чтобы уравнять естественные нормы тензоров второго ранга и изображающих их столбцов высотой шесть.

Асимптотическое разложение поля смещений вблизи вершины пика имеет вид [1, 3, 7]

Свойства малого остатка $\tilde {u}$ будут описаны в разд. 3 и 5, ${{e}_{{(k)}}}$ – орт оси ${{x}_{k}}$, $\theta (y)$ – поворот вокруг оси ${{x}_{3}}$, а комплексные число $\kappa \in \mathbb{C}$ и столбец $\mathcal{W}$ = ${{({{\mathcal{W}}_{1}},{{\mathcal{W}}_{2}},{{\mathcal{W}}_{3}},{{\mathcal{W}}_{4}})}^{ \top }}$ ∈ ${{\mathbb{C}}^{4}}$ подлежат определению вместе со слагаемыми суммы (2.4)

Причина введения вычитаемого 5/2 в показатели степеней переменной $z$ станет понятной в разд. 3. Согласно равенствам

градиент-оператор ${{\nabla }_{y}} = {{({{\partial }_{1}},{{\partial }_{2}})}^{ \top }}$ понижает показатель однородности $\tau $ сложной функции ${{z}^{\tau }}\mathcal{V}({{z}^{{ - 2}}}y)$ на два, а дифференцирование по продольной координате $z$ – только на единицу.

Обозначим $\nu = {{({{\nu }_{1}},{{\nu }_{2}})}^{ \top }}$ единичный вектор внешней нормали к контуру $\partial \omega \subset {{\mathbb{R}}^{2}}$. Трехмерная нормаль на поверхности ${{\Gamma }^{d}}$ = $\{ x:z \in (0,d)$, $\eta \in \omega \} $ принимает вид

Матричные дифференциальные операторы $L({{\nabla }_{x}})$ и $B(x,{{\nabla }_{x}})$ из уравнений (1.2) допускают расщепления

При этом операторы ${{L}^{q}}$ и ${{B}^{q}}$ понижают порядки однородностей вектор-функций (2.7) на $q - 4$ и $q - 2$ соответственно.

Подставим разложения (2.4) и (2.8) в уравнения (1.2) и соберем члены с одинаковыми порядками относительно переменной $z$. В результате получим последовательность плоских задач теории упругости на сечениях пика (1.1)

Здесь $q = - 2,\; \ldots ,\;2$, ${{U}^{p}} = 0$ при $p < - 2$, ${{\delta }_{{p,q}}}$ – символ Кронекера.

Вектор-функции (2.5) удовлетворяют задачам (2.9) при $q = - 2$ и $q = - 1$ соответственно. Проверено [1, 7], что поочередное решение задач (2.9), точнее, соблюдение условий их разрешимости

приводит к системе обыкновенных дифференциальных уравнений для вектор-функции w = ${{({{w}_{1}},{{w}_{2}},{{w}_{3}},{{w}_{4}})}^{ \top }}$. Для ее описания частично воспроизведем выкладки из [10], гл. 5, и [1, 7].

При учете связи

правые части задачи (2.9) с индексом $q = 0$ принимают вид

При помощи формулы интегрирования по частям проверено ([10], гл. 5, и [1, 7]), что выполнены все условия разрешимости (2.10) задачи (2.9) с индексом $q = 0$. Таким образом, справедливы соотношения

Матрица ${\mathbf{X}}$ размером 4 × 3 находится из разрешимой задачи

Установлено [1, 7], что первые два ($k = 1,2$) условия разрешимости задачи (2.9) с индексом $q = 1$ выполнены автоматически, а два остальных условия превращаются в две нижние строки искомой системы четырех обыкновенных дифференциальных уравнений

Две верхние строки системы (2.14), включающие спектральный параметр $\Lambda $ и площадь $\left| \omega \right|$ области $\omega \subset {{\mathbb{R}}^{2}}$, – результат выполнения первых двух условий разрешимости (2.10) задачи (2.9) с индексом $q = 2$. Доказано [1], что (4 × 4)-матрица ${\mathbf{A}}{\text{(1)}}$ симметрична и положительно определена.

Предельная одномерная задача на оси пика получена. В случае изотропного материала с модулем Юнга $E$ и модулем сдвига $\mu $ имеем

При этом $P$, $I$ и $G$ – центр тяжести, тензор инерции и жесткость кручения области $\omega \subset {{\mathbb{R}}^{2}}$ (см., например, [10], гл. 5 и приложение G в книге [11]). Задача (2.9) распадается на плоскую и антиплоскую задачи для плоского изотропного тела.

3. Упругие волны в пике. Разобьем матрицу ${\mathbf{A}}(z)$ на блоки размером 2 × 2 и введем (2 × 2)-матрицу ${\mathbf{M}}(z)$, также симметричную и положительно определенную:

Исключим неизвестные ${{w}_{ \bullet }} = {{({{w}_{3}},{{w}_{4}})}^{ \top }}$ из системы (2.14) и образуем систему двух уравнений для вектор-функции ${{w}_{\# }} = {{({{w}_{1}},{{w}_{2}})}^{ \top }}$

Пусть $0 < {{{\mathbf{m}}}_{1}} \leqslant {{{\mathbf{m}}}_{2}}$ – СЧ матрицы ${\mathbf{M}}{\text{(1)}}$, а $\mathcal{W}_{\# }^{1}$ и $\mathcal{W}_{\# }^{2}$ – соответствующие ортонормированные собственные векторы (СВ). Показатели однородности $\kappa - 5{\text{/}}2$ функций ${{w}_{1}}$ и ${{w}_{2}}$ из списка (2.6) подобраны так, что характеристические биквадратные уравнения для системы (3.2) эйлеровского типа принимают простой вид

При условии

уравнение (3.3) имеет два вещественных и два чисто мнимых корня

В случае $\Lambda < \Lambda _{j}^{\dag }$ все корни уравнения (3.3) вещественные.

Корни (3.5) и СВ $\mathcal{W}_{\# }^{j}$ формируют решения

укороченной системы уравнений (3.2), но проверенная ([7], разд. 2, § 3) формула восстанавливает недостающую часть вектора $w_{{(j)}}^{{b \pm }}$ высотой четыре.

Еще два решения системы (2.14)

подчинены соотношениям (2.6) с показателями ${{\kappa }_{3}} = 3{\text{/}}2$, ${{\kappa }_{4}} = 7{\text{/}}2$ и связаны с продольным жестким смещением пика и поворотом вокруг оси $z$. Наконец, решения отвечают продольной силе и крутящему моменту. При исследовании волновых процессов решения (3.8) и (3.9) не играют существенной роли.

Далее рассматриваем две принципиально разные ситуации

В случае (3.11) выполнены оба $(j = 1,2)$ требования (3.4), а значит, в списке (3.6) имеются четыре решения с комплексными показателями степени переменной $z$, но в случае (3.10) – только два, так как все корни уравнения (3.3) при $j = 2$ вещественные. При $\Lambda < {{\Lambda }^{\dag }}$ комплексных корней нет вообще, а на порогах $\Lambda = \Lambda _{j}^{\dag }$ нулевые корни уравнений (3.3) кратные, т.е. согласно правилу решения дифференциальных уравнений эйлеровского типа компоненты (2.6) вектор-функции $w$ приобретают линейную зависимость от $lnz$. Пороговые значения $\Lambda = \Lambda _{j}^{\dag }$ далее не анализируются, поскольку при них обсуждаемые эффекты исчезают.

Каждое решение $w$ системы (2.14) порождает [3, 7] трехмерное поле $w$, допускающее представление (2.4), например, в пике ${{\Pi }_{{3d/4}}}$ и удовлетворяет задаче (1.2), суженной на ${{\Pi }_{{d/2}}}$ и ${{\Gamma }_{{d/2}}}$ (уменьшение размеров до $3d{\text{/}}4$ и $d{\text{/}}2$ необходимо). Согласно формулам (2.5) и (2.12) столбец деформаций принимает вид

Оценки остатков в представлениях (3.12) и (2.4) зависят от инициирующего поле смещений $u$ вектора $w$, в частности, от показателя $\kappa $ в соотношениях (2.6) для его компонент. Обозначим $u_{{(j)}}^{{i \pm }}$ поле смещений, порожденное мнимыми корнями (3.5) биквадратных уравнений (3.3). Далее понадобятся известные [3, 7] оценки

Аналогичные оценки верны и для полей $u_{{(j)}}^{{r \pm }}$, инициированных вещественными корнями, однако множитель ${{z}^{{ - 3/2}}}$ в мажорантах превращается в множитель ${{z}^{{\kappa _{j}^{{r \pm }} - 3/2}}}$.

Формулы (3.13) и (2.15), (3.1) для столбца $\widetilde \varepsilon $ и матриц ${\mathbf{A}}$, ${\mathbf{M}}$ соответственно позволяют вычислить функционал упругой энергии на сечении (2.1)

Многоточие заменяет младшие по порядку слагаемые при $z \to + 0$.

Таким образом, погонная энергия (3.14), вычисленная для вектор-функции $w$ с компонентами (2.6), имеет порядок ${{z}^{{ - 1 + 2\operatorname{Re} \kappa }}}$, т.е. интеграл энергии в пике (1.1)

сходится при $\operatorname{Re} \kappa > 0$, но заведомо расходится при $\operatorname{Re} \kappa < 0$. Соответственно поле $u$ и вектор $w$ называем энергетическими и неэнергетическими. При чисто мнимом показателе $\kappa _{j}^{{i \pm }}$ величина (3.14) принимает [7] вид и также обеспечивает расходимость интеграла (3.15). Погонная упругая энергия (3.16) обладает примечательным свойством, характерным для волновых процессов: упругая энергия $E(u_{{(j)}}^{{i \pm }};{{\Pi }^{{2\rho }}}\backslash {{\Pi }^{\rho }})$, запасенная фрагментом пика ${{\Pi }^{d}}$, не зависит в главном от расстояния $\rho $ до вершины $\mathcal{O}$. Иными словами, волна $u_{{(j)}}^{{i \pm }}$ переносит энергию и потому называется распространяющейся. На основе принципов излучения Зоммерфельда и Умова–Мандельштама (см. [12], гл. 1, [13, 14] и др.) показано ([7], § 4), что волны $u_{{(j)}}^{{i - }}$ распространяются в сторону к вершине $\mathcal{O}$, а волны $u_{{(j)}}^{{i + }}$ – из вершины в сторону массивной части тела. Эти волны называются уходящими и приходящими соответственно.

4. Матрица рассеяния и коэффициент рассеяния; захваченные волны. Вычислен ([7], разд. 1, § 4) осредненный вектор Умова [15], проекция которого на ось $z$ пропорциональна симплектической (полуторалинейной и антиэрмитовой) форме переноса энергии

Показано ([7], разд. 1, § 4), что

Нормируем СВ $\mathcal{W}_{\# }^{j}$ матрицы ${\mathbf{M}}{\text{(1)}}$ так, чтобы правая часть соотношения (4.2) стала равной $ \pm i$. В результате приходим к условиям ортогональности и нормировки

Поля, порожденные разными чисто мнимыми показателями $i{{\kappa }_{{(1)}}}$ и $i{{\kappa }_{{(2)}}}$, ортогональны одно другому в смысле формулы (4.3) потому, что подынтегральное выражение приобретает осциллирующий множитель ${{e}^{{i({{\kappa }_{{(1)}}} - {{\kappa }_{{(2)}}})z}}}$, но сам интеграл (4.1) должен иметь предел, являясь фрагментом поверхностного интеграла в формуле Грина для решений задачи (1.2) в пике ${{\Pi }^{{d/2}}}$. По аналогичной причине ${{Q}_{0}}(u_{{(j)}}^{{r \pm }},u_{{(j)}}^{{r \pm }})$ = 0 для энергетических и неэнергетических упругих полей.

Определим дифракционные характеристики тела $\Omega $ с пиком. Сначала обратимся к ситуации (3.11), когда существуют две пары $u_{{(1)}}^{{i \pm }}$ и $u_{{(2)}}^{{i \pm }}$, т.е. $j,k = 1,2$ в формуле (4.3). Доказано ([16], гл. 5, [17], § 3, [7], § 5), что свойства (4.3) и $u_{{(j)}}^{{i - }}$ = $\overline {u_{{(j)}}^{{i + }}} $, упомянутых волн обеспечивают унитарность и симметричность (2 × 2)-матрицы рассеяния $S$, составленной из коэффициентов разложений специальных решений задачи (1.2)

При этом $\chi $ – гладкая срезающая функция, равная единице на ${{\Pi }^{{d/4}}}$ и нулю вне ${{\Pi }^{{d/2}}}$. Остаток ${{\tilde {Z}}^{j}}$ попадает в энергетическое гильбертово пространство $\mathcal{H}(\Omega )$, которое получается замыканием линейного пространства $C_{c}^{\infty }{{(\bar {\Omega }\backslash \mathcal{O})}^{3}}$ (бесконечно дифференцируемые функции, обращающиеся в нуль около точки $\mathcal{O}$) по норме

Более точная информация об остатках будет указана в разд. 5.

Установлено ([10], гл. 3, § 3, [1], § 3), что $\mathcal{H}(\Omega )$ шире пространства Соболева ${{H}^{1}}{{(\Omega )}^{3}}$ и вложение $\mathcal{H}{{(\Omega )}^{3}}$ ⊂ ${{L}^{2}}{{(\Omega )}^{3}}$ не является компактным. Для энергетических полей выполнено включение $\chi u_{{(k)}}^{{r + }}$ ∈ $\mathcal{H}(\Omega )$, но неэнергетические поля $\chi u_{{(k)}}^{{r - }}$ и распространяющиеся волны $\chi u_{{(j)}}^{{i \pm }}$, не принадлежат пространству $\mathcal{H}(\Omega )$.

В ситуации (3.10) имеется одна пара распространяющихся волн $u_{{(1)}}^{{i \pm }}$, и поэтому в формулах (4.3) и (4.4) фигурируют индексы $j,k = 1$, а матрица рассеяния вырождается в скаляр $S = {{S}_{{11}}}$:

Поля (4.4) и (4.5) порождены волнами, которые приходят из вершин $\mathcal{O}$ в тело $\Omega $, но затем рассеиваются в нем и возвращаются в вершину как уходящие волны. Закон сохранения энергии обеспечивает упомянутые свойства матрицы рассеяния, а в ситуации (3.10) показывает, что коэффициент рассеяния $S$ лежит на единичной окружности $\mathbb{S}$ в комплексной плоскости $\mathbb{C}$

Решения задачи (1.2) из энергетического класса $\mathcal{H}(\Omega )$ называются захваченными упругими волнами в теле $\Omega $. При геометрической и физической симметрии (например, изотропное тело с круговыми сечениями, перпендикулярными оси $z$) найдена [1] неограниченная последовательность частот собственных колебаний тела $\Omega $, причем соответствующие собственные моды экспоненциально затухают при $x \to \mathcal{O}$. Хотя конкретных примеров до сих пор не построено [7], в принципе у задачи (1.2) могут быть собственные вектор-функции, которые содержат в представлении на ${{\Pi }^{{d/2}}}$ нетривиальные энергетические поля и потому характеризуются степенным поведением при $x \to \mathcal{O}$. Указанные захваченные волны именуем экспоненциальными и степенным соответственно.

5. “Малоподвижные” собственные частоты. Захваченная волна, т.е. собственная вектор-функция ${{u}^{0}} \in \mathcal{H}(\Omega )$ задачи (1.2), отвечающая спектральному параметру ${{\Lambda }^{0}} > 0$, оставляет малые невязки в краевых условиях на торце ${{\omega }^{h}}$ обломанного пика, что обеспечивает существование СЧ $\Lambda _{{p(h)}}^{h}$ из последовательности (1.5) в непосредственной близости от ${{\Lambda }^{0}}$

При этом ${{\rho }_{h}} = {{e}^{{ - \beta ({{\Lambda }^{0}})/h}}}$ или ${{\rho }_{h}} = {{h}^{{{{\kappa }_{{min}}}({{\Lambda }^{0}})}}}$ в случаях экспоненциальной или степенной захваченной волны, $h({{\Lambda }^{0}})$, $c({{\Lambda }^{0}})$ и $\beta ({{\Lambda }^{0}})$ – некоторые положительные величины, зависящие от ${{\Lambda }^{0}}$, но не от $h$, а ${{\kappa }_{{min}}}({{\Lambda }^{0}})$ – наименьший положительный корень биквадратных уравнений (3.3).

Поясним как выводится неравенство (5.1). Снабдим энергетическое пространство $\mathcal{H}({{\Omega }^{h}})$ = ${{H}^{1}}{{({{\Omega }^{h}})}^{3}}$ скалярным произведением

Здесь ${{(\,,)}_{{{{\Omega }^{h}}}}}$ – скалярное произведение в пространстве Лебега ${{L}^{2}}({{\Omega }^{h}})$, а нужные свойства полуторалинейной формы (5.2) обеспечены [18] неравенством Корна в липшицевой области (1.4). Формула

определяет положительный, симметричный и непрерывный, а значит, самосопряженный оператор ${{\mathcal{K}}^{h}}$ в $\mathcal{H}({{\Omega }^{h}})$. Согласно определениям (5.3) и (5.2) вариационная формулировка задачи (1.3) равносильна абстрактному уравнению с новым спектральным параметром

Поскольку вложение $\mathcal{H}({{\Omega }^{h}}) \subset {{L}^{2}}{{({{\Omega }^{h}})}^{3}}$ компактно при $h > 0$, в силу общих результатов ([19], гл. 10) существенный спектр оператора ${{\mathcal{K}}^{h}}$ – единственная точка $K = 0$, а дискретный спектр – бесконечно малая положительная последовательность

образованная из последовательности (1.5) по правилу (5.4).

Утверждение

известно [20] как лемма о “почти собственных” числах и обеспечено ([19], гл. 6) спектральным разложением резольвенты.

Пусть ${{u}^{0}} \in \mathcal{H}(\Omega )$ – захваченная волна, ${{{\mathbf{u}}}^{h}}$ – ее сужение на ${{\Omega }^{h}}$ и ${{{\mathbf{K}}}^{h}} = {{(1 + {{\Lambda }^{0}})}^{{ - 1}}}$. При помощи одного из определений гильбертовой нормы находим

Здесь супремум вычисляется по единичному шару в $\mathcal{H}({{\Omega }^{h}})$, т.е. $\left\| {{{\text{v}}^{h}};\mathcal{H}({{\Omega }^{h}})} \right\| \leqslant 1$, а при переходе к интегралу по торцу ${{\omega }^{h}}$ была применена формула интегрирования по частям и учтено, что ${{u}^{0}}$ – решение задачи (1.2).

Для оценки величины (5.7) применим известное [1, 21] весовое анизотропное неравенство Корна

и сопутствующие следовые неравенства

В силу формул (3.12) и (2.11), (2.12) вектор-функция

удовлетворяет условиям ортогональности которые позволяют в интеграле по ${{\omega }^{h}}$ из соотношения (5.7) произвести замену $\text{v}_{j}^{h} \mapsto \text{v}_{j}^{h} - \bar {v}_{j}^{h}$ и затем применить уточненное неравенство (5.9). Поскольку ${{u}^{0}} \in \mathcal{H}({{\Omega }^{h}})$ – полиномиальная захваченная волна, в ее представлении около вершины пика отсутствуют неэнергетические и распространяющиеся волны, но присутствуют энергетические волны. Таким образом, справедливо [3] соотношение

В итоге получаем оценку величины (5.7)

Наконец, утверждение (5.6) подтверждает справедливость оценки (5.1), так как

Для экспоненциальных захваченных волн вычисления значительно упрощаются.

6. Пограничный слой вблизи обломанного кончика пика. Распространяющиеся волны $u_{{(j)}}^{{i \pm }}$ порождают вектор напряжений $T_{{(j)}}^{{i \pm }}$ = $D{{({{e}_{{(3)}}})}^{ \top }}AD(\nabla )u_{{(j)}}^{{i \pm }}$, для которых мажоранта в оценке (5.10) превращается в $c{{z}^{{ - 5/2}}}$ и не позволяет доказать, что величина ${{\delta }_{h}}$ – бесконечно малая при $h \to + 0$. Как обычно ([22], гл. 5 и гл. 16), для компенсации нежелательно большой невязки в краевом условии на ${{\omega }^{h}}$ приходится строить пограничный слой. Растяжение координат

и формальный переход к $h = 0$ трансформируют область (1.4) в полубесконечный цилиндр $\Xi = \omega \times {{\mathbb{R}}_{ + }}$ с боковой поверхностью $\Gamma = \partial \omega \times {{\mathbb{R}}_{ + }}$ и порождают задачу теории упругости

В силу классического принципа Сен-Венана (см., например, [23] и ср. математическую формулировку принципа [16], гл. 5) задача (6.1) имеет единственное решение $W \in {{H}^{1}}{{(\Xi )}^{3}}$, затухающее при ${{\xi }_{3}} \to + \infty $ с экспоненциальной скоростью, в том и только в том случае, если внешняя нагрузка на торце цилиндра самоуравновешена

Строение матрицы жестких смещений $d(\xi )$ согласовано со строением матриц $D$ и ${\mathbf{Y}}$ из списков (2.3) и (2.11)

Рассмотрим какое-либо решение $w$ системы (2.14) и восстановим [3] по нему трехмерное поле смещений $u$ в ${{\Pi }^{{d/2}}}$, главную часть невязки которого в краевом условии на ${{\omega }^{h}}$ нужно компенсировать слагаемым типа пограничного слоя и потому подчинить условию ортогональности (6.2). Представление (2.4) с начальными членами (2.5) дает соотношение

Вычислим интеграл (6.2). При учете формул (2.10), (2.11), (2.15) и (6.3) находим

Два нулевых столбца в (6 × 6)-матрице (6.4) – следствие равенств (2.13), которые вместе с представлениями (6.3) и (2.9), (2.8) приводят к формуле

Итак, согласно определению (3.1) матрицы ${\mathbf{M}}$ требование (6.2) затухания пограничного слоя, компенсирующего невязку поля $u$ в краевых условиях на ${{\omega }^{h}}$, эквивалентно равенствам

Соотношения (6.5) – естественные краевые условия (терминология [24]) для усеченной системы (3.2) двух обыкновенных дифференциальных уравнений четвертого порядка. Шесть скалярных равенств в списке (6.5), (6.6) – естественные краевые условия для полной системы (2.14).

7. “Мигающие” собственные частоты. Зафиксируем точку ${{\Lambda }^{0}} > {{\Lambda }^{\dag }}$ и сначала рассмотрим ситуацию (3.10), в которой имеются две распространяющиеся волны $u_{{(1)}}^{{i \pm }}$ с мнимыми показателями $\kappa _{1}^{{i \pm }} = \pm i\kappa _{1}^{i}$, а также три энергетические $u_{{(p)}}^{{r + }}$ и три неэнергетические $u_{{(p)}}^{{r - }}$ волны; здесь $p = 1,2,3$, а соответствующие показатели $ \pm \kappa _{1}^{r}$ и $ \pm \kappa _{2}^{r}$, $ \pm \kappa _{3}^{r}$ – вещественные корни биквадратных уравнений (3.3) при $j = 1$ и $j = 2$.

В качестве главного члена асимптотики собственной моды задачи (1.3) возьмем решение (4.5) задачи (1.2), а в качестве поправки – линейную комбинацию неэнергетических волн с малыми коэффициентами

Срезающая функция $\chi $ взята из разложения (4.5). В этом разложении поля $Z$ помимо слагаемых $u_{{(1)}}^{{i + }}$ и $Su_{{(1)}}^{{i - }}$ фигурируют энергетические волны, которые привносят в краевое условие на ${{\omega }^{h}}$ невязки следующего порядка по сравнению с $O({{h}^{{ - 5/2}}})$. Излишний рост $O({{h}^{{ - \kappa _{p}^{r} - 5/2}}})$ невязки, порожденной волной $u_{{(p)}}^{{r - }}$, компенсируется множителем ${{h}^{{\kappa _{p}^{r}}}}$. Таким образом, при построении пограничного слоя следует учесть решение системы (2.14)

Обозначив $a_{1}^{ - } = 1$ и $a_{1}^{ + } = S$, приводим соотношения (6.5) к виду

Согласно связи (3.7) фрагментов ${{w}_{\# }}$ и ${{w}_{ \bullet }}$ вектора (7.3) равенство (6.6) выполнено автоматически. Поскольку столбцы $\mathcal{W}_{\# }^{1}$ и $\mathcal{W}_{\# }^{2}$ взаимно ортогональны, выводим из системы (7.4) четырех линейных алгебраических уравнений, что ${{a}_{2}} = 0$ и ${{a}_{3}} = 0$. Исключив из системы еще одну неизвестную ${{a}_{1}}$, приходим к формулам при $j = 1$

Вернемся к обозначениям $1 = a_{1}^{ - }$, $S = a_{1}^{ + }$ и обнаружим, что вектор-функция (7.3) удовлетворяет ограничениям (6.5) и (6.6) в том и только в том случае, если

В результате для бесконечно малой последовательности

главный член невязки, оставленной суммой (7.1) в краевом условии на торце ${{\omega }^{h}}$, можно компенсировать экспоненциально затухающим пограничным слоем. Кроме того, согласно определению (7.2) малые невязки $O({{h}^{{{{\kappa }_{{min}}}({{\Lambda }^{0}})}}})$, порожденные произведением $\chi u_{{(ne)}}^{h}$ в задаче (1.2) обращаются в нуль на множестве ${{\Pi }^{{d/2}}}{\text{/}}{{\Pi }^{h}}$ и могут быть обработаны при помощи весового неравенства Корна (5.8). В результате некоторые усложнения выкладок из разд. 6 применительно к “почти собственному” вектору u^h = Z + $\chi u_{{(ne)}}^{h} + {{h}^{{ - 1/2}}}Z$ позволяют на основе утверждений (5.6) и (5.11) найти СЧ $\Lambda _{{p({{h}_{n}})}}^{{{{h}_{n}}}}$ задачи (1.3), для которого верна оценка (5.1) с бесконечно малым множителем

Итак, периодически в логарифмическом масштабе $\left| {lnh} \right|$ с периодом $\pi {\text{/}}\kappa _{1}^{i}({{\Lambda }^{0}})$ возникает СЧ задачи (1.3), расположенное в непосредственной близости к зафиксированной точке ${{\Lambda }^{0}} \in (\Lambda _{1}^{\dag },\Lambda _{2}^{\dag })$. В промежутках между критическими размерами (7.7) малая окрестность точки ${{\Lambda }^{0}}$ освобождается от СЧ из последовательности (1.5), если только вблизи нет “малоподвижных” СЧ (разд. 5). Такое поведение спектра при $h \to + 0$ можно ассоциировать с “миганием” СЧ.

8. “Планирующие” собственные частоты. Неравномерное растяжение координат

переводит множество ${{\Pi }^{d}}{\backslash }{{\Pi }^{h}}$ в множество ${{\Pi }^{{d{\mathbf{h}}/h}}}{\backslash }{{\Pi }^{{\mathbf{h}}}}$. Таким образом, при малой разности $h - {\mathbf{h}}$ существует “почти тождественный” диффеоморфизм области ${{\Omega }^{h}}$ на область ${{\Omega }^{{\mathbf{h}}}}$. Согласно общей теории возмущений линейных операторов ([25], гл. 7) в последовательностях (1.5) можно найти семейства СЧ $\{ \Lambda _{{p(h)}}^{h}\} $, непрерывно зависящих от малого параметра $h > 0$.

Пусть ${{\Lambda }^{0}} = \Lambda _{{p({{h}_{n}})}}^{{{{h}_{n}}}}$. Используя соотношение (7.6) и вытекающие из формул (3.5) и (3.4) равенства

вычисляем производную

Соотношение (8.1) означает, что СЧ из упомянутых семейств двигаются вниз вдоль интервала $(\Lambda _{1}^{\dag },\Lambda _{2}^{\dag })$ с большой скоростью $O({{h}^{{ - 1}}}{{\left| {lnh} \right|}^{{ - 1}}})$, пересекая каждую точку ${{\Lambda }^{0}}$ ∈ ∈ $(\Lambda _{1}^{\dag },\Lambda _{2}^{\dag })$ “почти периодически” в логарифмическом масштабе. Вместе с тем скорость спадает до нуля при приближении $\Lambda _{{p(h)}}^{h}$ к $\Lambda _{1}^{\dag }$, т.е. СЧ “плавно садятся” на порог $\Lambda _{1}^{\dag }$. Аналогичный режим свойственен парашютистам в затяжном прыжке, что отражено в термине “планирующие” СЧ.

Планирующие СЧ имеют общий предел $\Lambda _{1}^{\dag }$, т.е. при $h \to + 0$ происходит концентрация спектра (1.5) около нижнего порога непрерывного спектра задачи (1.2) в теле $\Omega $.

Тот факт, что каждая точка ${{\Lambda }^{0}} \in (\Lambda _{1}^{\dag },\Lambda _{2}^{\dag })$ – истинное СЧ задачи (1.3) для бесконечно малой последовательности длин обломков ${{\Pi }^{h}}$, во-первых, подтверждает правильность термина “мигающий” (в разд. 7 показано лишь то, что такое число расположено вблизи ${{\Lambda }^{0}}$) и, во-вторых, представляет новый способ формирования непрерывного спектра на участке $(\Lambda _{1}^{\dag },\Lambda _{2}^{\dag })$ из семейства дискретных спектров (1.5) задач (1.3) в ${{\Omega }^{h}}$.

9. “Блуждающие” собственные частоты. Пусть ${{\Lambda }^{0}} > \Lambda _{2}^{\dag }$, т.е. реализуется ситуация (3.11) и имеются две пары мнимых $ \pm i\kappa _{j}^{i}$ и две пары вещественных $ \pm \kappa _{j}^{r}$ корней биквадратных уравнений (3.3), $j = 1,2$. В качестве главного члена асимптотики (7.1) собственной вектор-функции ${{u}^{h}}$ задачи (1.3) возьмем линейную комбинацию $Z$ дифракционных решений (4.4), а основную поправку составим из неэнергетических полей $u_{{(j)}}^{{r \pm }}$

Равенства (6.6) для решения (9.1) системы (2.14) выполнены автоматически, а равенства (6.5), спроецированные на взаимно ортогональные СВ $\mathcal{W}_{\# }^{j}$ матрицы ${\mathbf{M}}(1)$, порождают систему четырех алгебраических уравнений

Исключив неизвестные ${{a}_{1}}$ и ${{a}_{2}}$, получаем связи (7.5) коэффициентов $a_{j}^{ - }$ и $a_{j}^{ + }$, которые согласно соотношениям (9.1) превращаем в систему двух уравнений для столбца b = = ${{({{b}_{1}},{{b}_{2}})}^{ \top }}$

Итак, условие экспоненциального затухания пограничного слоя, компенсирующего невязку суммы (7.1) в краевом условии на торце ${{\omega }^{h}}$ и позволяющего обосновать асимптотику СЧ задачи (1.3) в ${{\Omega }^{h}}$, привело к системе трансцендентных уравнений (9.2), т.е. длина $h$ обломка ${{\Pi }^{h}}$ находится из требования: единица – СЧ пучка

Если $\Omega $ – изотропное упругое тело, а сечение $\omega $ симметрично относительно обеих осей системы координат $y = ({{y}_{1}},{{y}_{2}})$, то $\Lambda _{1}^{\dag } = \Lambda _{2}^{\dag }$, реализуется именно ситуация (3.11) и

В итоге матрица (9.3) лишь постоянным множителем отличается от единичной $(2 \times 2)$-матрицы, а значит, при

соотношение (9.2) выполнено для СВ ${{b}^{k}}$ унитарной матрицы рассеяния $S$, отвечающих ее СЧ ${{e}^{{i{{\Theta }_{k}}}}}$. Таким образом, как и в разд. 7, наблюдаем эффект “мигания” СЧ.

Аналогичный вывод справедлив и для анизотропного тела с асимметричным пиком, если только $\kappa _{1}^{i} = \kappa _{2}^{i}$, причем в качестве ${{e}^{{i{{\Theta }_{k}}}}}$ в определении (9.4) критических длин ${{h}_{{nk}}}$ выступают СЧ унитарной матрицы ${{R}^{{ - 1/2}}}S{{R}^{{ - 1/2}}}$, где $R = {\text{diag}}\{ {{e}^{{i{{\theta }_{1}}}}},{{e}^{{i{{\theta }_{2}}}}}\} $. Кроме того, согласно формуле (9.3) СЧ пучка (9.4) при $h \to + 0$ обегают с большой скоростью единичную окружность $\mathbb{S} \subset \mathbb{C}$ в направлении против часовой стрелки.

В случае $\kappa _{1}^{i} \ne \kappa _{2}^{i}$ и ${{\Lambda }^{0}} > \Lambda _{2}^{\dag }$ СЧ пучка (9.4) хаотично двигаются по окружности $\mathbb{S}$ на комплексной плоскости, а направление их движения может изменяться сколь угодно много раз при $h \to + 0$. В двух ситуациях, когда семейства $\{ \Lambda _{{p(h)}}^{h}\} $, непрерывно зависящие от параметра $h > 0$, пересекают точку $ - 1 \in \mathbb{S}$ или приближаются к ней, в малой окрестности выбранной точки ${{\Lambda }^{0}}$ появляется элемент последовательности (1.5). Вместе с тем установить какой-либо закон движения семейств не удается, и поэтому соответствующие СЧ называем “блуждающими”. По доказанному [1, 3] непрерывный спектр задачи (1.2) покрывает луч ($\Lambda _{2}^{\dag }$, $ + \infty $) и правомочна гипотеза: для каждой точки ${{\Lambda }^{0}} > \Lambda _{2}^{\dag }$ найдется такая бесконечно малая последовательность $\{ {{h}_{n}}({{\Lambda }^{0}})\} $, что расстояние от –1 до СЧ пучка (9.4) при $h = {{h}_{n}}({{\Lambda }^{0}})$ стремится к нулю при $h \to + 0$.

Работа финансово поддержана Российским научным фондом (17-11-01003).