Прикладная математика и механика, 2019, T. 83, № 2, стр. 331-340

КОНТАКТНАЯ ЗАДАЧА ДЛЯ ЦИЛИНДРИЧЕСКОГО ВОЛНОВОДА ПЕРИОДИЧЕСКОЙ СТРУКТУРЫ

М. И. Чебаков^*, Е. М. Колосова^**

Институт математики, механики и компьютерных наук им. И.И. Воровича, Южный федеральный университет
Ростов-на-Дону, Россия

^* E-mail: michebakov@yandex.ru
^** E-mail: a_lena_ch@mail.ru

Поступила в редакцию 03.04.2018
После доработки 06.07.2018
Принята к публикации 25.12.2018

DOI: 10.1134/S0032823519020048

Полный текст (PDF)

Аннотация

Исследуется осесимметричная задача о возбуждении штампом крутильных колебаний в цилиндрическом волноводе с периодически изменяющимися механическими свойствами вдоль продольной координаты. Отрезок рассматриваемого волновода, соответствующий минимальному периоду изменения механических свойств, может состоять из любого количества однородных областей (конечные цилиндры) разной длины и с разными упругими постоянными. Использован метод, связанный с построением специального “оператора перехода”, который позволяет по значениям вектора перемещений и тензора напряжений на одном поперечном сечении волновода находить их значения на другом поперечном сечении, отстоящем от первого на расстоянии, равном величине минимального периода изменения свойств волновода. Получены соотношения для вычисления собственных чисел оператора перехода, исследование которых позволяет определить интервалы частот, когда в волноводе могут распространяться как затухающие, так и незатухающие колебания. Определены контактные напряжения под штампом для относительно больших радиусов цилиндра.

Ключевые слова: контактное взаимодействие, цилиндрический волновод, распространение колебаний, интегральное уравнение

Значительное число публикаций по проблеме распространения колебаний в телах периодической структуры появилось в 1950-х годах. Здесь, прежде всего, следует отметить исследования по распространению колебаний в периодических волноводах, связанные с проблемами акустики, механики, электромагнетизма и квантовой механики [1–4] и позволившие обнаружить при определенных условиях чередующиеся интервалы частот запирания волноводов и резонансы на этих частотах. Была вскрыта общность волновых явлений в акустике, механике, электромагнетизме и квантовой механике, причем общим для рассматриваемой широкой совокупности физических систем является периодичность их структуры [2].

В теории акустических волноводов с периодически меняющимися свойствами, по всей видимости, впервые, был применен [3] метод Флоке–Ляпунова. Этот метод также был использован [5] при изучении распространения сдвиговых стационарных волн в слое с периодической системой внешних разрезов. Рассматривались задачи о возбуждении волн и динамика разрушения в упругих системах периодической структуры [6]. В рамках одномерного приближения исследованы волноводные и резонансные свойства неоднородных одномерно-периодических структур, состоящих из двух различных сред, определены полосы пропускания и запирания, исследованы резонансные явления в периодических средах и структурах [7].

На основе подхода, излагаемого ниже, рассматривались плоская и антиплоская задачи для волновода в виде упругой полосы с периодической кусочно-однородной структурой механических свойств [8–10]. Для таких волноводов показано, что существуют чередующиеся промежутки изменения частоты, где волновод соответственно открыт или заперт, на тех промежутках изменения частоты, где волновод заперт, существуют резонансы. Также рассмотрена [10] задача о возбуждении штампом крутильных колебаний периодически кусочно-однородного сплошного цилиндра, подход к решению которой будет использован ниже.

Практическим приложениям теории распространения колебаний в периодических структурах также посвящены многие работы (см., например, [11–14]).

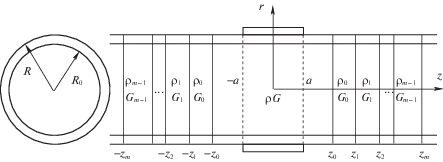
1. Постановка задачи. Рассмотрим полый упругий цилиндр ($r,\,\varphi ,z$ – цилиндрические координаты)

${{R}_{0}} \leqslant r \leqslant R,\quad {\text{|}}z{\text{|}} < \infty $

Его часть ${\text{|}}z{\text{|}} \leqslant {{z}_{0}}$ имеет модуль сдвига $G$ и плотность $\rho $, а части

${{z}_{n}} + kL < {\text{|}}z{\text{|}} < {{z}_{{n + 1}}} + kL;\quad n = 0,1,2,\;...,\;m - 1;\quad k = 0,1,2,\;...,\;\infty $

имеют соответственно модули сдвига ${{G}_{n}}$ и плотности ${{\rho }_{n}}$. Обозначим

${{z}_{{n + 1}}} - {{z}_{n}} = {{l}_{n}},\quad {{z}_{m}} - {{z}_{0}} = L,$

где L – период изменения упругих свойств материала цилиндра вдоль продольной координаты $z$ влево и вправо соответственно от точек $z = - {{z}_{0}}$ и $z = {{z}_{0}}$, m – количество однородных участков в периоде. На внешней поверхности $r = R$ цилиндра в области $\left| z \right| \leqslant a$ закреплен жесткий штамп, который совершает крутильные колебания вокруг оси $z$ под действием момента ${{M}_{0}} = M{{e}^{{ - i\omega t}}}$, а внутренняя и внешняя поверхности цилиндра вне штампа свободны от напряжений (см. фиг. 1).

Фиг. 1.

К постановке задачи

В случае установившихся колебаний угловое перемещение в цилиндре традиционно представим в виде

$v(r,z,t) = V(r,z){{e}^{{ - i\omega t}}}$

Тогда для определения функции $V(r,z)$ получим уравнение

(1.1)

$\begin{gathered} \Delta V(r,z) - \frac{1}{{{{r}^{2}}}}V(r,z) + \frac{{\partial G(z)}}{{\partial z}}V(r,z) + {{a}^{2}}(z)V(r,z) = 0 \\ \Delta = \frac{{{{\partial }^{2}}}}{{\partial {{r}^{2}}}} + \frac{1}{r}\frac{\partial }{{\partial r}} + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}},\quad {{a}^{2}}(z) = \frac{{\rho (z){{\omega }^{2}}}}{{G(z)}} \\ \end{gathered} $

Здесь $\omega $ – частота колебаний, $\rho (z)$ и $G(z)$ – плотность и модуль сдвига, представленные кусочно-однородными функциями координаты $z$.

В соответствии с поставленной задачей будем полагать, что

(1.2)

$\begin{gathered} \rho (z) = {{\rho }_{n}},\quad G(z) = {{G}_{n}}\quad {\text{п р и }}\quad {{z}_{n}} + kL < {\text{|}}z{\text{|}} < {{z}_{{n + 1}}} + kL \\ n = 0,1,\;...,\;m;\quad k = 0,1,\;... \\ \rho (z) = \rho ,\quad G(z) = G\quad {\text{п р и }}\quad {\text{|}}z{\text{|}} < {{z}_{0}}, \\ \end{gathered} $

где ${{\rho }_{n}}$, ${{G}_{n}}$, $\rho $, $G$ – постоянные величины, и введем обозначения

(1.3)

$a(z) = \left\{ {\begin{array}{*{20}{l}} {{{a}_{n}}\quad {\text{п р и }}\quad {{z}_{n}} + kL < \left| z \right| < {{z}_{{n + 1}}} + kL;\quad n = 0,1,\;...,\;m;\quad k = 0,1,...} \\ {{{a}_{*}}\quad {\text{п р и }}\quad \left| z \right| < {{z}_{0}}} \end{array}} \right.$

В итоге приходим к краевой задаче для уравнения (1.1) с граничными условиями

(1.4)

$\begin{gathered} V(r,z) = R\delta \quad {\text{п р и }}\quad {\text{|}}z{\text{|}} < a < {{z}_{0}},\quad r = R \\ \tau (r,z) = G\left( {\frac{\partial }{{\partial r}}V(r,z) - \frac{1}{r}V(r,z)} \right) = 0\quad\quad {\text{п р и }}\quad r = {{R}_{0}}\quad\quad {\text{и п р и }}\quad r = R,\quad {\text{|}}z{\text{|}} > a, \\ \end{gathered} $

где $\delta $ – амплитуда угла поворота штампа, $r = R$, ${\text{|}}z{\text{|}} < a$ – область контакта,

${{\tau }_{{r\varphi }}}(r,z,t) = \tau (r,z)\,{{e}^{{ - i\omega \;t}}},$

${{\tau }_{{r\varphi }}}(r,z,t)$ – касательные напряжения. Последнее условие (1.4) означает отсутствие напряжений на свободных поверхностях цилиндра.

2. Построение оператора перехода. Для того чтобы избежать решения дифференциального уравнения (1.1) с переменными коэффициентами, на первом этапе построим специальный оператор перехода, позволяющий по значениям вектора перемещений и тензора напряжений при $z = {{z}_{0}}$ находить их значения при $z = {{z}_{m}}$. На втором этапе будет дан анализ собственных чисел и собственных функций оператора перехода, что позволит проанализировать характер распространения колебания в цилиндре. В дальнейшем будут удовлетворены условия на бесконечности и построено интегральное уравнение поставленной динамической контактной задачи, для решения которого будет использован “метод больших $\lambda $”, предложенный В.М. Александровым [15].

Для построения оператора перехода рассмотрим уравнение (1.1) для полубесконечного полого однородного упругого цилиндра $z \geqslant {{z}_{n}}$ ($0 \leqslant n \leqslant m - 1$), ${{R}_{0}} < r < R$ с плотностью $\rho (z) = {{\rho }_{n}}$ и модулем Юнга $G(z) = {{G}_{n}}$ когда на цилиндрических поверхностях отсутствуют напряжения, а на торце при $z = {{z}_{n}}$ заданы касательные напряжения и перемещения. В этом случае получим соответствующую задачу для уравнения (1.1) с граничными условиями

(2.1)

$\begin{gathered} V(r,{{z}_{n}}) = {{f}_{1}}(r),\quad {{\tau }_{n}}(r) = \tau {\text{*}}(r,{{z}_{n}}) = {{\left. {{{G}_{n}}\frac{\partial }{{\partial z}}V(r,z)} \right|}_{{z = {{z}_{0}}}}} = {{f}_{2}}(r) \\ \tau {\text{*}}(r,z){{e}^{{ - i\omega t}}} = {{\tau }_{{z\varphi }}}(r,z,t) \\ \tau (r,z) = G\left( {\frac{\partial }{{\partial r}}V(r,z) - \frac{1}{r}V(r,z)} \right) = 0\quad {\text{п р и }}\quad r = {{R}_{0}}\quad {\text{и }}\quad r = R \\ \end{gathered} $

Для того чтобы удовлетворить граничным условиям (2.1), построим однородные решения для полого бесконечного цилиндра при отсутствии напряжений на цилиндрических поверхностях и возьмем их суперпозицию. Введя обозначения

${{\Delta }_{{\xi \eta }}}({{\kappa }_{k}};p,q) = {{J}_{\xi }}(p{{\kappa }_{k}}){{Y}_{\eta }}(q{{\kappa }_{k}}) - {{J}_{\eta }}(q{{\kappa }_{k}}){{Y}_{\xi }}(p{{\kappa }_{k}}),\quad \xi ,\eta = 1,2$

получим

(2.2)

$\begin{gathered} V(r,z) = \sum\limits_{k = 0}^\infty {({{C}_{k}}{{e}^{{ - i{{\alpha }_{{nk}}}z}}} + {{D}_{k}}{{e}^{{i{{\alpha }_{{nk}}}z}}}){{F}_{k}}} (r);\quad {{\alpha }_{{nk}}} = \sqrt {a_{n}^{2} - \kappa _{k}^{2}} \\ {{F}_{0}}(r) = r{\text{/}}R,\quad {{F}_{k}}(r) = {{\Delta }_{{12}}}({{\kappa }_{k}};r,R)\quad (k \geqslant 1), \\ \end{gathered} $

где ${{J}_{k}}(r)$ и ${{Y}_{k}}(r)$ – функции Бесселя, постоянные ${{\kappa }_{k}}$ – положительные корни уравнения

(2.3)

${{\Delta }_{{22}}}({{\kappa }_{k}};R,{{R}_{0}}) = 0$

Можно показать, что функции ${{F}_{k}}(r)$ ортогональны на отрезке $[{{R}_{0}},R]$, т.е. (${{\delta }_{{nk}}}$ – символ Кронекера)

(2.4)

$\begin{gathered} \int\limits_{{{R}_{0}}}^R {{{F}_{k}}(r){{F}_{n}}(r)rdr} = {{\delta }_{{nk}}}{{F}_{{kk}}};\quad {{F}_{{00}}} = \frac{{{{R}^{4}} - R_{0}^{4}}}{{4{{R}^{2}}}} \\ {{F}_{{kk}}} = \frac{1}{2}{{\left[ {\frac{{{{Y}_{2}}(R{{\kappa }_{k}})}}{{{{Y}_{2}}({{R}_{0}}{{\kappa }_{k}})}}} \right]}^{2}}\{ {{[R{{\Delta }_{{12}}}({{\kappa }_{k}};R,{{R}_{0}})]}^{2}} - {{[{{R}_{0}}{{\Delta }_{{12}}}({{\kappa }_{k}};{{R}_{0}},{{R}_{0}})]}^{2}}\} \quad (k \geqslant 1) \\ \end{gathered} $

Используя это условие ортогональности, из условий (2.1) получаем систему для определения ${{C}_{k}}$ и ${{D}_{k}}$

${{C}_{k}}{{e}^{{ - i{{\alpha }_{k}}{{z}_{n}}}}} + {{( - 1)}^{{\xi + 1}}}{{D}_{k}}{{e}^{{i{{\alpha }_{k}}{{z}_{n}}}}} = \frac{1}{{{{F}_{{kk}}}}}\left( {{{\delta }_{{1\xi }}} + {{\delta }_{{2\xi }}}\frac{i}{{{{G}_{n}}{{\alpha }_{k}}}}} \right)\int\limits_{{{R}_{0}}}^R {{{f}_{\xi }}(r){{F}_{k}}(r)rdr} ,\quad \xi = 1,2$

Выразив отсюда постоянные ${{C}_{k}}$ и ${{D}_{k}}$ и подставляя их значения в ряд (2.2), найдем $V(r,z)$ и $\partial V(r,z){\text{/}}\partial z$ при $z = {{z}_{{n + 1}}}$. После несложных преобразований построим оператор перехода

(2.5)

$\begin{gathered} {{{\mathbf{b}}}^{{n + 1}}}(r) = \sum\limits_{k = 0}^\infty {\frac{{{{F}_{k}}(r)}}{{{{F}_{{kk}}}}}} {\mathbf{A}}_{k}^{n}\int\limits_{{{R}_{0}}}^R {{{F}_{k}}(t){{{\mathbf{b}}}^{n}}(t)tdt} \\ {{{\mathbf{b}}}^{n}}(r) = \left( \begin{gathered} {{V}_{n}}(r) \hfill \\ {{\tau }_{n}}(r) \hfill \\ \end{gathered} \right),\quad {\mathbf{A}}_{k}^{n} = \left( {\begin{array}{*{20}{c}} {\cos {{\alpha }_{{nk}}}{{l}_{n}}}&{{{{({{G}_{n}}{{\alpha }_{{nk}}})}}^{{ - 1}}}\sin {{\alpha }_{{nk}}}{{l}_{n}}} \\ { - {{G}_{n}}{{\alpha }_{{nk}}}\sin {{\alpha }_{{nk}}}{{l}_{n}}}&{\cos {{\alpha }_{{nk}}}{{l}_{n}}} \end{array}} \right) \\ {{\tau }_{n}}(r) = \tau {\text{*}}(r,{{z}_{n}}),\quad {{V}_{n}}(r) = V(r,{{z}_{n}}),\quad {{l}_{n}} = {{z}_{{n + 1}}} - {{z}_{n}}, \\ \end{gathered} $

позволяющий находить перемещения и напряжения в сечениях $z = {{z}_{{n + 1}}}$ через их значения при $z = {{z}_{n}}$. Здесь ${{V}_{n}}(r){{e}^{{ - i\omega t}}}$ и ${{\tau }_{n}}(r){{e}^{{ - i\omega t}}}$ перемещения и напряжения в сечении $z = {{z}_{n}}$.

Применяя последовательно m-кратно оператор (2.5) для преобразования вектора ${{{\mathbf{b}}}^{k}}(r)$ в вектор ${{{\mathbf{b}}}^{{k + 1}}}(r)$ ($k = 0,1,\;...,\;m - 1$), можно теперь выразить вектор ${{{\mathbf{b}}}^{m}}(r)$ через ${{{\mathbf{b}}}^{0}}(r)$. В результате получим искомый оператор перехода

(2.6)

${{{\mathbf{b}}}^{m}}(r) = {{\Phi }^{m}}({{{\mathbf{b}}}^{0}}(\tau )) = \sum\limits_{k = 0}^\infty {\frac{{{{F}_{k}}(r)}}{{{{F}_{{kk}}}}}{\mathbf{\Phi }}_{k}^{m}\int\limits_{{{R}_{0}}}^R {{{F}_{k}}(\tau ){{{\mathbf{b}}}^{0}}(\tau )\tau d\tau } } ,\quad {\mathbf{\Phi }}_{k}^{m} = \prod\limits_{n = m - 1}^0 {{\mathbf{A}}_{k}^{n}} ,$

который позволяет находить перемещения и напряжения в сечении $z = {{z}_{m}}$ через их значения при $z = {{z}_{0}}$. Здесь ${\mathbf{\Phi }}_{k}^{m}$ – матрица второго порядка с элементами $a_{{ij}}^{{mk}}$ ($i = 1,2$, $j = 1,2$).

Если необходимо найти напряжения и перемещения в сечении $z \in \,({{z}_{n}},\;{{z}_{{n + 1}}})$, то в выражении для оператора (2.5) следует величину ${{l}_{n}}$ заменить ${{l}_{n}} = z - {{z}_{n}}$. Таким образом, соотношения (2.5) и (2.6) позволяют находить перемещения и напряжения в любом сечении $z \in ({{z}_{0}},{{z}_{{m + 1}}})$ через их значения в сечении $z = {{z}_{0}}$.

О собственных числах оператора ${{\Phi }^{m}}$. Напряжения и перемещения в сечениях $z = {{z}_{{m + iL}}}$ можно представить в виде разложений по собственным функциям оператора ${{\Phi }^{m}}$. Свойства рассматриваемого волновода будут определяться свойствами собственных функций (СФ) и собственных чисел (СЧ) этого оператора.

Используя представление единичного оператора в виде

$I(...) = \sum\limits_{k = 0}^\infty {\frac{{{{F}_{k}}(r)}}{{{{F}_{{kk}}}}}\int\limits_{{{R}_{0}}}^R {{{F}_{k}}(\tau ){\mathbf{I}}( \ldots )\tau d\tau } } ,\quad {\mathbf{I}} = \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right)$

из соотношения ${{\Phi }^{m}}({\mathbf{b}}) = \lambda \;{\mathbf{b}} = \lambda I({\mathbf{b}})$, где ${\mathbf{b}}$ – произвольный вектор, получим

(2.7)

$\sum\limits_{k = 0}^\infty {\frac{{{{F}_{k}}(r)}}{{{{F}_{{kk}}}}}({\mathbf{\Phi }}_{k}^{m} - \lambda {\mathbf{I}})\int\limits_{{{R}_{0}}}^R {{{F}_{k}}(\tau ){\mathbf{b}}(\tau )\tau d\tau } } = 0;\quad {\mathbf{\Phi }}_{k}^{m} = \{ a_{{ij}}^{k}\} $

СЧ $\lambda $ оператора ${{\Phi }^{m}}$ находятся из условия равенства нулю определителя некоторой клеточно-диагональной матрицы или ее диагональных матриц второго порядка:

(2.8)

${\text{|}}{\mathbf{\Phi }}_{k}^{m} - \lambda {\mathbf{I}}{\text{|}} = 0\quad {\text{и л и }}\quad \lambda _{k}^{2} - 2{{p}_{k}}{{\lambda }_{k}} + 1 = 0,\quad 2{{p}_{k}} = a_{{11}}^{k} + a_{{22}}^{k};\quad k = 0,1,2,\;...,$

где ${{p}_{k}} = {{p}_{k}}(\omega )$ – действительные числа. Здесь учтено, что определители матриц ${\mathbf{A}}_{k}^{n}$, а соответственно и матриц ${\mathbf{\Phi }}_{k}^{m}$, равны единице.

Обозначим через $\lambda _{k}^{1}$, $\lambda _{k}^{2}$ пары корней уравнения (2.8) для каждого k, при этом $\lambda _{k}^{1}\lambda _{k}^{2} = 1$. Расчеты СЧ показывают, что в зависимости от частоты $\omega $ и номера k их можно разделить на две группы: 1) $\operatorname{Im} (\lambda _{k}^{n})$ = 0 и $\lambda _{k}^{n} \ne \pm 1$, 2) $\operatorname{Im} (\lambda _{k}^{n})$ ≠ 0 и $\lambda _{k}^{n} = \pm 1$. При этом все комплексные СЧ находятся на единичной окружности. Будем считать, что в первой группе $\lambda _{k}^{1} < 1$, а $\lambda _{k}^{2} > 1$. Был проведен анализ СЧ $\lambda _{k}^{n}$ в зависимости от частоты $\omega $, номера k и числа m однородных областей с различными свойствами в периоде, который позволил установить существование чередующихся интервалов изменения частоты $\omega $, когда СЧ принадлежат к первой или второй группе. Возможны варианты, когда к первой группе принадлежат все СЧ. Ранее это было также отмечено для областей периодической структуры типа полуплоскости, полосы и сплошного цилиндра периодической структуры [3, 9, 10].

Условие на бесконечности. Используя представление перемещений и напряжений через линейную комбинацию СФ оператора перехода, для выполнения физически оправданных условий на бесконечности в группе СФ, соответствующих условию $\left| {\lambda _{k}^{n}} \right| \ne 1$, следует исключить в дальнейшем из рассмотрения СФ, соответствующие $\lambda _{k}^{2} > 1$ [10].

Для отбора СФ, соответствующих условию $\left| {\lambda _{k}^{n}} \right| = 1$, используем принцип фиктивного поглощения: в среду вводится малое внутреннее трение $\varepsilon \to 0$. В этом случае СЧ получат малое возмущение: $\lambda _{k}^{n}$ = $\lambda _{k}^{n}(\varepsilon )$, причем их модули будут больше или меньше единицы при разных n. Пусть $\left| {\lambda _{k}^{1}(\varepsilon )} \right| < 1$, а $\left| {\lambda _{k}^{2}(\varepsilon )} \right| > 1$. В этом случае также для выполнения физически оправданных условий на бесконечности в этой группе СФ следует в дальнейшем исключить из рассмотрения СФ, соответствующие $\left| {\lambda _{k}^{2}(\varepsilon )} \right| > 1$ [10].

3. Интегральное уравнение контактной задачи и его решение. Для нахождения контактных касательных напряжений под штампом в виде

(3.1)

${{\tau }_{{r\phi }}}(R,z,t) = q(z){{e}^{{ - i\omega t}}}$

построим интегральное уравнение, предварительно решив задачу для рассматриваемого в разд. 1 цилиндра, когда на части его внешней поверхности

(3.2)

$r = R,\quad \left| z \right| \leqslant a$

заданы контактные касательные напряжения (3.1), а остальная часть поверхности

(3.3)

$r = R,\quad \left| z \right| > a$

свободна от напряжений, также при этом свободна от напряжений и внутренняя поверхность $r = {{R}_{0}}$.

Решение такой задачи сконструируем из двух частей, содержащих неизвестные постоянные, которые будут определены из условия равенства напряжений и перемещений слева и справа от сечений $\left| z \right| = {{z}_{0}}$.

Первую часть решения при $\left| z \right| \leqslant {{z}_{0}}$ построим в виде следующей суммы: 1) решения задачи для бесконечного однородного цилиндра ${{R}_{0}} \leqslant r \leqslant R$ с параметрами $G$ и $\rho $, когда на части его внешней поверхности (3.2) заданы контактные касательные напряжения (3.1), а все остальные поверхности свободны от напряжений; с использованием преобразования Фурье по координате z получим ($\sigma $ – контур интегрирования, который совпадает почти везде с вещественной полуосью, обходя действительные положительные полюсы подынтегральной функции снизу, а отрицательные – сверху)

(3.4)

$\begin{gathered} {{V}_{N}}(r,z) = - \frac{1}{{2\pi G}}\int\limits_{ - a}^a {q(y)dy} \int\limits_\sigma {L(r,\alpha ){{e}^{{ - i\alpha \left( {z - y} \right)}}}d\alpha } \\ L(r,\alpha ) = \frac{{L_{{12}}^{ + }(r\tilde {\alpha },{{R}_{0}}\tilde {\alpha })}}{{\tilde {\alpha }L_{{22}}^{ - }({{R}_{0}}\tilde {\alpha },R\tilde {\alpha })}},\quad \tilde {\alpha } = \sqrt {{{\alpha }^{2}} - a_{{\text{*}}}^{2}} \\ L_{{\xi \eta }}^{ \pm }(p,q) = {{I}_{\xi }}(p){{K}_{\eta }}(q) \pm {{I}_{\eta }}(q){{K}_{\xi }}(p),\quad \xi ,\eta = 1,2, \\ \end{gathered} $

где ${{I}_{n}}(r)$ и ${{K}_{n}}(r)$ – модифицированные функции Бесселя, и 2) суперпозиции однородных решений для этого однородного полого цилиндра, когда его поверхности $r = R$ и $r = {{R}_{0}}$ свободны от напряжений:

(3.5)

${{V}_{0}}(r,z) = \sum\limits_{k = 0}^\infty {{{{\hat {C}}}_{k}}{{F}_{k}}(r)\cos {{\alpha }_{k}}z} ;\quad {{\alpha }_{k}} = \sqrt {a_{{\text{*}}}^{2} - \kappa _{k}^{2}} ,\quad a_{{\text{*}}}^{2} = \rho {{\omega }^{2}}{{G}^{{^{{ - 1}}}}}$

В итоге построим выражения

(3.6)

$\begin{array}{*{20}{c}} {{{\text{v}}_{ - }}(r,z,t) = {{V}_{ - }}(r,z){{e}^{{ - i\omega t}}},\quad {{\tau }_{{r\varphi }}}_{ - }(r,z,t) = {{\tau }_{ - }}(r,z){{e}^{{ - i\omega t}}}} \\ {{{V}_{ - }}(r,z) = {{V}_{N}}(r,z) + {{V}_{0}}(r,z),\quad {{\tau }_{ - }}(r,z) = G\frac{\partial }{{\partial z}}{{V}_{ - }}(r,z)} \end{array}$

Вторую часть решения

${{\text{v}}_{ + }}(r,z,t) = {{V}_{ + }}(r,z){{e}^{{ - i\omega t}}}$

при ${{z}_{0}} \leqslant z \leqslant {{z}_{1}}$ для цилиндра $z \geqslant {{z}_{0}}$ c периодически изменяющимися свойствами построим, воспользовавшись приведенными выше результатами для кусочно-однородного цилиндра $z \geqslant {{z}_{0}}$ с однородными граничными условиями.

Обозначим функцию $V(r,z)$, определенную равенствами (2.2), и $\tau (r,z)$ при $n = 0$ соответственно через ${{V}_{ + }}(r,z)$ и ${{\tau }_{ + }}(r,z)$, тогда

$\begin{gathered} {{V}_{ + }}(r,z) = \sum\limits_{k = 0}^\infty {({{C}_{k}}{{e}^{{ - i{{\alpha }_{{0k}}}z}}} + {{D}_{k}}{{e}^{{i{{\alpha }_{{0k}}}z}}}){{F}_{k}}(r)} \\ {{\tau }_{ + }}(r,z) = {{G}_{0}}\frac{\partial }{{\partial z}}{{V}_{ + }}(r,z) = i{{G}_{0}}\sum\limits_{k = 0}^\infty {{{\alpha }_{{0k}}}( - {{C}_{k}}{{e}^{{ - i{{\alpha }_{{0k}}}z}}} + {{D}_{k}}{{e}^{{i{{\alpha }_{{0k}}}z}}})} {{F}_{k}}(r) \\ \end{gathered} $

Подставляя в соотношение

(3.7)

${{{\mathbf{B}}}_{k}} = \int\limits_{{{R}_{0}}}^R {{{F}_{k}}(\tau ){{{\mathbf{b}}}^{0}}(\tau )\tau d\tau } = \left( \begin{gathered} {{B}_{{k1}}} \\ {{B}_{{k2}}} \\ \end{gathered} \right)$

значения вектора ${{{\mathbf{b}}}^{0}}(\tau )$ и используя условие ортогональности функций ${{F}_{k}}(\tau )$ (аналогичное условию (2.4)), получим

${{B}_{{k\xi }}} = \frac{{{{F}_{{kk}}}}}{2}({{\delta }_{{{\text{1}}\xi }}} + {{\delta }_{{{\text{2}}\xi }}}i{{G}_{0}}{{\alpha }_{{0k}}})({{( - 1)}^{{\xi + 1}}}{{C}_{k}}{{e}^{{ - i{{\alpha }_{{0k}}}{{z}_{0}}}}} + {{D}_{k}}{{e}^{{i{{\alpha }_{{0k}}}{{z}_{0}}}}}),\quad \xi = 1,2$

Согласно равенству (2.7) $({\mathbf{\Phi }}_{k}^{m} - \lambda {\mathbf{I}}){{\bar {B}}_{k}} = 0$, откуда найдем

(3.8)

${{B}_{{k2}}} = {{B}_{{k1}}}{{d}_{k}},\quad {{d}_{k}} = a_{{21}}^{{mk}}{\text{/}}(\lambda _{k}^{1} - a_{{22}}^{{mk}}),$

и соотношение (3.7) приводит к однородному уравнению, из которого выразим ${{C}_{k}}$ через ${{D}_{k}}$. В результате получим

(3.9)

${{C}_{k}} = {{D}_{k}}m_{k}^{{}}{{e}^{{2i{{\alpha }_{{0k}}}{{z}_{0}}}}},\quad {{m}_{k}} = \frac{{i{{\alpha }_{{0k}}}{{G}_{0}}(\lambda _{k}^{1} - a_{{22}}^{{mk}}) - a_{{21}}^{{mk}}}}{{i{{\alpha }_{{0k}}}{{G}_{0}}(\lambda _{k}^{1} - a_{{22}}^{{mk}}) + a_{{21}}^{{mk}}}},$

после чего найдем

(3.10)

$B_{k}^{1} = D_{k}^{{\text{*}}}(\lambda _{k}^{1} - a_{{22}}^{{mk}}),\quad B_{k}^{2} = D_{k}^{{\text{*}}}a_{{21}}^{{mk}},$

где $D_{k}^{{\text{*}}}$ – неизвестные постоянные.

Для нахождения напряжений и перемещений в сечениях $z = \operatorname{const} $ (${{z}_{0}} \leqslant z \leqslant {{z}_{1}}$) в формулах (2.5) положим $n = 1$ и ${{l}_{1}} = z - {{z}_{0}}$. В дальнейшем, перейдя к пределу в равенствах (2.5) при $z \to + {{z}_{0}}$, и с учетом того, что матрица $A_{k}^{1}$ станет единичной, получим

(3.11)

${{V}_{ + }}(r,{{z}_{0}}) = \sum\limits_{k = 0}^\infty {{{{\hat {D}}}_{k}}{{F}_{k}}(r){{\beta }_{k}}} ,\quad {{\tau }_{ + }}(r,{{z}_{0}}) = \sum\limits_{k = 0}^\infty {{{{\hat {D}}}_{k}}{{F}_{k}}(r)} ,\quad {{\beta }_{k}} = \frac{{\lambda _{k}^{1} - a_{{22}}^{{mk}}}}{{a_{{21}}^{{mk}}}},$

где $\hat {D}_{k}^{{}}$ – новые неизвестные постоянные.

Приравняв при $z = {{z}_{0}}$ соответствующие выражения (3.6) и (3.11), получим систему уравнений для определения неизвестных постоянных ${{\hat {C}}_{k}}$ и ${{\hat {D}}_{k}}$

(3.12)

${{V}_{ + }}(r,{{z}_{0}}) = {{V}_{ - }}(r,{{z}_{0}}),\quad {{\tau }_{ + }}(r,{{z}_{0}}) = {{\left. {G\frac{\partial }{{\partial z}}{{V}_{ - }}(r,z)} \right|}_{{z = {{z}_{0}}}}}$

Для построения интегрального уравнения (ИУ) относительно контактных напряжений понадобятся только величины ${{\hat {C}}_{k}}$.

Умножим правые и левые части уравнений (3.12) на $r{{F}_{n}}(r)$ и проинтегрируем по $r$ в пределах $[{{R}_{0}},R]$. Учитывая ортогональность функции ${{F}_{n}}(r)$, получим систему относительно ${{\hat {C}}_{k}}$ и ${{\hat {D}}_{k}}$

(3.13)

${{\hat {D}}_{k}}{{\beta }_{k}} - {{\hat {C}}_{k}}\cos {{\alpha }_{k}}{{z}_{0}} = {{T}_{{k1}}},\quad {{\hat {D}}_{k}} + G{{\alpha }_{k}}{{\hat {C}}_{k}}\sin {{\alpha }_{k}}{{z}_{0}} = {{T}_{{k2}}},$

где

(3.14)

${{T}_{{k1}}} = \frac{2}{{{{F}_{{kk}}}}}\int\limits_{{{R}_{0}}}^R {{{V}_{N}}(r,{{z}_{0}}){{F}_{k}}(r)rdr} ,\quad {{T}_{{k2}}} = {{\left. {\frac{{2G}}{{{{F}_{{kk}}}}}\frac{\partial }{{\partial z}}\int\limits_{{{R}_{0}}}^R {{{V}_{N}}(r,z){{F}_{k}}(r)rdr} } \right|}_{{z = {{z}_{0}}}}}$

Из системы (3.13) найдем

${{\hat {C}}_{k}} = ({{\beta }_{k}}{{T}_{{k2}}} - {{T}_{{k1}}}){\text{/}}{{\Delta }_{k}},\quad {{\Delta }_{k}} = \cos {{\alpha }_{k}}{{z}_{0}} + G{{\beta }_{k}}{{\alpha }_{k}}\sin {{\alpha }_{k}}{{z}_{0}}$

Проведя довольно громоздкие преобразования в формулах (3.14), получим

(3.15)

$\begin{gathered} {{{\hat {C}}}_{k}} = {{S}_{k}}\int\limits_{ - a}^a {q(y)\cos {{\alpha }_{k}}ydy} ,\quad {{S}_{k}} = - \frac{{{{L}_{k}}(\Delta _{k}^{{\text{*}}} - i{{\Delta }_{k}})}}{{G{{\Delta }_{k}}{{\alpha }_{k}}{{F}_{{kk}}}}},\quad {{L}_{k}} = \frac{{R{{Y}_{2}}({{\kappa }_{k}}R)}}{{{{Y}_{2}}({{\kappa }_{k}}{{R}_{0}})}}{{\Delta }_{{12}}}({{\kappa }_{k}};R,{{R}_{0}}) \\ \Delta _{k}^{{\text{*}}} = G{{\alpha }_{k}}{{\beta }_{k}}\cos {{\alpha }_{k}}{{z}_{0}} - \sin {{\alpha }_{k}}{{z}_{0}} \\ \end{gathered} $

Используя соотношения (3.4)–(3.7) и (3.15), найдем перемещения в неоднородном цилиндре $V(R,z)$ = ${{V}_{N}}(R,z)$ + ${{V}_{0}}(R,z)$ при $r = R$ в области $\left| z \right| \leqslant a$, а условие (1.4) позволит выписать ИУ для определения контактных напряжений $q(z)$. После преобразований получим искомое ИУ

(3.16)

$\begin{gathered} \int\limits_{ - 1}^1 {\varphi (y)k\left( {\frac{{z - y}}{\lambda }} \right)dy} = \pi {{a}^{{ - 1}}}G\delta (\left| z \right| \leqslant 1);\quad \varphi (y) = q(ay),\quad k(x) = {{k}_{1}}(x) + {{k}_{2}}(x) \\ {{k}_{1}}(x) = \int\limits_{{{\sigma }_{ + }}} {K(\alpha )\cos \alpha xd\alpha } ,\quad K(\alpha ) = \frac{{L(R,\alpha {\text{/}}R)}}{R} = \frac{{L_{{12}}^{ + }(\tilde {\eta },\mu \tilde {\eta })}}{{\tilde {\eta }L_{{22}}^{ - }(\mu \tilde {\eta },\tilde {\eta })}},\quad \tilde {\eta } = \sqrt {{{\alpha }^{2}} - {{\Omega }^{2}}} \\ {{k}_{2}}(x) = \sum\limits_{k = 0}^\infty {{{M}_{k}}\cos {{\alpha }_{k}}x} ,\quad {{M}_{k}} = \pi G{{S}_{k}}{{F}_{k}}(R), \\ \end{gathered} $

$\lambda = R{\text{/}}a$, $\mu = {{R}_{0}}{\text{/}}R$, ${{\Omega }^{2}} = \rho {{\omega }^{2}}{{R}^{2}}{{G}^{{ - 1}}}$, ${{\alpha }_{k}} = \sqrt {{{\Omega }^{2}} - {{R}^{2}}\kappa _{k}^{2}} $, ${{\sigma }_{ + }}$ – контур интегрирования, совпадающий с положительной действительной полуосью, обходя действительные полюса подынтегральной функции снизу. Можно показать, что

(3.17)

$K(\alpha ) = {{\alpha }^{{ - 1}}} + O({{\alpha }^{{ - 2}}})\quad (\alpha \to \infty )$

Можно также показать, что корни уравнения (2.3) имеют следующее асимптотическое поведение [16]

(3.18)

${{\kappa }_{k}} = \eta k + O({{k}^{{ - 1}}})\quad (k \to \infty ),\quad \eta = \pi {\text{/}}(R - {{R}_{0}})$

Можно показать, что при $k \to \infty $ с учетом (3.17)

(3.19)

$\begin{gathered} {{m}_{k}} = \frac{{\Delta _{k}^{{\text{*}}} - i{{\Delta }_{k}}}}{{{{\Delta }_{k}}{{\alpha }_{k}}}} = O\left( {\frac{1}{k}{{e}^{{ - 2\pi k{{z}_{0}}}}}} \right),\quad m_{k}^{{\text{*}}} = \frac{{{{L}_{k}}{{F}_{k}}(R)}}{{2{{F}_{{kk}}}}} = O(1) \\ {{M}_{k}} = O({{k}^{{ - 1}}}{{e}^{{ - 2\pi k{{z}_{0}}}}}) \\ \end{gathered} $

Как видно из ИУ (3.16), ядро ИУ состоит условно из двух слагаемых: первое соответствует ядру ИУ аналогичной контактной задачи для однородного цилиндра с параметрами $G$, $\rho $, а второе содержит информацию о периодических свойствах волновода и является гладкой функцией.

Нетрудно показать, что в случае $G = {{G}_{0}} = {{G}_{1}} = ... = {{G}_{N}}$ и $\rho = {{\rho }_{0}} = {{\rho }_{1}} = ... = {{\rho }_{N}}$ величина $\Delta _{k}^{{\text{*}}} - i{{\Delta }_{k}}$ обращается в нуль при любом $k$. Следовательно, в этом случае ${{k}_{2}}(x)$ = 0 и мы получаем интегральное уравнение для однородного пологого цилиндра.

Учитывая оценки (3.17) и (3.19), решение ИУ (3.16) можно получить с использованием широкого спектра известных аналитических методов (см., например, [10, 15, 17] и др.). Здесь применим “метод больших $\lambda $” [15]. Принимая во внимание представление

${{k}_{1}}(x) = \frac{\pi }{2}(i{{J}_{0}}(\Omega x) - {{N}_{0}}(\Omega x)) + \int\limits_{{{\sigma }_{ + }}} {{{K}_{1}}(t)\cos txdt} ;\quad {{K}_{1}}(t) = K(t) - {{({{t}^{2}} - {{\Omega }^{2}})}^{{ - 1/2}}}$

и представления функций Бесселя ${{J}_{0}}(x)$ и ${{N}_{0}}(x)$, а также $\cos tx$ и $\cos \,\,{{\alpha }_{k}}x$ в форме рядов, ядро ИУ (3.16) запишем следующим образом:

$k(y) = - \ln {\text{|}}y{\text{|}} + {{b}_{{20}}} + \ln {\text{|}}y{\text{|}}{{F}_{1}}(y) + {{F}_{2}}(y),\quad {{F}_{i}}(y) = \sum\limits_{k = 1}^\infty {{{b}_{{ik}}}{{y}^{{2k}}}} ,\quad i = 1,2$

${{b}_{{20}}} = {{m}_{0}} + {{T}_{0}} + \frac{{\pi i}}{2} - C - \ln \frac{\Omega }{2}$

${{b}_{{1k}}} = {{( - 1)}^{{k + 1}}}\frac{1}{{{{{(k!)}}^{2}}}}{{\left( {\frac{\Omega }{2}} \right)}^{{2k}}},\quad {{b}_{{2k}}} = {{( - 1)}^{k}}\frac{{{{m}_{k}} + {{T}_{k}}}}{{(2k)!}} - {{b}_{{1k}}}\left( {\sum\limits_{n = 1}^k {\frac{1}{n}} + \frac{{\pi i}}{2} - C - \ln \frac{\Omega }{2}} \right)$

${{m}_{k}} = \int\limits_{{{\sigma }_{ + }}} {{{t}^{{2k}}}{{K}_{1}}(t)dt} ,\quad {{T}_{k}} = \sum\limits_{n = 0}^\infty {\alpha _{n}^{{2k}}{{M}_{n}}} ,\quad C = 0.5772...$

и решение получим в виде [18]

(3.20)

$\varphi \,(t) = \frac{{G\delta }}{{a\sqrt {1 - {{t}^{2}}} }}\sum\limits_{k = 0}^\infty {\sum\limits_{n = 0}^{[k/2]} {{{w}_{{kn}}}(t){{\lambda }^{{ - k}}}{{{\ln }}^{n}}\lambda } } $

([k/2] – целая часть числа). Считая параметр $\lambda $ достаточно большим и ограничиваясь членами порядка ${{\lambda }^{{ - 4}}}{{\ln }^{2}}\lambda $, получим

(3.21)

$\begin{gathered} {{w}_{{00}}} = {{g}^{{ - 1}}}(\lambda ),\quad {{w}_{{10}}} = {{w}_{{30}}} = {{w}_{{31}}} = 0 \\ {{w}_{{20}}} = {{g}^{{ - 1}}}(\lambda )({{b}_{{11}}}(3{\text{/}}2 - \ln 2) + {{b}_{{21}}})(1 - 2{{t}^{2}}),\quad {{w}_{{21}}} = - {{g}^{{ - 1}}}(\lambda ){{b}_{{11}}}(1 - 2{{t}^{2}}) \\ g(\lambda ) = {{b}_{{20}}} + ({{b}_{{22}}} + {{b}_{{11}}}){{\lambda }^{{ - 2}}} + \ln (2\lambda )(1 - {{b}_{{11}}}{{\lambda }^{{ - 2}}}) \\ \end{gathered} $

Соотношения (3.24) и (3.25) позволяют исследовать решение поставленной задачи при достаточно больших относительных значениях внешнего радиуса полого цилиндра ($\lambda > 2$).

Работа выполнена при поддержке Министерства науки и высшего образования Российской Федерации (9.4726.2017/8.9).

Список литературы

Гельфанд И.М. Разложение по собственным функциям уравнения с периодическими коэффициентами // ДАН СССР. 1950. Т. 73. № 6. С. 1117–1120.
Brillouin L., Parodi M. Propagation des Ondes dans les Milieus Periodiques. Paris: Masson, 1956. 348 p. = Бриллюэн Л., Пароди М. Распространение волн в периодических структурах. М.: Изд-во иностр. лит. 1959. 457 с.
Крейн М.Г., Любарский Г.Я. К теории полос пропускания периодических волноводов // ПММ. 1961. Т. 25. Вып. 1. С. 24–37.
Крейн М.Г., Любарский Г.Я. Об аналитических свойствах мультипликаторов периодических канонических дифференциальных систем положительного типа // Изв. АН СССР. Сер. матем. 1962. Т. 26. Вып. 4. С. 549–572
Дьяков М.В., Устинов Ю.А. Дифракция сдвиговых волн на бесконечной и бесконечной периодической системах разрезов в упругом слое // Акуст. ж. 1997. Т. 43. № 2. С. 176–181.
Слепян Л.И. Возбуждение волн и динамика разрушения в упругих системах периодической структуры // Новожиловский сборник. СПб.: Судостр., 1992. С. 87–97.
Сухинин С.В. Распространение волн и резонансные явления в неоднородных средах // ПМТФ. 2001. Т. 42. № 3. С. 32–42.
Ворович И.И., Кучеров Л.В., Чебаков М.И. В-резонансы в задаче об установившихся колебаниях штампа на поверхности полосы периодической структуры // Изв. РАН. МТТ. 1992. № 3. С. 95–100.
Ворович И.И., Кучеров Л.В., Чебаков М.И. Динамические свойства слоя периодической структуры // Изв. вузов. Сев.-Кав. Регион. Спецвыпуск. 1994. С. 87–89.
Александров В.М., Чебаков М.И. Аналитические методы в контактных задачах теории упругости. М.: Физматлит, 2004. 315 с.
Zhibao Cheng, Zhifei Shi. Vibration attenuation properties of periodic rubber concrete panels // Construction and Building Materials. 2014. V. 50. P. 257–265.
Jiankun Huang, Wen Liu, Zhifei Shi. Surface-wave attenuation zone of layered periodic structures and feasible application in ground vibration reduction // Construction and Building Materials. 2017. V. 141. P. 1–11.
Xiang H.J., Shi Z.F., Wang S.J., Mo Y.L. Periodic materials-based vibration attenuation in layered foundations: experimental validation // Smart materials and structures. 2012. 21. 10 pp.
Pagneux V., Maurel A. Lamb wave propagation in inhomogeneous elastic waveguides // Proc. R. Soc. London. A. 2002. V. 458. P. 1913–1930.
Ворович И.И., Александров В.М., Бабешко В.А. Неклассические смешанные задачи теории упругости. М.: Наука, 1974. 456 с.
Абрамовиц М. Справочник по специальным функциям с функциями, графиками и математическими таблицами. М.: Наука, 1979. 832 с. = Abramovitz M., Stegan I. (Eds). Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables. New York: Dover Pub, 1972.
Механика контактных взаимодействий. Под редакцией Воровича И.И., Александрова В.М. М.: Физматлит, 2001. 672 с.
Александров В.М., Белоконь А.В. Асимптотическое решение одного класса интегральных уравнений и его применения к контактным задачам для цилиндрических упругих тел. ПММ. 1967. Т. 31. Вып. 4. С. 704–710.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал