Прикладная математика и механика, 2019, T. 83, № 3, стр. 468-477
ВЛИЯНИЕ ТЕПЛООБМЕННЫХ ПРОЦЕССОВ НА СНИЖЕНИЕ ИНТЕНСИВНОСТИ СФЕРИЧЕСКОГО ВЗРЫВА В ВОДНОЙ ПЕНЕ
Р. Х. Болотнова 1, *, Э. Ф. Гайнуллина 1, **
1 Институт механики им. Р.Р. Мавлютова УФИЦ РАН
Уфа, Россия
* E-mail: bolotnova@anrb.ru
** E-mail: elina.gef@yandex.ru
Поступила в редакцию 03.03.2019
После доработки 14.03.2019
Принята к публикации 19.03.2019
Аннотация
Разработана двухфазная модель поведения водной пены под воздействием сильной ударной волны (УВ) на основе законов сохранения массы и энергии для каждой фазы и уравнения импульса для смеси в лагранжевых переменных с учетом межфазного теплообмена и объемной вязкости. Численная реализация модели проведена с использованием метода сквозного счета с учетом псевдовязкости Неймана–Рихтмайера и условия устойчивости Куранта. Сферический взрыв моделируется в форме УВ, энергия которой совпадает с энергией заряда взрывчатого вещества, используемого в экспериментах. Численное решение задачи, полученное на основе предложенной модели, удовлетворительно согласуется с аналитическим автомодельным решением Л.И. Седова о точечном сферическом взрыве в газе и новыми экспериментальными данными по сферическому взрыву в водной пене. Детально исследованы причины значительного снижения амплитуды и скорости распространения УВ в изучаемой среде.
Введение. Демпфирующие свойства водных пен обусловлены их высокой сжимаемостью, которая существенно снижает амплитуду и скорость распространения акустических и ударных волн (УВ). Теплообменные процессы на межфазной структурной границе между газовой и жидкой компонентами пены также приводят к снижению интенсивности давления на фронте УВ. Изучение процессов ослабления УВ преградами из водных пен – актуальное направление исследований, связанных с учетом межфазных взаимодействий при построении математических моделей многофазных систем, численной реализацией этих моделей и верификацией полученных решений сравнением с новыми экспериментальными данными.
Распространение одномерных плоских [1, 2] и сферических [3, 4] УВ различной интенсивности в водных пенах с варьируемым начальным объемным водосодержанием исследовано в экспериментальных работах [1–4]. Установлено, что в таких пенах амплитуда УВ снижена на порядок по сравнению с газовой средой. В экспериментах также обнаружено уменьшение скорости распространения УВ. Уплотнение пены сопровождается разрушением жидких мостов, что приводит к образованию газокапельной смеси, в которой не наблюдаются процессы синерезиса (осаждения пены) [2].
Проводилось теоретическое исследование распространения УВ в газожидкостной среде с использованием вычислительных методов [3, 5–8]. Степень ослабления УВ в релаксирующих средах анализировалась [3] с применением смесевой модели водной пены. Также с использованием модели смеси при учете теплообмена между фазами численно моделировался [5] взрыв заряда взрывчатого вещества (ВВ) в пене. Были исследованы [6, 7] особенности взаимодействия ударно-волнового импульса со слоем пены в пространственной осесимметричной постановке на основе двухфазной модели газожидкостной смеси.
Настоящая работа, являющаяся продолжением предыдущего анализа [8], посвящена исследованию ослабления сильных УВ в водных пенах для условий экспериментов [4] с учетом объемной вязкости среды и процессов межфазной тепловой релаксации вследствие наличия контактного теплообмена.
1. Основные уравнения. Рассматривается однородная газожидкостная пенная среда, начальное объемное водосодержание которой принимается равным ${{\alpha }_{{10}}}$ в соответствии с условиями эксперимента [4] (рис. 1). В центре области инициируется взрыв заряда, который представлен в виде начального распределения давления
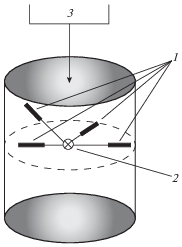
Рис. 1.
Схема экспериментальной установки: 1 – датчики давления, 2 – заряд ВВ, 3 – поступление пены.
Для случая сферической симметрии избыточная энергия в объеме, занимаемом УВ, определяется в виде [3]
(1.2)
$\Delta E = \int\limits_{x{\text{*}}}^{{{x}_{N}}} {4\pi {{x}^{2}}(\rho e - {{\rho }_{0}}{{e}_{0}} + \rho {{{v}}^{2}}{\text{/}}2)dx} ;\quad \rho e = \rho _{1}^{0}{{e}_{1}}{{\alpha }_{1}} + \rho _{2}^{0}{{e}_{2}}{{\alpha }_{2}},$Такая модель включает в себя [9]:
уравнения сохранения массы каждой фазы
(1.3)
${{\rho }_{0}}\frac{{\partial (\rho _{i}^{0}{{\alpha }_{i}})}}{{\partial t}} + \rho _{i}^{0}{{\alpha }_{i}}{{\rho }_{0}}\frac{{(\nu - 1){v}}}{x} + \rho \rho _{i}^{0}{{\alpha }_{i}}\frac{{\partial {v}}}{{\partial r}}{{\left( {\frac{x}{r}} \right)}^{{\nu - 1}}} = 0,\quad i = 1,2$уравнение сохранения импульса смеси
(1.4)
${{\rho }_{0}}\frac{{\partial {v}}}{{\partial t}} = - {{\left( {\frac{x}{r}} \right)}^{{\nu - 1}}}\frac{{\partial p}}{{\partial r}},$уравнения сохранения внутренних энергий фаз в двухтемпературном приближении
(1.5)
$\frac{{{{\rho }_{0}}}}{\rho }{{\alpha }_{i}}\rho _{i}^{0}\frac{{\partial {{e}_{i}}}}{{\partial t}} = {{\alpha }_{i}}\left( { - p{{{\left( {\frac{x}{r}} \right)}}^{{\nu - 1}}}\frac{{\partial {v}}}{{\partial r}} - p(\nu - 1)\frac{{v}}{r}\frac{{\partial x}}{{\partial r}}{{{\left( {\frac{x}{r}} \right)}}^{{(\nu - 1)(\nu - 2)/2}}}} \right) + {{( - 1)}^{{i + 1}}}q,\quad i = 1,2$Дифференциальная форма равенства давлений фаз p1= p2= p имеет вид
(1.6)
${{\left( {\frac{{\partial {{p}_{1}}}}{{\partial \rho _{1}^{0}}}} \right)}_{T}}\frac{{\partial \rho _{1}^{0}}}{{\partial t}} + {{\left( {\frac{{\partial {{p}_{1}}}}{{\partial {{T}_{1}}}}} \right)}_{{\rho _{1}^{0}}}}\frac{{\partial {{T}_{1}}}}{{\partial t}} - {{\left( {\frac{{\partial {{p}_{2}}}}{{\partial \rho _{2}^{0}}}} \right)}_{T}}\frac{{\partial \rho _{2}^{0}}}{{\partial t}} - {{\left( {\frac{{\partial {{p}_{2}}}}{{\partial {{T}_{2}}}}} \right)}_{{\rho _{2}^{0}}}}\frac{{\partial {{T}_{2}}}}{{\partial t}} = 0,$Оценим поведение водной пены под воздействием сильной УВ в зависимости от интенсивности межфазного теплообмена q. Поскольку в структуру пены входят жидкие пленки толщиной δ, то при ее разрушении за фронтом сильной УВ пена распадается на микрокапли диаметром d0 ≈ δ. Время разрушения жидких пленок ∼10 мкс толщиной δ ≈ 10–5 м оценивалось ранее [10]. Следовательно, в рассматриваемой модели можно предположить, что водная пена за фронтом сильной УВ распадается на монодисперсные микрокапли диаметра d, которые равномерно распределены в газе. Тогда интенсивность межфазного теплообмена q в уравнениях (1.5) определяется по аналогии с предложением Ждана [5]:
(1.7)
$\begin{gathered} q = \frac{{12\eta {{\alpha }_{1}}{{\gamma }_{2}}R}}{{{{d}^{2}}\Pr ({{\gamma }_{2}} - 1){{\mu }_{2}}}}({{T}_{2}} - {{T}_{1}});\quad \eta = {{\eta }_{{20}}}{{\left( {\frac{{{{T}_{2}}}}{{{{T}_{{20}}}}}} \right)}^{{0.85}}} \\ d = {{d}_{0}}{{\left( {\frac{{\rho _{{10}}^{0}}}{{\rho _{1}^{0}}}} \right)}^{{1/3}}},\quad \Pr = \frac{{4{{\gamma }_{2}}}}{{9{{\gamma }_{2}} - 5}} \\ \end{gathered} $Здесь $\eta $ – коэффициент динамической вязкости газа, η20 = 1.71 × 10–5 кг/м с и T20 = = 273 K – начальные значения динамической вязкости и температуры газа, ${{\gamma }_{2}}$, R, ${{\mu }_{2}}$ и Pr – показатель адиабаты газа, универсальная газовая постоянная, молекулярная масса воздуха и число Прандтля, d – текущий диаметр капли, где d0 = 3 × 10–5 м, $\rho _{{10}}^{0}$ – начальная плотность воды.
Уравнение состояния воды принято в форме Ми–Грюнайзена [11], где давление и внутренняя энергия записаны как сумма потенциальной (холодной) и тепловой компонент:
Свойства воздуха описываются уравнением состояния совершенного газа
(1.9)
${{p}_{2}} = \rho _{2}^{0}R{{T}_{2}} = \rho _{2}^{0}({{\gamma }_{2}} - 1){{c}_{V}}{{T}_{2}},\quad {{e}_{2}} = {{c}_{V}}{{T}_{2}},$В рассматриваемой задаче начальные и граничные условия выбраны в соответствии со схемой экспериментальной установки, изображенной на рис. 1. Эксперимент по сферическому взрыву в водной пене был проведен с использованием взрывчатого вещества PLANP массой ∼145 г, заключенного в пластиковую сферу диаметром 60 мм. Датчики давления, расположенные от центра взрыва на расстояниях li (i = 1, …, 4), использовались для измерения давления в УВ, вызванной сферическом взрывом. Осциллограммы давления, полученные в эксперименте, были представлены [4] с использованием шкалы расстояний Гопкинсона
(1.10)
$\tilde {x} = \frac{x}{{{{W}^{{1/3}}}}} = \frac{x}{{0.5689}}\;{\text{м/к}}{{{\text{г}}}^{{{\text{1/3}}}}}{\text{,}}$Численное решение задачи Коши, которая представлена системой пяти уравнений (1.3)–(1.7), замыкающими соотношениями для давления и внутренней энергии (1.8) и (1.9), начальными и граничными условиями, соответствующими экспериментам [4], было проведено на явной разностной сетке. Искусственная вязкость Неймана–Рихтмайера использовалась в виде добавки к давлению, что является аналогом объемной вязкости [13]. Устойчивость решения контролировалась условием Куранта.
2. Верификация модели. Для проверки достоверности предложенной модели было проведено сравнение автомодельного решения задачи о точечном сферическом взрыве в совершенном газе [14], полученного Л.И. Седовым, и численного решения, найденного по предложенной модели. Аналитические решения [14] для скорости ${v}$, давления p, плотности ρ, эйлеровой x, лагранжевой r координат и температуры T для случая сферической симметрии принимают вид
(2.1)
$\frac{x}{{{{r}_{f}}}} = {{\left[ {\frac{5}{4}(\gamma + 1)V} \right]}^{{ - \frac{2}{5}}}}{{\left[ {\frac{{\gamma + 1}}{{\gamma - 1}}\left( {\frac{5}{2}\gamma V - 1} \right)} \right]}^{{\frac{2}{{2\gamma + 1}}}}}{{\left[ {\frac{5}{2}\frac{{(\gamma + 1)(3V\gamma - V - 2)}}{{\gamma - 7}}} \right]}^{{\frac{{12{{\gamma }^{2}} - 68\gamma - 12}}{{5\left( {2\gamma + 1} \right)\left( {3\gamma - 1} \right)}}}}}$Условия на фронте УВ:
(2.2)
${{r}_{f}} = {{\left( {\frac{{{{E}_{0}}}}{{{{\rho }_{0}}}}} \right)}^{{1/5}}}{{t}^{{2/5}}},\quad {{{v}}_{f}} = \frac{4}{{5(\gamma + 1)}}{{\left( {\frac{{{{E}_{0}}}}{{{{\rho }_{0}}}}} \right)}^{{1/2}}}r_{f}^{{ - 3/2}},\quad {{p}_{f}} = \frac{{8{{E}_{0}}}}{{25(\gamma + 1)}}\frac{1}{{r_{f}^{3}}}$Скорость фронта УВ:
(2.3)
$D = \frac{2}{5}{{\left( {\frac{{{{E}_{0}}}}{{{{\rho }_{0}}}}} \right)}^{{1/5}}}{{t}^{{ - 3/5}}} = \frac{2}{5}{{\left( {\frac{{{{E}_{0}}}}{{{{\rho }_{0}}}}} \right)}^{{1/2}}}r_{f}^{{ - 3/2}}$Здесь E0= 10 Дж – энергия взрыва, ρ0 = 0.0125 кг/м3 – начальная плотность газа (воздух), γ = 1.4 – показатель адиабаты, $\frac{2}{{5\gamma }}$ ≤ V ≤ $\frac{4}{{5(\gamma + 1)}}$, $V = \frac{{{v}t}}{r}$ – безразмерный параметр.
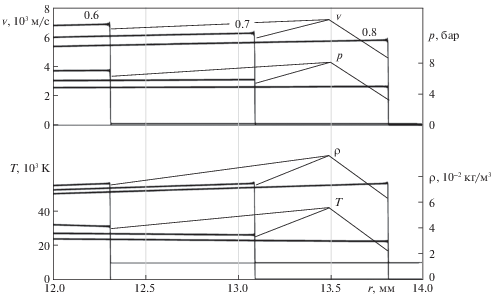
При численном решении задачи в качестве граничного условия на расстоянии r0 = = 12 мм от центра взрыва задавался закон движения поршня в виде массовой скорости лагранжевой точки ${{{v}}_{{{{r}_{0}}}}}(t)$ и давления ${{p}_{{{{r}_{0}}}}}(t)$ как функций от времени для лагранжевой координаты r0 в соответствии с решением (2.1)–(2.3). На рис. 2 представлено сравнение аналитического и численного решений по предлагаемой модели в однофазном приближении, которые удовлетворительно согласуются.
Рис. 2.
Сравнение аналитического и численного решений в указанные моменты времени (0.6, 0.7, 0.8 мкс) для скорости ${v}$, давления p, температуры T и плотности ρ: серые линии – решение Седова [14], черные – численные расчеты.
3. Результаты численного моделирования. В процессе численного исследования были проведены расчеты для условий экспериментов по сферическому взрыву в водной пене [4]. Согласование расчетной энергии взрыва заряда ВВ, вычисляемой по формуле (1.2), и ее экспериментального значения (1.11) достигнуто при следующих значениях амплитуды и ширины исходного импульса давления в пене (1.1): ∆p = 6 × 103 МПа, a = 0.07 м. В расчетах объемное водосодержание пены снижено до α10 = 0.0043 по сравнению с экспериментальными данными [4], вследствие учета эффекта синерезиса пены в процессе ее генерации с низкой скоростью, изменяющейся в диапазоне от 0.150 до 1 м3/мин, с коэффициентом расширения 1:120 [4].
Для сравнительного анализа на рис. 3 представлены расчетные зависимости давления от расстояния до центра взрыва для условий экспериментальных данных [4]. Здесь показаны численные результаты без учета (пунктирная линия) и с учетом межфазного теплообмена (1.7) и объемной вязкости [13] (сплошная линия). Пиковые значения давлений из эксперимента [4] отмечены точками 5. Обобщенные экспериментальные данные базы Кинни и Грэхэма для газа [14] и национальной лаборатории Сандиа для пены [16], представленные в аналитической форме, показаны линиями 3 и 4 соответственно. Как в экспериментах, так и в расчетах, после момента времени t ~ ~ 1.0 мс фиксируется второй скачок давления, который возникает в результате отражения волны сжатия от центра взрыва.
Рис. 3.
Результаты расчетов динамики давления в пене в указанные моменты времени (0.05, 0.2, …, 5, мс) с учетом (1) и без учета (2) теплообмена и вязкости; 3 и 4 – обобщение экспериментов по максимальным давлениям УВ в газе [14] и водной пене [16], 5 и 6 – экспериментальные точки [4] максимальных давлений в УВ в пене, l1, …, l4 – местоположения датчиков.
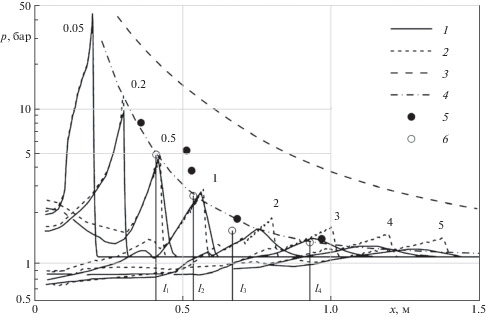
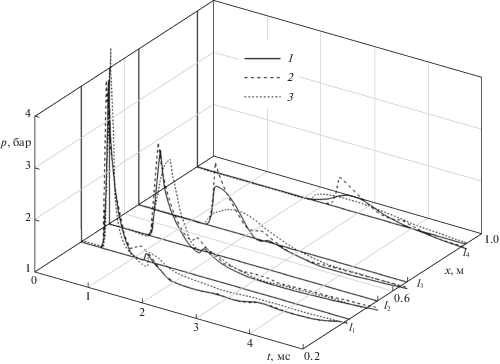
На рис. 4 приведены найденные зависимости давления от времени (линии 1 и 2) и соответствующие им экспериментальные данные для пены, полученные с помощью датчиков, расположенных на расстояниях l1 = 0.41, l2 = 0.53, l3 = 0.67, l4 = 0.93 (м) от точки взрыва. Профили давления в водной пене, обозначенные сплошными линиями, рассчитаны с учетом межфазного теплообмена и вязкости. На рис. 3 и 4 видно, что при x ≥ 0.5 м пиковые величины давлений, полученные в расчетах без учета межфазного теплообмена и вязкости, превышают экспериментальные значения. Добавочный член q в уравнениях сохранения внутренней энергии фаз (1.5), отвечающий за интенсивность межфазного теплообмена, дает дополнительное снижение амплитуды давления за счет уменьшения температуры газовой фазы, следствием чего является замедление скорости распространения фронта УВ по сравнению с расчетами без учета теплообмена. Учет вязкости в УВ приводит к дополнительной диссипации ударного импульса, что становится заметным при удалении УВ от центра взрыва.
Рис. 4.
Результаты расчетов динамики давления в пене в местоположениях датчиков на расстояниях l1, …, l4 от точки взрыва с учетом (1) и без учета (2) теплообмена и вязкости, 3 – экспериментальные данные [4].
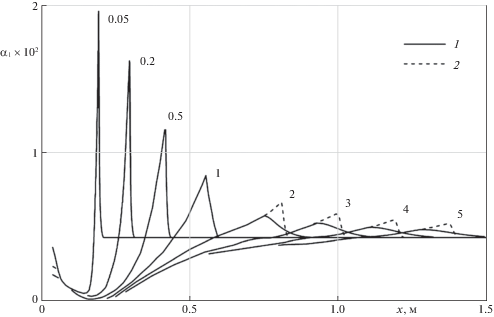
В процессе численного исследования был проведен анализ динамики объемного содержания ${{\alpha }_{1}}$ жидкости в пене. Расчетные профили ${{\alpha }_{1}}$ представлены на рис. 5 для моментов времени в мс. Сжатие пены за фронтом УВ увеличивает ее объемное водосодержание до α1 = 0.02 к моменту времени t = 0.05 мс, что приводит к уменьшению амплитуды и скорости распространения УВ по сравнению с соответствующими значениями при прохождении УВ в газе (см. рис. 3). Влияние межфазного теплообмена и вязкости снижает значение ${{\alpha }_{1}}$ за фронтом УВ за счет уменьшения амплитуды давления в УВ. Вблизи центра взрыва, после прохождения УВ, формируется газовая область с незначительным значением α1 < 0.001.
Рис. 5.
Результаты расчетов динамики объемного водосодержания в пене с учетом (1) и без учета теплообмена (2) в указанные моменты времени (0.05, 0.2, …, 5 мс).
Заключение. Проведено компьютерное исследование динамики сферической УВ, возникающей в результате взрыва заряда ВВ, в водной пене с применением предложенной модели двухфазной газокапельной смеси, учитывающей контактный теплообмен между фазами и вязкость. Численная реализация модели выполнена в открытой среде разработки Lazarus. Получена оценка энергии в УВ при моделировании сферического взрыва в виде начального импульса давления, согласующаяся с расчетным и экспериментальным значениями энергии взрыва. Расчетные зависимости давления и экспериментальные данные по сферическому взрыву в водной пене коррелируют по амплитуде, длительности и скорости распространения УВ. Показано, что при уплотнении пены наблюдается снижение скорости распространения УВ. Демпфирующие свойства водной пены усиливаются при увеличении начальной плотности пены [17]. Использование пены даже с невысоким водосодержанием α10 ≈ 0.004 способствует ослаблению амплитуды ударного импульса в шесть раз и уменьшению скорости распространения УВ по сравнению с газовой средой [8]. Анализ эволюции объемного водосодержания выявил увеличение ${{\alpha }_{1}}$ в пять раз на начальной стадии распространения УВ, приводящее к значительной диссипации энергии взрыва.
Работа выполнена при частичной финансовой поддержке грантов Российского фонда фундаментальных исследований (№ 17-41-020582 p_поволжье_а) и Республики Башкортостан молодым ученым (№ 8 ГР 18.03.2019), средствами государственного бюджета по госзаданию 0246-2019-0052 и программы ОЭ-4-4-12 ОЭММПУ РАН.
Список литературы
Borisov A.A., Gelfand B.E., Kudinov V.M. et al. // Shock waves in water foams // Acta Astron. 1978. V. 5. № 11. P. 1027–1033.
Jourdan G., Marian C., Houas L. et al. Analysis of shock-wave propagation in aqueous foams using shock tube experiments // Phys. Fluids. 2015. V. 27. P. 056101.
Вахненко В.А., Кудинов B.M., Паламарчук Б.И. К вопросу о затухании сильных ударных волн в релаксирующих средах // ФГВ. 1984. № 1. С. 105–111.
Del Prete E., Chinnayya A., Domergue L. et al. Blast Wave Mitigation by Dry Aqueous Foams // Shock Waves. 2013. V. 23. № 1. P. 39–53.
Ждан С.А. Численное моделирование взрыва заряда ВВ в пене // ФГВ. 1990. № 2. С. 103–110.
Болотнова Р.Х., Агишева У.О. Пространственное моделирование динамики газожидкостной пены на подвижных лагранжевых сетках в условиях ударно-волнового воздействия // Вычисл. методы и прогр. 2014. Т. 15. № 3. С. 427–440.
Агишева У.О., Болотнова Р.Х., Гайнуллина Э.Ф. и др. Особенности вихреобразования при воздействии импульса давления на газовую область, ограниченную пенным слоем // Изв. РАН. МЖГ. 2016. № 6. С. 47–56.
Болотнова Р.Х., Гайнуллина Э.Ф. Исследование демпфирующих свойств водной пены под воздействием сферической ударной волны // Изв. вузов. Поволжский регион. 2017. Т. 42. № 2. С. 108–121.
Нигматулин Р.И. Динамика многофазных сред. Ч. 1. Москва: Наука, 1987. 464 с.
Кудинов В.М., Паламарчук Б.И., Гельфанд Б.Е. и др. Ударные волны в газожидкостных средах пенистой структуры // Прикл. мех. 1977. Т. 13. № 3. С. 92–97.
Нигматулин Р.И., Болотнова Р.Х. Широкодиапазонное уравнение состояния воды и пара. Упрощенная форма // ТВТ. 2011. Т. 49. Вып. 2. С. 310–313.
Бесчастнов М.В. Промышленные взрывы: оценка и предупреждение. Москва: Химия, 1991. 432 с.
Neumann J.A., Richtmyer R. Method for the numerical calculation of hydrodynamical shocks // J. Appl. Phys. 1950. V. 21. № 3. P. 232–237.
Седов Л.И. Методы подобия и размерности в механике. Москва: Наука, 1977. 440 с.
Kinney G., Graham K. Explosives shocks in Air. Berlin: Springer, 1985. 282 p.
Hartman W., Boughton B., Larsen M. Blast mitigation capabilities of aqueous foam. Tech. Rep. SAND2006-0533. Sandia National Lab., 2006.
Агишева У.О., Болотнова Р.Х., Бузина В.А. и др. Параметрический анализ режимов ударно-волнового воздействия на газожидкостные среды // Изв. РАН. МЖГ. 2013. № 2. С. 15–28.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика


