Прикладная математика и механика, 2020, T. 84, № 3, стр. 273-279

Уравнения движения и первые интегралы рассматриваемой задачи приведены в [1]. Построение диаграмм Смейла [2] основано на анализе стационарных движений системы методом Рауса [3, 4] и Пуанкаре–Четаева [5, 6]. Частный случай этой задачи рассмотрен в [7].

1. Постановка задачи. Рассмотрим задачу о движении трех связанных твердых тел в однородном поле сил тяжести. Каждое из тел может вращаться только вокруг одной из осей: первое – вокруг неподвижной вертикали $OZ$, второе – вокруг горизонтали $Ox$, закрепленной на первом теле, а третье – вокруг оси $Oz$, закрепленной на втором теле и ортогональной оси $Ox$. Предположим, что $Oxyz$ – главные оси инерции (для точки $O$) второго тела (ось $Oy$ ортогональна плоскости $Oxz$), причем $Oz$ – ось симметрии эллипсоида инерции (для точки $O$) третьего тела.

Момент инерции первого тела относительно $OZ$ обозначим через ${{C}_{1}}$, а моменты инерции второго и третьего тел относительно осей $Oxyz$ – через ${{A}_{2}}$, ${{B}_{2}}$, ${{C}_{2}}$ и ${{A}_{3}}$, ${{B}_{3}} = {{A}_{3}}$, ${{C}_{3}}$ соответственно. Пусть центры масс второго и третьего тел лежат на оси $Oz$ в точках с координатами ${{c}_{2}}$ и ${{c}_{3}}$ соответственно, а ${{m}_{2}}$ и ${{m}_{3}}$ – массы этих тел. Положительное направление оси $Oz$ выбираем так, что ${{m}_{2}}{{c}_{2}} + {{m}_{3}}{{c}_{3}} = mc > 0$ (случай $c = 0$ тривиален и в статье не рассматривается).

Углы поворота первого, второго и третьего тел вокруг осей $OZ$, $Ox$ и $Oz$ соответственно обозначим через ${{{\varphi }}_{1}}$, ${{{\varphi }}_{2}}$ и ${{{\varphi }}_{3}}$. Очевидно, конфигурационное пространство системы – трехмерный тор (${{\mathbb{T}}^{3}}$).

Рассматриваемая система допускает интеграл энергии ($g$ – ускорение свободного падения)

и два циклических интеграла ($h$, $k$ и $l$ – произвольные постоянные; см. напр., [1]).

Напомним, что топологический анализ систем, допускающих первые интегралы, основан на построении (в пространстве констант этих интегралов) бифуркационного по Смейлу [2] множества, на котором эти интегралы зависимы. Учитывая структуру функций $H$, $K$ и $L$, задачу отыскания критических уровней интегралов $H = h$, $K = k$, $L = l$ можно свести к задаче определения всех критических точек эффективного потенциала ${{V}_{{kl}}}$ системы – минимума функции $H$ по скоростям на фиксированных уровнях интегралов $K = k$ и $L = l$. В рассматриваемой задаче этот минимум достигается при

и задается формулой [7]

Полагая, что $k \ne 0$, введем следующие обозначения

При этом ${{V}_{{kl}}} = mgc\,f(x) + {\text{const}}$, где

Отметим, что если второе тело – почти плоская рамка (как для гироскопа в кардановом подвесе), то $b \in ( - 1,0)$; этот случай рассмотрен в [7].

Если же второе тело достаточно сильно отличается от плоского, то параметр $b$ может принимать положительные значения, в том числе, достаточно большие.

Заметим также, что случай $k = 0$, $l \ne 0$ получается из общего случая предельным переходом при $a \to \infty $, а случай $k = l = 0$ тривиален и не рассматривается.

Таким образом, анализ критических уровней первых интегралов задачи сводится к анализу критических точек функции $f(x)$ (1.3), заданной на отрезке $[ - 1,\,\,1]$.

2. Анализ критических точек эффективного потенциала. Очевидно, $x = - 1\,\,({{{\varphi }}_{2}} = \pi )$ и $x = + 1\,\,({{{\varphi }}_{2}} = 0)$ – критические точки функции $f(x)$, причем $f( - 1) = \min \,(\max )$, если $f{\kern 1pt} '( - 1)$ > 0 (<0), а $f( + 1) = \min \,(\max )$, если $f{\kern 1pt} '( + 1)$ < 0 (>0). Здесь

Таким образом, $f( - 1) = \min $ при любом $p$, если $a \in [ - 1,b]$; если же $a \in ( - \infty , - 1)$ ∪ ∪ $(b, + \infty )$, то $f( - 1) = \min \,(\max )$ при $p < {{p}_{ - }}$ $(p > {{p}_{ - }})$. Аналогично, $f( + 1) = \max $ при любом $p$, если $a \in ( - \infty , - b]$ ∪ $[1, + \infty )$; если же $a \in ( - b,1)$, то $f( + 1) = \max \,(\min )$ при $p < {{p}_{ + }}$ $(p > {{p}_{ + }})$. Здесь

Значения ${{p}_{ + }}$ и ${{p}_{ - }}$ существуют одновременно (напомним, что $p > 0$), если $a \in (\left| b \right|,1)$ при ${\text{|}}b{\text{|}} < 1$ или $a \in ( - b, - 1)$ при $b > 1$, причем ${{p}_{ + }} > {{p}_{ - }}$ $({{p}_{ + }} < {{p}_{ - }})$ при $b > {{a}^{2}}$ $(b < {{a}^{2}})$.

Критические точки $x \in ( - 1,1)$ определяются из уравнения $f{\kern 1pt} '(x) = 0$, которое можно представить в виде

Очевидно, что если $x \in ( - 1,1)$ – решение уравнения (2.2), то $f{\kern 1pt} ''(x) = {{u{\kern 1pt} '(x)} \mathord{\left/ {\vphantom {{u{\kern 1pt} '(x)} {u(x)}}} \right. \kern-0em} {u(x)}}$. Следовательно, критическая точка $x \in ( - 1,1)$ доставляет функции $f(x)$ минимум (максимум), если функция $u(x)$ возрастает (убывает) в этой точке.

В зависимости от параметров задачи $a$ и $b$ область определения $\Delta \subseteq [ - 1,1]$ функции $u(x)$ имеет вид

Заметим, что критические точки $x \in ( - 1,1)$ функции $f(x)$, в отличие от точек $x = \pm 1$, зависят от параметра $p$, причем каждой такой точке отвечают два значения ${{{\varphi }}_{2}} = \pm \arccos x$.

Обозначим критические точки функции $f(x)$, принадлежащие интервалам $( - 1,1)$, $( - 1,{1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a})$, $( - {a \mathord{\left/ {\vphantom {a {b,1}}} \right. \kern-0em} {b,1}})$ и $( - {a \mathord{\left/ {\vphantom {a {b,{1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a}}}} \right. \kern-0em} {b,{1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a}}})$ – через ${{x}_{0}}(p)$, ${{x}_{\alpha }}(p)$, ${{x}_{\beta }}(p)$ и ${{x}_{{\alpha \beta }}}(p)$ соответственно; при этом

Поскольку $x(p)$ – решение уравнения (2.2), то свойства монотонности функций $x(p)$ и $u(x)$ совпадают.

Вычислим

Из соотношений (2.4) и (2.5) следует, что $u'(x)$ может обращаться в ноль на отрезке ${{\Delta }_{0}}$ и полуинтервалах ${{\Delta }_{\alpha }}$, ${{\Delta }_{\beta }}$ не более одного раза (в точках ${{x}_{0}}$, ${{x}_{\alpha }}$, ${{x}_{\beta }}$ соответственно), а в интервале ${{\Delta }_{{\alpha \beta }}}$ обращается в ноль ровно один раз (в точке ${{x}_{{\alpha \beta }}}$). Учитывая, что $u(x) \to + \infty $ при $x \to {1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a}$ и $x \to {{ - a} \mathord{\left/ {\vphantom {{ - a} b}} \right. \kern-0em} b}$, заключаем, что ${{x}_{0}}$ существует при $v( + 1)v( - 1) < 0$, ${{x}_{\alpha }}$ – при $v( - 1) < 0$, ${{x}_{\beta }}$ – при $v( + 1) > 0$ (${{x}_{{\alpha \beta }}}$ существует всегда). Здесь

В заключение этого раздела отметим, что критические точки функции $f(x)$ отвечают стационарным движениям системы ($x = \pm 1$ – вертикальным вращением при наинизшем для $x = - 1$ и наивысшем для $x = + 1$ положении центра масс, а $x(p) \in ( - 1,1)$ – прецессионным движениям; см. (1.1)), причем точки минимума (максимума) соответствуют устойчивым (неустойчивым) движениям.

3. Бифуркационная диаграмма. Приведенный выше анализ критических точек функции $f(x)$ позволяет построить полный атлас бифуркационных диаграмм Пуанкаре–Четаева [5, 6]. Каждая карта этого атласа на плоскости $\{ p;x\} $ ($p > 0$, $x \in [ - 1,1]$) состоит из прямых $x = \pm 1$ и кривых $x(p)$, где $x(p)$ – решение уравнения (2.2). Карты различаются видом кривых $x(p)$ и распределением точек минимума/максимума на этих кривых и на прямых $x = \pm 1$.

Для построения полного атласа бифуркационных диаграмм Смейла [2] необходим небольшой дополнительный анализ. Каждая карта этого атласа на плоскости $\{ p;q\} $ ($p > 0$, $q \geqslant - 1$) состоит из прямых

и кривых $q = q(p)$, заданных параметрически соотношениями $q = f(x)$, $p = u(x)$, которые (см. (1.3) и (2.2)) можно привести к виду ($x$ – параметр, принадлежащий соответствующему этой карте интервалу (2.3)).

Совокупность прямых (3.1) и кривых (3.2) определяет бифуркационное по Смейлу множество, на котором происходят перестройки топологического типа областей возможности движения, задаваемых соотношением $f(x) \leqslant q$ (${{V}_{{kl}}} \leqslant h$). Если $a < 0$, то прямые (3.1) не пересекаются; если же $a > 0$, то они пересекаются при $p = {{(1 + b)} \mathord{\left/ {\vphantom {{(1 + b)} a}} \right. \kern-0em} a}$. Очевидно,

Взаимное расположение точек ${{p}_{ + }}$, ${{p}_{ - }}$ и ${{(1 + b)} \mathord{\left/ {\vphantom {{(1 + b)} a}} \right. \kern-0em} a}$ тоже влияет на вид диаграммы Смейла.

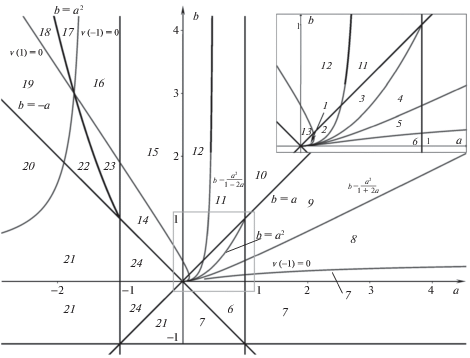
Таким образом, плоскость параметром задачи $a$ и $b$ ($a \in \mathbb{R}$, $b > - 1$) разбивается на 24 области (см. рис. 1), различающиеся видом бифуркационных диаграмм. Заметим, что при $x(p) \to {1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a}$ кривая (3.2) стремится к прямой $f({1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a}) = {1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a}$, а при $x \to - {a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}$ – к прямой

Очевидно, угол наклона прямой (3.3) больше углов наклона прямых (3.1).

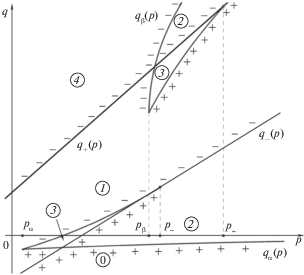
На рис. 2 приведена диаграмма Смейла для параметров задачи, принадлежащих области 18 (см. рис. 1), в которой $a < - 1$, $b < {{a}^{2}}$, $v( + 1) > 0$, $v( - 1) < 0$. На этой диаграмме кривые ${{q}_{\alpha }}(p)$ и ${{q}_{\beta }}(p)$ соответствуют полуинтервалам ${{\Delta }_{\alpha }}$ и ${{\Delta }_{\beta }}$ (см. (2.3)) существования решений уравнения (2.2), значение ${{p}_{ \pm }}$ задаются соотношениями (2.1), а значения ${{p}_{\alpha }}$ и ${{p}_{\beta }}$ – соотношениями ${{p}_{\alpha }} = u({{x}_{\alpha }})$, ${{p}_{\beta }} = u({{x}_{\beta }})$, где ${{x}_{\alpha }}$ и ${{x}_{\beta }}$ корни уравнения $v(x) = 0$ на полуинтервалах ${{\Delta }_{\alpha }}$ и ${{\Delta }_{\beta }}$ соответственно. Цифрами (0), (1), (2), (3), (4) обозначены топологические типы областей возможности движения ((0) – пустое множество, (1), (2) или (3) – один, два или три “толстых” двумерных тора (${{\mathbb{T}}^{2}} \times {{\mathbb{D}}^{1}}$), (4) – трехмерный тор (${{\mathbb{T}}^{3}}$)), а знаками плюс (минус) – точки минимума (максимума) функции $f(x)$.

Диаграммы, соответствующие областям 16, 17, 19, 22, 23, отличаются от приведенной на рис. 2, расположением точек ${{p}_{ + }}$, ${{p}_{ - }}$, ${{p}_{\alpha }}$ и ${{p}_{\beta }}$ и отсутствием точек возврата как на одной из кривых ${{q}_{\alpha }}(p),$ ${{q}_{\beta }}(p)$, так и на обеих. Для областей 20 (15) и 21 (14) исчезает ветвь ${{q}_{\beta }}(p)$ $({{q}_{\alpha }}(p))$; при этом для областей 20 и 15 есть точка возврата, а для областей 21 и 14 ее нет. Для областей 11 (${{(1 + b)} \mathord{\left/ {\vphantom {{(1 + b)} {a < {{p}_{ + }}}}} \right. \kern-0em} {a < {{p}_{ + }}}}$) и 12 (${{(1 + b)} \mathord{\left/ {\vphantom {{(1 + b)} {a > {{p}_{ + }}}}} \right. \kern-0em} {a > {{p}_{ + }}}}$) (13) диаграммы отличаются от диаграмм 15 (14) тем, что на них кривые (3.1) пересекаются. Для областей 1 – 6 кривые $q = {{q}_{0}}(p)$ = $f({{x}_{0}}(p))$, где ${{x}_{0}}(p)$ – решение уравнения (2.2) на ${{\Delta }_{0}}$, соединяют точки прямых (3.1), соответствующие значениям ${{p}_{ \pm }}$ и существуют только на ограниченном интервале изменения параметра $p$; при этом для областей 1 (${{p}_{ + }} < {{p}_{ - }}$) и 6 (${{p}_{ + }} > {{p}_{ - }}$) на кривой ${{q}_{0}}(p)$ нет точек возврата, а для областей 2 (${{p}_{ + }} < {{p}_{0}} < {{p}_{ - }}$), 3 (${{p}_{0}} < {{p}_{ + }} < {{p}_{ - }}$), 4 (${{p}_{0}} < {{p}_{ - }} < {{p}_{ + }}$) и 5 (${{p}_{ - }} < {{p}_{0}} < {{p}_{ + }}$) точки возврата есть (здесь ${{p}_{0}} = u({{x}_{0}})$, ${{x}_{0}}$ – корень уравнения $v(x)$ на ${{\Delta }_{0}}$). Для областей 7–9 не существует кривой ${{q}_{\beta }}(p)$, причем для области 7 на кривой ${{q}_{\alpha }}(p)$ нет точки возврата, а для областей 8 (${{p}_{ - }} < {{(1 + b)} \mathord{\left/ {\vphantom {{(1 + b)} a}} \right. \kern-0em} a}$) и 9 (${{p}_{ - }} > {{(1 + b)} \mathord{\left/ {\vphantom {{(1 + b)} a}} \right. \kern-0em} a}$) она есть. Для области 10, кроме прямых (3.1), есть только кривая $q = {{q}_{{\alpha \beta }}}(p)$ = = $f({{x}_{{\alpha \beta }}}(p))$, где ${{x}_{{\alpha \beta }}}(p)$ – корень уравнения (2.2) на интервале ${{\Delta }_{{\alpha \beta }}}$. Эта кривая состоит из двух ветвей, рождающихся в точке $p = {{p}_{{\alpha \beta }}}(p)$ = $u({{x}_{{\alpha \beta }}})$, где ${{x}_{{\alpha \beta }}}$ – корень уравнения $v(x) = 0$ на ${{\Delta }_{{\alpha \beta }}}$. При $p \to + \infty $ одна ветвь стремится к прямой $q = {1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a}$, а другая – к прямой (3.3). Для области 24 диаграмма состоит только из непересекающихся прямых (3.1). При этом для областей 10 и 24 все точки прямой ${{q}_{ - }}(p)$ (${{q}_{ + }}(p)$) являются точками минимума (максимума) функции $f(x)$.

Таким образом, общий случай гораздо богаче случая гироскопа в кардановом подвесе [7]: полный атлас бифуркационных диаграмм содержит 24 (а не 4) карты, а области возможного движения могут состоять из трех “толстых” двумерных торов (а не только одного) такого тора.

Работа выполнена при поддержке гранта РФФИ № 19-01-00140.