Прикладная математика и механика, 2020, T. 84, № 5, стр. 663-674
Мультирежимная модель развития усталостных повреждений
И. С. Никитин 1, *, Н. Г. Бураго 1, 2, **, А. Б. Журавлев 2, ***, А. Д. Никитин 1, ****
1 Институт автоматизации проектирования РАН
Москва, Россия
2 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: i_nikitin@list.ru
** E-mail: buragong@yandex.ru
*** E-mail: zhuravlev.alex2010@yandex.ru
**** E-mail: nikitin_alex@bk.ru
Поступила в редакцию 18.05.2020
После доработки 15.07.2020
Принята к публикации 21.07.2020
Аннотация
Предложена мультирежимная кинетическая модель развития повреждаемости при циклическом нагружении для описания развития процесса усталостного разрушения. Для определения коэффициентов кинетического уравнения повреждаемости использован известный критерий многоосного усталостного разрушения, в котором заложен механизм, связанный с развитием микротрещин нормального отрыва. На этой основе предложена процедура вычисления коэффициентов кинетического уравнения для различных режимов усталостного разрушения от малоцикловой до сверхмногоцикловой усталости. Разработан единообразный численный метод и приведены примеры расчета развития трещиноподобных зон повреждаемости и усталостного разрушения образцов, содержащих дефекты разного типа для различных режимов циклического нагружения.
Введение. Имеются две основные задачи теории усталостного разрушения – это задача определения локальной зоны и количества циклов нагружения до зарождения усталостных повреждений, а также задача определения скорости и направления их развития вплоть до выхода на поверхность образца или элемента конструкции и финального макроразрушения.
Основные способы их решения для случая многоосного циклического нагружения связаны с проведением испытаний образцов, обобщением закономерностей, установленных для одноосных нагружений и описываемых усталостными S–N кривыми типа Веллера и соотношениями типа Баскина [1].
Большое количество критериев (stress-based criteria) основано на прямом обобщении S–N кривых, построенных по результатам усталостных испытаний, и они делятся на две большие группы. В первую группу входят критерии, которые включают амплитуды инвариантных характеристик напряженного состояния в цикле нагружения – октаэдрических напряжений, главных напряжений и т.п. [2, 3], а во вторую группу входят те, которые учитывают значения амплитуд касательных и/или нормальных напряжений на так называемой критической плоскости [4–9]. Как правило, эта плоскость определяется из условия максимума амплитуд касательных, нормальных напряжений или их определенной комбинации по площадкам всевозможных ориентаций. Обзоры по этой тематике представлены в работах [10–13].
Для того чтобы исследовать процессы развития зон усталостных повреждений также существует два подхода. Первый основан на классических представлениях механики разрушения и связывает условия развития усталостных трещин при увеличении числа циклов с амплитудами коэффициентов интенсивности напряжений в вершине трещины. Основное уравнение было предложено Парисом [14], существует большое количество его модификаций [15, 16].
Второй подход использует представления теории повреждаемости, восходящей к работам [17, 18] и развитый впоследствии в [19, 20]. Он применялся [21–23] в приложении к задачам циклического нагружения и усталостного разрушения.
В данной работе предлагается мультирежимная модель развития усталостного разрушения, основанная на эволюционном уравнении для функции повреждаемости. Параметры модели определены для различных режимов усталостного разрушения – малоцикловой и многоцикловой усталости (МЦУ, МНЦУ), а также режима сверхмногоцикловой усталости (СВМУ), соответствующего высокочастотному низкоамплитудному нагружению.
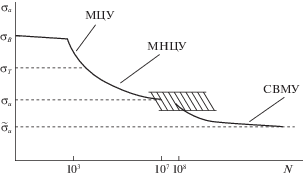
Для выделения различных режимов усталостного разрушения используется схема мультирежимной амплитудной усталостной кривой, представленная на рис. 1. Вплоть до значения N ~ 103 реализуется режим повторно-статического нагружения с амплитудой, мало отличающейся от статического предела прочности ${{\sigma }_{B}}$. Далее левая часть бимодальной усталостной кривой (кривая Веллера) описывает режимы МЦУ–МНЦУ вплоть до N ~ 107 и значений амплитуды порядка предела усталости ${{\sigma }_{u}}$. Затем начинается зона смены механизмов разрушения и дальнейшее падение усталостной прочности, начиная с величин N ~ 108, до нового предельного значения ${{\tilde {\sigma }}_{u}}$ в соответствии с правой ветвью бимодальной усталостной S–N кривой. Эта ветвь описывает режим СВМУ [24].
Отметим, что в настоящее время развиваются представления о явном разделении классической ветви Веллера еще на две части – собственно, МЦУ и МНЦУ. Граница этой переходной области определяется не значением величины N, а величиной амплитуды нагружения, равной пределу текучести материала ${{\sigma }_{T}}$ [25], так как при этом также происходит смена физического механизма усталостного разрушения.
Граница повторно-статического диапазона N ~ 103 довольно условна. Она уточняется в современных исследованиях [25] в зависимости от прочностных и пластических характеристик материала.
Тем не менее, в данной работе мы сохраним изложение предлагаемой модели развития повреждаемости, основанное на вышеописанной схеме.
Для того чтобы согласовать модель с известными критериями многоосного усталостного разрушения, был выбран основанный на напряженном состоянии (stress-based) критерий, который описывает усталостное разрушение, связанное с развитием микротрещин нормального отрыва. Это модифицированный критерий Smith–Watson–Topper (SWT) [26, 27], в котором определяющую роль в развитии усталостных повреждений играют амплитуды максимальных растягивающих напряжений. В исходном изложении этот и подобные ему stress-based критерии уже применялись для описания режимов МЦУ и МНЦУ. Был предложен [24] подход для обобщения многоосных критериев разрушения при описании правых ветвей усталостных кривых в режиме СВМУ, использующий опорные точки каждой из ветвей и обратную степенную зависимость от числа циклов N для выхода на асимптоту предела усталости. В данной работе для обобщения критерия SWT на случай СВМУ был также использован этот аналитический подход.
1. Кинетическое уравнение для повреждаемости в режиме МЦУ–МНЦУ.
1.1. Критерий многоосного усталостного разрушения в режиме МЦУ–МНЦУ с развитием микротрещин нормального отрыва (stress-based SWT), соответствующий левой ветви бимодальной усталостной кривой (рис. 1) имеет вид:
(1.1)
$\sqrt {\left\langle {{{\sigma }_{{{{1}_{{\max }}}}}}} \right\rangle \Delta {{\sigma }_{1}}{\text{/}}2} = {{\sigma }_{u}} + {{\sigma }_{L}}{{N}^{{ - {{\beta }_{{LH}}}}}},$Из критерия усталостного разрушения получаем число циклов до разрушения при однородном напряженном состоянии:
(1.2)
${{N}_{{LH}}} = {{10}^{3}}{{\left[ {({{\sigma }_{B}} - {{\sigma }_{u}}){\text{/}}\left\langle {{{\sigma }_{{LH}}} - {{\sigma }_{u}}} \right\rangle } \right]}^{{1/{{\beta }_{{LH}}}}}},\quad {{\sigma }_{{LH}}} = \sqrt {\left\langle {{{\sigma }_{{{{1}_{{\max }}}}}}} \right\rangle \Delta {{\sigma }_{1}}{\text{/}}2} $1.2. Для описания процесса развития усталостной поврежденности в режиме МЦУ–МНЦУ вводится функция повреждаемости $0 \leqslant \psi (N) \leqslant 1$, которая описывает процесс постепенного циклического (усталостного) разрушения материала. При $\psi = 1$ материальная частица считается полностью разрушенной. Ее модули Ламе становятся равными нулю. Функция повреждаемости $\psi $ в зависимости от числа циклов нагружения $N$ для режима МЦУ-МНЦУ описывается кинетическим уравнением:
где $\alpha $ и $0 < \gamma < 1$ – параметры модели, определяющие скорость процесса развития усталостных повреждений. Выбор знаменателя в этом двухпараметрическом уравнении задает бесконечно большую скорость роста зоны полного разрушения при $\psi \to 1$ и обусловлен известными экспериментальными данными по кинетическим кривым роста усталостных трещин, имеющим вертикальную асимптоту и отражающим факт их взрывного, неконтролируемого роста на последней стадии макроразрушения.Уравнение для повреждаемости сходного типа рассматривалось ранее [21, 22], его многочисленные параметры и коэффициенты определялись косвенно по результатам одноосных усталостных испытаний. Определим коэффициент ${{B}_{{LH}}}$ по процедуре, явно ассоциированной с выбранным критерием многоосного усталостного разрушения, которая выглядит следующим образом. Интегрируя уравнение для поврежденности при однородном напряженном состоянии
(1.3)
${{N}_{{LH}}} = \alpha {\text{/}}(1 + \alpha - \gamma ){\text{/}}(1 - \gamma ){\text{/}}{{B}_{{LH}}}$Приравнивая значения ${{N}_{{LH}}}$ из критерия разрушения (1.2) и из решения уравнения для повреждаемости (1.3) , получим выражение для коэффициента ${{B}_{{LH}}}$:
2. Кинетическое уравнение для повреждаемости в режиме СВМУ.
2.1. Критерий многоосного усталостного разрушения в режиме СВМУ, соответствующий правой ветви бимодальной усталостной кривой на рис. 2 (обобщенный stress-based SWT) имеет вид:
(2.1)
$\sqrt {\left\langle {{{\sigma }_{{{{1}_{{\max }}}}}}} \right\rangle \Delta {{\sigma }_{1}}{\text{/}}2} = {{\tilde {\sigma }}_{u}} + {{\sigma }_{V}}{{N}^{{ - {{\beta }_{{VH}}}}}},$Рис. 2.
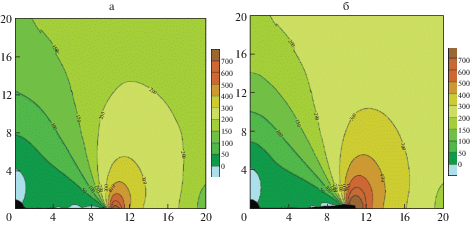
а – Режим СВМУ: $P = 160$ МПа, ${{N}_{k}} = 6.799 \times {{10}^{7}}$, ${{N}_{i}} = 1.007 \times {{10}^{6}}$, ${{N}_{f}} = 6.806 \times {{10}^{7}}$; б – Режим МНЦУ: $P = 210$ МПа, ${{N}_{k}} = 3.765 \times {{10}^{6}}$, ${{N}_{i}} = 7.229 \times {{10}^{4}}$, ${{N}_{f}} = 3.807 \times {{10}^{6}}$.
Из критерия усталостного разрушения получаем число циклов до разрушения при однородном напряженном состоянии:
(2.2)
${{N}_{{VH}}} = {{10}^{8}}{{\left[ {({{\sigma }_{u}} - {{{\tilde {\sigma }}}_{u}}){\text{/}}\left\langle {{{\sigma }_{{VH}}} - {{{\tilde {\sigma }}}_{u}}} \right\rangle } \right]}^{{1/{{\beta }_{{VH}}}}}},\quad {{\sigma }_{{VH}}} = {{\sigma }_{{LH}}} = \sqrt {\left\langle {{{\sigma }_{{{{1}_{{\max }}}}}}} \right\rangle \Delta {{\sigma }_{1}}{\text{/}}2} $Здесь ${{\tilde {\sigma }}_{u}}$ – предел усталости материала при реверсивном цикле для режима СВМУ, ${{\beta }_{{VH}}}$ – степенной показатель левой ветви бимодальной усталостной кривой.
2.2. Для режима СВМУ подобно п. 1.4 можно определить коэффициент в эволюционном уравнении для повреждаемости:
Аналогично уравнению (1.3) имеем:
(2.3)
${{N}_{{VH}}} = \alpha {\text{/}}(1 + \alpha - \gamma ){\text{/}}(1 - \gamma ){\text{/}}{{B}_{{VH}}}$Приравнивая значения ${{N}_{{VH}}}$ из критерия разрушения (2.2) и из решения уравнения для повреждаемости (2.3), получим выражение для коэффициента ${{B}_{{VH}}}$ в уравнении для повреждаемости:
Поведение поврежденного материала описывается уравнениями деградации его модулей упругости $\lambda (\psi ) = {{\lambda }_{0}}(1 - \psi )$, $\mu (\psi ) = {{\mu }_{0}}(1 - \psi )$. Материал становится полностью разрушенным, его модули упругости обнуляются при достижении функции повреждаемости $\psi (N)$ значения 1.
3. Условие переключения режимов накопления усталостной поврежденности. Точка перехода с левой ветви усталостной кривой на правую ветвь, при которой происходит смена механизма усталостного разрушения, находится чуть выше предела усталости ${{\sigma }_{u}}$ (рис. 1) и определяется значением ${{\sigma }_{*}} = {{\sigma }_{u}} + \Delta \sigma $. Для обеспечения непрерывного сопряжения левой и правой ветвей усталостной кривой необходимо выполнить условие ${{N}_{{LH}}} = {{N}_{{VH}}}$, которое эквивалентно уравнению для величины $\Delta \sigma $:
С учетом фактической малости поправочного члена в квадратных скобках, можно установить значение поправки $\Delta \sigma $ приближенной формулой:
Соответствующее приближенное значение ${{N}_{*}} = {{N}_{{LH}}}({{\sigma }_{*}})$ определяется величиной ${{N}_{*}} = {{10}^{3}}{{\left[ {({{\sigma }_{B}} - {{\sigma }_{u}}){\text{/}}\Delta \sigma } \right]}^{{1/{{\beta }_{{LH}}}}}} \approx {{10}^{8}}$, как и следовало ожидать.
С учетом полученных уточненных оценок для точки перехода с одной ветви усталостной кривой на другую, получим окончательные формулы для диапазонов и коэффициентов кинетических уравнений повреждаемости.
Для режима МЦУ–МНЦУ при ${{\sigma }_{u}} + \Delta {{\sigma }_{u}} < {{\sigma }_{{LH}}} < {{\sigma }_{B}}$, $\Delta \sigma = {{10}^{{ - 5{{\beta }_{{LH}}}}}}({{\sigma }_{B}} - {{\sigma }_{u}})$
Для режима СВМУ при ${{\tilde {\sigma }}_{u}} < {{\sigma }_{{VH}}} \leqslant {{\sigma }_{u}} + \Delta {{\sigma }_{u}}$
При ${{\sigma }_{{VH}}} \leqslant {{\tilde {\sigma }}_{u}}$ усталостного разрушения не происходит, при ${{\sigma }_{{LH}}} \geqslant {{\sigma }_{B}}$ оно наступает мгновенно.
4. Алгоритм расчета развития усталостных повреждений. Численная процедура решения дифференциального уравнения для функции повреждаемости состоит из следующих этапов. На первом этапе рассчитывается напряженное состояние упругого образца материала в одном цикле нагружения.
Для расчета цикла нагружения деформируемого образца с дефектами был использован программный пакет Астра, использующий высокоэкономичный безматричный вариант МКЭ [28] и дополненный кодом для расчета уравнения усталостной повреждаемости и изменения модулей упругости.
Ранее этот вариант МКЭ применялся для развития методов сквозного счета процессов динамического разрушения [29, 30]. С его использованием были построены [31] алгоритмы решения контактных задач. Он применялся [32] для решения задач прессования и спекания образцов при квазистатических или нестационарных (нециклических) нагрузках.
Для интегрирования уравнения $d\psi {\text{/}}dN = B{{\psi }^{\gamma }}{\text{/}}(1 - {{\psi }^{\alpha }})$, $B = {{B}_{{LH}}}$, ${{B}_{{VH}}}$ применялась аппроксимация функции повреждаемости в k-узле расчетной сетки при заданных дискретных значениях $\psi _{k}^{n}$ в моменты ${{N}^{n}}$ и искомых $\psi _{k}^{{n + 1}}$ в моменты ${{N}^{{n + 1}}}$.
Отметим, что вблизи состояния полного разрушения при $\psi \to 1$ знаменатель кинетического уравнения становится сколь угодно малым, уравнение становится “жестким” и обычные явные методы его численного решения становятся непригодными. При численном решении по неявным схемам возникает нелинейная алгебраическая система, решение которой при большом числе шагов затратно по времени расчета и достижению приемлемой точности.
Поэтому был выбран следующий метод расчета повреждаемости. Было замечено, что для значения $\alpha = 1 - \gamma $ путем аналитического интегрирования кинетического уравнения для повреждаемости на приращении числа циклов можно получить явное выражение для $\psi _{k}^{{n + 1}}(\psi _{k}^{n},\Delta {{N}^{n}})$. Кинетическое уравнение при этом становится однопараметрическим, но сохраняет желаемые особенности поведения скорости роста повреждаемости (заданный параметром $\gamma $ степенной рост в окрестности нуля, и бесконечный рост при $\psi \to 1$).
Выполним это интегрирование:
Обозначив ${{(\psi _{k}^{{n + 1}})}^{{1 - \gamma }}} = x$, $q = 2(1 - \gamma )B\Delta {{N}^{n}} + {{(\psi _{k}^{n})}^{{1 - \gamma }}} - 2{{(\psi _{k}^{n})}^{{2(1 - \gamma )}}}$, $\Delta {{N}^{n}} = {{N}^{{n + 1}}} - {{N}^{n}}$, получим уравнение ${{x}^{2}} - 2x + q = 0$ и его допустимый корень $x = 1 - \sqrt {1 - q} < 1$. Из него следует точная формула для повреждаемости на приращении числа циклов $\Delta {{N}^{n}}$:
Значение приращения $\Delta {{N}^{n}}$ определяется следующим образом.
На основе данных расчета напряженного состояния для каждого узла рассчитывается коэффициент В. Для определения приращения числа циклов выбираем точку с наиболее быстро растущей функцией поврежденности, то есть ту, в которой раньше других $\psi _{k}^{n}$ возрастет на заданную величину $\Delta {{\psi }_{0}}$. Выборка проводится по точкам, где $0 \leqslant \psi _{k}^{n} \leqslant 1$. Величину шага определяем следующим образом:
Величина шага ограничена заданным максимумом $\Delta {{N}_{{\max }}}$. В расчетах используются значения $\Delta {{\psi }_{0}} = 0.1$, $\Delta {{N}_{{\max }}} = {{10}^{5}}$.
Для каждого узла, исходя из его текущего уровня повреждаемости и эквивалентного напряжения, находится новый уровень повреждаемости с учетов вычисленного приращения $\Delta {{N}^{n}}$.
Деградация поврежденного материала при численных расчетах определялась зависимостью $E_{k}^{{n + 1}} = {{E}_{0}}(1 - \psi _{k}^{{n + 1}})(H({{\psi }_{0}} - \psi _{k}^{{n + 1}})$ + 0.001), где $E_{k}^{{n + 1}}$ – значение модуля Юнга на n + 1-м шаге по циклам нагружения при фиксированном значении коэффициента Пуассона, H – функция Хэвисайда, а ${{\psi }_{0}}\sim 1$ – критический параметр повреждаемости, по достижении которого материал переходит в полностью разрушенное состояние с околонулевыми модулями упругости. При расчетах выбиралось ${{\psi }_{0}} = 0.9$. Малое значение остаточного модуля Юнга – 0.001E для полностью разрушенного материала играет роль регуляризатора и вводится для того, чтобы сохранялась возможность вести сквозной счет для любого состояния поврежденности.
Расчет заканчивается при выходе границ области полностью разрушенного материала на поверхность образца (макроразрушение) или прекращении эволюции этой области.
С помощью мультирежимной модели и разработанной численной процедуры решены задачи о развитии зон усталостной поврежденности в окрестности типичных дефектов структуры материала (микропоры, различным образом ориентированные микротрещины).
Предложенную модель и численный метод можно считать развитием и распространением ранее разработанных алгоритмов сквозного счета процессов динамического разрушения [29, 30] на случай циклического нагружения и усталости материалов.
5. Примеры расчетов. Были проведены расчеты циклического нагружения пластин с дефектами для коэффициента асимметрии R = –1 (реверсивный цикл) c зарождением зон поврежденности, возникновения и развития трещиноподобных зон полного разрушения частиц материала (“квазитрещин”) вплоть до их выхода на боковую грань пластины (макроразрушения).
Нормальная нагрузка прикладывается с торцов, боковые грани пластины свободны от напряжений. Рассматривается плоское напряженное состояние. Упругие, прочностные и усталостные свойства материала пластины (титановый сплав) были взяты из [21]: ${{\sigma }_{B}} = {\text{116}}0$ МПа, ${{\sigma }_{u}} = 337$ МПа, ${{\tilde {\sigma }}_{u}} = 250$ МПа, ${{\beta }_{{LH}}} = 0.31$, ${{\beta }_{{VH}}} = 0.27$. Модули упругости неповрежденного сплава равны ${{\lambda }_{0}} = 77$ ГПа, ${{\mu }_{0}} = 44$ ГПа.
Степенной показатель кинетического уравнения $\gamma $ должен быть определен в процессе согласования результатов вычислительных и усталостных экспериментов. Для численных расчетов в уравнении для повреждаемости было принято среднее значение $\gamma $ = 0.5, $\alpha = 1 - \gamma $.
Размеры пластины 40 × 40 мм. Горизонтальная y = 0 и вертикальная x = 0 центральные оси пластины являются осями симметрии, поэтому расчет проводится для области x > 0, y > 0. Рассмотрены три вида дефектов в центре пластины: круговое отверстие радиусом r = 1 мм; узкое эллиптическое отверстие с горизонтальной осью a = 1 мм, вертикальной осью b = 0.2a; узкое эллиптическое отверстие с вертикальной осью b = 1 мм, горизонтальной осью a = 0.2b. На рис. 2 показаны результаты расчета для кругового отверстия. На этом и последующих рисунках представлены изолинии максимального главного напряжения вокруг “квазитрещины” в тот момент, когда она прошла примерно половину расстояния до боковой грани. В подписях к рисункам указаны значения количества циклов: ${{N}_{i}}$ – до начала разрушения, ${{N}_{f}}$ – до макроразрушения, ${{N}_{k}}$ – для положения, представленного на графике. Также указан максимальный уровень растягивающих напряжений Р в цикле приложенных нагрузок и соответствующий им режим усталостного разрушения.
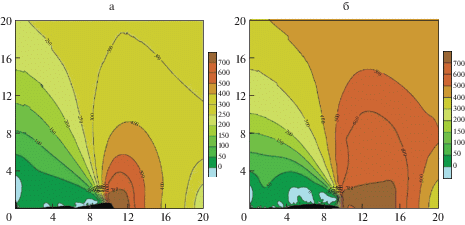
На рис. 3 показаны результаты расчета для горизонтально ориентированного узкого эллиптического отверстия; на рис. 4 – для вертикально ориентированного узкого эллиптического отверстия.
Рис. 3.
а – Режим СВМУ: $P = 100$ МПа, ${{N}_{k}} = 1.350 \times {{10}^{9}}$, ${{N}_{i}} = 2.903 \times {{10}^{4}}$, ${{N}_{f}} = 1.351 \times {{10}^{9}}$; б – Режим МНЦУ: $P = 180$ МПа, ${{N}_{k}} = 1.009 \times {{10}^{6}}$, ${{N}_{i}} = 1.971 \times {{10}^{4}}$, ${{N}_{f}} = 1.057 \times {{10}^{6}}$.
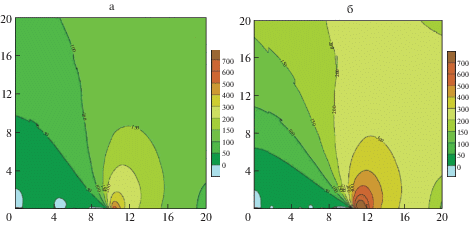
Рис. 4.
а – Режим СВМУ: $P = 264$ МПа, ${{N}_{k}} = 4.893 \times {{10}^{7}}$, ${{N}_{i}} = 2.619 \times {{10}^{7}}$, ${{N}_{f}} = 4.896 \times {{10}^{7}}$; б – Режим МНЦУ: $P = 400$ МПа, ${{N}_{k}} = 9.659 \times {{10}^{5}}$, ${{N}_{i}} = 8.701 \times {{10}^{5}}$, ${{N}_{f}} = 9.776 \times {{10}^{5}}$.
Отметим, что количество циклов ${{N}_{k}}$, соответствующее уровню продвижения трещиноподобных зон разрушения частиц материала (“квазитрещин”) примерно до середины образца (рис. 2–4), очень мало отличается от количества циклов ${{N}_{f}}$, что указывает на дальнейший финальный, быстропротекающий процесс макроразрушения.
Из рисунков видно, что близкий уровень циклических нагрузок, приложенных к образцу с дефектами разного типа и ориентации, может приводить к усталостному макроразрушению образца в совершенно различных режимах. Так, например, для вертикально ориентированного эллиптического дефекта при уровне P = 264 МПа имеем режим, переходный к СВМУ (рис. 4а) с долговечностью ${{N}_{f}} = 4.709 \times {{10}^{7}}$, а для горизонтально ориентированного эллиптического дефекта при существенно более низком P = 180 МПа макроразрушение происходит по механизму МНЦУ (рис. 3б) с долговечностью ${{N}_{f}} = 1.057 \times {{10}^{6}}$.
Также можно отметить, что при проведении расчетов по мультирежимной модели неоднократно проявлялся и моделировался эффект, наблюдаемый при фрактографических исследованиях элементов конструкций, разрушенных при эксплуатации [33]. При относительно небольшом уровне приложенных нагрузок, за счет внутренних дефектов зарождение и начальное развитие зон усталостного разрушения происходит по механизму СВМУ, а затем при концентрации и росте уровня напряжений в окрестности фронта распространяющейся “квазитрещины” происходит переход на другую ветвь (МЦУ–МНЦУ) усталостной кривой. При этом резко меняется скорость развития процесса усталостного разрушения.
Разработанная мультирежимная модель и численный метод позволяют проводить сквозной счет развития зон повреждаемости и трещиноподобных зон усталостного разрушения материала без явного выделения трещин в их классическом понимании, а также оценивать долговечность образцов от появления первых очагов до макроразрушения.
Заключение. Предложена мультирежимная кинетическая модель развития повреждаемости при циклическом нагружении для описания развития процесса усталостного разрушения. Для определения коэффициентов кинетического уравнения повреждаемости использован известный критерий многоосного усталостного разрушения SWT, в котором заложен механизм, связанный с развитием микротрещин нормального отрыва. На этой основе предложена процедура вычисления коэффициентов кинетического уравнения для различных режимов усталостного разрушения МЦУ–МНЦУ, СВМУ.
Разработан единообразный численный метод и приведены примеры расчета развития трещиноподобных зон повреждаемости и усталостного разрушения образцов, содержащих дефекты разного типа для различных режимов циклического нагружения от МЦУ до СВМУ.
Исследование выполнено за счет гранта Российского научного фонда (проект № 19-19-00705).
Список литературы
Basquin O.H. The exponential law of endurance tests // in: Proc. Amer. Soc. for Testing & Mater. 1910. V. 10. P. 625–630.
Sines G. Behavior of Metals under Complex Static and Alternating Stresses. Metal Fatigue. New York: McGraw-Hill, 1959. P. 145–169.
Crossland B. Effect of large hydrostatic pressures on torsional fatigue strength of an alloy steel // Proc. Intern. Conf. on Fatigue of Metals. London. 1956. P. 138–149.
Findley W. A theory for the effect of mean stress on fatigue of metals under combined torsion and axial load or bending// J. Eng. for Indust. 1959. P. 301–306.
Morel F. A critical plane approach for life prediction of high cycle fatigue under multiaxial variable amplitude loading // Intern. J. Fatigue. 2000. V. 22. № 2. P. 101–119.
Matake T. An explanation on fatigue limit under combined stress // Bull. JSME. 1977. V. 20. P. 257–263.
McDiarmid D.L. A shear stress based critical-plane criterion of multiaxial fatigue failure for design and life prediction // Fatigue Fract. Eng. Mater. Struct. 1999. V. 17 P. 1475–1484.
Papadopoulos I.V. Long life fatigue under multiaxial loading // Intern. J. Fatigue. 2001. V. 23. P. 839–849.
Carpinteri A., Spagnoli A., Vantadori S. Multiaxial assessment using a simplified critical plane based criterion // Intern. J. Fatigue. 2011. V. 33. P. 969–976.
Meggiolaro M.A., Miranda A.C., de Castro J. Comparison among fatigue life prediction methods and stress-strain models under multiaxial loading // Proc. 19th Intern. Congress Mech. Eng. 2007. Brasilia, DF.
Ying-Yu Wang, Wei-Xing Yao. Evaluation and comparison of several multiaxial fatigue criteria // Intern. J. Fatigue. 2004. V. 26. P. 17–25.
Karolczuk A., Papuga J., Palin-Luc T. Progress in fatigue life calculation by implementing life-dependent material parameters in multiaxial fatigue criteria // Intern. J. Fatigue. 2020. V. 134. 105509.
Bourago N.G., Zhuravlev A.B., Nikitin I.S. Models of multiaxial fatigue fracture and service life estimation of structural elements// Mech. Sol. 2011. V. 46. № 6. P. 828–838.
Paris P.C., Erdogan F. A Critical analysis of crack propagation laws // J. Basic Engng. 1963. V. 85. P. 528–533. https://doi.org/10.1115/1.3656900
Collins J.A. Failure of Materials in Mechanical Design: Analysis, Prediction, Prevention. New York: Wiley. 1993. 654 p.
Shlyannikov V.N. Creep-Fatigue crack growth rate prediction based on fracture damage zones models // Engng. Fract. Mech. 2019. V. 214. P. 449–463.
Качанов Л.М. О времени разрушения в условиях ползучести// Изв. АН СССР ОТН. 1958. Т. 8. С. 26–31.
Работнов Ю.Н. О механизме длительного разрушения. Вопросы прочности материалов и конструкций // АН СССР ОТН. 1959. С. 5–7.
Murakami S. Continuum Damage Mechanics. A Continuum Mechanics Approach to the Analysis of Damage and Fracture. Dordrecht: Springer, 2012.
Lemaitre J., Chaboche J.L. Mechanics of solid materials. Cambridge Univ. Press, 1994. 582 p.
Marmi A.K., Habraken A.M., Duchene L. Multiaxial fatigue damage modeling at macro scale of Ti6Al4V alloy // Intern. J. Fatigue. 2009. V. 31. P. 2031–2040.
Zhi Yong Huang, Wagner D., Bathias C., Chaboche J.L. Cumulative fatigue damage in low cycle fatigue and gigacycle fatigue for low carbon–manganese steel// Intern. J. Fatigue. 2011. V. 33. P. 115–121.
Plekhov O., Naimark O. et al. The study of a defect evolution in iron under fatigue loading in gigacycle fatigue regime// Frattura ed Integrita Strutturale. 2016. V. 10. № 35. P. 414–423.
Burago N.G., Nikitin I.S. Multiaxial fatigue criteria and durability of titanium compressor disks in low- and giga- cycle fatigue modes // in: Mathematical Modeling and Optimization of Complex Structures. Heidelberg: Springer, 2016. P. 117–130.
Shanyavskiy A.A., Soldatenkov A.P. The fatigue limit of metals as a characteristic of the multimodal fatigue life distribution for structural materials// Proc. Struct. Integr. 2019. 2011. V. 23. P. 63–68.
Smith R.N., Watson P., Topper T.H. A stress-strain parameter for the fatigue of metals // J. Mater. 1970. V. 5. № 4. P. 767–778.
Gates N., Fatemi A. Multiaxial variable amplitude fatigue life analysis including notch effects// Intern. J. Fatigue. 2016. V. 91. P. 337–351.
Бураго Н.Г., Никитин И.С. Безматричная реализация неявных схем методом сопряженных градиентов // ЖВММФ. 2018. Т. 58. № 8. С. 52–63.
Burago N.G., Nikitin I.S., Nikitin A.D., Stratula B.A. Algorithms for calculation damage processes // Frattura ed Integrità Strutturale. 2019. V. 49. P. 212–224.
Бураго Н.Г., Никитин И.С. Алгоритмы сквозного счета для процессов разрушения // Компьютерные исследования и моделирование. 2018. Т. 10. № 5. С. 645–666.
Burago N.G., Nikitin I.S., Nikitin A.D. Algorithms for calculating contact problems in the solid dynamics // in: Advances in Theory and Practice Computational Mechanics. Ed. by Jain L.C. Singapore: Springer, 2020. P. 185–198.
Бураго Н.Г., Никитин И.С. Математическая модель и алгоритм расчета прессования и спекания // Матем. модел. 2019. Т. 31. № 2. С. 3–17.
Шанявский А.А. Моделирование усталостных разрушений металлов. Уфа: Монография, 2007. 498 с.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика