Прикладная математика и механика, 2021, T. 85, № 2, стр. 172-192

УПРУГОПЛАСТИЧЕСКОЕ ДЕФОРМИРОВАНИЕ ВРАЩАЮЩЕГОСЯ СПЛОШНОГО ЦИЛИНДРА ИЗ ЛИНЕЙНО-УПРОЧНЯЮЩЕГОСЯ МАТЕРИАЛА

А. Н. Прокудин^a, *, А. А. Буренин^a, **

^a Институт машиноведения и металлургии Хабаровского федерального исследовательского центра ДВО РАН
г. Комсомольск-на-Амуре, Россия

^* E-mail: sunbeam_85@mail.ru
^** E-mail: mail@imim.ru

Поступила в редакцию 28.12.2020
После доработки 28.01.2021
Принята к публикации 02.02.2021

DOI: 10.31857/S0032823521020077

Полный текст (PDF)

Аннотация

Исследуется вращающийся сплошной цилиндр из упрочняющегося упругопластического материала. Постановка задачи основана на уравнениях Прандтля–Рейса и предположении об обобщенном плоском деформированном состоянии в цилиндре. Для определения пластических деформаций используется условие максимальных приведенных напряжений, ассоциированный с ним закон пластического течения, а также закон линейного изотропного упрочнения. Анализ ограничен активным нагружением цилиндра. Показано, что в общем случае в цилиндре возможно появление четырех пластических областей, соответствующих разным ребрам и граням поверхности текучести. Для каждой возможной области найдено точное аналитическое решение. Установлены зависимости критической скорости вращения, при которой весь цилиндр переходит в состояние пластичности, от параметра упрочнения. Приведено сравнение полученных результатов с решениями для условий пластичности Треска и Мизеса.

Ключевые слова: упругопластичность, малые деформации, вращающийся цилиндр, линейное изотропное упрочнение, условие максимальных приведенных напряжений

Вращающиеся цилиндры являются важным составным элементом многих механизмов и машин. В ходе эксплуатации цилиндры подвергаются действию значительных центробежных сил, что может приводить к появлению пластических деформаций. Поэтому для более точного прогнозирования прочности вращающихся деталей механизмов необходимо применять упругопластический анализ. Для решения данного класса задач обычно используется предположение о плоском либо обобщенном плоском деформированном состоянии в цилиндре, теория малых деформаций, условие пластичности Треска или Мизеса и ассоциированный с ним закон течения. В работах [1–8] представлено решение упругопластической задачи на основе условия Треска для вращающегося сплошного и полого цилиндра с различными типами условий на торцах. Установлены закономерности появления и развития пластических областей, а также критические скорости вращения, соответствующие полному переходу цилиндра в пластическое состояние. Схожая постановка задачи, отличающаяся тем, что материал цилиндра принят неоднородным, использовалась [9–11] для анализа упругопластического деформирования вращающихся полых цилиндров из функционально-градиентных материалов. Неоднородность свойств материала описывалась с помощью степенной зависимости от радиальной координаты, при этом данная зависимость использовалась [9, 10] только для модуля Юнга, а в [11] – для модуля Юнга, плотности и предела текучести. Показано [9–11], что неоднородность материала оказывает значительное влияние на напряженно-деформированное состояние в цилиндре и критические скорости вращения.

В работах [1–11] использовалась модель идеального упругопластического материала. Для описания пластического деформирования материалов в большей степени подходят модели упрочняющегося тела. С использованием условия Треска и закона линейного изотропного упрочнения получено [12] решение упругопластической задачи для вращающегося сплошного цилиндра. Автором рассматривались цилиндры, как с закрепленными, так и свободными торцами. Показано, что в цилиндрах из идеального и упрочняющегося материала возникают пластические области, соответствующие одинаковым граням и ребрам призмы Треска, однако в упрочняющемся цилиндре пластическое течение развивается медленней, а величина пластических деформаций – ниже. Исследовались [13] вращающиеся цилиндры из нелинейно-упрочняющегося материала. Рассматривались сплошные и полые цилиндры с различными типами условий на торцах. Для постановки задачи использовалась деформационная теория пластичности и условие пластичности Мизеса. Нелинейное изотропное упрочнение материала описывалось с помощью закона Свифта, частным случаям которого является линейный закон упрочнения. Решение задачи проводилось с помощью разработанного численного алгоритма на основе метода стрельбы. Автор показал, что использование условий Треска и Мизеса вместе с линейным законом упрочнения приводит к близкому распределению перемещений и напряжений в цилиндре, однако условие Мизеса предсказывает значительно меньшую величину пластических деформаций в цилиндре. Кроме того, для одинаковой скорости вращения пластическое течение при использовании условия Мизеса распространяется на меньшую область по сравнению с условием Треска. Также автором установлено, что параметры материала оказывают существенное влияние на напряженно-деформированное состояние вращающегося цилиндра из нелинейно-упрочняющегося материала.

На практике вращающиеся элементы механизмов, такие как роторы, находятся под действием не только центробежных сил, но и температурного воздействия. Рассмотрено [14, 15] упругопластическое деформирование вращающегося полого цилиндра при наличии стационарного температурного градиента между внутренней и внешней поверхностью цилиндра. Пластическая составляющая деформации определялась с помощью условия Треска, ассоциированного с ним закона течения и закона линейного упрочнения. Для расчета температурных деформаций использовалось уравнение теплопроводности и закон Дюамеля–Неймана. При этом предполагалось, что механические и теплофизические параметры материала не зависят от температуры. Установлено [14, 15], что неоднородное температурное поле оказывает существенное влияние на развитие пластического течения во вращающемся полом цилиндре. В частности, отмечено [14], что присутствие положительного градиента температуры приводит к уменьшению скорости начала пластического течения и незначительному увеличению скорости, при которой весь цилиндр переходит в пластическое состояние. С другой стороны, как показано [15], цилиндр, предварительно нагруженный отрицательным температурным градиентом практически до предела текучести, способен выдерживать значительные скорости вращения до возникновения пластического течения.

Использование более сложных моделей материалов затрудняет получение аналитического решения упругопластических задач, что приводит к необходимости применения численных методов. Следует отметить публикации [16–18], посвященные исследованию вращающихся полых цилиндров из нелинейно упрочняющегося материала в рамках жесткопластического анализа. Постановка задачи основана на теоремах предельного пластического состояния. Использовалось [16] условие пластичности Мизеса и экспоненциальный закон упрочнения Восе, который асимптотически (с увеличением эквивалентной пластической деформации) переходит в модель идеального пластического тела. Авторы [17, 18] рассматривали усложненные модели материала, включающие в себя учет эффектов вязкости материала [17] и его пластической анизотропии [18]. Решение поставленных в [16–18] задач проводилось с помощью метода конечных элементов. Кроме того, для ряда значений параметров материала найдены замкнутые аналитические решения в элементарных функциях.

Проведенный литературный обзор показал, что для расчета упругопластических деформаций вращающихся цилиндров наиболее часто используются условия текучести Треска и Мизеса. Условие максимальных приведенных напряжений (условие Ишлинского–Ивлева) [19] также относится к классическим условиям пластичности. Оно было сформулировано А.Ю. Ишлинским на основе гипотезы прочности формоизменения [20]. Аналогичное условие использовалось Шмидтом [21], Хиллом [22] и Ивлевым [23]. Это условие, как и условие Треска, является кусочно-линейным, но в его запись входят все три главных напряжения. Ранее с его помощью было получено распределение напряжений во вращающемся сплошном диске [24] и цилиндре [25] из идеального упругопластического материала. Из недавних работ также можно отметить [26–30].

Целью настоящей публикации является получение точного аналитического решения задачи об упругопластическом деформировании вращающегося сплошного цилиндра. Рассматривается цилиндр, как с закрепленными, так и свободными торцами. Для постановки задачи используется теория малых деформаций, условие максимальных приведенных напряжений, линейный закон изотропного упрочнения и ассоциированный закон пластического течения. Проведенное исследование ограничено случаем активного нагружения цилиндра. Полученные результаты дополняют работы Эразлана [12, 13], в которых использовались условия Треска и Мизеса вместе с линейным законом изотропного упрочнения, а также работу [25] в которой принималось условие максимальных приведенных напряжений и модель идеального упругопластического материала.

1. Постановка задачи. Рассматривается сплошной цилиндр, вращающийся вокруг собственной оси. Предполагается, что цилиндр находится в состоянии обобщенной плоской деформации (суммарная осевая деформация не зависит от $\beta $) и сохраняет осевую симметрию в процессе деформирования. Введем цилиндрическую систему координат $\left( {r,\theta ,z} \right)$ и безразмерные величины:

(1.1)

$\begin{gathered} \beta = \frac{r}{b},~\quad \bar {u} = \frac{E}{{{{\sigma }_{0}}}}\frac{{{{u}_{r}}}}{b},\quad ~{{{\bar {\varepsilon }}}_{{ij}}} = \frac{E}{{{{\sigma }_{0}}}}{{\varepsilon }_{{ij}}},\quad ~\bar {\varepsilon }_{{ij}}^{e} = \frac{E}{{{{\sigma }_{0}}}}\varepsilon _{{ij}}^{e},\quad \bar {\varepsilon }_{{ij}}^{p} = \frac{E}{{{{\sigma }_{0}}}}\varepsilon _{{ij}}^{p} \\ {{{\bar {\sigma }}}_{{ij}}} = \frac{{{{\sigma }_{{ij}}}}}{{{{\sigma }_{0}}}},\quad {{{\bar {\sigma }}}_{y}} = \frac{{{{\sigma }_{y}}}}{{{{\sigma }_{0}}}},\quad H = \eta \frac{{{{\sigma }_{0}}}}{E},\quad ~\Omega = \frac{{\rho {{b}^{2}}{{\omega }^{2}}}}{{{{\sigma }_{0}}}}, \\ \end{gathered} $

где $b$ – радиус цилиндра, $E$ – модуль Юнга, ${{\sigma }_{0}}$, ${{\sigma }_{y}}$ – начальный/актуальный предел текучести при одноосном растяжении-сжатии, ${{{\text{u}}}_{r}}$ – радиальное перемещение, ${{\varepsilon }_{{ij}}}$ – полные деформации, $\varepsilon _{{ij}}^{e}$ – упругие деформации, $\varepsilon _{{ij}}^{p}$ – пластические деформации, ${{\sigma }_{{ij}}}$ – напряжения, $\eta $ – параметр, характеризующий упрочнение материала, $\rho $ – плотность, $\omega $ – скорость вращения цилиндра. Параметр нагружения $\Omega $, зависящий от квадрата угловой скорости, монотонно возрастает от 0 до некоторого максимального значения ${{\Omega }_{{\max }}}$. Угловым ускорением пренебрегаем. Далее в статье все уравнения записаны в безразмерных переменных (1.1), а знак подчеркивания для краткости не используется.

Полные деформации ${{\varepsilon }_{{ij}}}$ являются малыми и складываются из упругих $\varepsilon _{{ij}}^{e}$ и пластических $\varepsilon _{{ij}}^{p}$ составляющих:

(1.2)

${{\varepsilon }_{{rr}}} = \frac{{\partial u}}{{\partial \beta }} = \varepsilon _{{rr}}^{e} + \varepsilon _{{rr}}^{p},\quad {{\varepsilon }_{{\theta \theta }}} = \frac{u}{\beta } = \varepsilon _{{\theta \theta }}^{e} + \varepsilon _{{\theta \theta }}^{p},\quad {{\varepsilon }_{{zz}}} = \varepsilon _{{zz}}^{e} + \varepsilon _{{zz}}^{p}$

Заметим, что случай ${{\varepsilon }_{{zz}}} = \operatorname{const} \ne 0$ соответствует цилиндру со свободными торцами, а ${{\varepsilon }_{{zz}}} = 0$ – цилиндру с закрепленными торцами (плоское деформированное состояние).

Напряжения связаны с упругими деформациями через закон Гука:

(1.3)

$\begin{gathered} {{\sigma }_{{rr}}} = \frac{1}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left( {\left( {1 - \nu } \right)\varepsilon _{{rr}}^{e} + \nu \varepsilon _{{\theta \theta }}^{e} + \nu \varepsilon _{{zz}}^{e}} \right) \\ {{\sigma }_{{\theta \theta }}} = \frac{1}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left( {\nu \varepsilon _{{rr}}^{e} + \left( {1 - \nu } \right)\varepsilon _{{\theta \theta }}^{e} + \nu \varepsilon _{{zz}}^{e}} \right) \\ {{\sigma }_{{zz}}} = \frac{1}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left( {\nu \varepsilon _{{rr}}^{e} + \nu \varepsilon _{{\theta \theta }}^{e} + \left( {1 - \nu } \right)\varepsilon _{{zz}}^{e}} \right) \\ \end{gathered} $

Здесь $\nu $ – коэффициент Пуассона.

Также в анализе используются соотношения, обратные к (1.3):

(1.4)

$\varepsilon _{{rr}}^{e} = {{\sigma }_{{rr}}} - \nu {{\sigma }_{{\theta \theta }}} - \nu {{\sigma }_{{zz}}},\quad \varepsilon _{{\theta \theta }}^{e} = {{\sigma }_{{\theta \theta }}} - \nu {{\sigma }_{{rr}}} - \nu {{\sigma }_{{zz}}},\quad \varepsilon _{{zz}}^{e} = {{\sigma }_{{zz}}} - \nu {{\sigma }_{{rr}}} - \nu {{\sigma }_{{\theta \theta }}}$

Единственное нетривиальное уравнение равновесия в цилиндре имеет вид:

(1.5)

$\frac{{\partial {{\sigma }_{{rr}}}}}{{\partial \beta }} + \frac{{{{\sigma }_{{rr}}} - {{\sigma }_{{\theta \theta }}}}}{\beta } = - \Omega \beta $

Для цилиндра со свободными концами необходимо использовать дополнительное ограничение на суммарную осевую силу:

(1.6)

$2\pi \int\limits_0^1 \beta {{\sigma }_{{zz}}}d\beta = 0$

Граничные условия задачи:

(1.7)

$u(0) = 0,\quad {{\sigma }_{{rr}}}(1) = 0$

Для расчета пластических деформаций используется условие максимальных приведенных напряжений:

$\max \left( {\left| {{{\sigma }_{1}} - \sigma } \right|,~\left| {{{\sigma }_{2}} - \sigma } \right|,~\left| {{{\sigma }_{3}} - \sigma } \right|} \right) = \frac{2}{3}{{\sigma }_{y}},$

где ${{\sigma }_{1}}$, $~{{\sigma }_{2}}$, $~{{\sigma }_{3}}$ – главные напряжения, упорядоченные по возрастанию: ${{\sigma }_{1}} \geqslant ~{{\sigma }_{2}} \geqslant ~{{\sigma }_{3}}$, $\sigma $ – гидростатическое напряжение. Приведенное условие далее используется в следующем виде:

(1.8)

$\begin{gathered} {{\sigma }_{1}} - \frac{1}{2}\left( {{{\sigma }_{2}} + {{\sigma }_{3}}} \right) = {{\sigma }_{y}},~\quad {\text{если}}\quad {{\sigma }_{2}} \leqslant \left( {{{\sigma }_{1}} + {{\sigma }_{3}}} \right){\text{/}}2 \\ \frac{1}{2}\left( {{{\sigma }_{1}} + {{\sigma }_{2}}} \right) - {{\sigma }_{3}} = {{\sigma }_{y}},\quad ~{\text{если}}\quad {{\sigma }_{2}} \geqslant \left( {{{\sigma }_{1}} + {{\sigma }_{3}}} \right){\text{/}}2 \\ \end{gathered} $

Главные напряжения ${{\sigma }_{1}}$, $~{{\sigma }_{2}}$, $~{{\sigma }_{3}}$ совпадают с координатными, поскольку касательные напряжения в цилиндре отсутствуют. Поверхность в пространстве главных напряжений, соответствующую условию (1.8) будем называть призмой Ивлева.

Для сравнения используются результаты [12, 13], полученные с помощью условий Треска и Мизеса, которые имеют вид:

(1.9)

$\max \left( {\left| {{{\sigma }_{1}} - {{\sigma }_{2}}} \right|,~\left| {{{\sigma }_{2}} - {{\sigma }_{3}}} \right|,~\left| {{{\sigma }_{1}} - {{\sigma }_{3}}} \right|} \right) = {{\sigma }_{y}}$

(1.10)

${{\left( {{{\sigma }_{1}} - {{\sigma }_{2}}} \right)}^{2}} + {{\left( {{{\sigma }_{2}} - {{\sigma }_{3}}} \right)}^{2}} + {{\left( {{{\sigma }_{1}} - {{\sigma }_{3}}} \right)}^{2}} = 2\sigma _{y}^{2}$

На рис. 1а изображены сечения поверхностей текучести (1.8)–(1.10) девиаторной плоскостью ${{\sigma }_{1}} + {{\sigma }_{2}} + {{\sigma }_{3}} = 0$. Условию Треска соответствует внутренний шестиугольник, а условию максимальных приведенных напряжений – внешний. Условие Мизеса имеет вид окружности, описанной вокруг внутреннего шестиугольника и вписанной во внешний.

Рис. 1.

Сечения поверхностей текучести девиаторной плоскостью ${{\sigma }_{1}} + {{\sigma }_{2}} + {{\sigma }_{3}} = 0$: а – условия Треска, Мизеса и Ишлинского–Ивлева; б – общее кусочно-линейное условие.

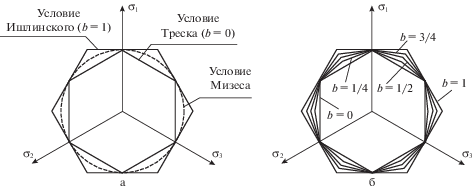
Условия (1.8) и (1.9) являются частными случаями общего кусочно-линейного условия пластичности [31]:

(1.11)

$\begin{gathered} {{\sigma }_{1}} - \frac{1}{{1 + b}}\left( {b{{\sigma }_{2}} + {{\sigma }_{3}}} \right) = {{\sigma }_{y}},\quad {\text{если}}\quad {{\sigma }_{2}} \leqslant \left( {{{\sigma }_{1}} + {{\sigma }_{3}}} \right){\text{/}}2 \hfill \\ \frac{1}{{1 + b}}\left( {{{\sigma }_{1}} + b{{\sigma }_{2}}} \right) - {{\sigma }_{3}} = {{\sigma }_{y}},\quad {\text{если}}\quad {{\sigma }_{2}} \geqslant \left( {{{\sigma }_{1}} + {{\sigma }_{3}}} \right){\text{/}}2 \hfill \\ \end{gathered} $

Условие (1.11) сводится к условию Треска (1.9), если принять $b = 0$ и к условию максимальных приведенных напряжений (1.8), если $b = 1$. Кроме того, условие, полученное из (1.11) при $b = \left( {\sqrt 3 - 1} \right){\text{/}}2$, называется условием Соколовского [32, 33] и представляет собой кусочно-линейную аппроксимацию условия Мизеса (1.10). Параметр $b\,$ зависит от отношения предела текучести при чистом сдвиге ${{\tau }_{y}}$ к пределу текучести при одноосном растяжении-сжатии ${{\sigma }_{y}}$:

$b = {{\left( {2\alpha - 1} \right)} \mathord{\left/ {\vphantom {{\left( {2\alpha - 1} \right)} {\left( {1 - \alpha } \right)}}} \right. \kern-0em} {\left( {1 - \alpha } \right)}},\quad \alpha = {{{{\tau }_{y}}} \mathord{\left/ {\vphantom {{{{\tau }_{y}}} {{{\sigma }_{y}}}}} \right. \kern-0em} {{{\sigma }_{y}}}},$

и его можно рассматривать как характеристику материала. Из предыдущего выражения можно найти отношение $\alpha = \left( {1 + b} \right){\text{/}}\left( {2 + b} \right)$.

Отсюда при $b\, = 1$ найдем для условия (1.8) $\alpha = 2{\text{/}}3$. Для условия Треска, как известно, $\alpha = 1{\text{/}}2$. Результаты экспериментов показывают, что для ряда материалов (алюминий, титан, никелевые сплавы, нержавеющая сталь) величина $\alpha $ лежит в диапазоне от 0.58 до 0.7 [31, 34]. Как следствие, для перечисленных материалов в большей степени подходит условие максимальных приведенных напряжений (1.8). Общее кусочно-линейное условие текучести для ряда значений параметра b изображено на рис. 1б.

Предел текучести является линейной функцией эквивалентной пластической деформации $\varepsilon _{{{\text{eq}}}}^{p}$:

(1.12)

${{\sigma }_{y}} = 1 + H\varepsilon _{{{\text{eq}}}}^{p}$

Ассоциированный закон течения имеет вид:

(1.13)

$d\varepsilon _{{ij}}^{p} = d\lambda \frac{{df}}{{d{{\sigma }_{{ij}}}}},$

здесь $d\varepsilon _{{ij}}^{p}$ – приращения пластических деформаций, $d\lambda $ – положительный множитель, $f$ – пластический потенциал, соответствующий грани поверхности текучести.

Если напряженное состояние в пластической области соответствует ребру поверхности текучести, то вместо закона (1.13) необходимо использовать его обобщение, предложенное Койтером [35]:

(1.14)

$d\varepsilon _{{ij}}^{p} = d{{\lambda }_{1}}\frac{{d{{f}_{1}}}}{{d{{\sigma }_{{ij}}}}} + d{{\lambda }_{2}}\frac{{d{{f}_{2}}}}{{d{{\sigma }_{{ij}}}}},$

где $d{{\lambda }_{1}}$ и $d{{\lambda }_{2}}$ – положительные множители, ${{f}_{1}}$ и ${{f}_{2}}$ – функции пластичности, соответствующие граням призмы текучести, на пересечении которых лежит рассматриваемое ребро.

Приращение эквивалентной пластической деформации $d\varepsilon _{{{\text{eq}}}}^{p}$ определяется из соотношения:

(1.15)

${{\sigma }_{y}}d\varepsilon _{{{\text{eq}}}}^{p} = {{\sigma }_{{rr}}}d\varepsilon _{{rr}}^{p} + {{\sigma }_{{\theta \theta }}}d\varepsilon _{{\theta \theta }}^{p} + {{\sigma }_{{zz}}}d\varepsilon _{{zz}}^{p}$

2. Упругое решение. Рассмотрим область чисто упругого деформирования, в которой $\varepsilon _{{rr}}^{p} = \varepsilon _{{\theta \theta }}^{p} = \varepsilon _{{zz}}^{p} = 0$. Решая уравнение равновесия (1.5) с учетом (1.2) и (1.3) найдем распределение перемещения:

(2.1)

$u = \frac{{{{D}_{1}}}}{\beta } + {{D}_{2}}\beta - \frac{1}{8}\frac{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}{{\left( {1 - \nu } \right)}}\Omega {{\beta }^{3}},$

где ${{D}_{1}}$, ${{D}_{2}}$ – константы интегрирования. Заметим, что полученное решение не зависит от полной осевой деформации ${{\varepsilon }_{{zz}}}$.

Далее с помощью кинематических соотношений (1.2) и закона Гука (1.3) найдем распределение напряжений в цилиндре:

(2.2)

$\begin{gathered} {{\sigma }_{{rr}}} = - \frac{{{{D}_{1}}}}{{\left( {1 + \nu } \right)}}\frac{1}{{{{\beta }^{2}}}} + \frac{{\left( {{{D}_{2}} + \nu {{\varepsilon }_{{zz}}}} \right)}}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}} - \frac{1}{8}\frac{{\left( {3 - 2\nu } \right)}}{{\left( {1 - \nu } \right)}}\Omega {{\beta }^{2}} \\ {{\sigma }_{{\theta \theta }}} = \frac{{{{D}_{1}}}}{{\left( {1 + \nu } \right)}}\frac{1}{{{{\beta }^{2}}}} + \frac{{\left( {{{D}_{2}} + \nu {{\varepsilon }_{{zz}}}} \right)}}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}} - \frac{1}{8}\frac{{\left( {1 + 2\nu } \right)}}{{\left( {1 - \nu } \right)}}\Omega {{\beta }^{2}} \\ {{\sigma }_{{zz}}}{\text{ }} = \nu \left( {{{\sigma }_{{rr}}} + {{\sigma }_{{\theta \theta }}}} \right) + {{\varepsilon }_{{zz}}} \\ \end{gathered} $

До наступления пластического течения решение (2.1), (2.2) остается справедливым во всем цилиндре, поэтому осевая деформация ${{\varepsilon }_{{zz}}}$ и константы интегрирования ${{D}_{1}}$, ${{D}_{2}}$ определяются из условий (1.6) и (1.7)

(2.3)

${{D}_{1}} = 0,\quad ~{{D}_{2}} = \frac{1}{8}\frac{{\left( {3 - 5\nu } \right)}}{{\left( {1 - \nu } \right)}}\Omega ,\quad {{\varepsilon }_{{zz}}} = - \frac{\nu }{2}\Omega $

С помощью соотношений (2.3) упругое решение (2.1), (2.2) в цилиндре со свободными концами запишется в следующем виде:

(2.4)

$\begin{gathered} u = \frac{1}{8}\frac{{\left( {3 - 5\nu } \right)}}{{\left( {1 - \nu } \right)}}\Omega \beta - \frac{1}{8}\frac{{\left( {1 - 2\nu } \right)\left( {1 + \nu } \right)}}{{\left( {1 - \nu } \right)}}\Omega {{\beta }^{3}},\quad ~{{\sigma }_{{rr}}} = \frac{{\left( {3 - 2\nu } \right)}}{{8\left( {1 - \nu } \right)}}\Omega \left( {1 - {{\beta }^{2}}} \right) \\ {{\sigma }_{{\theta \theta }}}{\text{ }} = \frac{{\left( {3 - 2\nu } \right)}}{{8\left( {1 - \nu } \right)}}\Omega \left( {1 - \frac{{1 + 2\nu }}{{3 - 2\nu }}{{\beta }^{2}}} \right),\quad ~{{\sigma }_{{zz}}} = \frac{\nu }{{4\left( {1 - \nu } \right)}}\Omega \left( {1 - 2{{\beta }^{2}}} \right) \\ \end{gathered} $

В цилиндре с закрепленными концами ${{\varepsilon }_{{zz}}} = 0$, а константы интегрирования ${{D}_{1}}$, ${{D}_{2}}$ определяются из граничных условий (1.7)

(2.5)

${{D}_{1}} = 0,\quad {{D}_{2}} = \frac{1}{8}\frac{{\left( {1 + \nu } \right)\left( {3 - 2\nu } \right)\left( {1 - 2\nu } \right)}}{{\left( {1 - \nu } \right)}}\Omega $

Упругое решение имеет такой же вид, как в цилиндре со свободными концами (2.4) за исключением осевого напряжения:

(2.6)

$\begin{gathered} u = \frac{1}{8}\frac{{\left( {3 - 5\nu } \right)}}{{\left( {1 - \nu } \right)}}\Omega \beta - \frac{1}{8}\frac{{\left( {1 - 2\nu } \right)\left( {1 + \nu } \right)}}{{\left( {1 - \nu } \right)}}\Omega {{\beta }^{3}},\quad ~{{\sigma }_{{rr}}} = \frac{{\left( {3 - 2\nu } \right)}}{{8\left( {1 - \nu } \right)}}\Omega \left( {1 - {{\beta }^{2}}} \right) \\ {{\sigma }_{{\theta \theta }}} = \frac{{\left( {3 - 2\nu } \right)}}{{8\left( {1 - \nu } \right)}}\Omega \left( {1 - \frac{{1 + 2\nu }}{{3 - 2\nu }}{{\beta }^{2}}} \right),\quad ~{{\sigma }_{{zz}}} = \frac{\nu }{{2\left( {1 - \nu } \right)}}\Omega \left( {\frac{{\left( {3 - 2\nu } \right)}}{2} - {{\beta }^{2}}} \right) \\ \end{gathered} $

Критические значения параметра нагружения $\Omega $, соответствующие началу пластического течения и полному переходу цилиндра в пластическое состояние, будем обозначать ${{\Omega }_{p}}$ и ${{\Omega }_{{fp}}}$ соответственно. В интервале ${{\Omega }_{p}} < \Omega < {{\Omega }_{{fp}}}$ в цилиндре сохраняется упругая область, в которой найденное решение (2.1), (2.2) остается справедливым, однако неизвестные величины ${{D}_{1}}$, ${{D}_{2}}$ и ${{\varepsilon }_{{zz}}}$ необходимо определять повторно, используя помимо условий (1.6) и (1.7) также условия непрерывности на границах между областями. Значения ${{\Omega }_{p}}$ и ${{\Omega }_{{fp}}}$ зависят от коэффициента Пуассона $\nu $ и от типа условий на торцах цилиндра.

Нетрудно показать, что пластическое течение во вращающемся сплошном цилиндре при условии текучести (1.9) начинается в центре цилиндре $\beta = 0$, где ${{\sigma }_{3}} = {{\sigma }_{{zz}}}$, $~{{\sigma }_{2}} \geqslant \left( {{{\sigma }_{1}} + {{\sigma }_{3}}} \right){\text{/}}2$. Используя (2.4) и (2.6) найдем выражение для ${{\Omega }_{p}}$ в цилиндре со свободными торцами:

(2.7)

$\Omega _{p}^{{fr}} = \frac{{8(1 - \nu )}}{{3 - 4\nu }},$

и с закрепленными:

(2.8)

$\Omega _{p}^{{fx}} = \frac{{8(1 - \nu )}}{{(3 - 2\nu )(1 - 2\nu )}}$

Очевидно, что $\Omega _{p}^{{fr}} < \Omega _{p}^{{fx}}$. Интересно отметить, что полученные выражения для критических величин $\Omega _{p}^{{fr}}$ и $\Omega _{p}^{{fx}}$ совпадают для всех условий (1.8)–(1.10), однако, как будет показано далее, для $\Omega _{{fp}}^{{fr}}$ и $\Omega _{{fp}}^{{fx}}$ это не так.

3. Упругопластическое решение. Развитие пластического течения во вращающемся сплошном цилиндре имеет свои особенности в зависимости от типа торцевых условий. Рассмотрим подробно цилиндр с закрепленными концами. При $\Omega = \Omega _{p}^{{fx}}$ в центре цилиндра $\beta = 0$ впервые выполняется условие (1.8), соответствующее грани призмы Ивлева ${{\sigma }_{3}} = {{\sigma }_{{zz}}}$, ${{\sigma }_{2}} \geqslant \left( {{{\sigma }_{1}} + {{\sigma }_{3}}} \right){\text{/}}2$, в результате чего появляется пластическая область I. С увеличением параметра нагружения $\Omega $ граница между пластической и упругой областями движется в сторону поверхности цилиндра. При $\Omega = {{\Omega }_{1}}$ на внешней поверхности цилиндра условие (1.8) выполняется в виде ${{\sigma }_{1}} = {{\sigma }_{{\theta \theta }}}$, $~{{\sigma }_{2}} \leqslant \left( {{{\sigma }_{1}} + {{\sigma }_{3}}} \right){\text{/}}2$, что приводит к появлению пластической области II. Последующее увеличение параметра нагружения $\Omega $ ведет к постепенному уменьшению упругой области между областями I и II, в результате чего при $\Omega = \Omega _{{fp}}^{{fx}}$ цилиндр полностью переходит в состояние пластичности, а между областями I и II появляется область III, напряженное состояние в которой соответствует ребру призмы Ивлева ${{\sigma }_{{rr}}} = \left( {{{\sigma }_{{\theta \theta }}} + {{\sigma }_{{zz}}}} \right){\text{/}}2$, ${{\sigma }_{{\theta \theta }}} > {{\sigma }_{{rr}}} > {{\sigma }_{{zz}}}$. Анализ можно продолжить и для бо́льших значений параметра нагружения $\Omega $. При $\Omega = \Omega _{{fp2}}^{{fx}}$ напряженное состояние на боковой поверхности цилиндра (область II) переходит с грани призмы Ивлева на ее ребро ${{\sigma }_{{zz}}} = \left( {{{\sigma }_{{rr}}} + {{\sigma }_{{\theta \theta }}}} \right){\text{/}}2$, ${{\sigma }_{{\theta \theta }}} > {{\sigma }_{{zz}}} > {{\sigma }_{{rr}}}$, в результате чего появляется пластическая область IV. Дальнейшее увеличение параметра $\Omega $ не приводит к появлению новых пластических областей, но границы между областями I–IV меняют свое положение, причем увеличиваются области III и IV, напряженное состояние в которых соответствует ребрам призмы Ивлева. Таким образом, в общем случае для достаточно высоких значений $\Omega $ во вращающемся цилиндре с закрепленными концами возможно появление четырех пластических областей, соответствующих различным граням и ребрам призмы Ивлева.

В цилиндре со свободными концами при $\Omega = \Omega _{p}^{{fr}}$ условие (1.8) выполняется в виде ${{\sigma }_{3}} = {{\sigma }_{{zz}}}$, ${{\sigma }_{2}} \geqslant \left( {{{\sigma }_{1}} + {{\sigma }_{3}}} \right){\text{/}}2$, что приводит к появлению пластической области I, соответствующей ребру призмы Ивлева. С увеличением параметра нагружения $\Omega $ упругопластическая граница движется в сторону боковой поверхности цилиндра и при $\Omega = \Omega _{{fp}}^{{fr}}$ весь цилиндр переходит в пластическое состояние. Следует отметить, что для определенного соотношения между параметрами $\nu $ и $H$ при $\Omega > \Omega _{{fp}}^{{fr}}$ возможно появление еще одной пластической области, однако в дальнейшем предполагается, что данное соотношение не выполняется, и пластическое течение происходит только в области I.

Рассмотрим общий принцип решения в пластических областях. В кинематических соотношениях (1.2) упругие $\varepsilon _{{ij}}^{e}$ и пластические $\varepsilon _{{ij}}^{p}$ составляющие деформаций выражаются через напряжения ${{\sigma }_{{ij}}}$ с помощью (1.4), (1.8) и (1.12)–(1.15). В результате получается линейная система, связывающая напряжения ${{\sigma }_{{ij}}}$ и полные деформации ${{\varepsilon }_{{ij}}}$. Из решения этой системы можно получить выражения для напряжений:

(3.1)

$\begin{gathered} {{\sigma }_{{rr}}} = {{a}_{0}} + {{a}_{1}}{{\varepsilon }_{{rr}}} + {{a}_{2}}{{\varepsilon }_{{\theta \theta }}} + {{a}_{3}}{{\varepsilon }_{{zz}}} \\ {{\sigma }_{{\theta \theta }}} = {{b}_{0}} + {{b}_{1}}{{\varepsilon }_{{rr}}} + {{b}_{2}}{{\varepsilon }_{{\theta \theta }}} + {{b}_{3}}{{\varepsilon }_{{zz}}} \\ {{\sigma }_{{zz}}} = {{c}_{0}} + {{c}_{1}}{{\sigma }_{{rr}}} + {{c}_{2}}{{\sigma }_{{\theta \theta }}} + {{c}_{3}}{{\varepsilon }_{{zz}}} \\ \end{gathered} $

Коэффициенты ${{a}_{i}}$, ${{b}_{i}}$ и ${{c}_{i}}$ в каждой области необходимо определять отдельно. Заметим, что в областях III и IV, соответствующих ребру призмы Ивлева, осевое напряжение ${{\sigma }_{{zz}}}$ выражается через ${{\sigma }_{{rr}}}$ и ${{\sigma }_{{\theta \theta }}}$ непосредственно из условия текучести (1.8). Далее уравнение равновесия (1.5) преобразуется с помощью (3.1). В полученном уравнении второго порядка неизвестной функцией является уже перемещение $u$. Из аналитического решения этого уравнения с помощью (1.2) определяются полные деформации ${{\varepsilon }_{{ij}}}$, далее с помощью (3.1) и (1.3) – упругие составляющие деформации $\varepsilon _{{ij}}^{e}$. Наконец, пластические деформации $\varepsilon _{{ij}}^{p}$ вычисляются как разница между полными ${{\varepsilon }_{{ij}}}$ и упругими $\varepsilon _{{ij}}^{e}$ деформациями.

Пластическое течение в цилиндре с закрепленными концами разбивается на следующие интервалы параметра нагружения $\Omega $: $\left( {\Omega _{p}^{{fx}},{{\Omega }_{1}}} \right)$, $\left( {{{\Omega }_{1}},\Omega _{{fp}}^{{fx}}} \right)$, $\left( {\Omega _{{fp}}^{{fx}},\Omega _{{fp2}}^{{fx}}} \right)$, $\left( {\Omega _{{fp2}}^{{fx}},{{\Omega }_{{\max }}}} \right)$. В случае цилиндра со свободными торцами необходимо рассматривать лишь два интервала: $\left( {\Omega _{p}^{{fr}},\Omega _{{fp}}^{{fr}}} \right)$ и $\left( {\Omega _{{fp}}^{{fr}},{{\Omega }_{{\max }}}} \right)$. В каждом из интервалов цилиндр состоит из разных пластических областей. Для вычисления констант интегрирования ${{D}_{i}}$ (в упругой области) и ${{C}_{i}}$ (в пластических областях), а также координат ${{\beta }_{i}}$ границ между областями используется система алгебраических уравнений, состоящая из граничных условий (1.7), а также условий непрерывности $u$, ${{\sigma }_{{rr}}}$ и ${{\sigma }_{{\theta \theta }}}$ на каждой границе. Для вычисления осевой деформации ${{\varepsilon }_{{zz}}}$ в систему дополнительно включается условие (1.6), при этом интеграл $\int \beta {{\sigma }_{{zz}}}d\beta $ вычисляется отдельно в каждой области. Полученная система уравнений является линейно относительно ${{C}_{i}}$, ${{D}_{i}}$, ${{\varepsilon }_{{zz}}}$и нелинейной относительно ${{\beta }_{i}}$. Часть уравнений системы решается точно для выражения ${{C}_{i}}$, ${{D}_{i}}$ и ${{\varepsilon }_{{zz}}}$ через параметры $\nu $, $H$ и $\Omega $. Для этого удобно использовать системы компьютерной алгебры (Wolfram Mathematica, Maple и др.). Получаемые выражения являются достаточно громоздкими и в статье не приводятся. В оставшиеся уравнения системы подставляются выражения для ${{C}_{i}}$, ${{D}_{i}}$ и ${{\varepsilon }_{{zz}}}$, а также численные значения параметров $\nu $ и $H$. Полученные уравнения решаются численно методом Ньютона для выбранных значений параметра нагружения $\Omega $ внутри интервала. Определение переходных величин ${{\Omega }_{1}}$, $\Omega _{{fp}}^{{fx}}$, $\Omega _{{fp2}}^{{fx}}$, $\Omega _{{fp}}^{{fr}}$ требует дополнительных условий.

В следующих подразделах получено аналитическое решение для каждой пластической области I–IV. Для большей общности использовалось предположение об обобщенном плоском деформированном состоянии в цилиндре. Найденные выражения сводятся к случаю плоского деформированного состояния, для этого достаточно положить ${{\varepsilon }_{{zz}}} = 0$.

Пластическая область I. В первой области пластического течения напряженное состояние соответствует грани призмы Ивлева ${{\sigma }_{3}} = {{\sigma }_{{zz}}}$, $~{{\sigma }_{2}} \geqslant \left( {{{\sigma }_{1}} + {{\sigma }_{3}}} \right){\text{/}}2$, тогда условие (1.8) примет вид:

$\frac{1}{2}\left( {{{\sigma }_{{rr}}} + {{\sigma }_{{\theta \theta }}}} \right) - {{\sigma }_{{zz}}} = {{\sigma }_{y}}\left( {\varepsilon _{{{\text{eq}}}}^{p}} \right)$

Из ассоциированного закона пластического течения (1.13) следует:

$d\varepsilon _{{rr}}^{p} = \frac{1}{2}d\lambda ;\quad d\varepsilon _{{\theta \theta }}^{p} = \frac{1}{2}d\lambda ;\quad d\varepsilon _{{zz}}^{p} = - d\lambda $

Соотношение (1.15) после преобразований запишется в виде:

${{\sigma }_{y}}d\varepsilon _{{{\text{eq}}}}^{p} = - \left( {\frac{1}{2}\left( {{{\sigma }_{{rr}}} + {{\sigma }_{{\theta \theta }}}} \right) - {{\sigma }_{{zz}}}} \right)d\varepsilon _{{zz}}^{p}$

Тогда для монотонного нагружения получим $\varepsilon _{{{\text{eq}}}}^{p} = - \varepsilon _{{zz}}^{p}$, $\varepsilon _{{rr}}^{p} = \varepsilon _{{\theta \theta }}^{p} = - \frac{1}{2}\varepsilon _{{zz}}^{p}$. Обратное соотношение к (1.15) запишется следующим образом:

(3.2)

$\varepsilon _{{{\text{eq}}}}^{p} = \frac{1}{H}\left( {\frac{1}{2}\left( {{{\sigma }_{{rr}}} + {{\sigma }_{{\theta \theta }}}} \right) - {{\sigma }_{{zz}}} - 1} \right)$

Кинематические соотношения (1.2) примут вид

${{\varepsilon }_{{rr}}} = \varepsilon _{{rr}}^{e} + \frac{1}{2}\varepsilon _{{{\text{eq}}}}^{p},\quad {{\varepsilon }_{{\theta \theta }}} = \varepsilon _{{\theta \theta }}^{e} + \frac{1}{2}\varepsilon _{{{\text{eq}}}}^{p},\quad {{\varepsilon }_{{zz}}} = \varepsilon _{{zz}}^{e} - \varepsilon _{{{\text{eq}}}}^{p}$

Преобразуем полученные соотношения с помощью (1.4) и (3.2)

$\begin{gathered} \left( {4H + 1} \right){{\sigma }_{{rr}}} - \left( {4\nu H - 1} \right){{\sigma }_{{\theta \theta }}} - \left( {4\nu H + 2} \right){{\sigma }_{{zz}}} = 4H{{\varepsilon }_{{rr}}} + 2 \\ - \left( {4\nu H - 1} \right){{\sigma }_{{rr}}} + \left( {4H + 1} \right){{\sigma }_{{\theta \theta }}} - \left( {4\nu H + 2} \right){{\sigma }_{{zz}}} = 4H{{\varepsilon }_{{\theta \theta }}} + 2 \\ - \left( {2\nu H + 1} \right){{\sigma }_{{rr}}} - \left( {2\nu H + 1} \right){{\sigma }_{{\theta \theta }}} + \left( {2H + 2} \right){{\sigma }_{{zz}}} = 2H{{\varepsilon }_{{zz}}} - 2 \\ \end{gathered} $

Решая полученную систему найдем коэффициенты в (3.1)

(3.3)

$\begin{gathered} {{a}_{0}} = {{b}_{0}} = \frac{1}{{3 + 2\left( {1 + \nu } \right)H}},\quad {{a}_{1}} = {{b}_{2}} = \frac{{\left( {5 - 4\nu + 4(1 - {{\nu }^{2}})H} \right)}}{{2\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)\left( {3 + 2\left( {1 + \nu } \right)H} \right)}} \\ {{a}_{2}} = {{b}_{1}} = - \frac{{\left( {1 - 4\left( {2 + H} \right)\nu - 4{{\nu }^{2}}H} \right)}}{{2\left( {1 + \nu } \right){\kern 1pt} \left( {1 - 2\nu } \right){\kern 1pt} \left( {3 + 2\left( {1 + \nu } \right){\kern 1pt} H} \right)}},\quad {{a}_{3}} = {{b}_{3}} = \frac{{\left( {1 + 2\nu H} \right)}}{{\left( {1 - 2\nu } \right){\kern 1pt} \left( {3 + 2\left( {1 + \nu } \right){\kern 1pt} H} \right)}} \\ {{c}_{0}} = - \frac{1}{{1 + H}},\quad {{c}_{1}} = {{c}_{2}} = \frac{{1 + 2\nu H}}{{2\left( {1 + H} \right)}},\quad {{c}_{3}} = \frac{H}{{\left( {1 + H} \right)}} \\ \end{gathered} $

Из решения уравнения равновесия (1.5) с помощью (3.1) и (3.3) найдем выражение для перемещения:

$u = {{C}_{1}}{{\beta }^{{ - 1}}} + {{C}_{2}}\beta - \frac{{\left( {1 - 2\nu } \right)\left( {1 + \nu } \right)\left( {3 + 2\left( {1 + \nu } \right)H} \right)}}{{4\left( {5 - 4\nu + 4\left( {1 - {{\nu }^{2}}} \right)H} \right)}}\Omega {{\beta }^{3}}$

Пластическая область II. Напряжения во второй пластической области лежат на грани призмы Ивлева ${{\sigma }_{1}} = {{\sigma }_{{\theta \theta }}}$, $~{{\sigma }_{2}} \leqslant \left( {{{\sigma }_{1}} + {{\sigma }_{3}}} \right){\text{/}}2$. Условие пластичности (1.8) имеет вид:

${{\sigma }_{{\theta \theta }}} - \frac{1}{2}\left( {{{\sigma }_{{rr}}} + {{\sigma }_{{zz}}}} \right) = {{\sigma }_{y}}\left( {\varepsilon _{{{\text{eq}}}}^{p}} \right)$

Ассоциированный закон течения (1.13) запишется как

$d\varepsilon _{{rr}}^{p} = - \frac{1}{2}d\lambda ,\quad ~d\varepsilon _{{\theta \theta }}^{p} = d\lambda ,\quad d\varepsilon _{{zz}}^{p} = - \frac{1}{2}d\lambda $

Отсюда получим:

${{\sigma }_{y}}d\varepsilon _{{{\text{eq}}}}^{p} = \left( {{{\sigma }_{{\theta \theta }}} - \frac{1}{2}\left( {{{\sigma }_{{rr}}} + {{\sigma }_{{zz}}}} \right)} \right)d\varepsilon _{{\theta \theta }}^{p}$

В результате для случая монотонного нагружения имеем: $\varepsilon _{{{\text{eq}}}}^{p} = \varepsilon _{{\theta \theta }}^{p}$, $\varepsilon _{{rr}}^{p} = \varepsilon _{{zz}}^{p}$ = $ - \frac{1}{2}\varepsilon _{{\theta \theta }}^{p}$.

Из закона линейного упрочнения (1.12) следует:

(3.4)

$\varepsilon _{{{\text{eq}}}}^{p} = \frac{1}{H}\left( {{{\sigma }_{{\theta \theta }}} - \frac{1}{2}\left( {{{\sigma }_{{rr}}} + {{\sigma }_{{zz}}}} \right) - 1} \right)$

Кинематические соотношения (1.2) с учетом последнего соотношения и (1.4) запишутся следующим образом:

$\begin{gathered} \left( {4H + 1} \right){{\sigma }_{{rr}}} - \left( {4\nu H + 2} \right){{\sigma }_{{\theta \theta }}} - \left( {4\nu H - 1} \right){{\sigma }_{{zz}}} = 4H{{\varepsilon }_{{rr}}} - 2 \\ - \left( {2\nu H + 1} \right){{\sigma }_{{rr}}} + \left( {2H + 2} \right){{\sigma }_{{\theta \theta }}} - \left( {2\nu H + 1} \right){{\sigma }_{{zz}}} = 2H{{\varepsilon }_{{\theta \theta }}} + 2 \\ - \left( {4\nu H - 1} \right){{\sigma }_{{rr}}} - \left( {4\nu H + 2} \right){{\sigma }_{{\theta \theta }}} + \left( {4H + 1} \right){{\sigma }_{{zz}}} = 4H{{\varepsilon }_{{zz}}} - 2 \\ \end{gathered} $

Решая вышеприведенную систему, найдем коэффициенты в (3.1)

(3.5)

$\begin{gathered} {{a}_{0}} = - \frac{1}{{3 + 2\left( {1 + \nu } \right)H}},\quad {{a}_{1}} = \frac{{\left( {5 - 4\nu + 4\left( {1 - {{\nu }^{2}}} \right)H} \right)}}{{2\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)\left( {3 + 2\left( {1 + \nu } \right)H} \right)}} \\ {{a}_{2}} = {{b}_{1}} = {{b}_{3}} = \frac{{\left( {1 + 2\nu H} \right)}}{{\left( {1 - 2\nu } \right){\kern 1pt} \left( {3 + 2{\kern 1pt} \left( {1 + \nu } \right){\kern 1pt} H} \right)}},\quad {{a}_{3}} = - \frac{{\left( {1 - 4\left( {2 + H} \right)\nu - 4{{\nu }^{2}}H} \right)}}{{2\left( {1 + \nu } \right)\left( {1 - 2\nu } \right){\kern 1pt} \left( {3 + 2{\kern 1pt} \left( {1 + \nu } \right){\kern 1pt} H} \right)}} \\ {{b}_{0}} = \frac{2}{{3 + 2\left( {1 + \nu } \right)H}},\quad ~{{b}_{2}} = \frac{{\left( {1 + 2\left( {1 - \nu } \right)H} \right)}}{{\left( {1 - 2\nu } \right)\left( {3 + 2\left( {1 + \nu } \right)H} \right)}} \\ {{c}_{0}} = - \frac{2}{{1 + 4H}},\quad {{c}_{1}} = - \frac{{1 - 4\nu H}}{{1 + 4H}},\quad {{c}_{2}} = \frac{{2 + 4\nu H}}{{1 + 4H}},\quad {{c}_{3}} = \frac{{4H}}{{1 + 4H}} \\ \end{gathered} $

Перемещение определяется из решения уравнения равновесия (1.5) с учетом соотношений (3.1) и (3.5):

$u = {{C}_{3}}{{\beta }^{{ - \kappa }}} + {{C}_{4}}{{\beta }^{\kappa }} + \left( {{{\varepsilon }_{{zz}}} + 2\left( {1 + \nu } \right)} \right)\beta - L\Omega {{\beta }^{3}}$

$\kappa = \sqrt {\frac{{2(1 + \nu + 2(1 - {{\nu }^{2}})H)}}{{(5 - 4\nu + 4(1 - {{\nu }^{2}})H)}}} ,\quad L = \frac{{2\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)\left( {3 + 2\left( {1 + \nu } \right)H} \right)}}{{\left( {43 - 38\nu + 32\left( {1 - {{\nu }^{2}}} \right)H} \right)}}$

Пластическая область III. В данной пластической области напряжения соответствуют ребру призмы Ивлева ${{\sigma }_{{rr}}} = \left( {{{\sigma }_{{\theta \theta }}} + {{\sigma }_{{zz}}}} \right){\text{/}}2$, ${{\sigma }_{{\theta \theta }}} > {{\sigma }_{{rr}}} > {{\sigma }_{{zz}}}$. Условие текучести (1.8) запишется в следующем виде:

${{\sigma }_{{\theta \theta }}} - \tfrac{1}{2}\left( {{{\sigma }_{{rr}}} + {{\sigma }_{{zz}}}} \right) = {{\sigma }_{y}}\left( {\varepsilon _{{{\text{eq}}}}^{p}} \right),\quad \tfrac{1}{2}\left( {{{\sigma }_{{\theta \theta }}} + {{\sigma }_{{rr}}}} \right) - {{\sigma }_{{zz}}} = {{\sigma }_{y}}\left( {\varepsilon _{{{\text{eq}}}}^{p}} \right),$

из которого следует, что

${{\sigma }_{{zz}}} = 2{{\sigma }_{{rr}}} - {{\sigma }_{{\theta \theta }}}$

Эквивалентная пластическая деформация

(3.6)

$\varepsilon _{{{\text{eq}}}}^{p} = \frac{1}{H}\left( {\frac{3}{2}({{\sigma }_{{\theta \theta }}} - {{\sigma }_{{rr}}}) - 1} \right)$

Ассоциированный закон пластического течения (1.13) примет вид:

$d\varepsilon _{{rr}}^{p} = - \frac{1}{2}d{{\lambda }_{1}} + \frac{1}{2}d{{\lambda }_{2}},\quad ~d\varepsilon _{{\theta \theta }}^{p} = d{{\lambda }_{1}} + \frac{1}{2}d{{\lambda }_{2}},\quad ~d\varepsilon _{{zz}}^{p} = - \frac{1}{2}d{{\lambda }_{1}} - d{{\lambda }_{2}}$

Отсюда следует:

$d{{\lambda }_{1}} = - d\varepsilon _{{rr}}^{p} + \frac{2}{3}d\varepsilon _{{\theta \theta }}^{p} = - \frac{4}{3}d\varepsilon _{{rr}}^{p} - \frac{2}{3}d\varepsilon _{{zz}}^{p} = \frac{4}{3}d\varepsilon _{{\theta \theta }}^{p} + \frac{2}{3}d\varepsilon _{{zz}}^{p}$

$d{{\lambda }_{2}} = \frac{4}{3}d\varepsilon _{{rr}}^{p} + \frac{2}{3}d\varepsilon _{{\theta \theta }}^{p} = \frac{2}{3}d\varepsilon _{{rr}}^{p} - \frac{2}{3}d\varepsilon _{{zz}}^{p} = - \frac{2}{3}d\varepsilon _{{\theta \theta }}^{p} - \frac{4}{3}d\varepsilon _{{zz}}^{p}$

Соотношение (1.15) после преобразований запишется в виде

$d\varepsilon _{{{\text{eq}}}}^{p} = d{{\lambda }_{1}} + d{{\lambda }_{2}}$

Отсюда для случая монотонного нагружения получим

(3.7)

$\varepsilon _{{{\text{eq}}}}^{p} = - \frac{2}{3}\varepsilon _{{rr}}^{p} - \frac{4}{3}\varepsilon _{{zz}}^{p},\quad \varepsilon _{{{\text{eq}}}}^{p} = \frac{2}{3}\varepsilon _{{\theta \theta }}^{p} - \tfrac{2}{3}\varepsilon _{{zz}}^{p}$

Преобразуем (1.2) с помощью (1.4), (3.6), (3.7) и получим

$\left( {9 + 4\left( {5 - 4\nu } \right)H} \right){{\sigma }_{{rr}}} - \left( {9 + 8\left( {1 + \nu } \right)H} \right){{\sigma }_{{\theta \theta }}} = 4H{{\varepsilon }_{{rr}}} + 8H{{\varepsilon }_{{zz}}} - 6,$

$ - \left( {9 + 8\left( {1 + \nu } \right)H} \right){{\sigma }_{{rr}}} + \left( {9 + 8\left( {1 + \nu } \right)H} \right){{\sigma }_{{\theta \theta }}} = 4H{{\varepsilon }_{{\theta \theta }}} - 4H{{\varepsilon }_{{zz}}} + 6$

Из решения данной системы найдем коэффициенты в (3.1):

(3.8)

$\begin{gathered} {{a}_{0}} = 0,\quad {{a}_{1}} = {{a}_{2}} = {{a}_{3}} = {{b}_{1}} = \frac{1}{3}\frac{1}{{\left( {1 - 2\nu } \right)}},\quad {{b}_{0}} = \frac{6}{{9 + 8\left( {1 + \nu } \right)H}} \hfill \\ {{b}_{2}} = \frac{{\left( {9 + 4\left( {5 - 4\nu } \right)H} \right)}}{{3\left( {1 - 2\nu } \right)\left( {9 + 8\left( {1 + \nu } \right)H} \right)}},\quad {{b}_{3}} = \frac{{\left( {9 - 4\left( {1 - 8\nu } \right)H} \right)}}{{3\left( {1 - 2\nu } \right)\left( {9 + 8\left( {1 + \nu } \right)H} \right)}} \hfill \\ \end{gathered} $

Из решения уравнения равновесия (1.5) с учетом (3.1) и (3.8) получим

$\begin{gathered} u = {{C}_{5}}{{\beta }^{{ - \tau }}} + {{C}_{6}}{{\beta }^{\tau }} + \left( {{{\varepsilon }_{{zz}}} - \frac{3}{2}{{H}^{{ - 1}}}} \right)\beta - M\Omega {{\beta }^{3}}, \\ \tau = \sqrt {\frac{{9 + 4(5 - 4\nu )H}}{{9 + 8(1 + \nu )H}}} ,\quad M = \frac{{3\left( {1 - 2\nu } \right)\left( {9 + 8\left( {1 + \nu } \right)H} \right)}}{{4\left( {18 + \left( {13 + 22\nu } \right)H} \right)}} \\ \end{gathered} $

Замечание: решение, найденное в пластической области III, не сводится к решению [25] для идеально пластического материала при $H = 0$.

Пластическая область IV. В последней области пластического деформирования напряжения лежат на ребре призмы Ивлева ${{\sigma }_{{zz}}} = \left( {{{\sigma }_{{rr}}} + {{\sigma }_{{\theta \theta }}}} \right){\text{/}}2$, ${{\sigma }_{{\theta \theta }}} > {{\sigma }_{{zz}}} > {{\sigma }_{{rr}}}$. Условие (1.8) имеет вид

${{\sigma }_{{\theta \theta }}} - \frac{1}{2}\left( {{{\sigma }_{{zz}}} + {{\sigma }_{{rr}}}} \right) = {{\sigma }_{y}}\left( {\varepsilon _{{{\text{eq}}}}^{p}} \right),\quad \frac{1}{2}\left( {{{\sigma }_{{\theta \theta }}} + {{\sigma }_{{zz}}}} \right) - {{\sigma }_{{rr}}} = {{\sigma }_{y}}\left( {\varepsilon _{{{\text{eq}}}}^{p}} \right)$

Откуда следует, что

${{\sigma }_{{zz}}} = \left( {{{\sigma }_{{rr}}} + {{\sigma }_{{\theta \theta }}}} \right){\text{/}}2$

Эквивалентная пластическая деформация

(3.9)

$\varepsilon _{{{\text{eq}}}}^{p} = \frac{1}{{\rm H}}\left( {\frac{3}{4}{{\sigma }_{{\theta \theta }}} - \frac{3}{4}{{\sigma }_{{rr}}} - 1} \right)$

Ассоциированный закон течения (1.13) запишется в виде

$d\varepsilon _{{rr}}^{p} = - \frac{1}{2}d{{\lambda }_{1}} - d{{\lambda }_{2}},\quad d\varepsilon _{{\theta \theta }}^{p} = d{{\lambda }_{1}} + \frac{1}{2}d{{\lambda }_{2}},\quad d\varepsilon _{{zz}}^{p} = - \frac{1}{2}d{{\lambda }_{1}} + \frac{1}{2}d{{\lambda }_{2}}$

Откуда следует, что

$d{{\lambda }_{1}} = \frac{2}{3}d\varepsilon _{{rr}}^{p} + \frac{4}{3}d\varepsilon _{{\theta \theta }}^{p} = - \frac{2}{3}d\varepsilon _{{rr}}^{p} - \frac{4}{3}d\varepsilon _{{zz}}^{p} = \frac{2}{3}d\varepsilon _{{\theta \theta }}^{p} - \frac{2}{3}d\varepsilon _{{zz}}^{p},$

$d{{\lambda }_{2}} = - \frac{4}{3}d\varepsilon _{{rr}}^{p} - \frac{2}{3}d\varepsilon _{{\theta \theta }}^{p} = - \frac{2}{3}d\varepsilon _{{rr}}^{p} + \frac{2}{3}d\varepsilon _{{zz}}^{p} = \frac{2}{3}d\varepsilon _{{\theta \theta }}^{p} + \frac{4}{3}d\varepsilon _{{zz}}^{p}$

Соотношение (1.15), как и в области III имеет вид

$d\varepsilon _{{{\text{eq}}}}^{p} = d{{\lambda }_{1}} + d{{\lambda }_{2}}$

Для монотонного нагружения имеем

(3.10)

$\varepsilon _{{{\text{eq}}}}^{p} = - \frac{4}{3}\varepsilon _{{rr}}^{p} - \frac{2}{3}\varepsilon _{{zz}}^{p},\quad \varepsilon _{{{\text{eq}}}}^{p}{\text{ }} = \frac{4}{3}\varepsilon _{{\theta \theta }}^{p} + \frac{2}{3}\varepsilon _{{zz}}^{p}$

C учетом (1.4), (3.9), (3.10) соотношения (1.2) примут вид

$\left( {9 + 4\left( {5 - 4\nu } \right)H} \right){{\sigma }_{{rr}}} - \left( {9 - 4\left( {1 - 8\nu } \right)H} \right){{\sigma }_{{\theta \theta }}} = 16H{{\varepsilon }_{{rr}}} + 8H{{\varepsilon }_{{zz}}} - 12,$

$ - \left( {9 - 4\left( {1 - 8\nu } \right)H} \right){{\sigma }_{{rr}}} + \left( {9 + 4\left( {5 - 4\nu } \right)H} \right){{\sigma }_{{\theta \theta }}} = 16H{{\varepsilon }_{{\theta \theta }}} + 8H{{\varepsilon }_{{zz}}} + 12$

Решая данную систему, найдем коэффициенты в (3.1)

(3.11)

$\begin{gathered} {{a}_{0}} = - {{b}_{0}} = - \frac{6}{{9 + 8\left( {1 + \nu } \right)H}},\quad ~{{a}_{1}} = {{b}_{2}} = \frac{{\left( {9 + 4\left( {5 - 4\nu } \right)H} \right)}}{{3\left( {1 - 2\nu } \right)\left( {9 + 8\left( {1 + \nu } \right)H} \right)}} \\ {{a}_{2}} = {{b}_{1}} = \frac{{\left( {9 - 4\left( {1 - 8\nu } \right)H} \right)}}{{3\left( {1 - 2\nu } \right)\left( {9 + 8\left( {1 + \nu } \right)H} \right)}},\quad {{a}_{3}} = {{b}_{3}} = \frac{1}{3}\frac{1}{{\left( {1 - 2\nu } \right)}} \\ \end{gathered} $

Из решения уравнения равновесия (1.5) с учетом (3.1) и (3.11) найдем

$\begin{gathered} u = {{C}_{7}}{{\beta }^{{ - 1}}} + {{C}_{8}}\beta + K\beta \ln \beta - N\Omega {{\beta }^{3}} \\ K = \frac{{18\left( {1 - 2\nu } \right)}}{{\left( {9 + 4\left( {5 - 4\nu } \right)H} \right)}},\quad ~N = \frac{{3\left( {1 - 2\nu } \right)\left( {9 + 8\left( {1 + \nu } \right)H} \right)}}{{8\left( {9 + 4\left( {5 - 4\nu } \right)H} \right)}} \\ \end{gathered} $

4. Результаты расчетов. Расчеты проводились для цилиндра, изготовленного из нержавеющей стали AISI 304, со следующими значениями параметров (1.1):

$\begin{gathered} b = 0.1\;м,\quad E = 200\;ГПа,\quad {{\sigma }_{0}} = 215\;МПА \\ \eta = 465,\quad \rho = 8000\;{\text{кг/}}{{м}^{3}},\quad \nu = 0.3 \\ \end{gathered} $

Отсюда безразмерный параметр упрочнения $H \cong 0.5$. Для сравнения рассматривается случай $H = 1.0$, а также идеальный упругопластический материал, который моделируется заданием значения $H = {{10}^{{ - 6}}} \approx 0$.

Пластическое течение в цилиндре с закрепленными концами начинается при $\Omega _{{fp}}^{{fx}}$ ≅ ≅ 5.8333 (2.8), а в цилиндре со свободными концами при $\Omega _{{fp}}^{{fr}} \cong 3.1111$ (2.7). Соответствующие скорости вращения: $\omega _{{fp}}^{{fx}} \cong 37\,800$ об./мин, $\omega _{{fp}}^{{fr}}$ ≅ 27 600 об./мин. Распределение напряжений в цилиндре с закрепленными концами в момент начала пластического течения представлено в работе [2].

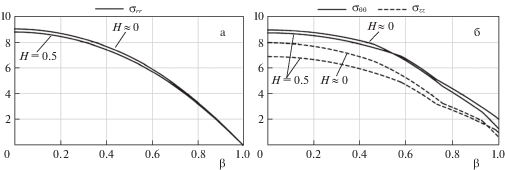
Цилиндр с закрепленными концами (${{\varepsilon }_{{zz}}} = 0$). Рассмотрим подробно пластическое деформирование вращающегося цилиндра с закрепленными концами. Установлено, что пластическая область II появляется на внешней поверхности цилиндра при $\Omega = {{\Omega }_{1}}$ ≅ ≅ 8.1663 (${{\omega }_{1}}$ ≅ 44 700 об./мин). Весь цилиндр переходит в пластическое состояние при $\Omega = \Omega _{{fp}}^{{fx}}$ ≅ 9.4035 (${{\omega }_{1}}$ ≅ 48 000 об./мин). Распределение напряжений и пластических деформаций при $\Omega = \Omega _{{fp}}^{{fx}}$ для разных значений параметра упрочнения $H$ изображено на рис. 2 и 3 соответственно. Разумеется, критическая величина $\Omega _{{fp}}^{{fx}}$ зависит от $H$, однако, как показали расчеты, зависит несущественно. Для $H = 0.0,\;1.0$ цилиндр полностью переходит в пластическое состояние при $\Omega _{{fp}}^{{fx}}$ ≅ 9.2672, 9.4771 соответственно. Видим, что упрочнение материала практически не влияет на распределение радиального и тангенциального напряжения в цилиндре и незначительно уменьшает величину осевого напряжения. Графики напряжений для $H = \;1.0$ не приведены на рис. 2 и 5 , поскольку они практически сливаются с графиками для $H = \;0.5$. С другой стороны, как видно из рис. 3, пластические деформации в цилиндре из упрочняющегося материала существенно ниже по сравнению с цилиндром из идеального материала. Сравнение полученных результатов с данными [12, 13] показывает, что условия Треска и Мизеса при одной и той же скорости вращения предсказывают бо́льшую величину напряжений и пластических деформаций в цилиндре.

Рис. 2.

Распределение напряжений при $\Omega = \Omega _{{fp}}^{{fx}}$: а – ${{\sigma }_{{rr}}}$; б – ${{\sigma }_{{\theta \theta }}}$, ${{\sigma }_{{zz}}}$.

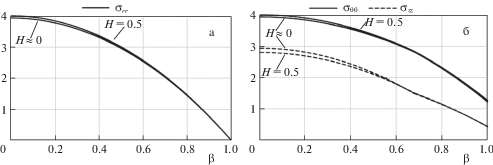
Рис. 3.

Распределение пластических деформаций при $\Omega = \Omega _{{fp}}^{{fx}}$: а – $\varepsilon _{{rr}}^{p}$; б – $\varepsilon _{{\theta \theta }}^{p}$, $\varepsilon _{{zz}}^{p}$.

Рис. 4.

Зависимость $\Omega _{{fp}}^{{fx}}$ от параметра упрочнения $H$ для условий (1.8)–(1.10).

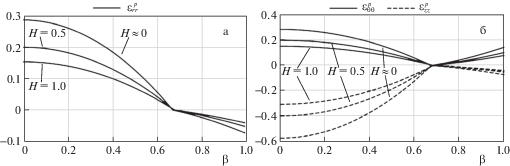
Рис. 5.

Распределение напряжений при $\Omega = \Omega _{{\max }}^{{fx}}$: а – ${{\sigma }_{{rr}}}$; б – ${{\sigma }_{{\theta \theta }}}$, ${{\sigma }_{{zz}}}$.

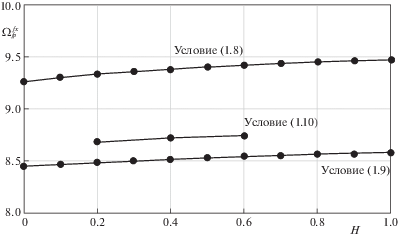
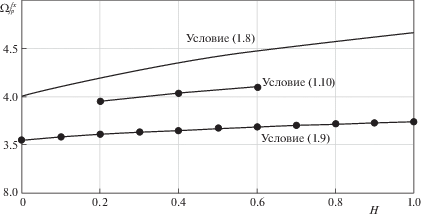
На рис. 4 изображены зависимости $\Omega _{{fp}}^{{fx}}$ от параметра упрочнения $H$ для условий Ишлинского–Ивлева, Треска и Мизеса. Графики, соответствующие условиям Треска и Мизеса, получены на основе работ [12] и [13] соответственно. Значения $\Omega _{{fp}}^{{fx}}$ и $\Omega _{{fp}}^{{fr}}$ приведены [13] только для трех значений параметра $H = 0.2;\,0.4;\,0.6$. Критические значения параметра нагружения $\Omega _{{fp}}^{{fx}}$ слабо зависит от параметра упрочнения $H$. Это справедливо для всех сравниваемых условий пластичности. Разница в значении $\Omega _{{fp}}^{{fx}}$ между условиями Ишлинского–Ивлева и Треска составляет около 10%, а между условиями Ишлинского–Ивлева и Мизеса – примерно 7%.

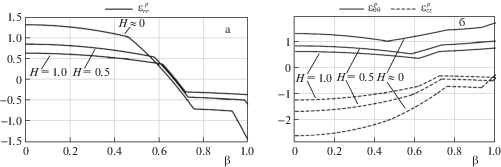
После полного перехода в пластическое состояние развитие пластического течения в упрочняющемся цилиндре существенно замедляется по сравнению с цилиндром из идеального материала. Так, для первой модели ($H \cong 0.5$) возникновение пластической области IV происходит при $\Omega = \Omega _{{fp2}}^{{fx}}$ ≅ 16.5679 ($\omega _{{fp2}}^{{fx}}$ ≅ 63 700 об./мин), а для второй ($H \approx 0.0$) при $\Omega = \Omega _{{fp2}}^{{fx}} \cong 12.1183$ ($\omega _{{fp2}}^{{fx}}$ ≅ 55 000 об. мин). Распределение напряжений и пластических деформаций в цилиндре для $\Omega = \Omega _{{\max }}^{{fx}} = 20$ ($\omega _{{\max }}^{{fx}}$ ≅ 70 000 об. мин) изображено на рис. 5 и 6 соответственно. Интересно отметить (рис. 5б), что упрочнение оказывает наибольшее влияние на осевое напряжение. Деформированное состояние цилиндра (рис. 6) существенно зависит от параметра упрочнения $H$: чем он выше, тем ниже пластические деформации в цилиндре.

Рис. 6.

Распределение пластических деформаций при $\Omega = \Omega _{{\max }}^{{fx}}$: а – $\varepsilon _{{rr}}^{p}$; б – $\varepsilon _{{\theta \theta }}^{p}$, $\varepsilon _{{zz}}^{p}$.

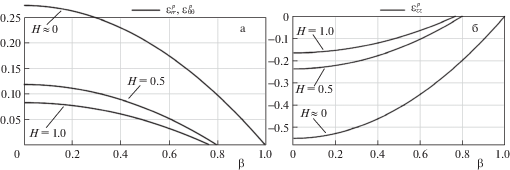
Цилиндр со свободными концами (${{\varepsilon }_{{zz}}} = \operatorname{const} $). Решение для цилиндра из идеально-пластического материала при использовании условия Треска и условия Ишлинского–Ивлева существует только для $\Omega < 4$. Для условия Ишлинского–Ивлева при указанном максимальном значении параметра нагружения цилиндр полностью переходит в пластическое состояние ($\Omega _{{fp}}^{{fr}} = 4$). Распределение напряжений и пластических деформаций при $\Omega = 4$ ($\omega $ ≅ 31 300 об./мин) для $H \approx 0.0$ и $H = 0.5$, 1.0 изображено на рис. 7 и 8 соответственно. При указанной скорости вращения координата упругопластической границы имеет следующие значения в зависимости от параметра упрочнения $H$: ${{\beta }_{1}}$ = 0.9995, 0.7983, 0.7671. Видим, что упрочнение материала оказывает на деформирование цилиндра со свободными торцами эффект, схожий рассмотренному выше в случае цилиндра с закрепленными концами. Радиальное и тангенциальное напряжения практически не зависят от параметра упрочнения $H$, и на рис. 7а показаны графики только для случая $H = 0.5$. Абсолютная величина осевого напряжения незначительно снижается с ростом $H$ (рис. 7б). Упрочнение материала главным образом влияет на пластические деформации в цилиндре: их величина существенно зависит от параметра $H$.

Рис. 7.

Распределение напряжений при $\Omega = 4$: а – ${{\sigma }_{{rr}}}$, ${{\sigma }_{{\theta \theta }}}$; б – ${{\sigma }_{{zz}}}$.

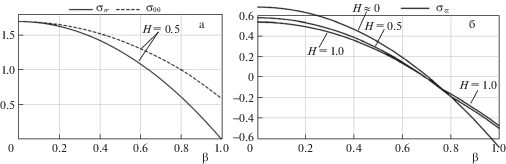
Рис. 8.

Распределение пластических деформаций при $\Omega = 4$: а – $\varepsilon _{{rr}}^{p}$, $\varepsilon _{{\theta \theta }}^{p}$; б – $\varepsilon _{{zz}}^{p}$.

Интересно отметить, что поскольку пластическое течение в линейно-упрочняющемся цилиндре при условии пластичности (1.8) происходит только в одной области (пластическая область I), то становится возможным получить следующее аналитическое выражение

$\Omega _{{fp}}^{{fr}} = 4\frac{{\left( {5 - 4\nu + 4H\left( {1 + \nu } \right)\left( {1 - \nu } \right)} \right)}}{{\left( {5 - 4\nu + 2H\left( {1 + \nu } \right)} \right)}}$

Для условия Треска подобное выражение получить затруднительно, поскольку в этом случае цилиндр состоит из двух пластических областей, и определение $\Omega _{{fp}}^{{fr}}$ сводится к решению системы двух нелинейных алгебраических уравнений относительно $\Omega $ и координаты ${{\beta }_{1}}$ границы между пластическими областями [12]. На рис. 9 приведены зависимости $\Omega _{{fp}}^{{fr}}$ от параметра упрочнения $H$ для условий Ишлинского–Ивлева, Треска и Мизеса. Видим, что с увеличением $H$ разница между критическими значениями $\Omega _{{fp}}^{{fr}}$ для условий пластичности Ишлинского–Ивлева и Треска также растет. Если для идеального материала эта разница составляет около 10%, то при $H = 0.5$ она составляет уже около 20%. При этом для условия Ишлинского–Ивлева величина $\Omega _{{fp}}^{{fr}}$ в большей степени зависит от параметра упрочнения $H$ по сравнению с условием Треска. Критическая величина $\Omega _{{fp}}^{{fr}}$, соответствующая условию Мизеса, примерно равна среднему между значениями $\Omega _{{fp}}^{{fr}}$ для условий Треска и Ишлинского–Ивлева. Здесь еще раз следует отметить, что для сравнения полученных результатов (рис. 4 и 9 ) с условием Мизеса используются данные [13], основанной на деформационной теории пластичности. Решение аналогичной упругопластической задачи, но с использованием условия Мизеса и ассоциированного с ним закона течения, представляет значительный интерес и к настоящему времени еще не опубликовано.

Рис. 9.

Зависимость $\Omega _{{fp}}^{{fr}}$ от параметра упрочнения $H$ для условий (1.8)–(1.10).

Для диапазона параметра нагружения $\Omega \geqslant \Omega _{{fp}}^{{fr}}$ из условий (1.6) и (1.7) можно получить точные выражения для констант интегрирования и осевой деформации в виде функций от $\nu $, $H$ и $\Omega $. Отсюда распределение напряжений в цилиндре имеет вид

$~{{\sigma }_{{rr}}} = \frac{{\left( {7 - 2\nu + 2H\left( {3 - 2\nu } \right)\left( {1 + \nu } \right)} \right)}}{{4\left( {5 - 4\nu + 4H\left( {1 - \nu } \right)\left( {1 + \nu } \right)} \right)}}\Omega \left( {1 - {{\beta }^{2}}} \right)$

${{\sigma }_{{\theta \theta }}} = \frac{{\left( {7 - 2\nu + 2H\left( {3 - 2\nu } \right)\left( {1 + \nu } \right) - \left( {1 + 10\nu + 2H\left( {1 + \nu } \right)\left( {1 + 2\nu } \right)} \right){{\beta }^{2}}} \right)}}{{4\left( {5 - 4\nu + 4H\left( {1 - \nu } \right)\left( {1 + \nu } \right)} \right)}}\Omega $

${{\sigma }_{{zz}}} = \frac{{\left( {1 + \nu } \right)\left( {1 + 2H\nu } \right)}}{{\left( {10 - 8\nu + 8H\left( {1 - \nu } \right)\left( {1 + \nu } \right)} \right)}}\Omega \left( {1 - 2{{\beta }^{2}}} \right)$

а актуальный предел текучести записывается как

$~{{\sigma }_{y}} = \frac{{\left( {5 - 4\nu + 2H\left( {1 + \nu } \right)\left( {3 - 4\nu - 2{{\beta }^{2}}\left( {1 - 2\nu } \right)} \right)} \right)}}{{4\left( {5 - 4\nu + 4H\left( {1 - \nu } \right)\left( {1 + \nu } \right)} \right)}}\Omega $

Работа выполнена в рамках государственного задания ХФИЦ ДВО РАН.

Список литературы

Gamer U., Sayir M. Elastic-plastic stress distribution in a rotating solid shaft // Zeitschrift für angewandte Mathematik und Physik ZAMP. 1984. V. 35. № 5. P. 601–617.
Gamer U., Mack W., Varga I. Rotating elastic-plastic solid shaft with fixed ends // Int. J. Eng. Sci. 1997. V. 35. № 3. P. 253–267.
Mack W. The rotating elastic–plastic solid shaft with free ends // Technische Mechanik. 1991. № 12. P. 119–124.
Mack W. Rotating elastic-plastic tube with free ends // Int. J. Solids & Struct. 1991. V. 27. № 11. P. 1461–1476.
Lindner T., Mack W. Residual stresses in an elastic-plastic solid shaft with fixed ends after previous rotation // ZAMM Zeitschrift fur Angewandte Mathematik und Mechanik. 1998. V. 78. № 2. P. 75–86.
Prokudin A.N. Exact elastoplastic analysis of a rotating cylinder with a rigid inclusion under mechanical loading and unloading // ZAMM Zeitschrift fur Angewandte Mathematik und Mechanik. 2020. V. 100. № 3. e201900213.
Prokudin A.N., Firsov S.V. Elastoplastic deformation of a rotating hollow cylinder with a rigid casing // PNRPU Mech. Bull. 2019. № 4. P. 120–135.
Прокудин А.Н., Фирсов С.В. Упругопластическое деформирование вращающегося полого цилиндра с жестким покрытием на внутренней и внешней стенках // Вестн. Инж. школы Дальнев. фед. ун-та. 2019. № 4 (41). С. 12–28.
Eraslan A.N., Arslan E. Plane strain analytical solutions to rotating partially plastic graded hollow shafts // Turkish J. Engng. & Environ. Sci. 2007. V. 31. № 5. P. 273–287.
Akis T., Eraslan A.N. Exact solution of rotating FGM shaft problem in the elastoplastic state of stress // Arch. Appl. Mech. 2007. V. 77. № 10. P. 745–765.
Nejad M.Z., Fatehi P. Exact elasto-plastic analysis of rotating thick-walled cylindrical pressure vessels made of functionally graded materials // Int. J. Engng. Sci. 2015. V. 86. № Suppl. C. P. 26–43.
Eraslan A.N. On the linearly hardening rotating solid shaft // Europ. J. Mech. A: Solids. 2003. V. 22. № 2. P. 295–307.
Eraslan A.N. Von Mises’ yield criterion and nonlinearly hardening rotating shafts // Acta Mechanica. 2004. V. 168. № 3–4. P. 129–144.
Eraslan A.N., Arslan E., Mack W. The strain hardening rotating hollow shaft subject to a positive temperature gradient // Acta Mechanica. 2007. V. 194. № 1–4. P. 191–211.
Arslan E., Mack W., Eraslan A.N. The rotating elastic-plastic hollow shaft conveying a hot medium // Forsch Ingenieurwes. 2010. V. 74. № 1. P. 27–39.
Leu S.-Y., Chen J.T. Sequential limit analysis of rotating hollow cylinders of nonlinear isotropic hardening // CMES – Comput. Model. in Engng.&Sci. 2006. V. 14. № 2. P. 129–140.
Leu S.-Y. Investigation of rotating hollow cylinders of strain-hardening viscoplastic materials by sequential limit analysis // Comput. Meth. in: Appl. Mech.&Engng. 2008. V. 197. № 51. P. 4858–4865.
Leu S.-Y., Hsu H.-C. Exact solutions for plastic responses of orthotropic strain-hardening rotating hollow cylinders // Int. J. Mech. Sci. 2010. V. 52. № 12. P. 1579–1587.
Ишлинский А.Ю., Ивлев Д.Д. Математическая теория пластичности. М.: Физматлит, 2003. 704 с.
Ишлинский А.Ю. Гипотеза прочности формоизменения // Уч. зап. МГУ. 1940. № 46. С. 104–114.
Schmidt R. Über den Zusammenhang von Spannungen und Formänderungen im Verfestigungsgebiet // Ingenieur-Archiv. 1932. V. 3. № 3. P. 215–235.
Hill R. On the inhomogeneous deformation of a plastic lamina in a compression test // The London, Edinburgh, and Dublin Phil. Mag. & J. Sci. 1950. V. 41. № 319. P. 733–744.
Ivlev D.D. On the development of a theory of ideal plasticity // JAMM. 1958. V. 22. № 6. P. 1221–1230.
Cai Q., Pang M., Zhang Y.-Q., Liu X. Elastic-plastic stress distribution of rotating annular disc based on twin-shear stress yield criterion // Zhejiang Daxue Xuebao (Gongxue Ban) / J. Zhejiang Univ. (Engng. Sci.). 2008. V. 42. № 9. P. 1540–1544.
Prokudin A.N. Elastic-plastic analysis of rotating solid shaft by maximum reduced stress yield criterion // Vestn. Samarsk. Gos. Tekhn. Univ., Ser. Fiz.-Mat. Nauki. 2020. V. 24. № 1. P. 74–94.
Zhao D.-w., Xie Y.-j., Liu X.-h., Wang G.-d. Three-dimensional analysis of rolling by twin shear stress yield criterion // J. Iron&Steel Res. Int. 2006. V. 13. № 6. P. 21–26.
Zhu X., Pang M., Zhang Y. Estimation of burst pressure of pipeline using twin-shear stress yield criterion // Yingyong Lixue Xuebao/Chinese J. Appl. Mech. 2011. V. 28. № 2. P. 135–138.
Буренин А.А., Ткачева А.В., Щербатюк Г.А. К расчету неустановившихся температурных напряжений в упругопластических телах // Выч. мех. сплошн. сред. 2017. Т. 10. № 3. С. 245–259.
Burenin A.A., Tkacheva A.V., Scherbatyuk G.A. To the use of piecewise-linear plastic potentials in the non-stationary theory of temperature stresses // Vestn. Samarsk. Gos. Tekhn. Univ., Ser. Fiz.-Mat. Nauki. 2018. V. 22. № 1. P. 23–39.
Буренин А.А., Каинг М., Ткачева А.В. К расчету плоских напряженных состояний в теории неустановившихся температурных напряжений в упругопластических телах // Дальнев. мат. ж. 2018. Т. 18. № 2. С. 131–146.
Yu M.-H. Unified Strength Theory and Its Applications. Singapore: Springer, 2018. 463 p.
Соколовский В.В. Теория пластичности. М.: Высшая школа, 1969. 608 с.
Писаренко Г.С., Лебедев А.А. Деформирование и прочность материалов при сложном напряженном состоянии. Киев: Наук. думка, 1976. 415 с.
Kolupaev V.A., Yu M.-H., Altenbach H. Fitting of the strength hypotheses // Acta Mechanica. 2016. V. 227. № 6. P. 1533–1556.
Koiter W.T. Stress-strain relations, uniqueness and variational theorems for elastic-plastic materials with a singular yield surface // Quart. Appl. Math. 1953. V. 11. № 3. P. 350–354.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал