1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 85, № 3, 2021

Прикладная математика и механика, 2021, T. 85, № 3, стр. 396-408

К определению термомеханических характеристик функционально-градиентного конечного цилиндра

А. О. Ватульян 1, 2, *, С. А. Нестеров 2, **

1 Южный федеральный университет
Ростов-на-Дону, Россия

2 Южный математический институт – филиал ВНЦ РАН
Владикавказ, Россия

* E-mail: aovatulyan@sfedu.ru
** E-mail: 1079@list.ru

Поступила в редакцию 02.02.2021
После доработки 18.03.2021
Принята к публикации 25.03.2021

Полный текст (PDF)

Аннотация

Сформулирована обратная задача об идентификации термомеханических характеристик конечного функционально-градиентного цилиндра по дополнительной информации, измеренной на внешней поверхности цилиндра на конечном временном интервале. Термоупругие характеристики считаются переменными по радиальной координате. Торцы цилиндра теплоизолированы и находятся в условиях скользящей заделки. Прямая задача после применения преобразования Лапласа решена на основе метода разделения переменных и метода пристрелки. Численное решение обратной задачи построено с помощью итерационного процесса, на каждом этапе которого решается интегральное уравнение Фредгольма 1-го рода.

Ключевые слова: обратная задача термоупругости, интегральное уравнение, функционально-градиентные материалы, конечный цилиндр, идентификация, метод пристрелки

1. Введение. В ходе анализа прочности различных элементов конструкций цилиндрической формы, находящихся в условиях термосилового нагружения, приходится решать задачи, связанные с нахождением полей температуры, перемещений и напряжений. Обычно такие расчеты проводят для однородных или слоистых термоупругих материалов. Однако в настоящее время все шире стали применяться функционально-градиентные материалы (FGM), которые изготавливают из-за необходимости оптимизировать термомеханические свойства конструкций [1, 2]. Однако технология изготовления FGM с заданными свойствами является многоступенчатой и поэтому требует на последнем этапе диагностики реальных свойств изделия. При этом материальные характеристики из-за неоднородности материалов могут быть определены только неразрушающими методами контроля, опирающимися на аппарат коэффициентных обратных задач (КОЗ).

К настоящему времени выполнено довольно много исследований по решению КОЗ теплопроводности [3, 4] и теории упругости [5–9] для тел цилиндрической формы. При этом наиболее распространенным методом решения КОЗ является построение функционала невязки и его минимизация каким-либо из градиентных методов [10–12] или генетическим алгоритмом [13]. Для некоторых материалов необходимо учитывать связанность полей и решать КОЗ термоупругости [14, 15].

В [16] для решения нелинейной КОЗ термоупругости на основе итерационного процесса были получены линеаризованные операторные уравнения в трансформантах Лапласа. С использованием этого подхода после перехода от трансформант Лапласа к оригиналам была проведена идентификация термомеханических характеристик [17, 18] и преднапряженного состояния [19, 20] бесконечного длинного полого цилиндра при задании информации о граничных полях на конечном временном интервале. При этом восстанавливалась только одна из термомеханических характеристик, остальные полагались известными. Однако для разработки теоретических основ неразрушающего контроля FGM тел цилиндрической формы при наличии радиальной неоднородности после изготовления более адекватной является модель цилиндра конечной длины. В работе [21] приведена постановка КОЗ конечного цилиндра в трансформантах Лапласа (это соответствует ситуации, когда дополнительная информация задана на полубесконечном интервале) в случае, когда торцы цилиндра теплоизолированы и находятся в условиях скользящей заделки, что позволяет при решении прямой задачи использовать метод разделения переменных. Для решения КОЗ на основе итерационного процесса операторные уравнения в трансформантах, полученные в [16] для произвольного конечного тела, упрощены и приведены к системе операторных уравнений для конечного цилиндра.

Однако постановка КОЗ в трансформантах требует информации на полубесконечном временном интервале, что создает сложности при реализации на практике, т.к. дополнительную информацию можно измерить на временном отрезке до выхода процесса на стационарный режим.

Данная работа посвящена постановке и решению КОЗ термоупругости для конечного цилиндра при задании информации на конечном временном интервале. Решение прямой задачи в трансформантах построено так же, как в [21]. Обращение преобразования Лапласа основано на методе разложения оригинала в ряд по смещенным многочленам Лежандра. В [21] получена система операторных уравнений в трансформантах, в правые части и ядра которых входят только нулевые гармоники радиальных перемещений и температуры. В данной работе, в дополнение к системе операторных уравнений, приведенных в [21], получена система операторных уравнений в трансформантах, в правые части и ядра которых входят гармоники радиальных перемещений и температуры при $n = 1,2,...$. Путем обращения операторных уравнений в трансформантах получены уравнения в оригиналах для восстановления теплофизических характеристик. Применен поэтапный итерационный процесс реконструкции двух характеристик. Даны практические рекомендации по выбору наиболее информативных временных интервалов для съема дополнительной информации.

2. Постановка задачи об идентификации термомеханических характеристик конечного FGM-цилиндра. Рассмотрим задачу для конечного термоупругого цилиндра, торцы которого теплоизолированы и находятся в условиях скользящей заделки, а термомеханические характеристики являются переменными только радиальной координаты. Цилиндр имеет высоту $2h$, внутренний радиус ${{r}_{1}}$, внешний радиус ${{r}_{2}}$. На внутренней поверхности цилиндра, свободной от механических нагрузок, поддерживается нулевая температура. На внешней поверхности цилиндра действует одна из двух типов нагрузки: 1) нормальная механическая нагрузка с амплитудой ${{p}^{0}}$; 2) тепловой поток с амплитудой ${{q}^{0}}$. Начально-краевая задача термоупругости после перехода к безразмерным параметрам и функциям по формулам

${{\xi }_{1}} = \frac{r}{{{{r}_{2}}}},\quad {{\xi }_{2}} = \frac{z}{{{{r}_{2}}}},\quad {{\xi }_{0}} = \frac{{{{r}_{1}}}}{{{{r}_{2}}}},\quad {{\beta }_{0}} = \frac{h}{{{{r}_{2}}}},\quad U = \frac{{{{u}_{r}}}}{{{{r}_{2}}}},\quad V = \frac{{{{u}_{z}}}}{{{{r}_{2}}}},\quad W = \frac{{{{\gamma }_{0}}\theta }}{{{{\lambda }_{0}}}}$
$\tau = \frac{t}{{{{r}_{2}}}}\sqrt {\frac{{{{\lambda }_{0}}}}{{{{\rho }_{0}}}}} ,\quad {{\delta }_{0}} = \frac{{\gamma _{0}^{2}{{T}_{0}}}}{{{{c}_{0}}{{\lambda }_{0}}}},\quad {{\Omega }_{{rr}}} = \frac{{{{\sigma }_{{rr}}}}}{{{{\lambda }_{0}}}},\quad {{\Omega }_{{\varphi \varphi }}} = \frac{{{{\sigma }_{{\varphi \varphi }}}}}{{{{\lambda }_{0}}}},\quad {{\Omega }_{{rz}}} = \frac{{{{\sigma }_{{rz}}}}}{{{{\lambda }_{0}}}},\quad {{\Omega }_{{zz}}} = \frac{{{{\sigma }_{{zz}}}}}{{{{\lambda }_{0}}}}$
$\bar {\lambda } = \frac{\lambda }{{{{\lambda }_{0}}}},\quad {{y}_{0}} = \frac{{{{\mu }_{0}}}}{{{{\lambda }_{0}}}},\quad \bar {\mu } = \frac{\mu }{{{{\mu }_{0}}}},\quad \bar {\rho } = \frac{\rho }{{{{\rho }_{0}}}},\quad \bar {\gamma } = \frac{\gamma }{{{{\gamma }_{0}}}},\quad \bar {k} = \frac{k}{{{{k}_{0}}}},\quad \bar {c} = \frac{c}{{{{c}_{0}}}}$
${{\chi }_{0}} = \frac{{{{p}^{0}}}}{{{{\lambda }_{0}}}},\quad {{\omega }_{0}} = \frac{{{{q}^{0}}{{r}_{2}}{{\gamma }_{0}}}}{{{{k}_{0}}{{\lambda }_{0}}}}$
имеет вид [21]:

(2.1)
$\frac{{\partial {{\Omega }_{{rr}}}}}{{\partial {{\xi }_{1}}}} + \frac{{\partial {{\Omega }_{{zr}}}}}{{\partial {{\xi }_{2}}}} + \frac{{{{\Omega }_{{rr}}} - {{\Omega }_{{\varphi \varphi }}}}}{{{{\xi }_{1}}}} = \bar {\rho }\frac{{{{\partial }^{2}}U}}{{\partial {{\tau }^{2}}}}$
(2.2)
$\frac{{\partial {{\Omega }_{{zr}}}}}{{\partial {{\xi }_{1}}}} + \frac{{\partial {{\Omega }_{{zz}}}}}{{\partial {{\xi }_{2}}}} + \frac{{{{\Omega }_{{zr}}}}}{{{{\xi }_{1}}}} = \bar {\rho }\frac{{{{\partial }^{2}}V}}{{\partial {{\tau }^{2}}}}$
(2.3)
$\frac{1}{{{{\xi }_{1}}}}\frac{\partial }{{\partial {{\xi }_{1}}}}(\bar {k}({{\xi }_{1}}){{\xi }_{1}}\frac{{\partial W}}{{\partial {{\xi }_{1}}}}) + \bar {k}({{\xi }_{1}})\frac{{{{\partial }^{2}}W}}{{\partial \xi _{2}^{2}}} = \bar {c}(\xi )\frac{{\partial W}}{{\partial \tau }} + {{\delta }_{0}}\bar {\gamma }(\xi )\left( {\frac{{{{\partial }^{2}}U}}{{\partial {{\xi }_{1}}\partial \tau }} + \frac{1}{{{{\xi }_{1}}}}\frac{{\partial U}}{{\partial \tau }} + \frac{{{{\partial }^{2}}V}}{{\partial {{\xi }_{2}}\partial \tau }}} \right)$
(2.4)
$V({{\xi }_{1}}, \pm {{\beta }_{0}},\tau ) = 0,\quad {{\Omega }_{{rz}}}({{\xi }_{1}}, \pm {{\beta }_{0}},\tau ) = 0,\quad \frac{{\partial W}}{{\partial {{\xi }_{2}}}}({{\xi }_{1}}, \pm {{\beta }_{0}},\tau ) = 0$
(2.5)
${{\Omega }_{{rr}}}({{\xi }_{0}},{{\xi }_{2}},\tau ) = 0,\quad {{\Omega }_{{rz}}}({{\xi }_{0}},{{\xi }_{2}},\tau ) = 0,\quad W({{\xi }_{0}},{{\xi }_{2}},\tau ) = 0$
(2.6)
$\begin{gathered} {{\Omega }_{{rr}}}(1,{{\xi }_{2}},\tau ) = {{\chi }_{0}}S({{\xi }_{2}}){{G}_{1}}(\tau ),\quad {{\Omega }_{{rz}}}(1,{{\xi }_{2}},\tau ) = 0 \\ - \bar {k}(1)\frac{{\partial W}}{{\partial {{\xi }_{1}}}}(1,{{\xi }_{2}},\tau ) = {{\omega }_{0}}R({{\xi }_{2}}){{G}_{2}}(\tau ) \\ \end{gathered} $
(2.7)
$W({{\xi }_{1}},{{\xi }_{2}},0) = U({{\xi }_{1}},{{\xi }_{2}},0) = \frac{{\partial U}}{{\partial \tau }}({{\xi }_{1}},{{\xi }_{2}},0) = V({{\xi }_{1}},{{\xi }_{2}},0) = \frac{{\partial V}}{{\partial \tau }}({{\xi }_{1}},{{\xi }_{2}},0) = 0$

Здесь ${{\lambda }_{0}}$, ${{\mu }_{0}}$ ${{\rho }_{0}}$, ${{\gamma }_{0}}$, ${{k}_{0}}$, ${{c}_{0}}$ – характерные величины.

Прямая задача термоупругости заключается в определении функций $W = W({{\xi }_{1}},{{\xi }_{2}},\tau )$, $U = U({{\xi }_{1}},{{\xi }_{2}},\tau )$, $V = V({{\xi }_{1}},{{\xi }_{2}},\tau )$ из (2.1)–(2.7) при известных термомеханических характеристиках $\bar {\lambda }$, $\bar {\mu }$, $\bar {\rho }$, $\bar {\gamma }$, $\bar {k}$, $\bar {c}$.

В обратной задаче требуется определить термомеханические характеристики $\bar {\lambda }$, $\bar {\mu }$, $\bar {\rho }$, $\bar {\gamma }$, $\bar {k}$, $\bar {c}$ из (2.1)–(2.7) по дополнительной информации, измеренной на внешней боковой поверхности цилиндра:

(2.8)
$U(1,{{\xi }_{2}},\tau ) = f({{\xi }_{2}},\tau );\quad \tau \in [a,b]$
(2.9)
$W(1,{{\xi }_{2}},\tau ) = g({{\xi }_{2}},\tau );\quad \tau \in [c,d]$

3. Исследование прямой задачи термоупругости. Применим преобразование Лапласа по $\tau $ к уравнениям (2.1)–(2.6), с учетом начальных условий (2.7). Полученная задача в трансформантах решается на основе метода разделения переменных [21]. Для этого полагаем:

(3.1)
$\begin{gathered} \tilde {U}({{\xi }_{1}},{{\xi }_{2}},p) = \sum\limits_{n = 0}^\infty {{{{\tilde {a}}}_{n}}} ({{\xi }_{1}},p)\cos ({{\nu }_{n}}{{\xi }_{2}}) \\ \tilde {V}({{\xi }_{1}},{{\xi }_{2}},p) = \sum\limits_{n = 0}^\infty {{{{\tilde {b}}}_{n}}} ({{\xi }_{1}},p)\sin ({{\nu }_{n}}{{\xi }_{2}}) \\ \tilde {W}({{\xi }_{1}},{{\xi }_{2}},p) = \sum\limits_{n = 0}^\infty {{{{\tilde {d}}}_{n}}} ({{\xi }_{1}},p)\cos ({{\nu }_{n}}{{\xi }_{2}});\quad {{\nu }_{n}} = \frac{{n\pi }}{{{{\beta }_{0}}}} \\ \end{gathered} $

Тогда граничные условия (2.4) выполняются тождественно. Полагаем, что функции $S({{\xi }_{2}})$ и $R({{\xi }_{2}})$ – четные, тогда их можно представить в виде:

(3.2)
$S({{\xi }_{2}}) = \sum\limits_{n = 0}^\infty {{{s}_{n}}} \cos ({{\nu }_{n}}{{\xi }_{2}}),\quad R({{\xi }_{2}}) = \sum\limits_{n = 0}^\infty {{{r}_{n}}} \cos ({{\nu }_{n}}{{\xi }_{2}}),$
где коэффициенты разложения имеют вид

${{s}_{n}} = \int\limits_{ - {{\beta }_{0}}}^{{{\beta }_{0}}} {S({{\xi }_{2}})\cos ({{\nu }_{n}}{{\xi }_{2}})} d{{\xi }_{2}},\quad {{r}_{n}} = \int\limits_{ - {{\beta }_{0}}}^{{{\beta }_{0}}} {R({{\xi }_{2}})\cos ({{\nu }_{n}}{{\xi }_{2}})} d{{\xi }_{2}}$

Компоненты тензора напряжений $\sigma $, распишем в виде:

(3.3)
${{\tilde {\Omega }}_{{rr}}} = \sum\limits_{n = 0}^\infty {{{{\tilde {R}}}_{{1n}}}} \cos ({{\nu }_{n}}{{\xi }_{2}}),\quad {{\tilde {\Omega }}_{{zr}}} = {{\tilde {\Omega }}_{{rz}}} = \sum\limits_{n = 0}^\infty {{{{\tilde {R}}}_{{2n}}}} \sin ({{\nu }_{n}}{{\xi }_{2}})$
(3.4)
${{\tilde {\Omega }}_{{\varphi \varphi }}} = \sum\limits_{n = 0}^\infty {{{{\tilde {R}}}_{{3n}}}} \cos ({{\nu }_{n}}{{\xi }_{2}}),\quad {{\tilde {\Omega }}_{{zz}}} = \sum\limits_{n = 0}^\infty {{{{\tilde {R}}}_{{4n}}}} \cos ({{\nu }_{n}}{{\xi }_{2}})$

Здесь

${{\tilde {R}}_{{1n}}} = (\bar {\lambda } + 2{{y}_{0}}\bar {\mu })\tilde {a}_{n}^{'} + \bar {\lambda }\left( {\frac{{{{{\tilde {a}}}_{n}}}}{{{{\xi }_{1}}}} + {{\nu }_{n}}{{{\tilde {b}}}_{n}}} \right) - \bar {\gamma }{{\tilde {d}}_{n}},\quad {{\tilde {R}}_{{2n}}} = {{y}_{0}}\bar {\mu }(\tilde {b}_{n}^{'} - {{\nu }_{n}}{{\tilde {a}}_{n}})$
${{\tilde {R}}_{{3n}}} = \frac{{\bar {\lambda } + 2{{y}_{0}}\bar {\mu }}}{{{{\xi }_{1}}}}{{\tilde {a}}_{n}} + \bar {\lambda }(\tilde {a}_{n}^{'} + {{\nu }_{n}}{{\tilde {b}}_{n}}) - \bar {\gamma }{{\tilde {d}}_{n}},\quad {{\tilde {R}}_{{4n}}} = (\bar {\lambda } + 2{{y}_{0}}\bar {\mu }){{\nu }_{n}}{{\tilde {b}}_{n}} + \bar {\lambda }\left( {\tilde {a}_{n}^{'} + \frac{1}{{{{\xi }_{1}}}}{{{\tilde {a}}}_{n}}} \right) - \bar {\gamma }{{\tilde {d}}_{n}}$

Тогда с учетом введенных обозначений, получим набор линейных систем дифференциальных уравнений относительно искомых функций ${{\tilde {a}}_{n}}$, ${{\tilde {b}}_{n}}$, ${{\tilde {d}}_{n}}$, ${{\tilde {Q}}_{n}}$, ${{\tilde {R}}_{{1n}}}$, ${{\tilde {R}}_{{2n}}}$. Решение системы уравнений при заданных функциях $\bar {\lambda }$, $\bar {\mu }$, $\bar {\rho }$, $\bar {\gamma }$, $\bar {k}$, $\bar {c}$ получено численно с помощью метода пристрелки [21] для любого численного значения параметра преобразования Лапласа $p$.

Для нахождения оригиналов функций $F(\tau )$ по их трансформантам $\tilde {F}(p)$ нужно применить обратное преобразование Лапласа, т.е. вычислить контурный интеграл:

(3.5)
$F(\tau ) = \frac{1}{{2\pi i}}\int\limits_{a - i\infty }^{a + i\infty } {\tilde {F}(p){{e}^{{p\tau }}}} dp$

Воспользуемся численным обращением преобразования Лапласа на основе метода разложения оригинала в ряд по смещенным многочленам Лежандра. Смещенные многочлены Лежандра $P_{n}^{*}$ отличаются от многочленов Лежандра ${{P}_{n}}$ тем, что область их определения сведена к отрезку [0, 1] вместо обычного [–1, 1], т.е. $P_{n}^{*}(x) = {{P}_{n}}(2x - 1)$. Смещенные многочлены Лежандра имеют вид:

(3.6)
$P_{n}^{*}(x) = {{( - 1)}^{n}}\sum\limits_{s = 0}^n {{{{( - 1)}}^{s}}\left( {\begin{array}{*{20}{c}} n \\ s \end{array}} \right)} \frac{{(n + s)!}}{{n!s!}}{{x}^{s}}$

Согласно [25] разложение функции $F(\tau )$ по смещенным многочленам Лежандра имеет вид:

(3.7)
$F(\tau ) = \sum\limits_{s = 0}^\infty {(2s + 1){{a}_{s}}} P_{s}^{*}({{e}^{{ - \tau }}})$

В [25] получено выражение для коэффициентов разложения ${{a}_{s}}$ через известные коэффициенты $c_{i}^{{(s)}}$ многочленов $P_{s}^{*}$ и значения изображения $\tilde {F}(p)$ в целых точках $p = 0,1,2,...$ в виде ${{a}_{s}} = \sum\nolimits_{i = 0}^s {c_{i}^{{(s)}}\tilde {F}(i)} $.

На конкретных примерах в системе Maple проведено тестирование процедуры обращения преобразования Лапласа. Выяснено, что для того, чтобы погрешность вычисления оригиналов для времени $\tau \geqslant 0.01$ не превосходила 1% достаточно ограничиться 80 членами ряда в разложении (3.7), используя при этом параметр $\operatorname{digits} = 60$, характеризующий повышенную точность вычислений.

Верификация предложенного метода решения прямой задачи (2.1)–(2.7) была проведена на примере FGM, свойства которого принимают свойства Ni при ${{\xi }_{1}} = {{\xi }_{0}}$ и свойства TiC при ${{\xi }_{1}} = 1$. Материальные характеристики композиции Ni–TiC имеют вид [23]: ${{E}_{{\operatorname{Ni} }}} = 2.06 \times {{10}^{{11}}}$ Па, ${{\nu }_{{\operatorname{Ni} }}} = 0.3$, ${{\rho }_{{\operatorname{Ni} }}} = 8890$ кг/м3, ${{\alpha }_{{\operatorname{Ni} }}} = 13.3 \times {{10}^{{ - 6}}}$ К–1, ${{k}_{{\operatorname{Ni} }}}$ = = 90 Вт/(м К), ${{c}_{{\operatorname{Ni} }}} = 439.5$ Дж(кг К), ${{E}_{{\operatorname{TiC} }}} = 3.2 \times {{10}^{{11}}}$ Па, ${{\nu }_{{\operatorname{TiC} }}} = 0.3$, ${{\rho }_{{\operatorname{TiC} }}}$ = 4940 кг/м3, ${{\alpha }_{{\operatorname{TiC} }}} = 7.4 \times {{10}^{{ - 6}}}$ К–1, ${{k}_{{\operatorname{TiC} }}} = 25$ Вт/(м К), ${{c}_{{\operatorname{TiC} }}} = 134$ Дж(кг К).

Для моделирования свойств FGM в работе используются законы вида [7, 24]: $\bar {a}({{\xi }_{1}}) = {{\bar {a}}_{{Ni}}}$ + $({{\bar {a}}_{{TiC}}} - {{\bar {a}}_{{Ni}}}){{\left( {\frac{{{{\xi }_{1}} - {{\xi }_{0}}}}{{1 - {{\xi }_{0}}}}} \right)}^{l}}$, $l = 1,2,...$. Полагая в расчетах ${{\lambda }_{0}} = {{\mu }_{0}} = {{10}^{{11}}}$ Па, ${{\gamma }_{0}} = {{10}^{6}}$ Па/К, ${{\rho }_{0}} = {{10}^{4}}$ кг/м3, ${{k}_{0}} = {{10}^{2}}$ Вт/(м К), ${{c}_{0}} = {{10}^{4}}$ Дж(кг К), $h = 0.5$ м, ${{r}_{1}} = 0.2$ м, ${{r}_{2}} = 0.25$ м, ${{p}^{0}} = {{10}^{{11}}}$ Па, ${{q}^{0}} = {{10}^{7}}$ Вт/м2, ${{T}_{0}} = 300$ К, получим следующие законы изменения безразмерных термомеханических характеристик:

$\bar {\mu }({{\xi }_{1}}) = 0.79 + 0.44{{\left( {5{{\xi }_{1}} - 4} \right)}^{l}},\quad \bar {\lambda }({{\xi }_{1}}) = 1.19 + 0.66{{\left( {5{{\xi }_{1}} - 4} \right)}^{l}}$
$\bar {\gamma }({{\xi }_{1}}) = 2.74 - 0.37{{\left( {5{{\xi }_{1}} - 4} \right)}^{l}},\quad \bar {\rho }({{\xi }_{1}}) = 0.89 - 0.4{{\left( {5{{\xi }_{1}} - 4} \right)}^{l}}$
$\bar {k}({{\xi }_{1}}) = 0.9 - 0.65{{\left( {5{{\xi }_{1}} - 4} \right)}^{l}},\quad \bar {c}({{\xi }_{1}}) = 0.44 - 0.3{{\left( {5{{\xi }_{1}} - 4} \right)}^{l}}$

Здесь $l = 1,2,...$ – показатель неоднородности.

Проведено сравнение полученного решения для материала $\operatorname{Ni} - TiC$ с решением в конечно-элементном пакете FlexPDE при значении показателя неоднородности $l = 1$. Выяснено, что для того, чтобы погрешность вычисления распределения перемещений $U$, $V$ и температуры $W$ по координате ${{\xi }_{1}}$ при ${{\xi }_{2}} = 0$, $\tau = 0.2$ не превосходила 1% достаточно ограничиться 5 членами ряда в разложениях (3.1).

При решении КОЗ важно, чтобы изменение восстанавливаемых функций отражалось на измеряемой в эксперименте дополнительной информации. На рис. 1 показан график изменения безразмерной температуры $W$ от $\tau $ в точке $({{\xi }_{1}},{{\xi }_{2}})$ = (1, 0) при нагружении тепловым потоком $Q(1,{{\xi }_{2}},\tau )$ = $\left( {1 - {{{\left( {\frac{{{{\xi }_{2}}}}{2}} \right)}}^{2}}} \right)H(\tau )$ FGM цилиндра с различными показателями неоднородности: $l = 1$ (сплошная линия) и $l = 2$ (точки).

Рис. 1.

Изменение безразмерной температуры $W$ от $\tau $ в точке (1, 0) при различных показателях законов неоднородности FGM-цилиндра.

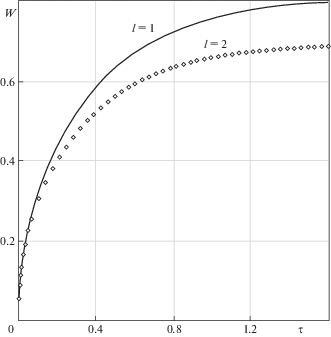
Из рис. 1 видно, что переменные свойства материала могут существенно влиять на граничные физические поля и их можно идентифицировать по дополнительной информации.

4. Схема решения обратной задачи термоупругости для цилиндра. КОЗ термоупругости (2.1)–(2.9) является нелинейной задачей. Построим ее решение на основе итерационного процесса, на каждом этапе которого решаются линеаризованные операторные уравнения или системы уравнений. Предположим, что функции $f({{\xi }_{2}},\tau )$, $g({{\xi }_{2}},\tau )$ в формулах (2.8), (2.9) допускают разложения в ряды: $f({{\xi }_{2}},\tau )$ = $\sum\nolimits_{n = 0}^\infty {{{f}_{n}}(\tau )\cos ({{\nu }_{n}}{{\xi }_{2}})} $, $g({{\xi }_{2}},\tau )$ = $\sum\nolimits_{n = 0}^\infty {{{g}_{n}}(\tau )\cos ({{\nu }_{n}}{{\xi }_{2}})} $.

Отметим, что при $n = 0$ система операторных уравнений для решения КОЗ термоупругости конечного цилиндра в трансформантах Лапласа, полученная в [21], имеет вид:

(4.1)
$\begin{gathered} \int\limits_{{{\xi }_{0}}}^1 {\left[ {{{{\bar {\lambda }}}^{{(m)}}}{{{\left( {\tilde {a}_{0}^{{'(m - 1)}} + \tfrac{{\tilde {a}_{0}^{{(m - 1)}}}}{{{{\xi }_{1}}}}} \right)}}^{2}} + 2{{{\bar {\mu }}}^{{(m)}}}{{g}_{0}}\left( {\tilde {a}_{0}^{{'{{{(m - 1)}}^{2}}}} + {{{\left( {\tfrac{{\tilde {a}_{0}^{{(m - 1)}}}}{{{{\xi }_{1}}}}} \right)}}^{2}}} \right) + {{p}^{2}}{{{\bar {\rho }}}^{{(m)}}}\tilde {a}_{0}^{{{{{(m - 1)}}^{2}}}}} \right]} - \\ - \;2{{\delta }_{0}}{{{\bar {\gamma }}}^{{(m)}}}\left( {\tilde {a}_{0}^{{'(m - 1)}} + \tfrac{{\tilde {a}_{0}^{{(m - 1)}}}}{{{{\xi }_{1}}}}} \right)\tilde {d}_{0}^{{(m - 1)}}{{\xi }_{1}}d{{\xi }_{1}} = {{s}_{0}}{{\chi }_{0}}{{{\tilde {G}}}_{1}}(p)({{{\tilde {f}}}_{0}}(p) - \tilde {a}_{0}^{{(m - 1)}}(1,p)) \\ \end{gathered} $
(4.2)
$\begin{gathered} \int\limits_{{{\xi }_{0}}}^1 {\left[ {{{{\bar {k}}}^{{(m)}}}\tilde {d}_{0}^{{'{{{(m - 1)}}^{2}}}} + p{{{\bar {c}}}^{{(m)}}}\tilde {d}_{0}^{{{{{(m - 1)}}^{2}}}} + 2p{{\delta }_{0}}{{{\bar {\gamma }}}^{{(m)}}}\left( {\tilde {a}_{0}^{{'(m - 1)}} + \tfrac{{\tilde {a}_{0}^{{(m - 1)}}}}{{{{\xi }_{1}}}}} \right)\tilde {d}_{0}^{{(m - 1)}}} \right]} {{\xi }_{1}}d{{\xi }_{1}} = \\ = {{r}_{0}}{{\omega }_{0}}{{{\tilde {G}}}_{2}}(p)({{{\tilde {g}}}_{0}}(p) - \tilde {d}_{0}^{{(m - 1)}}(1,p)),\quad p \in [0,\infty ) \\ \end{gathered} $

В правые части выражений (4.1), (4.2) входят трансформанты ${{\tilde {f}}_{0}}(p)$, ${{\tilde {g}}_{0}}(p)$, которые имеют вид: ${{\tilde {f}}_{0}}(p)$ = $\int_{ - \beta }^\beta {\tilde {f}({{\xi }_{2}},p)} d{{\xi }_{2}}$, ${{\tilde {g}}_{0}}(p)$ = $\int_{ - \beta }^\beta {\tilde {g}({{\xi }_{2}},p)d{{\xi }_{2}}} $.

Выполняя действия, аналогичные [21], получим системы операторных уравнений в трансформантах для различных гармоник $n = 1,2,...$ при каждом значении параметра $p \in [0,\infty )$:

(4.3)
$\begin{gathered} \int\limits_{{{\xi }_{0}}}^1 {{{{\bar {\lambda }}}^{{(m)}}}{{{\left( {\tilde {a}_{n}^{{'(m - 1)}} + \tfrac{{\tilde {a}_{n}^{{(m - 1)}}}}{{{{\xi }_{1}}}} + {{\nu }_{n}}\tilde {b}_{n}^{{(m - 1)}}} \right)}}^{2}}} + 2{{{\bar {\mu }}}^{{(m)}}}{{g}_{0}}\left( {\tilde {a}_{n}^{{'{{{(m - 1)}}^{2}}}} + {{{\left( {\tfrac{{\tilde {a}_{n}^{{(m - 1)}}}}{{{{\xi }_{1}}}}} \right)}}^{2}} + {{{({{\nu }_{n}}\tilde {b}_{n}^{{(m - 1)}})}}^{2}} + } \right. \\ \left. {\mathop + \limits_{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}} \frac{1}{2}{{{(\tilde {b}_{n}^{{'(m - 1)}} - {{\nu }_{n}}\tilde {a}_{n}^{{(m - 1)}})}}^{2}}} \right) + {{p}^{2}}{{{\bar {\rho }}}^{{(m)}}}\left( {\tilde {a}_{n}^{{{{{(m - 1)}}^{2}}}} + b_{n}^{{{{{(m - 1)}}^{2}}}}} \right) - \\ - \;2{{\delta }_{0}}{{{\bar {\gamma }}}^{{(m)}}}\left( {\tilde {a}_{n}^{{'(m - 1)}} + \tfrac{{\tilde {a}_{n}^{{(m - 1)}}}}{{{{\xi }_{1}}}} + {{\nu }_{n}}\tilde {b}_{n}^{{(m - 1)}}} \right)\tilde {d}_{n}^{{(m - 1)}}{{\xi }_{1}}d{{\xi }_{1}} = {{s}_{n}}{{\chi }_{0}}{{{\tilde {G}}}_{1}}(p)({{{\tilde {f}}}_{n}}(p) - \tilde {a}_{n}^{{(m - 1)}}(1,p)) \\ \end{gathered} $
(4.4)
$\begin{gathered} \int\limits_{{{\xi }_{0}}}^1 {\left[ {{{{\bar {k}}}^{{(m)}}}\left( {\tilde {d}_{n}^{{'{{{(m - 1)}}^{2}}}} + \nu _{n}^{2}\tilde {d}_{n}^{{{{{(m - 1)}}^{2}}}}} \right) + p{{{\bar {c}}}^{{(m)}}}\tilde {d}_{n}^{{{{{(m - 1)}}^{2}}}}} \right.} + \\ \left. { + \;2p{{\delta }_{0}}{{{\bar {\gamma }}}^{{(m)}}}\left( {\tilde {a}_{n}^{{'(m - 1)}} + \tfrac{{\tilde {a}_{n}^{{(m - 1)}}}}{{{{\xi }_{1}}}} + {{\nu }_{n}}\tilde {b}_{n}^{{(m - 1)}}} \right)\tilde {d}_{n}^{{(m - 1)}}} \right]{{\xi }_{1}}d{{\xi }_{1}} = {{r}_{n}}{{\omega }_{0}}{{{\tilde {G}}}_{2}}(p)({{{\tilde {g}}}_{n}}(p) - \tilde {d}_{n}^{{(m - 1)}}(1,p)) \\ p \in [0,\infty ) \\ \end{gathered} $

Выражения (4.1)–(4.4) представляют собой системы интегральных уравнений Фредгольма 1-го рода относительно поправок ${{\bar {\lambda }}^{{(m)}}}$, ${{\bar {\mu }}^{{(m)}}}$, ${{\bar {\rho }}^{{(m)}}}$, ${{\bar {\gamma }}^{{(m)}}}$, ${{\bar {k}}^{{(m)}}}$, ${{\bar {c}}^{{(m)}}}$ безразмерных термомеханических характеристик при известных значениях функций $\tilde {a}_{n}^{{(m - 1)}}$, $\tilde {b}_{n}^{{(m - 1)}}$, $\tilde {d}_{n}^{{(m - 1)}}$, найденных путем решения прямой задачи (2.1)–(2.7) на $(m - 1)$-й итерации. В правые части (43), (44) входят трансформанты ${{\tilde {f}}_{n}}(p)$, ${{\tilde {g}}_{n}}(p)$, которые имеют вид: ${{\tilde {f}}_{n}}(p)$ = $\int_{ - \beta }^\beta {\tilde {f}({{\xi }_{2}},p)\cos ({{\nu }_{n}}{{\xi }_{2}})} d{{\xi }_{2}}$, ${{\tilde {g}}_{n}}(p)$ = $\int_{ - \beta }^\beta {\tilde {g}({{\xi }_{2}},p)\cos ({{\nu }_{n}}{{\xi }_{2}})} d{{\xi }_{2}}$.

На основе системы операторных уравнений (4.1)–(4.4) можно организовать итерационный процесс для определения искомых характеристик. Итерационный процесс стартует с выбора начальных приближений, которые определяются в классе линейных функций исходя из априорной информации о значениях искомых характеристик только на внешней и внутренней границах, которые могут быть определены из экспериментов или заданы технологическим процессом [21]. Далее уточняются законы изменения термомеханической характеристики путем нахождения поправок из решения систем операторных уравнений 1-го рода в оригиналах, полученного на основе обращения систем уравнений в трансформантах (4.1)–(4.4).

Поскольку решение интегрального уравнения Фредгольма 1-го рода вида (4.1)–(4.4) является некорректной задачей, то для его регуляризации применяется метод Тихонова А.Н. с автоматическим выбором параметра регуляризации согласно алгоритму, описанному в [26]. Аппроксимация поправок осуществлялась с помощью сплайнов 4-го порядка.

Зашумление входной информации моделировалось с помощью соотношения

(4.5)
${{f}_{\alpha }}(\tau ) = f(\tau )(1 + \alpha \psi ),$
где $\alpha $ – величина зашумления, $\psi $ – случайная величина с равномерным законом распределения на отрезке [–1, 1].

Выход из итерационного процесса осуществляется по предельному числу итераций, равному 20.

5. Результаты вычислительных экспериментов. Особенности идентификации неоднородных механических характеристик конечного цилиндра подробно исследованы в [9]. В данном параграфе представлены результаты вычислительных экспериментов по реконструкции теплофизических характеристик в классах степенных и экспоненциальных функций, которыми наиболее часто моделируются законы изменения функционально-градиентных материалов. Цилиндр нагружается тепловым потоком $Q(1,{{\xi }_{2}},\tau )$ = ${{\omega }_{0}}(1 - {{\left( {{{\xi }_{2}}{\text{/}}{{\beta }_{0}}} \right)}^{2}})H(\tau )$. Механические характеристики цилиндра $\bar {\rho }({{\xi }_{1}})$, $\bar {\mu }({{\xi }_{1}})$, $\bar {\lambda }({{\xi }_{1}})$ полагаются известными и равными законам, рассмотренным в параграфе 2, с показателем неоднородности $l = 2$. В расчетах принято: ${{\xi }_{0}} = 0.8$, ${{\delta }_{0}} = 0.1$, ${{y}_{0}} = 1$, ${{\beta }_{0}} = 2$, ${{\omega }_{0}} = 1$.

Для одновременной идентификации теплофизических характеристик $\bar {\gamma }({{\xi }_{1}})$, $\bar {k}({{\xi }_{1}})$ и $\bar {c}({{\xi }_{1}})$ необходимо решить систему 3 интегральных уравнений, состоящих из обращенных в оригиналы уравнения (4.2) и двух уравнений (4.4) при $n = 1$ и $n = 2$, из-за чего возникают большие вычислительные проблемы. Возможности предлагаемого подхода проверим на решении упрощенной обратной задачи о реконструкции двух функций.

В первой серии экспериментов восстанавливались функции $\bar {\gamma }({{\xi }_{1}})$ и $\bar {k}({{\xi }_{1}})$ при известной $\bar {c}({{\xi }_{1}})$. В этом случае, полагая в уравнениях (4.2), (4.4) ${{\bar {с}}^{{(m)}}} = 0$, получим систему уравнений для нахождения поправок функций ${{\bar {\gamma }}^{{(m)}}}$ и ${{\bar {k}}^{{(т)}}}$. Однако, проведенные расчеты показали, что значение ядра при поправке ${{\bar {k}}^{{(т)}}}$ значительно больше, чем при ${{\bar {\gamma }}^{{(m)}}}$. Поэтому предложен поэтапный процесс идентификации теплофизических характеристик.

На первом этапе для всех итераций полагаем ${{\bar {\gamma }}^{{(т)}}} = 0$, что означает равенство коэффициента температурных напряжений выбранному начальному приближению. Далее на каждой итерации определялись поправки ${{\bar {k}}^{{(т)}}}$ как решение интегрального уравнения, полученного путем обращения уравнения в трансформантах (4.2) при ${{\bar {с}}^{{(m)}}} = {{\bar {\gamma }}^{{(m)}}} = 0$:

(5.1)
$\int\limits_{{{\xi }_{0}}}^1 {{{{\bar {k}}}^{{(m)}}}{{M}_{1}}({{\xi }_{1}},\tau )} {{\xi }_{1}}d{{\xi }_{1}} = {{r}_{0}}{{\omega }_{0}}({{g}_{0}}(\tau ) - d_{0}^{{(m - 1)}}(1,\tau ));\quad \tau \in [c,d],$
где ядро уравнения (5.1) имеет вид: ${{M}_{1}}({{\xi }_{1}},\tau ) = \int_0^\tau {\frac{{\partial d_{0}^{{(m - 1)}}({{\xi }_{1}},{{\tau }_{1}})}}{{\partial {{\xi }_{1}}}}\frac{{{{\partial }^{2}}d_{0}^{{(m - 1)}}({{\xi }_{1}},\tau - {{\tau }_{1}})}}{{\partial {{\xi }_{1}}\partial {{\tau }_{1}}}}} d{{\tau }_{1}}$.

На втором этапе фиксируется найденная функция $\bar {k}({{\xi }_{1}})$. Тогда, полагая поправки ${{\bar {k}}^{{(т)}}} = 0$, на каждой последующей итерации определяются поправки ${{\bar {\gamma }}^{{(т)}}}$ как решение интегрального уравнения, полученного путем обращения уравнения в трансформантах (4.2) при ${{\bar {с}}^{{(m)}}} = {{\bar {k}}^{{(m)}}} = 0$:

(5.2)
$2{{\delta }_{0}}\int\limits_{{{\xi }_{0}}}^1 {{{{\bar {\gamma }}}^{{(m)}}}} {{M}_{2}}({{\xi }_{1}},\tau ){{\xi }_{1}}d{{\xi }_{1}} = {{r}_{0}}{{\omega }_{0}}({{g}_{0}}(\tau ) - d_{0}^{{(m - 1)}}(1,\tau ));\quad \tau \in [c,d],$
где ядро уравнения (5.2) имеет вид: ${{M}_{2}}({{\xi }_{1}},\tau )$ = = $\int_0^\tau {\left( {\frac{{{{\partial }^{2}}a_{0}^{{(m - 1)}}({{\xi }_{1}},{{\tau }_{1}})}}{{\partial {{\xi }_{1}}\partial {{\tau }_{1}}}} + \frac{1}{{{{\xi }_{1}}}}\frac{{\partial a_{0}^{{(m - 1)}}({{\xi }_{1}},{{\tau }_{1}})}}{{\partial {{\tau }_{1}}}}} \right)} \frac{{\partial d_{0}^{{(m - 1)}}({{\xi }_{1}},\tau - {{\tau }_{1}})}}{{\partial {{\tau }_{1}}}}d{{\tau }_{1}}$.

Во второй серии экспериментов восстанавливались функции $\bar {k}({{\xi }_{1}})$ и $\bar {c}({{\xi }_{1}})$ при известной $\bar {\gamma }({{\xi }_{1}})$. В этом случае, полагая в уравнениях (4.2), (4.4) ${{\bar {\gamma }}^{{(m)}}} = 0$, получим систему уравнений для нахождения поправок функций  ${{\bar {c}}^{{(m)}}}$ и ${{\bar {k}}^{{(т)}}}$. Из-за того, что значение ядра при поправке ${{\bar {k}}^{{(т)}}}$ значительно больше, чем при ${{\bar {c}}^{{(m)}}}$, применен, как и в ходе первой серии экспериментов, поэтапный процесс идентификации теплофизических характеристик. На первом этапе для всех итераций полагая ${{\bar {c}}^{{(m)}}} = 0$, находим поправки ${{\bar {k}}^{{(т)}}}$ из решения интегрального уравнения (5.1). На втором этапе, полагая ${{\bar {k}}^{{(т)}}} = 0$, на каждой последующей итерации определяются поправки ${{\bar {c}}^{{(m)}}}$ как решение интегрального уравнения, полученного путем обращения уравнения в трансформантах (4.2) при ${{\bar {\gamma }}^{{(m)}}} = {{\bar {k}}^{{(m)}}} = 0$:

(5.3)
$\int\limits_{{{\xi }_{0}}}^1 {{{{\bar {c}}}^{{(m)}}}{{M}_{3}}({{\xi }_{1}},\tau )} {{\xi }_{1}}d{{\xi }_{1}} = {{r}_{0}}{{\omega }_{0}}({{g}_{0}}(\tau ) - d_{0}^{{(m - 1)}}(1,\tau ));\quad \tau \in [c,d],$
где ядро уравнения (5.3) имеет вид:

${{M}_{3}}({{\xi }_{1}},\tau ) = \int\limits_0^\tau {\frac{{\partial d_{0}^{{(m - 1)}}({{\xi }_{1}},{{\tau }_{1}})}}{{\partial {{\tau }_{1}}}}\frac{{\partial d_{0}^{{(m - 1)}}({{\xi }_{1}},\tau - {{\tau }_{1}})}}{{\partial {{\tau }_{1}}}}} d{{\tau }_{1}}$

Исходя из характера изменения дополнительной информации, был найден наиболее информативный временной отрезок для ее съема. В работе входная информация измерялось на временном отрезке $[c,d] = [0.1,0.8]$ в 8 равноотстоящих точках. При этом погрешность восстановления монотонных функций при отсутствии зашумления входной информации не превышала 8%. Наибольшая погрешность реконструкции функций $\bar {\gamma }({{\xi }_{1}})$ и $\bar {c}({{\xi }_{1}})$ возникала в окрестности $\xi = {{\xi }_{0}}$, что связано с особенностью ядер интегральных уравнений (5.2), (5.3). Они обращаются в нуль при $\xi = {{\xi }_{0}}$ в соответствии с граничным условием (2.5).

В ходе вычислительных экспериментов выяснено, что погрешность реконструкции теплофизических характеристик возрастает с увеличением величины зашумления $\alpha $. Так, зашумление входной информации $f(\tau )$ в 2% приводит к увеличению максимальной погрешности реконструкции монотонных функций до 17%. Выяснено влияние параметра термомеханической связанности ${{\delta }_{0}}$ на результаты реконструкции теплофизических характеристик. Реконструкция коэффициента теплопроводности и удельной теплоемкости оказалась успешной при любом значении параметра связанности $0.01 \leqslant {{\delta }_{0}} \leqslant 0.5$. В то же время реконструкция коэффициента температурного напряжения оказалась возможна только при параметре связанности ${{\delta }_{0}} \geqslant 0.16$.

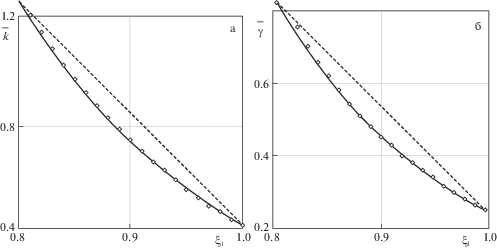
На рисунках ниже сплошной линией показан точный закон, штриховой линией – начальное приближение, точками – восстановленный закон.

На рис. 2 представлены результаты реконструкции убывающих функций $\bar {k}({{\xi }_{1}}) = 80{{e}^{{ - 5.2{{\xi }_{1}}}}}$ (рис. 2а) и $\bar {\gamma }({{\xi }_{1}}) = 100{{e}^{{ - 6.1{{\xi }_{1}}}}}$ (рис. 2б). Начальные приближения: ${{\bar {k}}^{{(0)}}}({{\xi }_{1}}) = - 4.05{{\xi }_{1}}$ + 4.49, ${{\bar {\gamma }}^{{(0)}}}({{\xi }_{1}}) = - 2.87{{\xi }_{1}}$ + 3.12. При отсутствии зашумления входной информации максимальная погрешность реконструкции $\bar {k}({{\xi }_{1}})$ не превысила 2%, а $\bar {\gamma }({{\xi }_{1}})$ – 7%.

Рис. 2.

Результат реконструкции функций: $\bar {k}({{\xi }_{1}}) = 80{{e}^{{ - 5.2{{\xi }_{1}}}}}$ (а), $\bar {\gamma }({{\xi }_{1}}) = 100{{e}^{{ - 6.1{{\xi }_{1}}}}}$ (б).

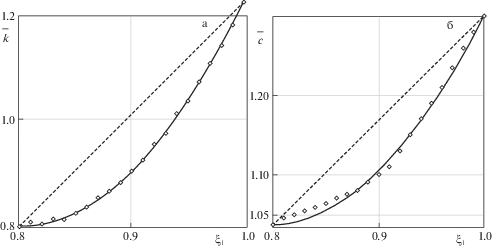
На рис. 3 представлены результаты реконструкции возрастающих функций $\bar {k}({{\xi }_{1}}) = - 9.3\xi _{1}^{2} + 14.8{{\xi }_{1}}$ – 3.18 (рис. 3а) и $\bar {c}({{\xi }_{1}}) = 6.4\xi _{1}^{2} - 10.2{{\xi }_{1}}$ + 5.1 (рис. 3б). Начальные приближения: ${{\bar {k}}^{{(0)}}}({{\xi }_{1}}) = 2.2{{\xi }_{1}}$ – 0.97, ${{\bar {c}}^{{(0)}}}({{\xi }_{1}}) = 1.32{{\xi }_{1}}$ – 0.02. При отсутствии зашумления входной информации погрешность реконструкции $\bar {k}({{\xi }_{1}})$ не превысила 3%, а $\bar {c}({{\xi }_{1}})$ – 8%.

Рис. 3.

Результат реконструкции функций: $\bar {k}({{\xi }_{1}}) = - 9.3\xi _{1}^{2} + 14.8{{\xi }_{1}}$ – 3.18 (а); $\bar {c}({{\xi }_{1}}) = 6.4\xi _{1}^{2} - 10.2{{\xi }_{1}}$ + 5.1 (б).

Заключение. Приведена постановка КОЗ об идентификации термомеханических характеристик для конечного неоднородного в радиальном направлении цилиндра на конечном временном интервале при граничных условиях в виде скользящей заделки и теплоизоляции на торцах. Решение нелинейной КОЗ построено на основе итерационного процесса, на каждом шаге которого решается линеаризованное интегральное уравнение Фредгольма 1-го рода. Вычислительные эксперименты показали, что монотонные законы изменения теплофизических характеристик восстанавливаются с погрешностью, не превышающей 8%.

Работа выполнена при поддержке гранта Правительства РФ № 075-15-2019-1928 и Южного математического института – филиала ВНЦ РАН, г. Владикавказ.

Список литературы

  1. Birman V., Byrd L.W. Modeling and analysis of functionally graded materials and structures // Appl. Mech. Rev. 2007. V. 60. P. 195–216.

  2. Wetherhold R.C., Seelman S., Wang J. The use of functionally graded materials to eliminated or control thermal deformation // Compos. Sci. Tech. 1996. № 56. P. 1099–1104.

  3. Chen W.L., Chou H.M., Yang Y.C. An inverse problem in estimating the space – dependent thermal conductivity of a functionally graded hollow cylinder // Composites: Pt. B. 2013. V. 50. P. 112–119.

  4. Nedin R., Nesterov S., Vatulyan A. On reconstruction of thermalphysic characteristics of functionally graded hollow cylinder // Appl. Math. Model. 2016. V. 40. Iss. 4. P. 271–279.

  5. Geymonat G., Pagano S. Identification of mechanical properties by displacement field measurement: a variational approach // Meccanica. 2003. V. 38. P. 535–545.

  6. Avril S., Pierron F. General framework for the identification of constitutive parameters from full-field measurements in linear elasticity // Int. J. Solids Struct. 2007. V. 44. P. 4978–5002.

  7. Vatulyan A.O., Dudarev V.V., Mnukhin R.M., Nedin R.D. Identification of the Lamé parameters of an inhomogeneous pipe based on the displacement field data // Europ. J. Mech. A/Solids. 2020. V. 81. https://doi.org/10.1016/j.euromechsol.2019.103939

  8. Vatulyan A.O., Bogachev I.V., Nedin R.D., Yavruyan O.V. Identification of inhomogeneous elastic properties of isotropic cylinder // ZAMM J. Appl. Math. Mech. / Zeitschrift fur Angewandte Mathematik und Mechanik. 2016. V. 97(3). P. 358–364.

  9. Dudarev V.V., Vatulyan A.O., Mnukhin R.M., Nedin R.D. Concerning an approach to identifying the Lame parameters of an elastic functionally graded cylinder // Math. Meth. Appl. Sci. 2020. P. 1–10. https://doi.org/10.1002/mma.6428

  10. Алифанов О.М., Артюхин Е.А., Румянцев С.В. Экстремальные методы решения некорректных задач. М.: Наука, 1988. 288 с.

  11. Hao D.N. Methods for Inverse Heat Conduction Problems. Frankfurt/Main: Peter Lang, 1998. 249 p.

  12. Kabanikhin S.I., Hasanov A., Penenko A.V. A gradient descent method for solving an inverse coefficient heat conduction problem // Num. Anal. Appl. 2008. № 1. P. 34–45.

  13. Raudensky M., Woodbary K.A., Kral J. Genetic algorithm in solution of inverse heat conduction problems // Num. Heat Transfer. Pt. B: Fundamentals. 1995. V. 28. P. 293–306.

  14. Ломазов В.А. Задачи диагностики неоднородных термоупругих сред. Орел: Из-во ОрелГТУ, 2002. 168 с.

  15. Lukasievicz S.A., Babaei R., Qian R.E. Detection of material properties in a layered body by means of thermal effect // J. Thermal Stresses. 2003. V. 26. № 1. P. 13–23.

  16. Ватульян А.О., Нестеров С.А. Коэффициентные обратные задачи термомеханики. Ростов-на-Дону; Таганрог: Изд-во Южного федерального университета, 2019. 146 с.

  17. Vatulyan A.O., Nesterov S.A. About the specifics of identification thermomechanical characteristics of functionally graded hollow cylinder // Mater. Phys.&Mech. 2015. V. 23. P. 71–75.

  18. Ватульян А.О., Нестеров С.А. К определению неоднородных термомеханических характеристик трубы // Инж.-физ. ж. 2015. Т. 88. № 4. С. 951–959.

  19. Ватульян А.О., Нестеров С.А. Об особенностях идентификации неоднородного предварительно напряженного состояния в термоупругих телах // ПММ. 2017. Т. 81. Вып. 1. С. 103–110.

  20. Vatulyan A.O., Nesterov S.A. On some features of identification of inhomogeneous prestressed state of thermoelastic hollow cylinder with coating // Mater. Phys.&Mech. 2019. V. 42. P. 54–64.

  21. Ватульян А.О., Нестеров С.А. О задаче идентификации термомеханических характеристик конечного функционально-градиентного цилиндра // Изв. Саратовского ун-та. Сер. Математика. Механика. Информатика. 2021. Т. 21. Вып. 1. С. 35–47.

  22. Новацкий В. Динамические задачи термоупругости. М.: Мир, 1970. 256 с.

  23. Vatulyan A., Nesterov S., Nedin R. Regarding some thermoelastic models of “coating-substrate” system deformation // Continuum Mech. Thermodyn. 2020. V. 32. P. 1173–1186.

  24. Reddy J.N. Analysis of functionally graded plates // Int. J. Num. Meth. Eng. 2000. V. 47(1–3). P. 663–684.

  25. Крылов В.И., Скобля Н.С. Методы приближенного преобразования Фурье и обращения преобразования Лапласа. М.: Наука, 1974. 224 с.

  26. Тихонов А.Н., Гончарский А.В., Степанов В.В., Ягола А.Г. Численные методы решения некорректных задач. М.: Наука, 1990. 230 с.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал