Прикладная математика и механика, 2021, T. 85, № 4, стр. 528-543

1. Введение. Описание свойств движения на поверхности небесных тел является важной и сложной задачей. Как было замечено ранее (см., например, [1–5]), среди многочисленных факторов, важных для описания такой динамики, следует выделить не только неоднородность поля притяжения, имеющую место из-за нерегулярности их формы и распределения масс, но и сопоставимость по величине сил притяжения и центробежных сил, обусловленных достаточно быстрым вращением изучаемых тел. Так, в частности, на поверхности тела могут существовать области, в которых незакрепленная частица не может оставаться в покое несмотря на наличие трения (аналоги крутых склонов гор). Такие области и их зависимость от параметров могут быть изучены с использованием общих методов исследования существования и бифуркаций неизолированных равновесий в системах с сухим трением, развитых в работах [6–11] и опробованных ранее на ряде механических систем [12–14].

В настоящей работе, как и в [15], рассматривается тело, простейшее по форме и распределению масс – однородный шар. Предполагается, что в шаре имеется сферическая полость, центр которой, вообще говоря, не совпадает с центром шара. Наличием такой полости обусловлена нецентральность порождаемого телом поля притяжения. Такое тело может как равномерно вращаться вокруг одной из своих центральных осей инерции, так и совершать прецессионное движение. Изучаемое тело представляет собой особенный случай гантелеобразного тела, являющегося удобной моделью для исследования движения в поле притяжения тел с нерегулярным распределением масс. Различные свойства таких движений в отсутствие контакта с поверхностью тела, в частности, точки либрации, были исследованы в [16–18].

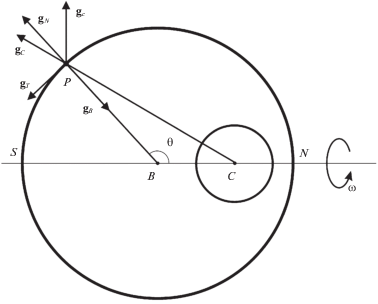
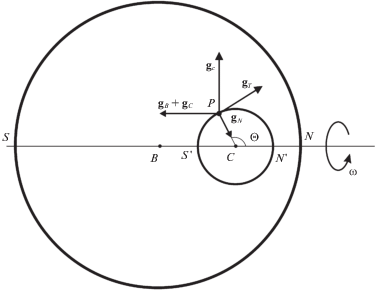
2. Постановка задачи. Рассмотрим твердое тело $\mathcal{A}$, получающееся изъятием содержимого сферической полости $\mathcal{C}$ с центром $C$ радиуса ${{r}_{C}}$ из однородного шара $\mathcal{B}$ с центром $B$ радиуса ${{r}_{B}}.$ Предположим, что тело $\mathcal{A}$ совершает вращение вокруг своей оси симметрии с постоянной угловой скоростью ω, а по поверхности $\partial{ \mathcal{A}}$ тела $\mathcal{A}$ движется частичка P. Ее движение осуществляется под действием силы притяжения со стороны тела $\mathcal{A}$, а также реакции со стороны поверхности тела, имеющей нормальную составляющую, препятствующую проникновению под поверхность тела, и касательную составляющую, представленную силой сухого трения. В дальнейшем считается, что частичка пренебрежимо мала по сравнению с телом, и она не оказывает влияния на его движение.

Введем правую систему отсчета $B{{x}_{1}}{{x}_{2}}{{x}_{3}}$ с началом в точке B, ось $B{{x}_{3}}$ которой совпадает с осью вращения. Поскольку нас интересуют прежде всего относительные равновесия точки P на поверхности вращающегося тела, а тело динамически и геометрически симметрично, то достаточно изучить положения относительного равновесия в любом из осевых сечений тела, например, в сечении плоскостью $B{{x}_{3}}{{x}_{1}}$.

Для описания положения частички в этой плоскости введем угол θ (см. рис. 1). Тогда, если $\left| {{\mathbf{CB}}} \right| = d$, то $\left| {{\mathbf{CP}}} \right| = {{\left( {r_{B}^{2} - 2{{r}_{B}}d\cos \theta + {{d}^{2}}} \right)}^{{1/2}}}$. Единичная внешняя нормаль и расположенная в рассматриваемой плоскости касательная к поверхности задаются как

соответственно. Кроме того,

Точки внешней поверхности тела, наименее и наиболее удаленные от полости, для удобства описания назовем полюсами и обозначим $N$ и $S$. Им отвечают углы ${{\theta }} = 0$ и ${{\theta }} = {{\pi }}$ соответственно. Также для удобства будем называть северным и южным полушариями части тела, прилегающие к точкам N и S соответственно. Будем считать, что центр полости располагается в северном полушарии. Тогда в случае касания полости и внешней поверхности тела такое касание происходит в точке N.

Точка P находится в относительном равновесии под действием нескольких сил. Среди них, во-первых, сила притяжения со стороны тела $\mathcal{A}$ напряженностью

Здесь и далее ${{g}_{X}}$ – величина напряженности поля притяжения на поверхности шара $X \in \left\{ {B,C} \right\}$:

Во-вторых, среди них – центробежная сила напряженностью

В-третьих, это реакция связи, нормальная и касательная составляющие которой, отнесенные к массе точки, имеют вид

Уравнения относительного равновесия в проекциях на нормаль и на касательную в точке P, соответственно, имеют вид

Далее будем изучать условие существования относительных равновесий, в данном случае имеющее вид

после подстановки выражений для ${{g}_{N}}$ и ${{g}_{T}}$ принимающее вид

После подстановки в (2.2) соотношений (2.1), введения обозначения

и преобразований это неравенство может быть представлено в виде

Знак функции ${{f}_{N}}$ определяет направление нормальной реакции: если ${{f}_{N}} > 0$, то нормальная реакция направлена вовне тела $\mathcal{A}$. Если это условие не выполнено, то возможные решения неравенства (2.3) согласно постановке задачи не имеют физического смысла. Однако в работе неравенство (2.3) будет рассматриваться в целом, а решения, на которых не выполнено указанное условие, будут выделяться и отбрасываться по мере появления.

3. Равновесия на внешней поверхности. Прежде всего исследуем зависимость областей, заполненных равновесиями, от коэффициента трения и от размеров и положения полости.

3.1. Зависимость равновесий от коэффициента трения. Неотрицательная функция $f = f\left( {{\theta }} \right) = {{f}_{T}}{\text{/}}{{f}_{N}}$ непрерывна на своем периоде и достигает на нем своего максимального значения ${{{{\mu }}}_{*}}$. Тогда, если ${{\mu }} \geqslant {{{{\mu }}}_{*}}$, то поверхность целиком заполнена равновесиями. Если ${{\mu }} < {{{{\mu }}}_{*}}$, то на поверхности имеются области, где равновесий нет. Эти области образуют кольцо, разделяющее приполярные области, заполненные равновесиями. Заметим, что приполярная область, прилегающая к северному полюсу N при любом значении d ýже приполярной области, прилегающей к южному полюсу S. При этом, если

то примыкающая к южному полюсу область содержит все южное полушарие и даже простирается в северное полушарие.

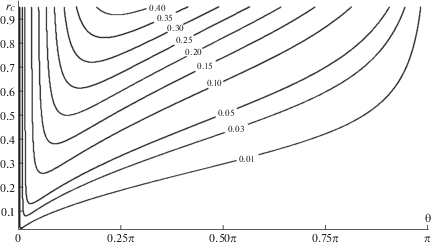
Кроме того, функция  f  также зависит от геометрических параметров ${{r}_{B}}$, ${{r}_{C}}$, $d$, а также от ${{\Omega }}$. Положим в дальнейшем ${{r}_{B}} = 1$ и изобразим на рис. 2 график функции $f\left( {{\theta }} \right)$ при ${{r}_{C}} = 0.25$ и различных значениях параметра d. В рассматриваемом случае полость относительно невелика по сравнению с размерами тела, и критические значения ${{{{\mu }}}_{*}}$ коэффициента трения, при котором образуются области, не содержащие равновесий, весьма малы и отвечают, например, скольжению металла по льду (${{\mu }} \approx 0.02$, см. например, [19]). В то же время, как показывают вычисления, для полостей больших размеров критическое значение коэффициента трения увеличивается и отвечает, например, скольжению резины по льду ${{\mu }} \approx 0.3$ (см., например, [20]) или по дороге ${{\mu }} \approx 0.4{\kern 1pt} - {\kern 1pt} 0.6$ (см., например, [19]).

3.2. Зависимость равновесий от размера полости. При исследовании множеств положений равновесия при различных значениях коэффициента трения ограничимся рассмотрением случая, когда полость касается внешней поверхности тела. В этом случае ${{r}_{C}} + d = 1$. Исследование множеств точек $f\left( {{{\theta }},{{r}_{C}}} \right) = {{\mu }}$ при различных значениях параметра $\mu $ показывает (см. рис. 3), что для каждого значения ${{\mu }}$ имеется минимальное значение ${{r}_{{C*}}}$ такое, что при ${{r}_{C}} \leqslant {{r}_{{C*}}}$ равновесия занимают всю внешнюю поверхность тела. При ${{r}_{C}} > {{r}_{{C*}}}$ область, заполненная равновесиями, распадается на две приполярных области. Заметим, что критическое значение ${{r}_{{C*}}}$ возрастает с ростом коэффициента трения. Также заметим, что приполярная область, прилегающая к северному полюсу N при исследованных значениях μ, ýже приполярной области, прилегающей к южному полюсу $S$.

Замечание. Из соотношения (2.3), в котором взят знак равенства, нетрудно выразить зависимость ${{r}_{C}}$ от остальных параметров задачи. Однако определение с помощью этой зависимости критического значения ${{r}_{{C*}}}$ оказывается задачей, не поддающейся аналитическому решению даже в случае, когда ${{\mu }} = 0$. Этим обусловлено применение численного счета для изучения такой, на первый взгляд – несложной, зависимости, в частности, при построении рис. 3.

4. Относительные равновесия на внешней поверхности: случай касания полости и внешней поверхности. В данном разделе изучается зависимость области, заполненной относительными равновесиями (ОЗОР), на внешней поверхности равномерно вращающегося тела от величины угловой скорости Ω. В примерах, для которых построены бифуркационные диаграммы, предполагается, что радиус внешней поверхности ${{r}_{B}} = 1$, а коэффициент трения ${{\mu }} = 0.05$.

Прежде всего, исследуем соотношение (2.3), рассматривая его как неравенство относительно $\Omega $ и переписав в виде (ср. [21])

Имеем

и неравенство (4.1) представимо в виде

Иными словами,

при ${{H}_{*}} > 0$ и при ${{H}_{*}} < 0$.

Эти неравенства определяют на полуполосе $\left\{ {{{\Omega }} \geqslant 0} \right\} \times \left\{ {0 \leqslant {{\theta }} \leqslant {{\pi }}} \right\}$ область, которую в дальнейшем будем называть бифуркационной диаграммой. В дальнейшем ограничимся рассмотрением случая, когда ${{\Omega }} \geqslant 0$. Кроме того, будем выделять случай ${{f}_{N}} < 0$ как физически нереализуемый. Предметом исследования будет зависимость ОЗОР, обозначаемой E, от величины угловой скорости Ω и геометрических параметров задачи.

Замечание. Особо выделим случай отсутствия трения (${{\mu }} = 0$, иначе говоря, “ледяной шар с полостью”). Несмотря на то, что аналитическое исследование зависимости решений от параметров, вообще говоря, затруднено, через них и переменную θ можно выразить величину Ω. Соответствующие этой зависимости кривые изображены штрих-пунктирными линиями на бифуркационных диаграммах рис. 4, 5 и 7. Эти линии являются “скелетными” для ОЗОР при отличных от нуля значениях коэффициента трения.

В качестве примеров прежде всего рассмотрим такие диаграммы на множестве тел, полость в которых касается их внешней поверхности.

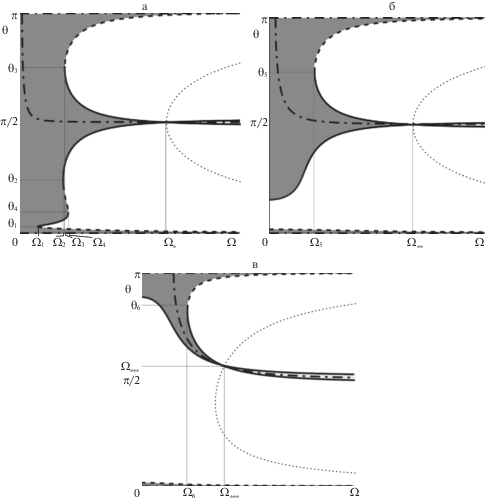
4.1. Случай a). Прежде всего рассмотрим случай, когда ${{r}_{C}} = 0.125$, которому отвечает рис. 4а. Здесь $\left( {{{{{\Omega }}}_{1}},{{{{\theta }}}_{1}}} \right)$ = (0.225, 0.103), $\left( {{{{{\Omega }}}_{2}},{{{{\theta }}}_{2}}} \right)$ = (0.312, 0.705), $\left( {{{{{\Omega }}}_{3}},{{{{\theta }}}_{3}}} \right)$ = (0.334, 2.365), $\left( {{{{{\Omega }}}_{4}},{{{{\theta }}}_{4}}} \right)$ = (0.341, 0.292), $({{{{\Omega }}}_{*}},{{{{\theta }}}_{*}})$ = (0.9995, 1.572). Если ${{\Omega }} = 0$, то область E совпадает со всей сферой: $E = {{S}^{2}}$. Это свойство остается выполненным при ${{\Omega }} < {{{{\Omega }}}_{1}}$ (см. рис. 4a). При ${{\Omega }} = {{{{\Omega }}}_{1}}$ происходит расщепление области $E$: ${{S}^{2}} \to {{D}_{S}} \cup {{D}_{N}}$, где ${{D}_{S}}$ и ${{D}_{N}}$ – диски, примыкающие, соответственно, к южному и северному полюсам. При изменении Ω между ${{{{\Omega }}}_{1}}$ и ${{{{\Omega }}}_{2}}$ топология области E не меняется. При ${{\Omega }} = {{{{\Omega }}}_{2}}$ происходит расщепление диска ${{D}_{S}}$: ${{D}_{S}} \to D_{S}^{'} \cup {{R}_{N}}$, т.е. от него отделяется кольцо ${{R}_{N}}$, расположенное в северном полушарии. При ${{\Omega }} \in \left( {{{{{\Omega }}}_{2}},{{{{\Omega }}}_{3}}} \right)$ топология изучаемых областей остается неизменной, в то время как при ${{\Omega }} = {{{{\Omega }}}_{3}}$ диск $D_{S}^{'}$ также претерпевает деление: $D_{S}^{'} \to D_{S}^{{''}} \cup {{R}_{e}}$, т.е. от него тоже отделяется кольцо ${{R}_{e}}$, прилегающее к экватору тела. Такая топология остается неизменной при ${{\Omega }} \in \left( {{{{{\Omega }}}_{3}},{{{{\Omega }}}_{4}}} \right)$, затем при ${{\Omega }} = {{{{\Omega }}}_{4}}$ кольцо ${{R}_{N}}$ стягивается в окружность и исчезает при ${{\Omega }} > {{{{\Omega }}}_{4}}$. Кольцо ${{R}_{e}}$ сохраняется до значения ${{\Omega }} = {{{{\Omega }}}_{*}}$, при котором на относительных равновесиях из этого кольца обращается в нуль нормальная реакция. Порожденное этим кольцом семейство решений при ${{\Omega }} > {{{{\Omega }}}_{*}}$ отвечает отрицательным значениям нормальной реакции и в дальнейшем не рассматривается, как не имеющее физического смысла. В противоположность физически осмысленным относительным равновесиям, изображенным на рис. 4 темно-серым цветом, эти равновесия изображены светло-серым цветом. Здесь и далее на рисунках точечная кривая отделяет области положительной и отрицательной нормальной реакции.

В дальнейшем, с увеличением ${{\Omega }} > {{{{\Omega }}}_{4}}$ южная приполярная область $D_{S}^{{''}}$ уменьшается в размерах, стягиваясь к южному полюсу. Северная приполярная область ${{D}_{N}}$ стягивается к северному полюсу: она уменьшается в размерах с увеличением Ω, начиная со своего выделения при ${{\Omega }} = {{{{\Omega }}}_{1}}$.

4.2. Случай б). Теперь рассмотрим случай $r = 0.25$, которому отвечает рис. 4б. На нем $\left( {{{{{\Omega }}}_{5}},{{{{\theta }}}_{5}}} \right)$ = (0.314, 2.347), $({{{{\Omega }}}_{{*{\kern 1pt} *}}},{{{{\theta }}}_{{*{\kern 1pt} *}}})$ = (0.996, 1.577). При ${{\Omega }} = 0$ область E сразу разделена на диски ${{D}_{S}}$ и ${{D}_{N}}$, примыкающие, соответственно, к южному и северному полюсам: $E = {{D}_{S}} \cup {{D}_{N}}$. Такая же топология области E сохраняется при ${{\Omega }} < {{{{\Omega }}}_{5}}$ (см. рис. 4б). При ${{\Omega }} = {{{{\Omega }}}_{5}}$ диск ${{D}_{S}}$ расщепляется на прилегающий к южному полюсу диск $D_{S}^{'}$ и прилегающее к экватору кольцо ${{R}_{e}}$: ${{D}_{S}} \to D_{S}^{'} \cup {{R}_{e}}$. При ${{\Omega }} \in ({{{{\Omega }}}_{5}},{{{{\Omega }}}_{{*{\kern 1pt} *}}})$ топология области E остается неизменной. При ${{\Omega }} = {{{{\Omega }}}_{{*{\kern 1pt} *}}}$ кольцо ${{R}_{e}}$ стягивается в окружность, и на отвечающих ему решениях нормальная реакция обращается в нуль. Это множество решений продолжается и для ${{\Omega }} > {{{{\Omega }}}_{{*{\kern 1pt} *}}}$, но для решений из этого множества нормальная реакция отрицательна, и такие решения в дальнейшем не рассматриваются, как не имеющие физического смысла. С увеличением ${{\Omega }} > {{{{\Omega }}}_{5}}$ южная приполярная область $D_{S}^{'}$ уменьшается в размерах, стягиваясь к южному полюсу. Северная приполярная область ${{D}_{N}}$ стягивается к северному полюсу: она уменьшается в размерах с увеличением ${{\Omega }}$, начиная со значения ${{\Omega }} = 0$.

Замечание. В случае, когда $r$ велико, естественно было ожидать какие-либо отличия в характере бифуркаций от рассмотренных выше случаев. Однако исследование случая $r = 0.9$ показало, что в этом случае топологические перестройки области $E$ совпадают с перестройками в случае b). При этом при ${{\Omega }} = 0$ оба диска ${{D}_{S}}$ и ${{D}_{N}}$, образующих множество E весьма малы, причем более крупный диск ${{D}_{S}}$ целиком располагается в южном полушарии. В отличие от предыдущего случая, при возрастании ${{\Omega }}$ от нуля до ${{{{\Omega }}}_{6}}$ область ${{D}_{S}}$ не убывает, а возрастает (см. рис. 4в).

Замечание. Применение в исследовании численных методов не дает возможности сделать вывод о том, что описаны все возможные типы бифуркаций. В этом плане на выполняемые исследования целесообразно смотреть как на описание уже выявленных перестроек ОЗОР при наличии осевой симметрии. Отказ от такой симметрии как правило делает картину бифуркаций куда более разнообразной (ср. [13]).

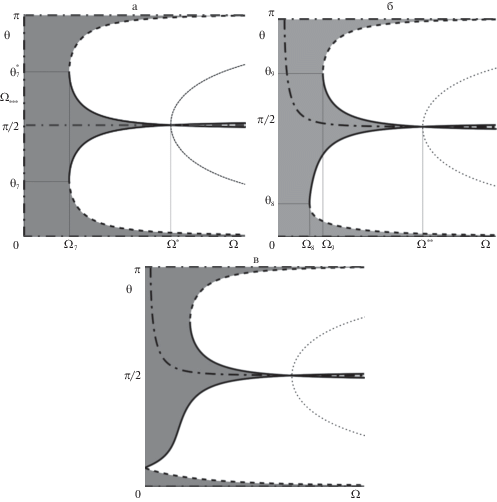
5. Относительные равновесия на внешней поверхности: полость целиком внутри тела. Теперь исследуем зависимость области E от расположения полости. Бифуркационные диаграммы для случаев радиуса полости ${{r}_{C}} = 0.25$ и расстояния между центром сферы и центром полости $d = 0$, $d = 0.6$ и $d = 0.6725$ при ${{\mu }} = 0.05$ показаны на рис. 5a–в, где $\left( {{{{{\Omega }}}_{7}},{{{{\theta }}}_{7}}} \right)$ = (0.355, 0.77), $({{{{\Omega }}}_{7}},{{\theta }}_{7}^{*})$ = (0.355, 2.308), $\left( {{{\Omega *}},{{\theta *}}} \right)$ = $\left( {1,\pi {\text{/2}}} \right)$, $\left( {{{{{\Omega }}}_{8}},{{{{\theta }}}_{8}}} \right)$ = (0.222, 0.508), $\left( {{{{{\Omega }}}_{9}},{{{{\theta }}}_{9}}} \right)$ = (0.313, 2.343), $\left( {{{\Omega *}}{\kern 1pt} {\text{*}},{{\theta *}}{\kern 1pt} {\text{*}}} \right)$ = (0.995, 1.577). В случае $d = 0$, то есть если центр полости совпадает с центром сферы, гравитационное поле однородно. Тогда бифуркационная диаграмма симметрична относительно прямой ${{\theta }} = {{\pi /2}}$, как и в случае шара без полости (см. [15]) (рис. 5a). При ${{\Omega }} < {{{{\Omega }}}_{7}}$ множество E покрывает всю внешнюю поверхность. При ${{\Omega }} = {{{{\Omega }}}_{7}}$ оно расщепляется сразу в двух точках на прилегающее к экватору кольцо ${{R}_{e}}$ и приполярные области ${{D}_{S}}$ и ${{D}_{N}}$. Приполярные области существуют при ${{\Omega }} > {{{{\Omega }}}_{7}}$. Они стягиваются к полюсам при ${{\Omega }} \to \infty $. Кольцевая область ${{R}_{e}}$ при ${{\Omega }} \to {{\Omega *}}$ стягивается в окружность, заполненную равновесиями, отвечающими нулевым значениям нормальной реакции. При ${{\Omega }} > {{\Omega *}}$ она вновь переходит в кольцо, заполненное решениями, отвечающими отрицательным значениям реакции, т.е. не имеющими физического смысла в рамках принятой постановки задачи.

При $d \ne 0$ диаграмма перестает быть симметричной. Так, при $0 < d < {{d}_{1}}$ (рис. 5б) можно указать значения ${{{{\Omega }}}_{8}}$ и ${{{{\Omega }}}_{9}}$ бифуркационного параметра, такие, что при ${{\Omega }} < {{{{\Omega }}}_{8}}$ множество E покрывает всю внешнюю поверхность. При ${{\Omega }} = {{{{\Omega }}}_{8}}$ область E расщепляется на приполярные области ${{D}_{S}}$ и ${{D}_{N}}$, существующие при ${{\Omega }}$: ${{{{\Omega }}}_{8}} < {{\Omega }} < {{{{\Omega }}}_{9}}$. При ${{\Omega }} = {{{{\Omega }}}_{9}}$ расщепляется область ${{D}_{S}}$: из нее выделяется экваториальное кольцо ${{R}_{e}}$. С дальнейшим ростом ${{\Omega }}$, как и в предыдущем случае, приполярные области стягиваются к полюсам, а кольцевая область ${{R}_{e}}$ при ${{\Omega }} \to {{\Omega *}}{\kern 1pt} {\text{*}}$ стягивается в окружность, заполненную равновесиями, отвечающими нулевым значениям нормальной реакции. При ${{\Omega }} > {{\Omega *}}{\kern 1pt} {\text{*}}$, как и в предыдущем случае, решениям из данного семейства отвечают равновесия, не обладающие физическим смыслом.

Если величина $d$ достигает некоторого критического значения $d = d{\kern 1pt} *$, то ${{{{\Omega }}}_{8}}$ из предыдущего рассуждения обращается в нуль (рис. 5в). При $d > d{\kern 1pt} *$ множество E изначально разделено на приполярные области ${{D}_{S}}$ и ${{D}_{N}}$, характер изменений которых с неограниченным увеличением ${{\Omega }}$ описан выше (рис. 4б).

6. Относительные равновесия на поверхности полости. Как известно из основ теории притяжения (см., например, [22], задача О-130), сила притяжения со стороны тела $\mathcal{A}$ внутри полости имеет напряженность

Иными словами, внутри полости поле сил притяжения постоянно и однородно. В этом случае с учетом симметрии относительно поворота вокруг диаметра $SN$ решение задачи об относительных равновесиях сводится к решению задачи об относительных равновесиях бусинки на круглом обруче, равномерно вращающемся вокруг своего вертикального диаметра. Эта задача была рассмотрена ранее ([23]), поэтому ограничимся тем, что воспроизведем коротко в используемых обозначениях аргументы из этой работы и построенные ранее бифуркационные диаграммы.

Пусть $d = 0$, и поле притяжения внутри полости отсутствует. Тогда внутренняя часть полости заполнена равновесиями, а на границах относительные равновесия определяются неравенством, которое после преобразований сводится к виду см. рис. 6.

При ${{\Omega }} = 0$ это неравенство выполнено всюду, и поверхность полости целиком заполнена равновесиями. При ${{\Omega }} \ne 0$ для любого значения коэффициента трения у неравенства имеются решения ${{\Theta }} = 0$ и ${{\Theta }} = {{\pi }}$, отвечающие, соответственно, полюсам полости $N{\kern 1pt} '$ и $S{\kern 1pt} '$, расположенным на оси симметрии тела. Также при любом ${{\Omega }} \ne 0$ имеются относительные равновесия, на которых $\left| {\Theta - \frac{\pi }{2}} \right| \leqslant \alpha $, где $\alpha = \operatorname{arctg} \mu $ – угол трения. Эти относительные равновесия, существование которых обеспечивается центробежной силой, располагаются в симметричном поясе вдоль экватора полости.

Пусть теперь $d \ne 0$. Вводя безразмерный параметр

представим уравнения относительного равновесия в проекциях на нормаль и на касательную в точке $P$, соответственно, в виде

Определяющее условие покоя неравенство (2.2) после преобразований записывается как

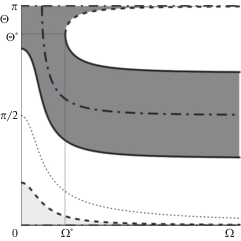
Если безразмерная угловая скорость ${{\hat {\Omega }}}$ равна нулю, то существует заполненная равновесиями приполярная область ${{{{\Delta }}}_{S}}$, примыкающая к полюсу $S{\kern 1pt} '$. Этот диск заполнен равновесиями, для которых $\pi - \alpha < \left| \Theta \right| \leqslant \pi $, где $\alpha $ – угол трения. С возрастанием ${{\hat {\Omega }}}$ до значения ${{\hat {\Omega }*}}$ (см. [23]) диск ${{\Delta }_{S}}$ становится шире, и при ${{\hat {\Omega }}} = {{\hat {\Omega }*}}$, которому отвечает значение ${{\Theta }} = {{{{\Theta }}}_{*}}$, разделяется на диск $\Delta _{S}^{'}\left( {\hat {\Omega }} \right)$, примыкающий к полюсу $S{\kern 1pt} '$, и на кольцевую область $R\left( {{{\hat {\Omega }}}} \right)$. При ${{\hat {\Omega }}} \to \infty $ приполярная область $\Delta _{S}^{'}\left( {\hat {\Omega }} \right)$ стягивается к полюсу $S{\kern 1pt} '$, а кольцевая область $R\left( {{{\hat {\Omega }}}} \right)$ стремится к предельному положению $R\left( \infty \right)$, для которого $\left| {\Theta - \frac{\pi }{2}} \right| \leqslant \alpha $.

Рис. 7 построен для ${{\mu }} = 0.7$. Для него ${{\Theta *}} = 2.723$, ${{\hat {\Omega }*}} = 2.188$ (ср. [23]). Область, заполненная механически осмысленными относительными равновесиями, на которых нормальная реакция направлена внутрь полости, отмечена темно-серым цветом. Область, отвечающая физически нереализуемым относительным равновесиям, на которых нормальная реакция направлена за пределы полости, обозначена светло-серым цветом.

7. Об устойчивости относительных равновесий. Устойчивость по Ляпунову относительных равновесий, расположенных внутри найденных областей, следует из результатов Г.К. Пожарицкого [24]. Можно, как и в [14], поставить вопрос об устойчивости связных компонент ОЗОР.

Будем считать связную компоненту устойчивой, если для каждой точки ее границы проекция суммы активных сил и центробежной силы на плоскость, касательную к поверхности в этой точке, направлена внутрь рассматриваемой связной компоненты ОЗОР. Это свойство можно трактовать следующим образом. Пусть в начальный момент точка P располагается в некоторой точке Q границы ОЗОР. “Отпустим” точку P без начальной скорости, “освободив” систему от трения, т.е. предположив, что коэффициент трения обратился в нуль. В случае устойчивости связной компоненты ОЗОР для всех точек Q ее границы точка P начнет движение внутрь этой компоненты или вдоль ее границы. Если найдется хотя бы одна точка Q границы рассматриваемой связной компоненты ОЗОР, для которой точка P начнет движение вовне этой компоненты, то речь идет о неустойчивости этой связной компоненты.

Замечание. В рассматриваемой задаче благодаря осевой симметрии это свойство достаточно проверить для любого меридионального сечения поверхности тела.

Введенное таким образом определение устойчивости проверяется путем анализа знака функции ${{f}_{T}}$ в точках границы ОЗОР. На бифуркационных диаграммах (рис. 4, 5, 7) точки границы ОЗОР, в которых упомянутая проекция суммы сил направлена вовне соответствующей связной компоненты ОЗОР, прорисованы пунктиром, в то время как точки границы ОЗОР, в которых эта проекция суммы сил направлена внутрь соответствующей связной компоненты ОЗОР, прорисованы сплошной линией.

Прокомментируем свойство устойчивости на примере случая a) из пункта (4.1). При выполнении условия $0 \leqslant {{\Omega }} < {{{{\Omega }}}_{1}}$ область $E$ состоит из единственной связной компоненты, совпадающей со всей сферой: $E = {{S}^{2}}$. Оно не имеет границ, т.е. устойчиво. При выполнении условия ${{{{\Omega }}}_{1}} < {{\Omega }} < {{{{\Omega }}}_{2}}$ область ${{D}_{S}}$ устойчива, а область ${{D}_{N}}$ неустойчива. При выполнении условия ${{{{\Omega }}}_{2}} < {{\Omega }} < {{{{\Omega }}}_{3}}$ область $D_{S}^{'}$ устойчива, а область ${{D}_{N}}$ неустойчива. Кольцевая область ${{R}_{N}}$ также неустойчива: условие устойчивости выполнено на одной ее границе и не выполнено на другой. При выполнении условия ${{\Omega }} > {{{{\Omega }}}_{3}}$ обе приполярные области $D_{S}^{{''}}$ и ${{D}_{N}}$ неустойчивы, равно как и кольцевая область ${{R}_{N}}$, существующая при ${{\Omega }} < {{{{\Omega }}}_{4}}$. При этом устойчивой оказывается приэкваториальная кольцевая область ${{R}_{e}}$, которая стягивается к окружности при ${{\Omega }} \to {{{{\Omega }}}_{*}}$. Наконец, при прохождении параметром ${{\Omega }}$ значения ${{{{\Omega }}}_{*}}$ нормальная реакция обращается в нуль. При ${{\Omega }} > {{{{\Omega }}}_{*}}$ устойчивых связных компонент ОЗОР больше нет – остаются только две неустойчивые приполярные области $D_{S}^{{''}}$ и ${{D}_{N}}$.

Замечание. В настоящей работе относительные равновесия рассмотрены в случае, когда тело вращается вокруг своей оси симметрии. Представляет интерес рассмотрение случая, когда тело совершает вращение вокруг оси инерции, перпендикулярной оси симметрии. В этом случае могут оказаться полезными результаты работы [25], в которой рассматривалось движение тяжелой бусинки по окружности, не совпадающей с ее вертикальным диаметром, а также работ [12, 14]. Особый интерес представляет случай, когда тело совершает прецессионные движения.

Замечание. Как любезно сообщил авторам рецензент, в работе [15] допущена ошибка: в конце 1980-х годов в рамках советского проекта освоения дальнего космоса “Фобос” были разработаны подвижные зонды ПРОП-ФП, изменяющие свое местоположение прыжками [26]. В.В. Белецкий, несомненно знавший о проекте таких зондов, совместно с О.П. Салимовой, вероятно, были первопроходцами, приступившими к систематическому изучению нелинейной динамики прыгающего космического аппарата [27, 28].

Данное исследование частично поддержано программой Президента Российской Федерации по федеральной поддержке молодых российских ученых, кандидатов наук (проект № МК-1712.2019.1) и РФФИ (проект № 18-01-00335).