Прикладная математика и механика, 2021, T. 85, № 4, стр. 516-527

1. Введение. Абсолютно твердое тело является одной из основных моделей теоретической механики, при этом считается, что при контакте выпуклых тел взаимодействие происходит в единственной точке. Кроме того, исходя из натурных экспериментов, в задачах часто используется предположение об отсутствии в этой точке проскальзывания. Это условие сводится к дифференциальной связи, в общем случае неголономной [1]. Изучению неголономных систем, в частности, теории общих уравнений аналитической механики, устойчивости движений, применимости вариационных принципов посвящены многие работы В.В. Румянцева (см. [2–5]).

Во втором томе классического учебника П. Аппеля по теоретической механике [6], п. 370, рассмотрена следующая задача: “Однородный круглый тяжелый диск, находящийся в вертикальной плоскости, поставлен на неподвижную прямую $Ox$, наклоненную к горизонту под углом ${{\varphi }}$, и предоставлен самому себе без начальной скорости. Предполагается, что имеется трение и спрашивается, будет ли диск катиться или скользить”. Взаимодействие между диском и прямой описывается следующим образом: если происходит качение (то есть скорость точки диска, находящейся в контакте с прямой, равна нулю), то касательная реакция должна быть меньше, чем произведение коэффициента трения ${{\mu }}$ на нормальную реакцию $P$; если это условие не выполняется, то “качение без скольжения невозможно; диск будет скользить, одновременно вращаясь”. В этом случае касательная реакция в точности равна произведению ${{\mu }}P$. Показано, что если $\operatorname{tg} \varphi \leqslant 3\mu $, то диск будет катиться без проскальзывания с постоянным ускорением центра диска

где $g$ – ускорение свободного падения. Если же $\operatorname{tg} \varphi > 3\mu $, то диск катится со скольжением, ускорение оси постоянно и равно $g\left( {\sin \varphi - \mu \cos \varphi } \right)$, а скорость скольжения линейно растет с течением времени. Таким образом, эта задача в классической постановке исследована полностью. (В кн. [6] угол наклона обозначен ${{\alpha }}$, нормальная реакция $N$, а коэффициент трения $f$. Здесь обозначения изменены для удобства последующего изложения.)

Указанная схема описания реакции опоры (трение покоя Кулона при качении и трение скольжения ${{\mu }}P$ при движении с проскальзыванием) является общепринятой при точечном контакте в рамках теоретической механики. Именно такая модель обычно используется при анализе экспериментов в учебном процессе (см., например, [7, 8]). Однако выпуклые тела при взаимодействии деформируются, и в области контактного взаимодействия действуют контактные напряжения, направленные по нормали и касательной к поверхности, которые могут существенно изменить динамику системы.

Изучение динамики качения со скольжением жесткого диска (цилиндра) в случае деформируемой опорной прямой (плоскости) проводится в работах [9, 10]: опорная прямая представляется в виде набора одномерных вязкоупругих элементов, описываемых моделями Максвелла или Кельвина–Фойгта, при деформации которых образуется область контактного взаимодействия. В работе [9] предполагается полное сцепление материалов и изучается влияние внешних сил (сопротивления воздуха, случайных возмущений) на устойчивость стационарного движения. В [10] исследуется качение диска с проскальзыванием: изучено движение в направлении, перпендикулярном основанию (в том числе прямой и косой удар диска и основания); показано, что при принятых предположениях о вязкоупругих свойствах основания, динамика в направлении, параллельном основанию, совпадает с классической постановкой.

Решения квазистатических задач механики контактных взаимодействий [12, 13] позволяют расширить спектр доступных моделей взаимодействия при изучении динамики твердых тел, установить границы применимости классических моделей и уточнить решения, полученные с их помощью. В предлагаемой статье изучение качения упругого цилиндра по наклонному основанию из того же материала проводится с использованием модели Картера [12]. Целью работы является исследование существования и устойчивости движения со сцеплением материалов в области контактного взаимодействия, а также сравнение полученного решения с классическим. Представленная работа продолжает исследования [14–18].

Структура работы следующая. Разд. 2–4 посвящены постановке задачи: составлены уравнения движения цилиндра; описана модель контактного взаимодействия упругих тел в условиях качения с проскальзыванием, предложенная Картером; введены безразмерные переменные задачи. В разд. 5 сформулирован основной результат работы о существовании и устойчивости стационарного решения динамических уравнений, которое соответствует движению оси цилиндра с постоянным ускорением, при этом в области контактного взаимодействия происходит частичное сцепление материалов. В разд. 6 проводится анализ полученного решения.

2. Динамические уравнения. Бесконечный упругий цилиндр с массой $m$ на единицу длины и радиусом $R$ движется плоскопараллельно по основанию из того же материала, недеформированная граница которого составляет угол φ с горизонтом. Введем инерциальную систему отсчета $O{{\xi \eta \zeta }}$, плоскость $O{{\xi \zeta }}$ является недеформированной границей основания, ось $O{{\eta }}$ направлена перпендикулярно ему, ось $O{{\zeta }}$ перпендикулярна плоскости движения и сонаправлена с осью цилиндра. Распределение масс в цилиндре предполагается осесимметричным, так что центр масс каждого сечения цилиндра $C$ лежит на его оси. Скорость оси цилиндра обозначим ${\mathbf{V}} = V{{{\mathbf{e}}}_{{{\xi }}}}$, а угловую скорость обозначим ${\mathbf{\omega }} = - {{\omega }}{{{\mathbf{e}}}_{{{\zeta }}}}$. Положительное значение ${{\omega }}$ соответствует вращению по часовой стрелке, если смотреть с конца оси $O{{\zeta }}$ (рис. 1).

Запишем динамические уравнения движения цилиндра:

где a – ускорение оси цилиндра, ${{{\mathbf{K}}}_{C}} = - J{{\omega }}{{{\mathbf{e}}}_{{{\zeta }}}}$ – кинетический момент относительно центра масс, $J$ – удельный момент инерции относительно оси цилиндра, ${\mathbf{g}}$ – ускорение свободного падения, Q и P – проекции равнодействующей сил взаимодействия цилиндра и основания на оси $O{{\xi }}$ и $O{{\eta }}$ соответственно, ${{{\mathbf{M}}}_{C}} = - {{M}_{C}}{{{\mathbf{e}}}_{{{\zeta }}}}$ – момент этих сил относительно оси цилиндра.

В скалярной форме уравнения движения (2.1) имеют вид:

Будем считать, что проекция ускорения оси цилиндра на нормаль к основанию пренебрежимо мала (движение квазистатическое), отсюда получим

Таким образом, прижимающая сила P обеспечивается силой тяжести и определяется углом наклона основания к горизонту φ.

Далее будем исследовать свойства некоторых решений задачи Коши для уравнений (2.2), при этом касательную силу $Q$ и момент ${{M}_{C}}$ будем определять из решения задачи теории упругости в квазистатической постановке, полученного Картером [12, 13]. Такой подход был применен при решении динамической задачи о движении цилиндра по горизонтальному основанию в [15]. Напомним далее постановку и основные результаты решения задачи Картера.

3. Определение сил и момента из решения задачи Картера. Модель Картера описывает взаимодействие упругого цилиндра с основанием из того же материала. Вследствие одинаковости механических характеристик контактирующих тел область контактного взаимодействия цилиндра и основания – это полоса $x \in \left[ { - a,a} \right]$, где $x$ отсчитывается от проекции оси цилиндра на опорное полупространство (рис. 1). Ширина этой полосы определяется прижимающей силой $P$, радиусом цилиндра $R$, а также модулем Юнга $E$ и коэффициентом Пуассона ${{\nu }}$ материалов цилиндра и основания:

Контактная область либо полностью состоит из области проскальзывания материалов цилиндра и основания (в этом случае касательные напряжения в каждой точке ${{{{\tau }}}_{{xy}}}\left( x \right)$ пропорциональны нормальным напряжениям $p\left( x \right)$, т.е. ${{{{\tau }}}_{{xy}}}\left( x \right) = {{\mu }}p\left( x \right)$, где ${{\mu }}$ – коэффициент трения), либо делится на участок проскальзывания и участок сцепления материалов (при сцеплении $\left| {{{{{\tau }}}_{{xy}}}\left( x \right)} \right| < {{\mu }}p\left( x \right)$). Участок сцепления материалов в области контактного взаимодействия возникает, если

по абсолютной величине не превышает некоторой постоянной величины, определяемой механическими характеристиками материала, коэффициентом трения, а также радиусом цилиндра и величиной прижимающей силы:

Параметр $\kappa \gg 1$ – безразмерный, его механический смысл – отношение радиуса цилиндра к ширине области контактного взаимодействия.

Результирующая касательных напряжений ${{{{\tau }}}_{{xy}}}$ имеет вид [12]

Распределение нормальных напряжений $p\left( x \right)$ симметрично: $p\left( x \right) = p\left( { - x} \right)$, поэтому момент сил взаимодействия относительно оси цилиндра определяется только касательными напряжениями и равен

Таким образом, из (2.2) получим

4. Анализ уравнений движения. Введем безразмерные переменные

Кроме того, обозначим

безразмерный момент инерции на единицу длины. Тогда уравнения движения (3.4) принимают вид где штрихом обозначена производная по безразмерному времени $\tilde {t}$, a $\tilde {Q} = Q{\text{/}}P$ – безразмерная результирующая касательных напряжений (см. (3.3)), которая задается соотношениями

График этой функции при положительных значениях $\tilde {V}$ показан синей сплошной линией на рис. 2 при ${{\mu }} = 0.4$, $\kappa = 2.9$; область $\left| \delta \right| < \mu {\text{/}}\left( {2\kappa } \right)$ показана на врезке справа.

Заметим, что при $\left| {{\delta }} \right| > {{\mu /}}\left( {2\kappa } \right)$ уравнения движения полностью совпадают с уравнениями движения классической задачи о движении с проскальзыванием твердого диска. Действительно, в этом случае сила трения $\tilde {Q}$ постоянна (в размерном виде равна ${{\mu }}P$) и направлена противоположно скорости проскальзывания $\left( {V - {{\omega }}R} \right){{{\mathbf{e}}}_{{{\xi }}}}$. Поэтому в указанной выше области фазового пространства $\left( {\tilde {V},{{\tilde {\omega }}}} \right)$ движение цилиндра происходит так же, как и в классической задаче.

Интерес представляет область фазового пространства, задаваемая неравенством $\left| {{\delta }} \right| \leqslant {{\mu /}}\left( {2\kappa } \right)$, в которой величина силы трения в соответствии с формулой (3.3) по модулю уменьшается при убывании $\left| {{\delta }} \right|$. Поэтому далее рассмотрим именно эту область фазового пространства.

5. Движение с постоянным относительным проскальзыванием. Докажем следующее утверждение.

Теорема. При углах наклона

основания к горизонту динамические уравнения (4.2) имеют решение, при котором ось цилиндра движется вдоль оси $O{{\xi }}$ с постоянным линейным ускорением $w* > 0$, при этом относительное проскальзывание также постоянно, то есть

Это решение асимптотически устойчиво по отношению к переменной δ.

Доказательство. Пользуясь определением относительного проскальзывания (3.1), составим дифференциальное уравнение, описывающее его изменение на решениях системы (4.2):

Найдем стационарное решение этого уравнения вида ${{\delta }}\left( {{\tau }} \right) \equiv {{\delta }}{\kern 1pt} *$. После подстановки получим уравнение

Функция ${{\Phi }}\left( {{\delta }} \right)$ зависит от угла наклона основания φ и параметра  j (см. (4.1)). На рис. 2 показаны графики этой функции при $\varphi = \pi {\text{/}}24$; $\pi {\text{/}}6$, $j = 0.5$, пунктирными линиями даны асимптоты.

Будем искать решения уравнения (5.3) на отрезке $\left| {{\delta }} \right| \leqslant {{\mu /}}\left( {2\kappa } \right)$, то есть когда происходит частичное сцепление материалов. Такое решение существует при

причем оно единственно и отрицательно: $\delta * \in \left[ { - \mu {\text{/}}\left( {2\kappa } \right),0} \right)$. Полученное выше неравенство приводится к виду (5.1), указанному в формулировке теоремы.

Если начальная скорость оси цилиндра ${{\tilde {V}}_{0}} > 0$ и угловая скорость ${{{{\tilde {\omega }}}}_{0}}$ соответствуют найденному решению

то уравнения (4.2) имеют решение (5.2), причем ускорение $w{\kern 1pt} *$ оси цилиндра постоянно и согласно уравнениям (4.2), (5.3) имеет вид:

Угловое ускорение на этом движении также постоянно и может быть вычислено из второго уравнения (4.2).

Устойчивость решения по переменной δ следует из теоремы об устойчивости по части переменных (теорема 5.1, [19]), если в качестве функции Ляпунова взять функцию ${{(\delta - \delta *)}^{2}}{\text{/2}}$. Доказательство асимптотической устойчивости и оценка асимптотики приведены в Приложении.

Замечание. При $\operatorname{tg} \varphi < \mu $ существует еще одно решение уравнения (5.3), которое соответствует движению цилиндра с полным проскальзыванием $\delta {\kern 1pt} *{\kern 1pt} * < - \left( {1 + j} \right){\text{/}}j$ (см. рис. 2). Фазовые переменные зависят от времени следующим образом:

Движение оканчивается за конечное время $\tau {\kern 1pt} *{\kern 1pt} * = {{\tilde {V}}_{0}}{\text{/}}\left( {\mu - \operatorname{tg} \varphi } \right)$: в этот момент оказываются равны нулю как линейная, так и угловая скорость цилиндра. Так как при ${{\varphi }} \ne 0$ условия равновесия цилиндра на наклонном основании не выполняются, то при $\tau \geqslant \tau {\kern 1pt} *{\kern 1pt} *$ начинается движение с малым относительным проскальзыванием, причем относительное проскальзывание δ стремится к значению δ* вследствие асимптотической устойчивости решения (5.2) по переменной δ. При ${{\varphi }} = 0$ после остановки цилиндра в момент ${{\tau }}{\kern 1pt} *{\kern 1pt} *$ движение прекращается [15].

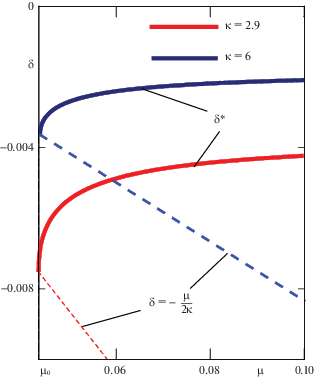
Графики решений уравнения (5.3) ${{\delta }}{\kern 1pt} *{\kern 1pt} \left( {{\mu }} \right)$ при ${{\varphi }} = {{\pi /}}24$ и $\kappa = 2.9$, $\kappa = 6$ (сплошные линии) и границы ${{\delta }} = - {{\mu /}}\left( {2\kappa } \right)$ существования области сцепления материалов (пунктирные линии) показаны на рис. 3 (численные значения остальных параметров указаны выше). Для фиксированного значения $\varphi $ решение (5.2) существует для всех ${{\mu }} > {{{{\mu }}}_{0}}$, где ${{{{\mu }}}_{0}}$ можно найти из неравенства (5.1). Анализ зависимости (4.3) показывает, что функция ${{\delta }}{\kern 1pt} *{\kern 1pt} \left( {{\mu }} \right)$ с ростом $\mu $ асимптотически приближается к значению $ - j\operatorname{tg} \varphi {\text{/}}\left[ {4\left( {1 + j} \right)\kappa } \right]$.

6. Свойства полученного решения. Проведенное выше исследование показывает, что в случае выполнения (5.1) при движении упругого цилиндра по основанию из того же материала существует асимптотически устойчивое по величине относительного проскальзывания решение, на котором ускорение оси цилиндра постоянно и положительно, а в зоне контактного взаимодействия существует участок сцепления материалов. При этом ускорение оси на величину порядка малой величины ${{\mu /}}\kappa $ больше, чем ускорение ${{w}_{d}}$ (см. (1.1)) в классической постановке. Действительно, возвращаясь к размерным переменным и считая цилиндр однородным $j = {\text{1/2}}$, получим:

Условие существования такого движения – выполнение неравенства (5.1) – чуть шире классического условия $\operatorname{tg} \varphi < 3\mu $ (также на малую величину порядка ${{\mu /}}\kappa $). Кроме того, решение (5.2) является асимптотически устойчивым по переменной δ. Важным отличием полученного здесь решения с постоянным относительным проскальзыванием от классического решения является тот факт, что абсолютное значение проскальзывания, то есть величина $V - {{\omega }}R$ в рассматриваемой задаче является линейной функцией времени: из определения (3.1) следует, что

а в классической задаче $V - {{\omega }}R \equiv 0$.

На рис. 4 построены изолинии относительного отклонения ускорения оси однородного ($j = {\text{1/2}}$) упругого цилиндра ${{w}_{{{\text{el}}}}}$ от ускорения, рассчитанного в классической задаче ${{w}_{d}}$ при пренебрежении упругостью контактирующих тел (в процентах)

при фиксированном значении угла наклона ${{\varphi }} = {{\pi /4}}$. Результаты расчетов показывают, что отклонение ${{e}_{w}}$ довольно мало (порядка 1$\% $), оно увеличивается при уменьшении коэффициента трения ${{\mu }}$ и параметра κ. Использованный на рис. 4 диапазон изменения параметра $\kappa \in \left[ {2.9,7} \right]$ соответствует диапазону модуля Юнга $E \in [1.9 \times {{10}^{5}}\;{\text{Па}}$, $1.1 \times {{10}^{6}}~\;{\text{Па}}]$ при следующих размерных параметрах (плотность соответствует плотности резины)

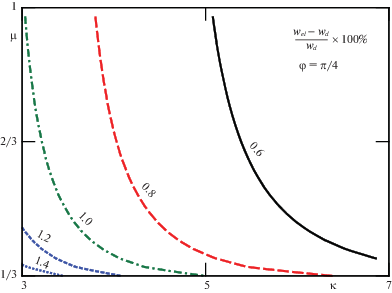
Поскольку параметр κ (см. (3.2)) пропорционален $\sqrt {ER} $, то найденные отличия в ускорении оси цилиндра будут более существенны для цилиндров малых радиусов и малых модулей Юнга E материала. Расчеты также показывают, что при увеличении угла наклона основания к горизонту ${{\varphi }}$ при фиксированных κ и ${{\mu }}$ величина ${{e}_{w}}$ увеличивается.

Заключение. В работе исследована задача о движении под действием силы тяжести упругого цилиндра по наклонному основанию из того же материала. Найдено асимптотически устойчивое (по части переменных) решение задачи Коши для динамических уравнений: оно соответствует качению цилиндра с постоянным ускорением его оси, при этом в части области контактного взаимодействия происходит сцепление материалов. Проведено сравнение параметров этого движения с решением классической задачи о качении без проскальзывания абсолютно твердого диска по недеформированной прямой. Показано, что ускорение оси упругого цилиндра увеличивается при уменьшении коэффициента трения, радиуса цилиндра и параметра, зависящего от механических характеристик контактирующих материалов (их модуля Юнга и коэффициента Пуассона), а также при увеличении угла наклона основания к горизонту. Полученные результаты позволяют оценить погрешности в определении ускорения оси цилиндра и углового ускорения, возникающие при использовании в этой задаче модели абсолютно твердого тела. Установлено, что указанные погрешности в достаточно широком диапазоне изменения механических характеристик материалов и коэффициента трения оказываются невелики; однако абсолютное значение проскальзывания при учете упругости материала растет линейно с течением времени, что существенно отличается от свойства решения в классической постановке, в которой оно принимается тождественно равным нулю. Этот факт представляется важным с теоретической точки зрения.

Часть работы, посвященная анализу решения контактной задачи, выполнена по теме государственного задания (№ госрегистрации AAAA-A20-120011690132-4); исследование стационарного решения и его устойчивости по части переменных – в рамках проекта Российского фонда фундаментальных исследований 19-01-00140-а.