Прикладная математика и механика, 2021, T. 85, № 4, стр. 414-425

1. Введение. В последние годы значительный интерес вызывают мобильные роботы, управляемые при помощи вспомогательных подвижных масс, снабженных актюаторами и способными перемещаться относительно корпуса робота [1–9]. Такие роботы, называемые капсульными, не имеют внешних подвижных элементов и могут быть герметичными. Они способны передвигаться в различных средах, включая агрессивные и ранимые среды, в сложной обстановке, в трубах, внутри живых организмов и выполнять операции доставки, мониторинга, диагностики и др. Большинство работ по динамике капсульных роботов посвящено одномерным поступательным движениям по прямой. Построены оптимальные законы движения, при которых достигается максимальная средняя скорость перемещения [1, 3].

Двумерные управляемые движения тела с внутренними массами вдоль горизонтальной плоскости исследованы в работах [10–15]. Здесь предполагается, что внутренние массы имеют две степени свободы относительно тела и состоят либо из двух осцилляторов [10, 14, 15], либо из ротора и подвижной материальной точки [11–13]. Случай одной внутренней точечной массы с двумя степенями свободы рассмотрен кратко в [13].

В данной работе также рассмотрен случай одной подвижной точечной массы, с помощью которой управляется движение твердого тела по горизонтальной плоскости при наличии сил сухого трения между телом и плоскостью. Установлено, что если подвижная точка может развивать достаточно большое ускорение относительно несущего тела, то система вполне управляема. Она может быть переведена из любого начального состояния покоя в произвольное терминальное состояние покоя в плоскости за конечное время. Описан способ управления и показано, что он может быть реализован в том случае, когда подвижная точка может двигаться по некоторой кривой относительно твердого тела, то есть имеет лишь одну степень свободы относительно тела.

Отметим, что двумерные плоские движения важны для реализации поворотов мобильного робота при его движении по плоскости.

2. Уравнения движения. Рассматриваемая система состоит из твердого тела P массы M и материальной точки Q массы m (рис. 1). Тело P может скользить по неподвижной горизонтальной плоскости OXY в поле тяжести, опираясь на эту плоскость в трех точках опоры ${{A}_{i}}$, $i = 1,2,3$. Как известно, в случае трех точек опоры твердое тело является статически определимой системой, и поэтому нормальные реакции ${{N}_{i}}$ в точках ${{A}_{i}}$ определяются однозначно.

Обозначим через C центр масс тела P и предположим, что проекция точки C на плоскость OXY лежит внутри треугольника ${{A}_{1}}{{A}_{2}}{{A}_{3}}$. Предполагаем также, что вертикальная ось, проходящая через точку C, является одной из главных центральных осей инерции тела P.

Материальная точка Q снабжена актюатором и может перемещаться относительно тела P вдоль горизонтальной плоскости, параллельной неподвижной плоскости OXY. Точка Q взаимодействует с телом P, но не взаимодействует с неподвижной плоскостью OXY. Таким образом, единственными внешними силами, действующими на систему $P + Q$, являются силы тяжести и реакции в точках опоры ${{A}_{i}}$.

Для упрощения предполагаем, что расстояние от центра масс C до неподвижной плоскости OXY, а также расстояние от точки Q до этой же плоскости малы по сравнению с линейными размерами тела P в горизонтальной плоскости. Тогда можно считать, что центр масс C и точка Q движутся в плоскости OXY, причем обе точки C и Q лежат внутри треугольника ${{A}_{1}}{{A}_{2}}{{A}_{3}}$. При сделанных предположениях нормальные реакции ${{N}_{i}}$ положительны, и “опрокидывание” тела P исключается.

Предполагаем, что касательные реакции ${{F}_{i}}$ в точках опоры подчиняются закону сухого трения Кулона с коэффициентом трения  f. Они удовлетворяют соотношениям:

где ${{v}_{i}}$ – скорость точки опоры ${{A}_{i}}$.

Составим уравнение движения системы $P + Q$. Обозначим через ${{v}_{C}}$ и ${{v}_{Q}}$ скорости точек C и Q относительно неподвижной плоскости OXY, а через F – силу, развиваемую актюатором и приложенную к точке Q. Следовательно, к телу P в точке Q приложена сила (–F). Уравнение движения центра масс C тела P имеет вид

где силы ${{F}_{i}}$ определены равенствами (2.1). Точками обозначаются производные по времени t.

Уравнение движения точки Q

запишем, представляя абсолютное ускорение ${{\dot {v}}_{Q}}$ как сумму переносного, кориолисова и относительного ускорений.

Обозначим через $r = \overline {CQ} $ радиус-вектор точки Q относительно центра масс C тела P, через v и w – скорость и ускорение точки Q, соответственно, относительно тела P, через $\omega = \omega k$ угловую скорость тела P, где k – единичный вектор, направленный вертикально вверх. В развернутом виде уравнение (2.3) запишется так:

Обозначая через J момент инерции тела P относительно вертикальной оси, проходящей через его центр масс C, запишем уравнение моментов для тела P относительно этой оси:

Уравнения динамики системы $P + Q$ заданы в виде (2.2), (2.4) и (2.5). В этих уравнениях в качестве управляющих воздействий можно рассматривать либо силу F, либо относительное ускорение w в зависимости от того, какие характеристики поддерживает принятая модель актюатора: силовые или кинематические. Если же ограничений на управление не налагается, то оба подхода эквивалентны, так как векторы F и w связаны уравнением (2.4).

Ниже для определенности относительное ускорение w рассматривается в качестве управляющего воздействия, причем предполагается, что вектор w может быть произволен по направлению в плоскости OXY и достаточно большим по величине.

Будут исследованы некоторые простые движения системы $P + Q$, при помощи которых будет установлена ее управляемость, то есть возможность ее перемещения из любого начального положения в произвольное заданное терминальное положение.

3. Типы движений. Рассмотрим некоторые простые возможные типы движений системы $P + Q$, при помощи которых будет установлена ее управляемость.

Медленные движения. Пусть точка Q движется относительно тела P внутри треугольника ${{A}_{1}}{{A}_{2}}{{A}_{3}}$ c достаточно малым по величине относительным ускорением. Тогда силы трения могут удерживать тело P в состоянии покоя, если оно было в этом состоянии в начале движения. Медленными движениями можно пользоваться для того, чтобы переместить точку Q из начального состояния покоя в произвольное терминальное положение относительно тела P, не изменяя его состояние покоя.

Остаточное движение. Пусть точка Q неподвижна относительно тела P, а само тело движется. Тогда систему $P + Q$ можно рассматривать как твердое тело массы $M + m$, которое находится под действием сил трения. Так как эти силы конечны по величине, то система $P + Q$ придет в состояние покоя за конечное время.

Прямолинейные движения. Пусть в начальный момент $t = 0$ вся система покоится, а точка Q находится на одной из прямых $C{{A}_{i}}$, $i = 1,2,3$. Если точка Q будет двигаться по этой прямой, то тело P будет двигаться прямолинейно и поступательно вдоль этой прямой.

Вращение. Пусть в начальный момент $t = 0$ вся система покоится, а точка Q находится на окружности S радиуса а с центром в точке C. Если точка Q будет двигаться по этой окружности относительно тела P, то само тело будет вращаться относительно неподвижной плоскости OXY.

Рассмотрим подробнее последние два типа движений.

4. Прямолинейные движения. Не нарушая общности, примем, что точка Q в начальный момент времени находится на прямой $C{{A}_{1}}$ (рис. 1). Обозначим через ξ ее смещение вдоль этой прямой, отсчитанное от ее начального положения. Покажем, что при движении точки Q по прямой $C{{A}_{1}}$ тело P совершает поступательное движение вдоль этой прямой. Для этого достаточно убедиться, что все уравнения (2.2), (2.4) и (2.5) удовлетворяются при таком движении.

Скорости ${{v}_{i}}$ всех точек опоры ${{A}_{i}}$, $i = 1,2,3$, при поступательном движении тела P равны ${{v}_{C}}$ и параллельны прямой $C{{A}_{1}}$. Согласно уравнениям (2.1), все силы трения ${{F}_{i}}$ также параллельны прямой $C{{A}_{1}}$ и направлены против скорости ${{v}_{C}}$. Следовательно, векторное уравнение (2.2) приводится к скалярному уравнению

где введено следующее обозначение, выражающее закон Кулона (2.1):

Сумма всех нормальных реакций равна весу системы $P + Q$. Имеем

где g – ускорение силы тяжести. Уравнение (4.1) с учетом равенства (4.3) примет вид

Уравнение (2.4) для поступательного движения тела P, при котором $\omega = 0$, сводится к скалярному уравнению

Исключая F из уравнений (4.4) и (4.5) и вводя обозначение

получим

Рассмотрим теперь уравнение (2.5). Согласно уравнению моментов для тела P относительно оси $C{{A}_{1}}$, имеет место равенство

где ${{b}_{2}}$ и ${{b}_{3}}$ – расстояния от точек опоры ${{A}_{2}}$ и ${{A}_{3}}$, соответственно, до прямой $C{{A}_{1}}$ (рис. 1). Так как силы трения ${{F}_{2}}$ и ${{F}_{3}}$ направлены параллельно прямой $C{{A}_{1}}$, то их моменты относительно точки C уравновешивают друг друга в силу равенства вытекающего из (2.1) и (4.8). Моменты относительно точки C сил ${{F}_{1}}$ и F, направленных по прямой $C{{A}_{1}}$, равны нулю. Поэтому правая часть уравнения (2.5) равна нулю, как и его левая часть при $\omega = 0$. Таким образом, все уравнения динамики (2.2), (2.4) и (2.5) удовлетворяются в случае прямолинейного движения точки Q вдоль прямой $C{{A}_{1}}$ и поступательного движения тела P вдоль этой же прямой. Эти уравнения сводятся к скалярному уравнению (4.7), к которому нужно добавить следующие кинематические соотношения: где х – абсолютное смещение центра масс C тела P вдоль направления $C{{A}_{1}}$.

Для уравнений (4.7) и (4.9) имеют место следующие начальные условия:

Ниже предлагается простой способ управления, при котором реализуется заданное абсолютное перемещение центра масс C вдоль направления $C{{A}_{1}}$ при ограниченном относительном перемещении точки Q по прямой $C{{A}_{1}}$. Зададим относительное ускорение w(t) точки Q, которое играет роль управления, в виде кусочно-постоянной функции времени:

Здесь ${{t}_{1}}$ и ${{t}_{2}}$ – некоторые моменты времени, а постоянные ${{w}_{1}}$ и ${{w}_{2}}$ удовлетворяют ограничениям:

Интегрируя второе уравнение (4.9) при w(t), определяемом соотношениями (4.11), при начальных условиях (4.10), получим

Потребуем, чтобы относительная скорость $v(t)$ точки Q из (4.13) обращалась в нуль в момент $t = {{t}_{2}}$. Найдем

Проинтегрируем теперь первое уравнение (4.9) при $v(t)$, определяемом соотношениями (4.13), при начальных условиях (4.10). Получим

Подставляя $t = {{t}_{2}}$ из (4.14) в соотношения (4.15), найдем полное относительное смещение точки Q за время ${{t}_{2}}$:

Обратимся к уравнению (4.7). В силу первого неравенства (4.12) имеем ${{\dot {v}}_{C}} < 0$ на интервале $t \in (0,{{t}_{1}})$. Согласно начальному условию ${{v}_{C}}(0) = 0$ из (4.10), получим ${{v}_{C}} < 0$ на интервале $t \in (0,{{t}_{1}})$ и в начале интервала $t \in ({{t}_{1}},{{t}_{2}})$. Будем исходить из того, что неравенство ${{v}_{C}} \leqslant 0$ выполняется на всем интервале $t \in (0,{{t}_{2}})$. Построенное ниже решение удовлетворяет этому условию.

Интегрируя уравнение (4.7) при w(t), определяемом равенствами (4.11), при начальных условиях (4.10), получим

Из последнего равенства (4.17) следует, что ${{v}_{C}}(t)$ обращается в нуль при $t = {{t}_{*}}$, где

Сравнивая равенства (4.14) и (4.18), нетрудно убедиться в том, что

Заметим, что если в какой-то момент времени ${{t}_{*}}$ выполнено условие ${{{v}}_{C}}({{t}_{*}}) = 0$, а относительное ускорение w(t) точки Q при $t > {{t}_{*}}$ удовлетворяет неравенству

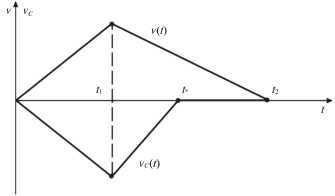
то тело P при $t > {{t}_{*}}$ будет оставаться в покое, и ${{{v}}_{C}}(t) = 0$ при $t > {{t}_{*}}$. Это следует из того, что второе слагаемое в правой части уравнения (4.7) в силу соотношения (4.2) компенсирует первое слагаемое. Другими словами, силы трения удерживают тело P в состоянии покоя на некотором интервале времени при выполнении условия (4.19), если ${{{v}}_{C}} = 0$ в начале этого интервала. Следовательно, имеем ${{{v}}_{C}} = 0$ на интервале $t \in ({{t}_{*}},{{t}_{2}})$.

Зависимости ${v}(t)$ и ${{{v}}_{C}}(t)$ на интервале $t \in (0,{{t}_{2}})$ показаны на рис. 2.

Определим еще перемещение тела P, для чего в третье уравнение (4.9) подставим ${{{v}}_{C}}(t)$ из (4.17). Принимая во внимание начальные условия (4.10), получим после интегрирования:

Полное перемещение тела P найдем, подставляя $t = {{t}_{*}}$ из (4.18) во второе соотношение (4.20):

Таким образом, управление w(t), заданное соотношениями (4.11) и (4.12), обеспечивает относительное перемещение точки Q по прямой $C{{A}_{1}}$ и одновременно поступательное перемещение тела P вдоль этого же направления по плоскости OXY. В начале и в конце этого маневра тело P и точка Q находятся в состоянии покоя. Время маневра ${{t}_{2}}$ определяется соотношением (4.14) и зависит от трех параметров: ${{w}_{1}}$, ${{w}_{2}}$ и ${{t}_{1}}$, причем ускорения ${{w}_{1}}$ и ${{w}_{2}}$ должны удовлетворять неравенствам (4.12), а величина ${{t}_{1}}$ может быть сколь угодно малой. Полное относительное перемещение Δξ точки Q и полное абсолютное перемещение Δх тела P определены соотношениями (4.16) и (4.21), соответственно. Эти перемещения противоположны по знаку и пропорциональны квадрату длины интервала ${{t}_{1}}$. Отсюда следует, что эти перемещения могут быть сделаны как угодно малыми.

После окончания описанного маневра перемещения, то есть при $t > {{t}_{2}}$, точка Q может быть при помощи медленного движения с ускорением w(t), удовлетворяющим неравенству (4.19), переведена в начальную точку $\xi = 0$. При этом тело P останется неподвижным. Повторяя описанный маневр нужное число раз и выбирая каждый раз его параметры ${{w}_{1}}$, ${{w}_{2}}$ и ${{t}_{1}}$, можно осуществить перемещение тела P на произвольное заданное расстояние вдоль направления $C{{A}_{1}}$ за конечное время. При этом точка Q будет совершать перемещения внутри любого сколь угодного малого отрезка прямой $C{{A}_{1}}$, а в конце движения она будет переведена в любое заданное положение на этой прямой при нулевой относительной скорости в конце движения.

Выше изложен один возможный способ управления совместным движением точки Q и тела P. Задачи оптимизации подобных движений применительно к уравнению типа (4.7), в котором участвуют силы сухого трения, рассмотрены и решены в работах [1, 3], где построены оптимальные движения, отвечающие максимальной средней скорости перемещения.

5. Вращение. Преобразуем уравнения движения (2.2), (2.4) и (2.5). Сначала выразим ${{\dot {v}}_{C}}$ из уравнения (2.2) и подставим его в (2.4). Получим

Здесь μ введено соотношением (4.6). Подставим выражение (5.1) для F в уравнение (2.5) и примем во внимание равенство $\omega = \omega k$. Имеем

В рассматриваемом вращательном движении точка Q движется относительно тела P по окружности S радиуса а с центром в точке С. Обозначим через φ угловую координату точки Q при этом движении, отсчитанную от некоторого начального положения этой точки, а через $\Omega = \dot {\varphi }$ угловую скорость точки Q относительно тела P (рис. 3). Относительная скорость v точки Q в рассматриваемом движении равна по величине $v = a\Omega $ и перпендикулярна радиусу-вектору $r = \overline {CQ} $. Так как справедливы равенства $rv = 0$, $\omega r = 0$, то имеем

Относительное ускорение w точки Q состоит из касательного ускорения ${\dot {v}} = a\dot {\Omega }$, направленного перпендикулярно вектору r, и из нормального ускорения, равного ${{v}^{2}}{\text{/}}a$ и направленного против вектора r. Поэтому получим

На основании равенств (5.3) и (5.4) уравнение (5.2) упрощается и приводится к виду

где угловое ускорение z точки Q, равное играет роль управляющего воздействия, и введены обозначения

Оценим сверху величину нормализованного момента сил трения R из (5.7). Вводя обозначение

получим

Пользуясь соотношениями (2.1) и равенством (4.3), получим оценку

Из оценки (5.8) следует, что размерность величины ${{R}_{O}}$ обратна квадрату времени. Поэтому можно ввести следующую характерную величину размерности времени:

Обозначим через ψ угол поворота тела P относительно неподвижной плоскости OXY и составим кинематические уравнения для вращений точки Q и тела P:

Так как точка Q и тело P начинают движение из состояния покоя, имеем начальные условия для уравнений (5.5) и (5.10):

Уравнения (5.5) и (5.10) вместе с начальными условиями (5.11) подобны уравнениям (4.7) и (4.9), соответственно, и начальным условиям (4.10) для прямолинейного движения.

Однако в рассматриваемом случае вращательных движений выражение R из (5.7) для момента сил трения более сложное, чем выражение для сил трения при прямолинейном движении. Поэтому здесь будет сделано более сильное предположение о величине управляющего воздействия z в уравнении (5.5). А именно, пусть функция z(t) задана в виде:

Здесь положительная постоянная Z и интервал времени τ таковы, что выполнены условия

где постоянные ${{R}_{O}}$ и Т введены соотношениями (5.8) и (5.9), а ε – малый параметр. При условиях (5.13) можно, с точностью $О({{\varepsilon }^{2}})$, на интервале $t \in (0,2\tau )$ пренебречь слагаемым R по сравнению с первым слагаемым в правой части уравнения (5.5). Тогда уравнения (5.5) и (5.6) приводятся к виду

Интегрируя это уравнение при начальных условиях (5.11), найдем

Подставляя z(t) из (5.12) в уравнения (5.10) и интегрируя эти уравнения при начальных условиях (5.11), найдем последовательно

Последнее соотношение (5.15) следует непосредственно из уравнения (5.14) и начальных условий (5.11).

Полные угловые перемещения точки Q и тела Р за время маневра 2τ определяются равенствами, вытекающими из (5.15):

Принимая во внимание (5.13) оценки, заключаем, что угловые перемещения (5.16) конечны при $\varepsilon \to 0$, пропорциональны друг другу и противоположны по знаку. За счет выбора интервала τ (при фиксированном Z) они могут быть сделаны сколь угодно малыми. Выполняя описанный маневр нужное число раз и выбирая каждый раз параметр τ, можно осуществить поворот тела P на заданный угол относительно неподвижной плоскости OXY. При этом движение точки Q по окружности S может быть заключено в заданных пределах, что также может регулироваться за счет выбора малого τ. После завершения описанного маневра, то есть при $t = 2\tau $, вращение тела P и движение точки Q относительно тела останавливаются, что следует из формул (5.15). Однако поступательное движение тела P может продолжаться, и будет иметь место остаточное движение, рассмотренное выше в разд. 2. Это движение завершается остановкой всей системы за конечное время. Затем точка Q может быть переведена в любое положение на окружности S при помощи медленного движения, после чего описанные вращательные движения могут быть продолжены. Итак, при помощи последовательности вращательных движений, чередующихся с остаточными и медленными движениями, можно за конечное время осуществить поворот тела P на заданный угол относительно неподвижной плоскости OXY. При этом точка Q будет двигаться относительно тела P по некоторой, в принципе любой, дуге окружности S с центром в точке С.

6. Управляемость. Покажем, как при помощи рассмотренных выше движений перевести систему, состоящую из твердого тела P и подвижной точки Q, из произвольного начального состояния покоя в заданное терминальное состояние покоя.

1) Сначала при помощи медленного движения переместим точку Q из начальной точки в произвольную точку на окружности S радиуса а с центром в точке С. Состояние покоя тела P и его положение на неподвижной плоскости OXY при этом не изменятся. Начальная и конечная скорости точки Q (как относительные, так и абсолютные) при этом равны нулю.

2) При помощи ряда описанных выше вращательных движений осуществим поворот тела P относительно неподвижной плоскости OXY так, чтобы его ориентация совпала с заданной терминальной ориентацией. Для этого может потребоваться несколько вращательных маневров, которые могут чередоваться с остаточными движениями и медленными движениями точки Q по окружности S. В конце этих движений система $P + Q$ придет в состояние покоя, причем тело P будет иметь заданную ориентацию, а точка Q будет находиться на окружности S.

3) Не изменяя ориентации тела P, при помощи поступательных движений по двум направлениям переведем тело P в заданное положение. Для этого используем прямолинейные движения по любым двум из трех возможных направлений $C{{A}_{i}}$, $i = 1,2,3$. Точку Q при помощи медленного движения сначала переместим с окружности S на одну из прямых $C{{A}_{i}}$, например, на $C{{A}_{1}}$. После окончания прямолинейных движений по прямой $C{{A}_{1}}$ переместим точку Q по дуге окружности S на другую прямую, например, на $C{{A}_{2}}$. После окончания прямолинейных движений по прямой $C{{A}_{2}}$ точку Q можно с помощью медленного движения переместить в любую заданную точку относительно тела P.

В результате, заданное перемещение системы $P + Q$ будет осуществлено за конечное время.

Для реализации данного перемещения, то есть для управляемости системы, достаточно, как показывает приведенный выше анализ, выполнения двух условий.

Во-первых, точка Q должна иметь возможность перемещаться относительно тела P с относительным ускорением, произвольным по величине и направлению.

Во-вторых, точка Q должна иметь возможность двигаться относительно тела P по некоторой (произвольной) дуге окружности S радиуса а с центром в точке С и по двум произвольным отрезкам каких-либо двух прямых $C{{A}_{i}}$.

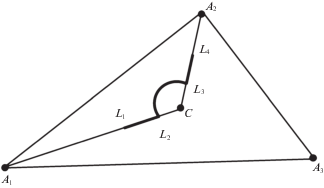
Для выполнения второго условия достаточно предположить, что точка Q может двигаться относительно тела P по кривой ${{L}_{1}}{{L}_{2}}{{L}_{3}}{{L}_{4}}$ (рис. 4), состоящей из отрезка ${{L}_{1}}{{L}_{2}}$ прямой $C{{A}_{1}}$, дуги ${{L}_{2}}{{L}_{3}}$ окружности S и отрезка ${{L}_{3}}{{L}_{4}}$ прямой $C{{A}_{2}}$. В этом случае точка Q имеет одну степень свободы относительно тела P.

Таким образом, если точка Q обладает достаточно большим относительным ускорением и имеет две или даже одну степень свободы относительно тела P, то система вполне управляема.

Заключение. Твердое тело, движущееся вдоль горизонтальной плоскости при наличии сил сухого трения между телом и плоскостью и управляемое при помощи вспомогательной подвижной точечной массы, может быть переведено из произвольного начального состояния в заданное конечное состояние покоя. Предложен способ управления подвижной массой, реализующей заданное перемещение. Управляемость системы имеет место, если подвижная масса может двигаться относительно тела по некоторой кривой с достаточно большим относительным ускорением.

Работа выполнена при финансовой поддержке РФФИ (гранты 20-01-00378 и 21-51-12004).