Прикладная математика и механика, 2021, T. 85, № 4, стр. 426-435

1. Введение. При подготовке кандидатского минимума в 1963-м году Валентин Витальевич Румянцев обратил внимание старшего из соавторов на раздел № 375 книги [1] под названием “О трудностях, возникающих при приложении обычно принимаемых эмпирических законов трения. Исследования Пенлеве.”. После некоторых изысканий, которые поддерживал Валентин Витальевич, возникла задача о динамике тормозной колодки, вошедшая в брошюру [2], в которой обосновано явление “удара трением”, как и в [3]. В [4] для “смягчения удара” введены упругие элементы в зону контакта и обнаружены некоторые особенности функционирования тормоза в условиях “удара”. В [5] описано поведение колодки после одноразового удара. Затем эта задача обсуждалась в рамках двух грантов РНФ [6, 7]. В [6], в частности, экспериментально подтверждены некоторые качественные выводы работы [5]. Но модель с упругими элементами [8] оказалась более богатой на эффекты. Динамическая система, описывающая взаимодействия силы упругости с силой трения, имеет переменную структуру. Изменчивость структуры даже после линеаризации уравнений придает системе свойства, характерные для нелинейных систем. В таких системах, в зависимости от режима движения, есть несколько особых точек. В частности, в [8] были обнаружены два характерных типа движения: демпфирование колебаний колодки после остановки колеса и колебания колодки с увеличением амплитуды и одновременное “дребезжание” колеса с постоянной амплитудой и частотой. Показано, что из-за сухого трения при наличии крутящего момента колодка начинает колебаться даже из предыдущего положения статического равновесия. Интерес к проявлению подобных свойств побудил авторов провести более детальный анализ взаимодействия сухого трения и упругих элементов конструкции в типовой задаче теоретической механики, частично описанных в [9] и дополненных в настоящей работе.

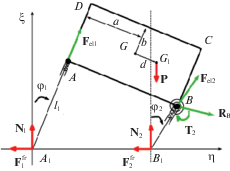
2. Объект исследования. Пусть тяжелое тело (рис. 1) массой m, для простоты, прямоугольной формы ABCD ($AB = 2a$, $AD = 2b$), с двумя одинаковыми телескопическими пружинными опорами AА₁ и BB₁ совершает плоско-параллельное движение, опираясь на горизонтальную шероховатую плоскость. Когда опоры не напряжены, их длина $A{{A}_{1}} = B{{B}_{1}} = {{l}_{0}}$. Центр тяжести G₁ прямоугольника смещен от центра прямоугольника G вдоль прямой DC на расстояние d. Пружины действуют на тело силами ${{F}_{{{\text{el1}}}}} = - k({{l}_{1}} - {{l}_{0}}) - h{{\dot {l}}_{1}}$, ${{F}_{{{\text{el2}}}}} = - k({{l}_{2}} - {{l}_{0}}) - h{{\dot {l}}_{2}}$, где k – коэффициент жесткости, h – коэффициент демпфирования пружин.

На систему кроме силы тяжести mg (g – ускорение свободного падения), действуют нормальные ${{N}_{1}}$, ${{N}_{2}}$ и тангенциальные ${{F}_{{{\text{fr1}}}}}$, ${{F}_{{{\text{fr2}}}}}$ реакции опор, которые в случае скольжения опорных ног связаны между собой по закону Кулона:

В случае, если опорная нога находится в покое, значение соответствующей тангенциальной реакции ${{F}_{{{\text{fr1}}}}} = {{F}_{{{\text{fr1stat}}}}}$, ${{F}_{{{\text{fr2}}}}} = {{F}_{{{\text{fr2stat}}}}}$ определяется из других характеристик движения.

Введем систему отчета Охy: ось Ох параллельна плоскости опоры и находится от нее на расстоянии ${{l}_{0}} + b$, ось Оу – вертикальна.

В качестве обобщенных координат выберем координаты центра масс ${{x}_{{{{G}_{1}}}}}$, ${{y}_{{{{G}_{1}}}}}$ и угол $\varphi $ между вертикалью и боковыми сторонами прямоугольника. Отметим, что координата ${{x}_{{{{G}_{1}}}}}$, очевидно, циклическая.

Исследуем возможные типы поведения системы.

Рассматриваемая система – система переменной структуры. В общем случае, при скольжении обеих ног, у нее три степени свободы. При этом у системы есть две колебательные координаты ${{y}_{{{{G}_{1}}}}}$, φ. Как минимум, система – двухчастотная. В условиях сильно разнесенных частот возможны разные типы переходов движения, в частности, угловые колебания могут затухнуть быстрее, чем продольные. При этом точки опоры тела начинают совершать быстрые колебания с изменением направления скорости, тело начинает “пританцовывать”.

В промежутки времени, когда одна из опор не скользит, у системы две степени свободы. Это эквивалентно наложению связи ${{x}_{{{{A}_{1}}}}} = \operatorname{const} $ или ${{x}_{{{{B}_{1}}}}} = \operatorname{const} $. Вторая опора останавливается только в те моменты времени, когда угловая скорость обратится в нуль.

Когда обе ноги не скользят, система имеет одну степень свободы, тело может перемещаться только поступательно вдоль линии $A{{A}_{1}}\;(B{{B}_{1}})$. При этом $\varphi = \operatorname{const} $, а координаты центра масс связаны между собой через эту постоянную угла наклона.

2.1. Первая особенность. Рассмотрим следующее положение тела:

Пусть пружины уравновешены силой тяжести. При $d = 0$ система симметрична и положение (2.2) является равновесием. Имеем N₁ = N₂ = mg/2, ${{F}_{{{\text{fr1}}}}} + {{F}_{{{\text{fr2}}}}} = 0$. Система статически неопределима.

Однако, если $d \ne 0$, то условия равновесия, очевидно, не выполняются ни при каком ${{y}_{{{{G}_{1}}}}}$. Это обстоятельство при большом желании можно счесть парадоксом. И для разрешения этого “парадокса”, следуя [9], введем податливость правой опоры на поворот. Предположим, что направляющая правой опоры крепится к корпусу с помощью цилиндрического шарнира, оснащенного спиральной пружиной (рис. 2) жесткости с, которую мы будем считать большим параметром, так как нас интересует предельный переход $c \to \infty $.

В этом случае число степеней свободы вырастает на единицу. Введем дополнительные координаты: $x = {{l}_{0}} - {{l}_{1}}$ – удлинение левого опорного стержня, и угол ${{\varphi }_{2}}$ между вертикалью и правым стержнем BB₁: ${{\varphi }_{2}}$ = $\operatorname{arctg} \left( {\frac{{2a(\cos \varphi - 1) + ({{l}_{0}} - x)\sin \varphi }}{{({{l}_{0}} - x)\cos \varphi - 2a\sin \varphi }}} \right)$ ≈ ≈ $\varphi + a{{\varphi }^{2}}{\text{/}}{{l}_{0}} + \ldots $. Длина правого стержня при этом:

Величина внутреннего крутящего момента T₂ спиральной пружины зависит от разности углов ориентации опорных стержней: ${{T}_{2}} = c({{\varphi }_{2}} - \varphi )$ ≈ $ca{{\varphi }^{2}}{\text{/}}{{l}_{0}} + o({{\varphi }^{2}})$.

Рассмотрим вновь равновесие тела. Выпишем потенциальную энергию системы:

Заметим, что потенциальная энергия спиральной пружины зависит от угла $\varphi $ в четвертой степени, поэтому традиционная процедура линеаризации уравнений равновесия здесь бесполезна даже при малых значениях параметра d, т.к. “большой” параметр не войдет в линейные уравнения.

Представим решение уравнений равновесия $\frac{{\partial \Pi }}{{\partial \varphi }} = 0$; $\frac{{\partial \Pi }}{{\partial x}} = 0$ в виде ряда по степеням ${{c}^{{ - 1/3}}}$:

Теперь определим реакции опор в положении равновесия из уравнений:

Из (2.4) получим выражение для тангенциальной реакции правой опоры:

Подставив решение (2.3) в (2.4), получим следующее приближение для силы ${{F}_{{{\text{fr2}}}}}$:

Очевидно, что при стремлении коэффициента с к бесконечности, величины тангенциальных реакций также стремятся к бесконечности. Действительно, пара бесконечных сил даже с нулевым плечом может создать момент, необходимый для равновесия системы при $\varphi = 0$ и $d \ne 0$. Во всяком случае, эти реакции не реализуемы силами сухого трения, и хотя бы одна из ног вынуждена начать скольжение.

Отметим, что в случае $\mu = 0$ скользить будут обе ноги. Из положения покоя (2.2) тело наклонится, а его центр масс опустится строго по вертикали.

2.2. Вторая особенность. Вернемся к исходной задаче ($c = \infty $). Положение равновесия $\{ \varphi {\kern 1pt} *,y_{{{{G}_{1}}}}^{*}\} $ системы не зависит от наличия тангенциальных реакций и может быть получено из следующих уравнений:

Очевидно, что при любом заданном $\varphi {\kern 1pt} *$ величина $d$ определяется однозначно. Причем в области малых значений $\varphi {\kern 1pt} *$ эти значения практически линейно зависят от d:

вследствие чего, в этой области зависимости $\varphi {\kern 1pt} *(d)$, $y_{{{{G}_{1}}}}^{*}(d)$ однозначные. Отметим, что у механической системы не существует другого положения равновесия, кроме положений (2.6), найденных для случая гладкой плоскости. В отличие от других задач с сухим трением, положение равновесия – изолированное! В этой задаче не существует привычной для задач с сухим трением “зоны застоя” по наклону!

3. Динамика системы.

3.1. Уравнения движения при скольжении обеих ног. Очевидно, если трение отсутствует или достаточно мало, то в процессе движения скользят обе точки опоры. Уравнения движения имеют вид:

Здесь $J$ – центральный момент инерции тела, ${{l}_{1}}$ – длина левого опорного стержня АА₁, ${{l}_{2}}$ – длина правого опорного стержня ВВ₁.

Величины нормальных реакций в точках опор определяем из следующих соотношений:

3.2. Скольжение одной ноги. Предположим, что скорость правой точки опоры оказалась равной нулю. Если в дальнейшие мгновения точка В₁ будет неподвижна, то число степеней свободы уменьшилось на единицу, динамическая система должна содержать два уравнения второго порядка. В качестве обобщенных переменных оставим вертикальную координату центра масс ${{y}_{{{{G}_{1}}}}}$ и угол $\varphi $. Уравнения движения принимают вид:

где ${{J}_{{{{B}_{1}}}}}$ – момент инерции тела относительно точки В₁.

Отметим, что при таком “вращении” системы вокруг точки В₁ скорость точки А₁ может быть равной нулю, только одновременно с равенством нулю угловой скорости $\dot {\varphi }$.

Теперь необходимо определить горизонтальную реакцию в точке В₁. Положение центра масс можно определить из следующего геометрического соотношения:

Дважды дифференцируя (3.3), получим зависимость ускорения центра масс:

Из первого уравнения (2.6) определим значение горизонтальной реакции в правой точке: ${{F}_{{{\text{fr2stat}}}}} = m\ddot {x} - {{F}_{{{\text{fr1}}}}}$ = $m\ddot {x} + \mu \operatorname{sign} ({{V}_{{{{x}_{{A1}}}}}})\left| {{{N}_{1}}} \right|$.

Вычислим знак разности $\Delta = \mu {{N}_{2}} - \operatorname{abs} ({{F}_{{{\text{fr2stat}}}}})$. Если выполнено:

то опорная точка находится в конусе трения и останется неподвижной в течение некоторого промежутка времени. В противном случае скорость опорной точки поменяет знак, и она продолжит движение в противоположную предыдущему движению сторону.

Выберем в качестве начальных условий для движения положение (2.2) с нулевыми скоростями:

Тогда неравенство (3.5) примет следующий вид:

В этом случае правая опора не начнет скользить. Для $\mu < {{\mu }_{2}}$ обе ноги с самого начала начнут скольжение. Аналогичные рассуждения возможно провести и в случае остановки левой точки А₁.

4. Численный счет. В силу жесткости механической системы при малых скоростях и углах вблизи положения равновесия могут возникать быстрые переключения действия сил (например, при изменении направления скорости опорной точки, движении опорных точек в разные стороны и т.д.). Эти переключения трудно контролировать при численном счете. Сказываются довольно случайные процессы, такие как ошибки счета, и всякие округления. Например, при расчете ускорения центра масс (соответственно и скоростей точек опоры) возникают нерегулярные, почти мгновенные отклонения (всплески, дергания) расчетных величин от основной расчетной траектории. Причем, при расчете методом Рунге–Кутта высокого порядка эти всплески ускорения могут быть абсолютно незаметны на поведении скорости и координаты центра масс, представляющие собой довольно гладкие функции времени.

Результаты численного счета продемонстрируем на следующем наборе параметров:

Решив систему (2.5), определим положения равновесия для выбранного набора параметров:

Выберем (3.6) в качестве начальных условий. Начальные координаты центра масс системы следующие: $({{x}_{{{{G}_{1}}}}}_{0},{{y}_{{{{G}_{1}}0}}})$ = $(d, - mg{\text{/}}2k)$ = (10, –0.5). Система при ненулевом трении будет совершать переход из начального положения в равновесное (4.1). Так как $d > 0$, правая опора более нагружена, чем левая. Поэтому следует ожидать, что после старта системы первой остановится правая опорная точка В₁.

Определим значение коэффициента трения, при котором для выбранных начальных условий правая точка опоры не начинает скольжение:

Численный расчет движения системы проведен для нескольких значений коэффициента демпфирования в широком диапазоне значений коэффициента трения $\mu $.

4.1. Расчет для малого трения. Для начала рассмотрим поведение системы при нулевом значении коэффициента демпфирования h и малых коэффициентов трения $\mu $. На рис. 3 изображены полученные колебания (красные кривые $\mu = 0$, зеленые кривые $\mu = 0.001$, синие кривые $\mu = 0.002$).

В отсутствие демпфирования и трения система консервативна и ее центр масс может двигаться только по вертикали. При этом тело совершает незатухающие угловые колебания около равновесного значения $\varphi {\kern 1pt} *$. Точки опоры колеблются с такой же частотой около некоторого их положения. При введении малого трения амплитуда этих колебаний убывает. Центр масс системы постоянно, хотя и неравномерно смещается вправо. Его горизонтальная скорость ${{V}_{{x{{G}_{1}}}}}$, отслеживая колебания опорных точек, “дребезжит”, чередуя участки практически линейного роста и линейного уменьшения. Разделяет эти участки кратковременное движение с почти постоянной скоростью ${{V}_{{x{{G}_{1}}}}}$. Это связано с тем, что опоры на этом интервале скользят в разные стороны. С увеличением трения амплитуда колебаний угла наклона уменьшается, амплитуда дребезга скорости центра масс увеличивается.

4.2. Влияние демпфирования. В случае гладкой опоры ($\mu = 0$) с увеличением коэффициента демпфирования система ведет себя как обычная колебательная система. Значение коэффициента демпфирования $h = h{\kern 1pt} * = 2\sqrt {2mk} $, назовем критическим. При $h{\kern 1pt} *$ затухание колебаний происходит апериодически (и быстрее, чем для любых других значений h). Для выбранного набора параметров $h{\kern 1pt} * = 0.{\text{89443}}$.

4.3. Влияние сухого трения. Рассмотрим эволюцию переходного движения с дальнейшим ростом коэффициента трения $\mu $. На рис. 4 показан результат расчета с учетом возможных остановок точек опоры при $h = 0.0001$ для $\mu = 0.{\text{02}}$ и $\mu = 0.{\text{05}}$ цветными кривыми (розовые кривые – расчет системы (3.1), синие кривые – расчет системы (3.2)) ($\mu = 0.{\text{02}}$), голубые кривые – расчет системы (3.2)) ($\mu = 0.{\text{05}}$). Оба этих значения далеки от критического значения коэффициента трения для левой точки. При этом $\mu = 0.{\text{02}}$ почти в 2 раза меньше, а $\mu = 0.{\text{05}}$ чуть больше критического значения ${{\mu }_{2}}$ коэффициента трения (4.2) для правой точки.

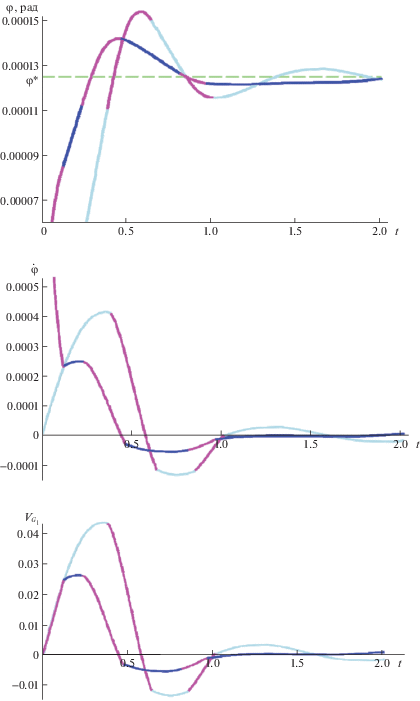
При $\mu = 0.{\text{02}}$ правая опора в начальный момент начинает скольжение. Однако в некоторых фазах качания тела эта опора останавливается. Происходит чередование режимов покоя и скольжения точки В₁.

При $\mu = 0.{\text{05}}$, наоборот, правая опора сначала покоится, но потом в некоторых фазах качания тела она начинает проскальзывать.

4.4. Коэффициент трения, при котором правая опора не начинает скольжение. Представляет интерес оценить значение коэффициента трения, при котором правая опора так и не начнет скольжение. Для получения такой оценки проведена серия расчетов. С ростом $\mu $ промежуток времени, на котором правая опора может скользить, уменьшается. Начиная с некоторого значения $\mu $, правая опора не будет скользить во все время переходного процесса. Мы не ставили задачу точного определения такого значения. Ниже (рис. 5) представлены графики расчета переходного процесса для значений $\mu = 0.{\text{1}}$ и $\mu = 0.{\text{25}}$.

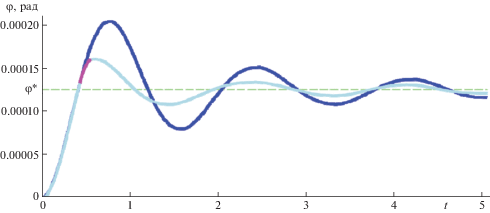
В отличие от случая $\mu = 0.{\text{1}}$, при $\mu = 0.{\text{25}}$ правая опора покоится все время переходного периода.

Заключение. Рассмотрена задача о поведении тела с упругими опорами на плоскости с сухим трением. Показано, что введение податливости лишь по части связей может вызвать внутренний “конфликт” со связями, которые остались твердыми, приводящий к резкому увеличению их необходимых реакций и практически к отсутствию возможности реализации этих связей.

Даже простейшее переходное движение тела из некоторого состояния покоя в положение равновесия сопровождается проскальзыванием одной или обеих опор в зависимости от величины коэффициента трения. Отличие между гладкой и шероховатой опорными плоскостями проявляется в том, что для последней центр масс тела имеет тенденцию смещения вправо при $d > 0$ (влево при $d < 0$).

Для коэффициента трения есть несколько областей значений, при которых процесс перехода к положению равновесия происходит качественно по-разному.