Прикладная математика и механика, 2021, T. 85, № 6, стр. 734-741

В трансзвуковой аэродинамике важное место занимают исследования течений со звуковыми линиями. Наиболее известные свойства звуковых линий получены для стационарных потенциальных течений [1, 2]. Для плоскопараллельных течений доказана теорема [1] (теорема Никольского–Таганова), из которой следует, что если двигаться вдоль звуковой линии так, чтобы область дозвуковых скоростей лежала слева, то вектор скорости будет монотонно (может быть, не строго монотонно) поворачиваться по часовой стрелке. В общем пространственном случае исследованы течения [2], в которых нет сверхзвуковых точек, но есть хотя бы одна звуковая точка. Доказано, что если звуковая точка лежит не на границе, а внутри течения, то через нее проходит плоская поверхность (в двухмерном случае – прямая линия или часть прямой линии), простирающаяся до границ течения и состоящая из звуковых точек, причем вектор (звуковой) скорости в каждой точке этой поверхности направлен по нормали к ней. Из этого факта для широкого класса обтекаемых тел следует [2], что первые звуковые точки при медленном (когда в каждый момент времени картину течения можно считать стационарной) увеличении скорости набегающего потока появляются именно на поверхности обтекаемых тел. Последнее обстоятельство учитывается при построении конфигураций с максимальным критическим числом Маха (например, [3]). Вопрос об изолированности таких точек на звуковой линии, в которых нарушается строгая монотонность поворота вектора скорости, рассмотрен в монографии [4]. В этой же монографии исследуется местная сверхзвуковая область, ограниченная обтекаемой поверхностью, слабой ударной волной и звуковой линией. В учебнике [5] можно найти решение задачи о звуковой струе. Это режим истечения дозвукового потока из сужающегося сопла в пространство с пониженным давлением, сопровождающийся дополнительным разгоном потока до скорости звука, при котором однородный звуковой поток (звуковая струя) образуется на конечном расстоянии от среза сопла и следует за плоской звуковой поверхностью перпендикулярно ей. Другие интересные факты, связанные со звуковыми линиями в соплах, можно найти в учебнике [6], где, в частности, отражены результаты [7] исследования звуковой линии в окрестности центра сопла Лаваля. Там же приведено доказательство двухмерной теоремы, аналогичной теореме [2] (о существовании и прямолинейности звуковой линии, проходящей через звуковую точку) для течений, в которых кроме звуковых и дозвуковых точек могут быть и сверхзвуковые точки. Следует заметить, что первые результаты о прямых звуковых линиях для симметричных сопел (например, [8, 9]) получены ранее результатов [1, 2]. Исследования [1, 2] упомянуты выше в первую очередь потому, что они относятся как к течениям в несимметричных каналах, так и к внешнему обтеканию. Более полный обзор работ по звуковым линиям в соплах можно найти в статье [10], где, в том числе, получена форма остроконечной головной части такого осесимметричного тела, при осесимметричном обтекании которого реализуется одновременно две звуковые линии. Прямая звуковая линия, ортогональная оси симметрии, и примыкающая к ней и проходящая по поверхности тела звуковая линия тока.

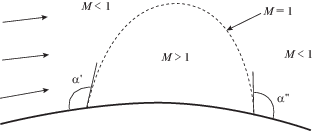
В статьях и монографиях, посвященных исследованию местных сверхзвуковых зон, примыкание звуковой линии к обтекаемой поверхности изображают обычно [1, 4–6] так, что углы примыкания звуковой линии с дозвуковой стороны больше 90 градусов (углы $\alpha {\kern 1pt} '$ и $\alpha {\kern 1pt} ''$ на рис. 1).

Такая же картина наблюдается не только при изображении местных сверхзвуковых зон. Показано [6], что в сопле Лаваля возможны два типа звуковых линий, одна из которых искривлена, а другая прямолинейна. На соответствующем рисунке [6] искривленная звуковая линия примыкает к стенке под углом больше 90 градусов с дозвуковой стороны, а прямая – по нормали. Факт примыкания прямой звуковой линии по нормали представляется очевидным, поскольку на всей прямой звуковой линии скорость газа ортогональна звуковой линии. Что касается угла примыкания искривленной звуковой линии, то, как в случае сопла Лаваля, так и в случае обтекаемой поверхности (рис. 1), данные об этом вопросе, основанные на строгом анализе полных уравнений Эйлера в окрестности точки примыкания, отсутствуют в доступной литературе, что и побудило провести настоящее исследование.

1. Обозначения и основные положения. Рассмотрим пространственное стационарное изоэнергетическое (поле полной энтальпии однородно) и изоэтропийное течение идеального (отсутствуют вязкость и теплопроводность) совершенного (выполняется закон Менделеева–Клапейрона) газа с постоянными теплоемкостями в области, в которой нет точек торможения, а параметры течения являются достаточно гладкими функциями координат. В силу известной теоремы Крокко [11] такое течение будет безвихревым. Используем обычные обозначения: V – скорость, $V = \left| {\mathbf{V}} \right|$, ρ – плотность, p – давление, γ – показатель адиабаты $(1 < \gamma \leqslant {5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3})$, $c = \sqrt {\gamma p{\text{/}}\rho } $ – адиабатическая скорость звука, ${\text{M}} = V{\text{/}}c$ – (местное) число Маха.

2. Кривизна линии тока и направление градиента числа Маха. Изоэнергетичность и изоэнтропийность означают, что полная энтальпия ${{h}_{0}}$ = $\gamma p{\text{/}}\rho {\text{/}}(\gamma - 1)$ + ${{{\mathbf{V}}}^{2}}{\text{/2}}$, которую также можно выразить формулой

и энтропийная функция $p{\text{/}}{{\rho }^{\gamma }}$ одинаковы во всех точках течения. Отсюда следует (см., например, [12], гл. V]), что где ${{p}_{0}} = {\text{const}}$ – давление торможения.

Поскольку скорость V отлична от нуля, в каждой точке рассматриваемой области течения существует единичный касательный к линии тока вектор $e = {V \mathord{\left/ {\vphantom {V V}} \right. \kern-0em} V}$. По определению кривизны и центра кривизны, вектор $({\mathbf{e}} \cdot \nabla ){\mathbf{e}}$ направлен в сторону центра кривизны линии тока, а его длина $\left| {(e \cdot \nabla )e} \right|$ равна кривизне линии тока.

Поскольку $(V \cdot \nabla )V$ = $V(e \cdot \nabla )(Ve)$ = $eV(e \cdot \nabla )\,V$ + ${{V}^{2}}(e \cdot \nabla )\,e$, уравнение Эйлера $(V \cdot \nabla )V$ = $ - (\nabla p){\text{/}}\rho $ можно представить в виде

Учитывая, что вектор $(e \cdot \nabla )\,e$ ортогонален $e$, из (2.3) получаем, что, если кривизна линии тока $\left| {(e \cdot \nabla )\,e} \right|$ отлична от нуля, то нормальная к линии тока составляющая $\nabla p$ отлична от нуля и направлена от центра кривизны. Вместе с уравнением (2.2) это означает следующее.

Утверждение 1. Если кривизна линии тока отлична от нуля, то нормальная к линии тока составляющая градиента числа Маха $\nabla M$ также отлична от нуля и направлена в сторону центра кривизны, а при нулевой кривизне она равна нулю.

Заметим, что утверждение 1 верно в общем пространственном случае (поскольку формулы (2.2) и (2.3) верны в общем пространственном случае).

3. Плоскопараллельное обтекание криволинейной поверхности. Пусть в некоторой точке $A$ на обтекаемой поверхности M = 1. И пусть кривизна поверхности (а вместе с ней и кривизна линии тока) в точке $A$ отлична от нуля так, что обтекаемая поверхность вогнута в сторону течения (направления от точки $A$ к внутренним точкам течения и к центру кривизны совпадают). Тогда, согласно утверждению 1, в некоторой окрестности точки $A$ на нормали к поверхности (кроме самой точки $A$) будут расположены только сверхзвуковые точки.

Теперь рассмотрим случай, когда звуковая точка $A$ есть точка примыкания звуковой линии к вогнутой в сторону внутренних точек течения обтекаемой поверхности. Если вектор $\nabla M$ отличен от нуля, то он направлен по нормали к звуковой линии. Поэтому, учитывая, что на нормали к поверхности расположены сверхзвуковые точки, из утверждения 1 получаем следующее.

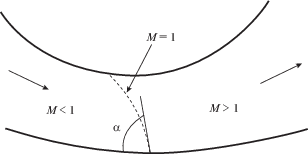
Утверждение 2. В случае вогнутой в сторону внутренних точек течения обтекаемой поверхности угол примыкания звуковой линии с дозвуковой стороны строго меньше 90 градусов (рис. 2), а в случае выпуклой в сторону внутренних точек течения обтекаемой поверхности этот угол строго больше 90 градусов (рис. 1).

В свою очередь, из утверждения 2 для случая прямой звуковой линии, т.е. для линии, во всех точках которой M = 1, а скорость газа перпендикулярна этой линии, получаем следующее.

Утверждение 3. Прямая звуковая линия всегда примыкает к поверхности под прямым углом и не может примыкать к поверхности в точках ненулевой кривизны.

4. Плоскопараллельное обтекание прямолинейного участка поверхности. Пусть звуковая линия примыкает в точке $A$ к прямолинейному участку обтекаемой поверхности. Рассмотрим отдельно два случая $\nabla M(A) \ne 0$ и $\nabla M(A) = 0$, учитывая то, что кривизна поверхности в точке A равна нулю.

При $\nabla M(A) \ne 0$, с одной стороны, вектор $\nabla M(A)$ направлен по нормали к звуковой линии, а с другой стороны, согласно утверждению 1, он направлен по касательной к обтекаемой поверхности. Поэтому угол примыкания звуковой линии равен 90 градусов.

Покажем, что в случае $\nabla M(A) = 0$ угол примыкания также равен 90 градусов. В [6] приведено достаточное условие прохождения прямой звуковой линии через звуковую точку. Оно сформулировано в виде теоремы ([6], глава IV, параграф 26, теорема 4), одно из условий которой требует, чтобы звуковая точка была центром течения, т.е. чтобы проходящая через нее звуковая линия была ортогональна линии тока. Но именно ортогональность нам и требуется доказать. Поэтому упомянутая теорема в данном случае неприменима. Однако идея доказательства этой теоремы в случае $\nabla M(A) = 0$ позволяет провести исследование без предположения об ортогональности звуковой линии и линии тока. Проведем доказательство аналогично [6]. Пусть u и ${v}$ есть x и y компоненты скорости V в прямоугольной декартовой системе координат, ось x которой направлена по касательной к линии тока в звуковой точке A. Начало координат поместим в точку A. Компоненты скорости и скорость звука удовлетворяют двум уравнениям

Если первое уравнение (4.1) продифференцировать по x, а второе последовательно продифференцировать по x дважды, то вместе с уравнениями (4.1) получится система из пяти уравнений. Непосредственной проверкой можно убедиться, что эту систему алгебраическими операциями можно преобразовать в систему обыкновенных дифференциальных уравнений ${\text{d}}{\kern 1pt} {g \mathord{\left/ {\vphantom {g {dy}}} \right. \kern-0em} {dy}}$ = Hg относительно пяти функций ${\mathbf{g}}(x,y)$ = (u – c, ${v},{{u}_{x}},{{{v}}_{x}},{{{v}}_{{xx}}})$, рассматриваемых как функции y при $x = 0$, где компоненты матрицы H зависят (при $x = 0$) только от $y$ и непрерывны в окрестности точки $A$ (в окрестности точки $y = 0$). Выражения для всех компонент матрицы H приводить не будем из-за их громоздкости. Ограничимся “самой простой” – третьей строкой матрицы, полученной дифференцированием по x первого уравнения (4.1). Эта строка имеет вид $(0,0,0,0,1)$.

В силу того, что ось x в окрестности точки $A$ совпадает с линией тока, в этой точке ${v} = {{{v}}_{x}} = {{{v}}_{{xx}}} = 0$. А в силу $\nabla M(A) = 0$ величина ${{u}_{x}}$ в точке $A$ также равна нулю. Поэтому, учитывая, что $u(0,0) - c(0,0) = 0$, имеем ${\mathbf{g}}(0,0)$ = $(0,0,0,0,0)$. В этом случае из теоремы существования и единственности для системы $d{\kern 1pt} {g \mathord{\left/ {\vphantom {g {dy}}} \right. \kern-0em} {dy}}$ = $Hg$ следует, что в некоторой окрестности точки $y = 0$ выполняется равенство ${\mathbf{g}}(0,y)$ = $(0,0,0,0,0)$, в частности $u(0,y) - c(0,y) = 0$ и ${v}(0,y) = 0$. Поэтому звуковая линия лежит на нормали, и угол примыкания звуковой линии равен 90 градусов.

Заметим, что отличие приведенного здесь доказательства от доказательства [6] состоит лишь в основаниях, из которых следует равенство ${\mathbf{g}}(0,0)$ = $(0,0,0,0,0)$. Также необходимо отметить, что из приведенного доказательства не следует, что звуковая линия единственна. Действительно, условие $\nabla M(A) = 0$ допускает однородный звуковой поток над прямолинейным участком поверхности. В этом случае к точке $A$ примыкает бесконечное число различных звуковых линий, в том числе и та звуковая линия, существование которой показано выше. Это обстоятельство будет учтено ниже при формулировке результата.

Таким образом, после рассмотрения двух возможных случаев $\nabla M(A) \ne 0$ и $\nabla {\text{M}}(A)$ = 0 можно сделать следующий вывод.

Утверждение 4. Если течение не является однородным звуковым потоком, и если к прямолинейному участку обтекаемой поверхности примыкает звуковая линия, то угол примыкания равен 90 градусам.

5. Осесимметричное незакрученное обтекание. Если под кривизной поверхности понимать кривизну сечения обтекаемой поверхности плоскостью, проходящей через ось симметрии течения, а под звуковой линией понимать сечение этой плоскостью звуковой поверхности, то три первых утверждения, полученные выше, остаются в силе для незакрученных осесимметричных течений. При этом их доказательства также остаются без изменений. Что касается угла примыкания к прямолинейному участку, то соответствующее утверждение отличается от утверждения 4. Чтобы разобраться в этом вопросе, как и в предыдущем разделе, рассмотрим отдельно два случая $\nabla {\text{M}}(A) \ne 0$ и $\nabla {\text{M}}(A) = 0$.

При $\nabla M(A) \ne 0$, как и для плоскопараллельного течения, из утверждения 1 получаем, что угол примыкания звуковой линии равен 90 градусам.

Перейдем к случаю $\nabla M(A) = 0$. Расположим прямоугольную декартову систему координат $Axy$ в плоскости, проходящей через ось симметрии течения. Ось $x$ направим вдоль прямолинейной образующей обтекаемой поверхности так, чтобы радиальная компонента положительного направления оси $y$ была направлена к оси симметрии. Тогда компоненты скорости и скорость звука будут удовлетворять двум уравнениям:

где $\varphi $ – острый угол между осью $x$ и осью симметрии течения. Знак этого угла нужно выбрать так, чтобы расстояние $r$ до оси симметрии выражалось формулой $r = {{r}_{A}} - x\sin \varphi - y\cos \varphi $. В силу того, что ось $x$ в окрестности звуковой точки $A$ совпадает с линией тока, в этой точке

В случае $\varphi = 0$, когда прямолинейные образующие обтекаемой поверхности параллельны оси симметрии, уравнения (5.1), (5.2) и условия (5.3) позволяют повторить с небольшими изменениями доказательство предыдущего раздела и прийти к следующему выводу.

Если прямолинейный участок образующей обтекаемой поверхности параллелен оси симметрии незакрученного осесимметричного течения, не являющегося однородным звуковым потоком, и если к этому участку примыкает звуковая линия, то угол примыкания равен 90 градусам.

Для случая $\varphi \ne 0$ в первую очередь исключим из рассмотрения течения с числом Маха $M \leqslant 1$, т.е. течения, в которых нет сверхзвуковых точек, а звуковая линия разделяет дозвуковые зоны. Дело в том, что, как показано в [2], такая линия будет прямой звуковой линией. Поэтому в точке $A$ величина ${{{v}}_{y}}$ должна равняться нулю, что противоречит равенству ${{{v}}_{y}}(A) = c\sin \varphi {\text{/}}r$, вытекающему из (5.1)–(5.3). То есть примыкание звуковой линии, разделяющей звуковые зоны к наклонному $(\varphi \ne 0)$ участку поверхности в незакрученных осесимметричных течениях невозможно. Следовательно, достаточно рассмотреть случаи, когда звуковая линия разделяет звуковую и сверхзвуковую зоны или две сверхзвуковые зоны. В этих случаях из $\nabla {\text{M}}(A) = 0$ следует, что ${{{\text{M}}}_{{xx}}}(A) \geqslant 0$ (иначе при отрицательных $x$ в некоторой окрестности точки $A$ были бы дозвуковые точки). Из $\nabla M(A) = 0$, а также из равенств (5.3) и из уравнения (2.1), продифференцированного по $x$, следует, что в точке $A$ производные ${{c}_{x}}$ и ${{u}_{x}}$ равны нулю. С учетом этого, из ${{M}_{{xx}}}(A) \geqslant 0$ и из уравнения (2.1), дважды продифференцированного по $x$, в точке $A$ имеем соответственно ${{u}_{{xx}}} \geqslant {{c}_{{xx}}}$ и 0 = $2{{c}_{{xx}}}{\text{/}}(\gamma - 1)$ + ${{u}_{{xx}}}$. Это возможно только, если ${{u}_{{xx}}}(A) \geqslant 0$.

Обозначим $\delta = {{u}^{2}} + {{{v}}^{2}} - {{c}^{2}}$ = $(\gamma + 1)({{u}^{2}} + {{{v}}^{2}}){\text{/2}}$ – $(\gamma - 1){{h}_{0}}$. На звуковой линии функция $\delta (x,y)$ равна нулю. Если уравнения (5.1) и (5.2) продифференцировать по $x$, то получится еще два уравнения. Вместе с (5.1)–(5.3) и с учетом условия $\nabla M(A) = 0$ эти два уравнения позволяют выразить первые и вторые производные функции $\delta $ в точке $A$:

Пусть функция $g(x)$ такова, что звуковая линия совпадает с ее графиком $(y = g(x))$. Если два раза продифференцировать тождество $\delta (x,{\text{g}}(x)) \equiv 0$ и подставить значения производных $\delta $ из (5.4), то получится, что в точке $A$ имеет место равенство $(\gamma + 1)\,c{{u}_{{xx}}}$ + + $[(\gamma + 1)\,{{c}^{2}}{{\sin }^{2}}\varphi {\text{/}}{{r}^{2}}]{{[{\text{g}}{\kern 1pt} '(0)]}^{2}}$ = 0. Вместе с ${{u}_{{xx}}}(A) \geqslant 0$ это означает, во-первых, что ${{u}_{{xx}}}(A) = 0$, во-вторых, что ${\text{g}}{\kern 1pt} '(0) = 0$. Т.е. угол примыкания звуковой линии с дозвуковой стороны равен или нулю или 180 градусам. Учитывая, что, согласно (5.4), значение ${{\delta }_{{yy}}}$ в точке $A$ положительно, а ${{\delta }_{y}} = 0$, приходим к заключению, что на оси $y$ в некоторой окрестности точки $A$ лежат сверхзвуковые точки. Поэтому из двух упомянутых углов возможен только нулевой угол примыкания с дозвуковой стороны. Таким образом, доказано следующее.

Утверждение 5. Если прямолинейный участок образующей обтекаемой поверхности не параллелен оси симметрии незакрученного осесимметричного течения, то звуковая линия может примыкать к нему, либо под нулевым, либо под прямым углом.

6. Замечание о первых звуковых точках. Исследование мест появления первых звуковых точек при медленном (когда в каждый момент времени картину течения можно считать стационарной) увеличении скорости набегающего потока проводится с помощью теорем, полученных ранее [1, 2]. Для плоскопараллельных течений из теоремы Никольского–Таганова [1] следует, что на вогнутой в сторону внутренних точек течения обтекаемой поверхности не могут появляться первые звуковые точки. Из утверждения 1 это свойство вытекает как для плоскопараллельных, так и для осесимметричных течений.

Утверждение 6. В плоскопараллельном течении на вогнутой в сторону внутренних точек течения обтекаемой поверхности, а в незакрученном осесимметричном течении на вогнутой в сторону внутренних точек течения линии пересечения обтекаемой поверхности с плоскостью, проходящей через ось симметрии, не могут появляться первые звуковые точки.

Заключение. Рассмотрены плоскопараллельные и незакрученные осесимметричные стационарные течения идеального совершенного газа в области, где параметры течения являются достаточно гладкими функциями координат, а полные энтальпия и энтропия постоянны. Исследовался угол примыкания звуковой линии к обтекаемой поверхности. Полученные результаты показывают, что угол примыкания звуковой линии к обтекаемой поверхности со звуковой стороны может быть как острым, так прямым или тупым. Определяющим фактором является кривизна обтекаемой поверхности (под кривизной поверхности в осесимметричных течениях понимается кривизна сечения обтекаемой поверхности плоскостью, проходящей через ось симметрии течения, а под звуковой линией понимается сечение этой плоскостью звуковой поверхности). Как для плоскопараллельных, так и для осесимметричных течений показано, что угол наклона с дозвуковой стороны на выпуклых в сторону течения поверхностях больше 90 градусов, на вогнутых – меньше 90 градусов. Для прямолинейных участков выводы различны для плоскопараллельных и для осесимметричных течений. Для плоскопараллельных течений угол примыкания к прямолинейному участку всегда равен 90 градусам. А для осесимметричных течений этот угол может быть или 90 градусов, или 0 градусов (примыкание по касательной). Полученные результаты строго обосновывают правильность изображения углов примыкания в статьях и монографиях [1, 4–6], упомянутых во введении.

Показано, что первые звуковые точки не могут возникать на вогнутых в сторону течения поверхностях (для плоскопараллельных течений этот вывод следует также из теоремы Никольского–Таганова).