Прикладная математика и механика, 2021, T. 85, № 6, стр. 792-812
Установившаяся ползучесть узкой мембраны внутри жесткой низкой матрицы
А. М. Локощенко 1, *, В. В. Терауд 1, 2, **, А. Ф. Ахметгалеев 1, ***
1 НИИ механики МГУ им. М.В. Ломоносова
Москва, Россия
2 Самарский государственный технический университет
Самара, Россия
* E-mail: loko@imec.msu.ru
** E-mail: ldrnww@gmail.ru
*** E-mail: Achmet206@yandex.ru
Поступила в редакцию 17.10.2020
После доработки 24.02.2021
Принята к публикации 10.03.2021
Аннотация
Исследуется задача об установившейся ползучести длинной узкой прямоугольной мембраны в стесненных условиях внутри жесткой матрицы при кусочно-постоянной зависимости величины поперечного давления от времени. В задаче рассматривается длинная жесткая матрица прямоугольного сечения, в которой высота меньше половины ширины. В качестве примера исследуется ползучесть мембраны при однократном изменении величины поперечного давления во времени. Рассматриваются два варианта условий контакта мембраны и матрицы: идеальное скольжение и прилипание. В данной работе исследованы четыре стадии ползучести мембраны. На первой стадии (упругое деформирование) мембрана, плоская в начальном состоянии, под действием давления мгновенно упруго деформируется, приобретая форму незамкнутой круговой цилиндрической оболочки. На второй стадии мембрана деформируется в условиях установившейся ползучести вплоть до момента касания верхней стенки матрицы. Третья стадия заканчивается в момент касания мембраной продольных стенок матрицы. На четвертой стадии мембрана контактирует с матрицей по поперечной и продольным сторонам. Расчет проводится до времени практически полного прилегания мембраны к матрице. Применительно к данной постановке задачи рассмотрено правило суммирования парциальных времен прилегания мембраны к матрице.
1. Введение. Аналитически исследуется установившаяся ползучесть в стесненных условиях длинной узкой прямоугольной мембраны, закрепленной вдоль длинных сторон и нагруженной равномерным поперечным давлением $q$, которое может изменяться во времени $t$ по заданному закону. Решение этой задачи в свободных условиях при различных физических и геометрических условиях приведено в монографиях Одквиста [1], Качанова [2] и др.
Приведено [3] моделирование формообразования панелей крыла самолета SSJ-100. Рассматриваются задачи неупругого деформирования трехмерных тел с большими перемещениями и поворотами. Дается экспериментальное обоснование предложенных определяющих уравнений установившейся ползучести для трансверсально изотропных материалов с различными характеристиками при растяжении и сжатии. Проведено [4] экспериментальное измерение деформации мембраны из разных эластомеров.
Исследовано [5] раздувание круглой мембраны при больших деформациях. Вязкоупругие характеристики материала мембраны описываются нелинейным интегральным определяющим уравнением. Представленный численный метод решения сочетает методы решения нелинейных интегральных уравнений Вольтерра и нелинейных обыкновенных дифференциальных уравнений.
Приведены [6–8] результаты теоретического исследования ползучести и длительной прочности мембран из анизотропных материалов. Предложена [6] математическая модель процесса изотермического свободного деформирования узкой прямоугольной мембраны из анизотропного листового материала, подчиняющегося энергетическому варианту кинетической теории ползучести и длительной прочности. Установлено, что с ростом коэффициента нормальной анизотропии предельные возможности исследованных процессов формоизменения возрастают. Приведена [6, 7] математическая модель процесса изотермического свободного деформирования узкой прямоугольной мембраны из анизотропного листового материала, подчиняющегося энергетическому варианту кинетической теории ползучести и длительной прочности. Показано влияние анизотропии механических свойств материала, геометрических размеров заготовки и накопления поврежденности на напряженное и деформированное состояние заготовки, силовые режимы и предельные возможности формообразования. На основе разработанных математических моделей деформирования выполнены теоретические исследования процессов изотермического свободного деформирования узкой прямоугольной мембраны, формообразования угловых элементов многослойных конструкций, штамповки и калибровки трапециевидных элементов трехслойных листовых конструкций из анизотропных высокопрочных материалов в режиме кратковременной ползучести [8]. Выполнено сопоставление результатов расчетов при анализе изотермического свободного деформирования узкой прямоугольной мембраны в предположении переменной и постоянной толщин стенки вдоль дуги окружности.
Особый интерес представляет исследование ползучести рассматриваемой мембраны внутри жесткой матрицы. Ефимов А.Б. с соавторами [9] составили обзор основных феноменологических закономерностей, описывающих постановку задачи контактного взаимодействия общего вида.
В монографиях [10, 11] рассмотрен цикл задач о ползучести такой мембраны внутри жесткой матрицы. Приведены [11] решения задач при учете различных форм матриц: клиновидной [12], криволинейной [13] и прямоугольной при различных условиях на контакте мембраны и матрицы. Во всех приведенных решениях величина равномерного поперечного давления $q$ не зависит от времени $t$. В различных решениях использовались разные модели ползучести: установившаяся, неустановившаяся, дробно-степенная. В случае применения дробно-степенной модели ползучести [14] в зависимости от контактных условий с течением времени мембрана либо заполняет пространство внутри матрицы за конечное или бесконечное время, либо разрушается внутри матрицы [12]. Решена [15] аналогичная задача об установившейся ползучести мембраны при кусочно-постоянной зависимости скорости изменения величины поперечного давления от времени.
Проведено [16] моделирование деформирования длинной узкой прямоугольной мембраны внутри жесткой клиновидной матрицы при различных подходах и различных краевых условиях. Получены все основные соотношения, характеризующие напряженно-деформированное состояние мембраны на различных стадиях деформирования. Приведены результаты численных экспериментов, в которых исследуются особенности деформирования мембран вплоть до разрушения. Аналогичное решение для П-образной матрицы приведено в [17].
Исследована [18] деформация нелинейной вязкоупругой однородной сферической мембраны, содержащей несжимаемую жидкость между двумя жесткими параллельными пластинами. Материал мембраны моделируется нелинейным интегральным определяющим соотношением, которое в частном случае включает квазилинейную вязкоупругость.
В статье Р.А. Васина с соавторами [19] приведено экспериментально-теоретическое исследование ползучести мембран в стесненных условиях. Сформулированы особенности процедуры идентификации определяющих соотношений (нахождения материальных констант) по результатам экспериментов. Приведены методика и результаты определения материальных констант из экспериментов по формовке цилиндрических и сферических оболочек из листовых заготовок.
Методика идентификации определяющих соотношений уравнения ползучести, основанная на использовании упрощенной инженерной модели процесса сверхпластической формовки листового проката в прямоугольную матрицу, построена в рамках основных предположений безмоментной теории оболочек [20]. Применимость этой упрощенной модели обоснована путем прямого сопоставления результатов аналитических расчетов с экспериментальными данными.
Авторы [21] представили теоретическое и численное исследование контакта нелинейной вязкоупругой прямоугольной мембраны, нагруженной равномерным давлением.
Описаны [22] большие контактные деформации и явление адгезии между раздутой гиперупругой мембраной и жесткой подложкой. Исходная форма мембраны – плоская, круглая, закрепленная по краю. Допустимы два условия контакта между мембраной и подложкой: контакт без трения и прилипание. Проведен анализ энергетического баланса без учета диссипации энергии.
Изучен [23] контакт длинной прямоугольной упругой мембраны с жесткой подложкой. Построенная точная модель основана на теории конечных деформаций. Учтены два условия контактов: идеальное скольжение и прилипание, для контакта без трения получено точное решение в замкнутой форме.
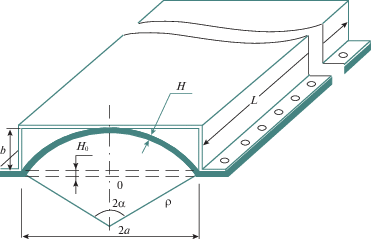
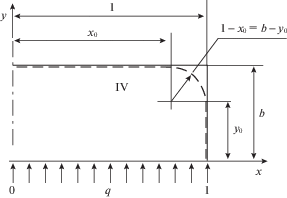
В данной работе исследуется установившаяся ползучесть мембраны толщины ${{H}_{0}}$ внутри жесткой матрицы прямоугольной формы. Ширина, длина и высота матрицы равны соответственно $2a$, $L$, $b$. Отношение высоты матрицы к половине ширины удовлетворяет неравенству $b{\text{/}}a < 1$ (рис. 1). Ширина мембраны $2a$ и ее длина $L$ удовлетворяет неравенству $2a{\text{/}}L \ll 1$. Здесь рассматривается не постоянная величина поперечного давления $q\left( t \right) = {\text{const}}$, а кусочно-постоянная зависимость величины $q\left( t \right)$ с однократным изменением величины $q\left( t \right)$. Представляет интерес рассмотреть особенности практически полного прилегания мембраны к пространству внутри матрицы при скачкообразном увеличении или уменьшении величины $q$.
Для исключения появления в начальный момент времени бесконечных напряжений в данном решении учитывается мгновенное упругое деформирование.
Для описания деформирования мембраны при $t > 0$ ($t$ – время) используется степенная модель установившейся ползучести материала
(1.1)
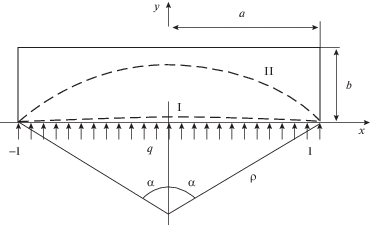
$\frac{{d{{p}_{u}}}}{{dt}} = \frac{1}{{{{t}_{0}}}}{{\left( {\frac{{{{\sigma }_{u}}}}{{{{\sigma }_{0}}}}} \right)}^{n}},$Координаты поперечного сечения мембраны и матрицы назовем $x$ и $y$ (рис. 2). Исследование свободного деформирования проводится в двух последовательных стадиях. На первой стадии (упругое деформирование) мембрана, плоская в начальном состоянии, под действием давления q мгновенно упруго деформируется, приобретая форму незамкнутой круговой цилиндрической оболочки с центральным углом $2{{\alpha }_{1}}$. На второй стадии мембрана деформируется в условиях установившейся ползучести вплоть до касания верхней стенки жесткой матрицы, так как $a > b$, то угол раствора мембраны в конце этой стадии равен $2{{\alpha }_{2}}$ = $2\arcsin \left( {\frac{{2ab}}{{{{a}^{2}} + {{b}^{2}}}}} \right)$. При моделировании напряженно-деформированного состояния мембраны рассматриваются главные напряжения (радиальное ${{\sigma }_{{rr}}}$, окружное ${{\sigma }_{{\theta \theta }}}$ и осевое ${{\sigma }_{{zz}}}$) и соответствующие компоненты тензора деформаций (${{\varepsilon }_{{rr}}}$, ${{\varepsilon }_{{\theta \theta }}}$ и ${{\varepsilon }_{{zz}}}$), при $t > 0$ учитываются только компоненты тензора деформаций ползучести ${{p}_{{rr}}}$, ${{p}_{{\theta \theta }}}$ и ${{p}_{{zz}}}$.
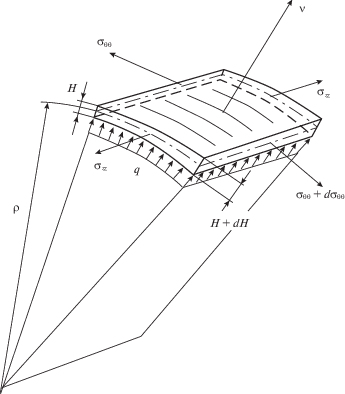
Рассматривая элемент мембраны (рис. 3), принимая напряжения в элементе равномерно распределенными по толщине и записывая уравнения равновесия в проекциях на нормаль и касательную, получаем:
(1.2)
${{\sigma }_{{\theta \theta }}} = \frac{{q\rho }}{H},\quad d\left( {{{\sigma }_{{\theta \theta }}}H} \right) = 0,$Следовательно,
Сопоставляя (1.2) и (1.3), заключаем, что в случае равномерного давления ($q = {\text{const}}$) радиус кривизны срединной поверхности во всех ее точках один и тот же ($\rho = {\text{const}}$), т.е. срединная поверхность мембраны при ее деформировании является частью поверхности кругового цилиндра с некоторым углом раствора $2\alpha $ [3]. В этом случае, очевидно, что если толщина мембраны до деформации постоянна, то она постоянна и после деформации. Следовательно, согласно (1.2) окружное напряжение по длине окружности радиуса $\rho $ не изменяется.
2. Мгновенное упругое деформирование мембраны (первая стадия). Упругое деформирование мембраны описывается с помощью закона Гука при сложном напряженном состоянии с учетом несжимаемости материала. При этом будут использоваться следующие обозначения: E – модуль Юнга, ${{\sigma }_{{ij}}}$ – компоненты тензора напряжений. Значения всех рассматриваемых в этом разделе параметров, полученные в результате приложения поперечного давления $q$, принимают дополнительный индекс 1.
Из условия несжимаемости материала получим значение толщины ${{H}_{1}}\left( {{{\alpha }_{1}}} \right)$:
(2.1)
${{H}_{0}}\left( {\sin {{\alpha }_{1}}} \right){{\rho }_{1}} = {{H}_{1}}{{\alpha }_{1}}{{\rho }_{1}},\quad \frac{{{{H}_{1}}}}{{{{H}_{0}}}} = \frac{{\sin {{\alpha }_{1}}}}{{{{\alpha }_{1}}}}$Из уравнений равновесия свободной мембраны получим значение напряжения ${{\sigma }_{{\theta \theta 1}}}$:
Из определения малой деформации получим выражение для окружной деформации ${{\varepsilon }_{{\theta \theta 1}}}$:
(2.2)
${{\varepsilon }_{{\theta \theta 1}}} = \frac{{{{\rho }_{1}}{{\alpha }_{1}} - a}}{a} = \frac{{{{\alpha }_{1}}}}{{\sin {{\alpha }_{1}}}} - 1$В соответствии с условием несжимаемости используем значение коэффициента Пуассона, равное 0.5. Считаем, что мембрана под поперечным давлением находится в условиях плоского деформированного состояния:
Для тонкостенных цилиндрических оболочек обычно принимается условие безмоментного напряженного состояния, при этом выполняется равенство ${{\sigma }_{{rr1}}} = 0$.
Из закона Гука при сложном напряженном состоянии следует связь компонент тензоров напряжений ${{\sigma }_{{ij}}}$ и упругих деформаций ${{\varepsilon }_{{ij}}}$:
(2.4)
${{\varepsilon }_{{zz{\text{1}}}}} = \frac{1}{E}\left( {{{\sigma }_{{zz{\text{1}}}}} - \frac{1}{2}{{\sigma }_{{\theta \theta {\text{1}}}}}} \right)$(2.5)
${{\varepsilon }_{{\theta \theta {\text{1}}}}} = \frac{1}{E}\left( {{{\sigma }_{{\theta \theta {\text{1}}}}} - \frac{1}{2}{{\sigma }_{{zz{\text{1}}}}}} \right)$Из равенства (2.4) при учете (2.3) получаем:
Подставляя (2.6) в (2.5) и учитывая (1.2) и (2.1), получаем:
Приравнивая это выражение выражению (2.2), получаем связь давления $q$ и угла ${{\alpha }_{1}}$:
(2.7)
$\frac{{3qa{{\alpha }_{1}}}}{{4E{{H}_{0}}{{{\sin }}^{2}}{{\alpha }_{1}}}} = \frac{{{{\alpha }_{1}}}}{{\sin {{\alpha }_{1}}}}\left( {1 - \frac{{\sin {{\alpha }_{1}}}}{{{{\alpha }_{1}}}}} \right),\quad \frac{q}{{{{\sigma }_{0}}}} = \frac{{4{{H}_{0}}k}}{{3a}}\left( {1 - \frac{{\sin {{\alpha }_{1}}}}{{{{\alpha }_{1}}}}} \right)\sin {{\alpha }_{1}},\quad k = \frac{E}{{{{\sigma }_{0}}}}$Так как упругое деформирование по определению происходит практически мгновенно, то длительность первой стадии принимается равной нулю: ${{t}_{1}} = 0$.
3. Свободное деформирование мембраны в условиях ползучести (вторая стадия).
Введем безразмерные переменные:
Далее черточки над всеми безразмерными переменными опустим. При этом под скоростями всюду понимаются производные по безразмерному времени.
В качестве связи компонент тензоров напряжений и скоростей деформаций ползучести примем гипотезу пропорциональности соответствующих девиаторов (см., например, [4]):
(3.1)
$\begin{gathered} {{{\dot {p}}}_{{ij}}} = \frac{{3f({{\sigma }_{u}})}}{{2{{\sigma }_{u}}}}({{\sigma }_{{ij}}} - \sigma ),\quad \sigma = \frac{1}{3}\left( {{{\sigma }_{{zz}}} + {{\sigma }_{{\theta \theta }}} + {{\sigma }_{{zz}}}} \right) \\ {{\sigma }_{u}} = \frac{1}{{\sqrt 2 }}\sqrt {{{{\left( {{{\sigma }_{{rr}}} - {{\sigma }_{{\theta \theta }}}} \right)}}^{2}} + {{{\left( {{{\sigma }_{{\theta \theta }}} - {{\sigma }_{{zz}}}} \right)}}^{2}} + {{{\left( {{{\sigma }_{{zz}}} - {{\sigma }_{{rr}}}} \right)}}^{2}} + 6\left( {\sigma _{{z\theta }}^{2} + \sigma _{{\theta z}}^{2} + \sigma _{{zr}}^{2}} \right)} \\ \end{gathered} $В рассматриваемом плоском деформированном состоянии скорость осевой деформации ползучести ${{\dot {p}}_{{zz}}}$ принимается равной нулю:
Далее всюду будем обозначать ${{H}_{i}}(t)$ толщину мембраны на $i$-й стадии ($i = 1{\kern 1pt} - {\kern 1pt} 4$).
Примем, как обычно, для тонкостенных цилиндрических оболочек равенство:
в этом случае из гипотезы пропорциональности девиаторов напряжений и скоростей деформаций ползучести (3.1) при учете (3.2) следует:Рассматривая два близких деформированных состояния мембраны, определим приращение окружной деформации ползучести, учитывая, что деформированное состояние однородное:
Следовательно, скорость окружной деформации ползучести равна
(3.3)
${{\dot {p}}_{{\theta \theta }}} = \frac{{\dot {\rho }}}{\rho } + \frac{{\dot {\alpha }}}{\alpha }$Используя дифференциальное следствие их соотношения
преобразуем выражение (3.3) к виду:(3.5)
${{\dot {p}}_{{\theta \theta }}} = \left( {\frac{1}{\alpha } - \operatorname{ctg} \alpha } \right)\dot {\alpha }$Из условия несжимаемости в случае плоского деформированного состояния получаем:
Так как скорость радиальной деформации ползучести равна
то согласно равенству (3.5) получаем:(3.6)
$ - \frac{{{{{\dot {H}}}_{2}}}}{{{{H}_{2}}}} = \left( {\frac{1}{\alpha } - \operatorname{ctg} \alpha } \right)\dot {\alpha }$Проинтегрируем уравнение (3.6) при начальных условиях: $t = 0$, $\alpha = {{\alpha }_{1}}$, ${{H}_{2}} = {{H}_{1}}$:
(3.7)
${{H}_{2}} = \frac{{\sin \alpha }}{\alpha }S\quad S = \frac{{{{\alpha }_{1}}}}{{\sin {{\alpha }_{1}}}}$Полученные выражения (1.2), (3.4) и (3.7) позволяют представить окружное напряжение ${{\sigma }_{{\theta \theta }}}$ и интенсивность напряжений ${{\sigma }_{u}}$ в зависимости от угла раствора $\alpha $:
(3.8)
${{\sigma }_{{\theta \theta }}} = \frac{{q\rho }}{{{{H}_{2}}{{H}_{0}}}} = \frac{{q\alpha }}{{S{{H}_{0}}{{{\sin }}^{2}}\alpha }},\quad {{\sigma }_{u}} = \frac{{\sqrt 3 }}{2}{{\sigma }_{{\theta \theta }}} = \frac{{\sqrt 3 }}{2}\frac{{q\alpha }}{{S{{H}_{0}}{{{\sin }}^{2}}\alpha }}$Из (1.1) при учете (3.5) и (3.8) получаем зависимость угла раствора $\alpha $ от времени $t$:
(3.9)
$t\left( \alpha \right) = \frac{2}{{\sqrt 3 }}\int\limits_{{{\alpha }_{1}}}^\alpha {\left( {\frac{1}{\alpha } - \operatorname{ctg} \alpha } \right){{{\left( {\frac{{2S{{H}_{0}}{{{\sin }}^{2}}\alpha }}{{\sqrt 3 q \cdot \alpha }}} \right)}}^{n}}d\alpha } ,\quad {{t}_{2}} = t\left( {{{\alpha }_{2}}} \right)$При исследовании второй стадии деформирования мембраны угол $\alpha $ изменяется в диапазоне от $\alpha = {{\alpha }_{1}}$ до ${{\alpha }_{2}}$ – угла, при котором происходит касание мембраной верхней стороны матрицы.
Так как угол ${{\alpha }_{1}}$ удовлетворяет условию ${{\alpha }_{1}} \ll \pi {\text{/}}2$ (т.е. постоянная $S$ незначительно отличается от единицы), то упростим соотношение (3.7) и введем дополнительно зависимость ${{H}_{2}}\left( \alpha \right)$ во время второй стадии деформирования мембраны в виде:
В конце второй стадии ($t = {{t}_{2}}$) максимальный раствор мембраны равен $2\alpha \left( {{{t}_{2}}} \right) = 2{{\alpha }_{2}}$. Так как значения ${{H}_{2}}$ при $S$ из (3.7) и (3.10) практически совпадают (и последующие вычисления подтвердят это), то далее под значением ${{t}_{2}}\left( \alpha \right)$ будем понимать соответствующее значение при $S = 1$. В связи с этим момент времени ${{t}_{2}}$, при котором происходит окончание второй стадии, и толщина мембраны $H_{{\text{2}}}^{^\circ } = H\left( {{{t}_{2}}} \right)$, вычисляемая с учетом зависимости (3.10), определяются согласно уравнениям:
Далее рассматривается ползучесть мембраны внутри жесткой матрицы при различных контактных условиях.
4. Идеальное скольжение мембраны вдоль сторон матрицы.
4.1. Третья стадия ($0 \leqslant {{x}_{0}} \leqslant 1 - b$).
Решение задачи имеет различный характер для относительно высокой матрицы ($b \geqslant 1$) и относительно низкой матрицы ($b < 1$). Для определенности здесь будет рассмотрена ползучесть мембраны внутри относительно низкой матрицы ($b < 1$).
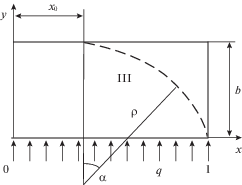
В связи с осевой симметрией мембраны и матрицы в процессе третьей стадии рассматривается ползучесть правой половины мембраны в координатах $0 \leqslant x \leqslant 1 - b$, $0 \leqslant y \leqslant b$ (рис. 4).
Свободное деформирование мембраны было рассмотрено в разд. 2 и 3. В некоторый момент времени ($t = t_{2}^{{}}$) мембрана соприкасается с поперечной стенкой матрицы. На этом свободное деформирование заканчивается, и в дальнейшем при $t > t_{2}^{{}}$ часть поверхности мембраны прилегает к верхней поверхности матрицы.
При исследовании третьей стадии ползучести мембраны выделим два близких деформированных состояния: одно характеризуется длиной участка контакта ${{x}_{0}}$, а другое – длиной участка контакта (${{x}_{0}} + d{{x}_{0}}$). С помощью геометрических соотношений (рис. 4) получим соотношение для приращения окружной деформации ползучести $d{{p}_{{\theta \theta }}}$ в виде:
(4.1)
$d{{p}_{{\theta \theta }}} = \frac{{\rho d\alpha + \alpha d\rho + d{{x}_{0}}}}{{\rho \alpha + {{x}_{0}}}}$Учитывая, что каждое из слагаемых числителя (4.1) содержит множитель $d{{x}_{0}}$, введем обозначения
(4.2)
$\rho d\alpha + \alpha d\rho + d{{x}_{0}} = {{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}},\quad \rho \alpha + {{x}_{0}} = {{B}_{2}}\left( {{{x}_{0}}} \right)$Тогда
(4.3)
$d{{p}_{{\theta \theta }}} = \frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}}}}{{{{B}_{2}}\left( {{{x}_{0}}} \right)}}$С помощью (4.3) вычислим характеристики деформированного состояния
(4.4)
${{\dot {p}}_{{\theta \theta }}} = \frac{{{{B}_{1}}}}{{{{B}_{2}}}}\frac{{d{{x}_{0}}}}{{dt}},\quad d{{\dot {p}}_{u}} = \frac{2}{{\sqrt 3 }}\frac{{{{B}_{1}}}}{{{{B}_{2}}}}\frac{{d{{x}_{0}}}}{{dt}}$Проектируя наклонный радиус $\rho $ (рис. 4) на горизонталь и вертикаль, получим следующие два уравнения:
Откуда следует, что
Подставляя $d\rho \left( {{{x}_{0}}} \right)$ и $d\alpha \left( {{{x}_{0}}} \right)$ в (4.2), получим
(4.5)
$\begin{gathered} \rho d\alpha = \frac{{{{{(a - {{x}_{0}})}}^{2}} + {{b}^{2}}}}{{2b}}\frac{{2b}}{{{{{(1 - {{x}_{0}})}}^{2}} + {{b}^{2}}}}d{{x}_{0}} = d{{x}_{0}} \\ \alpha d\rho = \alpha \left( { - \frac{{1 - {{x}_{0}}}}{b}} \right)d{{x}_{0}} = - \frac{{1 - {{x}_{0}}}}{b}\alpha d{{x}_{0}} \\ {{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}} = - \frac{{1 - {{x}_{0}}}}{b}\left( {\operatorname{arctg} \left( {\frac{{2b(1 - {{x}_{0}})}}{{{{{(1 - {{x}_{0}})}}^{2}} - {{b}^{2}}}}} \right)} \right)d{{x}_{0}} + 2d{{x}_{0}} \\ {{B}_{2}}\left( {{{x}_{0}}} \right) = \frac{{{{{(1 - {{x}_{0}})}}^{2}} + {{b}^{2}}}}{{2b}}\left( {\operatorname{arctg} \left( {\frac{{2b(1 - {{x}_{0}})}}{{{{{(1 - {{x}_{0}})}}^{2}} - {{b}^{2}}}}} \right)} \right) + {{x}_{0}} \\ \end{gathered} $Из условия несжимаемости при учете (3.2) получаем: $\,d{{\dot {p}}_{{\theta \theta }}} = \, - d{{\dot {p}}_{{rr}}}$.
Согласно определению ${{\dot {p}}_{{rr}}}$ имеем ${{\dot {p}}_{{rr}}} = {{\dot {H}}_{3}}{\text{/}}{{H}_{3}}$. Следовательно,
Последнее равенство следует из учета постоянства толщины $H$ мембраны вдоль всего рассматриваемого участка мембраны в конце третьей стадии. Интенсивности деформаций ползучести и напряжений определяются следующими выражениями:
Подставляя эти выражения в (1.1), получаем связь ${{x}_{0}}$ и $t$:
(4.6)
$t\left( {{{x}_{0}}} \right) = {{t}_{2}} + \int\limits_0^{{{x}_{0}}} {\frac{2}{{\sqrt 3 }}\frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)}}{{{{B}_{2}}\left( {{{x}_{0}}} \right)}}{{{\left[ {\frac{{\sqrt 3 }}{4}\frac{{q({{{(1 - {{x}_{0}})}}^{2}} + {{b}^{2}})}}{{{{H}_{0}}{{H}_{3}}\left( {{{x}_{0}}} \right)b}}} \right]}}^{{ - n}}}} d{{x}_{0}},\quad {{t}_{3}} = t\left( {{{x}_{0}} = 1 - b} \right)$4.2. Четвертая стадия ($1 - b \leqslant {{x}_{0}} \leqslant 1 - \Delta $).
На четвертой стадии ползучести мембрана касается обеих сторон матрицы ($1 - b \leqslant {{x}_{0}} \leqslant 1 - \Delta $, $0 \leqslant {{y}_{0}} \leqslant b$) (рис. 5). При этом профиль мембраны представляет собой полуокружность радиуса $(1 - {{x}_{0}})$ и размеры областей контакта по продольной и поперечной осям равны $({{x}_{0}} - (1 - b)) = {{y}_{0}}$. С учетом принятых допущений компоненты тензора деформаций ползучести примут вид:
Окончание четвертой стадии происходит при значении ${{x}_{0}}$, удовлетворяющем неравенству $\left( {1 - x_{{\text{0}}}^{{\text{0}}}} \right) = \Delta $, где $\left( {1 - x_{{\text{0}}}^{{\text{0}}}} \right)$ – радиус кривизны мембраны вблизи угла матрицы.
Интенсивность напряжений определяется следующим соотношением:
(4.6)
${{\sigma }_{u}}\left( {{{x}_{0}}} \right) = \frac{{\sqrt 3 }}{2}\frac{q}{{{{H}_{0}}}}\left[ {b + \tfrac{\pi }{2} - 1 + \left( {2 - \tfrac{\pi }{2}} \right){{x}_{0}}} \right]\left( {1 - {{x}_{0}}} \right)$Интенсивность скоростей деформаций ползучести согласно (4.6) равна:
(4.7)
${{\dot {p}}_{u}} = \frac{2}{{\sqrt 3 }}\frac{{2 - \frac{\pi }{2}}}{{b + \frac{\pi }{2} - 1 + \left( {2 - \frac{\pi }{2}} \right){{x}_{0}}}}\frac{{d{{x}_{0}}}}{{dt}}$Подставляя (4.6) и (4.7) в (1.1), получаем:
Отсюда следует, что
(4.8)
${{t}_{4}}\left( {{{x}_{0}}} \right) = {{t}_{3}} + {{\left( {\frac{2}{{\sqrt 3 }}} \right)}^{{\left( {n + 1} \right)}}}{{\left( {\frac{{{{H}_{0}}}}{q}} \right)}^{n}}\int\limits_{1 - b}^{{{x}_{0}}} {\frac{{\left( {2 - \frac{\pi }{2}} \right)d{{x}_{0}}}}{{{{{\left[ {b + \frac{\pi }{2} - 1 + \left( {2 - \frac{\pi }{2}} \right){{x}_{0}}} \right]}}^{{\left( {n + 1} \right)}}}{{{\left( {1 - {{x}_{0}}} \right)}}^{n}}}}} $Время ${{t}^{{\text{o}}}}$ практически полного заполнения матрицы мембраной определяется выражением (4.8) при замене в верхнем пределе интегрирования ${{x}_{0}}$ на $x_{0}^{0} = 1 - \Delta $:
5. Прилипание мембраны вдоль сторон матрицы.
5.1. Третья стадия ($0 \leqslant {{x}_{0}} \leqslant 1 - b$).
В случае постепенного прилипания материала мембраны к матрице ее контактная часть (с переменной толщиной) не деформируется, а свободная часть (с постоянной толщиной) представляет собой часть дуги окружности. Окружная деформация в свободной части мембраны имеет вид (рис. 4):
Аналогично (4.2) можно получить выражение
Как известно, ${{\dot {p}}_{{rr}}} = {{\dot {H}}_{3}}{\text{/}}{{H}_{3}}$. Из условия несжимаемости $\,{{\dot {p}}_{{\theta \theta }}} = \, - {{\dot {p}}_{{rr}}}$, так что $d{{p}_{{\theta \theta }}}$ = = $ - \frac{{d{{H}_{3}}}}{{{{H}_{3}}}}$ = $\frac{{{{B}_{1}}\left( {{{x}_{0}}} \right)d{{x}_{0}}}}{{{{B}_{3}}\left( {{{x}_{0}}} \right)}}$. После интегрирования, получаем
Интенсивности ${{\sigma }_{u}}$ и ${{\dot {p}}_{u}}$ равны соответственно:
Подставляя выражения ${{\sigma }_{u}}$ и ${{\dot {p}}_{u}}$ в (1.1), получаем:
5.2. Четвертая стадия ($1 - b \leqslant {{x}_{0}} \leqslant 1 - \Delta $).
На четвертой стадии ползучесть мембраны характеризуется касанием ею продольной и поперечной сторон матрицы (рис. 5), тогда
Окончание четвертой стадии происходит при значении $x_{{\text{0}}}^{{\text{0}}}$, удовлетворяющем неравенству $\left( {1 - x_{0}^{0}} \right)$ = $\Delta \ll 1$.
Интенсивность напряжений определяется следующим соотношением:
(5.1)
${{\sigma }_{u}}\left( {{{x}_{0}}} \right) = \frac{{\sqrt 3 }}{2}\frac{q}{{{{H}_{0}}}}\frac{{\left( {1 - {{x}_{0}}} \right)}}{{{{H}_{4}}\left( {{{x}_{0}}} \right)}}$Интенсивность скоростей деформаций ползучести равна:
(5.2)
${{\dot {p}}_{u}} = \frac{2}{{\sqrt 3 }}\frac{{\left( {4 - \pi } \right)}}{\pi }\frac{b}{{\left( {1 - {{x}_{0}}} \right)}}\frac{{d{{x}_{0}}}}{{dt}}$Подставляя (5.1) и (5.2) в (1.1), получаем:
Время практически полного прилегания мембраны к матрице определяется выражением:
6. Ползучесть мембраны при постоянном давлении $q$.
В качестве примера рассмотрим деформирование мембраны при матрице высотой $b = 0.5$ со следующими выбранными параметрами:
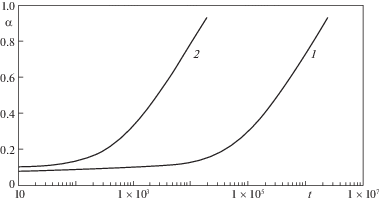
Величина $\Delta = 1 - x_{0}^{0}$ соответствует минимальному расстоянию между поперечной стороной матрицы и мембраной. Вычисления проводятся для трех значений $\Delta $. В качестве величин поперечного давления примем два значения $q$, различающихся в 5 раз: ${{q}_{1}} = 0.5 \times {{10}^{{ - 4}}}$ и ${{q}_{2}} = 2.5 \times {{10}^{{ - 4}}}$, в этом случае значения угла ${{\alpha }_{1}}$, полученные при мгновенном приложении внешнего давления $q$, равны соответственно ${{\alpha }_{1}} = 0.061$ и 0.104. На рис. 6 приведены зависимости $\alpha \left( t \right)$ при $q = {{q}_{1}}$ (кривая 1) и $q = {{q}_{2}}$ (кривая 2). Так как значения отношения $S$ в (3.7) очень незначительно отличаются от 1 (соответственно $S = 1.001$ и $S = 1.002$), то замена соотношения (3.7) на (3.10) является вполне обоснованной.
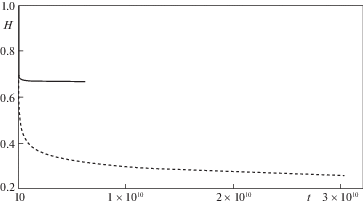
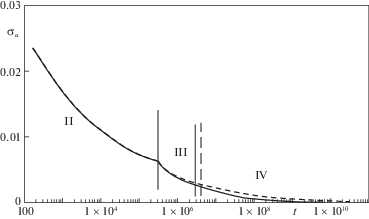
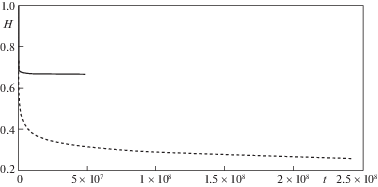
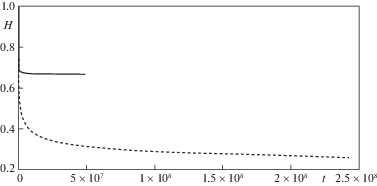
На рис. 7 и 8 соответственно приведены зависимости толщины мембраны $H\left( t \right)$ и интенсивности напряжений ${{\sigma }_{u}}\left( t \right)$ на свободной части мембраны от времени $t$ для всех четырех стадий деформирования при $q = {{q}_{1}}$. Для стадий стесненного деформирования (третья и четвертая стадии) зависимости $H\left( t \right)$ и ${{\sigma }_{u}}(t)$ приведены для идеального скольжения (сплошная линия) и прилипания (штриховая линия). На рис. 9 и 10 соответственно приведены аналогичные зависимости $H(t)$ и ${{\sigma }_{u}}(t)$. На рис. 11 приведены зависимости $x_{0}^{{}}(t)$ в случае идеального скольжения (кривая 1 – при $q = {{q}_{1}}$, кривая 2 – при $q = {{q}_{2}}$). На рис. 12 приведены аналогичные зависимости $x_{0}^{{}}(t)$ в случае прилипания. Значения основных параметров $t$, $H$, ${{\sigma }_{u}}$ в конце каждой стадии приведены в табл. 1 и 2 (колонки A и B) для идеального скольжения и прилипания соответственно.
Рис. 11.
Зависимости ${{x}_{0}}(t)$ в случае идеального скольжения (1 – $q = 0.5 \times {{10}^{{ - 4}}}$, 2 – $q = 2.5 \times {{10}^{{ - 4}}}$).
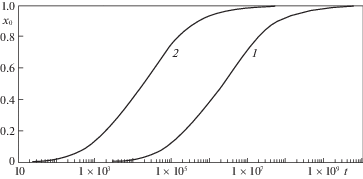
Рис. 12.
Зависимости ${{x}_{0}}(t)$ в случае прилипания (1 – $q = 0.5 \times {{10}^{{ - 4}}}$, 2 – $q = 2.5 \times {{10}^{{ - 4}}}$).
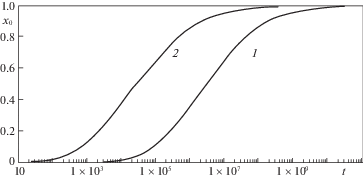
Таблица 1.
Характеристики ползучести мембраны в случае идеального скольжения в конце соответствующей стадии
| Δ | A ${{q}_{1}} = 0.5 \times {{10}^{{ - 4}}}$ |
B ${{q}_{2}} = 2.5 \times {{10}^{{ - 4}}}$ |
C ${{q}_{1}} = 0.5 \times {{10}^{{ - 4}}}$, $t \in \left[ {0,\frac{{\tau _{{\text{1}}}^{{\text{o}}}}}{2}} \right]$ ${{q}_{2}} = 2.5 \times {{10}^{{ - 4}}}$, $t \in [0.5\tau _{{\text{1}}}^{{\text{o}}},\tau _{{\text{2}}}^{{\text{o}}}]$ |
D ${{q}^{2}} = 2.5 \times {{10}^{{ - 4}}}$, $t \in \left[ {0,\frac{{\tau _{{\text{2}}}^{{\text{o}}}}}{2}} \right]$ ${{q}^{1}} = 0.5 \times {{10}^{{ - 4}}}$, $t \in [0.5\tau _{{\text{2}}}^{{\text{o}}},\tau _{{\text{1}}}^{{\text{o}}}]$ |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| № стадии | t | H | σu | t | H | σu | t | H | σu | t | H | σu | |
| 2 | – | 3.19 × 105 | 0.863 | 6.27 × 10–3 | 2.55 × 103 | 0.863 | 3.14 × 10–2 | 3.19 × 105 | 0.863 | 6.27 × 10–3 | 2.55 × 103 | 0.863 | 3.14 × 10–2 |
| 3 | – | 2.42 × 106 | 0.778 | 2.78 × 10–3 | 1.93 × 104 | 0.778 | 1.39 × 10–2 | 2.42 × 106 | 0.778 | 2.78 × 10–3 | 1.93 × 104 | 0.778 | 1.39 × 10–2 |
| 4 | 0.01 | 6.17 × 109 | 0.668 | 6.48 × 10–5 | 4.93 × 107 | 0.669 | 3.24 × 10–4 | 3.11 × 109 | 0.669 | 3.24 × 10–4 | 3.10 × 109 | 0.668 | 6.48 × 10–5 |
| 0.001 | 6.04 × 1011 | 0.667 | 6.49 × 10–5 | 4.83 × 109 | 0.667 | 3.25 × 10–4 | 3.04 × 1011 | 0.667 | 3.25 × 10–4 | 3.05 × 1011 | 0.667 | 6.49 × 10–5 | |
| 0.0001 | 6.03 × 1013 | 0.667 | 6.50 × 10–5 | 4.82 × 1011 | 0.666 | 3.25 × 10–4 | 3.04 × 1013 | 0.666 | 3.25 × 10–4 | 3.04 × 1013 | 0.667 | 6.50 × 10–5 | |
Таблица 2.
Характеристики ползучести мембраны в случае прилипании в конце соответствующей стадии
| Δ | A ${{q}^{1}} = 0.5 \times {{10}^{{ - 4}}}$ |
B ${{q}^{2}} = 2.5 \times {{10}^{{ - 4}}}$ |
C ${{q}^{1}} = 0.5 \times {{10}^{{ - 4}}}$, $t \in \left[ {0,\frac{{\tau _{{\text{1}}}^{{\text{o}}}}}{2}} \right]$ ${{q}^{2}} = 2.5 \times {{10}^{{ - 4}}}$, $t \in [0.5\tau _{{\text{1}}}^{{\text{o}}},{{t}^{{*2}}}]$ |
D ${{q}^{2}} = 2.5 \times {{10}^{{ - 4}}}$, $t \in \left[ {0,\frac{{\tau _{{\text{2}}}^{{\text{o}}}}}{2}} \right]$ ${{q}^{1}} = 0.5 \times {{10}^{{ - 4}}}$, $t \in [0.5\tau _{{\text{2}}}^{{\text{o}}},{{t}^{{*1}}}]$ |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| № стадии | t | H | σu | t | H | σu | t | H | σu | t | H | σu | |
| 2 | – | 3.19 × 105 | 0.863 | 6.27 × 10–3 | 2.55 × 103 | 0.863 | 3.14 × 10–2 | 3.19 × 105 | 0.863 | 6.27 × 10–3 | 2.55 × 103 | 0.863 | 3.14 × 10–2 |
| 3 | – | 3.30 × 106 | 0.752 | 2.88 × 10–3 | 2.63 × 104 | 0.752 | 1.44 × 10–2 | 3.30 × 106 | 0.752 | 2.88 × 10–3 | 2.63 × 104 | 0.752 | 1.44 × 10–2 |
| 4 | 0.01 | 3.06 × 1010 | 0.258 | 1.68 × 10–4 | 2.45 × 108 | 0.258 | 8.39 × 10–4 | 1.54 × 1010 | 0.258 | 8.39 × 10–4 | 1.55 × 1010 | 0.258 | 1.68 × 10–4 |
| 0.001 | 4.64 × 1012 | 0.138 | 3.15 × 10–5 | 3.71 × 1010 | 0.138 | 1.57 × 10–4 | 2.34 × 1012 | 0.138 | 1.57 × 10–4 | 3.32 × 1012 | 0.138 | 3.15 × 10–5 | |
| 0.0001 | 7.03 × 1014 | 0.073 | 3.90 × 10–6 | 5.62 × 1012 | 0.073 | 2.95 × 10–5 | 3.54 × 1014 | 0.073 | 2.95 × 10–5 | 3.04 × 1014 | 0.073 | 3.90 × 10–6 | |
Во всех случаях зависимости $H(t)$ являются монотонно убывающими функциями времени. Расчеты показывают, что интенсивность напряжений ${{\sigma }_{u}}(t)$ монотонно убывает. Толщины свободной части мембраны в конце деформирования при прилипании меньше, чем при идеальном скольжении, а интенсивности напряжений, наоборот, больше.
Вычисления показывают, что при заданных значениях используемых параметров основная длительность деформирования мембраны вплоть до практически полного прилегания мембраны к матрице соответствует четвертой стадии.
7. Ползучесть мембраны при кусочно-постоянном давлении $q$.
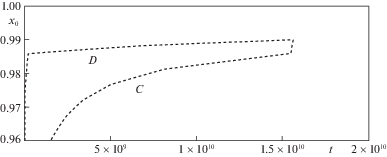
Рассмотрим две программы нагружения. В первой программе (см. колонки С в табл. 1 и 2) сначала деформирование происходит при $q = {{q}_{1}}$ в течение времени ${{\tau }_{1}}$, равного половине соответствующей длительности $\tau _{{\text{1}}}^{{\text{o}}}$ заполнения мембраны при постоянном давлении $q = {\text{const}}$, т.е. ${{\tau }_{1}} = 0.5\tau _{{\text{1}}}^{{\text{o}}}$ (колонка A в табл. 1), затем величина $q$ скачкообразно возрастает и становится равной ${{q}_{2}}$, при $\tau > {{\tau }_{1}}$ рассматривается ползучесть вплоть до практически полного прилегания мембраны к матрице при $t = {{t}^{{*1}}}$. Во второй программе нагружения (колонка D в табл. 1 и табл. 2) сначала мембрана деформируется при $q = {{q}_{2}}$ в течение $0 \leqslant t \leqslant 0.5\tau _{2}^{{\text{o}}}$ (где $\tau _{2}^{{\text{o}}}$ – длительность заполнения матрицы при $q = {\text{const}}$ (колонка В в табл. 1)), а затем мембрана деформируется при $q = {{q}_{1}}$ вплоть до практически полного прилегания мембраны к матрице при $t = {{t}^{{*2}}}$. На рис. 13 приведены зависимости $x_{0}^{{}}(t)$ в случае идеального скольжения при скачкообразном возрастании давления $q(t)$ от ${{q}_{1}}$ до ${{q}_{2}}$ (кривая С) и при мгновенном уменьшении давления от ${{q}_{1}}$ до ${{q}_{2}}$ в (кривая D), при этом в качестве характеристики предельной близости мембраны и матрицы использовано значение $\Delta = 0.01$. На рис. 14 приведены аналогичные кривые $x_{0}^{{}}(t)$ в случае прилипания. В момент мгновенного изменения давления происходит излом зависимости $x_{0}^{{}}(t)$ на рис. 13 и рис. 14.
Рис. 13.
Зависимость ${{x}_{0}}(t)$ при кусочно-постоянной величине $q(t)$ в случае идеального скольжения.
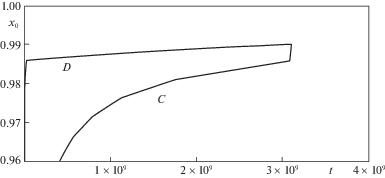
Согласно табл. 1 и 2 при данных значениях ${{q}^{{(1)}}}$ и ${{q}^{{(2)}}}$ скачкообразное изменение $q$ происходит в процессе III и IV стадий. Значение ${{x}_{0}}(0.5\tau _{{\text{1}}}^{{\text{o}}})$ вычисляется подбором такого значения ${{x}_{0}}$, которое соответствует заданному времени $t = 0.5\tau _{{\text{1}}}^{{\text{o}}}$.
Применим к этой задаче правило суммирования парциальных времен $\Sigma $, определяемое как сумма отношений длительностей ползучести при постоянных значениях $q$ к длительностям практически полного прилегания мембраны к матрице при этих значениях $q$:
Вычисления показывают, что как в случае идеального скольжения, так и в случае прилипания сумма парциальных времен $\Sigma = 1$.
Заключение. Приведено исследование ползучести длинной прямоугольной мембраны в стесненных условиях (внутри жесткой матрицы) под действием переменного поперечного давления. В качестве примера исследуется ползучесть мембраны при однократном мгновенном изменении величины поперечного давления. Рассматриваются два варианта условий на контакте мембраны и матрицы: идеальное скольжение и полное прилипание. В работе рассматриваются четыре последовательные стадии деформирования мембраны: мгновенное упругое деформирование, ползучесть в свободных условиях, ползучесть мембраны при контакте с поперечной стороной матрицы и ползучесть мембраны при контакте со всеми сторонами матрицы. Анализ проводится до времени практически полного прилегания мембраны к матрице. Получены зависимости толщины различных частей мембраны и интенсивности напряжений в мембране от времени. При анализе ползучести в случае кусочно-постоянной зависимости величины давления от времени рассмотрено соответствие правилу суммирования парциальных времен заполнения матрицы.
Представленные материалы могут быть использованы при моделировании процесса ползучести панели крыла современных самолетов.
Работа выполнена при частичной финансовой поддержке Российского научного фонда (проект № 19-19-00062).
Список литературы
Odqvist F.K.G. Mathematical Theory of Creep and Creep Rupture. Oxford: Clarendon, 1974. 200 p.
Качанов Л.М. Основы механики разрушения. М.: Наука, 1974. 312 с.
Аннин Б.Д., Олейников А.И., Бормотин К.С. Моделирование процессов формообразования панелей крыла самолета SSJ-100 // ПМТФ. 2010. Т. 51. № 4. С. 155–165.
Apratim Majumder, Chayanjit Ghosh, Mohit U., et al. Creep deformation in elastomeric membranes of liquid-filled tunable-focus lenses // Appl. Optics. 2019. V. 58. Iss. 23. 2019. P. 6446–6454.
lan Wineman. Nonlinear viscoelastic membranes // Comput.&Math. with Appl. 2007. V. 53. Iss. 2. P. 168–181.
Ларин С.Н., Бессмертный А.В. Изотермическое свободное деформирование узкой прямоугольной мембраны из анизотропного листового материала при кратковременной ползучести // Изв. ТулГУ. Сер. Технич. науки. 2010. № 1. С. 44–51.
Яковлев С.С., Ларин С.Н. Деформирование анизотропной прямоугольной мембраны в условиях ползучести // Изв. ТулГУ. Сер. Технич. науки. 2010. № 3. С. 37–46.
Бессмертный А.В. Изотермическое деформирование элементов многослойных листовых конструкций из высокопрочных анизотропных материалов в режиме кратковременной ползучести: диссертация кандидата технических наук. Дисс. … канд-та техн. наук. Тула, 2012. 206 с.
Ефимов А.Б., Романюк С.Н., Чумаченко Е.Н. Об определении закономерностей трения в процессах обработки металлов давлением // Изв. РАН. МТТ. 1995. № 6. С. 82–98.
Малинин Н.Н. Ползучесть в обработке металлов. М.: Машиностроение, 1986. 216 с.
Локощенко А.М. Ползучесть и длительная прочность металлов. М.: Физматлит, 2016. 504 с.
Локощенко А.М., Терауд В.В. Ползучесть длинной узкой мембраны в стесненных условиях вплоть до разрушения // ПМТФ. 2013. Т. 54. № 3. С. 126–133.
Демин В.А., Локощенко А.М., Жеребцов А.А. Ползучесть длинной прямоугольной мембраны внутри криволинейной матрицы // Изв. вузов. Машиностр. 1998. № 4–6. С. 41–46.
Шестериков С.А., Юмашева М.А. Конкретизация уравнения состояния в теории ползучести // Изв. АН СССР. МТТ. 1984. № 1. С. 86–91.
Локощенко А.М., Абросимова Е.А. Установившаяся ползучесть длинной мембраны внутри жесткой матрицы при кусочно-постоянной зависимости скорости поперечного давления от времени // ПМТФ. 2019. № 1. С. 103–113.
Локощенко А.М., Терауд В.В. Ползучесть длинной узкой мембраны в стесненных условиях вплоть до разрушения // ПМТФ. 2013. Т. 54. № 3. С. 126–133.
Терауд В.В., Локощенко А.М., Шеварова Е.А. Ползучесть мембраны внутри П-образной матрицы при переменном поперечном давлении // XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики. Сб. трудов. Т. 3: Уфа: РИЦ БашГУ. 2019. С. 382–384.
Nguyen N., Wineman A., Waas A. Contact problem of a non-linear viscoelastic spherical membrane enclosing incompressible fluid between two rigid parallel plates // Int. J. Non-Linear Mech. 2013. V. 50. P. 97–108.
Васин Р.А., Еникеев Ф.У., Круглов А.А., Сафиуллин Р.В. Об идентификации определяющих соотношений по результатам технологических экспериментов // Изв. РАН. МТТ. 2003. № 2. С. 111–123.
Сафиуллин Р.В., Еникеев Ф.У. Расчет режимов сверхпластической формовки протяженной прямоугольной мембраны // Кузнечно-штамп. пр-во. Обработка материалов давлением. 2001. № 3. С. 35–40.
Srivastava A., Hui C.-Y. Nonlinear viscoelastic contact mechanics of long rectangular membranes // Proc. Royal Soc. A. Math. Phys.&Engng. Sci. 2014. A 470: 20140528.
Rong Long, Kenneth Shull, Hui C.-Y. Large deformation adhesive contact mechanics of circular membranes with a flat rigid substrate // J. Mech.&Phys. Solids. 2010. V. 58. P. 1225–1242.
Srivastava A., Hui C.-Y. Large deformation contact mechanics of long rectangular membranes. I. Adhesionless contact // Proc. Royal Soc. A. Math. Phys.&Engng. Sci. 2013. A 469: 20130424.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика