Прикладная математика и механика, 2021, T. 85, № 6, стр. 779-791

1. Введение. Создание покрытий, обеспечивающих требуемые звукоотражающие свойства тел, является актуальной проблемой. В настоящее время предложены различные виды покрытий для тел разной геометрической формы. Например, рассмотрены [1] прямая и обратная задачи дифракции плоской звуковой волны на цилиндре с перфорированным покрытием. Обсуждается [2, 3] задача о нерассеивающем покрытии с протяженной реакцией, делающем цилиндрическое тело акустически невидимым. Выявлены [4] условия, при которых совместный выбор импедансов однородного покрытия и упругой цилиндрической оболочки позволяет минимизировать рассеянное поле. Предложено [5] изменять характеристики рассеяния тел с помощью непрерывно-неоднородных упругих покрытий при соответствующем подборе законов неоднородности для механических параметров покрытия. Такие непрерывно-неоднородные покрытия можно реализовать с помощью многослойной системы тонких однородных упругих слоев с различными значениями плотности и упругих постоянных. С математической точки зрения такое представление эквивалентно аппроксимации непрерывных функций, характеризующих переменные параметры непрерывно-неоднородного покрытия, кусочно-постоянными функциями.

Возможность изменения звукоотражающих свойств цилиндрических тел с помощью неоднородных упругих покрытий обсуждалась в ряде работ. Исследовано [5, 6] рассеяние плоских и цилиндрических звуковых волн абсолютно жестким цилиндром с радиально-неоднородным упругим покрытием. Решены [7, 8] задачи о рассеянии наклонно падающей плоской звуковой волны упругим цилиндром с радиально-неоднородным и дискретно-неоднородным упругими покрытиями. Исследована [9] дифракция цилиндрических звуковых волн на упругом цилиндре с радиально-неоднородным упругим покрытием. Осуществлено [10] моделирование неоднородного покрытия упругого цилиндра с заданными звукоотражающими свойствами. Найдены функциональные зависимости для плотности и модулей упругости материала покрытия, обеспечивающие наименьшее отражение звука в определенном угловом секторе и в заданном диапазоне частот. В указанных выше работах полагалось, что тела находятся в безграничном пространстве.

Исследование дифракции звуковых волн на упругих телах с неоднородными упругими покрытиями, расположенными вблизи границ раздела сред, имеет важное теоретическое и практическое значение. Результаты таких исследований представляют интерес для гидроакустики при создании покрытий тел с требуемыми звукоотражающими свойствами, при разработке функционально-градиентных и композитных материалов для борьбы с шумом.

Изучена дифракция плоской звуковой волны на упругом цилиндре с радиально-неоднородным покрытием, находящемся вблизи идеальной плоскости (абсолютно жесткой и акустически мягкой), при нормальном падении плоской волны на цилиндр [11] и при произвольном падении [12]. Решена задача [13] о рассеянии звуковых волн жестким цилиндром с неоднородным упругим покрытием в плоском волноводе, у которого одна граница является абсолютно жесткой, а другая – акустически мягкой. В настоящей работе рассматривается задача дифракции цилиндрической звуковой волны на упругом цилиндре с радиально-неоднородным покрытием, расположенным вблизи упругого полупространства.

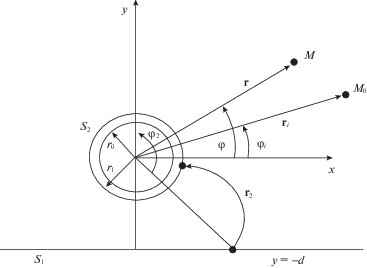
2. Постановка задачи. Рассмотрим бесконечный однородный и изотропный упругий цилиндр радиуса ${{r}_{0}}$, материал которого характеризуется плотностью ${{\rho }_{0}}$ и упругими постоянными ${{\lambda }_{0}}$ и ${{\mu }_{0}}$. Цилиндр имеет покрытие в виде радиально-неоднородного упругого изотропного слоя, внешний радиус которого равен ${{r}_{1}}$. Цилиндр с покрытием находится в идеальной жидкости с плотностью ${{\rho }_{ * }}$ и скоростью звука $c$, граничащей с однородным изотропным упругим полупространством с плотностью ${{\rho }_{1}}$ и упругими постоянными ${{\lambda }_{1}}$ и ${{\mu }_{1}}$. Ось цилиндра параллельна границе упругого полупространства и отстоит от неё на расстоянии $d$.

Введем прямоугольную декартову систему координат $x$, $y$, $z$ так, чтобы координатная ось $z$ совпадала с осью вращения цилиндра. С прямоугольной системой координат свяжем цилиндрическую систему координат $r$, $\varphi $, $z$.

Полагаем, что плотность материала покрытия $\rho $ является непрерывной функцией радиальной координаты $r$, а модули упругости материала покрытия $\lambda $ и $\mu $ – дифференцируемыми функциями координаты $r$. В системе координат $x$, $y$, $z$ граница упругого полупространства определяется уравнением $y = - d$ (рис. 1).

В полупространстве, заполненном идеальной жидкостью, находится линейный источник, параллельный оси $z$, который генерирует монохроматическую цилиндрическую звуковую волну с частотой $\omega $ и амплитудой $A$. Положение источника определяется точкой ${{M}_{0}}$, имеющей цилиндрические координаты (${{r}_{i}}$, ${{\varphi }_{i}}$). Точка наблюдения $M$ имеет координаты ($r$, $\varphi $).

Определим акустическое поле в жидком полупространстве.

3. Аналитическое решение задачи. Потенциал скорости гармонической звуковой волны, излучаемой осесимметричным цилиндрическим источником в свободном пространстве, представим в виде

где ${{G}_{0}}\left( {{\mathbf{r}},{{{\mathbf{r}}}_{i}}} \right) = \frac{i}{4}{{H}_{0}}\left( {k\left| {{\mathbf{r}} - {{{\mathbf{r}}}_{i}}} \right|} \right)$ – функция Грина для свободного пространства, ${{H}_{0}}\left( x \right)$ – цилиндрическая функция Ганкеля первого рода нулевого порядка, $k = \omega {\text{/}}c$ – волновое число жидкости, ${\mathbf{r}}$ и ${{{\mathbf{r}}}_{i}}$ – радиус-векторы точек $M$ и ${{M}_{0}}$, $t$ – время. Временной множитель $\exp \left( { - i\omega t} \right)$ далее опускается.

Потенциал скорости полного акустического поля в жидком полупространстве будем искать в виде

где ${{\Psi }_{{s1}}}$ – потенциал скорости волны, отраженной от границы полупространства, ${{\Psi }_{{s2}}}$ – потенциал скорости рассеянной цилиндром волны (с учетом многократного переотражения между цилиндром и упругим полупространством).

Скорость частиц ${\mathbf{v}}$ и акустическое давление $p$ в содержащей жидкости определяются формулами

Полное звуковое поле в верхнем полупространстве удовлетворяет интегральному уравнению Гельмгольца [14]

Здесь $G\left( {{\mathbf{r}},{{{\mathbf{r}}}_{2}}} \right)$ – двумерная функция Грина для уравнения Гельмгольца, $S = {{S}_{1}} + {{S}_{2}}$, ${{S}_{1}}$ – поверхность упругого полупространства, ${{S}_{2}}$ – внешняя поверхность покрытия цилиндра. При интегрировании по поверхности ${{S}_{1}}$ точка ${{{\mathbf{r}}}_{2}}$ находится на поверхности полупространства и дифференцирование выполняется по внешней нормали к поверхности ${{S}_{1}}$, а в интеграле по поверхности ${{S}_{2}}$ точка ${{{\mathbf{r}}}_{2}}$ находится на поверхности цилиндра и дифференцирование происходит по внешней нормали к поверхности ${{S}_{2}}$.

Для того, чтобы в (3.3) исключить интегрирование по бесконечной поверхности ${{S}_{1}}$ воспользуемся функцией Грина [14]

где [15]

Здесь $A_{1}^{'}\left( \xi \right) = \exp \left( {i2kd\eta } \right){{A}_{1}}\left( \xi \right)$, $\eta = \sqrt {1 - {{\xi }^{2}}} $, ${{A}_{1}}(\xi )$ – коэффициент отражения плоской волны единичной амплитуды, падающей на упругое полупространство. Коэффициент ${{A}_{1}}(\xi )$ находится при решении задачи об отражении плоской волны, направление распространения которой задается горизонтальной $k\xi $ и вертикальной $ - k\eta $ компонентами волнового вектора ${\mathbf{k}}$, в системе координат с началом отсчета, лежащим на границе упругого полупространства.

Функция Грина (3.4) удовлетворяет на поверхности раздела идеальной жидкости и упругого полупространства тем же граничным условиям, что и потенциал скорости акустического поля

где ${{u}_{{1y}}}$ и ${{\sigma }_{{1yy}}}$, ${{\sigma }_{{1xy}}}$ – нормальная компонента вектора смещения и компоненты тензора напряжений в упругом полупространстве. При таком выборе функции Грина интеграл по поверхности полупространства ${{S}_{1}}$ в (3.3) обращается в ноль, и остается только интеграл по поверхности цилиндра ${{S}_{2}}$.

При замене переменной $\xi = \sin \theta $ переходим от ${{A}_{1}}(\xi )$ к коэффициенту отражения плоской волны, падающей под углом $\theta $ на границу упругого полупространства, ${{A}_{1}}(\theta )$. Задача об отражении плоской звуковой волны от упругого полупространства решена в [16]. Коэффициент отражения имеет вид

где

Здесь ${{k}_{x}} = k\sin \theta $, ${{k}_{y}} = k\cos \theta $, ${{k}_{{1l}}} = \omega {\text{/}}{{c}_{{1l}}}$ и ${{k}_{{1\tau }}} = \omega {\text{/}}{{c}_{{1\tau }}}$ – волновые числа продольных и поперечных упругих волн в упругом полупространстве, ${{c}_{{1l}}} = \sqrt {\left( {{{\lambda }_{1}} + 2{{\mu }_{1}}} \right){\text{/}}{{\rho }_{1}}} $ и ${{c}_{{1\tau }}} = \sqrt {{{\mu }_{1}}{\text{/}}{{\rho }_{1}}} $ – скорости продольных и поперечных волн, ${{k}_{{1ly}}} = \sqrt {k_{{1l}}^{2} - k_{x}^{2}} $, ${{k}_{{1\tau y}}} = \sqrt {k_{{1\tau }}^{2} - k_{x}^{2}} $.

Используя теорему сложения для цилиндрических волновых функций, представим ${{G}_{0}}\left( {{\mathbf{r}},{{{\mathbf{r}}}_{2}}} \right)$ в виде разложения [17]

где ${{J}_{n}}(x)$ и ${{H}_{n}}(x)$ – цилиндрические функции Бесселя и Ганкеля первого рода порядка $n$ соответственно.

В (3.6) сделаем замену переменных $\xi = \sin \theta $, $\eta = \cos \theta $ и перейдем к цилиндрической системе координат $x = r\cos \varphi $, $y = r\sin \varphi $, ${{x}_{2}} = {{r}_{2}}\cos {{\varphi }_{2}}$, ${{y}_{2}} = {{r}_{2}}\sin {{\varphi }_{2}}$. Тогда ${{G}_{1}}$ примет вид

где $\Gamma $ – контур Зоммерфельда на комплексной плоскости $\theta $ (пределы интегрирования от $ - \pi {\text{/}}2 + i\infty $ до $\pi {\text{/}}2 - i\infty $).

Используя разложение [17]

из (3.9) получаем где

Определим потенциал скорости полного акустического поля на внешней поверхности покрытия цилиндра ${{S}_{2}}$. Представим его, а также нормальную составляющую скорости частиц жидкости на поверхности ${{S}_{2}}$ в виде разложений в ряды Фурье

где ${{p}_{q}}$ и ${{{v}}_{q}}$ – коэффициенты, подлежащие определению.

В уравнении (3.3) устремим точку наблюдения на поверхность ${{S}_{2}}$ и учтем, что при выборе функции Грина в виде (3.4) достаточно ограничиться интегрированием по поверхности ${{S}_{2}}$. Подставим в левую часть (3.3) разложение (3.12), а в первое слагаемое правой части (3.3) – функцию Грина в виде суммы (3.4), составленной из выражений (3.8) и (3.10), в которых заменим ${{r}_{2}}$, ${{\varphi }_{2}}$ на ${{r}_{i}}$, ${{\varphi }_{i}}$. Далее подставим разложения (3.12), (3.13) и функцию Грина (сумма (3.8) и (3.10)) в подынтегральное выражение уравнения (3.3). При этом дифференцирование по нормали будем выполнять по переменной ${{r}_{2}}$. При выполнении дифференцирования выражения (3.8) следует выбрать нижнюю строчку в формуле (3.8). После проведения указанных операций следует положить $r = {{r}_{2}} = {{r}_{1}}$.

Осуществив интегрирование по поверхности цилиндра ($d{{S}_{2}} = {{r}_{1}}d{{\varphi }_{2}}$, ${{\varphi }_{2}} \in \left[ {0,2\pi } \right]$) с учетом ортогональности экспоненциальных множителей и используя выражение для вронскиана [17]

получаем бесконечную систему линейных алгебраических уравнений относительно неизвестных коэффициентов ${{p}_{q}}$, ${{{v}}_{q}}$где

Отметим, что коэффициенты ${{p}_{q}}$ и ${{{v}}_{q}}$ связаны между собой. Эту связь через значения составляющих вектора смещения частиц покрытия на его внешней поверхности установим ниже.

Рассмотрим вычисление коэффициентов ${{g}_{l}}$, определяемых выражением (3.11). Интеграл (3.11) разобьем на три интеграла по участкам ($ - \pi {\text{/}}2 + i\infty $, $ - \pi {\text{/}}2$), ($ - \pi {\text{/}}2$, $\pi {\text{/}}2$), ($\pi {\text{/}}2$, $\pi {\text{/}}2 - i\infty $). Выполним замену переменных $\theta = - \pi {\text{/}}2 + i{{\gamma }_{1}}$ в первом и $\theta = \pi {\text{/}}2 - i{{\gamma }_{2}}$ в третьем интегралах.

В результате получаем

где

Здесь ${{A}_{1}}\left( {{{\gamma }_{j}}} \right)$ определяется по формуле (3.7), в которой следует положить

Теперь воспользуемся результатами [9], где радиальная ${{u}_{r}}$ и угловая ${{u}_{\varphi }}$ компоненты вектора смещения ${\mathbf{u}}$ в неоднородном упругом покрытии представляются в виде рядов Фурье

где функции ${{U}_{{1q}}}(r)$, ${{U}_{{2q}}}(r)$ для каждого $q$ являются решением следующей системы линейных обыкновенных дифференциальных уравнений второго порядка где ${{{\mathbf{U}}}_{q}} = {{\left( {{{U}_{{1q}}}(r),{{U}_{{2q}}}(r)} \right)}^{{\text{т}}}}$, ${{{\mathbf{\hat {A}}}}_{n}}$, ${{{\mathbf{\hat {B}}}}_{q}}$, ${{{\mathbf{\hat {C}}}}_{q}}$ – матрицы второго порядка с элементами [9].

Граничные условия на внешней поверхности покрытия заключаются в равенстве нормальных скоростей частиц неоднородной упругой среды и жидкости, равенстве на ней нормального напряжения и акустического давления, отсутствии касательного напряжения

где ${{u}_{r}}$ и ${{{v}}_{r}}$ – нормальные компоненты векторов смещения и скорости, ${{\sigma }_{{rr}}}$ и ${{\sigma }_{{r\varphi }}}$ – компоненты тензора напряжений в упругом неоднородном покрытии.

Используя обобщенный закон Гука [18] с учетом (3.16), будем иметь

Подставляя (3.12), (3.13), (3.16) и (3.19) в первые два граничных условия (3.18), получаем

Подставляя выражения (3.20) в систему (3.14), получаем краевое условие при $r = {{r}_{1}}$ для нахождения частного решения системы (3.17)

где

Второе краевое условие, которому должна удовлетворять система (3.17) при $r = {{r}_{1}}$, находим из третьего граничного условия (3.18) с учетом (3.19)

На внутренней поверхности покрытия при переходе через границу раздела упругих сред должны быть непрерывны составляющие вектора смещения частиц, нормальные и тангенциальные напряжения

где ${{u}_{{0r}}}$, ${{u}_{{0\varphi }}}$ и ${{\sigma }_{{0rr}}}$, ${{\sigma }_{{0r\varphi }}}$ – компоненты вектора смещения и компоненты тензора напряжений в однородном упругом цилиндре.

В результате преобразований, аналогичных [9], из (3.23) получаем еще два условия, которым должна удовлетворять система (3.17) при $r = {{r}_{0}}$

Выражения для коэффициентов в уравнениях (3.24) приведены в [5].

Найдем решение краевой задачи (3.17), (3.21), (3.22), (3.24) методом сплайн-коллокации [19] для $q = - N, - N + 1, \ldots ,0,1, \ldots ,N$, выбрав в качестве порядка усечения величину $N = 2\left[ {k{{r}_{1}}} \right] + 1$, где $[\;]$ – целая часть числа.

После нахождения ${{U}_{{1q}}}(r)$ и ${{U}_{{2q}}}(r)$ определяем по формулам (3.20) коэффициенты ${{p}_{q}}$, ${{{v}}_{q}}$. В результате получаем аналитическое описание потенциала скорости полного акустического поля и нормальной составляющей скорости на поверхности цилиндра в виде (3.12) и (3.13).

Теперь определим потенциал скорости полного акустического поля в точке наблюдения $M$. Обратимся к интегральному уравнению (3.3), используя представление потенциала $\Psi $ в виде (3.2). Запишем выражения для ${{\Psi }_{0}}$, ${{\Psi }_{{s1}}}$, ${{\Psi }_{{s2}}}$. Будем иметь

Подставим в (3.27) разложения (3.12), (3.13), а также функцию Грина в виде суммы (3.4), в которой первое слагаемое определяется нижней строкой формулы (3.8), а второе слагаемое – формулой (3.10). Интегрируя по поверхности цилиндра, получаем

где коэффициенты ${{p}_{q}}$ и ${{{v}}_{q}}$ определяются согласно (3.20).

Потенциал скорости рассеянного поля имеет вид

4. Численные исследования. На основе полученного решения были проведены расчеты угловых и частотных характеристик рассеянного акустического поля $\left| {{{\Psi }_{s}}{\text{/}}A} \right|$ в дальней зоне ($r = 100$ м).

Полагалось, что алюминиевый цилиндр (${{\rho }_{0}} = 2.7 \times {{10}^{3}}$ кг/м³, ${{\lambda }_{0}} = 5.3 \times {{10}^{{10}}}$ Н/м², ${{\mu }_{0}} = 2.6 \times {{10}^{{10}}}$ Н/м²) радиуса ${{r}_{0}} = 0.8$ м с неоднородным упругим покрытием толщиной 0.2 м располагается в полупространстве, заполненном водой (${{\rho }_{*}} = {{10}^{3}}$ кг/м³, $c = 1485$ м/с) и отстоит от границы полупространств на расстояние $d = 1 + {{r}_{1}}$. Упругое полупространство характеризуется параметрами: ${{\rho }_{1}} = 7.85 \times {{10}^{3}}$ кг/м³, ${{\lambda }_{1}} = 1.2 \times {{10}^{{11}}}$ Н/м², ${{\mu }_{1}} = 7.9 \times {{10}^{{10}}}$ Н/м² (сталь). Рассматривалось как однородное полимерное покрытие с характерной плотностью ${{\rho }^{0}} = 1.07 \times {{10}^{3}}$ кг/м³ и характерными модулями упругости ${{\lambda }^{0}} = 3.9 \times {{10}^{9}}$ Н/м², ${{\mu }^{0}} = 9.8 \times {{10}^{8}}$ Н/м² (поливинилбутираль), так и неоднородное покрытие, механические характеристики которого менялись по законам:

где

Предполагалось, что линейный источник излучает звуковую волну единичной амплитуды и располагается в точке с координатами ${{r}_{i}} = 4$ и ${{\varphi }_{i}} = \pi {\text{/}}4$.

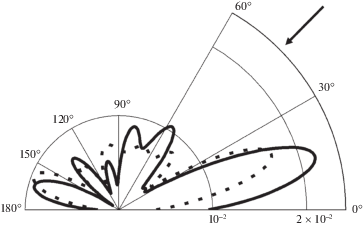
На рис. 2 представлены зависимости амплитуды рассеяния $\left| {{{\Psi }_{s}}{\text{/}}A} \right|$ от полярного угла $\varphi $ при волновом размере тела $k{{r}_{1}} = 5$. На лучах диаграмм отложены значения безразмерной амплитуды рассеяния, вычисленной для соответствующих значений угла $\varphi $. Стрелкой показано направление распространения падающей волны.

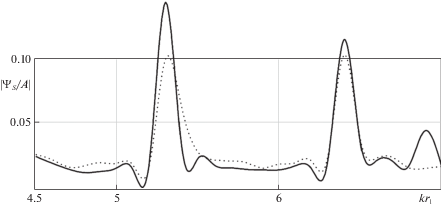
На рис. 3 представлены зависимости амплитуды рассеяния $\left| {{{\Psi }_{s}}{\text{/}}A} \right|$ в направлении на источник ($\varphi = \pi {\text{/}}4$) от волнового размера цилиндра $k{{r}_{1}}$ в интервале $4.5 \leqslant k{{r}_{1}} \leqslant 7$.

Сплошные линии на рис. 2 и 3 соответствуют случаю неоднородного покрытия, пунктирные – однородному покрытию.

Как видно из диаграмм направленности и частотных характеристик, свойства покрытия значительно влияют на характер рассеяния звука упругим цилиндром.

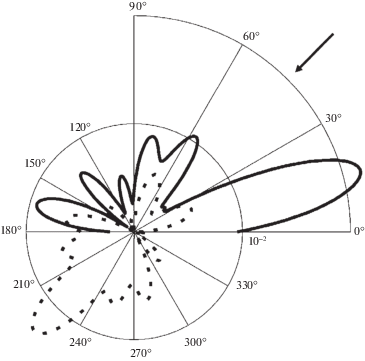
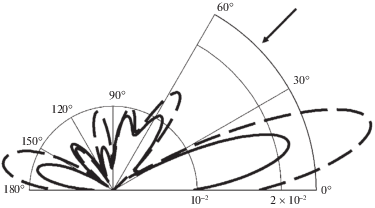
На рис. 4 приведены диаграммы направленности, рассчитанные при $k{{r}_{1}} = 5$ для случая цилиндра с неоднородным покрытием, расположенного вблизи границы упругого полупространства (сплошная линия), и для такого же цилиндра, расположенного в свободном пространстве (пунктирная линия).

Как показывают расчеты, присутствие подстилающей поверхности сильно влияет на дифракционную картину.

Отметим, что на основе предложенного решения можно рассмотреть случаи, когда рассеиватель расположен вблизи идеальных подстилающих поверхностей. Граничное условие при $y = - d$ для функции Грина (3.4) имеет вид

если поверхность является абсолютно жесткой, и если поверхность является акустически мягкой.

Условие (4.1) выполняется при ${{A}_{1}} = 1$, а условие (4.2) – при ${{A}_{1}} = - 1$ [14].

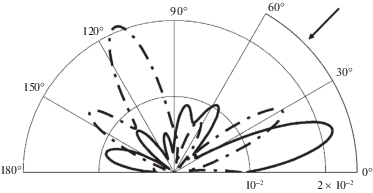
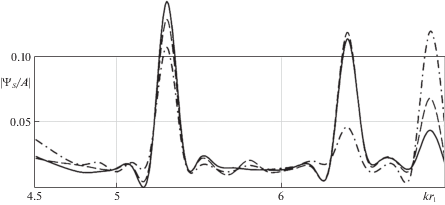
На рис. 5 и 6 представлены угловые зависимости $\left| {{{\Psi }_{s}}{\text{/}}A} \right|$ для цилиндра с неоднородным покрытием при значении волнового размера $k{{r}_{1}} = 5$. На рис. 7 приведены частотные зависимости $\left| {{{\Psi }_{s}}{\text{/}}A} \right|$ для цилиндра с неоднородным покрытием при $\varphi = \pi {\text{/}}4$ в интервале $4.5 \leqslant k{{r}_{1}} \leqslant 7$. На рис. 5–7 сплошные линии соответствуют случаю упругой поверхности, штриховые – абсолютно жесткой поверхности, штрихпунктирные – акустически мягкой поверхности.

Из графиков видно, что угловые и частотные зависимости в случае упругой подстилающей поверхности значительно отличаются от зависимостей, рассчитанных для идеальных поверхностей.

Исследование выполнено за счет гранта Российского научного фонда № 18-11-00199, https://rscf.ru/project/18-11-00199/.