Прикладная математика и механика, 2022, T. 86, № 2, стр. 276-290
Повреждаемость и усталостное разрушение элементов конструкций в различных режимах циклического нагружения
И. С. Никитин 1, *, Н. Г. Бураго 1, 2, **, А. Д. Никитин 1, ***
1 Институт автоматизации проектирования РАН
Москва, Россия
2 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: i_nikitin@list.ru
** E-mail: buragong@yandex.ru
*** E-mail: nikitin_alex@bk.ru
Поступила в редакцию 30.09.2021
После доработки 21.01.2022
Принята к публикации 27.01.2022
- EDN: EUOCPF
- DOI: 10.31857/S0032823522020084
Аннотация
На основе предложенной ранее мультирежимной двухкритериальной модели усталостного разрушения разработан метод расчета зарождения и развития узких локализованных зон поврежденности в элементах конструкций для различных режимов циклического нагружения. Такие узкие зоны повреждаемости можно рассматривать как квазитрещины двух типов, соответствующих механизму нормального отрыва и сдвига. Рассмотрен важный для приложений пример полетного цикла нагружения (многоцикловая усталость) и высокочастотного циклического нагружения при крутильно-изгибных колебаниях лопаток (сверхмногоцикловая усталость) диска компрессора авиационного газотурбинного двигателя. Дана оценка долговечности рассмотренного элемента авиационных конструкций. Также рассмотрен пример расчета усталостного разрушения при высокочастотных крутильных колебаниях экспериментального образца определенной формы, при котором удалось воспроизвести наблюдаемый эффект резкого изменения направления роста и типа квазитрещины в процессе циклического нагружения.
1. Введение. Ранее, в [1], была предложена мультирежимная модель развития усталостной повреждаемости, учитывающая бимодальный характер поведения усталостной кривой при циклическом нагружении. Там же был дан обзор основных работ по теории повреждаемости в квазистатических, динамических и циклических процессах нагружения [2–11]. Были приведены примеры расчета ряда модельных задач развития локализованных зон усталостной поврежденности (квазитрещин) в окрестности дефектов структуры материала и воспроизведены усталостные кривые для некоторых типов образцов в усталостных экспериментах на одноосное растяжение и кручение.
Затем, в работах [12, 13] эта модель была расширена на случай двух различных механизмов микроповрежденности материала – развития микротрещин нормального отрыва, микротрещин сдвига и, соответственно, рассмотрения двух типов функций макроскопической повреждаемости.
Отметим, что ранее предложенные рабочие модели развития усталостной повреждаемости различных авторов [6–9] описывают режим малоцикловой (МЦУ) и многоцикловой (МНЦУ) усталости.
Предложенная модель учитывает переход к режиму высокочастотного циклического нагружения – сверхмногоцикловой (СВМУ) усталости с учетом расположения опорных точек правой ветви бимодальной усталостной кривой (мультирежимность модели).
Кроме того, в моделях [6–9] многочисленные коэффициенты эволюционного уравнения для повреждаемости находятся чисто эмпирически по результатам серий испытаний на сложное циклическое нагружение, не всегда реализуемое в режиме СВМУ. В предложенной модели для нахождения коэффициентов кинетического уравнения для повреждаемости материала использовались известные, серьезно обоснованные многоосные критерии усталостного разрушения [14–16]. Эти коэффициенты определялись из того условия, чтобы результатом процесса развития повреждений до полного разрушения был выход на соответствующую ветвь бимодальной усталостной кривой. Никаких иных данных, кроме вида усталостной кривой, построенной по результатам одноосных реверсивных испытаний, не требуется.
Также отметим, что явного учета механизмов зарождения микротрещин различного типа (нормального отрыва и сдвига) с использованием ассоциированных критериев усталостного разрушения другими авторами не проводилось (двухкритериальность модели).
Можно отметить, что в модели Чоу [9] учитывается разница между растяжением и сжатием в накоплении усталостных повреждений за счет введения двух функций повреждаемости для деградации коэффициента Пуассона и модуля упругости Юнга. Это в какой-то степени отражает возможность развития усталостных повреждений по механизмам разного типа.
В данной работе предложенная ранее мультирежимная модель [12, 13] применяется к расчету и оценке долговечности эксплуатации реальных элементов конструкций.
В работах [17, 18] уже ставилась и решалась подобная практически важная задача для реального элемента конструкции компрессора газотурбинного двигателя (ГТД) Д30 – диска с лопатками первой ступени, для которого имелись данные по случаям летных происшествий в эксплуатации [19].
При этом использовались многоосные критерии усталостного разрушения [20–22], но только для того, чтобы на основе упругого решения задачи на цикле нагружения, с помощью соответствующего критерия указать зону зарождения разрушения и соответствующую этому моменту долговечность. При этом не учитывалась кинетика дальнейшего процесса развития усталостных повреждений в элементе конструкции.
В настоящей статье на основе предложенной мультирежимной двухкритериальной модели развития повреждаемости при циклическом нагружении приведены важные для приложений примеры расчета полетного цикла нагружения (малоцикловая и многоцикловая усталость) и высокочастотного циклического нагружения при крутильно-изгибных колебаниях лопаток (сверхмногоцикловая усталость) диска компрессора авиационного газотурбинного двигателя с учетом процесса зарождения и развития узких локализованных зон поврежденности (квазитрещин). Впервые проведен сравнительный анализ локализации очага зарождения и развития усталостных квазитрещин для различных циклических режимов нагружения и сравнение с результатами исследований реальных случаев разрушения в ободной части титановых дисков компрессора в эксплуатации.
Также рассмотрен пример расчета усталостного разрушения при высокочастотных крутильных колебаниях экспериментального образца определенной формы, при котором впервые удалось воспроизвести эффект резкого изменения направления роста и типа квазитрещины в процессе циклического нагружения, подтвержденный фрактографическими исследованиями по результатам СВМУ испытаний.
Данную работу можно рассматривать как развитие моделей и методов сквозного счета зарождения и развития множественных трещиноподобных зон повреждений (квазитрещин) разного типа при различных режимах циклического нагружения, подобных методам сквозного расчета возникновения и распространения ударных волн в задачах газовой динамики. В том и другом случае математические разрывы (трещины и скачки уплотнения) при расчете размазываются на некоторое (небольшое) число ячеек вычислительной сетки, что, тем не менее, дает возможность количественно и качественно отразить основные особенности поведения решений с учетом геометрии и типа разрывов (квазитрещин).
2. Описание мультирежимной модели усталостного разрушения на основе теории повреждаемости. Для того чтобы исследовать процессы развития зон усталостных повреждений существует два подхода. Первый основан на классических представлениях линейной механики разрушения и связывает условия развития усталостных трещин при увеличении числа циклов с амплитудами коэффициентов интенсивности напряжений в вершине трещины. Основное уравнение было предложено Парисом [23, 24].
Второй подход использует представления теории повреждаемости, восходящей к работам [2, 3] и развитый в [4, 5]. В приложении к задачам циклического нагружения и усталостного разрушения он применялся в [6–11].
В данной работе описывается мультирежимная модель развития усталостного разрушения, основанная на эволюционном уравнении для функции повреждаемости [1, 12, 13]. Предполагается, что в процессе повреждения материала (деградации его свойств, в частности, модулей упругости) реализуются два механизма – развития микротрещин нормального отрыва или микротрещин сдвига. Им соответствуют ассоциированные критерии многоосного усталостного разрушения при циклическом однородном нагружении. Усталостному разрушению при развитии поврежденности с микротрещинами нормального отрыва соответствует критерий Smith–Watson–Topper (SWT) [14, 15], а усталостному разрушению при развитии поврежденности с микротрещинами сдвига соответствует критерий Carpinteri–Spagnoli–Vantadori (CSV) [16].
Эти и иные подобные, основанные на расчете напряженного состояния (stress-based), многоосные критерии получены обобщением закономерностей, установленных для одноосных нагружений и описываемых усталостными S-N кривыми типа Веллера и соотношениями типа Баскина [25]. В [18] был предложен подход для экстраполяции многоосных критериев разрушения, построенных для режима МНЦУ, на правые ветви усталостных кривых в режиме СВМУ, и использующий опорные точки каждой из ветвей и обратную степенную зависимость от числа циклов N для выхода на асимптоту предела усталости. В данной работе для экстраполяции критериев SWT и CSV на случай СВМУ был также использован этот аналитический подход.
Принимается следующая схема мультирежимной (бимодальной) усталостной кривой с амплитудой ${{\sigma }_{a}}$ при одноосном реверсивном нагружении. Повторно-статическое нагружение до значения Ni ~ 103 с амплитудой, слабо убывающей от статического предела прочности ${{\sigma }_{B}}$. Далее левая часть бимодальной усталостной кривой описывает режимы МЦУ-МНЦУ до значений $N\sim {{10}^{7}}$ с выходом на предел усталости ${{\sigma }_{u}}$ (классическая усталостная кривая Веллера). Эти режимы на левой ветви усталостной кривой отделяются величиной амплитуды нагружения, равной пределу текучести материала ${{\sigma }_{T}}$. Затем, начиная с величин $N\sim {{10}^{8}}$, происходит дальнейшее падение усталостной прочности до нового предельного значения ${{\tilde {\sigma }}_{u}}$ (правая ветвь бимодальной усталостной кривой в режиме СВМУ [19]).
Кратко сформулируем мультирежимную модель развития повреждений при циклическом нагружении, все основные положения которой были развиты ранее [12].
При ее изложении мы ограничимся рассмотрением только части левой ветви усталостной кривой в режиме МНЦУ (напряжения не превышают предела текучести) и, следовательно, задачу определения напряженного состояния в пределах цикла нагружения можно решать в упругой постановке.
В общем виде в результате обобщения соотношения Баскина [25] ${{\sigma }_{a}} = {{\sigma }_{u}} + {{\sigma }_{L}}{{N}^{{ - {{\beta }_{L}}}}}$ на случай многоосного нагружения критерий в режиме МНЦУ выглядит следующим образом:
(2.1)
$\begin{gathered} {{\sigma }_{{eq}}} = {{\sigma }_{u}} + {{\sigma }_{L}}{{N}^{{ - {{\beta }_{L}}}}} \\ {{\sigma }_{L}} = {{10}^{{3{{\beta }_{L}}}}}({{\sigma }_{B}} - {{\sigma }_{u}}) \\ \end{gathered} $В этих формулах ${{\sigma }_{B}}$ – статический предел прочности материала, ${{\sigma }_{u}}$ – классический предел усталости материала при реверсивном цикле (коэффициент асимметрии цикла $R = {{\sigma }_{{\min }}}{\text{/}}{{\sigma }_{{\max }}}$ = –1).
С учетом подхода [18] для экстраполяции многоосных критериев разрушения на режим СВМУ путем замен ${{\sigma }_{B}} \to {{\sigma }_{u}}$, ${{\sigma }_{u}} \to {{\tilde {\sigma }}_{u}}$ получаются многоосные критерии усталостного разрушения в режиме СВМУ:
(2.2)
$\begin{gathered} {{\sigma }_{{{\text{eq}}}}} = {{{\tilde {\sigma }}}_{u}} + {{\sigma }_{V}}{{N}^{{ - {{\beta }_{V}}}}} \\ {{\sigma }_{V}} = {{10}^{{8{{\beta }_{V}}}}}({{\sigma }_{u}} - {{{\tilde {\sigma }}}_{u}}), \\ \end{gathered} $Кинетическое уравнение для функции повреждаемости материала $\psi $, предложенное в [1, 12], имеет вид:
(2.3)
${{\partial \psi } \mathord{\left/ {\vphantom {{\partial \psi } {\partial N = }}} \right. \kern-0em} {\partial N = }}{{B(\sigma ,\Delta \sigma ){{\psi }^{\gamma }}} \mathord{\left/ {\vphantom {{B(\sigma ,\Delta \sigma ){{\psi }^{\gamma }}} {\left( {1 - {{\psi }^{{1 - \gamma }}}} \right)}}} \right. \kern-0em} {\left( {1 - {{\psi }^{{1 - \gamma }}}} \right)}}$При ${{\sigma }_{u}} + \Delta {{\sigma }_{u}} < {{\sigma }_{{{\text{eq}}}}} < {{\sigma }_{B}}$ (режим МНЦУ, $\Delta {{\sigma }_{u}} = {{10}^{{ - 5{{\beta }_{L}}}}}({{\sigma }_{B}} - {{\sigma }_{u}})$)
При ${{\tilde {\sigma }}_{u}} < {{\sigma }_{{{\text{eq}}}}} \leqslant {{\sigma }_{u}} + \Delta {{\sigma }_{u}}$ (режим СВМУ)
При ${{\sigma }_{{{\text{eq}}}}} \leqslant {{\tilde {\sigma }}_{u}}$ усталостного разрушения не происходит, при ${{\sigma }_{{{\text{eq}}}}} \geqslant {{\sigma }_{B}}$ оно наступает мгновенно.
Здесь и далее приняты обозначения $\left\langle f \right\rangle = fH(f)$, $H(f)$ – функция Хэвисайда. Значение коэффициента $0 < \gamma < 1$ определяется по результатам согласования расчетных и экспериментально построенных усталостных кривых.
Выражения для эффективных напряжений ${{\sigma }_{{{\text{eq}}}}}$ определяются выбранными критериями полного усталостного разрушения для двух типов повреждаемости, связанных с механизмами развития микротрещин нормального отрыва или сдвига.
Многоосный критерий SWT описывает усталостное разрушение с развитием повреждений в виде микротрещин нормального отрыва [1, 15]:
(2.4)
$\sqrt {\left\langle {{{\sigma }_{{{{1}_{{\max }}}}}}} \right\rangle \Delta {{\sigma }_{1}}{\text{/}}2} = {{\sigma }_{u}} + {{\sigma }_{L}}{{N}^{{ - {{\beta }_{L}}}}},$Следовательно, в этом случае
Многоосный критерий CSV описывает усталостное разрушение с развитием повреждений в виде микротрещин сдвига [12, 16]:
(2.5)
$\sqrt {{{{(\left\langle {\Delta {{\sigma }_{n}}} \right\rangle {\text{/}}2)}}^{2}} + 3{{{(\Delta {{\tau }_{n}}{\text{/}}2)}}^{2}}} = {{\sigma }_{u}} + {{\sigma }_{L}}{{N}^{{ - {{\beta }_{L}}}}},$Следовательно, в этом случае
Начальное зарождение зоны повреждения в частице материала с ростом числа циклов нагружения, связанное с появлением отличного от нуля значения коэффициента $B$ в кинетическом уравнении, определяет дальнейший тип повреждаемости в этой частице по механизму развития микротрещин нормального отрыва при $\max ({{\sigma }^{n}},{{\sigma }^{\tau }}) = {{\sigma }^{n}}$ или по механизму развития микротрещин сдвига при $\max ({{\sigma }^{n}},{{\sigma }^{\tau }}) = {{\sigma }^{\tau }}$.
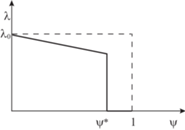
Развитие повреждаемости в материальной частице приводит к эффективному уменьшению модулей упругости, в общем случае по нелинейному закону, а в предложенном варианте модели – по кусочно-линейному закону следующего вида:
деградация материала при $\psi < {{\psi }_{*}}$
(2.6)
$\lambda (\psi ) = {{\lambda }_{0}}(1 - \kappa \psi ),\quad \mu (\psi ) = {{\mu }_{0}}(1 - \kappa \psi )$полное разрушение при ${{\psi }_{*}} \leqslant \psi \leqslant 1$
Здесь 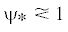 – критическое значение повреждаемости, при котором наступает состояние полного разрушения
(рис. 1).
– критическое значение повреждаемости, при котором наступает состояние полного разрушения
(рис. 1).
3. Численный метод расчета повреждаемости. Численный метод расчета зон повреждаемости заключается в пошаговом (по циклам нагружения) расчете упругого напряженного состояния образца материала или элемента конструкции, параллельно с численным решением нелинейного уравнения для повреждаемости (2.3) и корректировкой модулей упругости среды в областях, где функция повреждаемости отлична от нуля (2.6). Такие области становятся дополнительными развивающимися концентраторами напряжений, а локализованные зоны полного разрушения в указанном выше смысле трактуются как квазитрещины. Выход квазитрещин на границы нагружаемого тела рассматривается как его окончательное макроразрушение.
Для интегрирования уравнения (2.3) применялась аппроксимация функции повреждаемости в k-узле расчетной сетки при заданных дискретных значениях $\psi _{k}^{n}$ в моменты ${{N}^{n}}$ и искомых значениях $\psi _{k}^{{n + 1}}$ в моменты ${{N}^{{n + 1}}}$.
Была применена схема аппроксимации нелинейного уравнения для повреждаемости, построенная на пошаговом аналитическом интегрировании кинетического уравнения при фиксированном напряженном состоянии с предыдущего шага расчета по циклам нагружения:
Формула для функции повреждаемости на верхнем слое имеет вид:
(3.1)
$\psi _{k}^{{n + 1}} = {{\left( {1 - \sqrt {{{{\left( {1 - {{{(\psi _{k}^{n})}}^{{1 - \gamma }}}} \right)}}^{2}} - 2(1 - \gamma ){{B}^{n}}\Delta {{N}^{n}}} } \right)}^{{1/(1 - \gamma )}}}$(3.2)
$\begin{gathered} \Delta \tilde {N}_{k}^{n} = {{\left. {\left[ {{{{{{{\psi }^{{1 - \gamma }}}} \mathord{\left/ {\vphantom {{{{\psi }^{{1 - \gamma }}}} {(1 - \gamma ) - {{\psi }^{{2(1 - \gamma )}}}}}} \right. \kern-0em} {(1 - \gamma ) - {{\psi }^{{2(1 - \gamma )}}}}}} \mathord{\left/ {\vphantom {{{{{{\psi }^{{1 - \gamma }}}} \mathord{\left/ {\vphantom {{{{\psi }^{{1 - \gamma }}}} {(1 - \gamma ) - {{\psi }^{{2(1 - \gamma )}}}}}} \right. \kern-0em} {(1 - \gamma ) - {{\psi }^{{2(1 - \gamma )}}}}}} 2}} \right. \kern-0em} 2}{\text{/}}(1 - \gamma )} \right]} \right|_{{\psi _{k}^{n}}}^{1}} \mathord{\left/ {\vphantom {{\left. {\left[ {{{{{{{\psi }^{{1 - \gamma }}}} \mathord{\left/ {\vphantom {{{{\psi }^{{1 - \gamma }}}} {(1 - \gamma ) - {{\psi }^{{2(1 - \gamma )}}}}}} \right. \kern-0em} {(1 - \gamma ) - {{\psi }^{{2(1 - \gamma )}}}}}} \mathord{\left/ {\vphantom {{{{{{\psi }^{{1 - \gamma }}}} \mathord{\left/ {\vphantom {{{{\psi }^{{1 - \gamma }}}} {(1 - \gamma ) - {{\psi }^{{2(1 - \gamma )}}}}}} \right. \kern-0em} {(1 - \gamma ) - {{\psi }^{{2(1 - \gamma )}}}}}} 2}} \right. \kern-0em} 2}{\text{/}}(1 - \gamma )} \right]} \right|_{{\psi _{k}^{n}}}^{1}} {{{B}^{n}}}}} \right. \kern-0em} {{{B}^{n}}}} \\ \Delta {{N}^{n}} = \mathop {\min }\limits_k 0.5\Delta \tilde {N}_{k}^{n} \\ \end{gathered} $При численной реализации коэффициент Пуассона материала не меняется, а модуль упругости Юнга с ростом функции повреждаемости уменьшается по закону, в котором заложено его малое остаточное значение в состоянии полного разрушения, равное (для определенности) тысячной доле от начального значения:
(3.3)
$E_{k}^{{n + 1}} = {{E}_{0}}\left( {1 - \kappa \psi _{k}^{{n + 1}}} \right)\left( {H\left( {{{\psi }_{*}} - \psi _{k}^{{n + 1}}} \right) + 0.001} \right)$Такой алгоритм позволяет вести сквозной расчет усталостного разрушения с образованием и распространением квазитрещин без их явного выделения и на фиксированной сетке.
Упругие расчеты цикла нагружения в квазистатическом режиме (МНЦУ) и в динамическом режиме (высокочастотные осцилляции, СВМУ) выполнялись с помощью пакетов программ АСТРА и ANSYS. Пакет АСТРА – высокоэффективный программный комплекс, разработанный на основе безматричного варианта МКЭ, для решения широкого круга задач механики сплошных сред [26, 27].
Пакеты были дополнены кодом для расчета кинетики усталостной повреждаемости и изменения модулей упругости в соответствии с изложенным выше алгоритмом.
4. Примеры расчетов.
4.1. Расчет элемента конструкции ГТД.С использованием предложенной модели и вычислительного алгоритма было рассчитано зарождение и развитие квазитрещины при двух режимах циклического нагружения для важного элемента авиационной конструкции – диска и лопаток I ступени компрессора ГТД Д30КУ.
Характерный вид разрушенного диска, очаг зарождения в контактной зоне диска и лопатки показан на рис. 2 [28]. В этой работе на примере реального разрушения одного из таких дисков в эксплуатации отмечена необходимость многофакторного многокритериального подхода к оценке ресурса титановых дисков компрессоров.
Геометрия сектора диска и лопатки с бандажными полками показана на рис. 3 и ранее их упругое напряженно-деформированное состояние (НДС) было рассчитано в [17, 18] без учета развития процесса повреждаемости.
Рис. 3.
а – Сектор диска и лопатка, б – зона концентрации напряжений в окрестности паза “ласточкин хвост”.
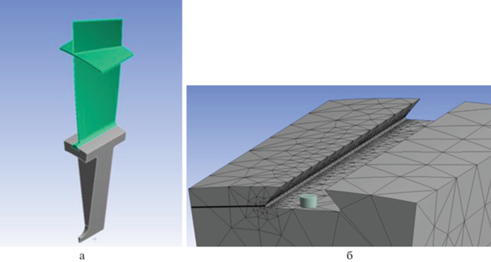
Алюминиевая лопатка вставлена в паз типа “ласточкин хвост” титанового диска и дополнительно скреплена с ним стальным цилиндрическим штифтом (рис. 3б). Контактные поверхности диска и лопатки допускают проскальзывание с коэффициентом трения q, на контактной границе со штифтом выполняется условие полного прилипания.
Математическая постановка соответствующей задачи теории упругости с нелинейными контактными условиями приведена в [17, 18].
В первом циклическом процессе полетного цикла нагружения “взлет-полет-посадка” (пульсирующий цикл, коэффициент асимметрии $R = 0$, режим МНЦУ) сектор диска с лопаткой нагружается центробежными силами при вращении с угловой скоростью ω и аэродинамическим давлением на лопатку, оценочно вычисленным по гипотезе изолированного профиля, при обтекании каждого сечения лопатки под переменным углом атаки [17, 18].
Конечно-элементная сетка при расчете одного сектора с лопаткой показана на рис. 3б. Сетка значительно сгущена в окрестности ожидаемой зоны повреждаемости. Общее количество элементов не превосходит 100 000.
Были прияты следующие параметры расчета: угловая скорость вращения ω = 419 рад/с (4000 об./мин), скоростной напор на бесконечности $\rho {v}_{\infty }^{2}{\text{/}}2$ = 26 000 Н/м2, что соответствует скорости потока 200 м/с при плотности 1.3 кг/м3. Свойства материалов принимались следующими: диск (титановый сплав): модуль Юнга E = 116 ГПa, коэффициент Пуассона ν = 0.32, плотность $\rho $ = 4370 кг/м3; лопатка (алюминиевый сплав): E = 69 ГПa, $\nu $ = 0.33, $\rho $ = 2700 кг/м3; фиксирующий штифт (сталь): $E$ = 207 ГПa, $\nu $ = 0.27, $\rho $ = = 7860 кг/м3, коэффициент трения $q$ = 0.1. Прочностные и усталостные параметры титанового сплава равны: предел прочности ${{\sigma }_{B}}$ = 1160 МПа, классический предел усталости ${{\sigma }_{u}}$ = 340 МПа, ${{\tilde {\sigma }}_{u}}$ = 250 МПа, ${{\beta }_{L}}$ = 0.31, ${{\beta }_{V}}$ = 0.27. Параметры уравнения повреждаемости по результатам вычислительных экспериментов и согласования расчетных и экспериментальных усталостных кривых [12, 13] выбраны следующими: $\gamma $ = 0.5, $\kappa $ = = 0.5, ${{\psi }_{*}}$ = 0.98.
Результаты расчетов развития повреждаемости в диске при полетном цикле нагружения приведены на рис. 4, 5. На этих рисунках приведены распределения эффективных напряжений в двух сечениях. Во-первых, в поперечном сечении диска, проходящем через точку зарождения поврежденности. Во-вторых, в продольном сечении, проходящем от левого угла выреза “ласточкин хвост” до боковой поверхности сектора диска, это сечение показано на рис. 3б сплошной черной линией.
Рис. 4.
Распределение эффективных напряжений в диске в контактной зоне крепления лопатки, МНЦУ, а – вид в поперечном сечении, б – вид в продольном сечении в момент зарождения квазитрещины, $N = 5.2 \times {{10}^{4}}$.
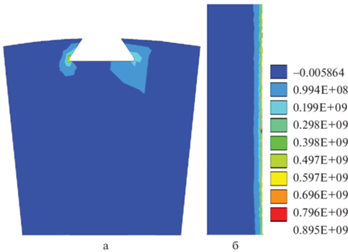
Рис. 5.
Распределение эффективных напряжений в диске в контактной зоне крепления лопатки, МНЦУ, а – вид в поперечном сечении, б – вид в продольном сечении при дальнейшем росте квазитрещины, $N = 2.0 \times {{10}^{5}}$.
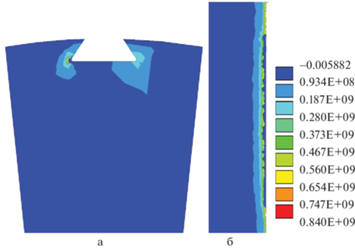
Максимальные эффективные напряжения в начале циклического процесса 913 МПа по критерию SWT и 615 МПа по критерию CSV. Следовательно, работает механизм развития микротрещин нормального отрыва. Квазитрещина зарождается после $N = 5.2 \times {{10}^{4}}$ циклов (рис. 4). Зона зарождения – в середине левого угла “ласточкиного хвоста” (малая черная точка на правом краю сечения, показанного на рис. 4б). Выход квазитрещины на торцевую поверхность диска происходит приблизительно при числе циклов $N = 2.0 \times {{10}^{5}}$ (рис. 5). Таким образом, удается описать процесс развития повреждений, который, в отличие от стандартных схем расчета долговечности по многоосным критериям усталостного разрушения и времени зарождения начального дефекта, позволяет проследить длительность и геометрию развития квазитрещин того или иного типа.
Во втором циклическом процессе проведен расчет наблюдаемых высокочастотных изгибно-крутильных колебаний лопатки, вызванных осевыми смещениями концов бандажных полок амплитуды $\Delta u$ ~ 0.5 мм (реверсивный цикл, коэффициент асимметрии $R = - 1$, режим СВМУ). Эти длительные вибрации поля напряжений в контактной зоне диска и лопаток также могут приводить к зарождению и развитию повреждений (альтернативный механизм разрушения [19]).
На рис. 6, 7 представлены результаты расчёта при изгибно-крутильных колебаниях лопатки с частотой 1000 Гц, вызванных осевыми колебаниями концов бандажной полки с амплитудой $\Delta u$ = 0.55 мм. Зона зарождения – в дальней от штифта зоне “ласточкиного хвоста”, возникает при числе циклов $N = 7.3 \times {{10}^{{10}}}$ (малая черная точка на правом краю сечения, показанного на рис. 6б). Эта характерное расположение очага зарождения наблюдается и в случае реального усталостного разрушения данного элемента конструкции (рис. 2а). Квазитрещина растет, доходит до торца диска и становится наблюдаемой извне при $N = 1.5 \times {{10}^{{11}}}$ (рис. 7), т.е. и в этом режиме процесс развития занимает достаточно продолжительное время, которое может быть оценено с помощью предложенной кинетической модели повреждаемости.
Рис. 6.
Распределение эффективных напряжений в диске в контактной зоне крепления лопатки, СВМУ, а – вид в поперечном сечении; б – вид в продольном сечении в момент зарождения квазитрещины, $N = 7.3 \times {{10}^{{10}}}$.
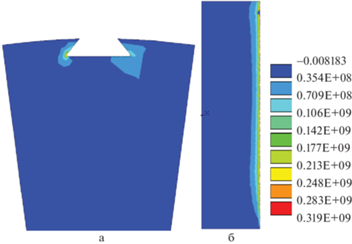
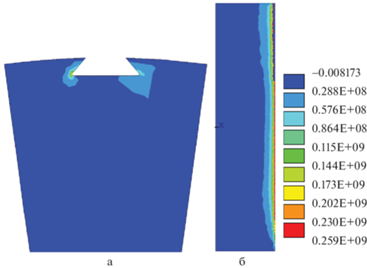
Рис. 7.
Распределение эффективных напряжений в диске в контактной зоне крепления лопатки, СВМУ. а – вид в поперечном сечении; б – вид в продольном сечении при дальнейшем росте квазитрещины, $N = 1.5 \times {{10}^{{11}}}$.
Можно провести оценки реального времени зарождения квазитрещины в каждом из режимов. В предположении, что средний полетный цикл приблизительно равен 3 часам, в режиме МНЦУ ${{T}_{1}} = 5.2 \times {{10}^{4}} \times 3$ ч ~ $1.6 \times {{10}^{5}}$ ч. В режиме СВМУ при частоте колебаний 1000 Гц ${{T}_{2}} = 7.3 \times {{10}^{{10}}}$ × 0.001 c ~ $2.0 \times {{10}^{4}}$ ч. Таким образом, эти оценки, а также специфическая локализация очага зарождения поврежденности, показывают, что зарождение начальной микротрещины более вероятно по механизму СВМУ.
4.2. Расчет высокочастотных крутильных колебаний образца в форме “песочных часов”. Также было проведено численное моделирование экспериментов по развитию СВМУ трещины и усталостному разрушению при высокочастотном кручении образцов из титанового сплава.
Испытания проводились с использованием прямой пьезоэлектрической усталостной торсионной машины [29]. Частота реверсивных колебаний составляла 20 кГц. Испытания были спланированы таким образом, чтобы обеспечить усталостную долговечность свыше 107 циклов. Геометрия образца – песочные часы с гладким сечением (рис. 8а). Материалом для испытаний на кручение являлся титановый сплав со следующими характеристиками: модуль Юнга E = 115 ГПа, плотность $\rho $ = 4500 кг/м3, коэффициент Пуассона $\nu $ = 0.3, классический предел усталости ${{\sigma }_{u}}$ = 440 МПа, предел усталости СВМУ ${{\tilde {\sigma }}_{u}}$ = 380 МПа. Амплитуда крутильных колебаний составляла 0.01 рад.
Рис. 8.
а – конечно-элементная сетка в корсетном образце, б – результат расчета зигзагообразной квазитрещины.
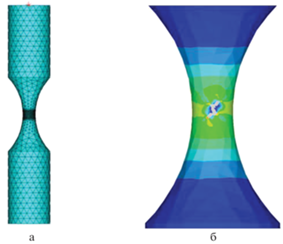
Основная цель математического моделирования – изучить траекторию и тип квазитрещины. Пример траектории трещины, развивающейся на боковой поверхности образца, представлен на рис. 8б.
Результаты расчета зоны повреждения в корсетном образце в режиме СВМУ представлены на рис. 8б, 9а. Характерный вид квазитрещины представлен на рис. 8б (серым цветом). Увеличенное изображение результата расчета показывает типичную для крутильного нагружения зигзагообразную траекторию трещины, рис. 9а. Было установлено, что на начальном этапе развития повреждений элементы разрушались по сдвиговому механизму. Это соответствует вертикальной квазитрещине вдоль оси образца (рис. 9а). Затем доминирующим механизмом разрушения стали квазитрещины нормального отрыва. Этот период соответствует наклонному участку траектории квазитрещины (рис. 9а).
Рис. 9.
а – смена типа квазитрещины в численном расчете; б – наблюдаемая траектория трещины в испытаниях на кручение.
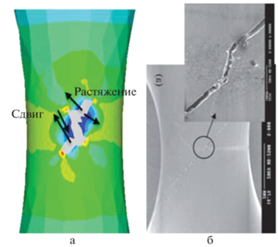
Сравнение результатов численного моделирования с экспериментальными данными [29], рис. 9б, показывает качественное совпадение траекторий и типов трещин, исследованных фрактографическим методом, в сходственные моменты процесса циклического нагружения. Это нетривиальный результат, так как он получен в соответствии с предложенной математической моделью по единообразному вычислительному алгоритму в результате сквозного счета. Таким образом, модель демонстрирует возможность расчета зарождения и развития различных типов квазитрещин в одном циклическом процессе, а также возможность резкой смены траектории и механизма повреждаемости в хорошем согласии с результатами экспериментов при многоосном нагружении.
Разработанная мультирежимная модель и численный метод позволяют проводить сквозной счет развития зон повреждаемости и трещиноподобных зон усталостного разрушения элементов конструкций и экспериментальных образцов без явного выделения трещин в их классическом понимании, а также оценивать долговечность элементов конструкции от появления первых очагов до макроразрушения в различных режимах усталостного разрушения.
Заключение. Предложена мультирежимная двухкритериальная кинетическая модель развития повреждаемости при циклическом нагружении для описания развития процесса усталостного разрушения. Для определения коэффициентов кинетического уравнения повреждаемости использованы известные критерии многоосного усталостного разрушения SWT, в котором заложен механизм, связанный с развитием микротрещин нормального отрыва, и CSV, в котором заложен механизм, связанный с развитием микротрещин сдвига.
Разработан единообразный численный метод и приведен пример расчета развития трещиноподобных зон повреждаемости и усталостного разрушения диска компрессора авиационного газотурбинного двигателя в полетном цикле нагружения (многоцикловая усталость) и при высокочастотных крутильно-изгибных колебаниях лопаток (сверхмногоцикловая усталость). Дана оценка долговечности рассмотренного элемента конструкции.
Также приведены результаты расчета усталостного разрушения при высокочастотных крутильных колебаниях экспериментального образца в форме “песочных часов”, при котором удалось воспроизвести наблюдаемый эффект резкого изменения направления роста и типа квазитрещины в процессе циклического нагружения.
Полученные результаты качественно и количественно совпадают с данными фрактографических исследований случаев усталостного разрушения дисков компрессора в эксплуатации и экспериментов по высокочастотным крутильным колебаниям образцов в режиме СВМУ.
Авторы выражают признательность Б.А. Стратула за помощь в проведении расчетов.
Исследование выполнено в рамках Госзадания ИАП РАН.
Список литературы
Никитин И.С., Бураго Н.Г., Журавлев А.Б., Никитин А.Д. Мультирежимная модель развития усталостных повреждений // ПММ. 2020. Т. 84. № 5. С. 687–698.
Качанов Л.М. О времени разрушения в условиях ползучести // Изв. АН СССР ОТН. 1958. 8. С. 26–31.
Работнов Ю.Н. О механизме длительного разрушения. Вопросы прочности материалов и конструкций // АН СССР ОТН. 1959. С. 5–7.
Lemaitre J., Chaboche J.L. Mechanics of Solid Materials. Cambridge: Univ. Press, 1994. 582 p.
Burago N.G., Nikitin I.S., Nikitin A.D., Stratula B.A. Algorithms for calculation damage processes // Frattura ed Integrità Strutturale. 2019. V. 49. P. 212–224.
Marmi A.K., Habraken A.M., Duchene L. Multiaxial fatigue damage modeling at macro scale of Ti6Al4V alloy // Int. J. Fatigue. 2009. V. 31. P. 2031–2040.
Chaboche J.L., Lesne P.M. A non-linear continuous fatigue damage model// Fatigue & Fracture of Engng. Mater.&Struct.1988. V. 11. P. 1–17.
Peerlings R.H., Brekelmans W.A., de Borst R., Geers M.G. Gradient-enhanced damage modelling of high-cycle fatigue // Int. J. Numer. Method in Engng. 2000. V. 49. P. 1547–1569.
Chow C.L., Wei Y. Constitutive modeling of material damage for fatigue failure prediction// Int. J. Damage Mech.1999. V. 8 (4). P. 355–375.
Plekhov O., Naimark O. et al. The study of a defect evolution in iron under fatigue loading in gigacycle fatigue regime // Frattura ed Integrita Strutturale. 2016. V. 10. № 35. P. 414–423.
Shlyannikov V.N. Creep-Fatigue crack growth rate prediction based on fracture damage zones models // Engng. Fracture Mech. 2019. V. 214. V. 449–463.
Nikitin I.S., Burago N.G., Nikitin A.D., Stratula B.A. On kinetic model of damage development // Proc. Struct. Integr. 2020. V. 28. P. 2032–2042.
Nikitin I.S., Nikitin A.D., Stratula B.A. Study on the Resonant Torsion Vibration in Hourglass Specimens under VHCF Loading // J. Physics: Conf. Ser. 2021. 1945 (1), 012043
Smith R.N., Watson P., Topper T.H. A stress-strain parameter for the fatigue of metals // J. Materials. 1970. V.5. № 4. P. 767–778.
Gates N., Fatemi A. Multiaxial variable amplitude fatigue life analysis including notch effects // Int. J. Fatigue. 2016. V. 91. P. 337–351.
Carpinteri A., Spagnoli A., Vantadori S. Multiaxial assessment using a simplified critical plane based criterion // Int. J. Fatigue. 2011. V. 33. P. 969–976.
Бураго Н.Г., Журавлев А.Б., Никитин И.С. Модели многоосного усталостного разрушения и оценка долговечности элементов конструкций // Изв. РАН. МТТ. 2011. № 6. С. 22–33.
Burago N.G., Nikitin I.S. Multiaxial Fatigue criteria and durability of titanium compressor disks in low- and giga-cycle fatigue modes // in: Mathematical Modeling and Optimization of Complex Structures. Heidelberg: Springer, 2016. P. 117–130.
Шанявский А.А. Моделирование усталостных разрушений металлов. Уфа: Монография, 2007. 498 с.
Sines G. Behavior of metals under complex static and alternating stresses // in: Metal Fatigue. McGraw-Hill, 1959. P. 145–169.
Crossland B. Effect of large hydrostatic pressures on torsional fatigue strength of an alloy steel // Proc. Int. Conf. on Fatigue of Metals. London: 1956. P. 138–149.
Findley W. A theory for the effect of mean stress on fatigue of metals under combined torsion and axial load or bending // J. Eng. for Indust. 1959. P. 301–306.
Paris P.C., Erdogan F. A Critical analysis of crack propagation laws // J. Basic Engng. 1963. V. 85. P. 528–533.
Collins J.A. Failure of Materials in Mechanical Design: Analysis, Prediction, Prevention. New York: Wiley, 1993. 654 p.
Basquin O.H. The exponential law of endurance tests // in: Proc of the Amer. Soc. for Testing & Material. 1910. V. 10. P. 625–630.
Бураго Н.Г., Никитин И.С., Якушев В.Л. Гибридный численный метод решения нестационарных задач механики сплошной среды с применением адаптивных наложенных сеток // ЖВММФ. 2016. Т. 56. № 6. С. 1082–1092.
Бураго Н.Г., Никитин И.С. Алгоритмы сквозного счета для процессов разрушения// Компьют. исслед. и моделир. 2018. Т. 10. № 5. С. 645–666.
Шанявский А.А. Безопасная эксплуатация дисков I ступени КНД двигателей семейства Д-30КУ по критерию роста усталостных трещин // Пробл. безопасн. полетов. 2011. № 1. С. 20–48.
Nikitin A., Bathias C., Palin-Luc T. A new piezoelectric fatigue testing machine in pure torsion for ultrasonic fatigue tests: application to forged and extruded titanium alloys// Fatigue & Fracture of Engng. Mater.&Struct. 2015. V. 38. № 11. P. 1294–1304.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика