Прикладная математика и механика, 2022, T. 86, № 4, стр. 612-621

Тонкослойные асимптотики в обобщенной задаче Прандтля для неоднородного по толщине пластического материала

Д. В. Георгиевский^1, 2, *

¹ МГУ им. М.В. Ломоносова
Москва, Россия

² Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

³ Московский центр фундаментальной и прикладной математики
Москва, Россия

^* E-mail: georgiev@mech.math.msu.su

Поступила в редакцию 20.04.2022
После доработки 11.05.2022
Принята к публикации 20.05.2022

EDN: SLUMGD
DOI: 10.31857/S0032823522040087

Полный текст (PDF)

Аннотация

Рассматривается обобщенная краевая задача Прандтля, моделирующая квазистатический технологический процесс сдавливания в одном направлении и быстром растекании в другом тонкого несжимаемого идеально жесткопластического слоя (плоское деформированное состояние), соответствующего критерию пластичности Мизеса–Генки с переменным по толщине пределом текучести. Стратификация может быть непрерывной либо кусочно-постоянной, в последнем случае задача моделирует прессование слоистых пластических композитов (ламинатов, “сэндвичей”) и прецизионное доведение их до нужной толщины. На основе тонкослойных сингулярных асимптотик по малому геометрическому параметру с помощью развиваемого в работе метода асимптотического интегрирования находится приближенное решение для кинематических и силовых величин. Обсуждается применимость квазистатического подхода на различных временных диапазонах процесса сдавливания.

Ключевые слова: идеально жесткопластический материал, задача Прандтля, тонкослойные асимптотики, квазистатика, неоднородность, стратификация, слоистый композит, “сэндвич”, число Эйлера

В плоской теории идеальной пластичности важное теоретическое значение имеют задача Прандтля и различные ее обобщения [1], моделирующие технологические процессы прессования и растекания тонких слоев при их обработке давлением [2, 3], в том числе и высокоскоростной. Классическое решение Прандтля может служить основой для получения более общих решений применительно к неоднородным по толщине тонким пластическим слоям как с непрерывной стратификацией, так и к слоистым композитам [4, 5].

1. Описание технологического процесса и постановка задачи. Положим, что в начальный момент времени $t = 0$ плоский тонкий слой

(1.1)

${{\Omega }_{0}} = \{ - {{l}_{0}} < {{x}_{1}} < {{l}_{0}}, - {{h}_{0}} < {{x}_{2}} < {{h}_{0}}\} ,\quad \alpha = \frac{{{{h}_{0}}}}{{{{l}_{0}}}} \ll 1$

был занят несжимаемым идеально жесткопластическим материалом, подчиняющимся критерию пластичности Мизеса–Генки. Материал неоднороден по толщине слоя, так что его предел текучести ${{\sigma }_{s}}$ – заданная непрерывная либо кусочно-непрерывная функция координаты ${{x}_{2}}$ в начальный момент. Без сильного ограничения общности примем, что эта функция четная.

При $t > 0$ начинается квазистатический процесс сжатия слоя ${{\Omega }_{0}}$ абсолютно жесткими плитами, движущимися вдоль оси ${{x}_{2}}$ навстречу друг другу, каждая с постоянной скоростью $V$. К моменту $t < {{h}_{0}}{\text{/}}V = t{\kern 1pt} *$ растекающийся с большой скоростью вдоль оси ${{x}_{1}}$ пластический слой занимает плоскую область

(1.2)

$\Omega = \{ - l < {{x}_{1}} < l, - h < {{x}_{2}} < h\} ;\quad h = {{h}_{0}} - Vt,\quad l = \frac{{{{h}_{0}}{{l}_{0}}}}{{{{h}_{0}} - Vt}}$

Замкнутая система уравнений теории идеальной пластичности при плоской деформации в квазистатическом приближении имеет вид

(1.3)

$ - {{p}_{{,1}}} + {{s}_{{11,1}}} + {{s}_{{12,2}}} = 0,\quad - {\kern 1pt} {{p}_{{,2}}} - {{s}_{{11,2}}} + {{s}_{{12,1}}} = 0$

(1.4)

${{s}_{{11}}}({{v}_{{1,2}}} + {{v}_{{2,1}}}) = 2{{s}_{{12}}}{{v}_{{1,1}}}$

(1.5)

$s_{{11}}^{2} + s_{{12}}^{2} = \frac{1}{2}{\kern 1pt} \sigma _{s}^{2}({{\xi }_{2}}({{x}_{1}},{{x}_{2}}))$

(1.6)

${{v}_{{1,1}}} + {{v}_{{2,2}}} = 0,$

где $p$ – давление, ${{s}_{{11}}}$ и ${{s}_{{12}}}$ – компоненты девиатора тензора напряжений ${{\sigma }_{{ij}}} = - p{{\delta }_{{ij}}} + {{s}_{{ij}}}$, а ${{v}_{1}}$ и ${{v}_{2}}$ – компоненты вектора скорости. Система, состоящая из уравнений равновесия (1.3), условия (1.4) пропорциональности девиаторов напряжений и скоростей деформаций, критерия Мизеса–Генки (1.5) и условия несжимаемости (1.6) относительно пяти функций $p$, ${{s}_{{11}}}$, ${{s}_{{12}}}$, ${{v}_{1}}$ и ${{v}_{2}}$ эйлеровых координат ${{x}_{1}}$ и ${{x}_{2}}$, осложнена тем, что единственная материальная характеристика среды – предел текучести ${{\sigma }_{s}}$ – известная функция лагранжевой координаты ${{\xi }_{2}}$, но заранее неизвестная функция ${{x}_{1}}$ и ${{x}_{2}}$. В аргумент этой функции в (1.5) входит обратный закон движения ${{\xi }_{i}} = {{\xi }_{i}}({{x}_{1}},{{x}_{2}})$, $i = 1,2$. Таким образом, систему (1.3)–(1.6) необходимо дополнить кинематическими уравнениями

(1.7)

$\frac{{d{{x}_{i}}}}{{dt}} = {{v}_{i}}({{x}_{1}},{{x}_{2}}),\quad {{\left. {{{x}_{i}}} \right|}_{{t = 0}}} = {{\xi }_{i}}$

для нахождения сначала закона движения ${{x}_{i}} = {{x}_{i}}({{\xi }_{1}},{{\xi }_{2}},t)$, а затем необходимого для (1.5) обратного закона ${{\xi }_{i}} = {{\xi }_{i}}({{x}_{1}},{{x}_{2}},t)$.

Кинематические граничные условия соответствуют равномерному сближению жестких плит:

(1.8)

${{\left. {{{v}_{2}}} \right|}_{{{{x}_{2}} = \pm h}}} = \mp V$

Кроме того, на границах слоя ${{x}_{2}} = \pm h$ модуль касательного напряжения равен

(1.9)

${\text{|}}{{s}_{{12}}}{{{\text{|}}}_{{{{x}_{2}} = \pm h}}} = \frac{m}{{\sqrt 2 }}{{\sigma }_{s}}({{\xi }_{2}}({{x}_{1}}, \pm h));\quad 0 < m \leqslant 1,$

где $m$ – известный из технологических соображений коэффициент сцепления пластического материала с плитами. Значение $m = 1$ реализуется в случае полного сцепления (абсолютной шероховатости), когда всю интенсивность напряжений на границах занимает касательная составляющая. Постоянная $m$ может рассматриваться в данной задаче как управляющий напряженным состоянием параметр.

Квазистатический режим деформирования имеет место не на всем временном интервале $0 < t < {{t}_{*}}$. При подходе к правому концу этого интервала даже при сколь угодно медленном движении плит начинают проявляться и играть существенную роль динамические эффекты, приводящие к перестройке силовых режимов, необходимых для осуществления процесса [6, 7].

Введем безразмерные координаты на плоскости $({{x}_{1}}{{x}_{2}})$ и время:

(1.10)

${{\eta }_{1}} = \frac{{{{x}_{1}}}}{{{{l}_{0}}}},\quad {{\eta }_{2}} = \frac{{{{x}_{2}}}}{{{{h}_{0}}}},\quad {{\eta }_{{10}}} = \frac{{{{\xi }_{1}}}}{{{{l}_{0}}}},\quad {{\eta }_{2}} = \frac{{{{\xi }_{2}}}}{{{{h}_{0}}}},\quad \tau = \frac{{Vt}}{{{{h}_{0}}}},$

изменяющиеся в области $\Omega $ в пределах

(1.11)

$\begin{gathered} - \frac{1}{{1 - \tau }} < {{\eta }_{1}} < \frac{1}{{1 - \tau }},\quad - {\kern 1pt} (1 - \tau ) < {{\eta }_{2}} < 1 - \tau ;\quad 0 < \tau < 1 \\ - 1 < {{\eta }_{{10}}} < 1,\quad - {\kern 1pt} 1 < {{\eta }_{{20}}} < 1 \\ \end{gathered} $

Представляя переменный предел текучести ${{\sigma }_{s}}$ в виде

(1.12)

${{\sigma }_{s}} = \sigma _{s}^{0}f({{\eta }_{{20}}}({{\eta }_{1}},{{\eta }_{2}})){\kern 1pt} ;\quad \sigma _{s}^{0} = {{\sigma }_{s}}( \pm h),\quad f( \pm 1) = 1$

введем в рассмотрение безразмерную функцию $f({{\eta }_{{20}}}({{\eta }_{1}},{{\eta }_{2}}))$, отвечающую за распределение пластического материала по толщине в начальной конфигурации ${{\Omega }_{0}}$ (1.1). Как функция одной безразмерной лагранжевой координаты ${{\eta }_{{20}}}$ она задана и является четной по ${{\eta }_{{20}}}$, но изначально она неизвестна как функция безразмерных эйлеровых координат ${{\eta }_{1}}$ и ${{\eta }_{2}}$.

2. Асимптотические разложения. Представим пять функций, входящих в систему (1.3)–(1.6), в виде степенных рядов по постоянному малому геометрическому параметру $\alpha $, определенному в (1.1):

${{{v}}_{1}} = V\sum\limits_{n = - 1}^\infty {{\alpha }^{n}}{\bar {v}}_{1}^{{\{ n\} }}({{\eta }_{1}},{{\eta }_{2}}),\quad {{{v}}_{2}} = V\sum\limits_{n = 0}^\infty {{\alpha }^{n}}{\bar {v}}_{2}^{{\{ n\} }}({{\eta }_{1}},{{\eta }_{2}})$

(2.1)

${{s}_{{11}}} = \frac{{\sigma _{s}^{0}}}{{\sqrt 2 }}\sum\limits_{n = 0}^\infty {{\alpha }^{n}}\bar {s}_{{11}}^{{\{ n\} }}({{\eta }_{1}},{{\eta }_{2}}),\quad {{s}_{{12}}} = \frac{{\sigma _{s}^{0}}}{{\sqrt 2 }}\sum\limits_{n = 0}^\infty {{\alpha }^{n}}\bar {s}_{{12}}^{{\{ n\} }}({{\eta }_{1}},{{\eta }_{2}})$

$p = \frac{{\sigma _{s}^{0}}}{{\sqrt 2 }}\sum\limits_{n = - 1}^\infty {{\alpha }^{n}}{{\bar {p}}^{{\{ n\} }}}({{\eta }_{1}},{{\eta }_{2}})$

Сингулярность рядов для ${{{v}}_{1}}$ и $p$ обусловлена физическим смыслом технологического процесса сжатия-растекания и стремлением в бесконечность двух этих функций при $\alpha \to 0$. Три оставшиеся функции ведут себя при этом регулярно. Строгое обоснование нижних границ суммирования рядов, аналогичных (2.1), применительно к классической задаче Прандтля приведено в [8].

Разложим также в ряды по $\alpha $ функции ${{\eta }_{1}}$ и ${{\eta }_{2}}$, входящие в безразмерный закон движения ${{\eta }_{1}} = {{\eta }_{1}}({{\eta }_{{10}}},{{\eta }_{{20}}},\tau )$, ${{\eta }_{2}} = {{\eta }_{2}}({{\eta }_{{10}}},{{\eta }_{{20}}},\tau )$:

(2.2)

${{\eta }_{1}} = \sum\limits_{n = - 1}^\infty {{\alpha }^{n}}\bar {\eta }_{1}^{{\{ n\} }}(\tau ),\quad {{\eta }_{2}} = \sum\limits_{n = 0}^\infty {{\alpha }^{n}}\bar {\eta }_{2}^{{\{ n\} }}(\tau )$

Подставляя ряды (2.1) в пять уравнений системы (1.3)–(1.6) и ряды (2.2) в кинематические уравнения (1.7), получим

(2.3)

$\sum\limits_{n = 0}^\infty {{\alpha }^{n}}( - \bar {p}_{{|1}}^{{\{ n - 1\} }} + \bar {s}_{{11|1}}^{{\{ n - 1\} }} + \bar {s}_{{12|2}}^{{\{ n\} }}) = 0$

(2.4)

$ - \frac{1}{\alpha }{\kern 1pt} \bar {p}_{{|2}}^{{\{ - 1\} }} + \sum\limits_{n = 0}^\infty {{\alpha }^{n}}( - \bar {p}_{{|2}}^{{\{ n\} }} - \bar {s}_{{11|2}}^{{\{ n\} }} + \bar {s}_{{12|1}}^{{\{ n - 1\} }}) = 0$

(2.5)

$\left( {\sum\limits_{n = 0}^\infty {{\alpha }^{n}}\bar {s}_{{11}}^{{\{ n\} }}} \right) \cdot \left( {\frac{1}{\alpha }{\bar {v}}_{{1|2}}^{{\{ - 1\} }} + \sum\limits_{n = 0}^\infty {{\alpha }^{n}}({\bar {v}}_{{1|2}}^{{\{ n\} }} + {\bar {v}}_{{2|1}}^{{\{ n - 1\} }})} \right) = 2\left( {\sum\limits_{n = 0}^\infty {{\alpha }^{n}}\bar {s}_{{12}}^{{\{ n\} }}} \right) \cdot \left( {\sum\limits_{n = 0}^\infty {{\alpha }^{n}}{\bar {v}}_{{1|1}}^{{\{ n - 1\} }}} \right)$

(2.6)

${{\left( {\sum\limits_{n = 0}^\infty {{\alpha }^{n}}\bar {s}_{{11}}^{{\{ n\} }}} \right)}^{2}} + {{\left( {\sum\limits_{n = 0}^\infty {{\alpha }^{n}}\bar {s}_{{12}}^{{\{ n\} }}} \right)}^{2}} = {{f}^{2}}({{\eta }_{{20}}}({{\eta }_{1}},{{\eta }_{2}},\tau ))$

(2.7)

$\sum\limits_{n = 0}^\infty {{\alpha }^{n}}({\bar {v}}_{{1|1}}^{{\{ n - 1\} }} + {\bar {v}}_{{2|2}}^{{\{ n\} }}) = 0$

(2.8)

$\begin{gathered} \frac{{d\eta _{1}^{{\{ n - 1\} }}}}{{d\tau }} = {\bar {v}}_{1}^{{\{ n - 1\} }},\quad \frac{{d\eta _{2}^{{\{ n\} }}}}{{d\tau }} = {\bar {v}}_{2}^{{\{ n\} }};\quad n = 0,1,2, \ldots \\ {{\left. {\eta _{1}^{{\{ n - 1\} }}} \right|}_{{\tau = 0}}} = {{\eta }_{{10}}}{{\delta }_{{n0}}},\quad {{\left. {\eta _{2}^{{\{ n\} }}} \right|}_{{\tau = 0}}} = {{\eta }_{{20}}}{{\delta }_{{n0}}}, \\ \end{gathered} $

где ${{\delta }_{{n0}}}$ – символ Кронекера; вертикальная черта в нижних индексах означает частное дифференцирование по безразмерным координатам ${{\eta }_{1}}$ и ${{\eta }_{2}}$. Функции $s_{{12}}^{{\{ - 1\} }}$ и ${v}_{2}^{{\{ - 1\} }}$, встречающиеся в (2.4) и (2.5), следует положить тождественно нулевыми.

Граничные условия (1.8) и (1.9) запишутся следующим образом:

(2.9)

${{\left. {{\bar {v}}_{2}^{{\{ n\} }}} \right|}_{{{{\eta }_{2}} = \pm (1 - \tau )}}} = \mp {{\delta }_{{n0}}}$

(2.10)

${{\left. {\left| {\bar {s}_{{12}}^{{\{ n\} }}} \right|} \right|}_{{{{\eta }_{2}} = \pm (1 - \tau )}}} = m{{\delta }_{{n0}}}$

3. Метод асимптотического интегрирования. Для нахождения неизвестных коэффициентов в рядах (2.1) и закона движения частиц воспользуемся методом асимптотического интегрирования [9]. Он заключается в получении и анализе цепочки замкнутых систем уравнений относительно данных коэффициентов путем приравнивания нулю коэффициентов при различных степенях $\alpha $ в (2.3)–(2.7). Начало цепочки связано с обнулением двух сингулярных слагаемых в (2.4) и (2.5) с отрицательными степенями $\alpha $:

(3.1)

$\bar {p}_{{|2}}^{{\{ - 1\} }} = 0,\quad {\bar {v}}_{{1|2}}^{{\{ - 1\} }} = 0$

Заметим, что в уравнениях (2.3), (2.4) и (2.7), порожденных линейными уравнениями (1.3) и (1.6), метод асимптотического интегрирования позволяет перейти от рядов к итерационным цепочкам постоянной длины по $n = 0,1,2, \ldots $:

(3.2)

$ - \bar {p}_{{|1}}^{{\{ n - 1\} }} + \bar {s}_{{11|1}}^{{\{ n - 1\} }} + \bar {s}_{{12|2}}^{{\{ n\} }} = 0,\quad - {\kern 1pt} \bar {p}_{{|2}}^{{\{ n\} }} - \bar {s}_{{11|2}}^{{\{ n\} }} + \bar {s}_{{12|1}}^{{\{ n - 1\} }} = 0,\quad {\bar {v}}_{{1|1}}^{{\{ n - 1\} }} + {\bar {v}}_{{2|2}}^{{\{ n\} }} = 0$

Первое уравнение третьей цепочки в (3.2) ${v}_{{1|1}}^{{\{ - 1\} }} + {\bar {v}}_{{2|2}}^{{\{ 0\} }} = 0$ вместе со вторым уравнением (3.1) и двумя граничными условиями (2.9) приводит к линейному по координатам полю скоростей в главных в (2.1) приближениях по $\alpha $:

(3.3)

${v}_{1}^{{\{ - 1\} }} = \frac{{{{\eta }_{1}}}}{{1 - \tau }},\quad {\bar {v}}_{2}^{{\{ 0\} }} = - \frac{{{{\eta }_{2}}}}{{1 - \tau }}$

Это поле соответствует плоскому сжатию-растеканию несжимаемой сплошной среды.

Подставим функции (3.3) в систему (2.8) при $n = 0$ и, интегрируя ее по $\tau $, придем к закону движения в главном приближении

(3.4)

$\eta _{1}^{{\{ - 1\} }} = \frac{{{{\eta }_{{10}}}}}{{1 - \tau }},\quad \eta _{2}^{{\{ 0\} }} = {{\eta }_{{20}}}(1 - \tau )$

Аргумент ${{\eta }_{{20}}}({{\eta }_{1}},{{\eta }_{2}},\tau )$ у функции ${{f}^{2}}$ в (2.6) на основании (3.4) будет следующий

(3.5)

${{\eta }_{{20}}}({{\eta }_{1}},{{\eta }_{2}},\tau ) = \frac{{{{\eta }_{2}}}}{{1 - \tau }}$

Правая часть (2.6) в главном приближении по $\alpha $ становится известной функцией одной безразмерной эйлеровой координаты ${{\eta }_{2}}$.

Первое уравнение первой цепочки (3.2) $ - \bar {p}_{{|1}}^{{\{ - 1\} }} + \bar {s}_{{12|2}}^{{\{ 0\} }} = 0$ вместе с первым уравнением (3.1) и двумя граничными условиями (2.10) при важном предположении о непрерывной дифференцируемости функции $\bar {s}_{{12}}^{{\{ 0\} }}$ по ${{\eta }_{2}}$ на всем интервале изменения ${{\eta }_{2}}$ (1.11) приводит к следующим коэффициентам в главных по $\alpha $ слагаемых в (2.1) для ${{s}_{{12}}}$ и $p$:

(3.6)

$\bar {s}_{{12}}^{{\{ 0\} }} = - sm{\kern 1pt} \frac{{{{\eta }_{2}}}}{{1 - \tau }},\quad {{\bar {p}}^{{\{ - 1\} }}} = \frac{m}{{1 - \tau }}\left( {\frac{1}{{1 - \tau }} - \left| {{{\eta }_{1}}} \right|} \right),$

где $s = \operatorname{sign} {{\eta }_{1}} = \operatorname{sign} {{x}_{1}}$. Давление кусочно-линейно по простиранию слоя с изломом в срединном сечении ${{x}_{1}} = 0$, а касательное напряжение при любом ${{\eta }_{2}}$ кусочно-постоянно по простиранию и терпит разрыв при ${{x}_{1}} = 0$. Явная зависимость функции $\bar {s}_{{12}}^{{\{ 0\} }}$ (3.6) от $s$ говорит о достоверности получаемого решения лишь вдали от сечения ${{x}_{1}} = 0$. Этот факт известен в классической задаче Прандтля и математически объясняется тем, что в окрестности сечения ${{x}_{1}} = 0$ ряды (2.1) теряют асимптотичность в смысле Пуанкаре [10]. Расстановка знаков у $\bar {s}_{{12}}^{{\{ 0\} }}$ именно как в (3.6) и у некоторых других функций подробно обсуждена в [8] применительно к задаче Прандтля.

Приравняем далее коэффициенты при ${{\alpha }^{0}}$ в левой и правой частях (2.6) и с учетом (3.6) определим функцию $\bar {s}_{{11}}^{{\{ 0\} }}$:

(3.7)

$\bar {s}_{{11}}^{{\{ 0\} }} = \sqrt {{{f}^{2}}\left( {\frac{{{{\eta }_{2}}}}{{1 - \tau }}} \right) - \frac{{{{m}^{2}}\eta _{2}^{2}}}{{{{{(1 - \tau )}}^{2}}}}} $

Из (3.7) следует ограничение на заданную функцию $f$ для осуществимости идеально жесткопластического процесса деформирования. Как четная функция своего аргумента ${{\eta }_{{20}}} \in [ - 1;1]$ она должна удовлетворять неравенству

(3.8)

$f({{\eta }_{{20}}}) \geqslant m{{\eta }_{{20}}}$

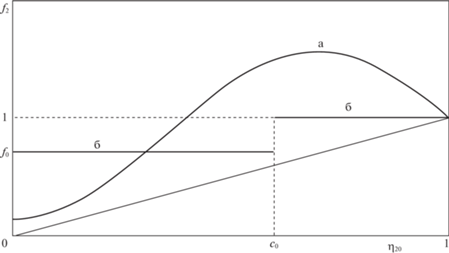
Напомним, что согласно (1.12) $f(1) = 1$, поэтому в точке ${{\eta }_{{20}}} = 1$, т.е. на границе области $\Omega $ (1.2) неравенство (3.8) заведомо выполняется и становится равенством при максимальном значении $m = 1$ коэффициента сцепления. На рисунке для $m = 1$ изображены возможные согласованные с (3.8) распределения по толщине предела текучести (а – непрерывно стратифицированный слой; б – слоистый композит).

Рис. 1.

Приравнивание нулю коэффициентов при ${{\alpha }^{0}}$ в (2.4) и (2.5) приводит к уравнениям

(3.9)

${{({{\bar {p}}^{{\{ 0\} }}} + \bar {s}_{{11}}^{{\{ 0\} }})}_{{|2}}} = 0,\quad \bar {s}_{{11}}^{{\{ 0\} }}{\bar {v}}_{{1|2}}^{{\{ 0\} }} = 2\bar {s}_{{12}}^{{\{ 0\} }}{\bar {v}}_{{1|1}}^{{\{ - 1\} }},$

из которых после интегрирования по ${{\eta }_{2}}$ определяются функции ${{\bar {p}}^{{\{ 0\} }}}$ и ${\bar {v}}_{1}^{{\{ 0\} }}$ – коэффициенты при первых регулярных по $\alpha $ слагаемых в разложениях $p$ и ${{{v}}_{1}}$ в (2.1):

(3.10)

${{\bar {p}}^{{\{ 0\} }}} = - \sqrt {{{f}^{2}}\left( {\frac{{{{\eta }_{2}}}}{{1 - \tau }}} \right) - \frac{{{{m}^{2}}\eta _{2}^{2}}}{{{{{(1 - \tau )}}^{2}}}}} + a({{\eta }_{1}})$

(3.11)

${\bar {v}}_{1}^{{\{ 0\} }} = - \frac{{2sm}}{{{{{(1 - \tau )}}^{2}}}}\int {{\eta }_{2}}{{\left[ {{{f}^{2}}\left( {\frac{{{{\eta }_{2}}}}{{1 - \tau }}} \right) - \frac{{{{m}^{2}}\eta _{2}^{2}}}{{{{{(1 - \tau )}}^{2}}}}} \right]}^{{ - 1/2}}}d{{\eta }_{2}} + b({{\eta }_{1}}),$

где $a$ и $b$ – пока произвольные функции от ${{\eta }_{1}}$.

Для нахождения этих функций приравняем нулю коэффициенты при $\alpha $ в (2.3) и (2.7):

(3.12)

${{( - {{\bar {p}}^{{\{ 0\} }}} + \bar {s}_{{11}}^{{\{ 0\} }})}_{{|1}}} + \bar {s}_{{12|2}}^{{\{ 1\} }} = 0,\quad {v}_{{1|1}}^{{\{ 0\} }} + {\bar {v}}_{{2|2}}^{{\{ 1\} }} = 0$

Продифференцируем равенства (3.12) по ${{\eta }_{2}}$ и, пользуясь выражениями (3.7), (3.10) и (3.11) для $\bar {s}_{{11}}^{{\{ 0\} }}$, ${{\bar {p}}^{{\{ 0\} }}}$ и ${\bar {v}}_{1}^{{\{ 0\} }}$, придем к дифференциальным уравнениям

(3.13)

$\bar {s}_{{12|22}}^{{\{ 1\} }} = 0,\quad {\bar {v}}_{{2|22}}^{{\{ 1\} }} = 0$

с однородными граничными условиями (2.9), (2.10) на поверхностях слоя, касающихся движущихся плит. Следовательно, всюду в слое

(3.14)

$\bar {s}_{{12}}^{{\{ 1\} }} \equiv 0,\quad {\bar {v}}_{2}^{{\{ 1\} }} \equiv 0$

Подставляя теперь нулевые функции (3.14) в (3.12), получим что $da{\text{/}}d{{\eta }_{1}} = 0$ и $db{\text{/}}d{{\eta }_{1}} = 0$, т.е. с точностью до движения всего слоя как недеформируемого целого вдоль оси ${{x}_{1}}$ можно положить $a \equiv 0$ и $b \equiv 0$.

Таким образом, определены несколько первых членов в каждом из разложений (2.1):

$\frac{{{{{v}}_{1}}}}{V} = \frac{{{{\eta }_{1}}}}{{\alpha (1 - \tau )}} - \frac{{2sm}}{{{{{(1 - \tau )}}^{2}}}}\int {{\eta }_{2}}{{\left[ {{{f}^{2}}\left( {\frac{{{{\eta }_{2}}}}{{1 - \tau }}} \right) - \frac{{{{m}^{2}}\eta _{2}^{2}}}{{{{{(1 - \tau )}}^{2}}}}} \right]}^{{ - 1/2}}}d{{\eta }_{2}} + O(\alpha )$

(3.15)

$\begin{gathered} \frac{{{{{v}}_{2}}}}{V} = - \frac{{{{\eta }_{2}}}}{{1 - \tau }} + O({{\alpha }^{2}}),\quad \frac{{\sqrt 2 {{s}_{{11}}}}}{{\sigma _{s}^{0}}} = \sqrt {{{f}^{2}}\left( {\frac{{{{\eta }_{2}}}}{{1 - \tau }}} \right) - \frac{{{{m}^{2}}\eta _{2}^{2}}}{{{{{(1 - \tau )}}^{2}}}}} + O(\alpha ) \\ \frac{{\sqrt 2 {{s}_{{12}}}}}{{\sigma _{s}^{0}}} = - sm\frac{{{{\eta }_{2}}}}{{1 - \tau }} + O({{\alpha }^{2}}) \\ \end{gathered} $

$\frac{{\sqrt 2 p}}{{\sigma _{s}^{0}}} = \frac{m}{{\alpha (1 - \tau )}}\left( {\frac{1}{{1 - \tau }} - \left| {{{\eta }_{1}}} \right|} \right) - \sqrt {{{f}^{2}}\left( {\frac{{{{\eta }_{2}}}}{{1 - \tau }}} \right) - \frac{{{{m}^{2}}\eta _{2}^{2}}}{{{{{(1 - \tau )}}^{2}}}}} + O(\alpha )$

4. Случай трехслойного “сэндвича”. Если идеально жесткопластический слой непрерывно стратифицирован по пределу текучести, т.е. функция $f$ в (1.12) непрерывна по своему единственному аргументу ${{\eta }_{{20}}}$, то все члены разложений (3.15) непрерывны по поперечной координате. Рассмотрим подробнее важный в приложениях случай кусочно-постоянной зависимости $f$ от ${{\eta }_{{20}}}$, означающий, что плоский слой ${{\Omega }_{0}}$ (1.1) – слоистый композит. Для определенности положим, что этот композит трехслойный и представляет собой так называемый “сэндвич” [11, 12] (график б на рисунке):

(4.1)

$f = \left\{ \begin{gathered} {{f}_{0}},\quad - {\kern 1pt} {{c}_{0}} < {{\eta }_{{20}}} < {{c}_{0}};\quad {{c}_{0}} < 1 \hfill \\ 1,\quad {{c}_{0}} < \left| {{{\eta }_{{20}}}} \right| \leqslant 1 \hfill \\ \end{gathered} \right.$

Здесь учтено требование масштабирования $f( \pm 1) = 1$. Условие (3.8) приводит к ограничению на константы ${{c}_{0}}$ и ${{f}_{0}}$ в (4.1):

(4.2)

${{f}_{0}} \geqslant m{{c}_{0}},$

т.е. средний слой сэндвича” не должен иметь слишком низкий предел текучести.

Заметим, что из (2.8) при $n = 1$ и (3.14) следует, что $\eta _{2}^{{\{ 1\} }} \equiv 0$ и с точностью уже до ${{\alpha }^{2}}$ обратный закон движения (3.5) по-прежнему имеет место. Независимость правой части (3.5) от ${{\eta }_{1}}$ говорит о том, что изначально прямолинейные границы раздела прослоек “сэндвича” ${{\eta }_{{20}}} = \pm {{c}_{0}}$ в процессе сжатия ($\tau > 0$) остаются прямолинейными: ${{\eta }_{2}} = \pm c$, где $c = {{c}_{0}}(1 - \tau )$.

Подстановка (4.1) в разложения (3.15) приводит к тому, что функции ${{s}_{{11}}}$, $p$ и ${{{v}}_{1}}$ оказываются разрывными по толщине слоя. При этом у $p$ и ${{{v}}_{1}}$ разрыв претерпевают неглавные слагаемые разложений, а главные, сингулярные, от поперечной координаты не зависят. Функции ${{s}_{{12}}}$ и ${{{v}}_{2}}$ остаются непрерывными. Вычисляя интеграл в выражении для ${{{v}}_{1}}$ в (3.15), получим

(4.3)

$\frac{{{{{v}}_{1}}}}{V} = \frac{{{{\eta }_{1}}}}{{\alpha (1 - \tau )}} - \left\{ \begin{gathered} \frac{{2s}}{m}\sqrt {f_{0}^{2} - \frac{{{{m}^{2}}\eta _{2}^{2}}}{{{{{(1 - \tau )}}^{2}}}}} ,\quad - {\kern 1pt} c < {{\eta }_{2}} < c;\quad c < 1 - \tau \hfill \\ \frac{{2s}}{m}\sqrt {1 - \frac{{{{m}^{2}}\eta _{2}^{2}}}{{{{{(1 - \tau )}}^{2}}}}} ,\quad c < \left| {{{\eta }_{2}}} \right| \leqslant 1 \hfill \\ \end{gathered} \right.$

В размерном виде разложения (3.15) в случае “сэндвича” имеют вид

${{{v}}_{1}} = V\left( {\frac{{{{x}_{1}}}}{h} - \frac{{2s}}{m}\sqrt {{{f}^{2}} - \frac{{{{m}^{2}}x_{2}^{2}}}{{{{h}^{2}}}}} + O(\alpha )} \right),\quad {{{v}}_{2}} = V\left( { - \frac{{{{x}_{2}}}}{h} + O({{\alpha }^{2}})} \right)$

(4.4)

${{s}_{{11}}} = \frac{{\sigma _{s}^{0}}}{{\sqrt 2 }}\left( {\sqrt {{{f}^{2}} - \frac{{{{m}^{2}}x_{2}^{2}}}{{{{h}^{2}}}}} } \right) + O(\alpha ),\quad {{s}_{{12}}} = \frac{{\sigma _{s}^{0}}}{{\sqrt 2 }}\left( { - sm{\kern 1pt} \frac{{{{x}_{2}}}}{h} + O({{\alpha }^{2}})} \right)$

$p = \frac{{\sigma _{s}^{0}}}{{\sqrt 2 }}\left( {\frac{m}{h}(l - \left| {{{x}_{1}}} \right|} \right) - \sqrt {{{f}^{2}} - \frac{{{{m}^{2}}x_{2}^{2}}}{{{{h}^{2}}}}} + O(\alpha )),$

где безразмерная четная кусочно-постоянная функция $f$ согласно (4.1) следующая:

(4.5)

$f = \left\{ \begin{gathered} {{f}_{0}},\quad - {\kern 1pt} {{c}_{0}}h < {{x}_{2}} < {{c}_{0}}h \hfill \\ 1,\quad {{c}_{0}}h < \left| {{{x}_{2}}} \right| \leqslant 1 \hfill \\ \end{gathered} \right.$

5. Применимость квазистатического приближения. В работах [6, 7, 13] подробно аналитически обсуждаются условия достоверности квазистатического приближения в классической задаче Прандтля и некоторых ее обобщениях. На основе анализа сингулярных асимптотик по малому геометрическому параметру выводятся необходимые и достаточные неравенства применимости квазистатического подхода, заключающегося в рассмотрении уравнений равновесия (1.3), а не уравнений движения:

(5.1)

$\frac{1}{{{\text{Eu}}}} \ll \frac{{{{h}^{2}}}}{{{{l}^{2}}}} \ll 1,$

где ${\text{Eu}} = {{\sigma }_{s}}{\text{/}}(\rho {{V}^{2}})$ – характерное в задаче число Эйлера, $\rho $ – постоянная плотность пластического материала.

Правое неравенство в (5.1) соответствует тонкослойному приближению. Если оно выполняется в начальный момент времени, то в силу специфики кинематики тем более верно и в последующие моменты. С левым же неравенством в (5.1) ситуация не такая тривиальная. Число $1{\text{/Eu}}$ постоянно в данной краевой задаче, в то время как дробь ${{h}^{2}}(t){\text{/}}{{l}^{2}}(t)$ монотонно убывает до нуля на интервале $t \in [0;{{t}_{*}})$. Следовательно, в некотором временном диапазоне перед моментом схлопывания плит ${{t}_{*}}$ левое неравенство заведомо нарушится.

Подставляя из соотношений (1.2) в неравенства (5.1) функции времени $h$ и $l$, получим, что применительно к задаче о сжатии неоднородного по толщине слоя эти неравенства таковы:

(5.2)

$\frac{1}{{{\text{Eu}}}} \ll \frac{{{{{({{h}_{0}} - Vt)}}^{4}}}}{{h_{0}^{2}l_{0}^{2}}} \ll 1,\quad {\text{Eu}} = \frac{{\sigma _{s}^{{{\text{min}}}}}}{{\rho {{V}^{2}}}},$

где число Эйлера построено по минимальному по толщине значению $\sigma _{s}^{{{\text{min}}}}$ предела текучести. В силу малости параметра $\alpha $ (1.1) правое неравенство (5.2) выполнено. Левое же будет удовлетворяться на следующем диапазоне времени:

(5.3)

${{t}_{*}} - t \ll \frac{{\sqrt {{{h}_{0}}{{l}_{0}}} }}{{V\sqrt[4]{{{\text{Eu}}}}}}$

При значительном приближении $t$ к ${{t}_{*}}$, когда условие (5.3) нарушается, происходит качественная перестройка силовых режимов сдавливания слоя, что влияет на технологию процесса.

Работа выполнена при поддержке РНФ (грант 22-21-00077).

Список литературы

Ишлинский А.Ю., Ивлев Д.Д. Математическая теория пластичности. М.: Физматлит, 2001. 704 с.
Ильюшин А.А. Полная пластичность в процессах течения между жесткими поверхностями, аналогия с песчаной насыпью и некоторые приложения // ПММ. 1955. Т. 19. Вып. 6. С. 693–713.
Колмогоров В.Л. Механика обработки металлов давлением. Екатеринбург: Изд-во УрГТУ–УПИ, 2001. 836 с.
Победря Б.Е., Гузей И.Л. Математическое моделирование деформирования композитов с учетом термодиффузии // Матем. моделир. систем и процессов. 1998. № 6. С. 82–91.
Георгиевский Д.В. Избранные задачи механики сплошной среды. М.: Ленанд, 2018. 560 с.
Георгиевский Д.В. Асимптотическое интегрирование задачи Прандтля в динамической постановке // Изв. РАН. МТТ. 2013. № 1. С. 97–105.
Georgievskii D.V., Mueller W.H., Abali B.E. Thin-layer inertial effects in plasticity and dynamics in the Prandtl problem // ZAMM. 2019. V. 99. № 12. P. 1–11.
Георгиевский Д.В. Асимптотические разложения и возможности отказа от гипотез в задаче Прандтля // Изв. РАН. МТТ. 2009. № 1. С. 83–93.
Гольденвейзер А.Л. Построение приближенной теории оболочек при помощи асимптотического интегрирования уравнений теории упругости // ПММ. 1963. Т. 27. Вып. 4. С. 593–608.
Кравченко В.Ф., Несененко Г.А., Пустовойт В.И. Асимптотики Пуанкаре решения задач нерегулярного тепло- и массопереноса. М.: Физматлит, 2006. 420 с.
Asmus M., Naumenko K., Oechsner A., Eremeyev V.A., Altenbach H. A generalized framework towards structural mechanics of three-layered composite structures // Technische Mechanik. 2019. V. 39. № 2. P. 202–219.
Asmus M., Altenbach H. On dynamic optimality of anti-sandwiches // in: Dyn.&Control of Adv. Struct.&Machines. Ser. Adv. Struct. Mater. V. 156. Springer, 2021. P. 1–11.
Кийко И.А., Кадымов В.А. Обобщение задачи Л. Прандтля о сжатии полосы // Вестн. МГУ. Сер. 1. Математика, механика. 2003. № 4. С. 50–56.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал