Прикладная математика и механика, 2022, T. 86, № 5, стр. 765-778
Об оценке вклада вторичных вихревых структур в перенос аэрозолей в атмосферном пограничном слое
М. А. Давыдова 1, *, О. Г. Чхетиани 2, **, Н. Т. Левашова 1, ***, А. Л. Нечаева 1, ****
1 Московский государственный университет им. М.В. Ломоносова
Москва, Россия
2 Институт физики атмосферы им. А.М. Обухова РАН
Москва, Россия
* E-mail: m.davydova@physics.msu.ru
** E-mail: ochkheti@ifaran.ru
*** E-mail: levashovant@physics.msu.ru
**** E-mail: nechaeva.al15@physics.msu.ru
Поступила в редакцию 30.05.2022
После доработки 20.07.2022
Принята к публикации 20.07.2022
- EDN: DIKFMZ
- DOI: 10.31857/S0032823522050071
Аннотация
В настоящей работе рассматриваются два обоснованных подхода к задаче численного моделирования распределения концентрации мелкодисперсного аэрозоля в спиралевидных вихревых структурах (роллах) в атмосферном пограничном слое с целью оценивания вклада вихревых структур в перенос аэрозолей через пограничный слой. С использованием методов теории возмущений получено приближенное решение стационарной пространственно-периодической сингулярно возмущенной задачи типа реакция–диффузия–адвекция, моделирующей распределение аэрозоля в вихрях, оценен остаточный член и предложен метод численного решения задачи нулевого приближения. В качестве альтернативного подхода к задаче численного моделирования поля концентраций аэрозоля в роллах рассмотрена реализация метода эволюционной факторизации. С использованием модельных данных получена оценка количества аэрозоля, переносимого вихревыми структурами.
1. Введение. Во второй половине XX века было обнаружено, что большая часть турбулентного атмосферного пограничного слоя (АПС) занята роллами – упорядоченными спиралевидными вихрями (валами) с горизонтальной осью, по направлению близкой к среднему направлению геострофического ветра (см., например, [1]). На спутниковых снимках пограничного слоя роллы выглядят, как “облачные улицы” – вытянувшиеся на сотни километров параллельные ряды с периодом в несколько километров, сохраняющиеся в течение нескольких суток. Облака в таком случае формируются в области восходящих движений между роллами при соответствующих термодинамических условиях (см. рис. 1). Возникновение роллов, как правило, является следствием развития гидродинамических неустойчивостей в АПС [1, 2], в том числе и конвективной неустойчивости при умеренных ветрах (2–3.5 м/с), развивающейся как в умеренных и южных широтах, так и в высоких при холодных вторжениях [3–7].
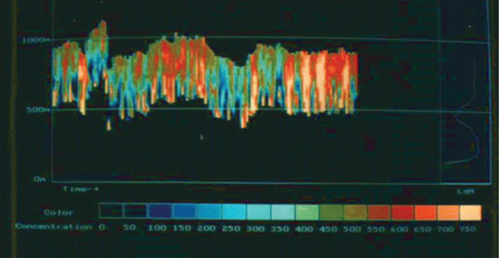
В безоблачных условиях спиралевидные вихри также хорошо наблюдаются средствами дистанционного зондирования в других диапазонах волн [3, 4, 8, 9]. На рис. 2 представлено пространственно-периодическое распределение аэрозоля (мелкая фракция), зафиксированное с помощью лидарных измерений коэффициента обратного рассеяния на пыли в пустынях Калмыкии [10], где из-за низкой влажности образование облачности в области локализации вихревых структур не происходит. Пространственный масштаб квазипериодичности зафиксированных аэрозольных слоев составляет 2–5 км, что характерно для валиковой циркуляции, высота роллов – не более 2 км [11]. Периодичность в распределении аэрозоля отмечается на всех высотах лидарного зондирования – от 300 м до 1000 м.
Рис. 2.
Пространственная структура распределения аэрозолей в пограничном слое атмосферы–лидарные измерения коэффициента обратного рассеяния c самолета на высоте 1 км, Калмыкия.
Согласно оценкам, вклад мезомасштабных роллов в тепломассоперенос через АПС составляет от 20 до 60%, причем вклад в вертикальный перенос в высоких широтах превалирует над турбулентным [6, 7, 12]. Роллы играют важную роль в индуцировании формирования новых частиц и, соответственно, образования ядер облачной конденсации [13]. В океаническом пограничном слое наблюдаются схожие движения (ленгмюровская циркуляция) [14]. Совокупность этих факторов и того, что оценки мощности антропогенных выбросов аэрозолей в атмосферу составляют порядка 107–108 т. в год [15, 16], делают задачу моделирования распределения концентраций мелкодисперсных аэрозолей в роллах существенной для моделирования процессов переноса и химической трансформации антропогенных примесей в АПС в целом.
Особый интерес представляет задача переноса аэрозолей в случае, когда тяжелый аэрозоль вступает в реакцию с внешней средой или распадается. Распространяясь в атмосфере, он диффундирует и под действием силы тяжести опускается на землю с постоянной скоростью, которая предвычисляется из задачи Стокса [17, 18].
В настоящей работе предлагаются два обоснованных метода расчета полей концентраций мелкодисперсных аэрозолей в вихревых структурах, использующих результаты моделирования поля скоростей в вихрях [19]. На основе методов теории возмущений [20] получено приближенное решение стационарной пространственно-периодической сингулярно возмущенной задачи реакция–диффузия–адвекция, моделирующей распределений аэрозоля, оценен остаточный член и предложен метод численного решения задачи нулевого приближения. В качестве альтернативного подхода к задаче численного моделирования поля концентраций рассмотрена реализация метода эволюционной факторизации, на основе которого исследован вопрос о влиянии величин скоростей распада и оседания аэрозоля на распределение концентрации этой примеси в роллах. Использование этих двух подходов строго обосновано с привлечением методов и результатов [20–23]. Таким образом, описано единственное устойчивое стационарное состояние системы путем описания распределения концентрации аэрозоля, отвечающего этому состоянию. С использованием модельных данных получена оценка количества переносимого аэрозоля.
В заключение этого параграфа отметим другие примеры эффективного использования методов асимптотического анализа при решении прямых и обратных задачах атмосферной диффузии малых примесей [24–26], связанных с получением оценок эмиссий локальных и распределенных источников загрязняющих примесей и параметров турбулентной диффузии для устойчивого или нейтрального АПС, а также при решении обратных задач по восстановлению параметров моделей реакция–диффузия–адвекция других приложений [27–32].
2. Постановка задачи. Изменение концентрации $C({{x}_{1}},{{x}_{2}},{{x}_{3}},t)$ аэрозоля при миграции через АПС описывается уравнением типа реакция–диффузия–адвекция [17]:
(2.1)
$\begin{gathered} \frac{{\partial C}}{{\partial t}} = \left\langle k \right\rangle \sum\limits_{i = 1}^2 {\frac{{{{\partial }^{2}}C}}{{\partial x_{i}^{2}}}} + \frac{\partial }{{\partial {{x}_{3}}}}\left( {{{k}_{3}}(x)\frac{{\partial C}}{{\partial {{x}_{3}}}}} \right) - \sum\limits_{i = 1}^2 {{{u}_{i}}} (x)\frac{{\partial C}}{{\partial {{x}_{i}}}} - ({{u}_{3}}(x) - {{{v}}_{g}})\frac{{\partial C}}{{\partial {{x}_{3}}}} + F(C,x) \\ x \in {{\mathbb{R}}^{2}} \times (a,b),~\quad t > 0, \\ \end{gathered} $В качестве масштабов длины, скорости и времени выберем толщину экмановского слоя $L = {{\left( {K{\text{/}}f} \right)}^{{1/2}}}\sim 1000$ м, скорость геострофического ветра $G$ ~ 10 м/с [2] и $1{\text{/}}f$, где $f = \Omega \sin \theta $, Ω – угловая скорость вращения Земли, $\theta - $ широта, K – характерная вертикальная турбулентная вязкость (подробнее см. [1, 2, 33, 34]). Поскольку характерные горизонтальные масштабы развивающихся структур кратны высоте экмановского слоя, то в качестве характерного пространственного масштаба по трем измерениям используется высота слоя Экмана (см., например, [2, 11, 19]).
Заметим, что детальный анализ данных позволяет говорить о сосуществовании в АПС наряду со структурами, горизонтальный масштаб $\lambda $ которых в несколько раз превосходит вертикальный $h$, где ${\lambda \mathord{\left/ {\vphantom {\lambda h}} \right. \kern-0em} h} \geqslant 2$, структур, вертикальный масштаб которых равен и меньше горизонтального ${\lambda \mathord{\left/ {\vphantom {\lambda h}} \right. \kern-0em} h} \leqslant 1$ [6, 35].
Определим безразмерные переменные посредством соотношений: $x{\kern 1pt} ' = \frac{x}{L}$, $t{\kern 1pt} ' = \frac{t}{T}$, $C{\kern 1pt} ' = \frac{C}{{\tilde {C}}}$, где T – характерное время существования валиковых структур (несколько суток), $\tilde {C}$ – характерная концентрация, например, фоновое значение концентрации (или ее среднее на некоторой высоте). Тогда в безразмерных переменных уравнение (2.1) принимает вид:
(2.2)
$\begin{gathered} \frac{L}{{TG}}\frac{{\partial C{\kern 1pt} '}}{{\partial t{\kern 1pt} '}} = \frac{{\left\langle k \right\rangle }}{{LG}}\sum\limits_{i = 1}^2 {\frac{{{{\partial }^{2}}C{\kern 1pt} '}}{{\partial x_{i}^{{'2}}}}} + \frac{{{{k}_{3}}(x)}}{{LG}}\frac{{{{\partial }^{2}}C{\kern 1pt} '}}{{\partial x_{3}^{{'2}}}} - \sum\limits_{i = 1}^2 {\frac{{{{u}_{i}}(x)}}{G}} \frac{{\partial C{\kern 1pt} '}}{{\partial x_{i}^{'}}} + \\ + \;\left( {\frac{1}{G}\frac{{\partial {{k}_{3}}}}{{\partial {{x}_{3}}}} - \frac{{{{u}_{3}}(x) - {{{v}}_{g}}}}{G}} \right)\frac{{\partial C{\kern 1pt} '}}{{\partial x_{3}^{'}}} + \frac{{F(C,x)L}}{{G\tilde {C}}} \\ \end{gathered} $Согласно [18] на высоте более 100 м над поверхностью Земли изменчивостью коэффициента обмена можно пренебречь. Следовательно
(2.3)
${{({{\Pr }_{D}}\operatorname{Re} )}^{{ - 1}}}\Delta C - ({\mathbf{u}}(x),\nabla C) + {{{v}}_{g}}\frac{{\partial C}}{{\partial {{x}_{3}}}} + \frac{{F(C,x)L}}{{G\tilde {C}}} = 0$Заметим, что валиковыми структурами переносятся в основном мелкодисперсные аэрозоли, для которых скорость оседания ∼1 см/с [34]. В таком случае безразмерная скорость оседания ${{{v}}_{g}}$ ~ ${{10}^{{ - 3}}}$.
Пусть в уравнении (2.1) $F(C,x) = - \gamma (C - \tilde {C})$, где $\gamma > 0$ – скорость распада аэрозоля (величина, обратно пропорциональная времени жизни примеси), а слагаемое $F(C,x)$ описывает распад вещества за счет столкновения частиц при миграции аэрозоля. Тогда уравнение (2.3) примет следующий вид:
(2.4)
${{({\text{P}}{{{\text{r}}}_{D}}{\text{Re}})}^{{ - 1}}}\Delta C - ({\mathbf{\bar {u}}}(x),\nabla C) - \gamma (C - 1) = 0,$Поскольку поле скоростей ${\mathbf{\bar {u}}}(x)$ в уравнении (2.4) предполагается гладким, то решение краевой задачи для уравнения в ограниченной области с гладкой границей, включающей в себя гряду роллов, и граничным условием смешанного типа [17], которое соответствует заданию концентрации или нулевого потока вещества на различных частях границы, существует и единственно [21, 22], а также глобально устойчиво по Ляпунову [23] как стационарное решение соответствующей начально-краевой задачи для уравнения:
(2.5)
$\frac{L}{{TG}}\frac{{\partial C}}{{\partial t}} = {{({\text{P}}{{{\text{r}}}_{D}}{\text{Re}})}^{{ - 1}}}\Delta C - ({\mathbf{\bar {u}}}(x),\nabla C) - \gamma (C - 1),$С целью выбора рациональных средств численного моделирования распределения аэрозоля внутри вихревых структур, перейдем к эквивалентной (в области локализации вихревых структур) пространственно-периодической задаче для уравнения (2.4) в полосе:
(2.6)
$\begin{gathered} \varepsilon \Delta C - ({\mathbf{\bar {u}}}(x),\nabla C) - \gamma (C - 1) = 0;\quad ({{x}_{1}},{{x}_{2}}) \in {{\mathbb{R}}^{2}},\quad {{x}_{3}} \in (a,b) \\ C({{x}_{1}} + {{L}_{1}},{{x}_{2}},{{x}_{3}}) = C({{x}_{1}},{{x}_{2}},{{x}_{3}});\quad ({{x}_{1}},{{x}_{2}}) \in {{\mathbb{R}}^{2}},\quad {{x}_{3}} \in [a,b] \\ C({{x}_{1}},{{x}_{2}} + {{L}_{2}},{{x}_{3}}) = C({{x}_{1}},{{x}_{2}},{{x}_{3}});\quad ({{x}_{1}},{{x}_{2}}) \in {{\mathbb{R}}^{2}},\quad {{x}_{3}} \in [a,b] \\ {{\left. C \right|}_{{{{x}_{3}} = a}}} = {{C}^{a}}({{x}_{1}},{{x}_{2}}),\quad {{\left. {(\nabla C,{\mathbf{n}})} \right|}_{{{{x}_{3}} = b}}} = 0;\quad ({{x}_{1}},{{x}_{2}}) \in {{\mathbb{R}}^{2}}, \\ \end{gathered} $3. Численное моделирование распределения концентрации аэрозоля. Существуют разные возможности (в смысле выбора средств) в моделировании распределения аэрозоля внутри вихревых структур. Рассмотрим два возможных подхода к решению этой задачи.
Алгоритм построения численного решения задачи (2.6) основан на использовании свойства единственности и глобальной устойчивости решения этой задачи как стационарного решения соответствующей начально-краевой задачи для уравнения (2.5) и реализуется путем стационирования решения задачи для уравнения (2.5) к решению задачи (2.6). В свою очередь, численное решение задачи для уравнения (2.5) выполняется с использованием метода эволюционной факторизации [37] в расчетной области, представляющей собой прямоугольный параллелепипед $\Pi = \{ ({{x}_{1}},{{x}_{2}},{{x}_{3}})$: $0 \leqslant {{x}_{1}},{{x}_{2}} \leqslant 49$, $0.3 \leqslant {{x}_{3}} \leqslant 12\} $, в котором введена равномерная сетка, состоящая из ${{N}_{1}} \times {{N}_{2}} \times {{N}_{3}}$ узлов. Безразмерный шаг сетки соответствует пространственному расстоянию в 0.1 км. Пространственные шаги сетки одинаковы по каждому из трех направлений: ${{h}_{x}} = {{h}_{y}} = {{h}_{z}}$ = = 0.1 (в безразмерных переменных). Безразмерный шаг по времени выбирается равным $\tau = 0.01$. Точность метода эволюционной факторизации при таком выборе пространственного и временного шага составляет $O\left( {{{\tau }^{2}} + h_{x}^{2} + h_{y}^{2} + h_{z}^{2}} \right)$ [37]. Поэтому численные расчеты проводились с точностью 0.01. По вертикали расчетная область начинается с уровня ${{x}_{3}} = 0.3$, поскольку вынос аэрозоля возникает на субмезомасштабных движениях, которые “не разрешимы” в используемом приближении. К структурам, обеспечивающим такое движение относятся, например, спонтанные вихри с вертикальной осью – пыльные дьяволы и термики. Они тянут частицы аэрозоля вверх.
В ходе реализации метода эволюционной факторизации трехмерный оператор Лапласа заменяется на произведение трех одномерных, что позволяет решить уравнение в три этапа, на каждом из которых решение уравнения сводится к решению ${{N}_{i}} \times {{N}_{j}}$, $i,j = 1,2,3$ обыкновенных дифференциальных уравнений методом прогонки. Метод прогонки реализуется в соответствии с алгоритмом из работы [38].
На рис. 3–4 а)–в) представлены компоненты u1, u2, u3 вектора скорости переноса [33], рассчитанные при условиях нейтральной стратификации для достаточно характерных для АПС значениях ${\text{Re}} = 200$, угле поворота по отношению к геострофическому ветру 15°. На рис. 3–4 г)–е) представлены результаты по расчету безразмерной концентрации $C(x)$, полученные при численном решении задачи (2.6) при различных значениях безразмерных параметров ${{{v}}_{g}}$, $\gamma $ и $\varepsilon = 0.004$ (в сечении вертикальной плоскостью). Рисунки 3–4 ж) или з) – разности безразмерных концентраций, которые представлены распределениям г) (уменьшаемое) и д) (вычитаемое) или д) (уменьшаемое) и е) (вычитаемое). Расчеты выполнены при различных граничных значениях концентрации ${{C}^{a}}$, равных 10 и 100.
Рис. 3.
Результаты расчетов при граничном условии ${{C}^{a}} = 10$, $a = 0,3$: а–в) – компоненты скорости переноса; г–е) – поле концентраций при различных значениях ${{{v}}_{g}}$, $\gamma $ в случае $\varepsilon = 0.004$; ж) разность концентраций, г) (уменьшаемое) и д) (вычитаемое), з) разность концентраций, д) (уменьшаемое) и е) (вычитаемое).
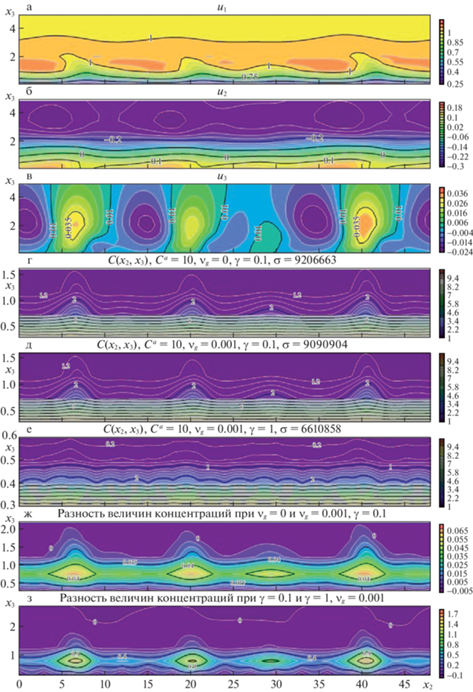
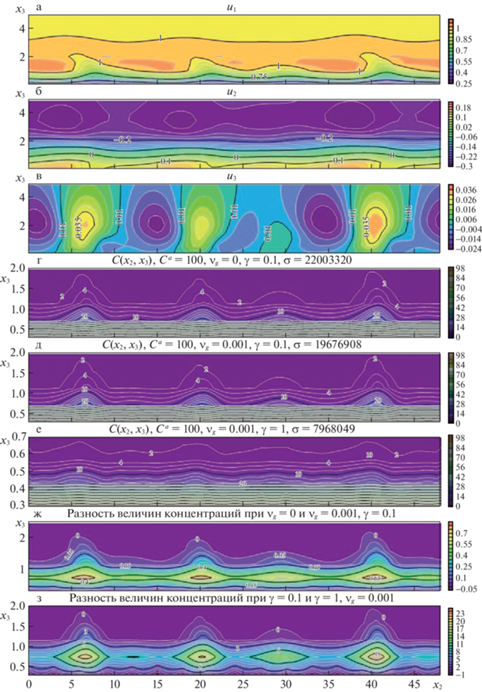
Рис. 4.
Результаты расчетов при граничном условии ${{C}^{a}} = 100$, $a = 0,3$: а–в) – компоненты скорости переноса; г–е) – поле концентраций при различных значениях ${{{v}}_{g}}$, $\gamma $ в случае $\varepsilon = 0.004$; ж) разность концентраций г) (уменьшаемое) и д) (вычитаемое), з) разность концентраций д) (уменьшаемое) и е) (вычитаемое).
Отметим, что согласно использованным данным [33] на верхней границе ${{x}_{3}} = 12$ (в безразмерных единицах) величина компоненты скорости u3 равна нулю, а рассчитанная концентрация постоянна и совпадает с фоновой. В связи с этим на рисунках представлены только те области изменения соответствующих физических величин, на которых наблюдаются распределения, отличные от постоянных.
В работах [13, 34] показано, что значительное количество аэрозоля попадает в приосевую область вихрей. Согласно численным расчетам, представленным на рис. 3, 4, распределение концентрации аэрозоля имеет пространственно-периодическую структуру (что соответствует данным наблюдений [10]), согласованную с периодической структурой поля скоростей [19, 33]. Основная масса увлекаемого вихрями аэрозоля удерживается ими и переносится в горизонтальной плоскости. Смещение области локализации вещества к нижней границе (по сравнению с результатами моделирования [13, 34]) связано с учетом распада и оседания вещества в модели (2.6). Учет процесса оседания аэрозоля приводит к незначительным изменениям в распределении концентрации этой примеси, не превышающим $1\% $ от граничного значения ${{C}^{a}}$ (по данным моделирования), причем наибольшее отличие величин концентраций при ${{{v}}_{g}} = 0$ и ${{{v}}_{g}} = 0.001$ приходится на области с наибольшими значениями компонент скорости переноса ${{u}_{2}}$ и ${{u}_{3}}$, которые определяют структуру распределения примеси по вертикали (см. рис. 3 б), в), ж) и рис. 4 б), в), ж)). На эти же области приходится наибольшее отличие величин концентраций при различных скоростях распада: $\gamma = 0.1$ и $\gamma = 1$ (см. рис. 3 д), е), з) и рис. 4 д), е), з)). Покажем, что при таком выборе параметров модели (2.6) процессы распада и переноса аэрозоля превалируют над диффузией и определяют структуру поля концентраций аэрозоля в вихрях.
Рассмотрим следующую задачу Коши
(3.1)
$\begin{gathered} \left( {{\mathbf{\bar {u}}}(x),\nabla {{{\bar {C}}}_{0}}} \right) + \gamma \left( {{{{\bar {C}}}_{0}} - 1} \right) = 0;\quad x \in {{\mathbb{R}}^{2}} \times (a,b) \\ {{{\bar {C}}}_{0}}({{x}_{1}},{{x}_{2}},{{x}_{3}}) = {{{\bar {C}}}_{0}}({{x}_{1}} + {{L}_{1}},{{x}_{2}},{{x}_{3}});\quad ~x \in {{\mathbb{R}}^{2}} \times [a,b] \\ {{{\bar {C}}}_{0}}({{x}_{1}},{{x}_{2}},{{x}_{3}}) = {{{\bar {C}}}_{0}}({{x}_{1}},{{x}_{2}} + {{L}_{2}},{{x}_{3}});\quad x \in {{\mathbb{R}}^{2}} \times [a,b] \\ {{{\bar {C}}}_{0}}({{x}_{1}},{{x}_{2}},a) = {{C}^{a}}({{x}_{1}},{{x}_{2}});\quad ({{x}_{1}},{{x}_{2}}) \in {{\mathbb{R}}^{2}}, \\ \end{gathered} $Определение. Упорядоченная пара ${{L}_{1}}$-периодических по переменной ${{x}_{1}}$ и ${{L}_{2}}$-периодических по переменной ${{x}_{2}}$ функций $\beta (x,\varepsilon )$, $\alpha (x,\varepsilon )$ ∈ ${{C}^{1}}\left( {{{\mathbb{R}}^{2}} \times [a,b]} \right)$ ∩ ${{C}^{2}}\left( {{{\mathbb{R}}^{2}} \times (a,b)} \right)$ называется соответственно верхним и нижним решениями задачи (2.6), если при $0 < \varepsilon \ll 1$ выполняются следующие дифференциальные неравенства:
Известно, что если существуют верхнее и нижнее решения задачи (2.6), то решение $C(x,\varepsilon )$ этой задачи заключено между верхним и нижним решениями (см. напр., [20]):
(3.2)
$\alpha (x,\varepsilon ) \leqslant C(x,\varepsilon ) \leqslant \beta (x,\varepsilon );\quad x \in {{\mathbb{R}}^{2}} \times [a,b]$Верхнее и нижнее решения задачи (2.6) получим путем модификации приближенного решения $\hat {C}(x,\varepsilon )$ определенным образом:
(3.3)
$\begin{gathered} \beta (x,\varepsilon ) = {{{\bar {C}}}_{0}}(x) + \delta + \varepsilon B\exp (\xi ) \\ \alpha (x,\varepsilon ) = {{{\bar {C}}}_{0}}(x) - \delta - \varepsilon B\exp (\xi );\quad x \in {{\mathbb{R}}^{2}} \times [a,b],\quad \xi \leqslant 0, \\ \end{gathered} $Лемма. Функции $\beta (x,\varepsilon )$, $\alpha (x,\varepsilon )$, определяемые равенствами (3.3), являются верхним и нижним решениями задачи (2.6).
Для доказательства леммы достаточно проверить выполнение неравенств 1)–3). Подставляя функции (3.3) в неравенства 1)–2), имеем:
При ${{x}_{3}} = a$ и ${{x}_{3}} = b$ имеем неравенства:
Получим оценку остаточного члена. Поскольку $\beta (x,\varepsilon ) - \alpha (x,\varepsilon ) = O(\mu )$ и β(x, ε) – ‒ ${{\bar {C}}_{0}}(x)$ = $O(\mu )$, где $\mu \sim {{10}^{{ - 2}}}$, то в силу неравенства треугольника:
(3.4)
$\left| {\left| {C(x,\varepsilon ) - {{{\bar {C}}}_{0}}(x)} \right|} \right| \leqslant \left| {\left| {C(x,\varepsilon ) - \beta (x,\varepsilon )} \right|} \right| + \left| {\left| {\beta (x,\varepsilon ) - {{{\bar {C}}}_{0}}(x)} \right|} \right| = O(\mu )$в равномерной норме.
Теорема. Существует единственное классическое решение $C(x,\varepsilon )$ задачи (2.6), удовлетворяющее при $\gamma = 1$ оценке (3.4), где ${{\bar {C}}_{0}}(x)$ – решение задачи (3.1).
Заметим, что в случае $\gamma = 0.1$ справедлива аналогичная теорема с оценкой (3.4), в которой $\mu \sim {{10}^{{ - 1}}}$. Доказательство теоремы легко получить, если положить $\delta $ = $2 \times {{10}^{{ - 1}}}$.
Таким образом, в качестве модельной задачи может быть использована задача (3.1), причем допущенная при этом ошибка в решении определяется неравенством (3.4). Для численного решения задачи (3.1) можно использовать метод конечных элементов [40], реализуемый в FEniCS Project (вычислительная платформа с открытым исходным кодом (LGPLv3) для решения уравнений в частных производных) через API для Python, дающий результат вычислений близкий (в соответствии с теоремой) к результату, представленному на рис. 3, 4.
4. Обсуждение результатов. Оценка количества переносимого аэрозоля. Из общих теорем теории линейных уравнений 2-го порядка в частных производных [21–23] следует, что состояние системы, которому соответствует стационарное распределение концентрации аэрозоля, изменившись по причине внешнего возмущения, возвращается в исходное стационарное состояние в силу устойчивости и единственности стационарного решения, описывающего это состояние. Таким образом, стационарное распределение концентрации аэрозоля отвечает наиболее вероятному состоянию этой системы.
В результате численного моделирования установлено, что поле концентрации аэрозоля в вихревых структурах имеет пространственно-периодическую структуру, согласованную с периодическим изменением поля скоростей [19, 33], что также согласуется с данными наблюдений [10]. Учет распада и оседания аэрозоля приводит к смещению области локализации вещества по вертикали в направлении нижней границы расчетной области (по сравнению с данными моделирования [13, 34]).
Количество вещества Q, переносимое через сечение $S \approx (50 \times 4)$ км2 за 1 мин определяется формулой (в размерных переменных):
В разд. 3 на рис. 3, 4 приведены вычисленные значения интеграла
для поля скоростей [19, 33] и различных значений параметров модели (2.6).Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-29-10080 и Фонда развития теоретической физики и математики “Базис” в рамках гранта № 19-2-6-178-1.
Авторы выражают глубокую благодарность проф. В.Ф. Бутузову за внимание к работе и полезные рекомендации.
Список литературы
Lilly D.K. On the stability of Ekman boundary flow // J. Atmos. Sci. 1966. V. 23. № 5. P. 481–494.
Пономарев В.М., Хапаев А.А., Чхетиани О.Г. Роль спиральности в формировании вторичных структур в экмановском пограничном слое // Изв. РАН. ФАО. 2003. Т. 39. № 4. С. 435–444.
Thompson T.W., Liu W.T., Weissman D.E. Synthetic aperture radar observation of the ocean roughess from rolls in an unstable marine boundary layer // J. Geophys. Res. 1983. V. 10. P. 172–175.
Mourad P.D., Walter B.A. SAR streaks vs cloud streets: viewing a cold air outbreak using satelite-based SAR and AVHRR imagery // J. Geophys. Res. 1996. V. 101. P. 16391–16400.
Atkinson B.W., Wu Zhang J. Mesoscale shallow convection in the atmosphere // Rev. Geophys. 1996. V. 34. № 4. P. 403–431.
Brummer B. Structure, dynamics and energetics of boundary layer from Kontur aircraft observations// Beitr. Phys. Atmos. 1985. V. 58. P. 237–254.
Chou S.-H., Ferguson M.P. Heat fluxes and roll circulation over the western gulf stream during an intense cold-air outbreak // Bound. Lay. Meteor. 1991. V. 55. № 3. P. 255–281.
Gerling T.W. Structure of the surface wind fields from Seasat SAR // J. Geophys. Res. 1986. V. 91. P. 2308–2320.
Alpers W., Brummer B. Atmospheric boundary layer rolls observed by the synthetic aperture radar aboard the ERS-1 satellite // J. Geophys. Res. 1994. V. 99. P. 12613–12621.
Golitsyn G.S., Granberg I.G., Andronova A.V., Ponomarev V.M., Zilitinkevich S.S., Smirnov V.V., Yablokov M.Yu. Investigation of boundary layer fine structure in arid regions: injection of fine dust into the atmosphere // Water, Air&Soil Pollut.: Focus 3. 2003. P. 245–257.
Вазаева Н.В., Чхетиани О.Г., Шестакова Л.В., Максименков Л.О. Нелинейное развитие структур в экмановском слое // Вычисл. мех. сплошных сред. 2017. Т. 10. № 2. С. 197–211.
LeMone M.A. The structure and dynamics of horizontal roll vortices in the planetary boundary layer // J. Atmos. Sci. 1973. V. 30. P. 1077–1091.
Lampilahti J., Manninen H.E., Leino K. et al. Roll vortices induce new particle formation bursts in the planetary boundary layer // Atmos. Chem. Phys. 2020. V. 20. № 20. P. 11841–11854.
Zedel L., Farmer D.M. Organised structures in subsurface bubble clouds: Langmuir circulation in the open ocean // J. Geophys. Res. 1991. V. 96. P. 8889–8900.
Ивлев Л.С., Довгалюк Ю.А. Физика атмосферных аэрозольных систем. СПб.: НИИХ СПбГУ, 1999. 194 с.
Joint MSC-W&CCC&CEIP Rep. Transboundary particulate matter, photo-oxidants, acidifying and eutrophying components. https://emep.int/publ/reports/2019/EMEP\_Status\_Report\_1\_2019.pdf
Марчук Г.И. Математическое моделирование в проблеме окружающей среды. М.: Наука, 1982. 319 с.
Берлянд М.Е. Прогноз и регулирование загрязнения атмосферы. Гидрометеоиздат, 1985. 272 с.
Пономарев В.М., Чхетиани О.Г., Шестакова Л.В. Нелинейная динамика крупномасштабных вихревых структур в турбулентном экмановском слое // Изв. РАН. МЖГ. 2007. № 2. С. 81–91.
Нефедов Н.Н. Метод дифференциальных неравенств для некоторых сингулярно возмущенных задач в частных производных // Дифф. уравн. 1995. Т. 31. № 4. С. 719–722.
Ладыженская О.А., Уральцева Н.Н. Линейные и квазилинейные уравнения эллиптического типа. М.: Наука, 1973. 576 с.
Миранда К. Уравнения с частными производными эллиптического типа. М.: Изд-во иностр. лит., 1957. 256 с.
Фридман А. Уравнения с частными производными параболического типа. М.: Мир, 1968. 427 с.
Давыдова М.А., Еланский Н.Ф., Захарова С.А., Постыляков О.В. Применение численно-асимптотического подхода в задаче восстановления параметров локального стационарного источника антропогенного загрязнения // Докл. РАН. 2021. Т. 496. С. 34–39.
Zakharova S.A., Davydova M.A., Lukyanenko D.V. Use of asymptotic analysis for solving the inverse problem of source parameters determination of nitrogen oxide emission in the atmosphere // Inverse Problems in Sci.&Engng. 2021. V. 29. № 3. P. 365–377.
Давыдова М.А., Еланский Н.Ф., Захарова С.А. О новом подходе к задаче восстановления вертикального коэффициента турбулентной диффузии в пограничном слое атмосферы // Докл. РАН. 2020. Т. 490. № 2. С. 51–56.
Davydova M.A., Zakharova S.A. Multidimensional thermal structures in the singularly perturbed stationary models of heat and mass transfer with a nonlinear thermal diffusion coefficient // J. Comput.&Appl. Math. 2022. V. 400. P. 113731.
Lukyanenko D.V., Borzunov A.A., Shishlenin M.A. Solving coefficient inverse problems for nonlinear singularly perturbed equations of the reaction-diffusion-advection type with data on the position of a reaction front // Commun. in Nonlin. Sci.&Numer. Simul. 2021. V. 99. P. 105824.
Argun R., Gorbachev A., Levashova N., Lukyanenko D. Inverse problem for an equation of the reaction-diffusion-advection type with data on the position of a reaction front: features of the solution in the case of a nonlinear integral equation in a reduced statement // Mathematics. 2021. V. 9. № 18. P. 2342.
Lukyanenko D., Yeleskina T., Prigorniy I., Isaev T., Borzunov A., Shishlenin M. Inverse problem of recovering the initial condition for a nonlinear equation of the reaction–diffusion–advection type by data given on the position of a reaction front with a time delay // Mathematics. 2021. V. 9. № 4. P. 342.
Levashova N., Gorbachev A., Argun R., Lukyanenko D. The problem of the non-uniqueness of the solution to the inverse problem of recovering the symmetric states of a bistable medium with data on the position of an autowave front // Symmetry. 2021. V. 13. № 5. P. 860.
Lukyanenko D.V., Prigorniy I.V., Shishlenin M.A. Some features of solving an inverse backward problem for a generalized burgers’ equation // J. Inverse&Ill-Posed Problems. 2020. V. 28. № 5. P. 641–649.
Пономарев В.М., Чхетиани О.Г., Шестакова Л.В. Численное моделирование развитой горизонтальной циркуляции в атмосферном пограничном слое // Вычисл. мех. сплошных сред. 2009. Т. 2. № 1. С. 68–80.
Вазаева Н.В., Чхетиани О.Г., Максименков Л.О. Организованная валиковая циркуляция и перенос минеральных аэрозолей в атмосферном пограничном слое // Изв. РАН. ФАО. 2019. Т. 55. № 2. С. 17–31.
Mourad P.D., Brown R.A. On multiscale large eddy states in weakly stratified boundary layers // J. Atmos. Sci. 1990. V. 47. P. 414–438.
Чхетиани О.Г., Вазаева Н.В. Об алгебраических возмущениях в атмосферном пограничном слое // Изв. РАН. ФАО. 2019. Т. 55. № 5. С. 62–75.
Калиткин Н.Н., Корякин П.В. Численные методы: в 2 кн. Кн 2. Методы математической физики. М.: ИЦ Академия, 2013. 303 с.
Абрамов А.А., Андреев В.Б. О применении метода прогонки к нахождению периодических решений дифференциальных и разностных уравнений // ЖВММФ. 1963. Т. 3. № 2. С. 377–381.
Камке Э. Справочник по дифференциальным уравнениям в частных производных первого порядка. М.: Наука. Физматлит, 1966. 260 с.
Guermond J.L. A finite element technique for solving first-order PDEs in Lp // SIAM J. Numer. Anal. 2004. V. 42. № 1. P. 714–737.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика



