Прикладная математика и механика, 2022, T. 86, № 5, стр. 753-764
Формирование вихревых структур внутри области сильного взрыва в неоднородной атмосфере на его ранней стадии
В. А. Андрущенко 1, *, В. А. Головешкин 2, 3, **, И. В. Мурашкин 1, ***, Н. Н. Холин 2, ****
1 Институт автоматизации проектирования РАН
Москва, Россия
2 Российский технологический университет МИРЭА
Москва, Россия
3 Институт прикладной механики РАН
Москва, Россия
* E-mail: andrusviktor@ya.ru
** E-mail: vag-1953@ya.ru
*** E-mail: murashkin@inbox.ru
**** E-mail: mostu@bk.ru
Поступила в редакцию 09.04.2022
После доработки 22.07.2022
Принята к публикации 22.07.2022
- EDN: GQEEQW
- DOI: 10.31857/S0032823522050034
Аннотация
Аналитически решается задача о сильном точечном взрыве с учетом неоднородности атмосферы. Полученное авторами ранее численное решение подобной задачи показало, что уже на начальной стадии процесса в сферическом слое газа внутри области взрыва, прилегающем к фронту ударной волны, образуются вихревые структуры. Поскольку для этих малых времен решение незначительно отличается от точного решения Л.И. Седова, методом возмущений проводится теоретическое исследование течения во внутренней области взрыва, позволившее объяснить возникновение таких вихревых образований.
1. Введение. В настоящее время задачи теории точечного взрыва вновь выдвинулись в ряд задач первостепенной значимости в связи с реальностью вторжения в атмосферу Земли малых космических тел и их возможном взрыве в ней, что подтвердилось в ходе падения, фрагментации [1] и последующими взрывами осколков челябинского болида 15 февраля 2013 г. [2].
В данной работе исследуется эволюция объема газа, охваченного фронтом ударной волны, при сильном точечном взрыве в экспоненциальной атмосфере для малых моментов времени. Как известно, для достаточно большого промежутка времени, когда ударная волна уходит на значительное расстояние от точки взрыва, под действием конвекции “огненный” шар около его центра трансформируется в вихревую топологическую структуру типа тора [3, 4]. В ходе численного эксперимента, проведенного авторами в [5], было выявлено, что вихревые тороидальные структуры в сферическом слое, прилегающем к фронту ударной волны, в задаче о сильном точечном взрыве образуются уже и на начальной стадии (порядка нескольких десятых секунды) при учете неоднородности атмосферы. Этот факт означает, что для момента времени, близкого к началу взрыва, малые возмущения (незначительное проявление стратификации атмосферы по высоте), возникающие только на фронте ударной волны (см. ниже), оказывают заметное влияние на решение исходной системы уравнений в некоторой части газа внутри области взрыва. Здесь проводится теоретическое исследование течения во внутренней области сильного точечного взрыва методом возмущений. Полученное аналитическое решение поставленной задачи позволяет объяснить причину возникновения тороидальных вихревых структур на ранней стадии точечного взрыва в неоднородной атмосфере.
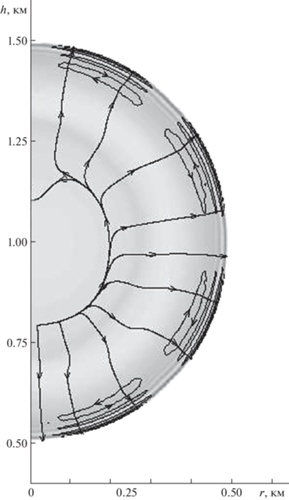
2. Постановка задачи. Рассматривается задача о сильном точечном взрыве в экспоненциальной атмосфере: $\rho = {{\rho }_{0}}\exp \left( { - z{\text{/}}H} \right)$, где ${{\rho }_{0}}$ – плотность на высоте взрыва, $H$ параметр неоднородности атмосферы. Численное решение задачи показало образование вихревых структур внутри области взрыва уже на ранней стадии процесса (см. рис. 1, на котором представлены линии равной завихренности (замкнутые структуры около фронта УВ) $ \pm \left| {\operatorname{rot} u} \right|$ и линии тока (расходящиеся веером от центральной области направленные линии) в вертикальной плоскости сечения области взрыва для момента времени $t = 0.6$ c в задаче о сильном точечном взрыве с энергией $E = 15$ кТ на высоте 1 км в неоднородной атмосфере в отсутствие гравитации и противодавления) [5]. Из рис. 1 видно, что уже на начальном этапе эволюции взрыва в сферическом слое, прилегающем к фронту ударной волны, возникли четыре тороидальные вихревые области некругового сечения, в которых направления движения чередуются (в верхнем тороиде направление по часовой стрелке – отрицательные значения компоненты завихренности, в следующем против – положительные значения компоненты завихренности, и т.д.; величины завихренности безразмерны и поэтому их численные значения порядка сотых от единицы малоинформативны).
Исходная система уравнений в сферических координатах ($R$, $\theta $) для газодинамических функций $\rho $, $P$, ${{u}_{R}}$, ${{u}_{\theta }}$ – плотности, давления, радиальной и азимутальной компонент скорости ($c$ – скорость фронта ударной волны, $R = S\left( {\theta ,t} \right)$ – уравнение фронта ударной волны) такова:
1. Уравнение неразрывности
(2.1)
$\frac{\partial }{{\partial t}}\left( {\ln \rho } \right) + {{u}_{R}}\frac{\partial }{{\partial R}}\left( {\ln \rho } \right) + \frac{{{{u}_{\theta }}}}{R}\frac{\partial }{{\partial \theta }}\left( {\ln \rho } \right) + \frac{{\partial {{u}_{R}}}}{{\partial R}} + \frac{1}{R}\frac{{\partial {{u}_{\theta }}}}{{\partial \theta }} + \frac{{2{{u}_{R}}}}{R} - \frac{{{{u}_{\theta }}}}{R}\operatorname{tg} \theta = 0$2. Уравнения движения ($g$ – ускорение свободного падения)
(2.2)
$\frac{{\partial {{u}_{R}}}}{{\partial t}} + {{u}_{R}}\frac{{\partial {{u}_{R}}}}{{\partial \lambda }} + \frac{{{{u}_{\theta }}}}{R}\frac{{\partial {{u}_{R}}}}{{\partial \theta }} - \frac{{{{u}^{2}}\theta }}{R} = - \frac{1}{\rho }\frac{{\partial P}}{{\partial R}} - ag\sin \theta $(2.3)
$\frac{{\partial {{u}_{\theta }}}}{{\partial t}} + {{u}_{R}}\frac{{\partial {{u}_{\theta }}}}{{\partial R}} + \frac{{{{u}_{\theta }}}}{R}\frac{{\partial {{u}_{R}}}}{{\partial \theta }} - \frac{{{{u}_{R}}{{u}_{\theta }}}}{R} = - \frac{1}{{\rho R}}\frac{{\partial P}}{{\partial \theta }} - ag\cos \theta $3. Закон сохранения энергии
(2.4)
$\frac{\partial }{{\partial t}}\ln \left( {\frac{P}{{{{\rho }^{\gamma }}}}} \right) + {{u}_{R}}\frac{\partial }{{\partial R}}\ln \left( {\frac{P}{{{{\rho }^{\gamma }}}}} \right) + \frac{{{{u}_{\theta }}}}{R}\frac{\partial }{{\partial \theta }}\ln \left( {\frac{P}{{{{\rho }^{\gamma }}}}} \right) = 0$Уравнение фронта
Уравнение движения фронта
(2.6)
$\frac{{\partial S}}{{\partial t}} = c\sqrt {1 + \frac{1}{{{{S}^{2}}}}{{{\left( {\frac{{\partial S}}{{\partial \theta }}} \right)}}^{2}}} $Условия на фронте
(2.7)
$\begin{gathered} {{u}_{\theta }}\sqrt {1 + \frac{1}{{{{S}^{2}}}}{{{\left( {\frac{{\partial S}}{{\partial \theta }}} \right)}}^{2}}} = \frac{2}{{\gamma + 1}}c\frac{1}{S}\frac{{\partial S}}{{\partial \theta }}\left( {1 - \beta \gamma \frac{{{{P}_{0}}}}{{{{\rho }_{0}}{{c}^{2}}}}} \right) \\ P = {{\rho }_{0}}\frac{2}{{\gamma + 1}}{{c}^{2}}\left( {1 - \beta \gamma \frac{{{{P}_{0}}}}{{{{\rho }_{0}}{{c}^{2}}}}} \right)\exp \left( { - \mu \frac{{S\sin \theta }}{H}} \right) \\ \end{gathered} $Из закона сохранения энергии следует
(2.8)
$\begin{gathered} 2\pi \int\limits_{ - \pi /2}^{\pi /2} {\cos \theta d\theta \int\limits_0^S {\left\{ {\rho \left[ {U_{R}^{2} + U_{\theta }^{2}} \right] + \frac{1}{{\gamma - 1}}\left[ {P - {{P}_{0}}\exp \left( { - \mu \frac{{R\sin \theta }}{H}} \right)} \right]} \right.} } + \\ + \;\alpha gR\sin \theta \left. {\left[ {\rho - \rho _{0}^{{^{{^{{}}}}}}\exp \left( { - \mu \frac{{R\sin \theta }}{H}} \right)} \right]} \right\}{{R}^{2}}dR = {{E}_{0}}, \\ \end{gathered} $При $t \to 0$ решение определяется из решения данной системы уравнений (2.1)–(2.8) при условиях: ${{u}_{\theta }} = 0$, $\frac{\partial }{{\partial t}} = 0$, $\frac{\partial }{{\partial \theta }} = 0$, $F\left( {\theta ,t} \right) = 1$ – сильный точечный взрыв в однородной атмосфере [6].
Предварительно поставленная таким образом задача (2.1)–(2.8) исследовалась качественно методом возмущений для случая сильного взрыва в неоднородной атмосфере в отсутствие гравитации и противодавления. Было выявлено наличие вихревых движений внутри области газа, возмущенного ударной волной без явного представления выражения для функции $\operatorname{rot} u$, то есть было доказано, что уже на раннем этапе развития взрыва $\left| {\operatorname{rot} u} \right| \ne 0$ [5].
Целью настоящей работы является исследование начального этапа развития процесса с явным определением функции $rotu$. В [5] было показано, что на этом этапе главный вклад вносит неоднородность атмосферы, поэтому ниже полагается $\alpha = \beta = 0$, то есть исключается влияние силы тяжести и противодавления. Также было доказано, что образование вихревых структур – реальное физическое явление, а не эффект схемной вязкости в численных расчетах.
3. Методика исследования задачи. Асимптотики. Итоговые результаты. После ввода безразмерной координаты $\lambda $ по формуле $R = \lambda {{s}_{0}}\left( t \right)$; и неизвестных функций $\bar {\rho }$, $\bar {P}$, ${{\bar {u}}_{R}}$, ${{\bar {u}}_{\theta }}$, $\bar {c}$:
(3.1)
$\begin{gathered} \frac{{5\left( {\gamma + 1} \right)}}{4}t\frac{\partial }{{\partial t}}\left( {\ln \rho } \right) + \left( {{{u}_{R}} - \frac{{\gamma + 1}}{2}\lambda } \right)\frac{\partial }{{\partial \lambda }}\left( {\ln \rho } \right) + \\ + \;\frac{{{{u}_{\theta }}}}{\lambda }\frac{\partial }{{\partial \theta }}\left( {\ln \rho } \right) + \frac{{\partial {{u}_{R}}}}{{\partial \lambda }} + \frac{1}{\lambda }\frac{{\partial {{u}_{\theta }}}}{{\partial \theta }} + \frac{{2{{u}_{R}}}}{\lambda } - \frac{{{{u}_{\theta }}}}{\lambda }\operatorname{tg} \theta = 0 \\ \end{gathered} $(3.2)
$\begin{gathered} \frac{{5\left( {\gamma + 1} \right)}}{4}t\frac{{\partial {{u}_{R}}}}{{\partial t}} + \left( {{{u}_{R}} - \frac{{\gamma + 1}}{2}\lambda } \right)\frac{{\partial {{u}_{R}}}}{{\partial \lambda }} + \frac{{{{u}_{\theta }}}}{\lambda }\frac{{\partial {{u}_{R}}}}{{\partial \theta }} - \\ - \;\frac{{{{u}^{2}}\theta }}{\lambda } - \frac{3}{4}\left( {\gamma + 1} \right){{u}_{R}} = - \frac{{\left( {\gamma - 1} \right)}}{2}\frac{1}{\rho }\frac{{\partial P}}{{\partial \lambda }} \\ \end{gathered} $(3.3)
$\begin{gathered} \frac{{5\left( {\gamma + 1} \right)}}{4}t\frac{{\partial {{u}_{\theta }}}}{{\partial t}} + \left( {{{u}_{R}} - \frac{{\gamma + 1}}{2}\lambda } \right)\frac{{\partial {{u}_{\theta }}}}{{\partial \lambda }} + \frac{{{{u}_{\theta }}}}{\lambda }\frac{{\partial {{u}_{\theta }}}}{{\partial \theta }} + \frac{{{{u}_{R}}{{u}_{\theta }}}}{\lambda } - \\ - \;\frac{3}{4}\left( {\gamma + 1} \right){{u}_{\theta }} = - \frac{{\left( {\gamma - 1} \right)}}{2}\frac{1}{{\lambda \rho }}\frac{{\partial P}}{{\partial \theta }} \\ \end{gathered} $(3.4)
$\frac{{5\left( {\gamma + 1} \right)}}{4}t\ln \frac{\partial }{{\partial t}}\left( {\frac{P}{{{{\rho }^{\gamma }}}}} \right) + \left( {{{u}_{R}} - \frac{{\gamma + 1}}{2}\lambda } \right)\frac{\partial }{{\partial \lambda }}\ln \left( {\frac{P}{{{{\rho }^{\gamma }}}}} \right) + \frac{{{{u}_{\theta }}}}{\lambda }\frac{\partial }{{\partial \theta }}\ln \left( {\frac{P}{{{{\rho }^{\gamma }}}}} \right) - \frac{3}{2}\left( {\gamma + 1} \right) = 0$Уравнение фронта волны представляется в виде
Уравнение движения фронта
(3.6)
$\frac{5}{2}t\frac{{\partial F}}{{\partial t}} + F = c\sqrt {1 + \frac{1}{{{{F}^{2}}}}{{{\left( {\frac{{\partial F}}{{\partial \theta }}} \right)}}^{2}}} $Условия на фронте
(3.7)
$\begin{gathered} {{u}_{R}}\sqrt {1 + \frac{1}{{{{F}^{2}}}}{{{\left( {\frac{{\partial F}}{{\partial \theta }}} \right)}}^{2}}} = c,\quad {{u}_{\theta }}\sqrt {1 + \frac{1}{{{{F}^{2}}}}{{{\left( {\frac{{\partial F}}{{\partial \theta }}} \right)}}^{2}}} = \frac{1}{F}\frac{{\partial F}}{{\partial \theta }}c, \\ P = {{c}^{2}}\exp \left( { - \mu \frac{{A{{t}^{{2/5}}}F\sin \theta }}{H}} \right),\quad \rho = \exp \left( { - \mu \frac{{A{{t}^{{2/5}}}F\sin \theta }}{H}} \right) \\ \end{gathered} $Соотношение (2.8) примет вид
(3.8)
$\frac{{32}}{{25\pi }}\frac{{{{\rho }_{0}}{{A}^{5}}}}{{{{\gamma }^{2}} - 1}}\int\limits_{ - \pi /2}^{\pi /2} {\cos \theta } d\theta \int\limits_0^F {\left\{ {\rho \left( {U_{R}^{2} + U_{\theta }^{2}} \right) + P} \right\}{{\lambda }^{2}}d\lambda = {{E}_{0}}} $Начальные условия при $t = 0$ соответствуют автомодельному решению при $\alpha = \beta = \mu = 0$ [6]. В момент, близкий к начальному наиболее значительное влияние оказывают слагаемые с параметром $\mu $ [5] поэтому положим $\alpha = \beta = 0$.
Представим неизвестные функции в виде
(3.9)
${{U}_{R}} = \lambda u,\quad {{U}_{\theta }} = \lambda {v},\quad \rho = G{\text{/}}{{\lambda }^{2}}$Сделаем замену переменной
Тогда система (3.1)–(3.8) примет вид
(3.11)
$\begin{gathered} \frac{{5\left( {2 + \varepsilon } \right)}}{4}t\frac{\partial }{{\partial t}}\left( {\ln G} \right) - \frac{1}{\varepsilon }\left( {u - \frac{{2 + \varepsilon }}{2}} \right)\frac{\partial }{{\partial s}}\left( {\ln G} \right) + V\frac{\partial }{{\partial \theta }}\left( {\ln G} \right) - \\ - \;\frac{1}{\varepsilon }\frac{{\partial u}}{{\partial s}} + \frac{{\partial {v}}}{{\partial \theta }} + u + 2 + \varepsilon - {v}\operatorname{tg} \theta = 0 \\ \end{gathered} $(3.12)
$\frac{{5\left( {2 + \varepsilon } \right)}}{4}t\frac{{\partial u}}{{\partial t}} - \frac{1}{\varepsilon }\left( {u - \frac{{2 + \varepsilon }}{2}} \right)\frac{{\partial u}}{{\partial s}} + V\frac{{\partial u}}{{\partial \theta }} + \left[ {u - \frac{{5\left( {2 + \varepsilon } \right)}}{4}} \right]u - {{{v}}^{2}} = \frac{1}{{2G}}\frac{{\partial P}}{{\partial S}}$(3.13)
$\frac{{5\left( {2 + \varepsilon } \right)}}{4}t\frac{{\partial {v}}}{{\partial t}} - \frac{1}{\varepsilon }\left( {u - \frac{{2 + \varepsilon }}{2}} \right)\frac{{\partial {v}}}{{\partial s}} + {v}\frac{{\partial {v}}}{{\partial \theta }} + \left[ {2u - \frac{{5\left( {2 + \varepsilon } \right)}}{4}} \right]u = - \frac{\varepsilon }{{2G}}\frac{{\partial P}}{{\partial \theta }}$(3.14)
$\begin{gathered} \frac{{5\left( {2 + \varepsilon } \right)}}{4}t\left( {\frac{1}{P}\frac{{\partial P}}{{\partial t}} - \frac{{1 + \varepsilon }}{G}\frac{{\partial G}}{{\partial t}}} \right) - \frac{1}{\varepsilon }\left( {u - \frac{{2 + \varepsilon }}{2}} \right)\left( {\frac{1}{P}\frac{{\partial P}}{{\partial s}} - \frac{{1 + \varepsilon }}{G}\frac{{\partial G}}{{\partial s}}} \right) + \\ + \;\left( {\frac{1}{P}\frac{{\partial P}}{{\partial \theta }} - \frac{{1 + \varepsilon }}{G}\frac{{\partial G}}{{\partial \theta }}} \right) + 2\left( {1 + \varepsilon } \right)\left( {u - \frac{{2 + \varepsilon }}{2}} \right) - \frac{3}{2}\left( {2 + \varepsilon } \right) = 0 \\ \end{gathered} $Уравнение фронта
Уравнение движения фронта
(3.16)
$\frac{5}{2}t\frac{{\partial F}}{{\partial t}} + F = c\sqrt {1 + \frac{1}{{{{F}^{2}}}}{{{\left( {\frac{{\partial F}}{{\partial \theta }}} \right)}}^{2}}} $Условия на фронте $s = - \frac{1}{\varepsilon }\ln F$
(3.17)
$P = {{c}^{2}}\exp \left( { - \mu \frac{{A{{t}^{{2/5}}}F\sin \theta }}{H}} \right),\quad G = {{F}^{2}}\exp \left( { - \mu \frac{{A{{t}^{{2/5}}}F\sin \theta }}{H}} \right)$(3.18)
$\frac{{32}}{{25}}\pi \frac{{{{\rho }_{0}}{{A}^{5}}}}{{2 + \varepsilon }}\int\limits_{ - \pi /2}^{\pi /2} {\cos \theta d\theta } \int\limits_0^F {\left\{ {G\left( {{{u}^{2}} + {{{v}}^{2}}} \right) + P} \right\}\exp ( - 3\varepsilon s)ds = {{E}_{0}}} $Представим неизвестные функции в виде
где $G = N\left( s \right)$, $P = K\left( s \right)$, $u = T\left( s \right)$ решение соответствующей системы при $t \to 0$. Разлагая по параметру $\mu $ для членов первого порядка, получим систему уравнений.Согласно (3.11)–(3.14)
(3.19)
$\begin{gathered} \frac{{5\left( {2 + \varepsilon } \right)}}{4}t\frac{1}{N}\frac{{\partial \delta G}}{{\partial t}} - \frac{1}{\varepsilon }\left( {T - \frac{{2 + \varepsilon }}{2}} \right)\frac{1}{N}\frac{{\partial \delta G}}{{\partial s}} - \frac{1}{\varepsilon }\frac{{\partial \delta u}}{{\partial s}} + \frac{{\partial \delta {v}}}{{\partial \theta }} + \\ + \;\frac{1}{\varepsilon }\left( {T - \frac{{2 + \varepsilon }}{2}} \right)\frac{1}{{{{N}^{2}}}}\delta G + \left( {1 - \frac{1}{\varepsilon }\frac{1}{N}\frac{{dN}}{{ds}}} \right)\delta u - \delta {v}\operatorname{tg} \theta = 0 \\ \end{gathered} $(3.20)
$\begin{gathered} \frac{{5\left( {2 + \varepsilon } \right)}}{4}t\frac{{\partial \delta u}}{{\partial t}} - \frac{1}{\varepsilon }\left( {T - \frac{{2 + \varepsilon }}{2}} \right)\frac{{\partial \delta u}}{{\partial s}} + \left[ {2T - \frac{1}{\varepsilon }\frac{{dT}}{{ds}} - \frac{{5\left( {2 + \varepsilon } \right)}}{4}} \right]\delta u = \\ = \;\frac{1}{{2N}}\frac{{\partial \delta P}}{{\partial s}} - \frac{1}{{2{{N}^{2}}}}\frac{{dK}}{{ds}}\delta G \\ \end{gathered} $(3.21)
$\frac{{5\left( {2 + \varepsilon } \right)}}{4}t\frac{{\partial \delta {v}}}{{\partial t}} - \frac{1}{\varepsilon }\left( {T - \frac{{2 + \varepsilon }}{2}} \right)\frac{{\partial \delta {v}}}{{\partial s}} + \left[ {2T - \frac{{5\left( {2 + \varepsilon } \right)}}{4}} \right]\delta {v} = - \frac{\varepsilon }{{2N}}\frac{{\partial \delta P}}{{\partial \theta }}$(3.22)
$\begin{gathered} \frac{{5\left( {2 + \varepsilon } \right)}}{4}t\left( {\frac{1}{K}\frac{{\partial \delta P}}{{\partial t}} - \frac{{1 + \varepsilon }}{N}\frac{{\partial \delta G}}{{\partial t}}} \right) - \frac{1}{\varepsilon }\left( {T - \frac{{2 + \varepsilon }}{2}} \right)\left[ {\frac{1}{K}\frac{{\partial \delta P}}{{\partial s}}} \right. - \frac{{1 + \varepsilon }}{N}\frac{{\partial \delta G}}{{\partial s}} - \\ - \;\frac{1}{{{{K}^{2}}}}\frac{{dK}}{{ds}}\delta P + \left. {\frac{{1 + \varepsilon }}{{{{N}^{2}}}}\frac{{dN}}{{ds}}\delta G} \right] + \left[ {2\left( {1 + \varepsilon } \right) - \frac{1}{\varepsilon }\left( {\frac{1}{K}\frac{{dK}}{{ds}} - \frac{{1 + \varepsilon }}{N}\frac{{dN}}{{ds}}} \right)} \right]\delta u = 0 \\ \end{gathered} $Уравнение фронта
Уравнение движения фронта
Условия на фронте при $s = 0$
(3.25)
$\delta P - \frac{{dK}}{{ds}}\frac{1}{\varepsilon }\delta F = 2\delta c - \frac{{A{{t}^{{2/5}}}}}{H}\sin \theta ,\quad \delta G - \frac{{dN}}{{ds}}\frac{1}{\varepsilon }\delta F = 2\delta F - \frac{{A{{t}^{{2/5}}}}}{H}\sin \theta $(3.26)
$\begin{gathered} \frac{{32}}{{25}}\pi \frac{{{{\rho }_{0}}{{A}^{5}}}}{{2 + \varepsilon }}\int\limits_{ - \pi /2}^{\pi /2} {\cos \theta d\theta \int\limits_0^F {\left( {\delta G{{T}^{2}} + 2NT\delta u + \delta P} \right)\exp \left( { - 3\varepsilon s} \right)ds + } } \\ + \;\frac{{32}}{{25}}\pi \frac{{{{\rho }_{0}}{{A}^{5}}}}{{2 + \varepsilon }}\int\limits_{ - \pi /2}^{\pi /2} {{{{\left. {\left( {N{{T}^{2}} + K} \right)} \right|}}_{{s = 0}}}\frac{{\delta F}}{\varepsilon }\cos \theta d\theta } = 0 \\ \end{gathered} $Представим неизвестные функции в виде
(3.27)
$\begin{gathered} \delta P = \delta P\left( s \right){{t}^{{2/5}}}\sin \theta ,\quad \delta G = \delta G\left( s \right){{t}^{{2/5}}}\sin \theta ,\quad \delta u = \delta u\left( s \right){{t}^{{2/5}}}\sin \theta \\ \delta {v} = \delta {v}\left( s \right){{t}^{{2/5}}}\cos \theta ,\quad \delta F = \delta F{{t}^{{2/5}}}\sin \theta ,\quad \delta c = \delta c{{t}^{{2/5}}}\sin \theta \\ \end{gathered} $Для их определения, используя (3.19)–(3.27), получим следующую систему соотношений:
Согласно (3.19)–(3.22)
(3.28)
$\begin{gathered} - \frac{1}{\varepsilon }\left( {T - \frac{{2 + \varepsilon }}{2}} \right)\frac{1}{N}\frac{{d\delta G}}{{ds}} - \frac{1}{\varepsilon }\frac{{d\delta u}}{{ds}} + \\ + \;\left[ {\frac{1}{\varepsilon }\left( {T - \frac{{2 + \varepsilon }}{2}} \right)\frac{1}{{{{N}^{2}}}} + \frac{{\left( {2 + \varepsilon } \right)}}{2}\frac{1}{N}} \right]\delta G + \left( {1 - \frac{1}{\varepsilon }\frac{1}{N}\frac{{dN}}{{ds}}} \right)\delta u - 2\delta {v} = 0 \\ \end{gathered} $(3.29)
$\begin{gathered} - \frac{1}{\varepsilon }\left( {T - \frac{{2 + \varepsilon }}{2}} \right)\frac{{d\delta u}}{{ds}} + \left[ {2T - \frac{1}{\varepsilon }\frac{{dT}}{{ds}} - \frac{{3\left( {2 + \varepsilon } \right)}}{4}} \right]\delta u = \\ = \;\frac{1}{{2N}}\frac{{d\delta P}}{{ds}} - \frac{1}{{2{{N}^{2}}}}\frac{{dK}}{{ds}}\delta G \\ \end{gathered} $(3.30)
$ - \frac{1}{\varepsilon }\left( {T - \frac{{2 + \varepsilon }}{2}} \right)\frac{{d\delta {v}}}{{ds}} + \left[ {2T - \frac{{3\left( {2 + \varepsilon } \right)}}{4}} \right]\delta {v} = - \frac{\varepsilon }{{2N}}\delta P$(3.31)
$\begin{gathered} - \frac{1}{\varepsilon }\left( {T - \frac{{2 + \varepsilon }}{2}} \right)\left[ {\frac{1}{K}\frac{{d\delta P}}{{ds}} - \frac{{1 + \varepsilon }}{N}\frac{{d\delta G}}{{ds}} - \frac{1}{{{{K}^{2}}}}\frac{{dK}}{{ds}}\delta P + \frac{{1 + \varepsilon }}{{{{N}^{2}}}}\frac{{dN}}{{ds}}\delta G} \right] + \\ + \;\frac{{2 + \varepsilon }}{2}\left( {\frac{1}{K}\delta P - \frac{{1 + \varepsilon }}{N}\delta G} \right) + \left[ {2\left( {1 + \varepsilon } \right) - \frac{1}{\varepsilon }\left( {\frac{1}{K}\frac{{dK}}{{ds}} - \frac{{1 + \varepsilon }}{N}\frac{{dN}}{{ds}}} \right)} \right]\delta u = 0 \\ \end{gathered} $Согласно (3.24)
Согласно (3.25) условия на фронте при $s = 0$
(3.33)
$\begin{gathered} \delta u - \frac{{dT}}{{ds}}\frac{1}{\varepsilon }\delta F = \delta c - \delta F,\quad \delta {v} = \delta F \\ \delta P - \frac{{dK}}{{ds}}\frac{1}{\varepsilon }\delta F = 2\delta c - \frac{A}{H},\quad \delta G - \frac{{dN}}{{ds}}\frac{1}{\varepsilon }\delta F = 2\delta c - \frac{A}{H} \\ \end{gathered} $Соотношение (3.26) удовлетворяется тождественно.
Представим искомые функции в виде
В дальнейшем волну опускаем.
При $\varepsilon \to 0$ функции $L$, $N$, $K$ стремятся к следующим значениям [5]:
(3.34)
$L = 2 - \omega ,\quad K = \frac{1}{{2 - \omega }},\quad N = \frac{\omega }{{{{{\left( {2 - \omega } \right)}}^{2}}}},$При $\varepsilon \to 0$ система (3.28)–(3.33) примет вид
(3.35)
$\frac{L}{2}\frac{{d\delta G}}{{ds}} + \delta G - L\frac{{d\delta u}}{{ds}} - \left( {\frac{1}{L}\frac{{dL}}{{ds}} + \frac{1}{N}\frac{{dN}}{{ds}}} \right)L\delta u = 0$(3.36)
$\frac{1}{K}\frac{{dK}}{{ds}}\delta G - \frac{1}{K}\frac{{dK}}{{ds}}\delta P - \frac{{d\delta P}}{{ds}} = 0$(3.37)
$\frac{{d\delta {v}}}{{ds}} + \left( {\frac{1}{L} + \frac{1}{L}\frac{{dL}}{{ds}}} \right)\delta {v} + \frac{K}{{{{L}^{2}}N}}\delta P = 0$(3.38)
$\frac{L}{2}\left( {\frac{{d\delta P}}{{ds}} - \frac{{d\delta G}}{{ds}}} \right) + \delta P - \delta G - \left( {\frac{1}{K}\frac{{dK}}{{ds}} - \frac{1}{N}\frac{{dN}}{{ds}}} \right)L\delta u = 0$Согласно (3.32)
Согласно (3.33) условия на фронте при $s = 0$ примут вид
(3.40)
$\begin{gathered} \delta u + \frac{1}{2}\frac{{dL}}{{ds}}\delta F = \delta c - \delta F,\quad \delta {v} = \delta F \\ \delta P - \frac{{dK}}{{ds}}\delta F = - \frac{A}{H},\quad \delta G - \frac{{dN}}{{ds}}\delta F = - \frac{A}{H} \\ \end{gathered} $Отметим, что использовать приближенную оценку разложения по $\varepsilon $ можно лишь вблизи границы фронта волны $s = 0$, поскольку при $s \to \infty $ значение $G$ стремится к нулю и приближенное представление $1{\text{/}}G$ в виде ряда невозможно.
Используя явные выражения для функций (3.34), систему (3.35)–(3.40) представим в виде:
(3.41)
$\frac{{\left( {2 - \omega } \right)}}{2}\frac{{d\delta G}}{{ds}} + \delta G - \left( {2 - \omega } \right)\frac{{d\delta u}}{{ds}} + 6\delta u = 0$(3.42)
$\frac{{ - 3\omega }}{{\left( {2 - \omega } \right)}}\delta G + \frac{{3\omega }}{{\left( {2 - \omega } \right)}}\delta P - \frac{{d\delta P}}{{ds}} = 0$(3.43)
$\left( {2 - \omega } \right)\frac{{d\delta {v}}}{{ds}} + \left( {1 + 3\omega } \right)\delta {v} + \delta P{\text{/}}\omega = 0$(3.44)
$\frac{{\left( {2 - \omega } \right)}}{2}\left( {\frac{{d\delta P}}{{ds}} - \frac{{d\delta G}}{{ds}}} \right) + \delta P - \delta G - 6\delta u = 0$Согласно (3.39), (3.40) условия при $s = 0$ примут вид
(3.45)
$\delta u = - \frac{1}{2}\delta F,\quad \delta {v} = \delta F,\quad \delta P = - 3\delta F - \frac{A}{H},\quad \delta G = - 9\delta F - \frac{A}{H}$Система дифференциальных уравнений (3.41)–(3.44) решается по следующей схеме:
Согласно (3.41)
Используя (3.42), получим
Интегрируя данное соотношение с условиями (3.45), получим
(3.46)
$\frac{\omega }{{\left( {2 - \omega } \right)}}\delta G - \frac{8}{3}\frac{1}{{\left( {2 - \omega } \right)}}\delta P - \frac{{2\omega }}{{\left( {2 - \omega } \right)}}\delta u = \frac{5}{3}\frac{A}{H}$Согласно (3.46)
(3.47)
$\delta u = \frac{1}{2}\delta G - \frac{4}{3}{{\omega }^{{ - 1}}}\delta P - \frac{5}{6}\frac{A}{H}\left( {2{{\omega }^{{ - 1}}} - 1} \right)$Согласно (3.42)
(3.48)
$\delta G = \delta P - \frac{1}{3}\left( {2{{\omega }^{{ - 1}}} - 1} \right)\frac{{d\delta P}}{{ds}}$Согласно (3.47)–(3.48)
(3.49)
$\delta u = - \frac{1}{6}\left( {2{{\omega }^{{ - 1}}} - 1} \right)\frac{{d\delta P}}{{ds}} - \frac{1}{6}\left( {8{{\omega }^{{ - 1}}} - 3} \right)\delta P - \frac{5}{6}\frac{A}{H}\left( {2{{\omega }^{{ - 1}}} - 1} \right)$Используя (3.44), получим дифференциальное уравнение для определения $\delta P$
(3.50)
$\begin{gathered} {{\left( {2{{\omega }^{{ - 1}}} - 1} \right)}^{2}}\frac{{{{d}^{2}}\delta P}}{{d{{s}^{2}}}} + 14\left( {2{{\omega }^{{ - 1}}} - 1} \right){{\omega }^{{ - 1}}}\frac{{d\delta P}}{{ds}} + 6\left( {8{{\omega }^{{ - 1}}} - 3} \right){{\omega }^{{ - 1}}}\delta P = \\ = - 30\frac{A}{H}\left( {2{{\omega }^{{ - 1}}} - 1} \right){{\omega }^{{ - 1}}} \\ \end{gathered} $Неизвестную функцию $\delta P$ представим в виде $\delta P = {{\left( {2{{\omega }^{{ - 1}}} - 1} \right)}^{{2/3}}}\psi $.
Тогда для отыскания $\psi $ имеем дифференциальное уравнение
(3.51)
$\begin{gathered} {{\left( {2{{\omega }^{{ - 1}}} - 1} \right)}^{2}}\frac{{{{d}^{2}}\psi }}{{d{{s}^{2}}}} + 22\left( {2{{\omega }^{{ - 1}}} - 1} \right){{\omega }^{{ - 1}}}\frac{{d\psi }}{{ds}} + \left( {120{{\omega }^{{ - 2}}} - 30{{\omega }^{{ - 1}}}} \right)\psi = \\ = - 30\frac{A}{H}{{\left( {2{{\omega }^{{ - 1}}} - 1} \right)}^{{1/3}}}{{\omega }^{{ - 1}}} \\ \end{gathered} $С начальными условиями $\psi = - 3\delta F - \frac{A}{H}$, $\frac{{d\psi }}{{ds}} = 30\delta F + 4\frac{A}{H}$ при $s = 0$. Уравнение преобразуется к виду
Интегрируя с учетом начальных условий, получим
Далее введем обозначение $\sigma = \exp \left( {3t} \right)$
Следовательно
(3.52)
$\delta P = \frac{1}{{\left( {2{{\omega }^{{ - 1}}} - 1} \right)}}\left[ { - \frac{5}{2}\frac{A}{H}{{\omega }^{{ - 1}}} + \frac{{15}}{4}\frac{A}{H}s - \frac{9}{4}\frac{A}{H}\int\limits_0^s {\frac{{dt}}{{{{{\left( {2\sigma - 1} \right)}}^{{1/3}}}}}} + \frac{3}{2}\frac{A}{H} - 3\delta F} \right]$Согласно (3.48), (3.52)
(3.53)
$\begin{gathered} \delta G = \frac{{2{{\omega }^{{ - 1}}} + 1}}{{\left( {2{{\omega }^{{ - 1}}} - 1} \right)}}\left[ { - \frac{5}{2}\frac{A}{H}{{\omega }^{{ - 1}}} + \frac{{15}}{4}\frac{A}{H}s - \frac{9}{4}\frac{A}{H}\int\limits_0^s {\frac{{dt}}{{{{{\left( {2\sigma - 1} \right)}}^{{1/3}}}}}} + \frac{3}{2}\frac{A}{H} - 3\delta F} \right] + \\ + \;\frac{5}{4}\frac{A}{H}\left( {2{{\omega }^{{ - 1}}} - 1} \right) + \frac{3}{4}\frac{A}{H}\frac{1}{{{{{\left( {2{{\omega }^{{ - 1}}} - 1} \right)}}^{{1/3}}}}} \\ \end{gathered} $Согласно (3.47), (3.52), (3.53)
(3.54)
$\begin{gathered} \delta u = \frac{{3 - 2{{\omega }^{{ - 1}}}}}{{6\left( {2{{\omega }^{{ - 1}}} - 1} \right)}}\left[ { - \frac{5}{2}\frac{A}{H}{{\omega }^{{ - 1}}} + \frac{{15}}{4}\frac{A}{H}s - \frac{9}{4}\frac{A}{H}\int\limits_0^s {\frac{{dt}}{{{{{\left( {2\sigma - 1} \right)}}^{{1/3}}}}}} + \frac{3}{2}\frac{A}{H} - 3\delta F} \right] + \\ + \;\frac{5}{8}\frac{A}{H}\left( {2{{\omega }^{{ - 1}}} - 1} \right) + \frac{3}{8}\frac{A}{H}\frac{1}{{{{{\left( {2{{\omega }^{{ - 1}}} - 1} \right)}}^{{1/3}}}}} - \frac{5}{6}\frac{A}{H}\left( {2{{\omega }^{{ - 1}}} - 1} \right) \\ \end{gathered} $Согласно (3.43)
(3.55)
$\left( {2{{\omega }^{{ - 1}}} - 1} \right)\frac{{d\delta {v}}}{{ds}} + \left( {{{\omega }^{{ - 1}}} + 3} \right)\delta {v} = - {{\omega }^{{ - 2}}}\delta P$Решение соответствующего однородного уравнения
Тогда решение (3.55) (после подстановки значений $\omega $ и $\sigma $) имеет вид
(3.56)
${v} = \frac{1}{{{{{\left( {2\exp \left( {3s} \right) - 1} \right)}}^{{1/6}}}\left( {2 - \exp \left( { - 3s} \right)} \right)}}\left[ {\delta F - \int\limits_0^s {\frac{{\left( {2 - \exp \left( { - 3t} \right)} \right)}}{{{{{\left( {2\exp \left( {3t} \right) - 1} \right)}}^{{5/6}}}}}} \exp \left( {6t} \right)\delta P(t)dt} \right]$При этом, поскольку ротор имеет единственную ненулевую составляющую, она может быть представлена в виде:
При $\varepsilon \to 0$ имеем $M = \frac{{d\delta {v}}}{{ds}}$. Следовательно, значение ротора скорости непосредственно за фронтом УВ отлично от нуля.
Заключение. В статье дано качественное объяснение возникновения завихренности, вызванное только неоднородностью атмосферы по высоте, уже для малых значений времени (несколько десятых секунды). Дальнейшее исследование предполагает изучение процесса для больших значений времени и учета влияния гравитации и противодавления на развитие завихренности внутри области, охваченной фронтом УВ.
Работа Андрущенко В.А., Мурашкина И.В. выполнена в рамках госзадания Института автоматизации проектирования РАН, работа Головешкина В.А. выполнена в рамках госзадания Института прикладной механики РАН.
Список литературы
Егорова Л.А. Напряженно-деформированное состояние и разрушение метеороида при движении в атмосфере // ПММ. 2011. Т. 75. Вып. 3. С. 513–518.
Андрущенко В.А., Сызранова Н.Г., Шевелев Ю.Д. Моделирование падения Челябинского метеорита // Компьютерные исследования и моделирование. 2013. Т. 5. № 6. С. 927–940.
Зельдович Я.Б., Райзер Ю.П. Физика ударных волн и высокотемпературных газодинамических явлений. М.: Физматгиз, 1963. 632 с.
Андрущенко В.А., Кестенбойм Х.С., Чудов Л.А. Движение газа, вызванное точечным взрывом в неоднородной атмосфере // Изв. АН СССР. МЖГ. 1981. № 6. С. 144–151.
Андрущенко В.А., Головешкин В.А., Холин Н.Н. О формировании вихревых структур внутри области сильного взрыва в неоднородной атмосфере / XI Всерос. съезд по фундам. проблемам теоретич. и прикл. мех. Сб. докл. Казань, 20–24 августа 2015 г. Казань: АН РТ, 2015. С. 162–163.
Седов Л.И. Методы подобия и размерности в механике. М.: Наука, 1977. 438 с.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика