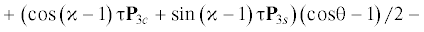Прикладная математика и механика, 2022, T. 86, № 6, стр. 872-886
Регулярная прецессия гиростата в суперпозиции трех однородных полей
1 ИПТМУ РАН
Саратов, Россия
* E-mail: olshanskiy_vlad@mail.ru
Поступила в редакцию 05.04.2022
После доработки 15.07.2022
Принята к публикации 30.07.2022
- EDN: YJAKIY
- DOI: 10.31857/S0032823522060121
Аннотация
В статье описаны все возможные случаи регулярной прецессии при движении твердого тела и гиростата вокруг неподвижной точки под действием трех однородных полей. Получено обобщение известных условий Яхья, когда скорости прецессии и собственного вращения равны друг другу. Найден новый случай регулярной прецессии, когда скорость прецессии вдвое больше скорости собственного вращения и ось прецессии не ортогональна оси собственного вращения. Рассмотрено применение результатов в частном случае, когда силовые линии трех полей взаимно ортогональны, и в случае, когда ось прецессии коллинеарна силовым линиям одного из полей.
1. Введение. Задача о движении твердого тела вокруг неподвижной точки в суперпозиции однородных полей является одним из обобщений задачи интегрирования уравнений Эйлера–Пуассона. После указания [1] новых случаев интегрируемости вращающегося намагниченного твердого тела в однородных гравитационном и магнитном полях, во многих работах были изучены различные аспекты задачи о движении твердого тела вокруг неподвижной точки в суперпозиции нескольких полей. Были найдены [2, 3], в частности, новые интегрируемые случаи движения под действием потенциальных и гироскопических сил без осевой симметрии и движения симметричного тела и гиростата в случае Ковалевской в гравитационном, электрическом и магнитном полях. Для гиростата в двух постоянных полях определены положения равновесия и построены периодические решения [4, 5]. Позже были получены достаточные условия устойчивости гиростата в постоянном гравитационном и однородном магнитном полях [6, 7]. Анализ интегрируемых систем выполнен [8] для волчка Ковалевской в двух полях. Уравнения движения твердого тела под действием обобщенных консервативных и гироскопических сил были использованы при построении новых решений в задаче о движении в идеальной несжимаемой жидкости свободного многосвязного тела [9] и при изучении устойчивости движения гиростата под действием гравитационной и выталкивающей сил [10].
Важным простым и нетривиальным случаем, который встречается при описании движения некоторых технических объектов и естественных космических тел, является регулярная прецессия. При таком движении тело вращается с постоянной скоростью вокруг некоторой оси, связанной с телом (ось собственного вращения), и эта ось вращается с постоянной скоростью вокруг оси, неподвижной в инерциальном пространстве (ось прецессии). Угол между осью прецессии и осью собственного вращения постоянен.
Регулярная прецессия динамически симметричного свободного и тяжелого тел хорошо изучена (см. например [11]). Возможность регулярной прецессии несимметричного тяжелого твердого тела, движущегося вокруг неподвижной точки, была показана Гриоли в 1947 году [12]. В этом случае оси прецессии и собственного вращения взаимно перпендикулярны, скорости прецессии и собственного вращения одинаковы, ось прецессии не вертикальна. Решение Гриоли было перенесено [13] на задачу о движении тела в жидкости. Отметим, что несимметричное тело с эллипсоидальной полостью, заполненной идеальной жидкостью, также может совершать прецессионное движение при отсутствии внешних сил [14–17]. Обзор регулярных и нерегулярных прецессий гиростата под действием потенциальных и гироскопических сил, при движении в жидкости, при движении в магнитном поле, приведен в [18, 19].
Недавно была указана возможность регулярной прецессии вокруг невертикальной оси несимметричного твердого тела и гиростата в суперпозиции двух [20] и трех [21] однородных полей, а также выделен случай трех однородных полей при анализе условий регулярной прецессии твердого тела в суперпозиции трех (гравитационного, электрического и магнитного) полей, одно из которых – неоднородное [22]. В отмеченных работах [20–22] рассматривается частный случай регулярной прецессии, когда скорости прецессии и собственного вращения совпадают, силовые линии полей взаимно ортогональны и ось прецессии коллинеарна силовым линиям одного из полей.
В настоящей статье проанализированы все возможные случаи регулярной прецессии твердого тела с неподвижной точкой в суперпозиции трех независимых однородных полей. Для случая равенства скоростей прецессии и собственного вращения получено обобщение известных условий [21, 22] и приведены условия для динамически симметричного тела. Найден новый случай регулярной прецессии, для которого скорость прецессии вдвое больше скорости собственного вращения. Получены общие условия существования прецессии для этого случая, показано, что угол между осями прецессии и собственного вращения задается равенством $\cos \theta = {\text{1/6}}$.
2. Постановка задачи и предварительный анализ. Рассмотрим движение гиростата вокруг неподвижной точки O под действием трех однородных постоянных силовых полей. Обозначим ${{{\mathbf{\alpha }}}_{i}}$ – единичные векторы направлений сил каждого из полей, ${{C}_{i}}$ – центры приведения сил, $~{{{\mathbf{u}}}_{{\text{i}}}} = {{p}_{i}}{\mathbf{O}}{{{\mathbf{C}}}_{i}}$, ${{p}_{i}}$ – суммарная сила действия на тело поля номер i.
Теорема об изменении кинетического момента дает уравнение
(2.1)
${\mathbf{I\dot {\omega }}} + {\mathbf{\omega }} \times \left( {{\mathbf{I\omega }} + {\mathbf{\sigma }}} \right) = {\mathbf{M}},\quad {\mathbf{M}} = {{{\mathbf{\alpha }}}_{1}} \times {{{\mathbf{u}}}_{1}} + {{{\mathbf{\alpha }}}_{2}} \times {{{\mathbf{u}}}_{2}} + {{{\mathbf{\alpha }}}_{3}} \times {{{\mathbf{u}}}_{3}}$Здесь ${{\left( ~ \right)}^{ \bullet }}$ – производная по времени в системе отсчета, связанной с телом; векторы ${{{\mathbf{u}}}_{i}}$ постоянны в этой системе, векторы ${{{\mathbf{\alpha }}}_{i}}$ постоянны в инерциальной системе. ${\mathbf{I}}$ и ${\mathbf{\omega }}$ – оператор инерции тела в неподвижной точке и угловая скорость тела, ${\mathbf{M}}$ – сумма моментов внешних сил, ${\mathbf{\sigma }}$ – гиростатический момент.
Для векторов ${{{\mathbf{\alpha }}}_{i}}$ в подвижной системе отсчета имеем уравнения
(2.2)
${{{\mathbf{\dot {\alpha }}}}_{i}} + {\mathbf{\omega }} \times {{{\mathbf{\alpha }}}_{i}} = 0;\quad i = 1,2,3$Если векторы ${{{\mathbf{\alpha }}}_{1}},{{{\mathbf{\alpha }}}_{2}}$, ${{{\mathbf{\alpha }}}_{3}}$ компланарны или векторы ${{{\mathbf{u}}}_{1}},{{{\mathbf{u}}}_{2}}$, ${{{\mathbf{u}}}_{3}}$ компланарны, то задача (2.1), (2.2) может быть заменена эквивалентной задачей о движении в двух однородных полях; эти случаи будем называть приводимыми, в данной статье они не рассматриваются.
При регулярной прецессии угловая скорость тела имеет два компонента, один – постоянный в системе, связанной с телом, другой – постоянный в инерциальной системе отсчета
Здесь векторы m и ${\mathbf{\rho }}$ постоянны, соответственно, в подвижной и инерциальной системах; $\left| {\mathbf{m}} \right| = \left| {\mathbf{\rho }} \right| = 1$. Величины ${{{{\omega }}}_{r}}$ и ${{{{\omega }}}_{p}}$ – это скорости собственного вращения (относительная скорость) и прецессии (переносная скорость).
Ниже решается следующая задача: при заданных в инерциальной системе отсчета направлениях ${{{\mathbf{\alpha }}}_{i}}$ силовых линий полей и заданном положении оси прецессии ${\mathbf{\rho }}$ определить гиростатический момент и векторы ${{{\mathbf{u}}}_{i}}$, при которых тело может совершать регулярную прецессию.
Решение может быть формально упрощено, если считать направления полей ${{{\mathbf{\alpha }}}_{i}}$ взаимно ортогональными; поскольку этого всегда можно добиться линейным преобразованием, обычно считается, что такое преобразование уже выполнено и (${{{\mathbf{\alpha }}}_{i}},{{{\mathbf{\alpha }}}_{j}}$) = 0, $i \ne j$. Это затрудняет интерпретацию результатов, поскольку в реальных задачах как взаимное расположение силовых линий полей, так и положения центров приведения сил могут быть любыми. Ниже задача решается для произвольных заданных углов между силовыми линиями полей.
Векторная функция ${\mathbf{\rho }}\left( t \right)$ удовлетворяет уравнению (2.2), которое, при учете равенства (2.3), становится линейным
Пусть $\left( {{{{\mathbf{l}}}_{1}},{{{\mathbf{l}}}_{2}},{{{\mathbf{l}}}_{3}}} \right)$ – некоторый связанный с телом ортонормированный правый базис и ${{{\mathbf{l}}}_{1}} = {\mathbf{m}}$. Решение уравнения (2.4) можно записать в виде
(2.5)
${\mathbf{\rho }} = \cos \theta {{{\mathbf{l}}}_{1}} + \sin \theta \left( {\sin \tau {{{\mathbf{l}}}_{2}} + \cos \tau {{{\mathbf{l}}}_{3}}} \right),\quad \tau = {{\omega }_{r}}t + \operatorname{const} $Произвольный параметр ${{\theta }}$ – это угол между осями собственного вращения и прецессии, $\cos \theta = \left( {{\mathbf{m}},{\mathbf{\rho }}} \right)$.
Из формул (2.3) и (2.5) получаем компоненты угловой скорости
(2.6)
${{\omega }^{{\left( 1 \right)}}} = \Omega \left( {1 + \kappa \cos \theta } \right),\quad {{\omega }^{{\left( 2 \right)}}} = \Omega \kappa \sin \theta \sin \tau ,\quad {{\omega }^{{\left( 3 \right)}}} = \Omega \kappa \sin \theta \cos \tau $Здесь и далее ${{d}^{{\left( i \right)}}}$ – компонента ${\mathbf{d}}$ в базисе $\left( {{{{\mathbf{l}}}_{1}},{{{\mathbf{l}}}_{2}},{{{\mathbf{l}}}_{3}}} \right)$, $~\kappa = {{\omega }_{p}}{\text{/}}{{\omega }_{r}}$, $\Omega = {{\omega }_{r}}$.
Скалярная форма уравнений (2.2) в осях $({{{\mathbf{l}}}_{j}})$ следующая:
(2.7)
$\frac{{d\alpha _{i}^{{\left( 2 \right)}}}}{{d\tau }} + \kappa \sin \theta \cos \tau \alpha _{i}^{{\left( 1 \right)}} - \left( {\kappa \cos \theta + 1} \right)\alpha _{i}^{{\left( 3 \right)}} = 0$Общее решение запишем, с учетом нормировки $\left| {{{{\mathbf{\alpha }}}_{i}}} \right| = 1$, в виде
(2.8)
$\alpha _{i}^{{\left( 2 \right)}} = \sin \theta \cos {{\theta }_{i}}\sin \tau + \sin {{\theta }_{i}}\left( {\cos \tau \cos {{\tau }_{i}} - \cos \theta \sin \tau \sin {{\tau }_{i}}} \right)$Здесь ${{\theta }_{i}},{{\varphi }_{i}}$ – произвольные постоянные, геометрический смысл которых указан ниже.
Формулы (2.5) и (2.8) допускают векторную запись
(2.9)
${{{\mathbf{\alpha }}}_{i}} = - {\mathbf{R}}{{{\mathbf{s}}}_{i}};\quad i = 1,2,3,\quad {\mathbf{\rho }} = - {\mathbf{R}}{{{\mathbf{l}}}_{1}}$Здесь ${\mathbf{R}}\left( t \right)$ – поворот, ${{{\mathbf{s}}}_{i}}$ – единичные векторы, заданные сферическими координатами ${{{{\theta }}}_{i}},{{{{\varphi }}}_{i}}$ в базисе (${{{\mathbf{l}}}_{i}}$)
(2.10)
${{{\mathbf{s}}}_{i}} = \cos {{\theta }_{i}}{{{\mathbf{l}}}_{1}} + \sin {{\theta }_{i}}\left( {\cos {{\varphi }_{i}}{{{\mathbf{l}}}_{2}} + \sin {{\varphi }_{i}}{{{\mathbf{l}}}_{3}}} \right);\quad i = 1,2,3$Элементы ${{r}_{{ij}}} = \left( {{{{\mathbf{l}}}_{i}},{\mathbf{R}}{{{\mathbf{l}}}_{j}}} \right)$ ортогональной матрицы ${\mathbf{R}}$ следующие
Из формул (2.9) и (2.10) получаем
(2.12)
$ + \;\cos {{\theta }_{2}}\sin {{\theta }_{1}}\sin {{\theta }_{3}}\sin \left( {{{\varphi }_{3}} - {{\varphi }_{1}}} \right) + \cos {{\theta }_{3}}\sin {{\theta }_{1}}\sin {{\theta }_{2}}\sin \left( {{{\varphi }_{1}} - {{\varphi }_{2}}} \right)$(2.13)
$\left\langle {{\mathbf{\rho }},{{{\mathbf{\alpha }}}_{1}},{{{\mathbf{\alpha }}}_{2}}} \right\rangle = \sin {{\theta }_{1}}\sin {{\theta }_{2}}\sin \left( {{{\varphi }_{1}} - {{\varphi }_{2}}} \right)\quad \left( {1\;2\;3} \right)$Для дальнейшего анализа условий регулярной прецессии суммарный момент внешних сил, учитывая равенства (2.9), удобно представить в виде
(2.14)
${\mathbf{M}} = {{{\mathbf{v}}}_{1}} \times {\mathbf{R}}{{{\mathbf{l}}}_{1}} + {{{\mathbf{v}}}_{2}} \times {\mathbf{R}}{{{\mathbf{l}}}_{2}} + {{{\mathbf{v}}}_{3}} \times {\mathbf{R}}{{{\mathbf{l}}}_{3}}$(2.15)
${{{\mathbf{v}}}_{i}}\mathop = \limits^{{\text{def}}} s_{1}^{{\left( i \right)}}{{{\mathbf{u}}}_{1}} + s_{2}^{{\left( i \right)}}{{{\mathbf{u}}}_{2}} + s_{3}^{{\left( i \right)}}{{{\mathbf{u}}}_{3}};\quad i = 1,2,3$Запись суммарного момента в виде (2.14) позволяет выполнить декомпозицию поставленной в работе задачи нахождения конфигурационных условий прецессии: сначала, при анализе тригонометрических тождеств, находим векторы ${{{\mathbf{v}}}_{i}}$ и ограничения, налагаемые на тензор инерции ${\mathbf{I}}$ твердого тела, гиростатический момент ${\mathbf{\sigma }}$ и угол ${{\theta }}$ между осями собственного вращения и прецессии. Эти ограничения, как и векторы ${{{\mathbf{v}}}_{i}}$, не зависят от значений параметров ${{{{\theta }}}_{i}},{{{{\varphi }}}_{i}}$ и, следовательно, не зависят от взаимного расположения силовых линий полей ${{{\mathbf{\alpha }}}_{i}}$ и от положения оси прецессии в инерциальном пространстве. Затем из системы (2.15) находим векторы ${{{\mathbf{u}}}_{i}}$, определяющие центры приведения сил.
Решение системы (2.15) имеет вид
(2.16)
${{{\mathbf{u}}}_{i}} = n_{i}^{{\left( 1 \right)}}{{{\mathbf{v}}}_{1}} + n_{i}^{{\left( 2 \right)}}{{{\mathbf{v}}}_{2}} + n_{i}^{{\left( 3 \right)}}{{{\mathbf{v}}}_{3}};\quad i = 1,2,3$(2.17)
${{{\mathbf{n}}}_{1}}\mathop = \limits^{{\text{def}}} \frac{{{{{\mathbf{s}}}_{2}} \times {{{\mathbf{s}}}_{3}}}}{{\left\langle {{{{\mathbf{s}}}_{1}},{{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}}} \right\rangle }},\quad {{{\mathbf{s}}}_{1}} = \frac{{{{{\mathbf{n}}}_{2}} \times {{{\mathbf{n}}}_{3}}}}{{\left\langle {{{{\mathbf{n}}}_{1}},{{{\mathbf{n}}}_{2}},{{{\mathbf{n}}}_{3}}} \right\rangle }}\quad \left( {1\;2\;3} \right)$Здесь $\left\langle {{\mathbf{a}},{\mathbf{b}},{\mathbf{c}}} \right\rangle $ – смешанное произведение, $\left\langle {{\mathbf{a}},{\mathbf{b}},{\mathbf{c}}} \right\rangle = \left( {{\mathbf{a}},{\mathbf{b}} \times {\mathbf{c}}} \right)$.
Первая группа равенств (2.17) определяет векторы ${{{\mathbf{n}}}_{i}}$ по заданным векторам ${{{\mathbf{s}}}_{i}}$, вторая группа равенств, выражающая ${{{\mathbf{s}}}_{i}}$ через ${{{\mathbf{n}}}_{i}}$, следует из первой. Допустимые при прецессионном движении положения центров приведения сил существенным образом зависят от параметров ${{\theta }_{i}},{{\varphi }_{i}}$, то есть от взаимного расположения силовых линий полей.
Отметим, что если направления силовых полей и ось прецессии заданы в инерциальном пространстве, то формулы (2.10) задают в теле однопараметрическое множество троек векторов (${{{\mathbf{s}}}_{1}},{{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{3}}$); любая тройка из этого множества отличается от другой поворотом вокруг оси собственного вращения l1. Действительно, при заданных векторах ${{{\mathbf{\alpha }}}_{1}},{{{\mathbf{\alpha }}}_{2}},{{{\mathbf{\alpha }}}_{3}},{\mathbf{\rho }}$ формулы (2.12) определяют углы ${{{{\theta }}}_{i}}$ и разности между углами ${{{{\varphi }}}_{i}}$ и ${{{{\varphi }}}_{j}}$. Формулы (2.17) также определяют множество троек векторов ${{{\mathbf{n}}}_{i}}$, отличающихся одна от другой поворотом вокруг l1.
Для анализа условий, при которых уравнение (2.1) обращается в тождество, запишем явно оператор ${\mathbf{R}}$ как функцию времени
(2.18)
$ - \;\sin \theta \left( {\cos \kappa \tau {{{\mathbf{P}}}_{{2c}}} + \sin \kappa \tau {{{\mathbf{P}}}_{{2s}}} + \cos \tau {{{\mathbf{P}}}_{{1c}}} + \sin \tau {{{\mathbf{P}}}_{{1s}}}} \right) - \cos \theta {{{\mathbf{P}}}_{0}}$У используемых в правой части равенства (2.18) операторов отличны от нуля только следующие элементы их матриц в базисе (li):
(2.19)
$\begin{gathered} p_{{33}}^{{4c}} = - p_{{22}}^{{4c}} = p_{{23}}^{{4s}} = p_{{32}}^{{4s}} = p_{{22}}^{{3c}} = p_{{33}}^{{3c}} = p_{{32}}^{{3s}} = - p_{{23}}^{{3s}} = p_{{13}}^{{2c}} = p_{{12}}^{{2s}} = \\ = p_{{31}}^{{1c}} = p_{{21}}^{{1s}} = p_{{11}}^{0} = 1 \\ \end{gathered} $Здесь, например, $p_{{ij}}^{{4c}} = \left( {{{{\mathbf{l}}}_{i}},{{{\mathbf{P}}}_{{4c}}}{{{\mathbf{l}}}_{j}}} \right)$.
Обозначим через ${\mathbf{L}}$ левую часть равенства (2.1) и, используя формулу (2.6) для угловой скорости, получим
(2.20)
${{{\mathbf{L}}}_{{1c}}} = {{{{\Omega }}}^{2}}\left( {\left( {2 + \kappa \cos \theta } \right){{{\mathbf{l}}}_{1}} \times {\mathbf{I}}{{{\mathbf{l}}}_{3}} + \kappa \cos \theta {{{\mathbf{l}}}_{3}} \times {\mathbf{I}}{{{\mathbf{l}}}_{1}} + {{{\mathbf{l}}}_{2}}\operatorname{tr} {\mathbf{I}}} \right) + {{\Omega }}{{{\mathbf{l}}}_{3}} \times {\mathbf{\sigma }}$После нахождения конфигурации, допускающей регулярную прецессию, для описания движения тела в инерциальном пространстве используем формулу
(2.21)
${{{\mathbf{l}}}_{q}} = - {{{\mathbf{\alpha }}}_{1}}\,\mathop \sum \limits_i \,n_{1}^{{\left( i \right)}}{{r}_{{qi}}} - {{{\mathbf{\alpha }}}_{2}}\,\mathop \sum \limits_i \,n_{2}^{{\left( i \right)}}{{r}_{{qi}}} - {{{\mathbf{\alpha }}}_{3}}\,\mathop \sum \limits_i \,n_{3}^{{\left( i \right)}}{{r}_{{qi}}}{\text{\;}};\quad q = 1,2,3$Для проверки данной формулы подставим в правую часть выражения ${{{\mathbf{\alpha }}}_{i}}$ и $n_{j}^{{\left( i \right)}}$ из формул (2.9) и (2.17), правая часть запишется в виде ${\mathbf{R}}{{{\mathbf{R}}}^{T}}{{{\mathbf{l}}}_{q}}$, где ${\mathbf{R}}{{{\mathbf{R}}}^{T}} = {\mathbf{E}}$.
Функции ${{r}_{{ij}}}\left( t \right)$ заданы равенствами (2.11). Формулы (2.21) задают движение связанного с телом базиса $\left( {{{{\mathbf{l}}}_{i}}} \right)$ в инерциальном пространстве и, следовательно, позволяют описать в явном виде движение каждой точки тела.
Отметим следующее. Векторы ${{{\mathbf{\beta }}}_{i}} = {\mathbf{R}}{{{\mathbf{l}}}_{i}}$ постоянны в инерциальной системе отсчета. Из формулы (2.14) следует, что суммарное действие трех полей с неортогональными силовыми линиями при регулярной прецессии может быть интерпретировано, как действие трех взаимно ортогональных полей с направлениями ${{{\mathbf{\beta }}}_{1}},{{{\mathbf{\beta }}}_{2}},{{{\mathbf{\beta }}}_{3}}$.
Покажем теперь, что регулярная прецессия в трех независимых полях при $\left| \kappa \right| \ne 1$, $\left| \kappa \right| \ne 2$ невозможна. Действительно, пусть ${{\kappa }} > 0$, тогда суммарный момент ${\mathbf{M}}$, заданный формулой (2.14), не должен содержать слагаемые с $\cos \left( {\kappa + 1} \right)\tau $, $\sin \left( {\kappa + 1} \right)\tau $, $\cos \kappa \tau $, $\sin \kappa \tau $, так как левая часть уравнения (2.1), заданная формулами (2.20), таких слагаемых не содержит. Учитывая равенства (2.18), получаем следующие условия
(2.22)
${{{\mathbf{v}}}_{1}} \times {\mathbf{P}}{{{\mathbf{l}}}_{1}} + {{{\mathbf{v}}}_{2}} \times {\mathbf{P}}{{{\mathbf{l}}}_{2}} + {{{\mathbf{v}}}_{3}} \times {\mathbf{P}}{{{\mathbf{l}}}_{3}} = 0,$Учитывая формулы (2.19), условия (2.22) запишем в виде
(2.23)
${{{\mathbf{v}}}_{2}} \times {{l}_{2}} - {{{\mathbf{v}}}_{3}} \times {{l}_{3}} = 0,\quad {{{\mathbf{v}}}_{2}} \times {{l}_{3}} + {{{\mathbf{v}}}_{3}} \times {{l}_{2}} = 0$Эти условия могут быть выполнены, только если ${{{\mathbf{v}}}_{2}} = {{{\mathbf{v}}}_{3}} = 0$. В этом случае из формулы (2.16) следует, что векторы ${{{\mathbf{u}}}_{i}}$ коллинеарны вектору ${{{\mathbf{v}}}_{1}}$ и система полей приводима к одному полю.
Таким образом, регулярная прецессия в трех независимых полях может быть возможна, только если скорость прецессии равна скорости собственного вращения или вдвое больше скорости собственного вращения. Примеры прецессий в случае $\kappa = 1$ приведены в работах [21, 22]. Возможность регулярной прецессии в случае $\kappa = 2$ впервые указана в настоящей работе. Рассмотрим эти случаи по отдельности.
3. Конфигурационные условия прецессии при равных скоростях прецессии и собственного вращения. Сравнивая при $\kappa = 1$ коэффициенты при соответствующих гармониках в уравнении (2.1), получим, учитывая равенства (2.14), (2.18) и (2.20), что равенство ${\mathbf{L}} = {\mathbf{M}}$ тождественно выполнено, только если
Учитывая равенства (2.19) и (2.20), эти условия запишем при $\kappa = 1$ в виде
(3.1)
$\begin{gathered} = {{{\mathbf{l}}}_{3}} \times {{{\mathbf{v}}}_{1}} + {{{\mathbf{l}}}_{1}} \times {{{\mathbf{v}}}_{3}} \\ {{{{\Omega }}}^{2}}\left( {\left( {2 + \cos \theta } \right){{{\mathbf{l}}}_{1}} \times {\mathbf{I}}{{{\mathbf{l}}}_{2}} + \cos {{\theta }}{{{\mathbf{l}}}_{2}} \times {\mathbf{I}}{{{\mathbf{l}}}_{1}} - {{{\mathbf{l}}}_{3}}\operatorname{tr} {\mathbf{I}}} \right) + {{\Omega }}{{{\mathbf{l}}}_{2}} \times {\mathbf{\sigma }} = ~ \\ \end{gathered} $Перейдем к векторным параметрам ${{{\mathbf{w}}}_{i}}$ по формулам
(3.2)
$\begin{gathered} {{{\mathbf{v}}}_{1}} = {{{\mathbf{w}}}_{1}} + {{\Omega }^{2}}\cos \theta {\mathbf{I}}{{{\mathbf{l}}}_{1}} + {{\Omega }}{\mathbf{\sigma }} \\ {{{\mathbf{v}}}_{2}} = {{{\mathbf{w}}}_{2}} + {{{{\Omega }}}^{2}}\left( {\cos \theta - 1} \right){\mathbf{I}}{{{\mathbf{l}}}_{2}},\quad {{{\mathbf{v}}}_{3}} = {{{\mathbf{w}}}_{3}} + {{{{\Omega }}}^{2}}\left( {\cos \theta - 1} \right){\mathbf{I}}{{{\mathbf{l}}}_{3}} \\ \end{gathered} $Условия (3.1) преобразуются к виду
(3.3)
${{{\mathbf{w}}}_{2}} \times {{{\mathbf{l}}}_{2}} - {{{\mathbf{w}}}_{3}} \times {{{\mathbf{l}}}_{3}} = 0,\quad {{{\mathbf{w}}}_{2}} \times {{{\mathbf{l}}}_{3}} + {{{\mathbf{w}}}_{3}} \times {{{\mathbf{l}}}_{2}} = 0$(3.4)
$\begin{gathered} {{{{\Omega }}}^{2}}(3{{{\mathbf{l}}}_{1}} \times {\mathbf{I}}{{{\mathbf{l}}}_{3}} + {{{\mathbf{l}}}_{2}}\operatorname{tr} {\mathbf{I}}) = {{{\mathbf{l}}}_{3}} \times {{{\mathbf{w}}}_{1}} + {{{\mathbf{l}}}_{1}} \times {{{\mathbf{w}}}_{3}} \\ {{{{\Omega }}}^{2}}\left( {3{{{\mathbf{l}}}_{1}} \times {\mathbf{I}}{{{\mathbf{l}}}_{2}} - {{{\mathbf{l}}}_{3}}\operatorname{tr} {\mathbf{I}}} \right) = {{{\mathbf{l}}}_{2}} \times {{{\mathbf{w}}}_{1}} + {{{\mathbf{l}}}_{1}} \times {{{\mathbf{w}}}_{2}} \\ \end{gathered} $(3.5)
${{\Omega }^{2}}3\cos \theta {{{\mathbf{l}}}_{1}} \times {\mathbf{I}}{{{\mathbf{l}}}_{1}} + {{\Omega }}{{{\mathbf{l}}}_{1}} \times {\mathbf{\sigma }} = \cos \theta {{{\mathbf{l}}}_{1}} \times {{{\mathbf{w}}}_{1}} + \frac{{1 - \cos \theta }}{2}\left( {{{{\mathbf{l}}}_{2}} \times {{{\mathbf{w}}}_{2}} + {{{\mathbf{l}}}_{3}} \times {{{\mathbf{w}}}_{3}}} \right)$Условия (3.3) выполнены, только если справедливы равенства
(3.6)
${{{\mathbf{w}}}_{2}} = \mu {{{\mathbf{l}}}_{2}} + \nu {{{\mathbf{l}}}_{3}},\quad {{{\mathbf{w}}}_{3}} = - \nu {{{\mathbf{l}}}_{2}} + \mu {{{\mathbf{l}}}_{3}}$Условия (3.4) с учетом формул (3.6) записываются в виде
Координатная форма этих условий следующая
Отсюда получаем
(3.8)
$w_{1}^{{\left( 1 \right)}} - {{\mu }} = {{{{\Omega }}}^{2}}\left( {{{I}_{{11}}} - {{I}_{{22}}}} \right),\quad {{\nu }} = 0,\quad {{{\mathbf{w}}}_{1}} = w_{1}^{{\left( 1 \right)}}{{{\mathbf{l}}}_{1}}$Из равенств (3.6), (3.8) находим векторы ${{{\mathbf{w}}}_{i}}$
(3.9)
${{{\mathbf{w}}}_{1}} = \left( {\mu + {{\Omega }^{2}}\left( {{{I}_{{11}}} - {{I}_{{22}}}} \right)} \right){{{\mathbf{l}}}_{1}},\quad {{{\mathbf{w}}}_{2}} = {{\mu }}{{{\mathbf{l}}}_{2}},\quad {{{\mathbf{w}}}_{3}} = {{\mu }}{{{\mathbf{l}}}_{3}}$Условие (3.5) принимает вид
Это условие эквивалентно системе двух условий
(3.10)
${{\sigma }^{{\left( 2 \right)}}} = - 3\Omega \cos \theta {{I}_{{12}}},\quad {{\sigma }^{{\left( 3 \right)}}} = - 3\Omega \cos \theta {{I}_{{13}}}$Таким образом, для того чтобы уравнение (2.1) обратилось в тождество, необходимо и достаточно, чтобы были выполнены условия (3.7), функции ${{{\mathbf{w}}}_{i}}$ были заданы формулами (3.9), где ${{\mu }}$ – некоторый скалярный параметр и компоненты гиростатического момента определялись по формулам (3.10).
Известно (см. п. 6), что условия (3.7) означают ортогональность вектора ${{{\mathbf{l}}}_{1}} = {\mathbf{m}}$ круговому сечению эллипсоида инерции и, следовательно, при их выполнении ось собственного вращения ортогональна данному сечению. В случае Гриоли [12] на данной оси находится и центр тяжести тела. В рассмотренном в статье общем случае прецессии нахождение какого-то из центров приведения сил на оси собственного вращения не является обязательным.
Векторные параметры ${{{\mathbf{v}}}_{i}}$ выражаются через ${{{\mathbf{w}}}_{i}}$ по формулам (3.2):
(3.11)
$\begin{gathered} {{{\mathbf{v}}}_{1}} = \left( {{{\mu }} + {{{{\Omega }}}^{2}}\left( {{{I}_{{11}}} - {{I}_{{22}}}} \right)} \right){{{\mathbf{l}}}_{1}} + {{{{\Omega }}}^{2}}\cos \theta {\mathbf{I}}{{{\mathbf{l}}}_{1}} + {{\Omega }}{\mathbf{\sigma }} \\ {{{\mathbf{v}}}_{2}} = {{\mu }}{{{\mathbf{l}}}_{2}} + {{{{\Omega }}}^{2}}\left( {\cos \theta - 1} \right){\mathbf{I}}{{{\mathbf{l}}}_{2}},\quad {{{\mathbf{v}}}_{3}} = {{\mu }}{{{\mathbf{l}}}_{3}} + {{{{\Omega }}}^{2}}\left( {\cos \theta - 1} \right){\mathbf{I}}{{{\mathbf{l}}}_{3}} \\ \end{gathered} $Учитывая формулы (2.16), теперь получим запись допустимых векторов ${{{\mathbf{u}}}_{i}}$ $\left( {i = 1,2,3} \right)$ в виде
(3.12)
${{{\mathbf{u}}}_{i}} = {{\mu }}{{{\mathbf{n}}}_{i}} + {{{{\Omega }}}^{2}}\left( {\cos \theta - 1} \right){\mathbf{I}}{{{\mathbf{n}}}_{i}} + n_{i}^{{\left( 1 \right)}}\Omega ({\mathbf{\sigma }} + {{\Omega }}\left( {{\mathbf{I}}{{{\mathbf{l}}}_{1}} + \left( {{{I}_{{11}}} - {{I}_{{22}}}} \right){{{\mathbf{l}}}_{1}}} \right)$4. Конфигурационные условия прецессии при скорости прецессии вдвое большей скорости собственного вращения. В случае κ = 2 суммарный момент ${\mathbf{M}}$ не должен содержать слагаемые с $\cos 3\tau $, $\sin 3\tau $ (они отсутствуют в левой части ${\mathbf{L}}$ уравнения (2.1)). Учитывая формулы (2.14) и (2.18), получим, что указанные слагаемые отсутствуют, если выполнены условия (2.22) при ${\mathbf{P}} = {{{\mathbf{P}}}_{{4c}}}$ и ${\mathbf{P}} = {{{\mathbf{P}}}_{{4s}}}$, что снова приводит к условиям (2.24).
При выполнении условий (2.24) равенство ${\mathbf{M}} = {\mathbf{L}}$ тождественно выполнено, только если
(4.1)
$\begin{gathered} 2\sin \theta {{{\mathbf{L}}}_{{2c}}} = - \sum {{{{\mathbf{v}}}_{i}}} \times {{{\mathbf{P}}}_{{2c}}}{{{\mathbf{l}}}_{i}},\quad 2\sin \theta {{{\mathbf{L}}}_{{2s}}} = - \sum {{{{\mathbf{v}}}_{i}}} \times {{{\mathbf{P}}}_{{2s}}}{{{\mathbf{l}}}_{i}} \\ 2\sin \theta {{{\mathbf{L}}}_{{1c}}} = \sum {{{{\mathbf{v}}}_{i}}} \times {\mathbf{P}}_{{3c}}^{'}{{{\mathbf{l}}}_{i}},\quad 2\sin \theta {{{\mathbf{L}}}_{{1s}}} = \sum {{{{\mathbf{v}}}_{i}}} \times {\mathbf{P}}_{{3s}}^{'}{{{\mathbf{l}}}_{i}},\quad {{{\mathbf{L}}}_{0}} = - ~\cos \theta \sum {{{{\mathbf{v}}}_{i}}} \times {{{\mathbf{P}}}_{0}}{{{\mathbf{l}}}_{i}} \\ \end{gathered} $Здесь
Условия (4.1) при учете равенств (2.19) и (2.20) принимают вид
(4.2)
$ = \frac{{\cos \theta - 1}}{2}\left( {{{{\mathbf{v}}}_{2}} \times {{{\mathbf{l}}}_{2}} + {{{\mathbf{v}}}_{3}} \times {{{\mathbf{l}}}_{3}}} \right) - \sin \theta {{{\mathbf{v}}}_{1}} \times {{{\mathbf{l}}}_{3}}$Из условий (2.24) следует, что векторы ${{{\mathbf{v}}}_{2}},{{{\mathbf{v}}}_{3}}$ можно представить в виде
(4.3)
${{{\mathbf{v}}}_{2}} = {{{{\xi }}}_{3}}{{{\mathbf{l}}}_{2}} + {{{{\xi }}}_{2}}{{{\mathbf{l}}}_{3}},\quad {{{\mathbf{v}}}_{3}} = - {{{{\xi }}}_{2}}{{{\mathbf{l}}}_{2}} + {{{{\xi }}}_{3}}{{{\mathbf{l}}}_{3}}$Записывая, при учете формул (4.3), систему (4.2) в проекциях на ${{{\mathbf{l}}}_{i}}$, получим систему, состоящую из условий (3.7) и следующих условий ($j = 2,3$)
(4.5)
$2\Omega \sin \theta \left( {2\Omega \cos \theta {{I}_{{1j}}} + {{\sigma }^{{\left( j \right)}}}} \right) = - \left( {1 - \cos \theta } \right){{\xi }_{j}} + \sin \theta {v}_{1}^{{\left( j \right)}}$(4.6)
${{\Omega }^{2}}({{\left( {1 + 2\cos \theta } \right)}^{2}} - 2{{\sin }^{2}}\theta ){{I}_{{1j}}} + \Omega \left( {1 + 2\cos \theta } \right){{\sigma }^{{\left( j \right)}}} = \cos \theta {v}_{1}^{{\left( j \right)}}$(4.7)
$2{{\Omega }^{2}}\left( {\left( {1 + 2\cos \theta } \right){{I}_{{11}}} - 2\cos \theta {{I}_{{22}}}} \right) + 2\Omega {{\sigma }^{{\left( 1 \right)}}} = {v}_{1}^{{\left( 1 \right)}}$Условия (4.5), после подстановки ${{{{\xi }}}_{j}}$ из формул (4.4), преобразуем к виду
(4.8)
${{\Omega }^{2}}\left( {6\cos \theta - 2} \right){{I}_{{1j}}} + 2\Omega {{\sigma }^{{\left( j \right)}}} = {v}_{1}^{{\left( j \right)}};\quad j = 2,3$Подставляя отсюда ${v}_{1}^{{\left( j \right)}}$ в равенства (4.6), получим
(4.9)
${{\sigma }^{{\left( j \right)}}} = \Omega \left( {1 - 6\cos \theta } \right){{I}_{{1j}}};\quad j = 2,3$Из формул (4.8) и (4.9) следует
Из равенств (4.3), (4.4), (4.7) и (4.8) находим
(4.11)
$\begin{gathered} {{{\mathbf{v}}}_{1}} = 2{{\Omega }}{\mathbf{\sigma }} + {{{{\Omega }}}^{2}}\left( {2\left( {3\cos \theta - 1} \right){\mathbf{I}}{{{\mathbf{l}}}_{1}} + 2\left( {\left( {2 - \cos \theta } \right){{I}_{{11}}} - 2\cos \theta {{I}_{{22}}}} \right){{{\mathbf{l}}}_{1}}} \right) \\ {{{\mathbf{v}}}_{2}} = - 2{{{{\Omega }}}^{2}}\sin \theta \left( {{{I}_{{13}}}{{{\mathbf{l}}}_{2}} + {{I}_{{12}}}{{{\mathbf{l}}}_{3}}} \right),\quad {{{\mathbf{v}}}_{3}} = 2{{\Omega }^{2}}\sin \theta \left( {{{I}_{{12}}}{{{\mathbf{l}}}_{2}} - {{I}_{{13}}}{{{\mathbf{l}}}_{3}}} \right) \\ \end{gathered} $Таким образом, имеем условия (3.7) и (4.9). Множество векторов ${{{\mathbf{u}}}_{i}}$ задается формулами (2.16) и (4.11).
5. Прецессия твердого тела. В случае, когда гиростатический момент равен нулю, получим условия прецессии твердого тела. Эти условия мало отличаются от случая, когда гиростатический момент коллинеарен оси собственного вращения, поэтому рассмотрим оба случая совместно. Пусть
Условия (3.7) остаются необходимыми.
Случай κ = 1. Имеется две возможности выполнения условий (3.10):
a) $\cos \theta = 0$, ось собственного вращения ортогональна оси прецессии;
b) ${{I}_{{12}}} = {{I}_{{13}}} = 0$, эллипсоид инерции имеет осевую симметрию, ось симметрии является осью собственного вращения.
В первом случае формулы (3.12), задающие допустимое множество векторов ${{{\mathbf{u}}}_{i}}$ $\left( {i = 1,2,3} \right)$, записываются в виде
(5.2)
${{{\mathbf{u}}}_{i}} = {{\mu }}{{{\mathbf{n}}}_{i}} - {{{{\Omega }}}^{2}}{\mathbf{I}}{{{\mathbf{n}}}_{i}} + n_{i}^{{\left( 1 \right)}}\left( {{{{{\Omega }}}^{2}}\left( {{\mathbf{I}}{{{\mathbf{l}}}_{1}} + \left( {{{I}_{{11}}} - {{I}_{{22}}}} \right)} \right){{{\mathbf{l}}}_{1}}} \right) + {{\Omega }}{{{{\sigma }}}^{{\left( 1 \right)}}}{{{\mathbf{l}}}_{1}})$Во втором случае, учитывая условия (3.7) получим, что li – собственные векторы оператора инерции и l1 – ось симметрии. Обозначив
из формул (3.11) получимДопустимое множество векторов ${{{\mathbf{u}}}_{i}}$ записывается, при учете формул (2.16), в виде
(5.3)
${{{\mathbf{u}}}_{i}} = {{\tilde {\mu }}}{{{\mathbf{n}}}_{i}} + n_{i}^{{\left( 1 \right)}}\left( {\Omega {{\sigma }^{{\left( 1 \right)}}} + {{\Omega }^{2}}\left( {\left( {1 + \cos \theta } \right){{I}_{1}} - \cos \theta {{I}_{2}}} \right)} \right){{{\mathbf{l}}}_{1}};\quad i = 1,2,3$Случай κ = 2. Условия (5.1) и (4.9) могут быть выполнены, только если
Иначе ${{I}_{{12}}} = {{I}_{{13}}} = 0$ и три поля приводятся к одному полю.
Таким образом, регулярная прецессия в суперпозиции трех независимых полей твердого тела или гиростата, гиростатический момент которого направлен по оси собственного вращения, в случае, когда скорость прецессии в два раза больше скорости собственного вращения, возможна, только если косинус угла между осями прецессии и собственного вращения равен одной шестой.
Из формул (2.16) и (4.11) находим допустимое множество векторов ${{{\mathbf{u}}}_{i}}$
(5.5)
$\begin{gathered} {{{\mathbf{u}}}_{i}} = 2\Omega {{\sigma }^{{\left( 1 \right)}}}n_{i}^{{\left( 1 \right)}}{{{\mathbf{l}}}_{1}} + {{{{\Omega }}}^{2}}\left( {n_{i}^{{\left( 1 \right)}}\left( {\frac{2}{3}\left( {4{{I}_{{11}}} - {{I}_{{22}}}} \right){{{\mathbf{l}}}_{1}} - {{I}_{{12}}}{{{\mathbf{l}}}_{2}} - {{I}_{{13}}}{{{\mathbf{l}}}_{3}}} \right)} \right. + \\ \left. {^{{^{{^{{}}}}}} + \;2\sin \theta \left( {n_{i}^{{\left( 2 \right)}}\left( {{{I}_{{13}}}{{{\mathbf{l}}}_{2}} - {{I}_{{12}}}{{{\mathbf{l}}}_{3}}} \right) - n_{i}^{{\left( 3 \right)}}\left( {{{I}_{{12}}}{{{\mathbf{l}}}_{2}} + {{I}_{{13}}}{{{\mathbf{l}}}_{3}}} \right)} \right)} \right);\quad i = 1,2,3 \\ \end{gathered} $Угол ${{\theta }}$ задан равенством (5.4).
В случае твердого тела в формуле (5.5) следует положить ${{{{\sigma }}}^{{\left( 1 \right)}}} = 0$.
Замечание. В рассмотренном выше случае κ = 1 векторы ${{{\mathbf{u}}}_{i}}$ включают в себя слагаемые ${{\mu }}{{{\mathbf{n}}}_{i}}$ (формулы (3.12), (5.2), (5.3)), содержащие произвольный параметр ${{\mu }}$. Получаем, что при заданных в инерциальном пространстве направлениях ${{{\mathbf{\alpha }}}_{i}}$ силовых линий постоянных полей, заданном расположении оси прецессии ${\mathbf{\rho }}$ относительно этих линий, заданном тензоре инерции твердого тела существуют различные расположения центров приведения сил и различные величины сил, для которых прецессионное движение будет совпадающим (при одинаковых начальных условиях).
Данное свойство обусловлено тем, что оператор поворота ${\mathbf{R}}$, заданный формулами (2.11), при κ = 1 является симметрическим. Момент внешних сил можно задать формулой (2.14), где векторы ${{{\mathbf{v}}}_{i}}$, в соответствии с формулой (3.11), содержат слагаемые ${{\mu }}{{{\mathbf{l}}}_{i}}$. Эти слагаемые не вносят вклад в суммарный момент, так как при любом симметрическом операторе ${\mathbf{R}}$ имеем
В случае κ = 2 оператор ${\mathbf{R}}\left( t \right)$ не является симметрическим и аналогичное свойство отсутствует.
6. Частный случай: регулярная прецессия в суперпозиции трех ортогональных полей. Пусть векторы ${{{\mathbf{\alpha }}}_{i}}$, задающие направления силовых линий полей, образуют правую ортонормированную тройку. В соответствии с формулами (2.9) векторы ${{{\mathbf{s}}}_{i}}$ тогда образуют левую ортонормированную тройку, при этом
Из формул (2.17) получаем
Таким образом, формула (2.10) определяет векторы ${{{\mathbf{n}}}_{i}}$, присутствующие в формулах (2.16), которые задают множества допустимых векторов ${{{\mathbf{u}}}_{i}}$.
Как было отмечено выше, в п. 2, при заданном положении оси прецессии относительно силовых линий полей можно определить все параметры ${{{{\theta }}}_{i}}$ и только разности между параметрами ${{{{\varphi }}}_{i}}$ (но не сами эти параметры). При этом формула (2.10) определяет тройку векторов (${{{\mathbf{s}}}_{i}}$) с точностью до произвольного поворота вокруг оси l1.
Параметры ${{{{\theta }}}_{i}}$ – это углы вектора ${\mathbf{\rho }}$ с осями ${{{\mathbf{\alpha }}}_{i}}$; приведем явные формулы для разностей ${{{{\varphi }}}_{i}} - {{{{\varphi }}}_{j}}$.
В случае ортогонального базиса имеем формулу
и из формул (2.13) также следуют условияДанные условия при $\sin {{\theta }_{1}}\sin {{\theta }_{2}}\sin {{\theta }_{3}} \ne 0$ приводят к формулам
(6.2)
$\cos \left( {{{\varphi }_{1}} - {{\varphi }_{2}}} \right) = - \frac{{\cos {{\theta }_{1}}\cos {{\theta }_{2}}}}{{\sin {{\theta }_{1}}\sin {{\theta }_{2}}}},\quad \sin \left( {{{\varphi }_{1}} - {{\varphi }_{2}}} \right) = \frac{{\cos {{\theta }_{3}}}}{{\sin {{\theta }_{1}}\sin {{\theta }_{2}}}}\quad \left( {1\;2\;3} \right)$Если $\sin {{\theta }_{i}} = 0$, то ${\mathbf{\rho }} = {{{\mathbf{\alpha }}}_{i}}$; этот случай рассмотрен ниже.
Обозначим ${{{{\varphi }}}_{2}} = {{\varepsilon }}$ и используем очевидные формулы
Из формул (2.10), (6.1) и (6.2) получаем
(6.3)
${{{\mathbf{n}}}_{2}} = \cos {{\theta }_{2}}{{{\mathbf{l}}}_{1}} + \sin {{\theta }_{2}}{\mathbf{l}}_{2}^{'},\quad {\mathbf{l}}_{2}^{'} = \cos \varepsilon {{{\mathbf{l}}}_{2}} + \sin \varepsilon {{{\mathbf{l}}}_{3}},\quad {\mathbf{l}}_{3}^{'} = {{{\mathbf{l}}}_{1}} \times {\mathbf{l}}_{2}^{'}$Для рассматриваемого случая трех ортогональных полей выделим частный случай, когда ось прецессии ортогональна силовым линиям одного из полей. Пусть, например, $\left( {{\mathbf{\rho }},{{{\mathbf{\alpha }}}_{2}}} \right) = 0$. В соответствии с формулами (2.9) получим $\left( {{{{\mathbf{l}}}_{1}},{{{\mathbf{s}}}_{2}}} \right)$ = 0. Учитывая равенства (6.1) и (6.3), получим $\cos {{\theta }_{2}}$ = 0. Положим
Формулы (6.3) примут вид
(6.4)
${{{\mathbf{n}}}_{1}} = \cos \beta {{{\mathbf{l}}}_{1}} + \sin \beta {\mathbf{l}}_{3}^{'},\quad {{{\mathbf{n}}}_{2}} = {\mathbf{l}}_{2}^{'},\quad {{{\mathbf{n}}}_{3}} = \sin \beta {{{\mathbf{l}}}_{1}} - \cos \beta {\mathbf{l}}_{3}^{'}$При ${{\beta }} = {{\pi /}}2$ получим ${\mathbf{\rho }} = {{{\mathbf{\alpha }}}_{3}}$, при ${{\beta }} = 0$ – ${\mathbf{\rho }} = {{{\mathbf{\alpha }}}_{1}}$ и, если ось прецессии коллинеарна силовым линиям ${{{\mathbf{\alpha }}}_{1}}$, векторы ${{{\mathbf{n}}}_{i}}$ имеют вид
(6.5)
${{{\mathbf{n}}}_{1}} = {{{\mathbf{l}}}_{1}},\quad {{{\mathbf{n}}}_{2}} = {\mathbf{l}}_{2}^{'},\quad {{{\mathbf{n}}}_{3}} = - {\mathbf{l}}_{3}^{'}$Эти равенства получены с использованием формул (6.2), то есть при $\sin {{\theta }_{i}} \ne 0$. Нахождение ${{{\mathbf{n}}}_{i}}$ непосредственно из формул (2.10) и (6.1) при ${{\theta }_{1}} = 0$, ${{\theta }_{2}} = {{\theta }_{3}} = \pi {\text{/}}2$, ${{\varphi }_{2}} = \varepsilon $, ${{\varphi }_{3}} = \varepsilon - \pi {\text{/}}2$ приводит снова к формулам (6.5).
Перейдем теперь к записи полученных условий в главных осях инерции. Обозначим ${{I}_{i}}$, ${{{\mathbf{e}}}_{i}}$ собственные значения и собственные векторы оператора инерции ${\mathbf{I}}$. При условиях (3.7) одним из собственных значений является ${{\lambda }} = {{I}_{{22}}} = {{I}_{{33}}}$ и соответствующий этому значению собственный вектор ортогонален l1. Пронумеруем собственные значения Ik оператора ${\mathbf{I}}$ так, что
Используемый выше ортобазис $\left( {{{{\mathbf{l}}}_{i}}} \right)$ ограничен только условием ${{{\mathbf{l}}}_{1}} = {\mathbf{m}}$. Учитывая, что ${{{\mathbf{e}}}_{2}} \bot {{{\mathbf{l}}}_{1}}$, можно выбрать базис $\left( {{{{\mathbf{l}}}_{i}}} \right)$ такой, что
(6.7)
${{{\mathbf{l}}}_{1}} = {\mathbf{m}},\quad {{{\mathbf{l}}}_{2}} = {{{\mathbf{e}}}_{2}},\quad {{{\mathbf{l}}}_{3}} = {\mathbf{m}} \times {{{\mathbf{e}}}_{2}}$Вектор ${\mathbf{m}}$ можно представить в виде
Если $\left( {{{I}_{2}} - {{I}_{1}}} \right)\left( {{{I}_{3}} - {{I}_{2}}} \right) \geqslant 0$, то ${{{\mathbf{e}}}_{2}}$ – средняя ось эллипсоида инерции и ${\mathbf{m}}$ – нормаль одного из круговых сечений эллипсоида. Справедливы формулы
(6.9)
${{I}_{{12}}} = {{I}_{{23}}} = 0,\quad {{I}_{{13}}} = \left( {{{I}_{3}} - {{I}_{1}}} \right)\sin \xi \cos \xi ,\quad {{I}_{{11}}} = {{I}_{1}} + {{I}_{3}} - {{I}_{2}}$Для сравнения с известными результатами [21, 22] приведенные выше при κ = 1 формулы (3.12) запишем для случая, когда ось прецессии коллинеарна силовым линиям поля ${{{\mathbf{\alpha }}}_{1}}$. Учитывая формулы (6.5), где ${\mathbf{l}}_{2}^{'},{\mathbf{l}}_{3}^{'}$ заданы формулами (6.3), получим
(6.10)
${{{\mathbf{u}}}_{2}} = {{\mu }}\left( {\cos \varepsilon {{{\mathbf{l}}}_{2}} + \sin \varepsilon {{{\mathbf{l}}}_{3}}} \right) + {{{{\Omega }}}^{2}}\left( {\cos \theta - 1} \right){\mathbf{I}}\left( {\cos \varepsilon {{{\mathbf{l}}}_{2}} + \sin \varepsilon {{{\mathbf{l}}}_{3}}} \right)$Выделим случай прецессии твердого тела или гиростата с гиростатическим моментом, коллинеарным оси собственного вращения. Полагая $\cos \theta = 0$, формулы (6.10) запишем в виде
Если здесь положить ${{\varepsilon }} = {{\pi }}$ и выполнить замену индексов $\left( {123} \right) \mapsto \left( {321} \right)$, то получим пример Яхья [21]. В этом случае ${{{\mathbf{u}}}_{2}}||{{{\mathbf{l}}}_{2}}$, ${{{\mathbf{l}}}_{2}} = {{{\mathbf{e}}}_{2}}$ и центр приведения сил поля ${{{\mathbf{\alpha }}}_{2}}$ лежит на средней оси эллипсоида инерции.
Таким образом, из возможных случаев регулярной прецессии твердого тела с гиростатом в суперпозиции трех полей решение Яхья [21] выделяет частный случай, заданный следующими условиями:
1) силовые линии трех полей взаимно ортогональны, $({{{\mathbf{\alpha }}}_{i}},{{{\mathbf{\alpha }}}_{j}}) = 0$, $i \ne j$;
2) ось прецессии коллинеарна силовым линиям одного из полей, ${\mathbf{\rho }}||{{{\mathbf{\alpha }}}_{1}}$;
3) ось собственного вращения перпендикулярна оси прецессии, $\left( {{\mathbf{m}},{\mathbf{\rho }}} \right) = 0$;
4) скорость собственного вращения равна скорости прецессии, κ = 1;
5) гиростатический момент ортогонален плоскости кругового сечения эллипсоида инерции твердого тела, ${\mathbf{\sigma }}||{\mathbf{m}}$;
6) центр приведения сил одного из полей лежит на средней оси эллипсоида инерции, ${{{\mathbf{u}}}_{2}}||{{{\mathbf{e}}}_{2}}$.
Как показано выше, каждое из этих условий не является обязательным.
В работе [22] рассмотрена возможность прецессии гиростата (с одинаковыми скоростями прецессии и собственного вращения) в трех полях, два из которых однородные, и выделен частный случай, когда третье поле тоже однородное. Выполненная нами проверка показывает, что условия прецессии [22] в трех однородных полях могут быть записаны в виде (6.10) при ${{\varepsilon }} = {{\pi }}$. Таким образом, решение [22] выделяет частный случай, заданный приведенными выше условиями 1, 2, 4, 6.
Заключение. Решение задачи о вращении твердого тела (гиростата) в суперпозиции нескольких полей важно при конструировании различных приборов навигации и управления. Во многих режимах работы таких устройств удобно использовать регулярную прецессию, как в классическом случае движения в поле тяжести. Возможность регулярной прецессии несимметричного твердого тела и гиростата в суперпозиции двух и трех полей была показана Яхья [20, 21], который привел примеры для случая, когда скорости прецессии и собственного вращения совпадают и оси прецессии и собственного вращения перпендикулярны. В настоящей работе описаны все возможные случаи регулярной прецессии при вращении гиростата вокруг неподвижной точки под действием трех независимых однородных полей. Случай двух полей должен быть рассмотрен отдельно. Конфигурационные условия прецессии получены без предположения о взаимной ортогональности полей. Получено обобщение условий Яхья. Показано, что регулярная прецессия несимметричного твердого тела и гиростата возможна и когда скорость прецессии вдвое больше скорости собственного вращения. Выделен случай, когда ось прецессии коллинеарна силовым линиям одного из полей.
Список литературы
Bogoyavlensky O.I. Euler equations on finite dimensional Lie algebras arising in physical problems // Math. Phys. Commun. 1984. V. 95. P. 307–315.
Yehia H. New integrable cases in the dynamics of rigid bodies // Mech. Res. Commun. 1986. V. 13. Iss. 3. P. 169–172.
Yehia H.M. New integrable problems in the dynamics of rigid bodies with the Kovalevskaya configuration. II – The case of asymmetric forces // Mech. Res. Commun. 1996. V. 23. Iss. 5. P. 429–431.
Kharlamov M.P. Bifurcation diagrams of the Kowalevski top in two constant fields // Reg. Chaot. Dyn. 2005. V. 10. Iss. 4. P. 381–398.
Kharlamov M.P. Periodic motions of the Kowalevski gyrostat in two constant fields // J. Phys. A. 2008. V. 41. Iss. 27.
Elmandouh A.A. On the stability of the permanent rotations of a charged rigid body-gyrostat // Acta Mech. 2017. V. 228. P. 3947–3959.
Elmandouh A.A., Ibrahim A.G. Hamiltonian structure, equilibria, and stability for an axisymmetric gyrostat motion in the presence of gravity and magnetic fields // Acta Mech. 2019. V. 230. P. 2539–2548.
Kharlamov M.P., Ryabov P.E. Topological atlas of the kovalevskaya top in a double field // J. Math. Sci. 2017. V. 233. P. 775–809.
Yehia H.M., Saleh E., Megahid S.F. New solutions of classical problems in rigid body dynamics // Mech. Res. Commun. 2015. V. 69. P. 40–44.
Elmandouh A.A. On the stability of certain motions of a rigid body-gyrostat in an incompressible ideal fluid // Int. J. Non-lin. Mech. 2020. V. 120. Art. no. 103419.
Goldstein H. Classical Mechanics. Addison – Wesley. 1951.
Grioli G. Esistenza e determinazione delle prezessioni regolari dinamicamente possibili per un solido pesante asimmetrico // Ann. mat. pura e appl. 1947. V. 26. Iss. 3–4. P. 271–281.
Рубановский В.Н. Об одном новом частном решении уравнений движения тяжелого твердого тела в жидкости // ПММ. 1985. Т. 49. Вып. 2. С. 212–219.
Ольшанский В.Ю. О регулярных прецессиях несимметричного твердого тела с жидким наполнением // ПММ. 2018. Т. 82. Вып. 5. С. 559–571.
Ol’shanskii V.Yu. New cases of regular precession of an asymmetric liquid-filled rigid body // Celest. Mech. Dyn. Astron. 2019. V. 131. Iss. 12. Art. no. 57.
Ol’shanskii V.Yu. Analysis of regular precession conditions for asymmetrical liquid-filled rigid bodies // Celest. Mech. Dyn. Astron. 2020. V. 132. Iss. 9. Art. no. 46.
Ольшанский В.Ю. Полурегулярная прецессия несимметричного твердого тела с жидким наполнением // ПММ. 2021. Т. 85. Вып. 5. С. 547–564.
Горр Г.В. Прецессионные движения в динамике твердого тела и динамике систем связанных твердых тел // ПММ. 2003. Т. 67. Вып. 4. С. 573–587.
Горр Г.В., Мазнев А.В., Щетинина Е.К. Прецессионные движения в динамике твердого тела и в динамике систем связанных твердых тел. Донецк: ДНГУ. 2009.
Yehia H.M. On the regular precession of an asymmetric rigid body acted upon by uniform gravity and magnetic fields // Egypt. J. Bas. Appl. Sci. 2015. V. 2. Iss.3. P. 200–205.
Yehia H.M. Regular precession of a rigid body (gyrostat) acted upon by an irreducible combination of three classical fields // J. Egypt. Math. Soc. 2017. V. 25. Iss. 2. P. 216–219.
ussein A.M. Precessional motion of a rigid body acted upon by three irreducible fields // Rus. J. Nonlin. Dyn. 2019. V. 15. Iss. 3. P. 285–292
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика