Прикладная математика и механика, 2022, T. 86, № 6, стр. 857-871

1. Введение. В небесной механике рассматриваются различные задачи о движении тел под действием сил взаимного притяжения. Как правило, рассматривается задача о движении нескольких тел, находящихся во внешнем пространстве друг относительно друга и, возможно, соприкасающихся друг с другом или приходящих в такое соприкосновение. В задачах другого типа предполагается, что те или иные тела проницаемы, и движение одного тела внутри другого осуществляется под действием силы притяжения и выталкивающий силы. Задачи такого типа называют задачами Роба, поскольку их исследование восходит к публикации [1]. В работе [1] предполагается, что шар движется внутри сферической оболочки, заполненной однородной несжимаемой жидкостью, под действием выталкивающей силы со стороны жидкости, а также силы притяжения со стороны точки, находящейся вне оболочки. Различные задачи о точках либрации в близкой постановке изучались в [2–4]. К этому же классу задач относится задача о движении звезды в неоднородной вращающейся эллиптической галактике [5], для которой были определены точки либрации и исследована их устойчивость.

В настоящей работе внимание сосредоточено на задаче, отличающейся по постановке от задач описанных выше типов. В ней предполагается, что в одном из тел имеется полость, и другое тело совершает движение внутри этой полости, соприкасаясь с предполагаемой непроницаемой поверхностью этой полости. Изучается простейший по постановке случай, когда одно тело представляет собой однородный шар, внутри которого расположена сферическая полость, не выходящая на поверхность. Предполагается, что размеры другого, находящегося внутри полости, тела пренебрежимо малы по сравнению с его размерами, т.е. это тело рассматривается как материальная точка. Считается, что в точке соприкосновения действует сила сухого трения. В предположении о равномерном вращении объемлющего тела изучаются свойства относительных равновесий (точек либрации) в зависимости от параметров задачи. Постановка задачи о движении внутри полости в идейном плане восходит, вероятно, к работе [6], где был описан потенциал притяжения в случае, когда одно тело находится внутри другого.

Как известно (см., например, [7–11]), среди факторов, важных для описания движения по внутренней или внешней поверхности быстро вращающегося малого небесного тела неправильной формы, можно выделить как возможную неоднородность поля притяжения, так и сопоставимость по величине силы притяжения и центробежной силы. Так, в частности, на поверхности тела могут существовать области, в которых незакрепленная частица не может оставаться в покое несмотря на наличие трения (аналоги крутых склонов гор). Общие методы исследования систем с такими свойствами, разработанные в [12–18], были опробованы ранее на ряде задач о движении систем, содержащих вращающиеся элементы [9–12].

2. Движение по инерции динамически симметричного твердого тела. Прежде всего напомним некоторые факты, относящиеся к вращению по инерции динамически симметричного твердого тела вокруг центра масс. Пусть $I = \operatorname{diag} ({{I}_{1}},{{I}_{*}},{{I}_{*}})$ главный центральный тензор инерции тела, ψ, $\theta $ и $\varphi $ – задающие положение тела углы прецессии, нутации и собственного вращения соответственно,

отвечающие им импульсы. Как известно (см., например, [23]), движение такого тела описывается каноническими уравнениями Гамильтона с функцией Гамильтона

Координаты $\psi $ и $\varphi $ – циклические. Отвечающие им импульсы сохраняют свои значения во все время движения.

Установившимися движениями оказываются прецессии. При фиксированных значениях отвечающих циклическим координатам импульсов постоянный угол нутации находится как критическая точка приведенного потенциала

При этом уравнение имеет вид

Так как косинус по абсолютной величине не превосходит единицы, то при ${{p}_{\psi }} \ne {{p}_{\varphi }}$ может иметь место лишь одно из двух решений относительно $cos\theta $: либо

либо

В случае, когда ${{p}_{\psi }} = {{p}_{\varphi }}$, имеет место единственный кратный корень $cos\theta = 1$, отвечающий равномерному вращению тела вокруг оси динамический симметрии.

Вычисляя вторые производные по углу нутации на движениях (2.3) и (2.4), находим

Таким образом, обсуждаемые прецессионные движения устойчивы по углу нутации. По углам прецессии и собственного вращения устойчивости естественно не наблюдается.

Подстановка (2.1) в (2.4) приводит к зависимости угла нутации от угловых скоростей прецессии и собственного вращения на прецессионных движениях. Эта зависимость имеет вид

В частности, при $\theta = \frac{\pi }{2}$ прецессия оказывается перманентным вращением с ${{\dot {\varphi }}_{0}} = 0.$ Именно этот случай, для которого ось прецессии перпендикулярна оси симметрии тела, составляет предмет дальнейшего рассмотрения.

Замечание. В случае, когда $\theta = \frac{\pi }{2}$, перманентные вращения образуют однопараметрическое семейство неизолированных движений, отличающихся углом поворота тела вокруг его оси симметрии.

3. Постановка задачи и основные обозначения. Пусть $\mathcal{A}$ – твердое тело, получающееся из однородного шара $\mathcal{B}$ радиуса ${{r}_{B}}$ с центром $B$ изъятием содержимого сферической полости $\mathcal{C}$ радиуса ${{r}_{C}}$ с центром $C$: $\mathcal{A} = \mathcal{B}{{\backslash }}\mathcal{C}$. Предположим, что тело $\mathcal{A}$ совершает вращение вокруг оси, перпендикулярной оси $BC$ и проходящей через точку $O$ – центр масс тела – c постоянной угловой скоростью $\omega $. Пусть частичка $P,$ размеры которой пренебрежимо малы по сравнению с размерами тела $A$, движется по внутренней $\partial {{\mathcal{A}}_{i}}$ или внешней $\partial {{\mathcal{A}}_{e}}$ поверхности тела $\mathcal{A}$ под действием притяжения со стороны тела, нормальной реакции и силы сухого трения. В дальнейшем считается, что движение частички $P$ не оказывает влияния на движение тела $\mathcal{A}$.

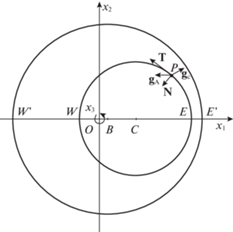
Введем вращающуюся вместе с телом правую систему отсчета $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ (ВСО), ось $O{{x}_{3}}$ которой совпадает с осью вращения, ось $O{{x}_{1}}$ направлена вдоль оси симметрии тела, а ось $O{{x}_{2}}$ дополняет их до правой тройки (см. рис. 1). Для удобства описания точки внутренней (внешней) поверхности тела, располагающиеся на оси $O{{x}_{1}}$, наименее и наиболее удаленные от оси вращения, обозначим $W$ и $E$ (W ' и E ') соответственно. Единичные векторы осей ВСО обозначим ${{e}_{1}}$, ${{e}_{2}}$ и ${{e}_{3}}$ соответственно.

Пусть центр полости $C$ располагается на положительной полуоси $O{{x}_{1}}$. В дальнейшем предполагается, что полость $\mathcal{C}$ не выходит за пределы внешней поверхности тела, т.е. если ${\text{|}}BC{\text{|}} = d$, то $d + {{r}_{C}} \leqslant {{r}_{B}}$. Тогда

где

Относительно неинерциальной системы отсчета $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ точка $P$ движется по поверхности тела под действием силы притяжения с его стороны, центробежной и кориолисовой сил, а также нормальной и касательной составляющих реакции. Касательная составляющая реакции – не что иное, как сила трения.

Уравнения движения имеют вид

где ${{{\mathbf{g}}}_{c}}$ – напряженность центробежных сил с потенциалом ${{{\mathbf{g}}}_{a}}$ – напряженность сил притяжения с потенциалом $U = U\left( {\mathbf{x}} \right)$, векторы N и T задают нормальную реакцию поверхности и силу трения, отнесенную к массе точки.

Ставится задача об определении точек либрации – равновесий точки $P$, находящейся в соприкосновении с поверхностью $\partial{ \mathcal{A}}$ тела $\mathcal{A}$ относительно вращающейся вместе с телом системы отсчета $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$. Исследованию точек либрации, расположенных внутри полости, посвящена работа [24], в которой были обнаружены семейства как изолированных, так и неизолированных относительных равновесий точек, исследованы устойчивость и бифуркации таких равновесий, а также построены области возможного движения.

4. Поле притяжения. Как известно (см., например, [25], задача O-130, а также [26], задача 1.215) напряженность поля притяжения со стороны тела $A$ внутри полости имеет вид

где $G$ – постоянная тяготения, $\rho $ – плотность тела $\mathcal{A}$. Иными словами, внутри полости поле сил притяжения постоянно и однородно. Для сравнения, вне тела напряженность поля притяжения имеет вид

Сила притяжения потенциальна, и ее потенциал записывается как

причем на внешней поверхности $\partial {{\mathcal{A}}_{e}}$ тела $\mathcal{A}$ первое слагаемое в (4.2) постоянно.

Замечание. Главные центральные моменты инерции тела $\mathcal{A}$

определяются с помощью теоремы Гюйгенса–Штейнера (см., например, [27]). Из соотношений (4.3) видно, что осевой момент инерции $I_{1}^{A}(O)$ является наибольшим:

5. Относительные равновесия. Пусть $\mu = {\text{tg}}\alpha \geqslant 0$ – коэффициент трения, $\alpha $ – угол трения. Для определения относительных равновесий точки $P$, находящейся в соприкосновении с поверхностью полости, выпишем условия их существования в виде

где ${{g}_{N}}$ и ${{g}_{T}}$ – нормальная и касательная составляющие вектора напряженности g. Нетрудно видеть, что задаваемое неравенством условие существования относительных равновесий представимо в виде

Для точек поверхности полости $\partial {{\mathcal{A}}_{i}}$, задаваемой уравнением

единичный вектор внутренней нормали имеет вид

Введем безразмерную угловую скорость $\Omega \geqslant 0$:

при этом напряженность ${\mathbf{g}}$ на относительных равновесиях записывается как

Эти соотношения в дальнейшем используются для исследования свойств нормальной и касательной составляющих реакции связи, а также условий равновесия (5.1).

5.1. Свойства нормальной составляющей реакции. На равновесиях условие напряженности связи принимает вид $\left( {{\mathbf{g}},{{{\mathbf{e}}}_{N}}} \right) < 0$ или

Здесь и далее

и имеет место неравенство

В дальнейшем будем подробно рассматривать случай $\alpha \in \left\langle {0;\pi {\text{/}}4} \right\rangle ,$ как физически более осмысленный. Для него $\mu \in [0,\;1]$.

При $\Omega = 0$ соотношение (5.3) задает полупространство, ограниченное плоскостью, ортогональной оси симметрии тела $\mathcal{A}$ и пересекающей полость $\mathcal{C}$ по окружности большого круга. Для всех точек полусферы, содержащей полюс $W$, нормальная составляющая реакции направлена внутрь полости, т.е. частица $P$ находится на связи.

При $0 < \Omega < {{\Omega }_{0}}$ соотношение (5.3) задает внешность прямого кругового цилиндра $\mathcal{L}$ с осью, параллельной оси вращения. Направляющая цилиндра – расположенная в плоскости $O{{x}_{1}}{{x}_{2}}$ окружность с центром в точке $\left( {c\frac{{{{\Omega }^{2}} + \Omega _{0}^{2}}}{{2{{\Omega }^{2}}}},0,0} \right)$ и радиусом $r(\Omega ) = \frac{{c\left| {{{\Omega }^{2}} - \Omega _{0}^{2}} \right|}}{{2{{\Omega }^{2}}}}$. Цилиндр $\mathcal{L}$ содержит прямую, параллельную оси вращения и проходящую через точку $C$ – центр полости $\mathcal{C}$. Кроме того, этот цилиндр содержит прямую, параллельную оси вращения и проходящую через точку $\left( {c\frac{{\Omega _{0}^{2}}}{{{{\Omega }^{2}}}},0,0} \right)$. При $\Omega = {{\Omega }_{ + }}$ точка $E$ и проходящая через нее образующая также будут принадлежать цилиндру $\mathcal{L}$.

При $\Omega \to {{\Omega }_{0}}$ цилиндр $\mathcal{L}$ стягивается в прямую, проходящую через точку $\left( {c,0,0} \right)$ и параллельную оси вращения, и исчезает при $\Omega = {{\Omega }_{0}}$: нормальная составляющая реакции при этом всюду направлена внутрь полости.

С дальнейшим увеличением угловой скорости цилиндр вновь появляется. При этом точка пересечения оси цилиндра с осью $O{{x}_{1}}$ пробегает отрезок от $C$ до $O$. С увеличением угловой скорости радиус цилиндра увеличивается. При $\Omega = {{\Omega }_{ - }}$ точка $W$ оказывается на одной из образующих цилиндра. Наконец, при $\Omega \to \infty $ цилиндр в пределе касается оси $O{{x}_{3}}$. При этом его радиус оказывается равным $c{\text{/}}2$, а ось проходит через точку $(c{\text{/}}2,0,0)$. Заметим, что если $d = 0$, то и $c = 0$, и соотношение (5.3) выполнено тождественно.

5.2. Условия существования относительных равновесий. Как было показано выше, относительные равновесия существуют при выполнении неравенства (5.2), которое согласно выполненным вычислениям принимает вид

Область ${{\mathcal{F}}_{i}}$, задаваемая неравенством (5.6), ограничена прямым цилиндром $\partial {{\mathcal{F}}_{i}}$, направляющая которого задается уравнением ${{F}_{i}} = 0$, а образующие параллельны оси $O{{x}_{3}}$. Цилиндрическая поверхность $\partial {{\mathcal{F}}_{i}}$, в частности, содержит прямые, параллельные оси вращения и проходящие через точки $\left( {c - {{r}_{C}}cos\alpha ,0,0} \right)$ и $\left( {c\frac{{\Omega _{0}^{2}}}{{{{\Omega }^{2}}}},0,0} \right)$.

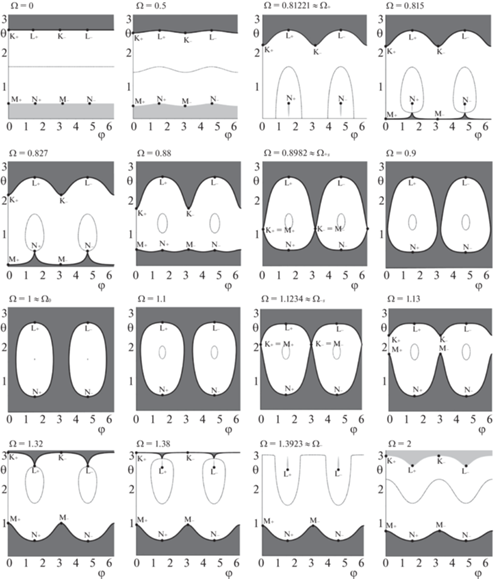
Опишем топологические перестроения областей, заполненных неизолированными равновесиями, на каждом из интервалов, задаваемых неравенствами (5.4) или (5.5), зависящих от угла трения $\alpha $. Обозначим ${{\mathcal{R}}_{W}}(\Omega )$ и ${{\mathcal{R}}_{E}}(\Omega )$ области, в которых удовлетворяется неравенство (5.6) и которые примыкают, соответственно, к точкам $W$ и $E$. Границы этих областей – кривые $\partial W$ и $\partial E$. Введем величины

существующие при $\Omega \in \left[ {0,{{\Omega }_{{ + s}}}} \right] \cup \left\langle {{{\Omega }_{{ - s}}},\infty } \right\rangle $ и $c > {{r}_{C}}sin\alpha $ или при $\Omega \in \left[ {0,{{\Omega }_{{ + s}}}} \right]$ и $c < {{r}_{C}}sin\alpha $.

Граница $\partial W$ содержит точки ${{K}_{ \pm }}(\Omega )$, такие, что

а граница $\partial E$ – точки

Положение точек ${{K}_{ \pm }}(\Omega )$ и ${{M}_{ \pm }}(\Omega )$ существенно зависит от величины угловой скорости $\Omega $. Кроме того, границы $\partial W$ и $\partial E$ содержат пары точек

соответственно. Положение этих точек фиксировано и не меняется с изменением угловой скорости $\Omega $.

Прежде всего, рассмотрим случай $\Omega = 0$, т.е. тело не вращается. В этом случае величина ${{F}_{i}}$ принимает вид

Тогда неравенство (5.6) определяет пару параллельных плоскостей, ортогональных оси $O{{x}_{1}}$ и отстоящих от центра полости $\mathcal{C}$ на расстоянии ${{r}_{C}}cos\alpha $. Эти плоскости высекают из границы $\partial{ \mathcal{C}}$ полости $\mathcal{C}$ два симметричных сферических сегмента высотой ${{r}_{C}}\left( {1 - cos\alpha } \right)$, содержащих точки $W$ и $E$ соответственно. При $\mu = 0$ пересечение этих плоскостей и полости $\mathcal{C}$ состоит ровно из точек $W$ и $E$.

В точках области, примыкающей к полюсу $E$, нормальная реакция направлена во внешность полости, т.е. частица $P$ не находится на связи. Такие области в данной постановке не имеют физического смысла и далее не рассматриваются.

Пусть теперь $\Omega > 0$. При $0 \leqslant \Omega < {{\Omega }_{ + }}$ область ${{\mathcal{R}}_{W}}(\Omega )$ заполнена неизолированными относительными равновесиями, в то время как при тех же значениях $\Omega $ в точках области ${{\mathcal{R}}_{E}}(\Omega )$ связь ослаблена, и относительных равновесий нет.

При $\Omega = {{\Omega }_{ + }}$ поверхность $\partial {{\mathcal{F}}_{i}}$ и полость $\mathcal{C}$ имеют, в частности, общую точку $E$, но нормальная реакция в этой точке равна нулю.

При ${{\Omega }_{ + }} < \Omega < {{\Omega }_{{ + c}}}$ область ${{\mathcal{R}}_{E}}(\Omega )$ представляется в виде трех связных компонент, пересекающихся по граничным точкам

причем, если $\Omega = {{\Omega }_{ + }}$, то эти точки порождаются из точки $E$; если $\Omega = {{\Omega }_{{ + c}}}$, то это точки ${{N}_{ \pm }}$.

Одна компонента, содержащая точку $E$, пересекается с двумя оставшимися компонентами, располагающимися в разных полупространствах относительно плоскости ${{x}_{3}} = 0$. При этом, лишь в точках компоненты связности, содержащей точку $E$, нормальная реакция направлена внутрь полости.

При ${{\Omega }_{{ + c}}} < \Omega < {{\Omega }_{{ + s}}}$ во всех точках область ${{\mathcal{R}}_{E}}(\Omega )$ нормальная реакция теперь направлена внутрь полости, и заполняющие это множество относительные равновесия обретают физический смысл.

При $\Omega = {{\Omega }_{{ + s}}}$ области ${{\mathcal{R}}_{W}}({{\Omega }_{{ + s}}})$ и ${{\mathcal{R}}_{E}}({{\Omega }_{{ + s}}})$ смыкаются в попарно совпадающих точках ${{K}_{ \pm }}({{\Omega }_{{ + s}}}) = {{M}_{ \pm }}({{\Omega }_{{ + s}}})$, причем

и образуют кольцо $\mathcal{R}(\Omega )$, существующее при ${{\Omega }_{{ + s}}} < \Omega < {{\Omega }_{{ - s}}}$.

Замечание. При $\Omega = {{\Omega }_{0}}$ бифуркация не происходит. Однако функция ${{F}_{i}}$, принимающая вид

задает круговой цилиндр радиуса ${{r}_{C}}cos\alpha $ с осью, параллельной оси вращения и проходящей через центр полости $\mathcal{C}$. Границы кольца $\mathcal{R}({{\Omega }_{0}})$ в этом случае – две симметричные окружности. Они принадлежат пересечениям плоскостей ${{x}_{3}} = \pm {{r}_{C}}sin\alpha $ и сферы (5.2). Отметим, что угол, который составляет радиус-вектор любой точки этих окружностей с плоскостью ${{x}_{3}} = 0$, и есть угол трения $\alpha $.

Дальнейшие случаи следует рассматривать в зависимости от того, где находится центр масс $O$. Так как предполагается, что $\alpha \in \left\langle {0;\pi {\text{/}}4} \right\rangle $, то возможны следующие случаи:

I. строго вне полости, т.е. $c > {{r}_{C}}$,

II. на границе полости, т.е. $c = {{r}_{C}}$,

III.а. внутри полости, и ${{r}_{C}}cos\alpha < c < {{r}_{C}}$,

III.б. внутри полости, и ${{r}_{C}}sin\alpha < c \leqslant {{r}_{C}}cos\alpha $,

III.в. внутри полости, и $0 < c \leqslant {{r}_{C}}sin\alpha $.

Рассмотрим перечисленные случаи более подробно.

I. Пусть $c > {{r}_{C}}$. При ${{\Omega }_{0}} < \Omega < {{\Omega }_{{ - s}}}$ кольцо $\mathcal{R}(\Omega )$ продолжает существовать, но деформируется, и при $\Omega > {{\Omega }_{{ - s}}}$ вновь размыкается в точках

на области ${{R}_{W}}(\Omega )$ и ${{R}_{E}}(\Omega )$, существующие при ${{\Omega }_{{ - s}}} < \Omega < {{\Omega }_{{ - c}}}$.

При ${{\Omega }_{{ - c}}} < \Omega < {{\Omega }_{ - }}$ область ${{\mathcal{R}}_{W}}(\Omega )$ представляется в виде трех связных компонент, пересекающихся по граничным точкам (5.7), причем, если $\Omega = {{\Omega }_{{ - c}}}$, то имеют место две точки ${{L}_{ \pm }}$; если $\Omega = {{\Omega }_{ - }}$, то точки сливаются в точке $W$. Одна компонента, содержащая точку $W$, пересекается с двумя оставшимися компонентами, располагающимися симметрично в разных полупространствах относительно плоскости ${{x}_{3}} = 0$. При этом, лишь в точках компоненты связности, содержащая точку $W$, нормальная реакция направлена внутрь полости.

При $\Omega = {{\Omega }_{ - }}$ поверхность $\partial {{\mathcal{F}}_{i}}$ и полость $\mathcal{C}$ пересекаются, в частности, в точке $W$, и нормальная реакция в этой точке равна нулю.

При $\Omega > {{\Omega }_{ - }}$ в точках области ${{\mathcal{R}}_{W}}(\Omega )$ нормальная реакция направлена во внешность полости, и такие решения более интереса не представляют, в то время как область ${{\mathcal{R}}_{E}}(\Omega )$ остается существовать. При $\Omega \to \infty $ в пределе имеют место соотношения

В точках области $\mathcal{R}_{W}^{\infty } = {{\left. {{{\mathcal{R}}_{W}}(\Omega )} \right|}_{{\Omega \to \infty }}}$ нормальная реакция направлена во внешность полости. При этом с областью $\mathcal{R}_{E}^{\infty } = {{\left. {{{\mathcal{R}}_{E}}(\Omega )} \right|}_{{\Omega \to \infty }}}$ такого не происходит: в точках из $\mathcal{R}_{E}^{\infty }$ нормальная составляющая реакции направлена внутрь полости.

Описанные перестройки областей неизолированных равновесий проиллюстрированы на рис. 2. Для удобства демонстрации введены сферические координаты $x = {{r}_{C}}cos\theta + c$, $y = {{r}_{C}}sin\theta cos\varphi $, $z = {{r}_{C}}sin\theta \sin \varphi $ и показана серия разверток на плоскости ($\theta ,\varphi $) при возрастании угловой скорости вращения тела $\Omega $, при этом выбраны параметры $\mu = 0.5$, ${{r}_{C}} = 0.25$, $d = 0.5$, ${{r}_{B}} = 1$. Светло-серым цветом выделены области, на которых нормальная реакция направлена во внешность полости, темно-серым – внутрь полости. Пунктирной линией показана граница смены знака нормальной реакции.

II. Пусть $c = {{r}_{C}}$. При ${{\Omega }_{0}} < \Omega < {{\Omega }_{{ - s}}}$ кольцо $\mathcal{R}(\Omega )$ продолжает существовать, и при $\Omega > {{\Omega }_{{ - s}}}$ вновь размыкается в точках ${{K}_{ \pm }}\left( {{{\Omega }_{{ - s}}}} \right) = {{M}_{ \pm }}\left( {{{\Omega }_{{ - s}}}} \right)$ на области ${{\mathcal{R}}_{W}}(\Omega )$ и ${{\mathcal{R}}_{E}}(\Omega )$, существующие при ${{\Omega }_{{ - s}}} < \Omega < {{\Omega }_{{ - c}}}$. При ${{\Omega }_{{ - c}}} < \Omega < \infty $ область ${{\mathcal{R}}_{W}}(\Omega )$ представляется в виде трех связных компонент, пересекающихся по граничным точкам, причем одна компонента, содержащая точку $W$, пересекается с двумя оставшимися компонентами, располагающимися в разных полупространствах относительно плоскости ${{x}_{3}} = 0$. При этом лишь в точках компоненты связности, содержащей точку $W$, нормальная реакция направлена внутрь полости. Значение угловой скорости $\Omega = {{\Omega }_{ - }}$ более не определено. При $\Omega \to \infty $ имеем ${{p}_{ - }} \to 0$, и область $\mathcal{R}_{W}^{\infty }$ состоит только из точки $W$, совпадающей с центром масс $O$. Нормальная составляющая реакции в этой точке обращается в нуль. При этом ${{p}_{ + }} \to 2{{r}_{C}}{{\cos }^{2}}\alpha $ при $\Omega \to \infty $ и, как и прежде, в точках из области $\mathcal{R}_{E}^{\infty }$ нормальная составляющая реакции направлена внутрь полости.

III.a. Пусть ${{r}_{C}}cos\alpha < c < {{r}_{C}}$. В этом случае наблюдается картина, аналогичная картине из пункта II. При ${{\Omega }_{0}} < \Omega < {{\Omega }_{{ - s}}}$ кольцо $\mathcal{R}(\Omega )$ продолжает существовать, и при $\Omega > {{\Omega }_{{ - s}}}$ вновь размыкается в точках ${{K}_{ \pm }}\left( {{{\Omega }_{{ - s}}}} \right) = {{M}_{ \pm }}\left( {{{\Omega }_{{ - s}}}} \right)$ на области ${{\mathcal{R}}_{W}}(\Omega )$ и ${{\mathcal{R}}_{E}}(\Omega )$, существующие при ${{\Omega }_{{ - s}}} < \Omega < {{\Omega }_{{ - c}}}$. При ${{\Omega }_{{ - c}}} < \Omega \leqslant \infty $ область ${{\mathcal{R}}_{W}}(\Omega )$ представляется в виде трех связных компонент. При этом компонента связности, содержащая точку $W$, не вырождается, и в ее точках нормальная реакция направлена внутрь полости.

III.б. Пусть ${{r}_{C}}sin\alpha < c \leqslant {{r}_{C}}cos\alpha $. При ${{\Omega }_{0}} < \Omega < {{\Omega }_{{ - s}}}$ кольцо $\mathcal{R}(\Omega )$ продолжает существовать, и при $\Omega > {{\Omega }_{{ - s}}}$ вновь размыкается в точках ${{K}_{ \pm }}\left( {{{\Omega }_{{ - s}}}} \right) = {{M}_{ \pm }}\left( {{{\Omega }_{{ - s}}}} \right)$ на области ${{\mathcal{R}}_{W}}(\Omega )$ и ${{\mathcal{R}}_{E}}(\Omega )$, существующие при ${{\Omega }_{0}} < \Omega < {{\Omega }_{{ - s}}}$. Значение угловой скорости $\Omega = {{\Omega }_{{ - c}}}$ более не определено. При ${{\Omega }_{{ - s}}} < \Omega \leqslant \infty $ существует односвязная область ${{\mathcal{R}}_{W}}(\Omega )$, во всех точках которой нормальная составляющая реакции направлена внутрь полости.

III.в. Пусть $0 \leqslant c \leqslant {{r}_{C}}sin\alpha $. Значение угловой скорости $\Omega = {{\Omega }_{ - }}$ более не определено. Кольцо $\mathcal{R}(\Omega )$ продолжает существовать при ${{\Omega }_{0}} < \Omega < \infty $. При $\Omega \to \infty $ точки ${{K}_{ \pm }} = {{\left. {{{K}_{ \pm }}(\Omega )} \right|}_{{\Omega \to \infty }}}$ и ${{M}_{ \pm }} = {{\left. {{{M}_{ \pm }}(\Omega )} \right|}_{{\Omega \to \infty }}}$ не существуют, и имеет место кольцо ${{\mathcal{R}}^{\infty }}$, во всех точках которого нормальная составляющая реакции направлена внутрь полости, т.е. частица $P$ находится на связи.

Отметим, что в случае $\alpha \in \left( {\pi {\text{/}}4;\pi {\text{/}}2} \right)$, по сравнению c предыдущим, критические значения угловой скорости ${{\Omega }_{{ \pm s}}}$ и ${{\Omega }_{{ \pm c}}}$ меняются местами, ср. неравенства (5.4) и (5.5). При $\alpha = \pi {\text{/}}4$ имеем ${{\Omega }_{{ \pm c}}} = {{\Omega }_{{ \pm s}}}$. Вместе с этим меняется местами порядок перестроения соответствующих областей, заполненных неизолированными равновесиями.

Замечание. При $d = 0$ величина ${{F}_{i}}$ из соотношения (5.6) принимает вид

и определяет прямую, параллельную оси вращения и проходящую через точку $O$, и круговой цилиндр с осью, совпадающей с осью вращения, радиуса ${{r}_{C}}cos\alpha $. Этот цилиндр вырезает из сферы (5.2) кольцо $\mathcal{R}({{\Omega }_{0}})$, рассмотренное выше. При этом во всех точках кольца выполнено соотношение $\left( {{\mathbf{g}},{{{\mathbf{e}}}_{N}}} \right) < 0$.

6. Об устойчивости относительных равновесий. Для относительных равновесий, расположенных внутри найденных областей, устойчивость по Ляпунову следует из результатов Г.К. Пожарицкого [28]. Как и в [22, 29], можно ставить вопрос об устойчивости связных компонент областей, заполненных равновесиями.

Будем считать связную компоненту устойчивой, если для каждой точки ее границы проекция суммы активных сил и центробежной силы на плоскость, касательную к поверхности в этой точке, направлена внутрь рассматриваемой связной компоненты. Это свойство можно трактовать следующим образом. Пусть в начальный момент точка $P$ располагается в некоторой точке границы области, заполненной равновесиями. “Освободив” систему от трения, т.е. предположив, что коэффициент трения обратился в нуль, “отпустим” точку $P$ без начальной скорости. Если для всех точек границы связной компоненты точка $P$ начнет движение внутрь этой компоненты или вдоль ее границы, то скажем, что эта связная компонента устойчива. Если найдется хотя бы одна точка границы рассматриваемой компоненты, для которой точка $P$ начнет движение вовне этой компоненты, то речь идет о неустойчивости этой связной компоненты.

Введенное таким образом определение устойчивости проверяется путем анализа знака скалярного произведения касательной проекции активных сил при нулевой начальной скорости на внешнюю нормаль к границе области, заполненной равновесиями, в точках границы. В рассмотренном на рис. 2 примере оказывается, что на всех компонентах областей равновесия, на которых нормальная реакция направлена внутрь сферы, упомянутая проекция суммы сил направлена внутрь компоненты. Границы этих компонент выделены жирной сплошной линией.

Выводы. Как показало исследование, области, заполненные неизолированными относительными равновесиями, в зависимости от значений параметров могут заполнять на поверхности полости подобласти различных топологических типов. Иными словами, области на поверхности полости, пригодные “для эксплуатации”, также существенно зависят от параметров.

Аналитическое исследование аналогичных перестроек множеств неизолированных относительных равновесий возможно и в случае, когда тело – однородный эллипсоид с шаровой полостью. Эта задача представляется более трудной из-за большого числа параметров, определяющих как размеры и положение полости, так и размеры эллипсоидального тела.

Заметим, что выполненное исследование носит академический характер. Для реальных небесных тел таких, как кометы, потоки исходящих газов говорят в пользу наличия полостей, из которых они исходят. Существующие методы в принципе позволяют вычислять гравитационные поля внутри небесных тел и численно исследовать особенности динамики внутри полостей при их наличии. Однако вопрос об обнаружении полостей и об описании их геометрии для конкретных небесных тел остается открытым.

Исследование выполнено при поддержке Российского научного фонда (проект № 22-21-00297).