Прикладная математика и механика, 2023, T. 87, № 3, стр. 343-368
Высокоточные численные схемы решения плоских краевых задач для полигармонического уравнения и их применение к задачам гидродинамики
1 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: petrovipmech@gmail.com
Поступила в редакцию 14.12.2022
После доработки 17.04.2023
Принята к публикации 24.04.2023
- EDN: ZUMQQK
- DOI: 10.31857/S0032823523030128
Аннотация
Рассматриваются краевые задачи для гармонического, бигармонического уравнений, а также общего полигармонического уравнения для многосвязных областей на плоскости. Задачи сводятся к решению линейных интегральных уравнений на граничных контурах, которые предполагаются гладкими. Представлен алгоритм вывода аппроксимации интегральных уравнений линейной системой с учетом логарифмических особенностей ядер интегральных операторов, через которые выражаются интегральные уравнения. В алгоритме используется периодичность функций, заданных на замкнутых граничных контурах. С ростом числа точек сетки погрешность аппроксимации убывает быстрее чем шаг сетки в любой фиксированной степени. Рассматриваются приложения к решению задач гидродинамики, фильтрации и другим задачам теоретической физики.
1. Введение. Одним из распространенных подходов к постановке краевых задач является сведение к системам интегральных уравнений. Преимущества, как правило, объясняют тем, что возможно добиться численной аппроксимации уравнений лучше всякой аппроксимации степенного порядка с любой наперед заданной степенью. Например, этого добиваются за счет использования квадратур Гаусса. Вокруг этого свойства часто выстроены такие алгоритмы, как метод граничных интегральных уравнений (также известный как метод граничных элементов) и метод спектральных элементов (см. [1, 2], также обзор современных работ приведен в [3]). В типичном случае для популярного метода спектральных элементов само уравнение выражается в терминах дифференциального оператора. Интегрирование же вводится уже в процессе построения численного алгоритма его решения. Для этого дифференциальный оператор из исходного уравнения следует рассмотреть как оператор над Гильбертовым пространством со скалярным произведением, имеющим интегральный вид. Тогда сведение к системе линейных уравнений может выполняться, например, по методу Галеркина на основе базисных функций, выражаемых в терминах многочленов Чебышева (точность аппроксимации при этом достигается за счет использования соответствующих квадратур). Для метода граничных интегральных уравнений более характерен иной подход. В этом случае к интегральному виду обычно приводится само исходное уравнение. Например, уравнение Лапласа можно переформулировать в интегральном виде с использованием операторов простого и двойного слоев. В плоском случае это интегралы по одномерной границе (что позволяет рассматривать функции на границе как периодические). Их аппроксимация однако затруднена тем, что функции ядра могут иметь особенности. По этой причине основной задачей для метода граничных интегральных уравнений является развитие методов построения квадратурных формул для интегральных операторов с ядром. Для построения численных схем решения краевых задач в областях, ограниченных гладкими замкнутыми контурами, в работе учитывается периодичность и аналитичность функций, определенных на этих контурах.
Предлагаемое исследование имеет следующую структуру.
В разд. 2 формулируется основная Теорема, которая представляет собой конструктивный алгоритм построения квадратурной формулы линейного интегрального оператора, действующего на периодическую функцию. Для квадратурной формулы доказывается экспоненциальная оценка погрешности.
В разд. 3 приведены три квадратурные формулы для линейных интегральных операторов гармонического и бигармонического уравнений.
В разд. 4 формулируется теорема 2 о квадратурной формуле линейного интегрального оператора системы Векуа для произвольного полигармонического уравнения.
В разд. 5 выводится численная схема с экспоненциальной сходимостью решения краевых задач для уравнения Лапласа.
В разд. 6 выводится численная схема с экспоненциальной сходимостью решения краевых задач для бигармонического уравнения.
В разд. 7 выводится численная схема с экспоненциальной сходимостью решения краевых задач для полигармонического уравнения.
В разд. 8 и 9 приведены численные схемы расчета течения вязкой жидкости в приближении Стокса в многосвязной области. Сходимость метода иллюстрируется на примерах.
2. Основная Теорема. Граничные интегральные уравнения выражаются через линейные операторы вида
(2.1)
$\Phi (z) = L(F(z)) = \int\limits_0^1 {H(z{\kern 1pt} '\; - z)F(z{\kern 1pt} ')dz{\kern 1pt} '} $(2.2)
$H(z) = \frac{{{{h}_{0}}}}{2} + \sum\limits_{n = 1}^\infty {({{h}_{n}}\cos nx + {{r}_{n}}\sin nx)} ;\quad x = 2\pi z$Коэффициенты ряда Фурье определяются по известным формулам
(2.3)
${{h}_{n}} = 2\int\limits_0^1 {H(z)\cos 2\pi nzdz} ,\quad {{r}_{n}} = 2\int\limits_0^1 {H(z)\sin 2\pi nzdz} $Линейные операторы действуют на функции $F(z)$ единичного периода, и в результате действия получается функция $\Phi (z)$ единичного периода.
Назовем частичной суммой ряда Фурье функции $H(z)$ выражение
(2.4)
$\begin{gathered} {{H}_{N}}(z) = \frac{{{{h}_{0}}}}{2} + \frac{{{{h}_{M}}}}{2}\cos Mx + \sum\limits_{n = 1}^{M - 1} {({{h}_{n}}\cos nx} + {{r}_{n}}\sin nx) \\ M = N{\text{/}}2,\quad x = 2\pi z \\ \end{gathered} $В частичную сумму входят члены ряда Фурье с коэффициентами ${{h}_{n}}$, ${{r}_{n}}$, $n = 1,2, \ldots ,N{\text{/}}2 - 1$, а коэффициент последнего члена ${{h}_{M}}$ делится на 2.
Формула вычисления интеграла для оператора (2.2)
(2.5)
$\begin{array}{*{20}{c}} {{{\Phi }_{i}} = \int\limits_0^1 {H(z - {{z}_{i}})F(z)dz} = \sum\limits_{i = 1}^N {{{g}_{{j - i}}}} {{F}_{j}},\quad {{\Phi }_{i}} = \Phi ({{z}_{i}}),\quad {{F}_{i}} = F({{z}_{i}})} \\ {{{z}_{j}} = j{\text{/}}N,\quad j = 1,2, \ldots ,N = 2M} \end{array}$(2.6)
${{\rho }_{N}} = \max \left( {\left| {{{\rho }_{{Ni}}}} \right|} \right),\quad {{\rho }_{{Ni}}} = \int\limits_0^1 {H(z - {{z}_{i}})F(z)dz} - \sum\limits_{j = 1}^N {{{g}_{{j - i}}}} {{F}_{j}};\quad i = 1,2, \ldots ,N$Конструированию квадратурных формул для таких операторов посвящена обширная литература [4–11]. Обычно квадратурные формулы имеют степенной порядок точности. Особый интерес вызывают квадратурные формулы, погрешность которых убывает быстрее любой степени шага сетки. В монографии [4] они называются квадратурными формулами без насыщения и имеют погрешность, убывающую экспоненциально с ростом числа точек сетки.
Алгоритм построения таких формул достаточно сложен [11]. Пользуясь же периодичностью можно получить простую общую формулу для коэффициентов квадратурной формулы ${{g}_{m}}$.
Предлагаемый алгоритм с экспоненциально малой погрешностью сформулирован в теореме 1, вытекающей из результатов [12, 13].
Теорема 1. Для периодического ядра $H$ (2.2) коэффициенты квадратурной формулы (2.5) выражаются через частичные суммы (2.4) его ряда Фурье (2.2)
(2.7)
$\begin{gathered} {{g}_{m}} = \frac{1}{N}{{H}_{N}}({{z}_{m}}) = \\ = \frac{1}{N}\left[ {\frac{{{{h}_{0}}}}{2} + \frac{{{{h}_{M}}}}{2}{{{( - 1)}}^{m}} + \sum\limits_{n = 1}^{M - 1} {({{h}_{n}}\cos (} 2\pi nm{\text{/}}N) + {{r}_{n}}\sin (2\pi nm{\text{/}}N))} \right] \\ \end{gathered} $Тогда квадратурная формула (2.5) с коэффициентами ${{g}_{{j - i}}}$ обладает следующими свойствами.
1. В дискретных точках ${{x}_{i}} = 2\pi {{z}_{i}} = 2\pi i{\text{/}}N$; $i = 1,2, \ldots ,N$ она определяет точные значения оператора (2.1), действующего на функции
(2.8)
$\begin{gathered} F(z) = 1,\;\cos x,\;\cos 2x, \ldots ,\cos (M - 1)x,\;\cos Mx \\ \sin x,\;\sin 2x, \ldots ,\sin (M - 1)x;\quad x = 2\pi z,\quad M = N{\text{/2}} \\ \end{gathered} $2. Если функция $F(z)$ и ядро $H(z)$ периодичны $F(z + 1) = F(z)$, $H(z + 1) = H(z)$, а интеграл по периоду
(2.8a)
$\int\limits_0^1 {\left. {H(z - {{z}_{i}})} \right|} dz \leqslant h\quad {\text{и сумма}}\quad \sum\limits_{j = 1}^N {\left| {{{g}_{{j - i}}}} \right|} = \frac{1}{N}\sum\limits_{j = 1}^N {\left| {{{H}_{N}}({{z}_{j}} - {{z}_{i}})} \right|} \leqslant \sigma $(2.9)
${{\rho }_{N}} = \int\limits_0^1 {H(z - {{z}_{i}})F(z)dz} - \sum\limits_{j = 1}^N {{{g}_{{j - i}}}} {{F}_{j}},\quad \left| {{{\rho }_{N}}} \right| < C{{e}^{{ - sN}}},$Для доказательства свойства 1 теоремы 1 последовательно проверяется точность значений оператора (2.1), действующего на каждую отдельную функцию системы (2.8) (доказательство в приложении).
Экспоненциальная оценка (2.9) (свойство 2) доказывается следующим образом.
Представим функцию суммой частичной суммы ряда Фурье и ее остаточного члена
(2.10)
$\begin{gathered} F(z) = {{F}_{N}}(z) + {{R}_{N}}(z) \\ {{F}_{N}}(z) = \frac{{{{A}_{0}}}}{2} + \sum\limits_{n = 1}^{M - 1} {({{A}_{n}}\cos nx + {{B}_{n}}\sin nx)} + {{A}_{M}}\cos Mx \\ {{R}_{N}}(z) = \sum\limits_{n = M + 1}^\infty {({{A}_{n}}\cos nx + {{B}_{n}}\sin nx)} + {{B}_{M}}\sin Mx;\quad x = 2\pi z \\ \end{gathered} $С помощью оценок коэффициентов Фурье аналитической функции, имеющей единичный период (см. [14], стр. 89)
(2.11)
${\text{|}}{{A}_{n}}{\text{|}} \leqslant C{{\theta }^{n}},\quad {\text{|}}{{B}_{n}}{\text{|}} \leqslant C{{\theta }^{n}};\quad 0 < \theta < 1$(2.12)
${\text{|}}{{R}_{N}}{\text{|}} < C\left( {{{\theta }^{M}} + \sum\limits_{n = M + 1}^\infty {2{{\theta }^{n}}} } \right) = C\frac{{1 + \theta }}{{1 - \theta }}{{\theta }^{M}};\quad 0 < \theta < 1$С помощью (2.10) разбиваем погрешность (2.6) на два слагаемых ${{\rho }_{{Ni}}} = {{\rho }_{a}} + {{\rho }_{b}}$
(2.13)
$\begin{gathered} {{\rho }_{a}} = \int\limits_0^1 {H(z{\kern 1pt} '\; - {{z}_{i}}){{F}_{N}}(z{\kern 1pt} ')dz{\kern 1pt} '} - \sum\limits_{j = 1}^N {{{g}_{{j - i}}}} {{F}_{N}}({{z}_{j}}) \\ {{\rho }_{b}} = \int\limits_0^1 {H(z{\kern 1pt} '\; - {{z}_{i}}){{R}_{N}}(z{\kern 1pt} ')dz{\kern 1pt} '} - \sum\limits_{j = 1}^N {{{g}_{{j - i}}}} {{R}_{N}}({{z}_{j}}) \\ \end{gathered} $Функция ${{F}_{N}}(z)$ является линейной комбинацией функций (2.8) и в силу теоремы 1 квадратурная формула для ${{F}_{N}}(z)$ точна и имеет нулевую погрешность ${{\rho }_{a}} = 0$. Дадим оценку второго слагаемого ${{\rho }_{b}}$. В силу неравенства (2.12) и условий (2.8a) имеем
(2.14)
$\begin{array}{*{20}{c}} {{\text{|}}{{\rho }_{N}}{\text{|}} = {\text{|}}{{\rho }_{b}}{\text{|}} \leqslant \left| {\int\limits_0^1 {H(z{\kern 1pt} '\; - {{z}_{i}}){{R}_{N}}(z{\kern 1pt} ')dz{\kern 1pt} '} } \right| + \left| {\sum\limits_{j = 1}^N {{{g}_{{j - i}}}} {{R}_{N}}({{z}_{j}})} \right| \leqslant } \\ { \leqslant \int\limits_0^1 {\left| {H(z{\kern 1pt} '\; - {{z}_{i}})} \right|\left| {{{R}_{N}}(z{\kern 1pt} ')\,} \right|dz{\kern 1pt} '} + \sum\limits_{j = 1}^N {\left| {{{g}_{{j - i}}}} \right|} \left| {{{R}_{N}}({{z}_{j}})\,} \right| \leqslant (h + \sigma )C\frac{{1 + \theta }}{{1 - \theta }}{{\theta }^{M}}} \end{array}$После замен $(h + \sigma )C\frac{{1 + \theta }}{{1 - \theta }} = {{C}_{1}}$, $\theta = {{e}^{{ - s}}}$ получаем требуемую оценку.
С помощью теоремы 1 строятся квадратурные формулы с экспоненциальной сходимостью для интегральных операторов с логарифмическими особенностями, а также для операторов дифференцирования и интегрирования. Далее, применяя метод граничных элементов, строятся квадратурные формулы с экспоненциальной сходимостью для линейных операторов граничных интегральных уравнений.
3. Квадратурные формулы для линейных операторов. Приведем с помощью теоремы 1 вывод основных квадратурных формул для метода граничных эдементов.
Пример 1. Квадратурная формула для ядра $H = 1$. Находим ряд Фурье $H = 1$ и частичную сумму ${{H}_{N}}(z) = 1$ и по формуле (2.7) получим ${{g}_{m}} = 1{\text{/}}N$. Квадратурная формула примет простейший вид
В монографии [9] доказана экспоненциальная оценка убывания погрешности квадратурной формулы (3.1) для аналитической функции $F(z) = F(z + 1)$. Еще раньше в монографии Крылова [8] 1967 г. доказана абсолютная точность квадратурной формулы (3.1) для тригонометрических полиномов (2.8).
Пример 2. Квадратурная формула для ядра с логарифмической особенностью $H = \ln \left| {\sin \pi z} \right|$. Логарифмическая особенность имеет место в функции Грина для уравнения Лапласа. Ядро $H(z) = \ln \left| {\sin \pi z} \right|$ представляется следующим рядом Фурье
(3.2)
$H(z) = - \left( {\ln 2 + \sum\limits_{k = 1}^\infty {\frac{1}{k}} \cos kx} \right);\quad x = 2\pi z$Составляем частичную сумму (2.4) и по формуле (2.7) теоремы 1 находим коэффициенты ${{g}_{m}}$
(3.3)
$\begin{gathered} {{H}_{N}}(z) = - \ln 2 - \frac{1}{{2M}}\cos Mx - \sum\limits_{k = 1}^{M - 1} {\frac{1}{k}\cos kx} ;\quad M = N{\text{/}}2 \\ \alpha (m) = {{H}_{N}}({{z}_{m}}),\quad {{g}_{m}} = \frac{1}{N}\alpha (m) \\ \end{gathered} $Она дает точные значения интеграла для системы функций (2.8) и выведена в [15] и затем в [9].
Пример 3. Квадратурная формула для ядра $H = \frac{1}{2}{{\sin }^{2}}(\pi z)\ln {{(2\sin \pi z)}^{2}}$. Она имеет место в функции Грина для бигармонического уравнения [16] и выведена впервые в [13]. Более просто она выводится с помощью теоремы 1 следующим образом.
Ядро $H = \frac{1}{2}{{\sin }^{2}}(\pi z)\ln {{(2\sin \pi z)}^{2}}$ имеет ряд Фурье
(3.4)
$H(z) = \frac{1}{4} - \frac{3}{8}\cos x + \sum\limits_{k = 2}^\infty {\frac{{\cos (kx)}}{{2k({{k}^{2}} - 1)}}} ;\quad x = 2\pi z$Составляем частичную сумму (2.4) и по формуле (2.7) теоремы 1 находим коэффициенты ${{g}_{m}}$
(3.5)
$\begin{gathered} {{H}_{M}}(z) = \frac{1}{4} + \frac{{\cos (Mx)}}{{4M({{M}^{2}} - 1)}} - \frac{3}{8}\cos x + \sum\limits_{k = 2}^{M - 1} {\frac{{\cos (kx)}}{{2k({{k}^{2}} - 1)}}} \\ {{\alpha }_{1}}(m) = {{H}_{M}}({{z}_{m}}),\quad {{g}_{m}} = \frac{1}{N}{{\alpha }_{1}}(m);\quad M = N{\text{/}}2 \\ \end{gathered} $Квадратурная формула
(3.6)
$\int\limits_0^1 {\frac{1}{2}{{{\sin }}^{2}}(\pi (z - {{z}_{i}}))\ln {{{(2\sin \pi (z - {{z}_{i}}))}}^{2}}F(z)dz} = \frac{1}{N}\sum\limits_{j = 1}^N {{{\alpha }_{1}}} (j - i){{F}_{j}}$Выведенные формулы (3.3) и (3.5) для коэффициентов $\alpha (m)$ и ${{\alpha }_{1}}(m)$ используются при аппроксимации линейных интегральных уравнений для решения краевых задач гармонического и бигармонического уравнений.
Полезны также квадратурные формулы для операторов дифференцирования и интегрирования. Их можно также получить с помощью теоремы 1, пользуясь рядом Фурье периодической дельта-функции
и рядов Фурье для ее производной и интеграла.Представим производную в виде линейного оператора, разложим ядро в ряд Фурье и через его коэффициенты выпишем коэффициенты квадратурной формулы для оператора производной
Аналогично находятся коэффициенты квадратурной формулы для интеграла. Находим
Квадратурная формула для первообразной, интеграл по периоду которой равен нулю имеет вид $\int {F(z)dz} $ = $\int_0^1 {H(z{\kern 1pt} '\; - z)F(z{\kern 1pt} ')dz{\kern 1pt} '} $ = $\sum\nolimits_{j = 1}^N {{{g}_{{j - i}}}{{F}_{j}}} $.
4. Построение схем для решения полигармонического уравнения.
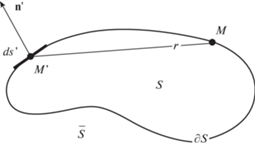
4.1. Система интегральных уравнений. Систему интегральных уравнений для функции $\Phi (x,y)$, удовлетворяющей в области $S$ произвольному полигармоническому уравнению ${{\Delta }^{m}}\Phi = 0$, вывел И.Н. Векуа [14]. Им введены функции Грина ${{G}^{{(k)}}}(r)$, зависящие от расстояния $r$ между двумя точками $M = M(x,y)$ и $M{\kern 1pt} ' = M(x{\kern 1pt} ',y{\kern 1pt} ')$ (рис. 1).
(4.1)
${{r}^{2}}(M,M{\kern 1pt} ') = {{(x{\kern 1pt} '\; - x)}^{2}} + {{(y{\kern 1pt} '\; - y)}^{2}}$Начальная функция Грина определяется формулой ${{G}^{{(0)}}} = G$ = $\ln (r(M,M{\kern 1pt} '))$, а остальные функции Грина ${{G}^{{(k)}}},$ $k = 1,2, \ldots $ находятся последовательно из рекуррентных уравнений
(4.2)
$\Delta {{G}^{{(k)}}} = \frac{1}{r}\frac{d}{{dr}}\left( {r\frac{{d{{G}^{{(k)}}}}}{{dr}}} \right) = {{G}^{{(k - 1)}}}(r)$Откуда получаем
(4.3)
${{G}^{{(k)}}} = \frac{{{{r}^{{2k}}}}}{{{{4}^{k}}{{k}^{2}}}}\left( {\ln r - \sum\limits_{i = 1}^k {\frac{1}{i}} } \right)$Приведем выражения для первых трех функций Грина $G$ и ${{G}^{{(1)}}}$ и ${{G}^{{(2)}}}$
(4.4)
$\begin{gathered} G(M,M{\kern 1pt} ') = \ln (r(M,M{\kern 1pt} ')) \\ {{G}^{{(1)}}}(M,M{\kern 1pt} ') = \frac{{{{r}^{2}}(M,M{\kern 1pt} ')}}{4}(\ln (r(M,M{\kern 1pt} ')) - 1) \\ {{G}^{{(2)}}}(M,M{\kern 1pt} ') = \frac{{{{r}^{4}}}}{{64}}\left( {\ln (r(M,M{\kern 1pt} ')) - \frac{3}{2}} \right) \\ \end{gathered} $Граничный контур области $\partial S$ определяется параметрическим уравнением $x\left( s \right),$ $y\left( s \right),$ где s – натуральный параметр контура (длина дуги) (рис. 1).
На границе определяются функции Грина ${{G}^{{(k)}}}(s,s{\kern 1pt} ')$ = ${{G}^{{(k)}}}(M(s),M(s{\kern 1pt} '))$ и ее нормальная производная
(4.5)
$G_{n}^{{(k)}}(s,s{\kern 1pt} ') = \frac{{\partial {{G}^{{(k)}}}}}{{\partial n{\kern 1pt} '}} = \frac{{\partial {{G}^{{(k)}}}}}{{\partial x{\kern 1pt} '}}n_{x}^{'} + \frac{{\partial {{G}^{{(k)}}}}}{{\partial y{\kern 1pt} '}}n_{y}^{'} = \frac{{\partial {{G}^{{(k)}}}}}{{\partial x{\kern 1pt} '}}\frac{{dy{\kern 1pt} '}}{{ds{\kern 1pt} '}} - \frac{{\partial {{G}^{{(k)}}}}}{{\partial y{\kern 1pt} '}}\frac{{dx{\kern 1pt} '}}{{ds{\kern 1pt} '}}$Система граничных уравнений Векуа для полигармонического уравнения имеет следующую структуру:
(4.6)
$\begin{gathered} \sum\limits_{i = 1}^m {({{A}^{{i - 1}}}{{V}^{{i - 1}}} + {{B}^{{i - 1}}}{{\Phi }^{{i - 1}}})} = 0 \\ \sum\limits_{i = 1}^{m - 1} {({{A}^{{i - 2}}}{{V}^{{i - 1}}} + {{B}^{{i - 2}}}{{\Phi }^{{i - 1}}})} = 0 \\ \ldots \\ A{{V}^{{(m - 1)}}} + B{{\Phi }^{{(m - 1)}}} = 0, \\ \end{gathered} $(4.7)
$\begin{gathered} {{A}^{{(k)}}}{{V}^{{(k)}}}(s) = - \int\limits_0^l {{{G}^{{(k)}}}} (s,s{\kern 1pt} '){{V}^{{(k)}}}(s{\kern 1pt} ')ds{\kern 1pt} ' \\ {{B}^{{(k)}}}{{\Phi }^{{(k)}}}(s) = \int\limits_0^l {\frac{{\partial {{G}^{{(k)}}}}}{{\partial n'}}} (s,s{\kern 1pt} '){{\Phi }^{{(k)}}}(s{\kern 1pt} ')ds{\kern 1pt} ';\quad k = 1,2, \ldots ,m - 1 \\ {{\Phi }^{{(k)}}}(M{\kern 1pt} ') = {{\Delta }^{{(k)}}}\Phi (M{\kern 1pt} '),\quad {{V}^{{(k)}}}(M{\kern 1pt} ') = \frac{{\partial {{\Phi }^{{(k)}}}}}{{\partial n{\kern 1pt} '}}, \\ \end{gathered} $4.2. Метод построения схемы с экспоненциальной сходимостью для решения полигармонического уравнения. Аргументом подынтегральных функций операторов ${{A}^{{(k)}}}$ и ${{B}^{{(k)}}}$ является длина дуги $s$, функции имеют период равный длине дуги $l$ граничного контура (рис. 1).
Координату точки $M(x,y)$ на контуре удобно задавать параметрическими уравнениями $x = \varphi (z)$, $y = \psi (z)$, где $\varphi (z)$ и $\psi (z)$ – функции параметра $z$ с единичным периодом. Параметр $z$ и координата $s$ связаны дифференциальным соотношением
(4.8)
$\frac{{ds}}{{dz}} = \sqrt {{{{\left( {\frac{{dx}}{{dz}}} \right)}}^{2}} + {{{\left( {\frac{{dy}}{{dz}}} \right)}}^{2}}} = lf(z),\quad \int\limits_0^1 {f(z){\mkern 1mu} {\kern 1pt} dz = 1} ,$Здесь следует обратить внимание на то, что благодаря произвольности функции $f(z)$ сетка на контуре по длине дуги произвольна, а по параметру $z$ – равномерна. По параметру $z$ шаг сетки всегда равен $1{\text{/}}N$, а по параметру $s$ шаг не равномерен и равен ${{h}_{i}} = lf{\kern 1pt} '({{z}_{i}}){\text{/}}N$. Точки сетки рекомендуется сгущать в окрестности наибольшей кривизны контура или в окрестности минимального расстояния двух соседних граничных контуров.
Заменой $ds = lf(z)dz$ интегральные операторы (4.7) приводятся к виду
(4.9)
$\begin{gathered} {{A}^{{(k)}}}{{V}^{{(k)}}}(z) = - \int\limits_0^1 {{{G}^{{(k)}}}} (z,z{\kern 1pt} '){{V}^{{(k)}}}(z{\kern 1pt} ')lf(z{\kern 1pt} ')dz{\kern 1pt} ' \\ {{B}^{{(k)}}}{{\Phi }^{{(k)}}}(z) = \int\limits_0^1 {G_{n}^{{(k)}}} (z,z{\kern 1pt} '){{\Phi }^{{(k)}}}(z{\kern 1pt} ')dz{\kern 1pt} ' \\ \end{gathered} $(4.10)
$G_{n}^{{(k)}}(z,z{\kern 1pt} ') = \frac{{\partial {{G}^{{(k)}}}}}{{\partial x{\kern 1pt} '}}\frac{{dy}}{{dz{\kern 1pt} '}} - \frac{{\partial {{G}^{{(k)}}}}}{{\partial y{\kern 1pt} '}}\frac{{dx}}{{dz{\kern 1pt} '}}$Для вывода квадратурных формул операторов (4.9) следует выделить особенность у ядра интегрального оператора и воспользоваться теоремой 2.
Теорема 2. Пусть функция $G({{z}_{i}},z)$ имеет в точке $z = {{z}_{i}}$ периодическую особенность и представляется в виде
(4.11)
${{G}^{{(k)}}}({{z}_{i}},z) = {{K}_{i}}H(z - {{z}_{i}}) + g({{z}_{i}},z);\quad {{z}_{i}} = \frac{i}{N},\quad i = 1,2, \ldots ,N,$Тогда
(4.12)
$\begin{gathered} \int\limits_0^1 F (z){{G}^{{(k)}}}({{z}_{i}},z)dz = \frac{1}{N}\sum\limits_{j = 1}^N {\left[ {{{K}_{i}}\beta \left( {\left| {i - j} \right|} \right) + {{G}_{{ij}}}} \right]} F({{z}_{j}}) + {{R}_{N}};\quad i,j = 1,2, \ldots ,N \\ \beta (m) = - H({{z}_{m}}) + {{H}_{N}}({{z}_{m}});\quad m = 1,2, \ldots ,N - 1,\quad \beta (0) = {{H}_{N}}(0) \\ {{G}_{{ij}}} = G({{z}_{i}},{{z}_{j}});\quad i \ne j,\quad {{G}_{{ii}}} = g({{z}_{i}},{{z}_{i}}) \\ \end{gathered} $Остаточный член ${{R}_{N}}$ убывает быстрее любой фиксированной степени $n$ шага сетки ${{R}_{N}} = o(1{\text{/}}{{N}^{n}})$.
Доказательство. Применяя теорему 1 к первому и второму слагаемым (4.11) функции $G({{z}_{i}},z)$, получаем
Вторая формула является квадратурной формулой (3.1) из примера 1. Остаточные члены обеих формул меньше любой степени шага сетки.
Суммируя эти две квадратурные формулы и подставляя $g({{z}_{i}},{{z}_{j}})$ = $G({{z}_{i}},{{z}_{j}})$ – ‒ ${{K}_{i}}H({{z}_{j}} - {{z}_{i}})$, $g({{z}_{i}},{{z}_{i}}) = G_{{ii}}^{{(k)}}$, получим квадратурную формулу (4.12) теоремы 2 , что и требовалось доказать.
Ниже более подробно описано применение изложенного метода к построению схем с экспоненциальной сходимостью для решений гармонического и бигармонического уравнений.
5. Схема для решения гармонического уравнения.
5.1. Интегральное граничное уравнение. Рассмотрим функцию $\Phi (x,y)$, гармоническую внутри области $S$, ограниченной гладким замкнутым контуром $\partial S$ (рис. 1).
Для этого случая система уравнений Векуа (4.6) сводится к одному уравнению
С помощью параметризации $ds = lf(z)dz$ интегральные операторы A и B приводятся к виду (4.9)
(5.2)
$\begin{gathered} AV(z) = - \int\limits_0^1 G (z,z{\kern 1pt} ')V(z{\kern 1pt} ')lf(z{\kern 1pt} ')dz{\kern 1pt} ' \\ B\Phi (z) = \int\limits_0^1 {{{G}_{n}}} (z,z{\kern 1pt} ')(\Phi (z{\kern 1pt} ') - \Phi (z))dz{\kern 1pt} ',\quad {{G}_{n}}(z,z{\kern 1pt} ') = \frac{{\partial G}}{{\partial x{\kern 1pt} '}}\frac{{dy{\kern 1pt} '}}{{dz{\kern 1pt} '}} - \frac{{\partial G}}{{\partial y{\kern 1pt} '}}\frac{{dx{\kern 1pt} '}}{{dz{\kern 1pt} '}} \\ \end{gathered} $Такая форма интегрального уравнения (5.1) и интегрального оператора $B$ (5.2) приведена в работе [17].
Во всех внутренних точках области $S$ функция $\Phi (M)$ представляется в виде суммы потенциалов простого и двойного слоев:
(5.3)
$2\pi \Phi (M) = \int\limits_{\partial S} {\left( { - G(M,M{\kern 1pt} ')\frac{{\partial \Phi }}{{\partial n{\kern 1pt} '}}(M{\kern 1pt} ') + \Phi (M{\kern 1pt} ')\frac{{\partial G(M,M{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}} \right)} ds{\kern 1pt} ';\quad M{\kern 1pt} ' \in \partial S$Эти же уравнения можно получить с помощью теории потенциалов простого и двойного слоев [18].
Ниже с помощью теоремы 2 получены квадратурные формулы для операторов A и B. Граничное интегральное уравнение (5.1) приводится к линейной системе уравнений.
5.2. Квадратурные формулы для оператора A. Для того, чтобы воспользоваться теоремой 2, необходимо выделить в функции $G(z,z{\kern 1pt} ')$ логарифмическую особенность при $z{\kern 1pt} ' = z$. С помощью асимптотических соотношений
(5.4)
$\begin{gathered} r(z{\kern 1pt} ',z) = {\text{|}}s{\kern 1pt} '\; - s{\text{|}}\left( {1 + \mathcal{O}{\text{|}}s - s{\text{|}}} \right) = lf(z)\left| {z{\kern 1pt} '\; - z} \right|\left( {1 + \mathcal{O}\left( {z{\kern 1pt} '\; - z} \right)} \right) = \\ = \frac{{lf(z)}}{\pi }\left| {\sin \pi (z - z)} \right|\left( {1 + \mathcal{O}\left| {\sin \pi (z{\kern 1pt} '\; - z)} \right|} \right) \\ \end{gathered} $(5.5)
$G(z,z{\kern 1pt} ') = \ln r(z{\kern 1pt} ',z) = \ln \frac{{lf(z)}}{\pi } + \ln \left| {\sin \pi (z{\kern 1pt} '\; - z)} \right| + \mathcal{O}\left| {\sin \pi (z{\kern 1pt} '\; - z)} \right|$В нем ${{K}_{i}} = 1$, $H(z) = \ln \left| {\sin \pi (z)} \right|$, ${{G}_{{ii}}} = \ln \frac{{lf({{z}_{i}})}}{\pi }$. Пользуясь рядом Фурье для функции $H(z)$ (3.3), с помощью теоремы 2 получим квадратурную формулу с экспоненциальной сходимостью для интегрального оператора (5.2). Ее удобно выразить через матрицу ${{A}_{{ij}}}$ размерности $N \times N$
(5.6)
$\begin{gathered} AV({{z}_{i}}) = \sum\limits_{j = 1}^N {{{A}_{{ij}}}} {{V}_{j}}l{{f}_{j}};\quad {{A}_{{ij}}} = - \frac{1}{N}\left( {\beta \left( {\left| {i - j} \right|} \right) + {{G}_{{ij}}}} \right) \\ \beta (m) = - \ln \left| {\sin \frac{{\pi m}}{N}} \right| + \alpha (m);\quad m = 1,2, \ldots ,N - 1,\quad \beta (0) = \alpha (0) \\ \alpha (m) = - \left( {\ln 2 + \frac{{{{{( - 1)}}^{m}}}}{N} + \sum\limits_{k = 1}^{N/2 - 1} {\frac{1}{k}} \cos \frac{{2\pi km}}{N}} \right);\quad m = 0,1,2, \ldots ,N, \\ \end{gathered} $Одномерный массив $\alpha (m)$ соответствует формуле (3.3) в примере 2.
5.3. Квадратурные формулы для оператора B. Покажем, что функция ${{G}_{n}}(z,z{\kern 1pt} ')(\Phi (z{\kern 1pt} ') - \Phi (z))$ в интегральном операторе $B$ (5.2) не имеет особенности при $z{\kern 1pt} ' = z$.
Для этого выпишем разложения по степеням $\Delta z = z{\kern 1pt} '\; - z$
(5.7)
$\begin{gathered} \frac{{\partial G}}{{\partial x{\kern 1pt} '}} = \frac{{x{\kern 1pt} '\; - x}}{{{{r}^{2}}(z{\kern 1pt} ',z)}} = \frac{{\frac{{\partial x}}{{\partial z}}\Delta z + \frac{1}{2}\left( {\frac{{{{\partial }^{2}}x}}{{\partial {{z}^{2}}}}} \right)\Delta {{z}^{2}} + \mathcal{O}(\Delta {{z}^{3}})}}{{{{l}^{2}}{{f}^{2}}\Delta {{z}^{2}} + \mathcal{O}(\Delta {{z}^{3}})}} \\ \frac{{\partial y}}{{\partial z{\kern 1pt} '}} = \frac{{\partial y}}{{\partial z}} + \frac{{{{\partial }^{2}}y}}{{\partial {{z}^{2}}}}\Delta z + \mathcal{O}(\Delta {{z}^{3}}) \\ \frac{{\partial G}}{{\partial x{\kern 1pt} '}}\frac{{\partial y}}{{\partial z{\kern 1pt} '}} = \frac{{\frac{{\partial x}}{{\partial z}}\frac{{\partial y}}{{\partial z}}\Delta z + \left( {\frac{{\partial x}}{{\partial z}}\frac{{{{\partial }^{2}}y}}{{\partial {{z}^{2}}}} + \frac{1}{2}\frac{{{{\partial }^{2}}x}}{{\partial {{z}^{2}}}}\frac{{\partial y}}{{\partial z}}} \right)\Delta {{z}^{2}} + \mathcal{O}(\Delta {{z}^{3}})}}{{{{l}^{2}}{{f}^{2}}\Delta {{z}^{2}} + \mathcal{O}(\Delta {{z}^{3}})}} \\ \end{gathered} $Переставляя x и y, находим $\frac{{\partial G}}{{\partial y{\kern 1pt} '}}\frac{{\partial x{\kern 1pt} '}}{{\partial z{\kern 1pt} '}}$. Подставляя эти выражения в формулу (4.10) для ${{G}_{n}}$, получим
(5.8)
${{G}_{n}}(z,z{\kern 1pt} ') = \frac{1}{{2{{l}^{2}}{{f}^{2}}}}\left( {\frac{{\partial x}}{{\partial z}}\frac{{{{\partial }^{2}}y}}{{\partial {{z}^{2}}}} - \frac{{\partial y}}{{\partial z}}\frac{{{{\partial }^{2}}x}}{{\partial {{z}^{2}}}}} \right) + \mathcal{O}(\Delta z),$Отсюда при $z{\kern 1pt} ' \to z$ для подынтегральной функции оператора $B$ получим
(5.9)
${{G}_{n}}(z,z{\kern 1pt} ')(\Phi (z{\kern 1pt} ') - \Phi (z)) = \mathcal{O}(z{\kern 1pt} '\; - z),$(5.10)
$B\Phi ({{z}_{i}}) = \sum\limits_{j = 1}^N {{{B}_{{ij}}}} {{\Phi }_{j}};\quad {{B}_{{ij}}} = \frac{1}{N}{{G}_{{nij}}},\quad i \ne j,\quad {{B}_{{ii}}} = - \sum\limits_{j = 1}^N {{{B}_{{ij}}}} ,$(5.11)
$\begin{gathered} {{G}_{n}}({{z}_{i}},{{z}_{j}}) = \frac{{{{x}_{j}} - {{x}_{i}}}}{{r_{{ij}}^{2}}}\frac{{dy}}{{d{{z}_{j}}}} - \frac{{{{y}_{j}} - {{y}_{i}}}}{{r_{{ij}}^{2}}}\frac{{dx}}{{d{{z}_{j}}}};\quad i \ne j \\ {{x}_{i}} = x({{z}_{i}}),\quad {{y}_{i}} = y({{z}_{i}}),\quad r_{{ij}}^{2} = {{({{x}_{i}} - {{x}_{j}})}^{2}} + {{({{y}_{i}} - {{y}_{j}})}^{2}} \\ \end{gathered} $5.3. Проверка сходимости. Проверим сходимость аппроксимации интегрального уравнения (5.1) с помощью искуственного точного решения.
Рассмотрим эллипс $x = a\cos 2\pi z$, $y = b\sin 2\pi z$ и функцию $\Phi = {{x}^{2}} - {{y}^{2}}$, гармоническую внутри эллипса. Вычисляем ее значения и значения нормальной производной ${{\Phi }_{j}}$, ${{V}_{j}}$ на эллипсе в точках ${{z}_{j}}$, $j = 1,2, \ldots ,N$.
Составляем аппроксимацию левой части интегрального уравнения (5.1)
(5.12)
${{\varepsilon }_{i}} = \sum\limits_{j = 1}^N {\left( {{{A}_{{ij}}}{{V}_{j}}{\mkern 1mu} {\kern 1pt} l{{f}_{j}} + {{B}_{{ij}}}{{\Phi }_{j}}} \right)} ,$Погрешностью аппроксимации интегрального уравнения является величина $\varepsilon = \max \left| {{{\varepsilon }_{i}}} \right|$, $i = 1,2, \ldots ,N$.
В табл. 1 приведены значения $\varepsilon $ в зависимости от числа точек сетки $N$ для эллипса $a = 1$, $b = 0.1$. В первой строке эти значения вычислены по предложенной схеме, а во второй строке по схеме второго порядка, предложенной в [19].
Таблица 1
| N | 32 | 48 | 64 | 80 | 96 | 112 | 128 |
|---|---|---|---|---|---|---|---|
| ε | 4.9 × 10–4 | 1.9 × 10–5 | 7.4 × 10–7 | 2.9 × 10–8 | 1.2 × 10–9 | 4.7 × 10–11 | 1.9 × 10–12 |
| ε1 | 7.2 × 10–3 | 3.5 × 10–3 | 2.0 × 10–3 | 1.3 × 10–3 | 9.2 × 10–4 | 6.8 × 10–4 | 5.2 × 10–4 |
Число точек сетки по схеме с экспоненциальной сходимостью растет по арифметической прогрессии, а погрешность – по геометрической. Тогда как в схеме второго порядка погрешность в зависимости от числа точек сетки $N$ убывает гораздо медленнее по степенному закону $\sim {\kern 1pt} {{N}^{{ - 2}}}$.
Значения функции $\Phi (M)$ во внутренних точках области $S$ определяются интегралом (5.3). Подынтегральная функция особенностей не имеет, и квадратурной формулой с экспоненциальной сходимостью является простейшая формула из примера 1 (3.1)
(5.13)
$2\pi \Phi (M) = \frac{1}{N}\sum\limits_{j = 1}^N {\left[ { - G(M,{{M}_{j}})V({{M}_{j}}) + \Phi ({{M}_{j}}){{G}_{n}}(M,{{M}_{j}})} \right]} l{{f}_{j}};\quad M \in S,$Если точка $M$ имеет координаты $(x,0)$, то ее точное значение равно ${{x}^{2}}$. Введем относительную погрешность $\Delta = (\Phi (M) - {{x}^{2}}){\text{/}}{{x}^{2}}$. Тогда максимальная погрешность равна
Интегральное уравнение внешней задачи выражается через те же самые операторы, что и для внутренней задачи. Быстрота сходимости численной схемы для внешней задачи демонстрируется в [23] сравнением определенных численно значений с точным решением задачи потенциального обтекания эллипса $x = a\cos 2\pi z$, $y = b\sin 2\pi z$, $z \in (0,1)$ с большим отношением его полуосей.
Заметим, что предложенная численная схема дает абсолютно точные значения для скорости ${{V}^{{(\Gamma )}}}$ чисто циркуляционного обтекания эллипса для любого числа точек сетки $N \geqslant 4$ и любых значениях полуосей эллипса $a$ и $b$. Это тем более удивительно, что точные значения получаются для достаточно сложной дробно иррациональной функции
6. Схема с экспоненциальной сходимостью для решения бигармонического уравнения. 6.1. Система интегральных уравнений. Системе граничных интегральных уравнений Векуа (4.6) при $n = 2$ соответствует случай бигармонического уравнения ${{\Delta }^{2}}\Phi (x,y)$. Эта система уравнений принимает вид:
(6.1)
$\begin{gathered} AV(s) + B\Phi (s) + {{A}^{{(1)}}}{{V}^{{(1)}}}(s) + {{B}^{{(1)}}}{{\Phi }^{{(1)}}}(s) = 0 \\ A{{V}^{{(1)}}}(s) + B{{\Phi }^{{(1)}}}(s) = 0 \\ \end{gathered} $Линейные операторы A и B определены в (4.9). Они аппроксимируются матрицами ${{A}_{{ij}}}$ (5.6) и ${{B}_{{ij}}}$ (5.10).
Выпишем операторы ${{A}^{{(1)}}}$ и B(1), определенные в (4.9)
(6.2)
${{A}^{{(1)}}}{{V}^{{(1)}}}(s) = - \int\limits_0^l {{{G}^{{(1)}}}} (s,s{\kern 1pt} '){{V}^{{(1)}}}(s{\kern 1pt} ')ds{\kern 1pt} ',\quad {{B}^{{(1)}}}{{\Phi }^{{(1)}}}(s) = \int\limits_0^l {\frac{{\partial {{G}^{{(1)}}}}}{{\partial n{\kern 1pt} '}}} (s,s{\kern 1pt} '){{\Phi }^{{(1)}}}(s{\kern 1pt} ')ds{\kern 1pt} '$(6.3)
$G_{n}^{{(1)}}(z,z{\kern 1pt} ') = \frac{{\partial {{G}^{{(1)}}}}}{{\partial x{\kern 1pt} '}}\frac{{\partial y{\kern 1pt} '}}{{\partial z{\kern 1pt} '}} - \frac{{\partial {{G}^{{(1)}}}}}{{\partial y{\kern 1pt} '}}\frac{{\partial x{\kern 1pt} '}}{{\partial z{\kern 1pt} '}}$Второе уравнение системы (6.1) является интегральным уравнением (5.1) для гармонической функции ${{\Phi }^{{(1)}}}$.
Значения функции во внутренних точках области $S$ находятся по формуле аналогичной
(6.4)
$\begin{array}{*{20}{c}} {2\pi \Phi (M) = \oint\limits_{\partial S} {\left[ { - G(M,M{\kern 1pt} ')\frac{{\partial \Phi }}{{\partial n{\kern 1pt} '}}(M{\kern 1pt} ') + \Phi (M{\kern 1pt} ')\frac{{\partial G(M,M{\kern 1pt} ')}}{{\partial n'}}} \right.} - } \\ { - \;\left. {{{G}^{{(1)}}}(M,M{\kern 1pt} ')\frac{{\partial {{\Phi }^{{(1)}}}}}{{\partial n{\kern 1pt} '}}(M{\kern 1pt} ') + {{\Phi }^{{(1)}}}(M{\kern 1pt} ')\frac{{\partial {{G}^{{(1)}}}(M,M{\kern 1pt} ')}}{{\partial n{\kern 1pt} '}}} \right]ds{\kern 1pt} ';\quad M \in S} \end{array}$6.2. Квадратурная формула для оператора ${{A}^{{(1)}}}$. Интегральный оператор (6.2) с помощью параметризации $ds = lf(z)dz$ можно представить в виде
(6.5)
${{A}^{{(1)}}}{{V}^{{(1)}}} = - \int\limits_0^1 {{{G}^{{(1)}}}} (z,z{\kern 1pt} '){{V}^{{(1)}}}(z{\kern 1pt} ')lf(z{\kern 1pt} ')dz{\kern 1pt} ',\quad {{G}^{{(1)}}} = \frac{{{{l}^{2}}{{f}^{2}}(z)}}{{4{{\pi }^{2}}}}H(z{\kern 1pt} '\; - z) + g(z,z{\kern 1pt} '),$(6.6)
$H(z) = \frac{1}{2}{{\sin }^{2}}(\pi z)\ln {{(2\sin \pi z)}^{2}} = \frac{1}{4} - \frac{{3\cos x}}{8} + \sum\limits_{k = 2}^\infty {\frac{{\cos (kx)}}{{2k({{k}^{2}} - 1)}}} ;\quad x = 2\pi z$Функция $g(z,z{\kern 1pt} ')$ – аналитическая функция единичного периода по обоим аргументам и удовлетворяет условию $g(z,z) = 0$.
По теореме 2 для интегрального оператора получаем следующую квадратурную формулу
(6.7)
$\begin{gathered} {{A}^{{(1)}}}{{V}^{{(1)}}}({{z}_{i}}) = \sum\limits_{j = 1}^N {A_{{ij}}^{{(1)}}} V_{j}^{{(1)}}l{{f}_{j}} \\ A_{{ij}}^{{(1)}} = - \frac{{{{l}^{2}}f_{i}^{2}}}{{4{{\pi }^{2}}N}}\left( {{{\beta }_{1}}\left( {\left| {i - j} \right|} \right) + G_{{ij}}^{{(1)}}} \right) \\ {{\beta }_{1}}(m) = - H({{z}_{m}}) + {{\alpha }_{1}}(m);\quad m = 1,2, \ldots ,N - 1, \\ \end{gathered} $Одномерный массив значений ${{\alpha }_{1}}(m)$ определяется по коэффициентам ряда Фурье (3.4) с помощью теоремы 1.
(6.8)
$\begin{gathered} {{\alpha }_{1}}(m) = \left( {\frac{1}{4} + \frac{{{{{( - 1)}}^{m}}}}{{4M({{M}^{2}} - 1)}} - \frac{{3\cos (2\pi m{\text{/}}N)}}{8} + \sum\limits_{n = 2}^{M - 1} {\frac{{\cos (2\pi nm{\text{/}}N)}}{{2n({{n}^{2}} - 1)}}} } \right) \\ {{\beta }_{1}}(0) = {{\alpha }_{1}}(0) = \frac{1}{{4 - 4{{M}^{2}}}} \\ \end{gathered} $6.3. Квадратурная формула для оператора ${{B}_{1}}$. Преобразуем ядро оператора ${{B}_{1}}$
(6.9)
$G_{n}^{{(1)}} = \frac{1}{4}\left( {\frac{{dy}}{{dz{\kern 1pt} '}}(x{\kern 1pt} '\; - x) - \frac{{dx}}{{dz{\kern 1pt} '}}(y{\kern 1pt} '\; - y)} \right)\left( {\frac{1}{2}\ln \left( {{{{(x{\kern 1pt} '\; - x)}}^{2}} + {{{(y{\kern 1pt} '\; - y)}}^{2}}} \right) - 1} \right)$Выделяем логарифмическую особенность
(6.10)
$G_{n}^{{(1)}}(z,z{\kern 1pt} ') = K(z)H(z{\kern 1pt} '\; - z) + g(z,z{\kern 1pt} ');\quad K(z) = - \frac{1}{{4{{\pi }^{2}}}}\left( {\frac{{{{d}^{2}}y}}{{d{{z}^{2}}}}\frac{{dx}}{{dz}} - \frac{{{{d}^{2}}x}}{{d{{z}^{2}}}}\frac{{dy}}{{dz}}} \right)$По теореме 2 находим матрицу, аппроксимирующую оператор ${{B}^{{(1)}}}$
(6.11)
$B_{{ij}}^{{(1)}} = K({{z}_{i}}){{\beta }_{1}}\left( {\left| {i - j} \right|} \right) + G_{n}^{{(1)}}({{z}_{i}},{{z}_{j}})$6.4. Проверка сходимости. Сходимость численной схемы для бигармонического уравнения можно проверить на искуственном точном решении также как и для гармонического уравнения в разд. 5. Выбирается бигармоническая функция $\Phi = {{x}^{3}} - {{y}^{3}}$ и для нее находятся значения в точках граничной сетки значения функции ${{\Phi }_{i}}$, ee нормальной производной ${{V}_{i}}$ функций $\Phi _{i}^{{(1)}}$ и $V_{i}^{{(1)}}$, $i = 1,2,...,N$. Погрешности численной схемы для системы уравнений (6.1) вычисляются по формулам
(6.12)
$\begin{gathered} {{\varepsilon }_{i}} = \sum\limits_{j = 1}^N {\left( {{{A}_{{ij}}}{{V}_{j}}l{{f}_{j}} + {{B}_{{ij}}}{{\Phi }_{i}} + A_{{ij}}^{{(1)}}V_{j}^{{(1)}}l{{f}_{j}} + B_{{ij}}^{{(1)}}\Phi _{j}^{{(1)}}} \right)} \\ {{\delta }_{i}} = \sum\limits_{j = 1}^N {\left( {{{A}_{{ij}}}V_{j}^{{(1)}}l{{f}_{j}} + {{B}_{{ij}}}\Phi _{i}^{{(1)}}} \right)} \\ \end{gathered} $В табл. 2 приведены значения максимальной погрешности $\varepsilon = \max \left| {{{\varepsilon }_{i}}} \right|$, $\delta = \max \left| {{{\delta }_{i}}} \right|$ в зависимости от числа точек сетки $N$ для эллипса $a = 1$, $b = 0.1$.
Таблица 2
| N | 32 | 48 | 64 | 80 | 96 | 112 |
|---|---|---|---|---|---|---|
| ε | 7 × 10–4 | 2.8 × 10–5 | 1.1 × 10–6 | 5.6 × 10–8 | 1.3 × 10–8 | 6 × 10–9 |
| δ | 1.4 × 10–2 | 5.5 × 10–4 | 2.2 × 10–5 | 8.7 × 10–7 | 3.5 × 10–8 | 1.4 × 10–9 |
| ε1 | 9.6 × 10–3 | 4.7 × 10–3 | 2.7 × 10–3 | 1.8 × 10–3 | 1.3 × 10–3 | 9.3 × 10–4 |
| δ1 | 2.6 × 10–2 | 1.2 × 10–2 | 6.9 × 10–3 | 4.4 × 10–3 | 3.1 × 10–3 | 2.2 × 10–3 |
В первых двух строках приведены погрешности схемы с экспоненциальной сходимостью ε и δ, а в следующих двух строках погрешности схемы второго порядка [22], обозначенные ${{\varepsilon }_{1}}$ и ${{\delta }_{1}}$. Как видно из таблицы, погрешность квадратурных формул при 112 точках сетки на пять порядков меньше погрешности схемы второго порядка, которая обычно используется для решения краевых задач бигармонического уравнения.
Все приведенные таблицы показывают убывание погрешности по геометрической прогрессии при увеличении числа узлов сетки по арифметической прогрессии так, как и должно быть в схеме с экспоненциальной сходимостью.
Cходимость вычислений бигармонической функции ${{x}^{3}} - {{y}^{3}}$ во внутренних точках проверяем так же, как и сходимость для гармонической функции. Если точка $M$ имеет координаты $(x,0)$, то ее точное значение равно ${{x}^{3}}$. Численные значения находим с помощью аппроксимации интегральной формулы (6.4). Введем относительную погрешность $\delta \Phi = (\Phi (M) - {{x}^{3}}){\text{/}}{{x}^{3}}$. Максимальная погрешность равна $\max \left| {\delta \Phi } \right| = 8 \times {{10}^{{ - 6}}}$ при $N = 128$; $\max \left| {\delta \Phi } \right| = 3.0 \times {{10}^{{ - 7}}}$ при $N = 160$; $\max \left| {\delta \Phi } \right| = 1.5 \times {{10}^{{ - 8}}}$ при $N = 192$; $\max \left| {\delta \Phi } \right| = 5.5 \times {{10}^{{ - 10}}}$ при $N = 224$.
Как видно из приведенных результатов вычислений, погрешности убывают также по геометрической прогрессии.
7. Схема с экспоненциальной сходимостью для решения полигармонического уравнения. Аналогично можно получить квадратурные формулы с экспоненциалной сходимостью для операторов ${{A}^{{(k)}}}$ и ${{B}^{{(k)}}}$ для любого натурального $k = 1,2,3, \ldots $ в системе уравнений Векуа Ф (4.6). Для этого достаточно заметить, что ядро ${{G}^{{(k)}}}$ (2.2) оператора ${{A}^{{(k)}}}$ c точностью до множителя $K$ имеет периодическую особенность
Ядро представляется в виде ${{G}^{{(k)}}}({{z}_{i}},z) = {{K}_{i}}{{H}_{k}}({{z}_{i}} - z) + g({{z}_{i}},z)$, $k = 0,1,2, \ldots ,$ где функция $g({{z}_{i}},z)$ аналитична и имеет единичный период по обоим аргументам.
Периодическую особенность можно разложить в ряд Фурье с помощью следующих формул
Приведем ряды для ${{H}_{k}}$, $k = 0,1,2,3$
Для ${{H}_{0}}$ и ${{H}_{1}}$ ряды Фурье приведены в (3.2) и (3.4).
С помощью теоремы 2 можно выписать квадратурные формулы с экспоненциальной сходимостью для операторов ${{A}^{{(k)}}}{{V}^{{(k)}}}$, $k = 1,2,3,4$. Особенности ядер $G_{n}^{{(k)}}$ (4.10) операторов ${{B}^{{(k)}}}$ отличаются от особенностей ядер $G_{{}}^{{(k)}}$ операторов ${{A}^{{(k)}}}$ только множителем и для них квадратурные формулы находятся аналогично.
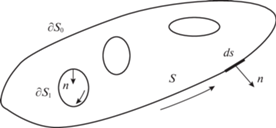
8. Численная схема для решения задач гидродинамики. Рассмотрим решение плоской задачи течения вязкой жидкости в приближении Стокса в многосвязной области $S$, ограниченной снаружи контуром $\partial {{S}_{0}}$, а изнутри контурами $\partial {{S}_{i}}$, $i = 1,2, \ldots n$ (рис. 2).
Краевая задача для функции тока $\Psi (x,y)$ ставится так. В области течения жидкости $S$ функция тока $\Psi (x,y)$ и давление $p(x,y)$ удовлетворяют уравнениям
(8.1)
$\mu \Delta \frac{{\partial \Psi }}{{\partial y}} = \frac{{\partial p}}{{\partial x}},\quad \mu \Delta \frac{{\partial \Psi }}{{\partial x}} = - \frac{{\partial p}}{{\partial y}};\quad (x,y) \in S$Из них следует гармоничность функции давления $\Delta p(x,y) = 0$ и бигармоничность функции тока
На границе области задаются значения функции тока $\Psi (s)$ и ее нормальной производной $\frac{{\partial \Psi }}{{\partial n}}(s)$
(8.2)
${{\left. \Psi \right|}_{{\partial S}}} = \psi (s),\quad {{\left. {\frac{{\partial \Psi }}{{\partial n}}} \right|}_{{\partial S}}} = {v}(s);\quad (x,y) \in {\text{ }}\partial S$Для многосвязных областей функции $\psi (s)$ на границах $\partial {{S}_{i}}$, $i = 1, \ldots n$ функции тока $\psi (s)$ определены с точностью до постоянных значений ${{c}_{i}}$, $i = 1, \ldots n$. Для определения этих постоянных значений требуется еще выполнение условий однозначности давления в области $S$. Из них следует выполнение следующих условий на каждом контуре $\partial {{S}_{i}}$, $i = 0,1, \ldots n$: $\int_{\partial {{S}_{i}}} {\frac{{\partial p}}{{\partial s}}ds} $ = 0, где $ds$ – элемент длины.
В силу тождества $\frac{{\partial p}}{{\partial s}} = - \mu \frac{{\partial \Delta \Psi }}{{\partial n}}$ условия однозначности давления принимают вид
(8.3)
$\int\limits_{\partial {{S}_{i}}} {\frac{{\partial \Delta \Psi }}{{\partial n}}} ds = 0;\quad i = 1,2, \ldots ,n$Задача сводится к решению системы интегральных уравнений (6.1), которая для граничных значений (8.2) функций $\psi (s)$, ${v}(s)$ и функций ${{\Psi }^{1}}(s)$ и ${{V}^{{(1)}}}(s)$ примет вид
(8.4)
$\begin{gathered} Av(s) + B\psi (s) + {{A}^{{(1)}}}{{V}^{{(1)}}}(s) + {{B}^{{(1)}}}{{\Psi }^{1}}(s) = 0 \\ A{{V}^{{(1)}}}(s) + B{{\Psi }^{{(1)}}}(s) = 0 \\ \end{gathered} $Из системы уравнений (8.3), (8.4) определяются функции ${{V}^{{(1)}}}(s)$, ${{\Psi }^{1}}(s)$ на границах $\partial {{S}_{i}}$, $i = 0,1,...,n$ и постоянные ${{c}_{i}}$ на границах $\partial {{S}_{i}}$, $i = 1, \ldots n$. Значения функции во внутренних точках области $S$ выражаются через контурные граничные интегралы (6.4). Подынтегральные функции на каждом контуре периодичны и не имеют особенностей. Поэтому квадратурные формулы для них имеют вид, аналогичный (5.13) для случая гармонического уравнения в разд. 5.
(8.5)
$\begin{array}{*{20}{c}} {2\pi \Phi (M) = \frac{1}{N}\sum\limits_{j = 1}^N {\left[ { - G(M,{{M}_{j}})V({{M}_{j}}) + \Phi ({{M}_{j}})G_{n}^{{}}(M,{{M}_{j}})} \right.} - } \\ { - \;\left. {{{G}^{1}}(M,{{M}_{j}}){{V}^{{(1)}}}({{M}_{j}}) + {{\Phi }^{1}}({{M}_{j}})G_{n}^{{(1)}}(M,{{M}_{j}})} \right]l{{f}_{j}};\quad M \in S,} \end{array}$9. Примеры решения задач гидродинамики. В качестве примера применения численных схем разд. 8 рассмотрим следующую задачу. Пусть внутри неподвижного эллиптического цилиндра: $\frac{{{{x}^{2}}}}{{{{a}^{2}}}} + \frac{{{{y}^{2}}}}{{{{b}^{2}}}} = 1$ с полуосями $a$ и $b$ вращается круговой цилиндр радиуса $R$: ${{(x - {{x}_{0}})}^{2}} + {{y}^{2}} = {{R}^{2}}$. Полость $S$ между цилиндрами заполнена вязкой жидкостью. Нужно определить функцию тока $\Psi (x,y)$.
Приведем численную схему решения. Граничные точки сетки распределяются следующим образом: на эллипсе ${{N}_{0}}$ точек с индексами $i = 1,2, \ldots ,{{N}_{0}}$, на окружности ${{N}_{1}}$ точек с индексами $i = {{N}_{0}} + 1$, ${{N}_{0}} + 2$, …, ${{N}_{0}} + {{N}_{1}} = N$. Система интегральных уравнений (8.4) аппроксимируется по предложенным квадратурным формулам линейной системой
(9.1)
$\begin{gathered} \sum\limits_{j = 1}^N {\left( {{{A}_{{ij}}}{{V}_{j}}l{{f}_{j}} + {{B}_{{ij}}}{{\Psi }_{j}} + A_{{ij}}^{{(1)}}V_{j}^{{(1)}}l{{f}_{j}} + B_{{ij}}^{{(1)}}\Psi _{j}^{{(1)}}} \right)} = 0 \\ \sum\limits_{j = 1}^N {\left( {{{A}_{{ij}}}V_{j}^{{(1)}}l{{f}_{j}} + {{B}_{{ij}}}\Psi _{j}^{{(1)}}} \right)} = 0 \\ \end{gathered} $К этой системе добавляется аппроксимация уравнения (8.3)
На эллипсе задаются условия ${{\Psi }_{j}} = {{V}_{j}} = 0$, $j = 1,2, \ldots ,{{N}_{0}}$ и на круге ${{\Psi }_{j}} = q$, ${{V}_{j}} = 1$, $j = {{N}_{0}} + 1,{{N}_{0}} + 2$, …, N. Из системы $2N + 1$ уравнений определяются $2N + 1$ неизвестных значений: $\Psi _{j}^{{(1)}}$, $V_{j}^{{(1)}}$, $j = 1, \ldots ,N$ = ${{N}_{0}} + {{N}_{1}}$ и q. Функция тока во внутренних точках области $S$ определяется по формуле (8.5). Погрешность аппроксимации определяется сравнением с точным решением, а если его нет, то с помощью искусственного точного решения погрешностей $\varepsilon $ и $\delta $ находятся по формулам (6.12). Рассмотрим частные случаи.
Пример 1. Пусть полость между двумя коаксиальными круговыми цилиндрами заполнена вязкой жидкостью. Внешний круг радиуса ${{R}_{0}} = 2$, а внутренний радиуса ${{R}_{1}}$. Внешний круг неподвижен, а внутренний вращается. На границах кругов задаются скорости ${{{v}}_{0}} = 0$ и ${{{v}}_{1}} = 1$ соответственно. Для функции тока задается значения равное нулю на внешнем круге и $q$ – на внутреннем. Значение $q$ и функция тока в области течения подлежат определению. Эта задача имеет точное решение [20]
На границах круга выполняются условия
Для численного решения этой задачи граничные условия (8.2) имеют вид
(9.3)
${{\left. \Psi \right|}_{{\partial {{S}_{0}}}}} = 0,\quad {{\left. \Psi \right|}_{{\partial {{S}_{1}}}}} = q,\quad {{\left. {\frac{{\partial \Psi }}{{\partial n}}} \right|}_{{\partial {{S}_{0}}}}} = 0,\quad {{\left. {\frac{{\partial \Psi }}{{\partial n}}} \right|}_{{\partial {{S}_{1}}}}} = 1$Из решения системы уравнений (9.1), (9.2) находятся значения $\Psi _{j}^{{(1)}}$, $V_{j}^{{(1)}}$, $j = 1$, …, $N = {{N}_{0}} + {{N}_{1}}$ на границе и величина расхода жидкости $q$. Функция тока внутри области $S$ определяется по найденным граничным значениям по формуле (8.5).
Ниже приведена табл. 3, демонстрирующая зависимость погрешности вычисления расхода $\delta q$ от чиcла точек $N$ для радиуса ${{R}_{0}} = 2$ и радиусов ${{R}_{1}} = 0.5$, 1 и 1.5.
Таблица 3
| R1 | N | 6 | 8 | 10 | 12 | 14 | 16 |
|---|---|---|---|---|---|---|---|
| 0.5 | δq | 1.8 × 10–4 | 1.1 × 10–5 | 6.9 × 10–7 | 4.3 × 10–8 | 2.7 × 10–9 | 1.7 × 10–10 |
| N | 12 | 16 | 20 | 24 | 28 | 32 | |
| 1 | δq | 1.8 × 10–4 | 1.1 × 10–5 | 6.9 × 10–7 | 4.3 × 10–8 | 2.7 × 10–9 | 1.6 × 10–10 |
| N | 32 | 40 | 48 | 56 | 64 | 72 | |
| 1.5 | δq | 4.8 × 10–5 | 4.6 × 10–6 | 4.6 × 10–7 | 4.6 × 10–8 | 4.5 × 10–9 | 4.5 × 10–10 |
Для всех значений радиусов характерна скорость убывания погрешности по геометрической прогрессии с ростом числа точек по арифметической прогрессии. Знаменатели геометрической прогрессии меньше единицы. Однако с увеличением радиуса знаменатель прогрессии увеличивается.
Пример 2. Полость между двумя круговыми цилиндрами, расположенными эксцентрично, заполнена вязкой жидкостью. Внешний круг радиуса ${{R}_{0}} = 2$, а внутренний радиуса ${{R}_{1}} = 0.5$. Краевые условия такие же как в предыдущем примере (9.3). Значение расхода $q$ и функция тока внутри области течения подлежат определению. Задача также имеет точное решение, но гораздо более сложное. Пользуясь точными формулами [21], находим: $q$ = –0.43157034963 при расстоянии между центрами кругов $\Delta x = 0.5$ и $q$ = –0.26752948323 при $\Delta x = 1$. В табл. 4 приведены погрешности вычисления расхода при различном числе узлов сетки $N$ для расстояний между центрами кругов 0.5 и 1.
Таблица 4
| $\Delta x$ | N | 8 | 12 | 16 | 20 |
|---|---|---|---|---|---|
| 0.5 | δq | 8.2 × 10–4 | 5.3 × 10–6 | 3.6 × 10–8 | 2.3 × 10–10 |
| N | 16 | 24 | 32 | 40 | |
| 1 | δq | 1.3 × 10–3 | 1.6 × 10–5 | 1.9 × 10–7 | 2.1 × 10–9 |
На рис. 3,а изображены линии тока для кругового цилиндра, радиуса ${{R}_{1}} = 0.5$, вращающегося с единичной скоростью внутри неподвижного кругового цилиндра радиуса ${{R}_{0}} = 2$. Расстояние между центрами кругов равно 1. Функция тока имеет значения 0 на внешнем цилиндре и $q = - 0.2675$ на внутреннем. Внутри области линии тока имеют отрицательные значения $(i{\text{/}}5)q$, $i = 0,1,...,5$ и положительные 0.01i, $i = 1,2, \ldots 5$. На внешней окружности 96 точек, а на внутреннем круге 64. Картина линий тока не отличается от построенной на точном решении.
Рис. 3.
Линии тока вязкой жидкости внутри эллиптической области, создаваемые а) вращением двух круговых цилиндров а) в одинаковом направлении, б) в противоположном направлении.
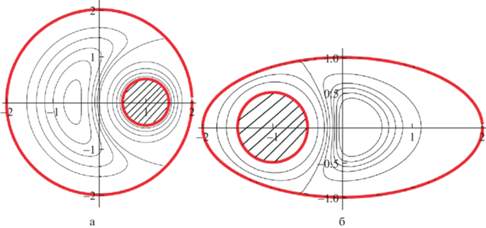
Пример 3. Полость между внешним эллиптическим и внутренним круговым цилиндрами заполнена вязкой жидкостью (рис. 3, б). Эллипc и круг задаются уравнениями
Круговой цилиндр вращается вогруг своей оси с постоянной угловой скоростью, а внешний эллиптический цилиндр покоится. Значения функции тока и скорости жидкости на неподвижной эллиптической границе полагаем нулем. Скорость на границе круга полагаем равной единице, а значение функции тока равным $q$. Для этой задачи точного решения не существует и точность аппроксимации линейной системы проверяется на искуственном точном решении бигармонической функции ${{x}^{3}} - {{y}^{3}}$.
В табл. 5 приводятся невязки $\varepsilon $ и $\delta $, а также погрешности во внутренних точках: в точке ${{M}_{1}}(1.9,0)$ погрешность $\Psi (1.9,0) - ({{1.9}^{3}})$ и в точке ${{M}_{2}}(0,0.08)$ погрешность $\Psi (0,0.8)$ + (0.83) при различных значениях числа точек на контурах ${{N}_{0}}$ и ${{N}_{1}}$.
Таблица 5
| N0, N1 | 32.64 | 48.96 | 64.128 |
|---|---|---|---|
| ε | 2.2 × 10–5 | 9.4 × 10–8 | 2.2 × 10–8 |
| δ | 3.8 × 10–5 | 6.0 × 10–8 | 9.5 × 10–11 |
| M1 | 6.2 × 10–3 | 1.7 × 10–4 | 4.6 × 10–6 |
| M2 | 1.5 × 10–3 | 5.7 × 10–5 | 2.1 × 10–6 |
Полагая ${{N}_{1}} = {{N}_{2}} = 64$, из решения линейной системы уравнений находим $q = 0.1698$ и неизвестные $\Psi _{i}^{{(1)}}$, $V_{i}^{{(1)}}$, $i = 1,2, \ldots {{N}_{1}} + {{N}_{2}}$, а функцию тока $\Psi (x,y)$ внутри области вычисляем по аппроксимации (5.3). На рис. 3,б приведены линии тока $\Psi (x,y)$ = = const. Два замкнутых семейства линий тока разделяет линия $\Psi (x,y) = 0$, примыкающая к границе эллипса. Из первого семейства выбраны три замкнутые линии тока $\Psi = q{\text{/}}3$, $2q{\text{/}}3$ и линия $\Psi = q$, совпадающая с границей круга. Для второго семейства выбраны линии с отрицательными значениями функции тока $\Psi = - 0.05i$, $i = 1,2,...,5$.
Пример 4. Полость между эллиптическим и двумя круговыми цилиндрами заполнена вязкой жидкостью (рис. 4). Эллипc и круги задаются уравнениями $\frac{{{{x}^{2}}}}{4} + \frac{{{{y}^{2}}}}{1} = 1$, ${{(x \pm 1)}^{2}} + {{y}^{2}} = 1{\text{/}}4$.
Рис. 4.
Линии тока вязкой жидкости внутри эллиптической области, создаваемые а) вращением двух круговых цилиндров а) в одинаковом направлении, б) в противоположном направлении.
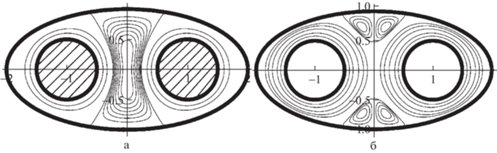
Круговые цилиндры вращаются вокруг своей оси с постоянной угловой скоростью в одном направлении (рис. 1,а) и в противоположных направлениях (рис. 1,б). Внешний цилиндр покоится. Значение функции тока и скорость жидкости на неподвижной эллиптической границе полагаем равными нулю. Скорость на границе каждого круга полагаем равной единице, а значение функции тока равным $q$. Это значение подлежит определению.
Задача сводится к решению системы уравнений (9.1) с двумя дополнительными условиями (8.3) равенство нулю циркуляций на каждой окружности. Они следуют из требования однозначности функции давления и с помощью квадратурной формулы (3.1) аппроксимируются следующим образом
Пример 5. Предложенная схема удобна также для расчета обтеканий периодических структур. Для учета этой периодичности надо учесть периодичность в функции Грина и решить задачу обтекания в периодической ячейке. Покажем это на решении задачи потенциального обтекания периодической решетки круговых цилиндров между двумя плоскостями. Задача ставится следующим образом. Между двумя пластинами расположенными на уровнях $y = \pm b$ помещена периодическая цепочка круговых цилиндров радиуса $R$ с центрами в точках $y = {{y}_{0}}$, $x = kL$, $k = ...{\kern 1pt} - {\kern 1pt} 1,0,1,2, \ldots $ Тогда периодическая функция тока $\Psi (x + L,y) = \Psi (x,y)$ потенциального обтекания найдется из решения следующей краевой задачи. В области течения функция тока должна удовлетворять уравнению Лапласа, на пластинах она должна принимать постоянные значения ${{\psi }_{1}}$ и ${{\psi }_{2}}$, а на круговом цилиндре ${{\psi }_{3}}$.
Для такой задачи доказывается теорема единственности также как для внутренней краевой задачи для уравнения Лапласа. Предполагая, что существуют два решения ${{\Psi }_{1}}$ и ${{\Psi }_{2}}$, получаем, что разность $\delta \Psi = {{\Psi }_{2}} - {{\Psi }_{1}}$ удовлетворяет уравнению Лапласа и нулевым краевым условиям. Тогда в прямоугольнике $S = x \in ( - L{\text{/}}2,L{\text{/}}2)$, $y \in ( - b,b)$ (ячейка периодичности): интеграл $\int_S {{{{(\operatorname{grad} \delta \Psi )}}^{2}}} dxdy$ приводится к интегралу по границе ячейки $\int_S {\left( {\delta \Psi \frac{{\partial \delta \Psi }}{{\partial n}}} \right)} ds.$ Он, очевидно, равен нулю, так как, на пластинах и на круге $\delta \Psi = 0$, а на сторонах $x = \pm L{\text{/2}}$ интегралы в силу периодичности сокращаются. $\int_S {{{{(\operatorname{grad} \delta \Psi )}}^{2}}} dxdy$ = 0. Отсюда получаем: $\operatorname{grad} \delta \Psi $ = $0 \Rightarrow \delta \Psi $ = const = 0.
Решение задачи сводится к интегральному уравнению (5.1)$AV(s) + B\Psi (s) = 0$, где $\Psi (x,y)$ – функция тока, а $V(s) = \partial \Psi {\text{/}}\partial n$ – скорость на границе. В интегральных операторах A и B – функцию Грина $G(x,y)$ = $\frac{1}{2}\ln ({{x}^{2}} + {{y}^{2}})$ нужно заменить на периодическую функцию Грина
Далее нужно воспользоваться квадратурными формулами (5.6) для оператора $A$ и (5.10) для оператора $B$.
На рис. 5 изображены линии тока для обтекания периодической системы кругов радиуса $R = 1$ с центрами в точках $y = {{y}_{0}}$, $x = k2\pi $, $k = ...{\kern 1pt} - {\kern 1pt} 1,0,1,2, \ldots $ между двумя пластинами, расположенными на уровнях $y = \pm \pi $. На пластинах задаются нулевые значения функции тока, а на окружности $\Psi = 1$. Значения функций тока на изображенных линиях меняются от нуля до единицы c шагом 0.1. Кроме того изображены критические линии тока, разделяющие направление скорости на них. На рис. 5,а центры кругов расположены на средней линии ${{y}_{0}} = 0$ между пластинами. В этом случае картина линий тока симметрична относительно линии центров. Критической линии тока соответствует значение функции тока 0.5576. В критической точке, расположенной на средней линии, критическая линия тока разделяется на две ветви нижнюю и верхнюю. Между нижней пластиной и нижней ветвью критической линии тока жидкость течет слева направо с расходом $Q = 0.5576$, а между верхней ветвью и верхней пластиной жидкость течет справа налево с отрицательным расходом $Q = - 0.5576$. Между окружностью и двумя ветвями критической линии тока жидкость движется по замкнутым линиям тока против часовой стрелки.
Рис. 5.
Линии тока потенциального циркуляционного обтекания решетки круговых цилиндров между двумя плоскостями: а) симметричное обтекание, б) ассимметричное обтекание.
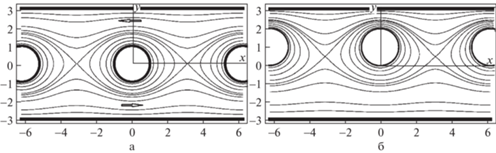
На рис. 5,б центры кругов расположены выше средней линии, т.е. ${{y}_{0}} = 1$. При этом течение не симметрично, но также как и в симметричном случае имеется критическая линия тока с иным значением функции тока 0.5365. Между нижней пластиной и нижней ветвью критической линии тока жидкость течет слева направо с расходом $Q = 0.5365$, а между верхней ветвью и верхней пластиной жидкость течет справа налево с отрицательным расходом $Q = - 0.5365$.
Заключение. Предложен конструктивный алгоритм получения численных схем с экспоненциальной сходимостью для решения краевых задач для полигармонического уравнения в произвольных многосвязных областях, ограниченных гладкими контурами. Матрицы ${{A}_{{ij}}}$, ${{B}_{{ij}}}$ квадратурных формул интегральных операторов $A$ и $B$ легко находятся с помощью выписанных рядов Фурье для функций Грина и применения теорем 1 и 2. По сравнению с известными, предложенный алгоритм проще программируется, так как все квадратурные формулы имеют явную и простую форму. Области, в которых решается краевая задача, могут быть самыми разнообразными, в том числе многосвязными. Достаточно задать границу области двумя параметрическими функциями или даже в оцифрованном табличном виде. Предложенный алгоритм позволяет решать как внутренние, так и внешние задачи без усложнения схем.
Если же сравнивать предложенную численную схему с экспоненциальной скоростью сходимости с другими разностными или с известными схемами второго порядка метода граничных элементов [22], то она существенно экономичнее, и позволяет достигать машинной точности при сравнительно малом числе элементов сетки (около сотни). Решение линейной системы сотого порядка решается практически мгновенно. Схема также удобна для расчета периодических структур. Для этого достаточно решить интегральное уравнение на одной ячейке периодичности и заменить функцию Грина на периодическую функцию Грина с сохранением ее особенности в нуле. Заметим, что в силу сохранения особенности коэффициенты квадратурных формул не меняются, а периодическая структура в численной схеме учитывается за счет периодичности функции Грина. Предлагаемые численные схемы можно применять не только в гидродинамике, но и для решения других задач математической физики, сводящихся к краевым задачам для эллиптических уравнений.
Например, краевые задачи для решения широкого класса теории упругости изложены в монографии [24]. В ней используется метод конформных отображений, достижимый для ограниченного класса задач, тогда как представленная численная схема применима для произвольных геометрических областей.
Исследование выполнено за счет гранта Российского научного фонда (проект № 22-21-00833).
Список литературы
Boyd J.P. Chebyshev and Fourier Spectral Methods. Dover: Mineola, 2001.
Orszag S.A., Gotlib D. Numerical Analysis of Spectral Methods. Theory and Applications. SIAM, Philadelphia, Pennsylvania: 19103, 1977. 169 p.
Hafeez M.B., Krawczuk M.A. Review: applications of the spectral finite element method // Arch. Comput. Meths in Engng. 2023. P. 1–13. https://doi.org/10.1007/s11831-023-09911-2
Бабенко К.И. Основы численного анализа. М.; Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2002. 848 с.
Бабенко К.И. Несколько замечаний о дискретизации эллиптических задач // Докл. АН СССР. 1975. Т. 221. № 1. С. 1114.
Алгазин С.Д. h-матрица, новый математический аппарат для дискретизации многомерных уравнений математической физики. M.: URSS, 2017. 246 с.
Алгазин С.Д. Численные алгоритмы без насыщения для уравнения Шрёдингера атома водорода // Вычисл. методы и програм. 2018. Т. 19. С. 215–218.
Крылов В.И. Приближенное вычисление интегралов. М.: Наука, 1967. 500 с.
Kress R. Linear Integral Equation. Springer, 1999. 380 p.
Калиткин Н.Н., Колганов С.А. Функции Ферми–Дирака. Прямое вычисление функций // Препр. ИПМ им. М.В. Келдыша. 2018. 235 с.
Белых В.Н. К проблеме конструирования ненасыщаемых квадратурных формул на отрезке // Матем. сб. 2019. Т. 210. № 1. С. 27–62.
Петров А.Г. Численные схемы без насыщения для периодических функций // Докл. РАН. 2018. Т. 481. № 4. С. 362–366.
Петров А.Г. Алгоритм построения квадратурных формул с экспоненциальной сходимостью для линейных операторов, действующих на периодические функции// Изв. вузов. Математика. 2021. № 2. С. 86–92.
Бари Н.К. Тригонометрические ряды. М.: Физматлит, 1961. 936 с.
Петров А.Г., Смолянин В.Г. Расчет профиля капиллярно-гравитационной волны на поверхности тяжелой жидкости конечной глубины // Вестн. МГУ. № 2. 1991. С. 92–96.
Векуа И.Н. Новые методы решения эллиптических уравнений. М.: Физматлит, 1948.
Воинов О.В., Воинов В.В. Численный расчет нестационарных движений идеальной несжимаемой жидкости со свободными поверхностями // Докл. АН СССР. 1975. Т. 221. № 3. С. 559–562.
Соболев С.Л. Уравнения математической физики. М.: Физматлит, 1966.
Казакова А.О., Терентьев А.Г. Численное решение краевых задач для полигармонического уравнения // ЖВММФ. 2012. Т. 52. № 11. С. 2050–2059.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986.
Казакова А.О., Петров А.Г. О поле скоростей вязкой жидкости между двумя цилиндрами, вращающимися и движущимися поступательно // Изв. РАН. МЖГ. 2016. № 3. С. 16–25.
Казакова А.О., Петров А.Г. Расчет течения вязкой жидкости между двумя произвольно движущимися цилиндрами произвольного сечения // ЖВММФ. 2019. Т. 59. № 6. С. 10631082.
Петров А.Г. Схема без насыщения для обтекания решетки профилей и вычисление точек отрыва в вязкой жидкости // ЖВММФ. 2011. Т. 51. № 7. С. 13261338.
Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости, М.: Наука, 1966.
Hamming R.W. Numerical Methods for Scientists and Engineers. New York: McGraw-Hill, 1962.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика