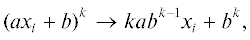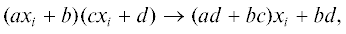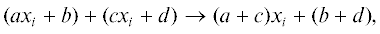Программирование, 2019, № 2, стр. 49-57
ПОДСЧЕТ ПОЧТИ СОВЕРШЕННЫХ ПАРОСОЧЕТАНИЙ НА ТОРАХ Cm × Cn НЕЧЕТНОГО ПОРЯДКА В СИСТЕМЕ MAPLE
С. Н. Перепечко *
Петрозаводский государственный университет
185910 Петрозаводск, пр. Ленина, 33, Россия
* E-mail: persn@newmail.ru
Поступила в редакцию 10.07.2018
После доработки 10.07.2018
Принята к публикации 12.09.2018
Аннотация
В системе компьютерной алгебры Maple получен набор рекуррентных соотношений и ассоциированных с ними производящих функций для числа почти совершенных паросочетаний в семействе торов ${{C}_{m}} \times {{C}_{n}}$ нечетного порядка при фиксированных значениях параметра $3 \leqslant m \leqslant 11$. Выявлена идентичность рекуррентных соотношений для числа совершенных и почти совершенных паросочетаний при одном и том же значении m. Приводится оценка числа почти совершенных паросочетаний при больших нечетных m когда $n \to \infty $.
I. ВВЕДЕНИЕ
В значительной части работ, посвященных подсчету паросочетаний, чаще всего обсуждаются совершенные паросочетания. Количественные характеристики других видов паросочетаний представлены в литературе менее подробно. В то же время паросочетания, структурно близкие к совершенным, естественным образом возникают при изучении задачи о димерах – одной из классических решеточных моделей статистической механики.
Как известно, необходимым условием существования в графе совершенного паросочетания является четность его порядка. Почти совершенные паросочетания являются непосредственным аналогом совершенных паросочетаний в графах нечетного порядка. В этом случае ненасыщенной паросочетанием оказывается ровно одна вершина, которую будем называть вакансией. Очевидно, что такие паросочетания всегда являются наибольшими.
В задаче о димерах наибольшие паросочетания служат моделью плотноупакованных димерных конфигураций. При равенстве активностей всех димеров статсумма этой решеточной модели идентична производящей функции для числа наибольших паросочетаний. Целью данной работы стал вывод рекуррентных соотношений и ассоциированных с ними производящих функций для числа почти совершенных паросочетаний в семействе торов ${{C}_{m}} \times {{C}_{n}}$ нечетного порядка при фиксированном значении параметра m.
Несмотря на трудоемкость подсчета паросочетаний в графах общего вида [1, 2], выяснилось, что при небольших m все необходимые вычисления могут быть выполнены в системе компьютерной алгебры. В силу своей компактности и универсальности алгоритмы, опирающиеся на символьные преобразования, по крайней мере, в графах умеренного порядка могут являться полезной альтернативой более специализированным, но сложным в реализации численным алгоритмам.
II. ОСНОВНЫЕ ОБОЗНАЧЕНИЯ И РАНЕЕ ИЗВЕСТНЫЕ РЕЗУЛЬТАТЫ
Для количественного описания совершенных паросочетаний воспользуемся обозначениями, согласованными с [3]. Поскольку в данной работе параметр m принимает только нечетные значения, то будем считать, что величина ${{K}_{{m,n}}}$ является числом совершенных паросочетаний на торе ${{C}_{m}} \times {{C}_{{2n}}}$. Как показано в [3], при фиксированном $m \geqslant 3$ числовая последовательность
является монотонно возрастающей и удовлетворяет линейному рекуррентному соотношению с постоянными коэффициентами. Основные свойства таких последовательностей приводятся в [4]. Из [4] следует, что производящие функцииЕсли порядок соотношения минимален, то полиномы ${{P}_{m}}(z)$ и ${{Q}_{m}}(z)$ будут взаимно просты. С ростом m порядки соотношений ${{q}_{m}} = deg{{Q}_{m}}(z)$ увеличиваются в геометрической прогрессии. Для нечетных m в [3] получена оценка сверху ${{q}_{m}} \leqslant {{3}^{{[m/2]}}}$, которая в большинстве случаев достигается.
Максимальный корень характеристического полинома ${{z}^{{{{q}_{m}}}}}{{Q}_{m}}(1{\text{/}}z)$ будем обозначать символом $\lambda (m)$. Его можно выразить в явном виде непосредственно через параметры тора
Опираясь на $\lambda (m)$, можно оценить значения ${{K}_{{m,n}}}$ при $n \to \infty $. Для нечетных фиксированных m имеем ${{K}_{{m,n}}} \sim 2{{\lambda }^{n}}(m)$.
Количество почти совершенных паросочетаний в произвольном двухпараметрическом семействе графов ${{\mathcal{L}}_{{m,n}}}$ нечетного порядка зависит от местоположения вакансии. Пусть $\mathcal{V}$ – множество вершин графа ${{\mathcal{L}}_{{m,n}}}$. Введем обозначение $\hat {K}_{{m,n}}^{{(\text{v})}}$ для числа почти совершенных паросочетаний в ${{\mathcal{L}}_{{m,n}}}$ при условии, что вакансия расположена в вершине $v \in \mathcal{V}$.
Отличительной особенностью торов, т.е. семейства ${{\mathcal{L}}_{{m,n}}} = {{C}_{m}} \times {{C}_{n}}$, является изоморфизм любой пары графов ${{\mathcal{L}}_{{m,n}}} - v'$ и ${{\mathcal{L}}_{{m,n}}} - v''$ при $v' \ne v''(v',v'' \in \mathcal{V})$. В такой ситуации величина $\hat {K}_{{m,n}}^{v}$ не зависит от $v$. Данное обстоятельство существенно упрощает расчет термодинамических параметров в модели димеров, так как для этого требуется выполнить суммирование по всем вершинам [5]. Поскольку $\hat {K}_{{m,n}}^{v} = {{\hat {K}}_{{m,n}}}$, то
поэтому в термодинамическом пределе интересующие нас величины могут быть получены непосредственно из асимптотики ${{\hat {K}}_{{m,n}}}$.Исходя из нечетности порядка графов, имеет смысл слегка переопределить ${{\hat {K}}_{{m,n}}}$ для того, чтобы избавиться от нулевых членов в последовательностях $\{ {{\hat {K}}_{{m,n}}}\} $. Если величину ${{\hat {K}}_{{m,n}}}$ положить равной количеству почти совершенных паросочетаний на торе ${{C}_{m}} \times {{C}_{{2n + 1}}}$, то последовательность $\{ {{\hat {K}}_{{m,n}}}\} $, также как и $\{ {{K}_{{m,n}}}\} $, будет монотонно возрастающей, а ее производящая функция ${{\hat {G}}_{m}}(z) = \sum\limits_{n = 1}^\infty {{{{\hat {K}}}_{{m,n}}}{{z}^{n}}} $ примет наиболее простой вид.
Важнейшим свойством ${{\hat {G}}_{m}}(z)$ является то, что эти функции являются рациональными. Данное свойство вытекает из результатов работы [5], в которой была предложена схема кодирования состояний в методе матрицы переноса для решеток вида ${{P}_{{2m + 1}}} \times {{P}_{{2n + 1}}}$ при наличии одной вакансии. С несущественными модификациями данная схема может быть использована и для построения матрицы переноса в семействе торов. В таком случае, применяя к этой матрице теорему Кэли–Гамильтона, приходим к тому, что последовательности $\{ {{\hat {K}}_{{m,n}}}\} $ удовлетворяют линейным рекуррентным соотношениям с постоянными коэффициентами [6] и, следовательно, производящие функции представимы в виде
Алгоритмы, использованные для вывода рекуррентных соотношений, всегда приводили к
соотношениям минимального порядка, что и обусловило взаимную простоту полиномов ${{\hat {P}}_{m}}(z)$ и ${{\hat {Q}}_{m}}(z)$. Остальные обозначения имеют тот же смысл, что и в случае совершенных паросочетаний,
отличаясь только наличием символа “ 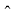 ”. В частности, последовательность $\{ {{\hat {K}}_{{m,n}}}\} $ удовлетворяет соотношению порядка ${{\hat {q}}_{m}} = \deg {{\hat {Q}}_{m}}(z)$.
”. В частности, последовательность $\{ {{\hat {K}}_{{m,n}}}\} $ удовлетворяет соотношению порядка ${{\hat {q}}_{m}} = \deg {{\hat {Q}}_{m}}(z)$.
III. СУЩНОСТЬ МЕТОДА УИЛФА
Несмотря на возможность построения матрицы переноса в семействе торов, непосредственное применение этого метода для нахождения ${{\hat {G}}_{m}}(z)$ непрактично. Как отмечалось в [3], даже при отсутствии вакансий порядок матрицы переноса возрастает гораздо быстрее чем qm. Отношение указанных величин, как правило, увеличивается в геометрической прогрессии и описанные в [3, 5] стандартные методы сжатия матрицы переноса не способны существенно изменить эту зависимость. В результате уже при небольших m затраты памяти на хранение матрицы переноса и некоторых вспомогательных величин могут оказаться неприемлемо велики.
При наличии нескольких или даже одной вакансии для подсчета числа паросочетаний в решеточных графах предпочтительно опираться на универсальные методы. Один из первых таких методов был предложен полвека назад Уилфом. Общая идея работы [7] состояла в унификации принципа включения–исключения, позволяющей выразить искомую величину через производящий полином особого вида. В рамках этого подхода сама формула включения–исключения порождалась из производящего полинома чисто “механически” по универсальной схеме.
Применительно к задаче подсчета паросочетаний предложенный Уилфом метод устанавливал связь между количеством совершенных паросочетаний и числом всевозможных непустых порожденных подграфов исходного графа с учетом их порядков и размеров. Однако в вычислительном контексте именно этот результат, сформулированный в теореме 2 [7], вряд ли можно признать практичным. Так, например, порожденные подграфы, имеющие по одному ребру, структурно близки к независимым множествам, которые трудно пересчитать даже в графах с максимальной степенью вершины 3.
Приведенное в теореме 2 выражение является результатом упрощения формулы включения–исключения и ее представления в “стандартном” виде как суммы по всем подмножествам множества вершин исходного графа. На этапе реализации, конечно, можно было бы воспользоваться исходным, неупрощенным вариантом, перебирая все подмножества или же их большую часть. Тогда потребовалось бы отслеживать лишь размеры соответствующих порожденных подграфов. Однако характер зависимости количества самих подмножеств от числа вершин накладывает сильные ограничения на порядки изучаемых графов – в лучшем случае, несколько десятков. Более того, количество слагаемых в формуле включения–исключения способно даже превзойти число подсчитываемых совершенных паросочетаний.
Современные системы компьютерной алгебры способны эффективно выполнять операции над полиномами от большого числа переменных, поэтому в настоящее время первостепенный интерес в методе Уилфа представляет как раз-таки “вспомогательный” производящий полином. Пусть $\mathcal{L}$ = = $(\mathcal{V},\mathcal{E})$ – неориентированный граф четного порядка N без петель и кратных ребер. Не умаляя общности можно считать, что вершины графа перенумерованы числами от 1 до N. Если каждой вершине $i \in \mathcal{V}$ поставить в соответствие переменную ${{x}_{i}}$, то подсчет совершенных паросочетаний в графе $\mathcal{L}$ сводится к нахождению определенного коэффициента полинома
где $h({{x}_{1}},{{x}_{2}}, \ldots ,{{x}_{N}}) = \sum\nolimits_{\{ i,j\} \in E}^{} {{{x}_{i}}{{x}_{j}}.} $Точное количество паросочетаний в $\mathcal{L}$ совпадает с результатом деления коэффициента при ${{x}_{1}}{{x}_{2}}\; \ldots \;{{x}_{N}}$ в (1) на $(N{\text{/}}2)!$. Наличие такой поправки обусловлено различными перестановками пар множителей в произведении ${{x}_{1}}{{x}_{2}}\; \ldots \;{{x}_{N}}$, порождающими одно и то же паросочетание.
В статье самого Уилфа производящий полином формировался на основе матрицы смежности графа, приобретая вид ${{(2h)}^{{N/2}}}$. Тогда искомый коэффициент следует разделить не только на $(N{\text{/}}2)!$, но и на ${{2}^{{N/2}}}$. Поскольку матрица смежности использовалась в [7] только для лаконичной записи $h({{x}_{1}},{{x}_{2}}, \ldots ,{{x}_{N}})$, то, фактически, затраты на ее построение и хранение избыточны.
Вместо вывода формулы включения–исключения в настоящей работе предлагается извлекать указанный выше коэффициент непосредственно из (1), опираясь на базовый набор простейших операций с полиномами, который поддерживается различными системами компьютерной алгебры. К достоинствам предложенной трактовки метода Уилфа следует отнести универсальность, простоту и компактность формулировки перечислительной задачи, позволяющей избежать трудоемкой фазы написания и отладки кода.
IV. ПОЛУКОЛИЧЕСТВЕННЫЕ ОЦЕНКИ СЛОЖНОСТИ АЛГОРИТМА
Далеко не очевидно, насколько эффективной окажется фактическая реализация метода Уилфа, завуалированная лаконичной формулой (1). Для графов, порядок которых мал, будут пригодны практически любые варианты метода, вплоть до обычного раскрытия скобок. В такой ситуации можно воспользоваться даже обсуждавшейся выше формулой включения–исключения. Однако по мере увеличения порядка графа резкий рост размерности задачи, обусловленный как увеличением количества слагаемых в основании степени, так и ее показателя, быстро дает о себе знать.
Уже сам факт наличия совершенных паросочетаний в изучаемом графе автоматически означает громоздкость явного представления (1) в виде суммы одночленов. Пусть M = {{i1, j1}, ..., $\{ {{i}_{{N/2}}},{{j}_{{N/2}}}\} \} \subseteq \mathcal{E}$ – одно из таких паросочетаний. Тогда приведенная в (1) сумма будет с точностью до коэффициентов включать все члены, входящие в выражение
(2)
$\begin{gathered} {{\left( {\sum\limits_{\{ i,j\} \in M} {{x}_{i}}{{x}_{j}}} \right)}^{{N/2}}} = \\ = \;\sum\limits_{{{k}_{1}}} \cdots \sum\limits_{{{k}_{{N/2}}}} \frac{{(N{\text{/}}2)!}}{{{{k}_{1}}!\; \cdots \;{{k}_{{N/2}}}!}}{{({{x}_{{{{i}_{1}}}}}{{x}_{{{{j}_{1}}}}})}^{{{{k}_{1}}}}}\; \cdots \;{{({{x}_{{{{i}_{{N/2}}}}}}{{x}_{{{{j}_{{N/2}}}}}})}^{{{{k}_{{N/2}}}}}}, \\ \end{gathered} $Независимо от особенностей представления полиномов в памяти компьютера, на практике столь быстрый рост приведет к тому, что развернутая запись (1) будет приемлема лишь для графов содержащих несколько десятков вершин.
С учетом полилинейности одночлена, коэффициент при котором требуется вычислить, естественно было бы прибегнуть к более “экономичной” процедуре, отбирая после каждого домножения на h только полилинейные члены. Однако и в таком случае пришлось бы столкнуться с экспоненциальным характером роста количества слагаемых. Весьма показателен промежуточный шаг, соответствующий перемножению [N/4] сумм. Действительно, в полиноме ${{h}^{{[N/4]}}}$ представлены, по меньшей мере,
Помимо резкого роста количества слагаемых в развернутой записи (1) дополнительные трудности в ходе проведения расчетов обусловлены большими значениями коэффициентов. Чтобы получить представление о величине этих коэффициентов, достаточно рассмотреть граф, имеющий единственное паросочетание, которое совпадает с самим графом. Тогда полином (1) будет равен (2), а сумма его коэффициентов составит ${{(N{\text{/}}2)}^{{N{\text{/}}2}}}$. В частности, при каждом полилинейном слагаемом рассмотренного выше промежуточного полинома ${{h}^{{[N/4]}}}$ образуется коэффициент [N/4]!, обусловленный числом перестановок пар множителей в произведении $\prod {{{x}_{i}}{{x}_{j}}} $. Наличие указанных числовых множителей факториального вида предопределено самой структурой производящего полинома (1).
Стоит отметить, что зависимость числа совершенных паросочетаний от порядка графа достаточно часто имеет экспоненциальный характер. Например, в любом регулярном двудольном графе степени 3 с N вершинами существует, по меньшей мере, $81{\text{/}}32 \times {{(4{\text{/}}3)}^{{N/2}}}$ таких паросочетаний [8]. Из аналогичных оценок для других классов графов следует, что коэффициенты полинома (1) в ряде практически важных случаев могут достигать очень больших значений.
Если возрастание числовых коэффициентов, обусловленное самой природой перечислительной задачи, является неизбежным фактором, усложняющим подсчет паросочетаний, то общий объем промежуточных выкладок допускает определенный контроль. За счет ряда манипуляций над исходной формулой (1), которые описаны в следующем разделе, становится возможным изучение графов с сотнями вершин и ребер, причем имеющих достаточно разнообразные структуры, а для специализированных семейств графов вполне достижимы порядки в несколько тысяч.
V. ОБЩИЕ РЕКОМЕНДАЦИИ ПО РЕАЛИЗАЦИИ МЕТОДА УИЛФА
Подход к обработке выражения (1), предлагаемый в данной работе, состоит в построении цепочки полиномов, начинающейся с (1) и оканчивающейся числом — коэффициентом (1) при ${{x}_{1}}{{x}_{2}} \ldots {{x}_{N}}$. Пронумеруем все полиномы этой цепочки, присвоив начальному номер 0. Тогда на очередной итерации алгоритма $i$-й полином будет строиться только из тех членов $(i - 1)$-го полинома, которые содержат переменную ${{x}_{i}}$ в первой степени. Сам множитель ${{x}_{i}}$, общий для всех указанных членов, удобно опустить. В таком случае i-й полином можно интерпретировать как коэффициент $(i - 1)$-го полинома при ${{x}_{i}}$, рассматривая остальные переменные ${{x}_{{i + 1}}},{{x}_{{i + 2}}}, \ldots ,{{x}_{N}}$ в роли параметров. Ключевой особенностью данного подхода является возможность обойтись без полного раскрытия скобок, сдерживая до некоторой степени рост объема промежуточных выкладок.
На каждой итерации этой вычислительной схемы очередной многочлен-коэффициент строящейся цепочки определяется посредством рекурсивного извлечения пар младших коэффициентов относительно ${{x}_{i}}$ согласно следующего простого набора правил:
где $a,b,c$ и d – не зависящие от xi полиномы. Данные преобразования допускают естественную интерпретацию в терминах операции дифференцирования: искомые коэффициенты являются значениями самого полинома от xi и его производной при xi = 0. В частности, формальное аналитическое выражение для числа совершенных паросочетаний представимо в виде(4)
$\frac{1}{{(N{\text{/}}2)!}}\frac{{{{\partial }^{N}}}}{{\partial {{x}_{1}}\partial {{x}_{2}}\; \ldots \;\partial {{x}_{N}}}}h{{({{x}_{1}},{{x}_{2}},\; \ldots ,\;{{x}_{N}})}^{{N/2}}}.$Вообще говоря, при отсутствии контроля за структурой промежуточных выражений, подобная стратегия вычислений сталкивается с теми же самыми проблемами, которые присущи и обычному раскрытию скобок. Залогом успешного выполнения преобразований выступает как раз-таки сохранение факторизованных форм для частей промежуточных выражений.
Отметим, что целесообразность использования предложенных правил – поочередной обработки переменных и “экономичного” раскрытия скобок – напрямую обусловлена чрезвычайно большим количеством слагаемых в развернутом представлении (1). Оба этих правила должны быть положены в основу любой практичной реализации метода.
Сама по себе поддержка полиномиальных вычислений еще не гарантирует реальной работоспособности метода Уилфа. Некоторые системы компьютерной алгебры могут оказаться заведомо непригодны, если в этих системах полиномы от нескольких переменных хранятся в памяти компьютера в виде суммы одночленов, поскольку уже ввод исходного выражения (1) обернется попыткой полного раскрытия скобок. В соответствии с оценками предыдущего раздела даже для графов с 30 вершинами объем задействованной памяти будет измеряться гигабайтами.
Эффективная реализация метода подразумевает возможность представления в системе произвольных выражений, образованных из чисел и переменных посредством операций сложения, умножения и возведения в натуральную степень, с сохранением их оригинальной структуры. Именно в такой класс попадают все элементы цепочки, порождаемые из (1) с применением правил (3). Несмотря на то, что в математическом смысле указанные выражения являются полиномами, с точки зрения реализации их следует трактовать как выражения общего вида, отличая от полиномов в стандартном развернутом представлении. Поддержка подобных формул свойственна многим универсальным системам компьютерной алгебры, к разряду которых относится и использовавшаяся в работе система Maple. Как правило, даже в рамках одной системы можно предложить несколько вариантов, количество которых определяется набором имеющихся в системе средств.
VI. РЕАЛИЗАЦИЯ МЕТОДА В СИСТЕМЕ MAPLE
Вычисления должны начинаться с ввода или же построения графа, когда формируется конкретное упорядочение его вершин. При использовании системы Maple графы, принадлежащие многим популярным семействам, могут быть сконструированы непосредственно с помощью пакета GraphTheory. Например, тор ${{C}_{m}} \times {{C}_{n}}$ может быть создан одной инструкцией
G := CartesianProduct(CycleGraph(n),
CycleGraph(m)):
Если при вызове CartesianProduct поменять местами аргументы, то получим изоморфный граф с таким же количеством совершенных паросочетаний. В следующем разделе будут приведены некоторые соображения, почему в контексте данной работы именно такой способ является предпочтительным.
Конструирование графа средствами пакета GraphTheory позволяет получить исходный полином (1) с помощью инструкций
V := Vertices(G):
N := nops(V):
g := add(x[e [1]]*x[e [2]], e = Edges(G))^(N/2):
На этапе тестирования алгоритма рассматривались и другие способы явной записи h: согласно оригинальной версии [7] с удвоенными коэффициентами и в виде сгруппированной версии
Результаты контрольных расчетов показали, что выбор того или иного способа не оказывает существенного влияния на производительность метода. Гораздо важнее оказалась возможность записи полинома h в форме функционального символа. Такой вариант представления h вытекает непосредственно из анализа структуры промежуточных выражений, порождаемых по цепочке из (1), так как для этих выражений характерно многократное вхождение h.
Для вычисления коэффициента многочлена в библиотеке Maple содержатся сразу несколько функций: coeftayl, coeff и diff. По формату вызова наиболее подходящей представляется функция coeftayl, позволяющая извлечь искомый коэффициент при ${{x}_{1}}{{x}_{2}}\; \ldots \;{{x}_{N}}$ непосредственно по формуле (4) и, следовательно, вычислить количество совершенных паросочетаний f:
f := coeftayl(g, [seq(x[v], v=V)] = [0$N],
[1$N])/(N/2)!:
Фактически выполнение данной команды с учетом специфики g сведется к пошаговому дифференцированию этого многочлена в соответствии с указанным списком переменных.
Итерационный процесс можно организовать и явно, воспользовавшись для выполнения элементарных операций двумя разными функциями: coeff или diff:
for v in V do g := coeff(g, x[v]) end:
f := g/(N/2)!:
Альтернативный вариант получается заменой coeff на diff.
Ручная организация цикла удобна, прежде всего, тем, что позволяет контролировать промежуточные выкладки, применяя при необходимости к выражению ряд дополнительных преобразований. Такие преобразования требуются, например, для удаления избыточных членов, порождаемых diff. Если coeff возвращает непосредственно коэффициент при заданной переменной в первой степени, то в результате применения diff образуется выражение, содержащее и коэффициенты при старших степенях переменной дифференцирования.
Возникающие издержки создают серьезные трудности, позволяя выполнять расчеты только для графов, содержащих несколько десятков вершин. По этой причине указанные выше подходы на основе coeftayl или diff оказываются крайне неудачны. Применение diff становится практичным лишь в сочетании с подстановкой нуля на место переменной дифференцирования
for v in V do
g := eval(diff(g, x[v]), x[v]=0)
end:
f := g/(N/2)!:
Отметим, что данная комбинация diff и eval только математически эквивалентна вызову функции coeff. Получаемые результаты, как правило, сильно различаются по структуре.
В то же время, достоинством diff является возможность дальнейшего усовершенствования кода. Вместо явного указания $h$ целесообразно ввести компактный функциональный символ h(x), где x – очередная переменная дифференцирования. С точки зрения программиста дополнительные усилия сведутся лишь к паре новых подстановок. Во-первых, следует явно указать, чему равна производная $h$ по текущей переменной, а во-вторых, подготовить h(x) к следующей итерации, обновив аргумент
g := h(x[V [1]])^(N/2):
for i to N–1 do
g := eval(diff(g, x[V[i]]),
[x[V[i]] = 0, h(x[V[i]]) = h(x[V[i+1]]),
'diff' (h(x[V[i]], x[V[i]]) = add(x[v],
v = Neighbors (G, V[i]))]):
x[V[i]] := 0
end
f := diff(g, x[V[N]])/(N/2)!
Присваивание x[V[i]] := 0 обеспечивает надлежащий набор слагаемых на выходе add, гарантируя отсутствие переменных, дифференцирование по которым уже выполнялось.
Представленные в этом разделе фрагменты кода отражают наиболее существенные модификации, которые могут встречаться в различных реализациях метода Уилфа. В ходе тестирования алгоритма изучалось влияние на эффективность вычислений и некоторых других факторов. В частности, оказалось, что замена eval на subs с последовательным выполнением подстановок приводила к замедлению расчетов.
VII. ПОДСЧЕТ ПОЧТИ СОВЕРШЕННЫХ ПАРОСОЧЕТАНИЙ
При подсчете почти совершенных паросочетаний следует исходить из того, что такие паросочетания структурно близки к совершенным. Если задан граф нечетного порядка, то после выбора вершины, в которой будет расположена вакансия, данную вершину вместе с инцидентными ей ребрами необходимо удалить из исходного графа. Затем в полученном графе четного порядка можно вычислить количество совершенных паросочетаний, применив метод Уилфа.
Как уже отмечалось в разделе 2, отличительной особенностью семейства торов является независимость полученного результата от местоположения вакансии. В связи с этим при любых значениях m и n из тора ${{C}_{m}} \times {{C}_{n}}$ всегда удалялась вершина под номером 1.
Поскольку в данной работе интерес представлял вывод рекуррентных соотношений, то вполне естественно, что наибольшие трудности были связаны с получением достаточно длинных начальных отрезков последовательностей $\{ {{\hat {K}}_{{m,n}}}\} $ при нечетных фиксированных m.
В ходе проведения расчетов, как правило, выполнялось условие $n > m$, а иногда даже $n \gg m$. При таких условиях для конструирования торов следует воспользоваться командой из предыдущего раздела. В результате ее выполнения вершинам графа присваиваются номера в соответствии с последовательным просмотром циклов длины m. Благодаря подобному способу разметки, затраты памяти при работе алгоритма будут зависеть от m экспоненциально. Однако зависимость от параметра n будет выражена весьма слабо. В области $n > 2m$ эта зависимость хорошо аппроксимируется степенной функцией с показателем меньше 1. На этапе тестирования при всех значениях m на данных зависимостях можно было также заметить несколько скачкообразных изменений, обусловленных неконтролируемой работой сборщика мусора Maple.
Алгоритм с указанными выше потребностями в оперативной памяти позволял строить фрагменты $\{ {{\hat {K}}_{{m,n}}}\} $, содержащие несколько сотен членов. Такого количества вполне хватало для вывода рекуррентных соотношений при небольших m. Если же при вызове функции CartesianProduct поменять местами аргументы, то потребность в памяти зависела бы от параметра $n$ экспоненциально и нахождение даже первых 20 значений ${{\hat {K}}_{{m,n}}}$ становилось бы невозможным в силу ограниченности имеющихся ресурсов.
Наличие экспоненциальной зависимости приводит к существенному ограничению диапазона параметров m и $n$, для которых возможно вычисление значений ${{\hat {K}}_{{m,n}}}$. По этой причине порядки соотношений ${{\hat {q}}_{m}}$, несмотря на сильную зависимость от $m$, окажутся не слишком велики, а сами рекуррентные соотношения могут быть найдены средствами системы Maple.
Сравнительный анализ эффективности встроенных в Maple функций вывода соотношений выполнен в [9]. Для быстрорастущих последовательностей предпочтительными являются методы, основанные на p-адических разложениях (см., например, [10]). Один из таких методов, опирающийся на вычислительную схему Диксона, реализован в процедуре rgf_findrecur из пакета genfunc. С помощью этой процедуры были найдены все рекуррентные соотношения, для которых удалось вычислить начальные отрезки $\{ {{\hat {K}}_{{m,n}}}\} $ достаточной длины. Например, при m = 3 имеем
Остальные члены $\{ {{\hat {K}}_{{m,n}}}\} $ могут быть получены из соотношения
Если рекуррентное соотношение уже известно, то ${{\hat {G}}_{m}}(z)$ находится путем обращения к процедуре rsolve с опцией 'genfunc'(z). Когда $m = 3$, производящая функция представима в виде
Вычисление фрагментов последовательностей $\{ {{\hat {K}}_{{m,n}}}\} $ оказалось наиболее трудоемкой частью проделанной работы. Вследствие экспоненциальной зависимости порядков ${{\hat {q}}_{m}}$ для восстановления соотношения из начальных данных даже при небольших m требовалось найти от нескольких десятков до нескольких сотен элементов ${{\hat {K}}_{{m,n}}}$. Для ускорения расчетов алгоритм Уилфа был запрограммирован в виде процедуры, имя которой передавалось на вход функции Seq из пакета Threads. Такой подход позволял одновременно вычислять сразу несколько значений ${{\hat {K}}_{{m,n}}}$, однако ценой существенного увеличения потребностей в оперативной памяти. При m = 11 многопоточные вычисления стали невозможны, поскольку даже однопоточная версия алгоритма работала на пределе возможностей имеющегося компьютера. Именно это ограничение и определило максимальное значение параметра m.
VIII. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Все расчеты в данной работе были выполнены на персональном компьютере с процессором Core i7 980 3.33GHz работающим под управлением 64-битовой версии Windows 7 SP1. Компьютер имел 24GB RAM и установленную на нем 64-битовую версию системы компьютерной алгебры Maple 17.02.
Имеющихся вычислительных ресурсов оказалось достаточно, чтобы вывести рекуррентные соотношения и ассоциированные с ними производящие функции в семействе торов нечетного порядка при $3 \leqslant m \leqslant 11$. В качестве примера приведем явное выражение для ${{\hat {G}}_{m}}(z)$ при m = 5
Наиболее интересный вывод, вытекающий из сопоставления ${{\hat {G}}_{m}}(z)$ с ${{G}_{m}}(z)$, состоит в том, что знаменатели ${{\hat {Q}}_{m}}(z)$ и ${{Q}_{m}}(z)$ идентичны при всех изученных значениях m. Ранее аналогичная закономерность была замечена на цилиндрах ${{C}_{m}} \times {{P}_{n}}$ нечетного порядка [11].
Несмотря на то, что проверка равенства знаменателей была выполнена в достаточно ограниченном диапазоне изменения параметра m, единый способ вывода всех рекуррентных соотношений дает основание выдвинуть и более общее предположение
Предположение. Последовательности $\{ {{\hat {K}}_{{m,n}}}\} $ и $\{ {{K}_{{m,n}}}\} $ удовлетворяют одному и тому же линейному рекуррентному соотношению при всех нечетных m.
Если данное предположение верно, то задача подсчета почти совершенных паросочетаний на различных модификациях прямоугольных решеток сводится к более простой задаче подсчета совершенных паросочетаний.
Из равенства ${{\hat {Q}}_{m}}(z) = {{Q}_{m}}(z)$ следует экспоненциальный рост порядков соотношений, поскольку ${{\hat {q}}_{m}} = {{q}_{m}} \leqslant {{3}^{{[m/2]}}}$. Как уже ранее отмечалось в [3], при умеренных значениях $m$ верхняя граница не достигается лишь при $m = 15(2k - 1)$, где k = $1,2, \ldots $.
Быстрый рост порядков ${{\hat {q}}_{m}}$ сопровождается столь же быстрым увеличением коэффициентов рекуррентных соотношений, не позволяя представить в явном виде все полученные в работе производящие функции. Однако $\{ {{K}_{{7,n}}}\} $ и $\{ {{K}_{{9,n}}}\} $ зарегистрированы в OEIS [12], где приводятся выражения для ${{Q}_{7}}(z)$ и ${{Q}_{9}}(z)$ (см. последовательности A230033, A281583), поэтому для иллюстрации отмеченной тенденции ограничимся числителем ${{\hat {P}}_{7}}(z)$
Учитывая простоту корней ${{Q}_{m}}(z)$, непосредственно из ${{\hat {G}}_{m}}(z)$ возможен вывод формул для ${{\hat {K}}_{{m,n}}}$ в традиционной форме, то есть в виде суммы геометрических прогрессий. В простейших случаях показатели этих прогрессий могут быть выражены в радикалах. Например, при m = 3 получаем следующий результат:
(5)
$\begin{gathered} {{{\hat {K}}}_{{3,n}}} = \left( {\frac{{2\sqrt 7 + 7\sqrt 3 }}{{21}}} \right){{\left( {\frac{{\sqrt 7 + \sqrt 3 }}{2}} \right)}^{{(2n + 1)}}} + \\ + \;\left( {\frac{{2\sqrt 7 - 7\sqrt 3 }}{{21}}} \right){{\left( {\frac{{\sqrt 7 - \sqrt 3 }}{2}} \right)}^{{(2n + 1)}}} - \frac{2}{3}. \\ \end{gathered} $С вычислительной точки зрения подобного рода формулы вовсе не обязаны быть оптимальными. Их основное достоинство заключается в возможности изучения асимптотики ${{\hat {K}}_{{m,n}}}$ в больших графах.
При больших значениях n доминирующий вклад в (5) вносит первое слагаемое. Поскольку $\Lambda (3) = (\sqrt 7 + \sqrt 3 ){\text{/}}2$, то для оценки числа почти совершенных паросочетаний можно воспользоваться простым выражением
В общем случае для нечетных m асимптотика ${{\hat {K}}_{{m,n}}}$ имеет вид ${{\hat {K}}_{{m,n}}} \sim c(m)\lambda {{(m)}^{n}}$. Так как λ(m) = = ${{\Lambda }^{2}}(m)$, то, принимая во внимание рациональность ${{\hat {G}}_{m}}(z)$, находим $c(m)$, опираясь на стандартную формулу
(6)
$c(m) = - \frac{{\lambda (m){{{\hat {P}}}_{m}}(1{\text{/}}\lambda (m))}}{{\hat {Q}_{m}^{'}(1{\text{/}}\lambda (m))}}.$Величину $c(m)$ удобно представить в виде произведения, выделив в ней быстрорастущий множитель равный некоторой целой степени $\Lambda (m)$ и медленно меняющуюся составляющую $\hat {c}(m)$. В силу неоднозначности данной процедуры, наложим условие нормировки $2{\text{/}}\Lambda (m) < \hat {c}(m) < \Lambda (m)$. Наличие коэффициента 2 в левом неравенстве обусловлено тем, что для совершенных паросочетаний ${{K}_{{m,n}}} \sim 2{{\lambda }^{n}}(m)$.
Оказалось, что для всех изученных в работе значений m условие нормировки будет выполнено, если положить $c(m) = \hat {c}(m)\Lambda (m)$. Тем самым, при фиксированных нечетных m для оценки ${{\hat {K}}_{{m,n}}}$ можно воспользоваться формулой
Набор значений $\hat {c}(m)$ образует монотонно убывающую последовательность. Эти значения могут быть вычислены точно, если выполнять расчеты в системе Maple, опираясь на (6). Однако даже при малых m полученные результаты оказываются чрезвычайно громоздкими и по этой причине малоинформативными. Например, при m = 5 имеем
Величина c(5) представляется аналогичным выражением, содержащим вложенные радикалы.
Попытаемся эмпирически описать зависимость $\hat {c}(m)$, опираясь на числовые данные из таблицы 1. По аналогии с другими модификациями прямоугольных решеток будем аппроксимировать $\hat {c}(m)$ степенными функциями вида $A{\text{/}}{{m}^{\alpha }}$. В результате применения процедуры PowerFit из пакета Statistics получаем $\hat {c}(m) \approx 1.077{\text{/}}{{m}^{{0.235}}}$.
Таблица 1.
| $m$ | $\hat {c}(m)$ |
|---|---|
| 3 | 0.829 326 5841 |
| 5 | 0.740 141 9370 |
| 7 | 0.682 823 0778 |
| 9 | 0.642 008 9077 |
| 11 | 0.610 918 7048 |
Хотя из полученного выражения невозможно определить явный вид главного члена асимптотического разложения $\hat {c}(m)$, весьма вероятно, что $\hat {c}(m) \sim 1{\text{/}}\sqrt[4]{m}$ при $m \to \infty $. Полученный результат свидетельствует о важной роли граничных условий, наложенных на решетку. Для сравнения отметим, что в семействе цилиндров ${{C}_{m}} \times {{P}_{n}}$ наличие вакансии на границе приводит к тому, что аналогичный $\hat {c}(m)$ множитель убывает пропорционально $\sqrt m $ [11].
IX. ЗАКЛЮЧЕНИЕ
Часть полученных результатов в силу их громоздкости не удалось разместить в основном тексте работы. По запросу автор готов предоставить заинтересованному читателю все необходимые данные.
В работе приведены лишь наиболее существенные рекомендации, которые должны учитываться в любой реализации метода Уилфа. В то же время для разработки эффективной реализации в графах с различными структурными особенностями необходимо более подробное обсуждение и некоторых других деталей метода, что предполагает написание отдельной статьи.
В список обсуждаемых тем желательно включить правила разметки вершин графа и способы более рационального использования оперативной памяти. Однако, как свидетельствуют результаты данной работы, в ряде случаев можно и без дополнительных оптимизаций получать решение перечислительной задачи, причем в таких ситуациях, когда применение других методов оказывается крайне затруднительным.
Список литературы
Valiant L.G. The complexity of enumeration and reliability problems // SIAM Journal on Computing. 1979. V. 8. № 3. P. 410–421.
Björklund A. Counting perfect matchings as fast as Ryser // Proceedings of SODA. 2012. P. 914–921.
Перепечко С.Н. Количество совершенных паросочетаний в графах ${{C}_{m}} \times {{C}_{n}}$. Информационные процессы. 2016. Т. 16. № 4. С. 333–361.
Петковшек М. Символьные вычисления над последовательностями. Программирование, 2006. Т. 32. № 2. С. 8–15.
Kong Y. Packing dimers on $(2p + 1) \times (2q + 1)$ lattices // Physical Review. 2006. V. E73. art. 016106.
Klarner D.A. Some remarks on the Cayley-Hamilton theorem. American Mathematical Monthly. 1976. V. 83. № 5. P. 367–369.
Wilf H.S. A mechanical counting method and combinatorial applications // Journal of Combinatorial Theory. 1968. V. 4. P. 246–258.
Voorhoeve M. A lower bound for the permanent of certain $(0,1)$-matrices // Indagationes Mathematicae. 1979. V. 82. № 1. P. 83–86.
Караваев А.М., Перепечко С.Н. Производящие функции в задаче о димерах на прямоугольных сеточных графах // Информационные процессы. 2013. Т. 13. № 4. С. 374–400.
Малашонок Г.И. О решении систем линейных уравнений $p$-адическим методом // Программирование. 2003. Т. 29. № 2. С. 8–22.
Perepechko S.N. Near-perfect matchings on cylinders ${{C}_{m}} \times {{P}_{n}}$ of odd order // EPJ Web of Conferences. 2018. V. 173. A. 02016.
The on-line encyclopedia of integer sequences. http:// oeis.org.
Дополнительные материалы отсутствуют.
Инструменты
Программирование