Программирование, 2020, № 4, стр. 3-13

1. ВВЕДЕНИЕ

Тестовые эквивалентности используются при сравнении поведения систем и проверке соответствия между заданной спецификацией и полученной реализацией, а также при установлении выполнимости логических формул. Понятие тестовой эквивалентности параллельных процессов было предложено М. Хеннеси и Р. де Николой в статье [1]. Тест – это специальный процесс, который выполняется параллельно с тестируемым процессом. Такое выполнение считается успешным, если тест достигает выделенного успешного состояния, и процесс проходит тест, если каждое его совместное выполнение с процессом является успешным. Два процесса считаются тестово эквивалентными, если они проходят одни и те же наборы тестов. Чтобы облегчить исследование и применение тестовых эквивалентностей, были найдены их альтернативные характеризации – например, сравнение проводится по совокупности всех тестов, которые представляют собой вычисления процессов и множества возможных их продолжений. Концепция тестовой эквивалентности интуитивно понятна и привела к появлению математической теории эквивалентностей и предпорядков на процессах.

Изначально тестовые эквивалентности были детально исследованы в контексте моделей систем переходов (см., например, [2, 3]), которые базируются на интерливинговой семантике – отношение параллелизма между действиями системы представляется не напрямую, а посредством недетерминированного выбора между выполнениями линейноупорядоченных поддействий. Интерливинговые тестовые эквивалентности для элементарных сетевых систем изучались в статье [4]. Чтобы преодолеть ограничения интерливингового подхода, отношение параллелизма часто моделируется как отсутствие причинной зависимости, представленной, как правило, частичным порядком, между действиями системы. В работах [5, 6] тестовые эквивалентности рассматривались в семантике частичного порядка в рамках моделей структур событий. Кроме того, тестовые эквивалентности активно изучались в контексте моделей структур событий для семантики причинных деревьев – поведение системы представляется в виде дерева, в котором дуги помечаются действиями и сведениями об их предшественниках, т.е. сохраняется информация о причинной зависимости. Взаимосвязи между семантиками частичного порядка и причинных деревьев были хорошо изучены для моделей структур событий в работах [6–8]. Чаще всего семантика частичного порядка сетей Петри представляется посредством так называемых причинных сетей-процессов, включающих события и условия, находящиеся в отношениях причинной зависимости и параллелизма (см. [9–11] среди других статей). Сравнение разновидностей тестовой эквивалентности в частично-упорядоченной семантике сетей Петри было проведено в статье [4]. Исследование семантики причинных деревьев в контексте сетей Петри, на сколько нам известно, не проводилось.

При верификации сложных систем, критичных с точки зрения безопасности, важно исследовать не только качественные, но и количественные характеристики поведения систем. Для этих целей тестовые эквивалентности были применены в контексте ряда моделей с реальным временем. Для систем переходов с дискретным временем в работах [12] и [13] были даны альтернативные характеризации временных тестовых эквивалентностей с использованием расширенного понятия, так называемых, допустимых множеств. Семантическая теория на основе тестовых эквивалентностей была предложена для алгебр процессов с временными ограничениями в статьях [14] и [15], где формулируются альтернативные характеризации тестовых предпорядков через, так называемые, трассы отказов. Авторы статьи [15] доказали возможность дискретизации в контексте разработанной ими временной алгебры процессов и, как следствие, сведение непрерывно-временных тестовых отношений к дискретно-временным. В работе [16] интерливинговые тестовые отношения, а также результаты по их альтернативной характеризации и дискретизации распространяются на модель сетей Петри с временными характеристиками, сопоставленными фишкам, и с временными интервалами, связанными с дугами из мест в переходы. Тестовые отношения исследуются одновременно для временных и причинно-зависимых семантик моделей структур событий в статье [17]. Кроме того, в [18–20] дается классификация эквивалентностей из спектра линейного/ветвящегося времени для семантик интерливинга, причинных деревьев и частичного порядка в контексте моделей непрерывно-временных структур событий. Частично-упорядоченная cемантика в работах [21, 22] была предложена для дискретно-временных сетей Петри, где с каждым переходом связана длительность его срабатывания, а также в статье [23] – для непрерывно-временных безопасных сетей Петри, где каждому переходу сопоставлен интервал временных задержек его срабатывания. Однако, насколько нам известно, в литературе по временным сетям Петри не представлены исследования тестовых эквивалентностей в семантиках причинных сетей-процессов и причинных деревьев. Только в работах [24, 25] изучались взаимосвязи трассовых и бисимуляционных эквивалентностей в интерливинговой и частично-упорядоченной семантиках непрерывно-временных безопасных сетей Петри.

Цель данной работы состоит в определении, изучении и сравнении тестовых эквивалентностей в семантиках интерливинга, причинных сетей и причинных деревьев в контексте непрерывно-временных безопасных сетей Петри (элементарных сетевых систем, переходы которых помечены временными интервалами и каждый переход, имеющий достаточное количество фишек во входных местах, должен срабатывать тогда, когда его счетчик достигнет некоторого значения, принадлежащего его временному интервалу). Устанавливаются взаимосвязи между рассматриваемыми эквивалентностями и показывается совпадение эквивалентностей в семантиках временных причинных сетей-процессов и временных причинных деревьев.

2. ВРЕМЕННЫЕ СЕТИ ПЕТРИ: СИНТАКСИС И ИНТЕРЛИВИНГОВАЯ СЕМАНТИКА

В этом разделе рассмотрим базовую терминологию непрерывно-временных сетей Петри и их интерливинговую семантику. Сначала напомним определения структуры и поведения сетей Петри. Пусть Act – множество действий.

Определение 1. (Помеченная над $Act$) сеть Петри (СП) – это набор $\mathcal{N} = (P,T,F,{{M}_{0}},L)$, где P – конечное множество мест, T – конечное множество переходов ($P \cap T = \emptyset $ и $P \cup T \ne \emptyset $), $F \subseteq (P \times T)$ ∪ ∪ (T × P) – отношение инцидентости, $\emptyset \ne {{M}_{0}}$ ⊆ ⊆ P – начальная разметка, L : T → $Act$ – помечающая функция. Для элемента $x \in P \cup T$ определим множество $^{ \bullet }x = \{ y\,|\,(y,x) \in F\} $ входных и множество ${{x}^{ \bullet }} = \{ y\,|\,(x,y) \in F\} $ выходных элементов, которые для подмножества $X \subseteq P \cup T$ элементов обобщаются соответственно до множеств $^{ \bullet }X$ = = ${{\bigcup\nolimits_{x \in X} }^{ \bullet }}x$ и ${{X}^{ \bullet }} = \bigcup\nolimits_{x \in X} {{x}^{ \bullet }}$.

Разметка M СП $\mathcal{N}$ – это произвольное подмножество P. Переход t ∈ T готов сработать при разметке M, если $^{ \bullet }t \subseteq M$¹¹. Обозначим через $En(M)$ множество всех переходов, готовых сработать при разметке M. Если переход t готов сработать при разметке M, то его срабатывание приводит к новой разметке $M{\text{'}}$ (обозначается $M\mathop \to \limits^t M{\text{'}}$), если M' = = $(M{{{\backslash }}^{ \bullet }}t) \cup {{t}^{ \bullet }}$. Будем использовать обозначение $M\mathop \to \limits^\vartheta M{\text{'}}$, если $\vartheta = {{t}_{1}} \ldots {{t}_{k}}$ и $M = {{M}^{0}}\mathop \to \limits^{{{t}_{1}}} {{M}^{1}}$ … M^{k – 1}$\mathop \to \limits^{{{t}_{k}}} $ $\mathop \to \limits^{{{t}_{k}}} $ M^k = M ' (k ≥ 0). Тогда, ϑ – это последовательность срабатываний из M (в $M{\text{'}}$) и $M{\text{'}}$ – разметка, достижимая из разметки M, в СП $\mathcal{N}$. Пусть $RM(\mathcal{N})$ – множество всех разметок, достижимых из M₀, в СП $\mathcal{N}$.

СП $\mathcal{N}$ называется T-ограниченной, если $^{ \bullet }t \ne \emptyset $ ≠ ${{t}^{ \bullet }}$ для всех переходов t ∈ T; свободной от контактов, если для произвольной разметки $M \in RM(\mathcal{N})$ и любого перехода t, готового сработать при разметке M, выполняется условие $M \cap {{t}^{ \bullet }} = \emptyset $.

Под непрерывно-временной сетью Петри (ВСП) [23] понимается СП, в которой с каждым переходом связан временной интервал, указывающий возможные временные моменты срабатывания перехода, готового по наличию фишек в его входных местах; готовый переход может сработать, только когда достигнута нижняя граница и не превышена верхняя граница его интервала, и, если он еще не сработал, то обязан сработать, когда достигнута верхняя граница его интервала.

Область $\mathbb{T}$ временных значений – множество неотрицательных рациональных чисел. Считаем, что $[{{\tau }_{1}},{{\tau }_{2}}]$ – замкнутый интервал между двумя временными значениями ${{\tau }_{1}},{{\tau }_{2}} \in \mathbb{T}$. Также, бесконечность может появляться как правая граница в открытых справа интервалах. Пусть Interv – множество всех таких интервалов.

Определение 2. (Помеченная над $Act$) временная сеть Петри (ВСП) – это пара $\mathcal{T}\mathcal{N} = (\mathcal{N},D)$, где $\mathcal{N}$ – (помеченная над Act) базовая сеть Петри и $D:T$ → Interv – статическая временная функция, сопоставляющая каждому переходу временной интервал. Границы временного интервала $D(t)$ ∈ Interv называются ранним (Eft) и поздним (Lft) временами срабатывания перехода t ∈ T.

Состояние ВСП $\mathcal{T}\mathcal{N}$ – это пара $S = (M,I)$, где M – разметка СП $\mathcal{N}$ и $I:En(M) \to \mathbb{T}$ – динамическая временная функция. Начальное состояние ВСП $\mathcal{T}\mathcal{N}$ – это пара ${{S}_{0}} = ({{M}_{0}},{{I}_{0}})$, где M₀ – начальная разметка СП $\mathcal{N}$ и ${{I}_{0}}(t) = 0$ для всех $t \in En({{M}_{0}})$. Переход t, готовый сработать при разметке M в СП $\mathcal{N}$, готов сработать в состоянии $S = (M,I)$ в относительный момент времени $\theta \in \mathbb{T}$ в ВСП $\mathcal{T}\mathcal{N}$, если ($Eft(t) \leqslant I(t)$ + θ) и верно, что ($I(t{\text{'}}) + \theta \leqslant Lft(t{\text{'}})$ для всех $t{\text{'}} \in En(M)$). Если переход t готов сработать в состоянии $S = (M,I)$ в относительный момент времени θ, то его срабатывание приводит в новое состояние $S{\text{'}} = (M{\text{'}},I{\text{'}})$ (обозначается $S\mathop \to \limits^{(t,\theta )} S{\text{'}}$) такое, что верно: $M\mathop \to \limits^t M{\text{'}}$ и $\forall t{\text{'}} \in {{T}_{\diamondsuit }}$

Будем писать $S\mathop \to \limits^\sigma S{\text{'}}$, если $\sigma = ({{t}_{1}},{{\theta }_{1}}) \ldots ({{t}_{k}},{{\theta }_{k}})$ и $S = {{S}^{0}}\xrightarrow{{({{t}_{1}},{{\theta }_{1}})}}{{S}^{1}}$ … ${{S}^{{k - 1}}}\xrightarrow{{({{t}_{k}},{{\theta }_{k}})}}{{S}^{k}} = S{\text{'}}$ ($k$ ≥ 0). Тогда, σ – последовательность срабатываний из S (в $S{\text{'}}$) и $S{\text{'}}$ – состояние, достижимое из S, в ВСП $\mathcal{T}\mathcal{N}$. Пусть $\mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})$ – множество всех последовательностей срабатываний из ${{S}_{0}}$ и $RS(\mathcal{T}\mathcal{N})$ – множество всех состояний, достижимых из ${{S}_{0}}$, в ВСП $\mathcal{T}\mathcal{N}$. Для $\sigma = ({{t}_{1}},{{\theta }_{1}})$ ... $({{t}_{k}},{{\theta }_{k}}) \in \mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})$ $L(\sigma )$ = (a₁, θ₁) ... (a_k, θ_k), если ${{a}_{i}} = L({{t}_{i}})$ для всех $1 \leqslant i \leqslant k$. Определим интерливинговый язык ВСП $\mathcal{T}\mathcal{N}$ следующим образом: $\mathcal{L}(\mathcal{T}\mathcal{N})$ = {L(σ) ∈ (Act × $\mathbb{T}){\text{*}}\,|\,\sigma \in \mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})\} $.

ВСП $\mathcal{T}\mathcal{N}$ называется T-ограниченной, если базовая СП T-ограничена; свободной от контактов, если для любого состояния $S = (M,I) \in RS(\mathcal{T}\mathcal{N})$ и любого перехода t, готового сработать в состоянии S в относительный момент времени θ, верно, что $(M{{{\backslash }}^{ \bullet }}t) \cap {{t}^{ \bullet }}$ = ∅²²; прогрессирующей по времени, если для любой последовательности переходов {t₁, ${{t}_{2}}, \ldots ,{{t}_{n}}\} \subseteq T$ такой, что $t_{i}^{ \bullet } \cap {{\,}^{ \bullet }}{{t}_{{i + 1}}}$ ≠ ∅ ($1 \leqslant i$ < n) и $t_{n}^{ \bullet } \cap {{\,}^{ \bullet }}{{t}_{1}}$ ≠ ∅ , выполяняется неравенство $\sum\nolimits_{1 \leqslant i \leqslant n} Eft({{t}_{i}})$ > > 0³³. В дальнейшем будем рассматривать только T-ограниченные, свободные от контактов и прогрессирующие по времени ВСП.

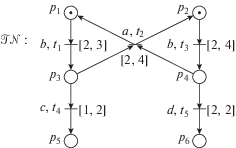
Пример 1. Пример помеченной над Act = = $\{ a,b,c,d\} $ ВСП $\mathcal{T}\mathcal{N}$ показан на рис. 1, где места представлены окружностями, переходы – барьерами; рядом с элементами ВСП размещены их имена; между элементами, включенными в отношение инцидентности, изображены стрелки; каждое место, входящее в начальную разметку, отмечено наличием в нем фишки (жирной точки); значения помечающей и статической временной функций указаны рядом с переходами. Нетрудно проверить, что переходы t₁ и t₃ готовы сработать при начальной разметке M₀ = ${\text{\{ }}{{p}_{1}},{{p}_{2}}{\text{\} }}$ и, более того, готовы сработать в начальном состоянии ${{S}_{0}} = ({{M}_{0}},{{I}_{0}})$, где I₀(t) = $\left\{ {\begin{array}{*{20}{l}} {0,\quad {\text{если}}\;t \in \{ {{t}_{1}},{{t}_{3}}\} ,} \\ {{\text{не}}\;{\text{определено}}\;{\text{иначе}},} \end{array}} \right.$ в относительный момент времени $\theta \in [2,3]$. При этом, $\sigma = ({{t}_{1}},3)$ $({{t}_{3}},0)$ $({{t}_{2}},2)$ $({{t}_{3}},2)$ $({{t}_{1}},0)$ $({{t}_{5}},2)$ $({{t}_{4}},0)$ – последовательность срабатываний из S₀ в ВСП $\mathcal{T}\mathcal{N}$. Кроме того, $\mathcal{T}\mathcal{N}$ является T-ограниченной, свободной от контактов и прогрессирующей по времени. □

Рис. 1.

Пример временной сети Петри.

3. ПРИЧИННО-ЗАВИСИМЫЕ СЕМАНТИКИ ВРЕМЕННЫХ СЕТЕЙ ПЕТРИ

3.2. Временные причинные сети-процессы временных сетей Петри

В этом разделе рассмотрим понятие временных причинных сетей-процессов ВСП, предложенное в статье [23].

Определение 4. Пусть $\mathcal{T}\mathcal{N}$ = ((P, T, F, M₀, L), D) – ВСП и $TN = (B,E,G,l,\tau )$ – временная причинная сеть. Отображение $\varphi {\kern 1pt} :\;B \cup E \to P \cup T$ называется гомоморфизмом из $TN$ в $\mathcal{T}\mathcal{N}$, если выполняются следующие условия:

• $\varphi (B) \subseteq P$, $\varphi (E) \subseteq T$;

• ограничение φ на $^{ \bullet }e$ является биекцией между $^{ \bullet }e$ и $^{ \bullet }\varphi (e)$ и ограничение φ на ${{e}^{ \bullet }}$ является биекцией между ${{e}^{ \bullet }}$ и $\varphi {{(e)}^{ \bullet }}$ для всех e ∈ E;

• ограничение φ на $^{ \bullet }TN$ является биекцией между $^{ \bullet }TN$ и M₀;

• $l(e) = L(\varphi (e))$ для всех $e \in E$.

Пара $\pi = (TN,\varphi )$ называется временным причинным сетью-процессом ВСП $\mathcal{T}\mathcal{N}$, если TN – временная причинная сеть и φ – гомоморфизм из TN в $\mathcal{T}\mathcal{N}$.

Пусть $\pi = (TN,\varphi )$ – временной причинный сеть-процесс ВСП $\mathcal{T}\mathcal{N}$, $B{\text{'}} \subseteq {{B}_{{TN}}}$ и $t \in En(\varphi (B{\text{'}}))$. Тогда глобальный момент времени, когда фишки появляются во всех входных местах перехода $t$, определяется следующим образом: ${\mathbf{TO}}{{{\mathbf{E}}}_{\pi }}(B{\text{'}},t)$ = = $max(\{ {{\tau }_{{TN}}}{{(}^{ \bullet }}b)\,|\,b \in B_{{[t]}}^{'}{{{\backslash }}^{ \bullet }}TN\} \cup \{ 0\} )$, где $B_{{[t]}}^{'}$ = = $\{ b \in B{\text{'}}\,|\,{{\varphi }_{{TN}}}(b) \in {{\;}^{ \bullet }}t\} $.

Для того, чтобы значения временных функций временных причинных сетей-процессов ВСП соответствовали временным интервалам срабатывания сетевых переходов, вводится понятие корректных временных причинных сетей-процессов ВСП.

Определение 5. Временной причинный сеть-процесс $\pi = (TN,\varphi )$ ВСП $\mathcal{T}\mathcal{N}$ называется корректным, если для каждого e ∈ E выполняются следующие условия:

• $\tau (e) \geqslant {\mathbf{TO}}{{{\mathbf{E}}}_{\pi }}{{(}^{ \bullet }}e,\varphi (e)) + Eft(\varphi (e))$,

• $\forall t \in En(\varphi ({{C}_{e}}))\diamondsuit \tau (e) \leqslant {\mathbf{TO}}{{{\mathbf{E}}}_{\pi }}({{C}_{e}},t) + Lft(t)$, где ${{C}_{e}} = Cut(Earlier(e))$.

Пусть $\mathcal{C}\mathcal{P}(\mathcal{T}\mathcal{N})$ – множество корректных временных причинных сетей-процессов ВСП $\mathcal{T}\mathcal{N}$. Через $\mathcal{T}\mathcal{P}os(\mathcal{T}\mathcal{N}) = \{ TP\,|\,\exists \pi = (TN,\varphi ) \in \mathcal{C}\mathcal{P}(\mathcal{T}\mathcal{N})$:TP ≃ ⁵⁵ ≃ $\eta (TN)\} $ обозначим множество ВЧУМов, изоморфных ВЧУМам, полученным из корректных временных причинных сетей-процессов ВСП $\mathcal{T}\mathcal{N}$.

Пример 3. Определим отображение φ из временной причинной сети TN (см. рис. 2) в ВСП $\mathcal{T}\mathcal{N}$ (см. рис. 1) следующим образом: $\varphi ({{b}_{i}}) = {{p}_{i}}$ (1 ≤ $i \leqslant 6$), $\varphi ({{b}_{i}}) = {{p}_{{i - 6}}}$ ($7 \leqslant i$ ≤ 10) и $\varphi ({{e}_{i}}) = {{t}_{i}}$ ($1 \leqslant i \leqslant 5$), $\varphi ({{e}_{6}}) = {{t}_{1}}$, $\varphi ({{e}_{7}}) = {{t}_{3}}$. Далее, для временной причинной сети $TN{\text{'}}$, заданной в примере 2, определим $\varphi {\text{'}} = \varphi \,|{{\,}_{{E{\text{'}} \cup B{\text{'}}}}}$. Легко видеть, что π = $(TN,\varphi )$ и $\pi {\text{'}} = (TN{\text{'}},\varphi {\text{'}})$ являются временными причинными сетями-процессами ВСП $\mathcal{T}\mathcal{N}$.

Рис. 2.

Пример временной причинной сети.

Для множества $\tilde {B} = \{ {{b}_{3}},{{b}_{4}}\} \subset B$ и перехода ${{t}_{2}}$ ∈ ∈ $En(\varphi (\widetilde B))$ вычислим ${\mathbf{TO}}{{{\mathbf{E}}}_{\pi }}(\widetilde B,{{t}_{2}})$ = $max(\{ {{\tau }_{{TN}}}{{(}^{ \bullet }}b)\,|\,b$ ∈ ∈ ${{\tilde {B}}_{{[{{t}_{2}}]}}}{{{\backslash }}^{ \bullet }}TN\} \cup \{ 0\} )$ = $\max (\{ \tau ({{e}_{1}})\, = \,3,\tau ({{e}_{3}})\, = \,3\} \, \cup \,\{ 0\} )$ = 3. Также, нетрудно проверить, что временные причинные сети-процессы $\pi = (TN,\varphi )$ и $\pi {\text{'}} = (TN{\text{'}},\varphi {\text{'}})$ являются корректными. □

Будем говорить, что $\pi = (TN,\varphi )$ и $\pi {\text{'}} = (TN{\text{'}},\varphi {\text{'}})$ из $\mathcal{C}\mathcal{P}(\mathcal{T}\mathcal{N})$ изоморфны (обозначается $\pi \simeq \pi {\text{'}}$), если существует изоморфизм $f{\kern 1pt} :\;TN \simeq TN{\text{'}}$ такой, что $\varphi (x) = \varphi {\text{'}}(f(x))$ для всех $x \in B \cup E$; а также будем писать $\pi \to \pi {\text{'}}$ в $\mathcal{T}\mathcal{N}$, если $TN \to TN{\text{'}}$ и $\varphi = \varphi {\text{'}}{{{\text{|}}}_{{B \cup E}}}$.

Рассмотрим взаимосвязи между последовательностями срабатываний и корректными временными причинными сетями-процессами ВСП. Для $\pi = (TN,\varphi ) \in \mathcal{C}\mathcal{P}(\mathcal{T}\mathcal{N})$ определим функцию FS_π, которая отображает линеаризацию $\rho = {{e}_{1}} \ldots {{e}_{k}}$ $TN$ в последовательность вида: FS_π(ρ) = $(\varphi ({{e}_{1}}),\tau ({{e}_{1}})$ – – 0) ... $(\varphi ({{e}_{k}}),\tau ({{e}_{k}}) - \tau ({{e}_{{k - 1}}}))$.

Утверждение 1. Пусть $\mathcal{T}\mathcal{N}$ – ВСП. Тогда

(а) если $\pi = (TN,\varphi ) \in \mathcal{C}\mathcal{P}(\mathcal{T}\mathcal{N})$ и ρ – линеаризация TN, то существует единственная последовательность срабатываний $F{{S}_{\pi }}(\rho ) \in \mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})$;

(б) если $\sigma \in \mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})$, то существует единственный (с точностью до изоморфизма) временной причинный сеть-процесс ${{\pi }_{\sigma }} = (TN,\varphi ) \in \mathcal{C}\mathcal{P}(\mathcal{T}\mathcal{N})$ и единственная линеаризация ${{\rho }_{\sigma }}$ TN такие, что $F{{S}_{{{{\pi }_{\sigma }}}}}({{\rho }_{\sigma }})$ = σ.

Доказательство. Пункт (а) без факта единственности последовательности срабатываний $F{{S}_{\pi }}(\rho )$ и пункт (б) без факта единственности линеаризации ${{\rho }_{\sigma }}$ – это переформулировки результатов, доказанных в теоремах соответственно 19 и 21, 22 в [23].

(а) Единственность последовательности срабатываний $F{{S}_{\pi }}(\rho )$ следует из определений гомоморфизма φ и функции $F{{S}_{\pi }}$.

(б) Пусть ${{\rho }_{\sigma }} = {{e}_{1}} \ldots {{e}_{n}}$ ($n \geqslant 0$) – линеаризация TN такая, что $F{{S}_{{{{\pi }_{\sigma }}}}}({{\rho }_{\sigma }})$ = σ = (t₁, θ₁)...(t_n, ${{\theta }_{n}}) \in \mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})$. Предположим обратное, т.е. существует линеаризация $\bar {\rho } = {{\bar {e}}_{1}} \ldots {{\bar {e}}_{n}}$ $TN$ такая, что $F{{S}_{{{{\pi }_{\sigma }}}}}(\bar {\rho }) = \sigma $ и $\bar {\rho } \ne {{\rho }_{\sigma }}$. Так как все линеаризации $TN$ конечны, то можно найти минимальное $k$ такое, что ${{e}_{k}} \ne {{\bar {e}}_{k}}$. Ясно, что $\varphi ({{e}_{k}}) = \varphi ({{\bar {e}}_{k}}) = {{t}_{k}}$. Поскольку $\mathcal{T}\mathcal{N}$ – T-ограниченная ВСП, то $^{ \bullet }{{t}_{k}} \ne \emptyset $. Возьмем произвольное место ${{p}_{k}} \in {{\;}^{ \bullet }}{\kern 1pt} {{t}_{k}}$. По определению гомоморфизма, существуют условия $b \in {{\;}^{ \bullet }}{{e}_{k}}$ и $\bar {b} \in {{\;}^{ \bullet }}{{\bar {e}}_{k}}$ такие, что φ(b) = = $\varphi (\bar {b})$ = p_k. В силу определения временной причинной сети, верно, что $b \ne \bar {b}$.

Рассмотрим возможные случаи.

– $\{ b,\bar {b}\} \subseteq {{\;}^{ \bullet }}TN$. Тогда верно, что ${{p}_{k}} \in {{M}_{0}}$. Это противоречит определению гомоморфизма φ.

– $b \in {{\;}^{ \bullet }}TN$ и (случай, когда $\bar {b} \in {{\;}^{ \bullet }}TN$ и , аналогичен). Поскольку $b \in {{\;}^{ \bullet }}TN$, то получаем, что ${{p}_{k}} \in {{M}_{0}}$, по определению гомоморфизма φ. Тогда имеем, что $b = {{b}_{{0,{{p}_{k}}}}}$, по построению ${{\pi }_{\sigma }}$ в [23]. Предполагая, что , найдем событие $\tilde {e}$ такое, что $\{ \tilde {e}\} = {{\;}^{ \bullet }}\bar {b}$. Так как k – минимальное, то в обеих линеаризациях $\rho $ и $\bar {\rho }$ событие $\tilde {e}$ имеет один и тот же порядковый номер, т.е. $\tilde {e} = {{e}_{i}} = {{\bar {e}}_{i}}$ для некоторого $0 < i$ < k. По определению функции $F{{S}_{{{{\pi }_{\sigma }}}}}$, верно, что $\varphi (\tilde {e}) = {{t}_{i}}$. Тогда ${{p}_{k}} \in t_{i}^{ \bullet }$, согласно определению φ. Кроме того, имеем, что $\bar {b} = {{b}_{{i,{{p}_{k}}}}}$, в силу построения ${{\pi }_{\sigma }}$ в [23]. Таким образом, получили противоречие со свойством (41) из [23]: не существует ${{b}_{{i,{{p}_{k}}}}}$ для любого 0 < i < k.

– . Cледовательно, существует событие $\tilde {e}$ ($\hat {e}$) такое, что $\{ \tilde {e}\} = {{\;}^{ \bullet }}b$ ($\{ \hat {e}\} {{ = }^{ \bullet }}\bar {b}$). В силу определения гомоморфизма φ, верно, что $\tilde {e} \ne \hat {e}$. Так как $k$ – минимальное, то в обеих линеаризациях $\rho $ и $\bar {\rho }$ событие $\tilde {e}$ ($\hat {e}$) имеет один и тот же порядковый номер, т.е. $\tilde {e} = {{e}_{i}} = {{\bar {e}}_{i}}$ для некоторого $1 \leqslant i < k$ ($\hat {e} = {{e}_{j}} = {{\bar {e}}_{j}}$ для некоторого $1 \leqslant j < k$). Тогда $i \ne j$, согласно определению линеаризации. По определению функции $F{{S}_{{{{\pi }_{\sigma }}}}}$, имеем, что $\varphi (\tilde {e}) = {{t}_{i}}$ ($\varphi (\hat {e})$ = = t_j). Из определения гомоморфизма следует, что ${{p}_{k}} \in t_{i}^{ \bullet }$ (${{p}_{k}} \in t_{j}^{ \bullet }$). По построению ${{\pi }_{\sigma }}$ в [23] верно, что $b = {{b}_{{i,{{p}_{k}}}}}$ ($\bar {b} = {{b}_{{j,{{p}_{k}}}}}$). В случае, когда i < j < k (j < i < k), получаем противоречие со свойством (41) из [23]: не существует ${{b}_{{l,{{p}_{k}}}}}$ для любого $i < l < k$ ($j < l < k$). □

Пример 4. Для временного причинного сети-процесса $\pi = (TN,\varphi )$ ВСП $\mathcal{T}\mathcal{N}$ (см. пример 3) и линеаризации $\rho = {{e}_{1}}{{e}_{3}}{{e}_{2}}{{e}_{7}}{{e}_{6}}{{e}_{5}}{{e}_{4}}$ временной причинной сети TN получаем, что $F{{S}_{\pi }}(\rho ) = ({{t}_{1}},3)$ $({{t}_{3}},0)$ $({{t}_{2}},2)$ $({{t}_{3}},2)$ $({{t}_{1}},0)$ $({{t}_{5}},2)$ $({{t}_{4}},0)$ является последовательностью срабатываний ВСП $\mathcal{T}\mathcal{N}$ (см. пример 1). □

Используя определение префикса временной причинной сети и утверждение 1, легко показать, что если последовательность срабатываний и временной причинный сеть-процесс ВСП взаимосвязаны, то их непосредственные расширения тоже взимосвязаны.

Лемма 2. Пусть $\sigma \in \mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})$ и $\pi \in \mathcal{C}\mathcal{P}(\mathcal{T}\mathcal{N})$ такие, что $\sigma = F{{S}_{\pi }}(\rho )$, где ρ – линеаризация $T{{N}_{\pi }}$. Тогда

(a) если $\sigma (t,\theta ) \in \mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})$, то существует $\tilde {\pi } \in \mathcal{C}\mathcal{P}(\mathcal{T}\mathcal{N})$ такой, что $\pi \to \tilde {\pi }$ в $\mathcal{T}\mathcal{N}$ и $\sigma (t,\theta )$ = = $F{{S}_{{\tilde {\pi }}}}(\rho e)$, где $\rho e$ – линеаризация $T{{N}_{{\tilde {\pi }}}}$;

(б) если $\pi \to \tilde {\pi }$ в $\mathcal{T}\mathcal{N}$, то существует σ(t, $\theta ) \in \mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})$ такая, что $\sigma (t,\theta ) = F{{S}_{{\widetilde \pi }}}(\rho e)$, где ρe – линеаризация $T{{N}_{{\tilde {\pi }}}}$.

4. ТЕСТОВЫЕ ЭКВИВАЛЕНТНОСТИ

При интерливинговом подходе к определению тестовой эквивалентности в качестве тестов рассматриваются последовательности $w$ выполняемых действий (вычисления системы) и множества $W$ возможных дальнейших действий. Процесс проходит тест, если после выполнения каждой последовательности w действий дальше может выполниться хотя бы одно действие из W. Два процесса тестово эквивалентны, если они проходят одно и то же множество тестов. Во временном варианте добавляется информация о временах выполнения действий.

Определение 7. Пусть $\mathcal{T}\mathcal{N}$ и $\mathcal{T}\mathcal{N}{\kern 1pt} '$ – ВСП.

Для последовательности $w \in (Act \times \mathbb{T}){\text{*}}$ и множества $W \subseteq (Act \times \mathbb{T})$, $\mathcal{T}\mathcal{N}$ after w MUST$_{{int}}$ W, если для всех $\sigma \in \mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})$ таких, что $L(\sigma ) = w$, существуют $(a,\theta ) \in W$ и $\sigma (t,\theta ) \in \mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N})$ такие, что $L(\sigma (t,\theta )) = w(a,\theta )$.

$\mathcal{T}\mathcal{N}$ и $\mathcal{T}\mathcal{N}{\kern 1pt} '$ называются ИНТ-тестово эквивалентными (обозначается $\mathcal{T}\mathcal{N}{{ \sim }_{{int}}}\mathcal{T}\mathcal{N}{\text{'}}$), если для любой последовательности $w \in (Act \times \mathbb{T}){\text{*}}$ и любого множества $W \subseteq (Act \times \mathbb{T})$, $\mathcal{T}\mathcal{N}$ after w MUST$_{{int}}$ $W$ $ \Leftrightarrow $ $\mathcal{T}\mathcal{N}{\kern 1pt} '$ after w MUST$_{{int}}$ W.

Пример 6. ВСП $\mathcal{T}{{\mathcal{N}}_{2}}$, $\mathcal{T}{{\mathcal{N}}_{3}}$ и $\mathcal{T}{{\mathcal{N}}_{4}}$, изображенные на рис. 3, ИНТ-тестово эквивалентны, тогда как $\mathcal{T}{{\mathcal{N}}_{1}}$ и $\mathcal{T}{{\mathcal{N}}_{2}}$ не являются таковыми. Легко проверить, что $TCT(\mathcal{T}{{\mathcal{N}}_{2}})$ after $w = (b,0)(b,0)$ ${\mathbf{MUS}}{{{\mathbf{T}}}_{{int}}}$ $W = \{ (a,3.9)\} $. Однако в $TCT(\mathcal{T}{{\mathcal{N}}_{1}})$ существует последовательность срабатываний, которая помечена w и после которой невозможно срабатывание перехода, помеченного a, в момент времени 3.9. Таким образом, не выполняется $TCT(\mathcal{T}{{\mathcal{N}}_{1}})$ after w ${\mathbf{MUS}}{{{\mathbf{T}}}_{{int}}}$ W. □

Рис. 3.

Тестовые эквивалентности, учитывающие отношение причинной зависимости между действиями, были впервые введены Асето и др. в статье [5] в контексте моделей структур событий. При этом в качестве вычислений процесса вместо последовательностей выполняемых действий рассматривались их частично-упорядоченные мультимножества (ЧУММы). В работе [6] вместо множеств дальнейших действий использовались непосредственные расширения выполняемых ЧУММов. Кроме того, в [6] была предложена еще одна версия причинной тестовой эквивалентности, которая использует в качестве вычислений ЧУМы выполняемых действий и которая, как было показано, является более строгой эквивалентностью. Следуя этому подходу, далее определяется временная ЧУМ-тестовая эквивалентность для ВСП с использованием ее корректных временных причинных сетей-процессов.

Определение 8. Пусть $\mathcal{T}\mathcal{N}$ и $\mathcal{T}\mathcal{N}{\kern 1pt} '$ – ВСП.

Для ВЧУМ TP и множества TP ВЧУМов такого, что $TP \prec \cdot $⁷⁷ $TP{\text{'}}$ для любого $TP{\text{'}} \in {\mathbf{TP}}$, $\mathcal{T}\mathcal{N}$ after TP MUST$_{{tpos}}$ TP, если для любого π = (TN, $\varphi ) \in \mathcal{C}\mathcal{P}(\mathcal{T}\mathcal{N})$ и для любого изоморфизма f: $\eta (TN) \to TP$ существуют $TP{\text{'}} \in {\mathbf{TP}}$, π' = (TN', $\varphi {\text{'}}) \in \mathcal{C}\mathcal{P}(\mathcal{T}\mathcal{N})$ и изоморфизм $f{\text{'}}{\kern 1pt} :\;\eta (TN{\text{'}}) \to TP{\text{'}}$ такие, что $\pi \to \pi {\text{'}}$ и $f \subseteq f{\text{'}}$.

$\mathcal{T}\mathcal{N}$ и $\mathcal{T}\mathcal{N}{\kern 1pt} '$ называются ВЧУМ-тестово эквивалентными (обозначается $\mathcal{T}\mathcal{N}{{ \sim }_{{tpos}}}\mathcal{T}\mathcal{N}{\text{'}}$), если для любого ВЧУМ TP и любого множества ${\mathbf{TP}}$ ВЧУМов такого, что $TP \prec \cdot TP{\text{'}}$ для всех $TP{\text{'}} \in {\mathbf{TP}}$, выполняется условие: $\mathcal{T}\mathcal{N}$ after TP MUST$_{{tpos}}$ ${\mathbf{TP'}}$ $ \Leftrightarrow $ $\mathcal{T}\mathcal{N}'$ after $TP$ MUST$_{{tpos}}$ ${\mathbf{TP}}$.

Пример 7. Рассмотрим ВСП $\mathcal{T}{{\mathcal{N}}_{2}}$, $\mathcal{T}{{\mathcal{N}}_{3}}$ и $\mathcal{T}{{\mathcal{N}}_{4}}$, изображенные на рис. 3. Легко видеть, что $\mathcal{T}{{\mathcal{N}}_{2}}$ и $\mathcal{T}{{\mathcal{N}}_{3}}$ ВЧУМ-тестово эквивалентны, тогда как $\mathcal{T}{{\mathcal{N}}_{3}}$ и $\mathcal{T}{{\mathcal{N}}_{4}}$ не являются таковыми. Убедимся в последнем. Определим ВЧУМ TP = ({x₁, x₂}, $ \preccurlyeq ,\lambda $, τ), где $ \preccurlyeq = \{ ({{x}_{i}},{{x}_{i}})\,|\,1 \leqslant i \leqslant 2\} $, $\lambda ({{x}_{1}}) = \lambda ({{x}_{2}}) = b$, $\tau ({{x}_{1}})$ = = τ'(x₂) = 0; и ВЧУМ $TP{\text{'}} = (\{ {{x}_{1}},{{x}_{2}},{{x}_{3}}\} , \preccurlyeq \,{\text{'}}$, λ', τ') где $ \preccurlyeq \,{\text{'}}\, = \,\{ ({{x}_{i}},{{x}_{i}})\,|\,1\, \leqslant \,i\, \leqslant \,3\} \, \cup \,\{ ({{x}_{2}},{{x}_{3}})\} $, $\lambda {\text{'}}({{x}_{1}})$ = λ'(x₂) = b, $\lambda {\text{'}}({{x}_{3}}) = a$, $\tau {\text{'}}({{x}_{1}}) = \tau {\text{'}}({{x}_{2}}) = 0$ и $\tau {\text{'}}({{x}_{3}})$ = 3.9. Для любого временного причинного сети-процесса π₃ = = $(T{{N}_{3}},{{\varphi }_{3}}) \in \mathcal{C}\mathcal{P}(\mathcal{T}{{\mathcal{N}}_{3}})$, в котором ${{E}_{{T{{N}_{3}}}}}$ состоит из двух параллельных событий с пометками b и временными значениями, равными 0, и для любого изоморфизма ${{f}_{3}}:\eta (T{{N}_{3}}) \to TP$ можно найти временной причинный сеть-процесс $\pi _{3}^{'} = (TN_{3}^{'},\varphi _{3}^{'}) \in \mathcal{C}\mathcal{P}(\mathcal{T}{{\mathcal{N}}_{3}})$, в котором ${{E}_{{TN_{3}^{'}}}}$ состоит из двух параллельных событий с пометками b и временными значениями 0 и третьего события с пометкой a и временным значением 3.9, находящегося в отношении причинной зависимости с одним из b, и изоморфизм $f_{3}^{'}{\text{:}}\eta (TN_{3}^{'}) \to TP{\text{'}}$ такие, что ${{\pi }_{3}} \to \pi _{3}^{'}$ и ${{f}_{3}} \subset f_{3}^{'}$. Однако, это не так в случае ВСП $\mathcal{T}{{\mathcal{N}}_{4}}$. □

Далее определим тестовую эквивалентность для ВСП на основе их временных причинных деревьев. При этом будем придерживаться метода, использованного для модели структур событий в [6]. Тесты будут строиться с учетом временных значений на основе множества пометок $Act \times \mathbb{T} \times {{2}^{\mathbb{N}}}$ дуг деревьев.

Определение 9. Пусть $\mathcal{T}\mathcal{N}$ и $\mathcal{T}\mathcal{N}'$ – ВСП и $TCT(\mathcal{T}\mathcal{N}) = (\mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N}),A,\phi )$ и $TCT(\mathcal{T}\mathcal{N}{\text{'}})$ = = $(\mathcal{F}\mathcal{S}(\mathcal{T}\mathcal{N}{\text{'}})$, A', ϕ') – их временные причинные деревья.

Для последовательности $w \in (Act \times \mathbb{T} \times {{2}^{\mathbb{N}}}){\text{*}}$ и множества ${\mathbf{W}} \subseteq (Act \times \mathbb{T} \times {{2}^{\mathbb{N}}})$, $TCT(\mathcal{T}\mathcal{N})$ after w MUST$_{{tct}}$ W, если для всех путей u в $TCT(\mathcal{T}\mathcal{N})$ из корня в вершину n таких, что $\phi (u) = w$, существуют пометка $(a,d,K) \in {\mathbf{W}}$ и дуга r из вершины n такие, что $\phi (r) = (a,d,K)$;

$\mathcal{T}\mathcal{N}$ и $\mathcal{T}\mathcal{N}'$ называются ВПД-тестово эквивалентными (обозначается $\mathcal{T}\mathcal{N}$ ${{ \sim }_{{tct}}}$ $\mathcal{T}\mathcal{N}'$), если для любой последовательности $w \in (Act \times \mathbb{T} \times {{2}^{\mathbb{N}}}){\text{*}}$ и для любого множества ${\mathbf{W}} \subseteq (Act \times \mathbb{T} \times {{2}^{\mathbb{N}}})$, $TCT(\mathcal{T}\mathcal{N})$ after w ${\mathbf{MUS}}{{{\mathbf{T}}}_{{tct}}}$ W $ \Leftrightarrow $ $TCT(\mathcal{T}\mathcal{N}{\kern 1pt} ')$ after w ${\mathbf{MUS}}{{{\mathbf{T}}}_{{tct}}}$ ${\mathbf{W}}$.

Пример 8. Рассмотрим ВСП $\mathcal{T}{{\mathcal{N}}_{2}}$, $\mathcal{T}{{\mathcal{N}}_{3}}$ и $\mathcal{T}{{\mathcal{N}}_{4}}$, изображенные на рис. 3. Легко видеть, что $\mathcal{T}{{\mathcal{N}}_{2}}$ и $\mathcal{T}{{\mathcal{N}}_{3}}$ ВПД-тестово эквивалентны, а $\mathcal{T}{{\mathcal{N}}_{3}}$ и $\mathcal{T}{{\mathcal{N}}_{4}}$ не являются таковыми. Убедимся в последнем факте. Для этого определим w = $(b,0,\emptyset )(b,0,\emptyset )$ и ${\mathbf{W}} = \{ (a,3.9,\{ 1\} )\} $. Легко проверить, что $TCT(\mathcal{T}{{\mathcal{N}}_{3}})$ after w ${\mathbf{MUS}}{{{\mathbf{T}}}_{{tct}}}$ W. В $TCT(\mathcal{T}{{\mathcal{N}}_{4}})$ существуют два пути, помеченных $(b,0,\emptyset )(b,0,\emptyset )$, один из них заканчивается в вершине, из которой есть дуга с пометкой $(a,3.9,\{ 1\} )$, а из вершины, в которую ведет другой путь, такой дуги нет. Таким образом, не выполняется $TCT(\mathcal{T}{{\mathcal{N}}_{4}})$ after w ${\mathbf{MUS}}{{{\mathbf{T}}}_{{tct}}}$ W. □

Из определений ИНТ-, ВЧУМ- и ВПД-тестовых эквивалентностей очевидным образом следует

Лемма 3. Пусть $\mathcal{T}{{\mathcal{N}}_{1}}$ и $\mathcal{T}{{\mathcal{N}}_{2}}$ – ВСП. Тогда

Установим связи между ИНТ- и ВПД-тестовыми эквивалентностями.

Теорема 1. $\mathcal{T}{{\mathcal{N}}_{1}}{{ \sim }_{{tct}}}\mathcal{T}{{\mathcal{N}}_{2}} \Rightarrow \mathcal{T}{{\mathcal{N}}_{1}}{{ \sim }_{{int}}}\mathcal{T}{{\mathcal{N}}_{2}}$.

Доказательство. Предположим, что $\mathcal{T}{{\mathcal{N}}_{1}}$ ~_tct$\mathcal{T}{{\mathcal{N}}_{2}}$. Покажем, что верно $\mathcal{T}{{\mathcal{N}}_{1}}{{ \sim }_{{int}}}\mathcal{T}{{\mathcal{N}}_{2}}$. Предположим обратное, т.е. существуют $w \in (Act \times \mathbb{T}){\text{*}}$ и $W \subseteq (Act \times \mathbb{T})$ такие, что $\mathcal{T}{{\mathcal{N}}_{1}}$ after w MUST$_{{int}}$ W, однако $\neg (\mathcal{T}{{\mathcal{N}}_{2}}$ after w MUST$_{{int}}$ W). Последнее означает, что существует σ₂ ∈ $\mathcal{F}\mathcal{S}(\mathcal{T}{{\mathcal{N}}_{2}})$ такая, что $L({{\sigma }_{2}})$ = w, и для любых $(a,\theta ) \in W$ и ${{\sigma }_{2}}(t{\text{'}},\theta )$ ∈ ∈ $\mathcal{F}\mathcal{S}(\mathcal{T}{{\mathcal{N}}_{2}})$ не верно, что $L({{\sigma }_{2}}(t{\text{'}},\theta ))$ = w(a, θ). Используя определения, получаем, что $w \in \mathcal{L}(\mathcal{T}{{\mathcal{N}}_{2}})$ и, более того, $\tilde {w} = {{\phi }_{2}}(path({{\sigma }_{2}}))$ ∈ ∈ $\mathcal{L}(TCT(\mathcal{T}{{\mathcal{N}}_{2}}))$, при этом $\tilde {w}{{{\text{|}}}_{{(Act \times \mathbb{T}){\text{*}}}}} = w$. Определим множество W =  $\{ (a,\theta ,K)\,{\text{|}}\,(a,\theta ) \in W$, $\exists \sigma \in \mathcal{F}\mathcal{S}(\mathcal{T}{{\mathcal{N}}_{1}})$ : L(σ) = w и ${{\phi }_{1}}(path(\sigma )) = \tilde {w}$, $\exists $ дуга r из $\sigma $ в $TCT(\mathcal{T}{{\mathcal{N}}_{1}})$ : ϕ₁(r) = = (a, θ, K)}. Покажем, что $\mathcal{T}{{\mathcal{N}}_{1}}$ after $\tilde {w}$ MUST$_{{tct}}$ W. Возьмем произвольную ${{\sigma }_{1}} \in \mathcal{F}\mathcal{S}(\mathcal{T}{{\mathcal{N}}_{1}})$ такую, что ${{\phi }_{1}}(path({{\sigma }_{1}}))$ = $\tilde {w}$. Такая σ₁ существует, поскольку $\tilde {w} \in \mathcal{L}(TCT(\mathcal{T}{{\mathcal{N}}_{1}}))$, по лемме 3. Более того, имеем, что $w \in \mathcal{L}(\mathcal{T}{{\mathcal{N}}_{1}})$, по утверждению 3. Так как $\mathcal{T}{{\mathcal{N}}_{1}}$ after w MUST$_{{int}}$ W, то существуют $(a,\theta ) \in W$ и σ₁(t, θ) ∈ $\mathcal{F}\mathcal{S}(\mathcal{T}{{\mathcal{N}}_{1}})$ такие, что $L({{\sigma }_{1}}(t,\theta )) = w(a,\theta )$. Согласно построению временного причинного дерева, найдется дуга $r = ({{\sigma }_{1}},{{\sigma }_{1}}(t,\theta ))$ в $TCT(\mathcal{T}{{\mathcal{N}}_{1}})$ такая, что ${{\phi }_{1}}(r) = (a,\theta ,K)$. Значит, имеем, что ${{\phi }_{1}}(r) \in {\mathbf{W}}$. В силу произвольности выбора ${{\sigma }_{1}}$, верно, что $\mathcal{T}{{\mathcal{N}}_{1}}$ after $\tilde {w}$ MUST$_{{tct}}$ W. Таким образом, пришли к противоречию, так как легко проверить, что $\neg (\mathcal{T}{{\mathcal{N}}_{2}}$ after $\tilde {w}$ MUST$_{{tct}}$ W). □

В заключение, покажем совпадение тестовых эквивалентностей для ВСП в семантиках временных частично-упорядоченных множеств и временных причинных деревьев.

Теорема 2. Пусть $\mathop {\mathcal{T}\mathcal{N}}\nolimits_1 $ и $\mathop {\mathcal{T}\mathcal{N}}\nolimits_2 $ – ВСП. Тогда

Доказательство. Рассмотрим доказательство слева направо (доказательство справа налево аналогично). Пусть $TCT(\mathcal{T}{{\mathcal{N}}_{i}}) = (\mathcal{F}\mathcal{S}(\mathcal{T}{{\mathcal{N}}_{i}}),{{A}_{i}},{{\phi }_{i}})$ (i = 1, 2). Предположим, что $\mathcal{T}{{\mathcal{N}}_{1}}{{ \sim }_{{tpos}}}\mathcal{T}{{\mathcal{N}}_{2}}$. Тогда, согласно лемме 3, имеем $\mathcal{T}\mathcal{P}os(\mathcal{T}{{\mathcal{N}}_{1}})$ = $\mathcal{T}\mathcal{P}os(\mathcal{T}{{\mathcal{N}}_{2}})$. По утверждению 3, получаем, что $\mathcal{L}(TCT(\mathcal{T}{{\mathcal{N}}_{1}}))$ = = $\mathcal{L}(TCT(\mathcal{T}{{\mathcal{N}}_{2}}))$. Покажем, что $\mathcal{T}{{\mathcal{N}}_{1}}{{ \sim }_{{tct}}}\mathcal{T}{{\mathcal{N}}_{2}}$. Возьмем произвольные w ∈ $(Act\, \times \,\mathbb{T}\, \times \,{{2}^{\mathbb{N}}}){\text{*}}$ и ${\mathbf{W}}\, \subseteq \,(Act\, \times \,\mathbb{T}\, \times \,{{2}^{\mathbb{N}}})$. Без потери общности полагаем, что $\left| w \right| = n$ (n ≥ 0). Предположим, что $TCT(\mathcal{T}{{\mathcal{N}}_{1}})$ after w MUST$_{{tct}}$ W. Проверим, что $TCT(\mathcal{T}{{\mathcal{N}}_{2}})$ after $w$ MUST$_{{tct}}$ ${\mathbf{W}}$.

Если $w \notin \mathcal{L}(TCT(\mathcal{T}{{\mathcal{N}}_{1}})) = \mathcal{L}(TCT(\mathcal{T}{{\mathcal{N}}_{2}}))$, то результат очевиден. Рассмотрим случай, когда $w \in \mathcal{L}(TCT(\mathcal{T}{{\mathcal{N}}_{1}})) = \mathcal{L}(TCT(\mathcal{T}{{\mathcal{N}}_{2}}))$. Тогда можно выбрать любой путь u из корня в некоторую вершину $\sigma \in \mathcal{F}\mathcal{S}(\mathcal{T}{{\mathcal{N}}_{1}})$ такую, что ${{\phi }_{1}}(u) = w$. Согласно утверждению 1(б), существует единственный (с точностью до изоморфизма) временной причинный сеть-процесс ${{\pi }_{\sigma }} = (T{{N}_{\sigma }},{{\varphi }_{\sigma }}) \in \mathcal{C}\mathcal{P}(\mathcal{T}{{\mathcal{N}}_{1}})$ и единственная линеаризация ${{\rho }_{\sigma }} = e_{1}^{\sigma } \ldots e_{n}^{\sigma }$ TN_σ такие, что $F{{S}_{{{{\pi }_{\sigma }}}}}({{\rho }_{\sigma }}) = \sigma $. Обозначим $T{{P}_{w}} = \eta (T{{N}_{\sigma }})$ ∈ ∈ $\mathcal{T}\mathcal{P}os(\mathcal{T}{{\mathcal{N}}_{1}})$.

Для каждой $(a,\theta ,K) \in {\mathbf{W}}$ сконструируем ВЧУМ $T{{P}_{{(a,\theta ,K)}}} = (X, \preccurlyeq ,\lambda ,\tau )$ следующим образом: X = = ${{E}_{{T{{N}_{\sigma }}}}} \cup \{ {{e}_{{(a,\theta ,K)}}}\} $ (); $ \preccurlyeq = {{ \preccurlyeq }_{{T{{N}_{\sigma }}}}} \cup \;\{ (e_{{n - k + 1}}^{\sigma }$, ${{e}_{{(a,\theta ,K)}}})\,|\,k \in K\} $; $\lambda {{{\text{|}}}_{{{{E}_{{T{{N}_{\sigma }}}}}}}} = {{\lambda }_{{T{{N}_{\sigma }}}}}$, $\lambda ({{e}_{{(a,\theta ,K)}}})$ = a; $\tau {{{\text{|}}}_{{{{E}_{{T{{N}_{\sigma }}}}}}}}$ = = ${{\tau }_{{T{{N}_{\sigma }}}}}$, $\tau ({{e}_{{(a,\theta ,K)}}}) = \tau (T{{N}_{\sigma }}) + \theta $. Обозначим множество всех построенных ВЧУМ как TP_W = $\{ T{{P}_{{(a,\theta ,K)}}}\,|\,(a$, θ, K) ∈ W}.

Проверим, что $\mathcal{T}{{\mathcal{N}}_{1}}$ after $T{{P}_{w}}$ MUST$_{{tpos}}$ TP_W. Возьмем произвольный временной причинный сеть-процесс ${{\pi }_{1}} = (T{{N}_{1}},{{\varphi }_{1}}) \in \mathcal{C}\mathcal{P}(\mathcal{T}{{\mathcal{N}}_{1}})$ и изоморфизм ${{f}_{1}}{\kern 1pt} :\;\eta (T{{N}_{1}}) \to T{{P}_{w}}$. Так как $T{{P}_{w}} \in \mathcal{T}\mathcal{P}os(\mathcal{T}{{\mathcal{N}}_{1}})$, то такие ${{\pi }_{1}}$ и f₁ существуют. Из утверждения 2(а) получаем, что $e_{1}^{1} \ldots e_{n}^{1}\, = \,{{\rho }_{1}}\, = \,{{({{f}_{1}})}^{{ - 1}}}:\eta (T{{N}_{\sigma }})$ → $\eta (T{{N}_{1}})({{\rho }_{\sigma }})$ является линеаризацией TN₁ такой, что w = ϕ(path(σ₁ = = $F{{S}_{{{{\pi }_{1}}}}}({{\rho }_{1}})))$. Так как $TCT(\mathcal{T}{{\mathcal{N}}_{1}})$ after w MUST$_{{tct}}$ W, то существует пометка $(a_{1}^{'},\theta _{1}^{'},K_{1}^{'}) \in {\mathbf{W}}$ и дуга r₁ из вершины σ₁ такие, что ${{\phi }_{1}}({{r}_{1}}) = (a_{1}^{'},\theta _{1}^{'},K_{1}^{'})$. Тогда можно найти $TP_{1}^{'} = T{{P}_{{(a_{1}^{'},\theta _{1}^{'},K_{1}^{'})}}} \in {\mathbf{T}}{{{\mathbf{P}}}_{{\mathbf{W}}}}$. Следовательно, по построению множества TP_W, получаем, что $\{ {{e}_{{(a_{1}^{'},\theta _{1}^{'},K_{1}^{'})}}}\} = {{E}_{{TP_{1}^{'}}}}{\backslash }{{E}_{{T{{N}_{\sigma }}}}}$, $a_{1}^{'} = {{\lambda }_{{TP_{1}^{'}}}}({{e}_{{(a_{1}^{'},\theta _{1}^{'},K_{1}^{'})}}})$, $\theta _{1}^{'}$ = = ${{\tau }_{{TP_{1}^{{{\kern 1pt} '}}}}}({{e}_{{(a_{1}^{'},\theta _{1}^{'},K_{1}^{'})}}})$ – τ(TN_σ), $K_{1}^{'}$ = {n – l + 1 | $e_{l}^{\sigma }$ ${{ \preccurlyeq }_{{TP_{1}^{'}}}}$ ${{e}_{{(a_{1}^{'},\theta _{1}^{'},K_{1}^{'})}}}\} $. Более того, по определению $TCT(\mathcal{T}{{\mathcal{N}}_{1}})$, существует ${{\sigma }_{1}}(t_{1}^{'},\theta _{1}^{'}) \in \mathcal{F}\mathcal{S}(\mathcal{T}{{\mathcal{N}}_{1}})$, ($t_{1}^{'} \in {{T}_{{\mathcal{T}{{\mathcal{N}}_{1}}}}}$), такая что r₁ = $({{\sigma }_{1}},{{\sigma }_{1}}(t_{1}^{'},\theta _{1}^{'}))$ и ${{\phi }_{1}}(\sigma _{1}^{'},{{\sigma }_{1}}(t_{1}^{'},\theta _{1}^{'}))$ = = $({{l}_{{\mathcal{T}{{\mathcal{N}}_{1}}}}}(t_{1}^{'}) = a_{1}^{'},\theta _{1}^{'},K_{1}^{'})$. Из леммы 2(а) следует наличие временного причинного сети-процесса $\pi _{1}^{'}$ = = $(TN_{1}^{'},\varphi _{1}^{'}) \in \mathcal{C}\mathcal{P}(\mathcal{T}{{\mathcal{N}}_{1}})$ такого, что ${{\pi }_{1}} \to \pi _{1}^{'}$ и ${{\sigma }_{1}}(t_{1}^{'},\theta _{1}^{'})$ = $F{{S}_{{\pi _{1}^{'}}}}({{\rho }_{1}}e_{1}^{'})$ для некоторой линеаризации ${{\rho }_{1}}e_{1}^{'}$ $TN_{1}^{'}$, т.е. $\varphi _{1}^{'}(e_{1}^{'})$ = $t_{1}^{'}$. Определим функцию $f_{1}^{'}{\kern 1pt} :\;\eta (TN_{1}^{'}) \to TP_{1}^{'}$ так: $f_{1}^{'}{{{\text{|}}}_{{{{E}_{{\eta (T{{N}_{1}})}}}}}}$ = f₁, $f_{1}^{'}(e_{1}^{'})$ = ${{e}_{{(a_{1}^{'},\theta _{1}^{'},K_{1}^{'})}}}$. Кроме того, ${{\lambda }_{{\eta (TN_{1}^{'})}}}(e_{1}^{'})$ = $a_{1}^{'}$ = ${{\lambda }_{{\mathop {TP}\nolimits_1 }}}({{e}_{{(a_{1}^{'},\theta _{1}^{'},K_{1}^{'})}}})$; ${{\tau }_{{\eta (TN_{1}^{'})}}}(e_{1}^{'})$ = = $\theta _{1}^{'}$ + τ(TN₁) = $\theta _{1}^{'} + \tau (T{{N}_{\sigma }}) = {{\tau }_{{TP_{1}^{'}}}}({{e}_{{(a_{1}^{'},\theta _{1}^{'},K_{1}^{'})}}})$; $e_{{n - k + 1}}^{1}$ ${{ \preccurlyeq }_{{\eta (TN_{1}^{'})}}}$ $e_{1}^{'}$ $ \Leftrightarrow $ $f_{1}^{'}(e_{{n - k + 1}}^{1})$ = $e_{{n - k + 1}}^{\sigma } \preccurlyeq {{\;}_{{\mathop {TP}\nolimits_1 }}}{{e}_{{(a_{1}^{'},\theta _{1}^{'},K_{1}^{'})}}}$, для всех $k \in K_{1}^{'}$. Следовательно, $f_{1}^{'}$ является изоморфизмом и ${{f}_{1}} \subseteq f_{1}^{'}$. Таким образом, $\mathcal{T}{{\mathcal{N}}_{1}}$ after TP_w MUST$_{{tpos}}$ TP_W. Тогда, по предположению теоремы, получаем, что $\mathcal{T}{{\mathcal{N}}_{2}}$ after TP_w MUST$_{{tpos}}$ TP_W.

Далее покажем, что $TCT(\mathcal{T}{{\mathcal{N}}_{2}})$ after w MUST$_{{tct}}$ W. Возьмем произвольный путь u₂ в $TCT(\mathcal{T}{{\mathcal{N}}_{2}})$ из корня в вершину ${{\sigma }_{2}}$ такой, что ${{\phi }_{2}}({{u}_{2}}) = w$. Так как $w \in \mathcal{L}(TCT(\mathcal{T}{{\mathcal{N}}_{2}}))$, то найдется хотя бы один такой путь u₂ в $TCT(\mathcal{T}{{\mathcal{N}}_{2}})$. Согласно утверждению 1(б), существует единственный (с точностью до изоморфизма) временной причинный сеть-процесс ${{\pi }_{{{{\sigma }_{2}}}}} = (T{{N}_{2}},{{\varphi }_{2}}) \in \mathcal{C}\mathcal{P}(\mathcal{T}{{\mathcal{N}}_{2}})$ и единственная линеаризация ${{\rho }_{2}} = e_{1}^{2} \ldots e_{n}^{2}$ $T{{N}_{2}}$ такие, что $F{{S}_{{{{\pi }_{{{{\sigma }_{2}}}}}}}}({{\rho }_{2}})$ = = σ₂. Используя утверждение 2(б), получаем наличие изоморфизма ${{f}_{2}}:\eta (T{{N}_{2}}) \to T{{P}_{w}}$ такого, что ${{f}_{2}}({{\rho }_{2}}) = {{\rho }_{\sigma }}$. Так как $\mathcal{T}{{\mathcal{N}}_{2}}$ after TP_w MUST$_{{tpos}}$ TP_W, то существуют $TP_{2}^{'} \in {\mathbf{T}}{{{\mathbf{P}}}_{{\mathbf{W}}}}$, $\pi _{{{{\sigma }_{2}}}}^{'}$ = $(TN_{2}^{'},\varphi _{2}^{'})$ ∈ $\mathcal{C}\mathcal{P}(\mathcal{T}{{\mathcal{N}}_{2}})$ и изоморфизм $f_{2}^{'}:\eta (TN_{2}^{'}) \to TP_{2}^{'}$ такие, что ${{\pi }_{{{{\sigma }_{2}}}}} \to \pi _{2}^{'}$ и ${{f}_{2}} \subseteq f_{2}^{'}$. Согласно лемме 2(б), найдется ${{\sigma }_{2}}(\widetilde t,\widetilde \theta ) \in \mathcal{F}\mathcal{S}(\mathcal{T}{{\mathcal{N}}_{2}})$ такая, что для некоторой линеаризации ${{\rho }_{2}}e_{2}^{'}$ $TN_{2}^{'}$ имеем, что ${{\sigma }_{2}}(\widetilde t,\widetilde \theta )$ = $F{{S}_{{\pi _{2}^{'}}}}({{\rho }_{2}}e_{2}^{'})$. По построению TP_W, существует пометка $(a,\theta ,K)$ ∈ ∈ W такая, что $TP_{2}^{'}$ = $T{{P}_{{(a,\theta ,K)}}}$, и, следовательно, ${\text{\{ }}{{e}_{{(a,\theta ,K)}}}{\text{\} }}\, = \,{{E}_{{TP_{2}^{'}}}}{\backslash }{{E}_{{T{{N}_{\sigma }}}}}$. Так как $T{{N}_{2}}\, \to \,TN_{2}^{'}$ и $T{{P}_{w}} \prec \cdot TP_{2}^{'}$, то $\{ e_{2}^{'}\} = {{E}_{{TN_{2}^{'}}}}{\backslash }{{E}_{{T{{N}_{2}}}}}$ и $f_{2}^{'}(e_{2}^{'}) = {{e}_{{(a,\theta ,K)}}}$. Поскольку $f_{2}^{'}$ – изоморфизм, верно: ${{\lambda }_{{\eta (TN_{2}^{'})}}}(e_{2}^{'}) = {{\lambda }_{{TP_{2}^{'}}}}({{e}_{{(a,\theta ,K)}}})$ = a, ${{\tau }_{{\eta (TN_{2}^{'})}}}(e_{2}^{'}){{\tau }_{{TP_{2}^{'}}}} = ({{e}_{{(a,\theta ,K)}}}) = \tau (T{{N}_{\sigma }})$ + θ = $\tau (T{{N}_{2}}) + \theta $, и $e_{i}^{\sigma }{{ \preccurlyeq }_{{TP_{2}^{'}}}}{{e}_{{(a,\theta ,K)}}}$ $ \Leftrightarrow $ ${{(f_{2}^{'})}^{{ - 1}}}(e_{i}^{\sigma }) = e_{i}^{2}{{ \preccurlyeq }_{{\eta (TN_{2}^{'})}}}e_{2}^{'}$ для всех $1 \leqslant i \leqslant n$. Тогда получаем, что $(\widetilde t,\widetilde \theta ) = (\varphi _{2}^{'}(e_{2}^{'}),\theta )$ и $e_{{n - k + 1}}^{2} \preccurlyeq {{\;}_{{\eta (TN_{2}^{'})}}}e_{2}^{'}$ для всех $k \in K$. Следовательно, в $TCT(\mathcal{T}{{\mathcal{N}}_{2}})$ существует дуга ${{r}_{2}} = ({{\sigma }_{2}},{{\sigma }_{2}}(\widetilde t,\widetilde \theta ))$ такая, что ${{\phi }_{2}}({{r}_{2}}) = (a,\theta ,K)$. Таким образом, имеем, что $TCT(\mathcal{T}{{\mathcal{N}}_{1}})$ after w MUST_tctW $ \Rightarrow $ $TCT(\mathcal{T}{{\mathcal{N}}_{2}})$ after w MUST_tctW.

В силу симметрии, верно, что $\mathcal{T}{{\mathcal{N}}_{1}}$ ~_tpos$\mathcal{T}{{\mathcal{N}}_{2}}$ $ \Rightarrow $ $ \Rightarrow $ $\mathcal{T}{{\mathcal{N}}_{1}}{{ \sim }_{{tct}}}\mathcal{T}{{\mathcal{N}}_{2}}$. □

5. ЗАКЛЮЧЕНИЕ

В данной статье было показано, что хорошо известные в теории безвременных и временных моделей структур событий причинно-зависимые тестовые эквивалентности могут быть обобщены на модели непрерывно-временных сетей Петри. В частности, были введены и изучены тестовые эквивалентности в интерливинговой, частично-упорядоченной и комбинированных семантиках в контексте безопасных сетей Петри, переходы которых помечены временными интервалами и каждый переход, имеющий достаточное количество фишек во входных местах, должен срабатывать тогда, когда его счетчик достигнет некоторого значения, принадлежащего его временному интервалу. При исследованиях были построены три представления вычислений непрерывно-временной сети Петри: последовательности срабатываний, представляющие интерливинговую семантику, временные сети-процессы, из причинных сетей которых выводятся частичные порядки, и причинное дерево, построенное из последовательностей срабатываний и частичных порядков причинных сетей. Были найдены взаимосвязи, с одной стороны, между последовательностями срабатываний и корректными временными причинными сетями-процессами, и, с другой стороны, между последними и помеченными путями во временных причинных деревьях. Было установлено, что интерливинговая тестовая эквивалентость слабее, чем тестовая эквивалентность, определенная с использованием временного причинного дерева. Как основной результат, доказано совпадение тестовых эквивалентностей в семантиках временного частичного порядка и временного причинного дерева. Заметим, что подобный результат верен и для безвременных версий тестовых эквивалентностей в контексте свободных от контактов элементарных сетевых систем.

В дальнейшем планируется исследовать взаимосвязи рассмотренных эквивалентностей и семантик с другими эквивалентностями из спектров линейного/ветвящегося времени и интерливинга/частичного порядка ([25]). Также следует изучить возможность расширения полученных результатов на модели непрерывно-временных сетей Петри с невидимыми действиями.