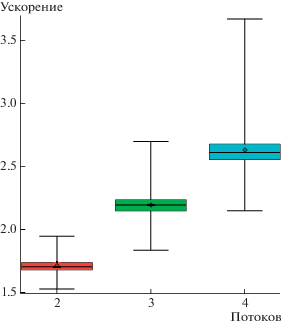Программирование, 2021, № 2, стр. 15-27
ФАКТОРИЗАЦИЯ БУЛЕВЫХ ПОЛИНОМОВ: ПАРАЛЛЕЛЬНЫЕ АЛГОРИТМЫ И ЭКСПЕРИМЕНТАЛЬНАЯ ОЦЕНКА
П. Г. Емельянов a, *, М. Кришна c, **, В. Кулкарни b, ***, С. К. Нанди b, ****, Д. К. Пономарев a, *****, С. Раха b, ******
a Институт систем информатики им. А.П. Ершова СО РАН; Новосибирский государственный университет
Новосибирск, Россия
b Department of Computational and Data Sciences, Indian Institute of Science,
Бангалор, Индия
c Morphing Machines Pvt Ltd
Бангалор, Индия
* E-mail: emelyanov@iis.nsk.su
** E-mail: madhava@iisc.ac.in
*** E-mail: vadirajk@iisc.ac.in
**** E-mail: nandy@iisc.ac.in
***** E-mail: ponom@iis.nsk.su
****** E-mail: raha@iisc.ac.in
Поступила в редакцию 02.04.2020
После доработки 06.05.2020
Принята к публикации 06.05.2020
Аннотация
Факторизация полиномов – классическая алгоритмическая проблема алгебры, имеюшая широкий спектр приложений. Особый интерес представляет факторизация над конечными полями, среди которых поле порядка два является, вероятно, наиболее важным в связи с представлением булевых функций полиномами Жегалкина. В частности, факторизация булевых полиномов соответствует конъюнктивной декомпозиции булевых функций, заданных в алгебраической нормальной форме. Кроме того, факторизация дает решение проблемы декомпозиции функций, заданных в СДНФ и позитивных ДНФ, а также декартовой декомпозиции реляционых данных. Эти приложения демонстрируют важность разработки быстрых алгоритмов факторизации. В статье мы рассматриваем некоторые недавно предложенные алгоритмы факторизации полиномиальной сложности и описываем параллельную MIMD-реализацию, которая использует как параллелизм уровня задачи, так и параллелизм уровня данных. Мы представляем эксперименты, выполненные на бенчмарках логического синтеза и на синтетических (случайных) полиномах, которые показывают значительное ускорение факторизации. В заключение представлены результаты тестирования параллельной реализации алгоритма на массивнопараллельной многоядерной архитектуре (Redefine).
1. ВВЕДЕНИЕ
Факторизация полиномов – классическая алгоритмическая проблема алгебры [1], которая имеет широкий спектр приложений. Один вариант проблемы, привлекающий особое внимание — факторизация булевых полиномов, т.е. мультилинейных полиномов над конечным полем порядка 2. Булев многочлен – это одно из широко известных представлений булевых функций, также известных в математической логике как полиномы Жегалкина [2] или каноническая форма Рида–Маллера [3] в синтезе логических схем и теории помехоустойчивого кодирования. В последнее время это представление становится все более популярным в связи со следующими преимуществами. Во-первых, это естественное и компактное представление некоторых важных классов булевых функций (например, арифметические функции, кодеры, и т.д.). Во-вторых, оно допускает естественное отображение в некоторых схемных технологиях (например, основанных на FPGA или в наноструктурной электронике), а также имеет хорошие свойства для тестирования.
Факторизация булевых полиномов является частным случаем конъюнктивной декомпозиции булевых функций (декомпозиция в конъюнкцию функций с непересекающимися множествами переменных или AND-декомпозиция). Действительно, для булева полинома, в котором всякая переменная имеет степень 1, факторизация дает факторы с непересекающимися наборами переменных: $F(X,Y) = {{F}_{1}}(X) \times {{F}_{2}}(Y)$, $X \cap Y = \emptyset $.
Недавно было показано [4, 5], что факторизация булевых полиномов решает задачу конъюнктивной декомпозиции функций, заданных в СДНФ и позитивных ДНФ. Кроме того, это дает метод декартовой декомпозиции таблиц реляционных баз данных [6, 7], т.е. отыскание таблиц таких, что их неупорядоченное декартово произведение совпадает с исходной таблицей (обращение оператора CROSS JOIN). Несколько примеров, иллюстрирующих указанные применения, приведены ниже.
Рассмотрим следующую ДНФ
Она эквивалентна
так как последняя конъюнкция избыточна. Можно видеть, что и компоненты декомпозиции $x \vee y$ и $u \vee {v}$ могут быть восстановлены из факторов полинома построенного для ψ.Следующая СДНФ
(1.1)
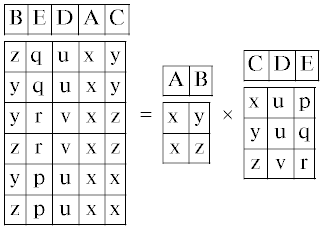
$\begin{gathered} {{F}_{\varphi }} = x\bar {y}u{\bar {v}} + x\bar {y}\bar {u}{v} + \bar {x}yu{\bar {v}} + \\ + \;\bar {x}y\bar {u}{v} = (x\bar {y} + \bar {x}y) \times (u{\bar {v}} + \bar {u}{v}), \\ \end{gathered} $Наконец, декартова декомпозиция следующей таблицы
может быть найдена факторизацией полиномаДекомпозиция позволяет находить более компактное представление булевых функций и таблиц данных, которые применяются в области синтеза логических схем, самоорганизующихся баз данных и поиска зависимостей в данных. Так как большие объемы входов – типичная ситуация в перечисленных задачах, чрезвычайно важно иметь эффективные на практике алгоритмы факторизации булевых полиномов.
В [8], изучая проблему факторизации полиномов над произвольными конечными полями, представленных в виде арифметических схем, Шпилька и Волкович показали связь между факторизацией полиномов и проверкой тождества полиномов. В частности, из их результата следует, что булев полином может быть факторизован за время $O({{l}^{3}})$, где l – размер полинома заданного как символьная последовательность. Подход использует умножение полиномов, полученных из исходного, и эта операция является дорогостоящей для больших входов. В [4] был предложен альтернативный подход к факторизации, где явного умножения можно избежать. В дальнейшем этот подход обсуждался в [9].
В данной статье мы рассматриваем параллельную версию алгоритма декомпозиции из [4, 9] и сравниваем его с параллельными реализациями аналогичных алгоритмов. В разделе 2 мы сначала приводим обзор последовательного алгоритма факторизации и его вариантов. В разделе 3 описывается параллельная MIMD реализация алгоритма и далее в разделе 4 представлен количественный анализ параллельного и последовательного алгоритмов. Наконец, в разделе 5 приведены результаты тестирования нашего алгоритма на массивнопараллельной многоядерной архитектуре (Redefine).
2. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ
Введем базовые определения и обозначения и рассмотрим последовательный алгоритм факторизации из [4, 9].
Полином $F \in {{\mathbb{F}}_{2}}[{{x}_{1}},\; \ldots ,\;{{x}_{n}}]$ называется факторизуемым если $F = {{F}_{1}} \times \; \ldots \times {{F}_{k}}$, где $k \geqslant 2$ и ${{F}_{1}}, \ldots ,{{F}_{k}}$ неконстантные полиномы. В противном случае F называется неприводимым. Полиномы ${{F}_{1}}, \ldots ,{{F}_{k}}$ называются факторами F. Важно отметить, что так как рассматриваются мультилинейные полиномы (каждая переменная может входить только в степени не более 1), факторы являются полиномами над непересекающимися множествами переменных. В дальнейшем мы полагаем, что полином F не имеет тривиальных факторов (делителей), т.е., ни x, ни x + 1 не делят F. Очевидно, тривиальные делители легко распознаваемы.
Пусть $F$ – полином. Для переменной $x$ из множества переменных $Var(F)$ полинома F и значения $a \in {\text{\{ }}0,\;1{\text{\} }}$, обозначим через ${{F}_{{x = a}}}$ полином, полученный из F посредством подстановки для $x$ значения a. $\tfrac{{\partial F}}{{\partial x}}$ обозначает формальную производную F по переменной $x$. Если дана переменная $z$, то $z|F$ означает, что $z$ делит F, т.е., $z$ входит в каждый моном F (заметим, что это эквивалентно условию $\tfrac{{\partial F}}{{\partial z}} = {{F}_{{z = 1}}}$). Если дано множество переменных Σ и моном $m$, то определим проекцию $m$ на Σ следующим образом. Она равна 1, если $m$ не содержит переменных из Σ, и в противном случае равна моному, полученному из $m$ удалением всех переменных, которые не входят в Σ. Проекция полинома F на Σ, обозначаемая ${{\left. F \right|}_{\Sigma }}$ – есть полином, полученный как сумма проекций мономов F на Σ, в которой мономы-дубликаты удалены.
2.1. Алгоритм факторизации
Алгоритм 1 описывает последовательную версию процедуры факторизации. Как уже было упомянуто, факторы булева полинома имеют непересекающиеся множества переменных. Это свойство используется в алгоритме, который пытается вычислить разбиение переменных по компонентам. Если разбиение построено, то соответствующие факторы могут быть найдены с помощью проекций исходного полинома на компоненты полученного разбиения. Далее мы полагаем, что входной полином F имеет, по крайней мере, две переменные и не содержит пары одинаковых мономов.
Algorithm 1. Последовательный алгоритм факторизации
Input Факторизуемый булев полином F
Output ${{F}_{{same}}}$ и ${{F}_{{other}}}$, которые являются факторами входного полинома $F$
1: Выбрать произвольную переменную $x$, входящую в $F$
2: Пусть $A = \tfrac{{\partial F}}{{\partial x}}$, $B = {{F}_{{x = 0}}}$
3: Пусть ${{\Sigma }_{{same}}} = x$, ${{\Sigma }_{{other}}} = \emptyset $, ${{F}_{{same}}} = 0$, ${{F}_{{other}}} = 0$
4: for each $y \in var(F){\backslash \{ }x{\text{\} }}$ do
5: Пусть $C = \tfrac{{\partial A}}{{\partial y}}$, $D = \tfrac{{\partial B}}{{\partial y}}$
6: if IsEqual($A,D,B,C$) then
7: ${{\Sigma }_{{other}}} = {{\Sigma }_{{other}}} \cup {\text{\{ }}y{\text{\} }}$
8: else
9: ${{\Sigma }_{{same}}} = {{\Sigma }_{{same}}} \cup {\text{\{ }}y{\text{\} }}$
10: end if
11: end for
12: Если ${{\Sigma }_{{other}}}$ = $\not {0}$, тогда F неприводим.
13: Вернуть полиномы ${{F}_{{same}}}$ и ${{F}_{{other}}}$ как проекции $F$ на ${{\Sigma }_{{same}}}$ и ${{\Sigma }_{{other}}}$, соответственно.
Таким образом, алгоритм выбирает произвольным образом переменную x из F и разбивает множество переменных F на два множества относительно x:
• первое множество ${{\Sigma }_{{same}}}$ содержит выбранную переменную x и соответствует фактору, представляющему неприводимый полином;
• второе множество ${{\Sigma }_{{other}}}$ соответствует второму фактору, который допускает дальнейшую факторизацию.
Факторы ${{F}_{{same}}}$ и ${{F}_{{other}}}$ получаются проекциями исходного полинома на ${{\Sigma }_{{same}}}$ и ${{\Sigma }_{{other}}}$, соответственно.
В строках 1–3 выбирается произвольная $x$ из F и вычисляются полиномы $A$ и $B$. $A$ – это производная F по переменной x, а $B$ – полином, полученный из F означиванием x нулем. Строки 4–11 занимают цикл над множеством переменных F, откуда исключена переменная x. Для переменной на очередной итерации вычисляются полиномы $C$ и $D$, где $C$ – производная $A$ и $D$ – производная $B$. Затем проверяется равенство $AD$ = BC. Для проверки этого равенства вызывается процедура IsEqual (строка 6). Она описывается в следующем разделе.
2.2. Процедура IsEqual
В Алгоритме 2 представлена последовательная версия процедуры IsEqual.
• Процедура принимает на вход полиномы A, B, $C$, $D$ и проверяет равенство $AD = BC$ посредством рекурсии.
• Строки 1–16 реализуют базовые случаи, когда равенство $AD = BC$ может быть определено простым образом.
• В строках 3–6 проверяется, делит ли переменная $z$ полиномы A, $B$, $C$, $D$ так, что условие в строке 4 верно. Если это не верно, то переменная $z$ из A, $B$, $C$, D удаляется (строка 7) и выполняется проверка на равенство произведений полученных полиномов.
• В строках 17–26 процедура IsEqual вызывается рекурсивно на полиномах меньших размеров.
2.3. Возможность параллелизма
Суть Алгоритма 1 заключена в цикле, представленном строками 4–11. Легко заметить, что различные итерации цикла независимы. Следовательно цикл обеспечивает параллелизм уровня потока, который может быть использован для улучшения производительности. Условный блок внутри цикла в строках 6–10 может быть использован для организации параллелизма уровня задачи между многими потоками.
Algorithm 2. Последовательная процедура IsEqual
Input Булевы полиномы A, B, C, D
Output TRUE если AD равно BC и FALSE иначе.
1: If A = 0 or D = 0 then return (B = 0 or C = 0)
2: If B = 0 or C = 0 then return FALSE
3: for each z, встречающуюся, по крайней мере, в одном из A, B, C, D do
4: if $z|A$ or $z|D$ x or $z|B$ or $z|C$ then
5: return FALSE
6: end if
7: Заменить каждый $X \in {\text{\{ }}A,B,C,D{\text{\} }}$ на $\tfrac{{\partial X}}{{\partial z}}$ при условии $z|X$
8: end for
9: if A = 1 and D = 1 then return (B = 1 and C = 1)
10: end if
11: if B = 1 and C = 1 then return FALSE
12: end if
13: if A = 1 and B = 1 then return (D = C)
14: end if
15: if D = 1 and C = 1 then return (A = B)
16: end if
17: Выбрать переменную z
18: if not(IsEqual(${{A}_{{z = 0}}},{{D}_{{z = 0}}},{{B}_{{z = 0}}},{{C}_{{z = 0}}}$)) then return FALSE
19: end if
20: if not(IsEqual$\left( {\frac{{\partial A}}{{\partial z}},\frac{{\partial D}}{{\partial z}},\frac{{\partial B}}{{\partial z}},\frac{{\partial C}}{{\partial z}}} \right)$) then return FALSE
21: end if
22: if IsEqual$\left( {\frac{{\partial A}}{{\partial z}},{{B}_{{z = 0}}},{{A}_{{z = 0}}},\frac{{\partial B}}{{\partial z}}} \right)$ then return TRUE
23: end if
24: if IsEqual$\left( {\frac{{\partial A}}{{\partial z}},{{C}_{{z = 0}}},{{A}_{{z = 0}}},\frac{{\partial C}}{{\partial z}}} \right)$ then return TRUE
25: else return FALSE
26: end if
Множество частей Алгоритма 2 поддаются параллелизму. Проверка делимости полиномов A, B, $C$, $D$ в строках 3–6 процедуры IsEqual может быть выполнено независимо. В строках 17–26 рекурсивные вызовы IsEqual независимы и представляют параллелизм уровня задачи. В следующем разделе рассматривается параллельный алгоритм, использующий эти наблюдения.
3. ПРЕДЛАГАЕМЫЙ ПОДХОД
3.1. Параллельный алгоритм факторизации
Алгоритм 3 описывает параллельную версию алгоритма факторизации. В строках 1–3 выбирается произвольная перменная x из множества переменных полинома F и вычисляются полиномы A и B. В строках 4–11 порождением нескольких потоков несколько итераций цикла выполняются параллельно. Каждый поток возвращает два множества $\Sigma _{{same}}^{{tid}}$ и $\Sigma _{{other}}^{{tid}}$, специфичные для потока и обозначаемые идентификатором потока tid. В строках 12–14, множества переменных ${{\Sigma }_{{same}}}$ и ${{\Sigma }_{{other}}}$ вычисляются как объединение данных соответствующих разным потокам. Отметим синхронизационный барьер для всех параллельных потоков.
Algorithm 3. Параллельный алгоритм факторизации
Input Факторизуемый булев полином F
Output ${{F}_{{same}}}$ и ${{F}_{{other}}}$, которые являются факторами входного полинома F
1: Выбрать произвольную переменную $x$ из F
2: Пусть $A = \tfrac{{\partial F}}{{\partial z}}$, $B = {{F}_{{z = 0}}}$
3: Пусть ${{\Sigma }_{{same}}} = x$, ${{\Sigma }_{{other}}} = \not {0}$, ${{F}_{{same}}} = 0$, ${{F}_{{other}}} = 0$
4: for each $y \in var(F){\backslash \{ }x{\text{\} }}$ do in parallel
5: Пусть $C = \tfrac{{\partial A}}{{\partial y}}$, $D = \tfrac{{\partial B}}{{\partial y}}$
6: if IsEqual($A,D,B,C$) then
7: $\Sigma _{{other}}^{{tid}} = \Sigma _{{other}}^{{tid}} \cup {\text{\{ }}y{\text{\} }}$
8: else
9: $\Sigma _{{same}}^{{tid}} = \Sigma _{{same}}^{{tid}} \cup {\text{\{ }}y{\text{\} }}$
10: end if
11: end for
12: Ждать пока все параллельные потоки не закончатся
13: ${{\Sigma }_{{other}}} = \bigcup\nolimits_{tid} {\Sigma _{{other}}^{{tid}}} $
14: ${{\Sigma }_{{same}}} = \bigcup\nolimits_{tid} {\Sigma _{{same}}^{{tid}}} $
15: Если ${{\Sigma }_{{other}}}$ = $\not {0}$, тогда F неприводим; остановиться.
16: Вернуть полиномы ${{F}_{{same}}}$ и ${{F}_{{other}}}$, полученные как проекции F на ${{\Sigma }_{{same}}}$ и ${{\Sigma }_{{other}}}$, соответственно.
3.2. Параллельная версия функции IsEqual
Алгоритм 4 описывает параллельную версию процедуры IsEqual. Алгоритм принимает на вход четыре полинома $A,D,B,C$ и проверяет равенство $AD = BC$. Строки 1–21 описывают случаи, когда определение равенства $AD = BC$ тривиально.
Algorithm 4. Параллельная версия функции IsEqual
Input Булевы полиномы A, B, C, D
Output TRUE если AD = BC и FALSE, иначе.
1: If A = 0 or D = 0 then return (B = 0 or C = 0)
2: If B = 0 or C = 0 then return FALSE
3: for each z, входящая в хотя бы один из A, B, C, D do in parallel
4: Положить flagtid = True
5: if z | A or z | D x or z | B or z | C then
6: Положить flagtid = FALSE
7: end if
8: Заменить каждый ${{X}^{{tid}}} \in {\text{\{ }}A,B,C,D{\text{\} }}$ на $\tfrac{{\partial {{X}^{{tid}}}}}{{\partial z}}$, при условии z | Xtid
9: end for
10: Ждать пока все параллельные потоки не закончатся
11: if $\mathop \wedge \limits_{tid} fla{{g}^{{tid}}} = FALSE$ then return FALSE
12: end if
13: $X = \bigcap\nolimits_{tid} {{{X}^{{tid}}}} $, for $X \in {\text{\{ }}A,B,C,D{\text{\} }}$
14: if A = 1 and D = 1 then return (B = 1 and C = 1)
15: end if
16: if B = 1 and C = 1 then return FALSE
17: end if
18: if A = 1 and B = 1 then return (D = C)
19: end if
20: if D = 1 and C = 1 return (A = B)
21: end if
22: Выбрать переменную z
23: Выполнять следующие 4 строки параллельно
24: x = not(IsEqual(${{A}_{{z = 0}}},{{D}_{{z = 0}}},{{B}_{{z = 0}}},{{C}_{{z = 0}}}$))
25: y = not(IsEqual$\left( {\tfrac{{\partial A}}{{\partial z}},\tfrac{{\partial D}}{{\partial z}},\tfrac{{\partial B}}{{\partial z}},\tfrac{{\partial C}}{{\partial z}}} \right)$)
26: z = IsEqual$\left( {\tfrac{{\partial A}}{{\partial z}},{{B}_{{z = 0}}},{{A}_{{z = 0}}},\tfrac{{\partial B}}{{\partial z}}} \right)$
27: w = IsEqual$\left( {\tfrac{{\partial A}}{{\partial z}},{{C}_{{z = 0}}},{{A}_{{z = 0}}},\tfrac{{\partial C}}{{\partial z}}} \right)$
28: Ждать пока все параллельные потоки не закончатся
29: if not(x) then return FALSE
30: end if
31: if not(y) then return FALSE
32: end if
33: if z then return TRUE
34: end if
35: if w then return TRUE
36: else return FALSE
37: end if
В строках 3–9 проверяется, делит ли переменная $z$ входные полиномы $A$, D, $B$, $C$ так, что условие в строке 5 выполнено. Если это не так, все они делятся на $z$ для того, чтобы получить приведенные полиномы (не содержащие тривиальных делителей). Вышеупомянутые операции выполняются для каждой переменной независимо в параллельно работающих потоках. В строке 8 в каждом потоке проверяется, является ли переменная ${{z}^{{tid}}}$ (tid – идентификатор потока) делителем какого-то полинома $A$, $B$, $C$, D. Если ${{z}^{{tid}}}$ делит какой-то из полиномов $A$, $B$, $C$, D, то вычисляются соответствующие приведенные полиномы ${{A}^{{tid}}}$, ${{D}^{{tid}}}$, ${{B}^{{tid}}}$, ${{C}^{{tid}}}$. В строке 13 берется попарное пересечение соответствующих мономов полиномов из потоков ${{A}^{{tid}}}$, ${{D}^{{tid}}}$, ${{B}^{{tid}}}$, ${{C}^{{tid}}}$ для того, чтобы сформировать полиномы, свободные от тривиальных делителей. Пересечение двух мономов ${{m}_{1}}$, ${{m}_{2}}$ равно 1, если ${{m}_{1}}$, ${{m}_{2}}$ не имеют общих переменных, в противном случае это моном, состоящий из переменных, которые входят в оба монома ${{m}_{1}}$ и ${{m}_{2}}$. В строках 23–27 выполняются четыре независимых рекурсивных вызова функции IsEqual в параллельных потоках. В строках 28–37 ожидается завершение всех потоков и сравнение их результатов для формирования окончательного результата. Отметим в строках 10 и 28 синхронизирующий барьер для всех параллельных потоков.
3.3. Оценка ускорения параллельного алгоритма, основанного на распределении переменных по параллельным потокам исполнения
Реализация параллелизма в Алгоритмах 3 и 4 исходит из предположения о неограниченных возможностях использования ресурсов — параллельно запускаются все достаточно объемные секции кода и коммуникация между ними не представляет никаких сложностей. Это интересно с теоретической точки зрения для исследования глубины параллелизма. Однако, с точки зрения оценки глубины “практического” параллелизма, следует рассмотреть некоторые ограничения. В частности, фиксированное количество процессоров/ядер, доступных для исполнения программы. В этой связи можно рассмотреть вариант Алгоритма 3, в котором распараллеливание в цикле по всем переменным $y \in var(F){\backslash \{ }x{\text{\} }}$ заменяется на параллелизм по блокам разбиения множества переменных $var(F){\backslash \{ }x{\text{\} }}$. Количество блоков определяется количеством доступных процессоров/ядер. Следует отметить, что параллельные потоки исполнения могут не взаимодействовать друг с другом (иметь изолированную память) что, например, может быть привлекательным при реализации алгоритма факторизации на входящих в широкую практику NUMA-архитектурах. Вопрос повышения эффективности вычислений за счет доступа к переиспользуемым общим данным на данный момент остается открытым.
Изучая поведение алгоритма факторизации полиномов, представленных в виде списка мономов (ESOP), было обнаружено, что IsEqual работает в разы больше времени для переменных из компоненты, которая противоположна компоненте, содержащей выбранную на первом шаге переменную: доказательство, что равенство не выполняется, заканчивается быстрее, чем доказательство равенства, когда нужно довести разбиение полиномов до “мельчайшего”, чтобы проверка равенства была тривиальной. Один из выводов, который из этого следует, – неприводимые полиномы будут обрабатываться быстрее, чем разложимые.
Оценим возможное ускорение в этом случае. Рассмотрим следующие параметры:
• $N$ – количество переменных в полиноме;
• $\mu \in (0 \ldots 1)$ – доля переменных из ${{\Sigma }_{{same}}}$ и $1 - \mu $ – доля переменных из ${{\Sigma }_{{other}}}$ среди всех $N$ переменных;
• $t$ – среднее время обработки переменной из ${{\Sigma }_{{same}}}$;
• $t\nu ,\nu > 1,$ – среднее время обработки переменной из ${{\Sigma }_{{other}}}$;
• P – количество доступных в параллельной версии процессоров (отметим, задачи, запущенные на них, никак не синхронизируются).
Время решения задачи факторизации (той части, где ищется разбиение на ${{\Sigma }_{{same}}}$ и ${{\Sigma }_{{other}}}$) на одном процессоре
Легко видеть, что ускорение вычислений зависит от того, насколько “удачно” распределились по потокам переменные (разумным предположением является, что каждый поток обрабатывает примерно одинаковое количество переменных). В данном случае самый удачный вариант – это когда в каждом потоке воспроизводится исходная пропорция переменных из ${{\Sigma }_{{same}}}$ и ${{\Sigma }_{{other}}}$:
Таким образом, в идеале возможно ускорение в P раз (это максимально возможное ускорение).
Худших варианта два:
1. Существует поток, который обрабатывает переменные только из ${{\Sigma }_{{other}}}$. Тогда
Аналитическая зависимость для ν пока не установлена, но на достаточно больших полиномах стабильно проявляется, что $\nu \gg 1$, а значит ускорение составляет примерно $P - \mu P$.
2. Все потоки кроме одного обрабатывают переменные только из ${{\Sigma }_{{same}}}$, а этот выделенный поток обрабатывает как переменные из ${{\Sigma }_{{same}}}$, т.е. $\mu > \tfrac{{P - 1}}{P}$, так и все из ${{\Sigma }_{{other}}}$.
Видно, что при таком распределении переменных по потокам и при $\nu \gg 1$ рост количества процессоров не будет оказывать значительное влияние на ускорение.
После анализа ускорения при таком распараллеливании в Maple-реализации алгоритма было сделано следующее. Перед разбиением множества переменных по k потокам – разрезания массива переменных на k частей – выполняется несколько случайных перестановок этого массива с целью балансировки распределения переменных в разных частях.
4. ЭКСПЕРИМЕНТЫ ПО РАСПАРАЛЛЕЛИВАНИЮ ОБРАБОТКИ ПЕРЕМЕННЫХ ПО ПОТОКАМ
Для экспериментальной оценки последовательного и параллельного алгоритмов, основанного на распределении проверки переменных по потокам, использовались известные бенчмарки для логического синтеза и искусственно сгенерированные (случайные) булевы полиномы.
4.1. Реализация полиномов с использованием Zero-suppressed Decision Diagrams
Для представления булевых полиномов используется ZDD из библиотеки CUDD версии 3.0.0 [10]. Его можно трактовать как представление в виде множества (сам полином) подмножеств (его мономы) некоторого конечного множества (переменные полинома). Реализация использует стандартный механизм потоков в С++. Для тестирования использовались 500 случайных полиномов со 100 переменными и 10 000 мономами (с различными пропорциями переменных и мономов в би-компонентах разложения). В табл. 1 приведены результаты тестирования ускорения алгоритма с распараллеливанием обработки переменных на 2, 3 и 4 потока. На рис. 1 основная статистическая информация приведена в графическом виде.
4.2. Реализация полиномов в виде списков мономов
Мы использовали бенчмарки логического синтеза ITC’99 [11], Iscas’85 [12] и бенчмарк $n$-битного сумматора с переносом [13]. Описания схем были конвертированы из формата Verilog в СДНФ, чтобы получить соответствующие булевы полиномы. Последовательный и параллельный алгоритмы тестировались на полученных полиномах. В табл. 2 показано усредненное по 5 запускам время работы последовательного и параллельного алгоритмов на процессоре Xeon 2.8 Ghz с четыремя потоками.
Таблица 2.
Результаты запуска на процессоре Xeon 2.8 GHz с 4-мя потоками
| Тест | Послед. | Многопот. | Ускорен. |
|---|---|---|---|
| ITC’99 | 4324(s) | 1441(s) | 3.01 |
| Iscas’85 | 7181(s) | 2633(s) | 2.73 |
| EPFL Adder | 1381(s) | 374(s) | 3.69 |
Для последовательного и параллельного алгоритмов также было проведено тестирование на случайных полиномах различной сложности (экспериментах число переменных полинома варьируется от десятков до пары сотен). В табл. 3 показано усредненное по 5 запускам время работы последовательного и параллельного алгоритмов на процессоре Xeon 2.8 Ghz с четыремя потоками.
Таблица 3.
Время факторизации случайных полиномов на процессоре Xeon 2.8 GHz с 4-мя потоками
| Мономов | Послед. | Многопот. | Ускорен. |
|---|---|---|---|
| 10 | 0.023(s) | 0.0074(s) | 3.12 |
| 50 | 16.29(s) | 5.07(s) | 3.21 |
| 100 | 103.5(s) | 30.44(s) | 3.4 |
| 500 | 483.6(s) | 178.1(s) | 2.7 |
| 1000 | 1165(s) | 520.9(s) | 2.2 |
| 5000 | 1430(s) | 735.11(s) | 1.91 |
| 10 000 | 12614(s) | 8034(s) | 1.57 |
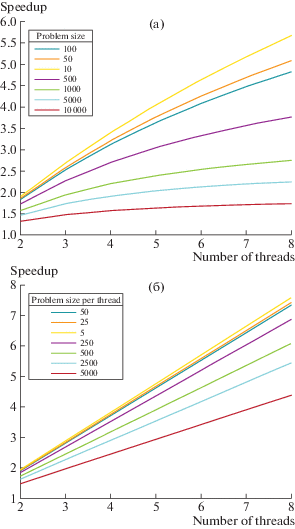
График 2а показывает ускорение, достигаемое параллельным алгоритмом по отношению к числу потоков. Размер входа фиксирован для того, чтобы проанализировать свойства сильной масштабируемости параллельного алгоритма. Можно заметить, что ускорение снижается в увеличением сложности входного полинома. С увеличением размера входа увеличивается число вызовов к узкому месту алгоритма, каковым является упрощение полиномов, что, в свою очередь, влечет снижение быстродействия.
Для результатов экспериментов, показанных на рис. 2б, размер входа фиксирован для каждого из потоков, чтобы проанализировать свойства слабой масштабируемости параллельного алгоритма. Прирост скорости с увеличением числа потоков оказывается меньше максимально возможного линейного ускорения. Это обусловлено узкими местами алгоритма, требующими последовательных вычислений (упрощение полиномов), а также затратами на коммуникацию между потоками.
5. РЕАЛИЗАЦИЯ НА REDEFINE
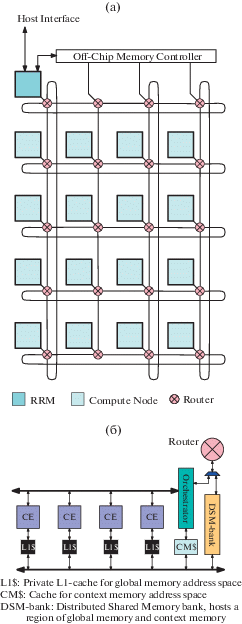
В основе архитектуры REDEFINE [14] лежит набор вычислительных модулей, соединенных в сеть на чипе (см. иллюстрацию 3a).
REDEFINE – это ускоритель, который может настраиваться на выполнение конкретной вычислительной задачи посредством реконфигурации. Настройка конфигурации REDEFINE возможна на двух уровнях: посредством агрегации узлов в вычислительные ядра для выполнения высокоуровневых операций с множественными входами и выходами, а также на уровне специализированных функциональных элементов, представленных на слое аппаратных абстракций в виде расширенных наборов инструкций. В отличие от традиционных архитектур, расширенные наборы инструкций могут быть определены на пост-производственном этапе. Эта специфика выделяет REDEFINE на фоне широко распространенных многоядерных решений, предоставляя возможность настройки на приложения различных типов.
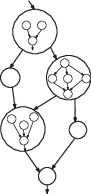
REDEFINE реализует исполнение в духе модели макропотоков данных. В ней исполнение представлено в виде иерархического графа потока данных (рис. 4), в котором вершинами являются гипероперации, а дуги представляют явное направление данных или порядок выполнения связанных гиперопераций. Гипероперация представляет собой макрооперацию с множественными входами и выходами. Гипероперация подлежит исполнению как только доступны все ее операнды, и все завимости порядка исполнения или синхронизации выполнены. Помимо арифметических, связанных с чтением/записью в память и управляющих инструкций, модель исполнения REDEFINE включает примитивы для явного обмена данными и синхронизации между гипероперациями, а также примитивы для добавления новых узлов (гиперопераций) и дуг графа в процессе исполнения. Таким образом, модель исполнения поддерживает динамический (зависимый от данных) параллелизм. В модели реализовано невытесняющее планирование гиперопераций, поэтому циклические зависимости между ними запрещены. Управляющий модуль планирует готовые гипероперации к выполнению на вычислительных узлах. Каждый узел содержит четыре вычислительных элемента, каждый из которых может выполнить ту или иную гипероперацию (рис. 2б). Обмен данными между гипероперациями является однонаправленным, т.е. только одна и та же гипероперация может инициировать и завершить обмен. Таким образом, в условиях достаточного параллелизма обмен данными может накладываться на вычисления. По сравнению с другими гибридными моделями потока данных и управления, модель REDEFINE упрощает управление ресурсами и моделью памяти, необходимыми для поддержки параллелизма любого типа.
Рис. 4.
Модель исполнения на уровне макропотоков данных. Исполнение представлено в виде иерархического графа потока данных, в котором вершинами являются гипероперации, а дуги представляют явное направление данных или порядок выполнения связанных гиперопераций.
5.1. Алгоритм факторизации на основе гиперопераций
Algorithm 5. Алгоритм декомпозиции на основе гиперопераций
Input Факторизуемый булев полином F
Output ${{F}_{{same}}}$ и ${{F}_{{other}}}$, которые являются факторами входного полинома F Глобальные переменные ${{\Sigma }_{{same}}},{{\Sigma }_{{other}}}$
1: Begin HyperOp
2: Входы: $A$, $B$, переменная $y$
3: Вычислить $C = \tfrac{{\partial A}}{{\partial y}}$, $D = \tfrac{{\partial B}}{{\partial y}}$
4: if IsEqual(A,D,B,C) then
5: ${{\Sigma }_{{other}}} = {{\Sigma }_{{other}}} \cup {\text{\{ }}y{\text{\} }}$
6: else
7: ${{\Sigma }_{{same}}} = {{\Sigma }_{{same}}} \cup {\text{\{ }}y{\text{\} }}$
8: end if
9: Call Sync HyperOp
10: End HyperOp
11: Выбрать произвольную переменную $x$ из F
12: Let $A = \tfrac{{\partial F}}{{\partial z}}$, $B = {{F}_{{z = 0}}}$
13: Let ${{\Sigma }_{{same}}} = x$, ${{\Sigma }_{{other}}} = \not {0}$, ${{F}_{{same}}} = 0$, ${{F}_{{other}}} = 0$
14: for each $y \in var(F){\backslash \{ }x{\text{\} }}$ do in parallel
15: Породить HyperOp со входами $A$, $B$, $y$
16: end for
17: Ждать исполнения Sync HyperOp
18: Если ${{\Sigma }_{{other}}}$ = $\not {0}$ то F неприводим; остановиться.
19: Вернуть полиномы ${{F}_{{same}}}$ и ${{F}_{{other}}}$, являющиеся проекциями F на ${{\Sigma }_{{same}}}$ и ${{\Sigma }_{{other}}}$, соответственно.
В Алгоритме 5 приведен псевдокод алгоритма факторизации в стиле реализации на языке C с гипероперациями. Фрагмент кода, соответствующий Алгоритму 5, представлен в распечатке ниже. В ней выражения вида __CMAddr, __Sync, __kernel, __WriteCM, CMADDR являются аннотациями, используемыми для REDEFINE. Строки 2–8 и 12–13 Алгоритма 5 соответствуют строкам 5–10 и 1–3 Алгоритма 1, соответственно.
В строках 14–16 Алгоритма 5 для каждой переменной y из $F$ (отличной от x) параллельно порождаются гипероперации, которые устанавливают, какому из множеств ${{\Sigma }_{{same}}}$ или ${{\Sigma }_{{other}}}$ принадлежит y. В строках 1–10 дано определение гипероперации, которая берет на вход булевы полиномы A, B и переменную $y$ и добавляет $y$ в ${{\Sigma }_{{same}}}$ или ${{\Sigma }_{{other}}}$. В строках 17–19 указано ожидание завер-шения всех гиперопераций и выдача полиномов ${{F}_{{same}}}$ и ${{F}_{{other}}}$.
В ПРИЛОЖЕНИИ 1 приведена реализация алгоритма факторизации на языке C с гипероперациями. Алгоритм был протестирован на эмуляторе REDEFINE, запущенном на процессоре Intel Xeon. В табл. 4 приведено время работы алгоритма факторизации на эмуляторе REDEFINE для случайных полиномов. Реализация на REDEFINE требует наименьшее число циклов ЦП.
6. ЗАКЛЮЧЕНИЕ И ДАЛЬНЕЙШАЯ РАБОТА
В статье рассмотрена проблема факторизации булевых полиномов, лежащая в основе декомпозиции булевых функций в ДНФ и реляционных данных. В связи с этой проблемой важным является построение эффективных алгоритмов факторизации. Мы рассмотрели алгоритм факторизации булевых полиномов, предложенный в [4], и предложили параллельную MIMD реализацию этого алгоритма, который использует параллелизм уровня задачи и параллелизм уровня данных для повышения быстродействия. Эксперименты с последовательным и параллельным алгоритмами факторизации на бенчмарках логического синтеза и случайных полиномах показали существенное ускорение вследствие параллелизации. Реализация параллельного алгоритма на эмуляторе REDEFINE продемонстрировало преимущество в быстродействии благодаря массивнопараллельной многоядерной архитектуре. Модель исполнения, реализуемая архитектурой REDEFINE, основана на принципах потока данных, что позволяет избежать необходимости барьерной синхронизации. Это дает повышение скорости MIMD задач (в частности, факторизации) на архитектуре REDEFINE. Указанные реализации будут применены для вычисления недизъюнктной декомпозиции ДНФ [15] и табличных данных [6], которая опирается на решение массовой задачи факторизации булевых полиномов.
Список литературы
von zur Gathen J., Gerhard J. Modern Computer Algebra. Third edition. New York, NY, USA: Cambridge University Press, 2013. P. 812.
Жегалкин И.И. Арифметизация символической логики // Математический сборник. 1928. Т. 35. № 1. С. 311–377.
Muller D.E. Application of Boolean algebra to switching circuit design and to error detection // IRE Transactions on Electronic Computers. 1954. V. EC-3. P. 6–12.
Емельянов П.Г., Пономарев Д.К. Алгоритмические вопросы конъюнктивной декомпозиции булевых формул // Программирование. 2015. Т. 41. № 3. С. 162–169.
Emelyanov P., Ponomaryov D. On tractability of disjoint AND–decomposition of boolean formulas // Proceedings of the PSI 2014: 9th Ershov Informatics Conference. V. 8974 of Lecture Notes in Computer Science. Springer, 2015. P. 92–101.
Emelyanov P. On two kinds of dataset decomposition // Proceedings of the 18th International Conference on Computational Science (ICCS 2018), Part II. V. 10861 of Lecture Notes in Computer Science. Springer, 2018. P. 171–183.
Emelyanov P., Ponomaryov D. Cartesian decomposition in data analysis // Proceedings of the Siberian Symposium on Data Science and Engineering (SSDSE 2017). 2017. P. 55–60.
Shpilka A., Volkovich I. On the relation between polynomial identity testing and finding variable disjoint factors // Proceedings of the 37th International Colloquium on Automata, Languages and Programming. Part 1 (ICALP 2010). V. 6198 of Lecture Notes in Computer Science. Springer, 2010. P. 408–419.
Emelyanov P., Ponomaryov D. On a polytime factorization algorithm for multilinear polynomials over ${{F}_{2}}$ // Proceedings of the 20th International Workshop on Computer Algebra in Scientific Computing (CASC 2018). V. 11077 of Lecture Notes in Computer Science. Springer, 2018. P. 164–176.
Somenzi F. CUDD: CU Decision Diagram package // https://github.com/ivmai/cudd. Accessed 2019-12-11.
Corno F., Reorda M. S., Squillero G. RT-level ITC’99 benchmarks and first ATPG results // IEEE Design & Test of Computers. 2000. V. 17. № 3. P. 44–53.
Hansen M.C., Yalcin H., Hayes J.P. Unveiling the ISCAS-85 benchmarks: A case study in reverse engineering // IEEE Design Test of Computers. 1999. V. 16. № 3. P. 72–80.
Fišer P., Schmidt J. A prudent approach to benchmark collection // Proceedings of the 12th International Workshop on Boolean Problems (IWSBP’2016). 2016. P. 129–136.
Redefine – reconfigurable silicon core description // http://morphing.in/redefine. Accessed 2018-12-07.
Ponomaryov D. A polynomial time delta-decomposition algorithm for positive DNFs // Proceedings of the 14th International Computer Science Symposium in Russia (CSR’2019). V. 11532 of Lecture Notes in Computer Science. Springer, 2019. P. 325–336.
Дополнительные материалы отсутствуют.
Инструменты
Программирование