Программирование, 2023, № 1, стр. 48-55
РЕАЛИЗАЦИЯ ГЕОМЕТРИЧЕСКОЙ АЛГЕБРЫ В СИСТЕМАХ СИМВОЛЬНЫХ ВЫЧИСЛЕНИЙ
М. Н. Геворкян a, *, А. В. Королькова a, **, Д. С. Кулябов a, b, ***, А. В. Демидова a, ****, Т. Р. Велиева a, *****
a Российский университет дружбы народов
117198 Москва, ул. Миклухо-Маклая, д. 6, Россия
b Объединенный институт ядерных исследований
141980 Московская область, Дубна, ул. Жолио-Кюри 6, Россия
* E-mail: gevorkyan-mn@rudn.ru
** E-mail: korolkova-av@rudn.ru
*** E-mail: kulyabov-ds@rudn.ru
**** E-mail: demidova-av@rudn.ru
***** E-mail: velieva-tr@rudn.ru
Поступила в редакцию 01.09.2022
После доработки 02.09.2022
Принята к публикации 08.09.2022
- EDN: GRTBSQ
- DOI: 10.31857/S0132347423010041
Аннотация
Для описания специализированных математических структур предпочтительнее использовать более специальный формализм вместо более общего. Однако, зачастую в этом вопросе превалирует традиция. Например, для описания вращений в трехмерном пространстве, или например, для описания движения в пространствах Гилилея или Минковского обычно используют векторный (или тензорный) формализм взамен более специализированных формализмов представлений алгебры Клиффорда. Этот подход является исторически обусловленным. Применение специализированных формализмов (таких как спиноры или кватернионы) не стало научным мейнстримом, однако заняло свое место при решении практических и инженерных задач. Следует также отметить, что все операции в теоретических задачах проводятся именно с формульными данными. А манипуляции с многомерными геометрическими объектами подразумевают большое количество операций с одинаковыми объектами. И именно в таких задачах сильна компьютерная алгебра. В данной работе авторы хотят обратить внимание на один из таких специализированных формализмов, формализм геометрической алгебры. А именно, предлагается рассмотреть варианты реализации геометрической алгебры в рамках парадигмы символьных вычислений.
1. ВВЕДЕНИЕ
Геометрическая алгебра основывается на работах Г.Г. Грассмана [1], У.Р. Гамильтона [2] и У.К. Клиффорда [3]. Клиффорд в своих работах обобщил алгебру Грассмана и алгебру кватернионов Гамильтона. В геометрической алгебре рассматривается конкретная реализация алгебры Клиффорда, основанная на мультивекторах, которая включает в себя реализацию алгебры Грассмана в виде внешней алгебры p-векторов (контравариантных антисимметричных тензоров с операцией внешнего умножения). Алгебра кватернионов также является частным случаем алгебры мультивекторов.
Долгое время работы Клиффорда не привлекали особого внимание физиков и математиков. Алгебра Клиффорда была известна [4], но математический аппарат не был разработан. Д. Хинстейн [5] судя по всему является первым исследователем, который формализовал разработки Клиффорда в виде современного математического аппарата. Основная волна исследований на эту тему началась уже в 21 веке.
Первоначально алгебра мультивекторов формулировалась с прицелом на использование в физике [6, 7], однако довольно быстро она обрела большую популярность у специалистов по компьютерной графике [8, 9]. Объясняется это тем, что алгебра мультивекторов включает в себя в виде частных случаев алгебру комплексных чисел, кватернионов и бикватернионов, которые используются в компьютерной графике для описания вращений в двумерном, трехмерном и однородном пространствах.
В настоящее время сведения из геометрической алгебры входят во многие учебники по компьютерной графике [10, 11], а методы описания вращений с помощью бивекторов могут потенциально вытеснить кватернионы и бикватернионы [12].
В целом следует отметить прикладной характер исследований по геометрической алгебре [13, 14]. Это объясняется сравнительной простотой математического аппарата, для освоения которого достаточно стандартного курса линейной алгебры и некоторые сведения из общей алгебры [15]. Следует также отметить, что изучаемые объекты допускают довольно наглядное визуальное представление, что делает их изучение проще.
Исследования по использованию геометрической алгебры в различных областях физики также продолжаются, см. например, статью [16].
В данной статье дается обзор библиотеки GAlgebra [17] для языка Python. Данная библиотека реализует основные операции и объекты геометрической алгебры. Авторы уже делали обзор на библиотеку Grassmann.jl в статье [18] и приводили необходимые математические сведения из геометрической алгебры. Однако символьные алгебраические вычисления в Grassmann.jl крайне ограничены, а некоторые функции и вовсе не работают. Поэтому возникла задача найти более функциональную альтернативу, какой и стал пакет символьных вычислений для задач геометрической алгебры GAlgebra.
1.1. Структура статьи
Раздел 2 дает краткое описание основных понятий и операций геометрической алгебры. В разделе 3 статьи дается краткий обзор библиотек для разных языков программирования, реализующих операции геометрической алгебры. Оставшаяся часть статьи посвящена библиотеке GAlgebra и ее использованию. Изложение ведется на основе примеров двумерного (раздел 4) и трехмерного (раздел 5) евклидова пространства, а также более специфического двумерного пространства Минковского (раздел 6). Для данного пространства также указывается связь геометрической алгебры с гиперболическими числами и с преобразованиями Лоренца (раздел 7), что иллюстрирует применение геометрической алгебры в физике.
Все примеры кода, представленные в статье, выполнялись в оболочке Jupyter Notebook с интерпретатором языка Python 3.9.7 и библиотекой SymPy [19] версии 1.9. Примеры кода приводятся вместе с возвращаемым результатом. Для лучшей читабельности мы делаем некоторые косметические улучшения формул в результатах, например, выделяем векторы полужирным шрифтом.
2. ОСНОВНЫЕ ПОНЯТИЯ И ОПЕРАЦИИ ГЕОМЕТРИЧЕСКОЙ АЛГЕБРЫ
В этом разделе напомним основные понятия операции, связанные с геометрическим произведением и мультивекторами. В статье [18] нами уже кратко была изложена основа внешней алгебры p-векторов, которая входит в расширенные курсы алгебры, например [20], обозначений которой мы будем придерживаться.
Будем рассматривать евклидово или псевдоевклидово пространство L с ортонормированным базисом $\langle {{{\mathbf{e}}}_{1}}, \ldots ,{{{\mathbf{e}}}_{n}}\rangle $, где буквой n всегда будем обозначать размерность пространства. Контрвариантные кососимметричные тензоры валентности (0, p) называются p-векторами или реже поливекторами. Пространство p-векторов и операция внешнего произведения $ \wedge $ образуют внешнюю алгебру т.е. ассоциативную алгебра над полем $\mathbb{R}$ – реализацию абстрактной алгебры Грассмана.
Объекты, состоящие из формальной суммы всех возможных p-векторов, называются мультивекторами и образуют градуированную алгебру, называемую геометрической алгеброй, которая является реализацией алгебры Клиффорда относительно операции геометрического произведения.
Геометрическим произведением двух векторов ${\mathbf{u}}$ и ${\mathbf{v}}$ назовем отображение $L \times L \to L$, которое имеет следующие свойства.
• Геометрическое умножение двух скаляров сводится к обычному умножению, определенному в поле этих скаляров.
• Геометрическое умножение скаляра на вектор из L сводится к обычному умножению на скаляр, определенному в L.
• Геометрическое произведение вектора ${\mathbf{u}}$ самого на себя равно скаляру, значения которого равно норме вектора (норме):
• Дистрибутивность: ${\mathbf{u}}({\mathbf{v}} + {\mathbf{w}}) = {\mathbf{uv}} + {\mathbf{uw}}$ и u(v + + w) = ${\mathbf{uv}} + {\mathbf{uw}}$. В силу того, что u может быть скаляром, из дистрибутивности следует линейность.
• Ассоциативность: ${\mathbf{v}}({\mathbf{uw}}) = ({\mathbf{vu}}){\mathbf{w}}$.
Коммутативность или антикоммутативность явным образом не требуется. По соглашению геометрическое произведение никаким специальным символом не обозначается. Заметим, что геометрическое произведение действует на все градуировки рассматриваемой градуированной алгебры.
Более полезно конструктивное определение геометрического произведения через скалярное и внешнее произведения:
Можно определить обратный вектор ${{{\mathbf{u}}}^{{ - 1}}} = \frac{{\mathbf{u}}}{{{{{\left\| {\mathbf{u}} \right\|}}^{2}}}}$ относительно геометрического произведения:
Наличие ортонормированного базиса в пространстве $L$ позволяет используя лишь формулу (1) вычислять геометрические произведения произвольных мультивекторов, разложенных по базисным p-векторам. Вычисления основываются на следующих двух формулах:
(2)
${{{\mathbf{e}}}_{i}}{{{\mathbf{e}}}_{j}} = - {{{\mathbf{e}}}_{j}}{{{\mathbf{e}}}_{i}},\quad i \ne j\quad {\text{и}}\quad {{{\mathbf{e}}}_{i}}{{{\mathbf{e}}}_{i}} = 1.$Оба соотношения можно получить, если рассмотреть геометрическое произведение двух ортонормированных базисных векторов: eiej = (ei, ej) + + ${{{\mathbf{e}}}_{i}} \wedge {{{\mathbf{e}}}_{j}} = {{\delta }_{{ij}}} + {{{\mathbf{e}}}_{i}} \wedge {{{\mathbf{e}}}_{j}}$.
Кроме того, если $i \ne j$, то ${{{\mathbf{e}}}_{i}}{{{\mathbf{e}}}_{j}} = {{{\mathbf{e}}}_{i}} \wedge {{{\mathbf{e}}}_{j}}$, то есть базис бивекторов можно выразить через геометрическое произведение. В общем случае для базиса p-вектора:
Используя (2) можно находить геометрические произведения любых мультивекторов, разложенных по базисным p-векторам. Например:
При раскрытии скобок использовалась ассоциативность и дистрибутивность, затем используя правила (2) упрощаем выражение e1e2e1e2e3 = = $ - {{{\mathbf{e}}}_{1}}\underbrace {{{{\mathbf{e}}}_{2}}{{{\mathbf{e}}}_{2}}}_1{{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{3}}$ = $ - \underbrace {{{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{1}}}_{ = 1}{{{\mathbf{e}}}_{3}} = - {{{\mathbf{e}}}_{3}}$. Аналогично поступаем и с ${{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{3}}{{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}{{{\mathbf{e}}}_{3}}$. В результате получаем мультивектор, разложенный по базисным p-векторам.
Таким образом, вводить формальное определение геометрического произведения произвольных мультивекторов при работе в пространстве L с ортонормированным базисом не требуется – оно вводится конструктивно из определения геометрического произведения для векторов.
3. КРАТКИЙ ОБЗОР СУЩЕСТВУЮЩИХ БИБЛИОТЕК ПО ГЕОМЕТРИЧЕСКОЙ АЛГЕБРЕ
Математический аппарат геометрической алгебры получил широкую популярность среди специалистов по компьютерной графике. Вследствие этого довольно быстро появилось большое количество библиотек для разных языков программирования, которые реализуют различные возможности геометрической алгебры.
Основным источником сведений о существующих библиотеках с открытым исходным кодом, является сайт bivector.net [21], на котором в разделе lib собрано большое количество ссылок на актуальные библиотеки разного плана. Перечислим здесь некоторые из них.
Большинство библиотек ориентированы на численные расчеты.
• Clifford [22] – библиотека для языка Python, реализующая все основные операции геометрической алгебры в численном виде. Библиотека довольно стабильна, последняя версии 1.4.0 вышла в июле 2020 года.
• Ganja.js [23] – библиотека для языка JavaScript. Имеет встроенные возможности визуализации и интерактивного взаимодействия геометрических объектов. Существуют библиотеки-обертки и для других языков: Python, C++, C# и Rust.
• Grassmann.jl [24] – библиотека для языка Julia, последняя версии 0.7.7 вышла в ноябре 2021 года. Поддерживает как численные, так и символьные вычисления. Однако библиотека довольно нестабильна и ряд заявленных функций работает с ошибками.
• Garamon [25], Klein [26], Versor [27] – библиотеки для языка C++. Большой выбор библиотек именно для этого языка объясняется его доминированием в области компьютерной графики.
Все вышеперечисленные библиотеки ориентированы на численные расчеты, а не на символьные вычисления. Исключение составляет только Grassmann.jl так как частично поддерживает символьные вычисления с помощью системы компьютерной алгебры Reduce. Мы уже делали обзор [18] Grassmann.jl и указывали, что поддержка символьных вычислений не доработана и крайне ограничена. Впрочем, учитывая перспективность языка Julia [28, 29], стоит в будущем еще вернуться к решениям на его основе.
Судя по всему, единственной библиотекой с открытым исходным кодом с поддержкой символьных вычислений для геометрической алгебры является библиотека GAlgebra [17].
4. ДВУМЕРНОЕ ЕВКЛИДОВО ПРОСТРАНСТВО
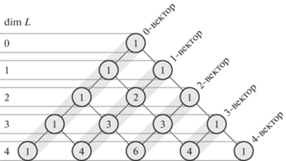
Рассмотрим случай двумерного евклидова пространства, для которого существуют четыре внешние алгебры, перечисленные в таблице 1. Размерность внешней алгебры $\dim {{\Lambda }^{p}}(L)$ зависит от ранга p (градуировки, grade) внешней алгебры и от размерности пространства L. При этом dimΛp(L) = = ${\text{C}}_{n}^{p}$ (см. рис. 1).
Таблица 1.
Базисы для двумерного случая
| p | ${{\Lambda }^{p}}(L)$ | Базис | Элемент | $\dim {{\Lambda }^{p}}(L)$ |
|---|---|---|---|---|
| 0 | $\mathbb{R}$ | 1 | $a = a \cdot 1$ | 1 |
| 1 | $L$ | ${{{\mathbf{e}}}_{1}}$, ${{{\mathbf{e}}}_{2}}$ | ${\mathbf{a}} = {{a}^{1}}{{{\mathbf{e}}}_{1}} + {{a}^{2}}{{{\mathbf{e}}}_{2}}$ | 2 |
| 2 | ${{\Lambda }^{2}}(L)$ | ${{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}$ | ${\mathbf{a}} = {{a}^{{12}}}{{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}$ | 1 |
| 3 | ${{\Lambda }^{3}}(L)$ | 0 | ${\mathbf{a}} = 0$ | 0 |
Рис. 1.
Зависимость размерности p-вектора от градуировки внешней алгебры и размерности пространства L.
Приведем примеры с помощью GAlgebra. Для начала подключим библиотеку и настроим механизм отображение формул.
import sympy as sp
from galgebra.ga import Ga
sp.init_printing(latex_printer=latex,
↪ use_latex='mathjax' )
Зададим двумерное пространство, указав символы для базисных элементов, для индексов, а также единичную диагональную метрику g, которая определяет ортонормированность пространства:
xy = sp.symbols('1 2' , real=True)
o2d = Ga('e' , g= [1, 1 ], coords=xy)
Следует отметить, что GAlgebra позволяет задавать метрики только диагонального вида, но не обязательно единичные.
После определения пространства L можно задавать p-векторы произвольного вида, например, скаляр, вектор и бивектор:
a_scalar = o2d.mv('a' , 0)
a_vect = o2d.mv('a' , 1)
a_bivect = o2d.mv('a' , 2)
a_scalar, a_vect, a_bivect
$(a,{{a}^{1}}{{{\mathbf{e}}}_{1}} + {{a}^{2}}{{{\mathbf{e}}}_{2}},{{a}^{{12}}}{{{\mathbf{e}}}_{1}} \wedge {{{\mathbf{e}}}_{2}})$
Также можно записать базисные векторы в отдельные переменные и использовать их для формирования произвольных мультивекторов, например:
e_1, e_2 = o2d.mv()
4*e_1 + 3*e_1*e_2
$4{{{\mathbf{e}}}_{1}} + 3{{{\mathbf{e}}}_{1}} \wedge {{{\mathbf{e}}}_{2}}$
В GAlgebra все базисные элементы записываются через внешнее произведение $ \wedge $, хотя при их задании мы использовали геометрическое умножение *.
Внешнее произведение двух векторов имеет простой геометрический смысл параллелограмма, построенного на этих векторах, а единственная компонента равна ориентированной площади этого параллелограмма.
a,b = o2d.mv('a' , 1), o2d.mv('b' , 2)
a ^ b # внешнее произведение
$({{a}^{1}}{{b}^{2}} - {{a}^{2}}{{b}^{1}}){{{\mathbf{e}}}_{1}} \wedge {{{\mathbf{e}}}_{2}}$
Мультивекторы со скалярной и бивекторной частями $a + b{{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}$ изоморфны комплексным числам. Это легко проверить, показав, что базисный бивектор ${{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}$ обладает свойствами эллиптической мнимой единицы:
i = e_1*e_2
i*i == –1 # True
Создав два мультивектора указанного типа, можно с помощью GAlgebra проверить, что операции сложения, умножения и деления дают результат, полностью аналогичный комплексным числам.
u = o2d.mv('u' , 0) + o2d.mv('u' , 2)
v = o2d.mv('v' , 0) + o2d.mv('v' , 2)
u, v
u + v, u * v
u / v
Часто используют обозначение ${\mathbf{i}} = {{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}$, что делает алгебру мультивекторов $a + b{\mathbf{i}}$ практически неотличимой от алгебры комплексных чисел (эллиптического типа) [30] даже на уровне обозначений. Так в GAlgebra для бивекторов определена функция экспоненты:
θ = sp.Symbol(' θ ' , real=True)
(θ*i).exp()
В результате возвращается мультивектор вида:
Отметим, что в GAlgebra для мультивекторов определены операции сложения +, разности –, скалярного произведения |, внешнего произведения ^. Использование знака * для геометрического произведения не вносит никаких противоречий, так как для скаляров геометрическое умножения эквивалентно обычному умножению чисел.
5. ТРЕХМЕРНОЕ ЕВКЛИДОВО ПРОСТРАНСТВО
Увеличим теперь размерность $L$ до трех и составим таблицу 2 всех возможных нетривиальных внешних алгебр.
Зададим трехмерное евклидово пространство с ортонормированным базисом и три произвольных вектора:
o3d = Ga('e' , g= [1, 1, 1 ], coords=xyz)
a, b, c = o3d.mv('a' , 1), o3d.mv('b' ,
↪ 1), o3d.mv('c' , 1)
В трехмерном пространстве внешнее произведение двух векторов дает бивектор с тремя компонентами, которые совпадают с компонентами псевдовектора векторного произведения a × b:
a ^ b
Заметим, что для получения точного соответствия векторному произведению, необходимо воспользоваться операцией правого или левого дополнения, которая в GAlgebra не реализована (собственно поэтому мы не упоминали ее в теоретическом введении). Этот недостаток для трехмерного пространства легко преодолим, так как операция дополнения эквивалентна умножению на обратный базисный тривектор ${\mathbf{I}} = {{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}{{{\mathbf{e}}}_{3}}$ или, иначе, делению на I.
Таблица 2.
Базисы для трехмерного случая
| p | ${{\Lambda }^{p}}(L)$ | Базис | Элемент | $\dim {{\Lambda }^{p}}(L)$ |
|---|---|---|---|---|
| 0 | $\mathbb{R}$ | 1 | $a = a \cdot 1$ | 1 |
| 1 | $L$ | ${{{\mathbf{e}}}_{1}}$, ${{{\mathbf{e}}}_{2}}$, ${{{\mathbf{e}}}_{3}}$ | ${\mathbf{a}} = {{a}^{1}}{{{\mathbf{e}}}_{1}} + {{a}^{2}}{{{\mathbf{e}}}_{2}} + {{a}^{3}}{{{\mathbf{e}}}_{3}}$ | 3 |
| 2 | ${{\Lambda }^{2}}(L)$ | ${{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}$, ${{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{3}}$, ${{{\mathbf{e}}}_{2}}{{{\mathbf{e}}}_{3}}$ | ${\mathbf{a}} = {{a}^{{12}}}{{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}} + {{a}^{{23}}}{{{\mathbf{e}}}_{2}}{{{\mathbf{e}}}_{3}} + {{a}^{{13}}}{{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{3}}$ | 3 |
| 3 | ${{\Lambda }^{3}}(L)$ | ${{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}{{{\mathbf{e}}}_{3}}$ | ${\mathbf{a}} = {{a}^{{123}}}{{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}{{{\mathbf{e}}}_{3}}$ | 1 |
I = e_1*e_2*e_3
(a^b) / I
В случае внешнего произведения трех векторов мы получим тривектор, единственная компонента которого совпадает со смешанным произведением трех векторов. Деление на I вновь дает точное значение, равное смешанному произведению.
a ^ b ^ c
(a ^ b ^ c) / I
Обозначение I для базисного тривектора выбрано из-за свойства эллиптической мнимой единицы II = –1. Кроме того, базисные бивекторы ${{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{2}}$, ${{{\mathbf{e}}}_{2}}{{{\mathbf{e}}}_{3}}$ и ${{{\mathbf{e}}}_{1}}{{{\mathbf{e}}}_{3}}$ проявляют свойства мнимых единиц кватернионов:
i, j, k = e_1*e_2, e_2*e_3, e_1*e_3
i*i == j*j == k*k == i*j*k == -1 # True
Подалгебра мультивекторов со скалярной и бивекторной частями изоморфна алгебре кватернионов. Заметим, что мультивекторы точно такого же вида в двумерном пространстве L были изоморфны алгебре комплексных чисел.
6. ДВУМЕРНОЕ ПСЕВДОЕВКЛИДОВО ПРОСТРАНСТВО
Рассмотрим подробно случай пространства $\Lambda (L)$, когда пространство I является двумерным пространством Минковского (двумерным псевдоевклидовым пространством $E_{{1,1}}^{2}$) с базисом $\langle {{{\mathbf{e}}}_{0}},{{{\mathbf{e}}}_{1}}\rangle $. В этом случае Λ(L) = ${{\Lambda }^{0}}(L) \oplus {{\Lambda }^{1}}(L) \oplus {{\Lambda }^{2}}(L)$ и общий вид мультивектора:
Задать такое пространство в GAlgebra можно следующим образом:
tx = (t, x) = sp.symbols('0 1' ,
↪ real=True)
m2d = Ga('e' , g=[1, -1], coords=tx)
e0, e1 = m2d.mv()
Базисный бивектор ${{{\mathbf{e}}}_{0}}{{{\mathbf{e}}}_{1}}$ обозначим буквой ${\mathbf{j}}$, так как он обладает свойствами гиперболической мнимой единицы [30] относительно геометрического умножения:
j = e0*e1
j*j == 1 # return True
Мультивектор, содержащий лишь скалярную и бивекторную части, можно записать в виде ${\mathbf{u}} = a + b{{{\mathbf{e}}}_{0}}{{{\mathbf{e}}}_{1}} = a + b{\mathbf{j}}$. Множество мультивекторов такого вида, изоморфно относительно геометрического произведения множеству комплексных чисел гиперболического типа [30], для которых определены те же алгебраические операции, что и для стандартных эллиптических комплексных чисел11. Покажем, как эти операции реализованы в GAlgebra. Зададим вначале два мультивектора нужного нам вида. Обратите внимание, что здесь мы используем альтернативный способ задания, без функции mv.
a, b, c, d = sp.symbols('a, b, c, d' ,
↪ real=True)
u = a + b*j
v = c + d*j
Теперь испробуем все стандартные алгебраические операции. Начнем со сложения и умножения.
u + v, u * v
Также определены сопряжение и норма (модуль)
~u, u.norm()
Вместо операции деления покажем, как найти обратный элемент:
u.inv()
В частности базисный бивектор j является обратным сам для себя так как ${\mathbf{jj}} = 1$, следовательно ${{{\mathbf{j}}}^{{ - 1}}} = {\mathbf{j}}$.
j = e0*e1
j.inv() == j # True
Для гиперболических чисел справедлив аналог формулы Эйлера ${{e}^{{{\mathbf{j}}\theta }}} = \theta + {\mathbf{j}}\theta ,\theta \in \mathbb{R}$. В GAlgebra для бивектора определена операция exp:
θ = sp.Symbol(' θ ' , real=True)
(θ*j).exp();
которая как раз возвращает результат в виде аналога формулы Эйлера:
В евклидовом пространстве мультивекторы состоящие из скалярной и бивекторной частей изоморфны комплексным числам (двумерный случай) и кватернионам (трехмерный случай) и с помощью них задаются вращения на плоскости и в трехмерном пространстве. В случае псевдоевклидового пространства аналогичный мультивектор задает преобразования Лоренца и в двумерном случае изоморфен гиперболическим комплексным числам.
7. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА И РЕЛЯТИВИСТСКОЕ СЛОЖЕНИЕ СКОРОСТЕЙ
Релятивистские операции можно рассматривать как в представлении гиперболических комплексных чисел [30, 32], так и в представлении геометрической алгебры. Рассмотрим мультивектор ${\mathbf{u}} = \exp \{ \theta {\mathbf{j}}\} $ и умножим его на произвольный вектор ${\mathbf{x}} = {{x}^{0}}{{{\mathbf{e}}}_{0}} + {{x}^{1}}{{{\mathbf{e}}}_{1}}$ пользуясь геометрическим умножением:
Мы получили преобразование Лоренца:
В GAlgebra данные операции выполняются следующим образом:
θ1 = sp.Symbol(' θ1 ' , real=True)
θ2 = sp.Symbol(' θ2 ' , real=True)
u = (θ*j).exp()
x = m2d.mv(' x ' , 1)
u*x
Релятивистскую формулу сложения скоростей можно получить выполнив преобразования Лоренца два раза подряд:
Так как ${\text{th}}\theta = \frac{{v}}{c}$, то ${\text{th}}{{\theta }_{3}} = {\text{th}}({{\theta }_{1}} + {{\theta }_{2}})$ и по формуле тангенса суммы:
Сложение скоростей свелось к сложению гиперболических углов. Естественно, что в двумерном случае это сложение коммутативно и ассоциативно (в отличии от случая полного пространства Минковского).
То же самое легко повторить с помощью GAlgebra:
u1 = (' θ1 ' *j).exp()
u2 = (' θ2 ' *j).exp()
u1*u2*x
Фактически, применяя специализированный формализм геометрической алгебры мы смогли вместо громоздких (векторных) операций с леренцовыми коэффициентами применить элегантные операции поворотов в соответствующем пространстве.
8. ЗАКЛЮЧЕНИЕ
Мы рассмотрели практически весь основной функционал модуля GAlgebra для языка Python и пакета компьютерной алгебры SymPy. За рамками статьи остались лишь примеры использования дифференциального исчисления ввиду их объемности. В рамках геометрической алгебры вводится оператор градиента, который обобщает стандартные операторы векторного анализа. Примером его использования может служить запись уравнений Максвелла в виде единственного уравнения и крайне простая процедура получения волнового уравнения (подробнее см. [7]).
Если ограничиться рассмотрением лишь свободного программного обеспечения, то модуль GAlgebra является безальтернативным. Существуют и другие библиотеки для разных языков программирования, но практически все они ограничены численными вычислениями.
Укажем также и некоторые недостатки модуля. Так, например, в нем отсутствует операция дополнения, что впрочем компенсируется геометрическим делением на базисный элемент максимального ранга.
Более существенным недостатком является невозможность задания метрики с нулями на диагонали. Такая метрика описывает проективное пространство, для которого в рамках геометрической алгебры развита довольно проработанная теория. Проективная геометрическая алгебра (PGA – Projective geometric algebra) наиболее удобна для использования в задачах компьютерной графики.
Список литературы
Grassmann H.G. Die mechanik nach den principien der ausdehnungslehre // Mathematische Annalen. 1877. Bd. 12. S. 222–240.
Kuipers J.B. Quaternions and rotation sequences. Princeton University Press, 1999.
Clifford W.K. Applications of grassmann’s extensive algebra // American Journal of Mathematics. 1878. V. 1. № 4. P. 350–358.
Казанова Г. Векторная алгебра / Под ред. М.К. Поливанова. Современная математика. М.: Мир, 1979.
Hestenes D., Sobczyk G. Clifford Algebra to Geometric Calculus: A Unified Language for Mathematics and Physics. Fundamental Theories of Physics. Springer Netherlands, 1987. ISBN: 9789027725615.
Delanghe R., Sommen F., Soucek V. Clifford algebra and spinor-valued functions. Mathematics and Its Applications. Kluwer Academic Publishers, 1992.
Doran C., Lasenby A. Geometric Algebra for Physicists. Morgan Kaufmann Publishers, 2003. ISBN: 9780123694652.
Dorst L., Fontijne D., Mann S. Geometric algebra for computer science. The Morgan Kaufmann Series in Computer Graphics. Morgan Kaufmann, 2007. ISBN: 0123694655.
Vince J. Geometric algebra for computer graphics. Springer-Verlag, 2008. ISBN: 9781846289965.
Lengyel E. Mathematics. Lincoln, California: Terathon Software LLC, 2016. V. 1. ISBN: 9780985811747.
Kanatani K. Understanding Geometric Algebra. Taylor and Francis Group/CRC, 2015. ISBN: 9781482259513.
ten Bosch M. Let’s remove quaternions from every 3d engine. URL: https://marctenbosch.com/quaternions/.
Perwa C.B.U. Geometric Algebra with Applications in Engineering. Geometry and Computing. Springer-Verlag Berlin Heidelberg, 2009. ISBN: 9783540890676.
Joot P. Geometric Algebra for Electrical Engineers: Multivector Electromagnetism. CreateSpace Independent Publishing Platform, 2019. ISBN: 9781987598971.
Winitzki S. Linear Algebra via Exterior Products. 2020. URL: https://github.com/winitzki/linear-algebra-book.
Chappell J.M., Drake S.P., Seidel C.L. et al. Geometric algebra for electrical and electronic engineers // Proceedings of the IEEE. 2014. V. 102. № 9. P. 1340–1363.
Galgebra – symbolic geometric algebra/calculus package for sympy. 2022. URL: https://galgebra.readthedocs.io/en/latest/index.html.
Геворкян М.Н., Демидова А.В., Велиева Т.Р. и др. Аналитико-численная реализация алгебры поливекторов на языке julia // Программирование. 2022. № 1. С. 54–64.
Sympy. 2022. URL: http://www.sympy.org/ru/index.html.
Кострикин А.И. Линейная алгебра. М.: МЦНМО, 2009. Т. 2. ISBN: 9785940574545.
Bivector.net: Geometric algebra resources. 2022. URL: https://bivector.net/index.html.
Hadfield H., Wieser E., Arsenovic A. et al. pygae/clifford. 2022.
De Keninck S. ganja.js. 2020.
Grassmann.jl. 2022. URL: https://github.com/chakravala/Grassmann.jl.
Breuils S., Nozick V., Fuchs L. Garamon: A geometric algebra library generator // Advances in Applied Clifford Algebras. 2019. 7. V. 29. № 4. P. 69.
Gunn C.G., Keninck S.D. Geometric algebra and computer graphics // ACM SIGGRAPH 2019. Courses. ACM, 2019. 7.
Colapinto P. Versor: Spatial computing with conformal geometric algebra. 2011. Available at http://versor.mat.ucsb.edu. URL: http://versor.mat.ucsb.edu.
Кулябов Д.С., Королькова А.В. Компьютерная алгебра на julia // Программирование. 2021. № 2. С. 44–50. 2108.12301.
Gevorkyan M.N., Kulyabov D.S., Korolkova A.V. et al. Symbolic implementation of multivector algebra in julia language // Computer algebra: 4th International Conference Materials. LCC MAKS Press, 2021. 5. P. 57–60.
Kulyabov D.S., Korolkova A.V., Sevastianov L.A. Complex numbers for relativistic operations. MDPI AG, 2021. 12.
Зи Э. Квантовая теория поля в двух словах. Регулярная и хаотическая динамика, 2009. ISBN: 978-5-93972-770-9.
Kulyabov D.S., Korolkova A.V., Gevorkyan M.N. Hyperbolic numbers as einstein numbers // Journal of Physics: Conference Series. 2020. 5. V. 1557. P. 012027.
Дополнительные материалы отсутствуют.
Инструменты
Программирование


