Программирование, 2023, № 1, стр. 56-60

1. ВВЕДЕНИЕ

Дискриминантом многочлена степени n:

называется неприводимый многочлен ${{\Delta }_{n}}({{a}_{0}},{{a}_{1}}$, ..., a_n) с целочисленными коэффициентами, который обращается в нуль тогда и только тогда, когда f имеет кратные корни. Иногда дискриминант многочлена  f  будем обозначать ${{\Delta }_{n}}(f)$.

Структура многогранника Ньютона дискриминанта отражает геометрию дискриминантной гиперповерхности. В частности, асимптотическое поведение гиперповерхности “на бесконечности” контролируется “экстремальными” мономами дискриминанта, которые соответствуют вершинам многогранника Ньютона. Дискриминанты, в свою очередь, играют фундаментальную роль в теории алгебраических функций, в теории особенностей, в алгебраической геометрии и математической физике, о чем свидельствует значительное число публикаций (см., например, [1–6]).

В работах [7–9] было доказано интересное свойство срезок дискриминанта на грани его многогранника Ньютона, а именно, они допускают фактороизацию в дискриминанты многочленов меньших степеней. Данная работа посвящена алгоритму вычисления этих срезок. Также приводится результат факторизации полученных срезок в дискриминанты других многочленов. В основе алгоритма лежат формулы, приведенные и доказанные в статьях [8, 10] для граней многогранника Ньютона дискриминанта общего многочлена одного переменного. Используются факторизационные формулы, полученные в недавних статьях [7, 8].

Отметим, что количество слагаемых в дискриминанте многочлена быстро растет с увеличением степени многочлена. Так, если дискриминант кубического уравнения содержит пять слагаемых, то дискриминант многочлена четвертой степени состоит из шестнадцати слагаемых, для многочлена пятой степени дискриминант содержит 59 слагаемых, а для многочлена 10-й степени он состоит из 133 881 монома. Поэтому вычисление срезки дискриминанта весьма затруднительно без специальной программы.

2. МНОГОГРАННИК НЬЮТОНА ДЛЯ ДИСКРИМИНАНТА МНОГОЧЛЕНА

Напомним, что многогранником Ньютона $\mathcal{N}({{\Delta }_{n}})$ дискриминанта многочлена (1.1) называется выпуклая оболочка в ${{\mathbb{R}}^{{n + 1}}}$ множества всех показателей $k = ({{k}_{0}},{{k}_{1}}, \ldots ,{{k}_{n}})$ мономов, участвующих в ${{\Delta }_{n}}$.

Доказанная в [1] теорема показывает, что каждая вершина многогранника Ньютона $\mathcal{N}({{\Delta }_{n}})$ для дискриминанта многочлена  f  определяется некоторым разбиением отрезка [0, n] набором целых точек

Теорема 1 ([1], с. 412). Многогранник Ньютона дискриминанта многочлена (1.1) комбинаторно эквивалентен (n – 1)-мерному кубу; он содержит ${{2}^{{n - 1}}}$ вершин, которые находятся в биективном соответствии со всевозможными подмножествами

Вершина ${{v}_{I}}$, соответствующая подмножеству $I = \{ {{i}_{1}} < {{i}_{2}} < \ldots < {{i}_{s}}\} $, имеет координаты

Пусть ${{l}_{q}} = {{i}_{{q + 1}}} - {{i}_{q}}$ $(0 \leqslant q \leqslant s)$. Тогда моном

встречается в ${{\Delta }_{n}}$ с коэффициентом

Проиллюстрируем утверждение теоремы на примере кубического многочлена

Дискриминант Δ этого многочлена имеет вид:

В рассматриваемом случае имеется 4 подмножества $I \subset \{ 1,2\} $:

Соответствующие мономы будут следующими:

Отметим, что моном $18{{a}_{0}}{{a}_{1}}{{a}_{2}}{{a}_{3}}$ соответствует внутренней целочисленной точке (1, 1, 1, $1) \subset \mathcal{N}(\Delta )$ и теорема о нем ничего не утверждает.

Многогранник $\mathcal{N}({{\Delta }_{n}})$ имеет n – 1 гиперграней $\{ h_{k}^{0}\} $, лежащих в координатных гиперплоскостях $\{ {{t}_{k}} = 0\} $, $k = 1, \ldots ,n - 1$ (предполагается, что в объемлющем пространстве ${{\mathbb{R}}^{{n + 1}}}$ выбраны координаты $t = ({{t}_{0}},{{t}_{1}}, \ldots ,{{t}_{{n - 1}}},{{t}_{n}})$), и n – 1 некоординатных гиперграней. Здесь речь идет о гипергранях наивысшей размерности, т.е. коразмерности 1. Обозначим через h_k некоординатную грань многоранника $\mathcal{N}({{\Delta }_{n}})$, противоположную к координатной грани $h_{k}^{0}$.

В работах [8] и [10] показано, что многоранник $\mathcal{N}({{\Delta }_{n}})$ в пространстве ${{\mathbb{R}}^{{n + 1}}}$ переменных ${{t}_{0}},{{t}_{1}}, \ldots ,{{t}_{n}}$ высекается следующими неравенствами:

$k = 1,2, \ldots ,n - 1.$ Каждая его некоординатная гипергрань h_k определяется уравнением

Согласно известному свойству биоднородности дискриминанта, переменные ${{t}_{0}},{{t}_{n}}$ однозначно восстанавливаются через переменные ${{t}_{1}}, \ldots ,{{t}_{{n - 1}}}$ по формулам

Отметим, что при вычислении дискриминанта многочлена (1.1) мы можем сокращать число переменных на два. А потом, по формулам (2.2), сокращенные переменные восстанавливать (см. пример в конце этого параграфа).

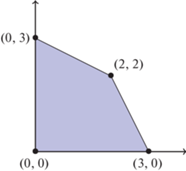
На рисунке 1 изображен многогранник Ньютона дискриминанта приведенного кубического многочлена

Это есть проекция многоранника $\mathcal{N}({{\Delta }_{3}})$ полного кубического многочлена на плоскость ${{t}_{0}} = 0$, ${{t}_{3}} = 0$. Для рассматриваемого многочлена дискриминант $\Delta $ равен

Согласно формулам (2.1) многогранник Ньютона приведенного дискриминанта рассматриваемого кубического многочлена задается системой неравенств

Что же касается дискриминанта полного кубического многочлена, то он находится из дискриминанта (2.3) приведенного кубического многочлена по формулам

которые получаются из (2.2), и имеет вид

3. ФАКТОРИЗАЦИЯ СРЕЗОК ДИСКРИМИНАНТА НА ГРАНИ МНОГОГРАННИКА НЬЮТОНА

Срезкой дискриминанта Δ на гипергрань h_k его многогранника Ньютона мы называем многочлен $\Delta {{{\text{|}}}_{{{{h}_{k}}}}}$, состоящий из всех мономов Δ, показатели которых принадлежат h_k. В качестве примера вычислим срезку дискриминанта многочлена четвертой степени

на гипергрань h₂. Как показывают вычисления, дискриминант многочлена (3.1) следующий:

Грань h₂ многогранника Ньютона многочлена (3.1) определяется системой:

Тогда срезка дискриминанта рассматриваемого многочлена будет иметь вид:

В статье [7] доказано свойство факторизуемости срезки дискриминанта $\mathcal{N}({{\Delta }_{n}})$ на любую из некоординатных гиперграней в произведение двух дискриминантов меньших степеней. В частности, последняя срезка факторизуется в произведение двух дискриминантов квадратных уравнений:

В статье [8] доказано свойство факторизуемости срезок дискриминанта на грани его многогранника Ньютона большей коразмерности. Именно, пусть

грань $\mathcal{N}({{\Delta }_{n}})$, полученная пересечением p некоординатных гиперграней. Здесь мультииндекс K = = $\{ {{k}_{1}}, \ldots ,{{k}_{p}}\} $ определяет разбиение набора $\{ 0,1, \ldots ,n\} $ на p + 1 поднаборов (отрезков) считая ${{k}_{0}} = 0$, ${{k}_{{p + 1}}} = n$. Обозначим через l_i := := ${{k}_{{i + 1}}} - {{k}_{i}}$ длину K_i и

Приведем результат, доказанный в работе [8].

Теорема 2. Срезка Δ_n на грань h_K факторизуется в виде произведения

где $a_{K}^{2} = a_{{{{k}_{1}}}}^{2} \ldots a_{{{{k}_{p}}}}^{2}$, а ${{\Delta }_{{{{l}_{i}}}}}$ – дискриминанты многочленов ${{f}_{{{{K}_{i}}}}}$ степеней ${{l}_{i}}$.

Проиллюстрируем данную теорему на примере. Для многочлена седьмой степени f(y) = = $\sum\nolimits_{k = 0}^7 {{{a}_{k}}{{y}^{k}}} $ срезка ${{\Delta }_{7}}{{{\text{|}}}_{{{{h}_{{2,5}}}}}}$ на грань ${{h}_{2}} \cap {{h}_{5}}$ представится в виде произведения трех дискриминантов:

т.е. дискриминантов многочленов ${{a}_{0}} + {{a}_{1}}y + {{a}_{2}}{{y}^{2}}$, ${{a}_{2}} + {{a}_{3}}y + {{a}_{4}}{{y}^{2}} + {{a}_{5}}{{y}^{3}}$ и ${{a}_{5}} + {{a}_{6}}y + {{a}_{7}}{{y}^{2}}$.

4. ОПИСАНИЕ АЛГОРИТМА

Алгоритм MAIN1(n, $facets1$, $facets2$) построения срезки по определению:

1. по заданному натуральному числу n строим многочлен $f(y)$ степени n и его дискриминат $Dsc$ по переменной y;

2. строим список $ListOfTerms$ из мономов дискриминанта $Dsc$;

3. по заданному n формируем матрицу $MTRX$ и столбец $CLMN$ из коэффициентов в правой части системы (2.1);

4. из списка $ListOfTerms$ выбираем мономы, у которых показатели степеней переменных ${{a}_{1}}, \ldots ,{{a}_{{n - 1}}}$ удовлетворяют системе (2.1) уравнений и неравенств, знаки которой задаются списком $facets1$; формируем многочлен $truncation$, являющийся искомой срезкой многочлена;

5. возвращаем факторизацию срезки, используя встроенную функцию factor;

6. если множество координатных граней $facets2$ непустое, то определенные в нем коэффициенты приравниваем к нолю; возвращаем факторизованную срезку на координатные грани.

Алгоритм MAIN2(n, $facets1$, $facets2$) построения срезки по Теореме 2:

1. по заданному натуральному числу n и номерам граней $facets = \{ {{k}_{1}}, \ldots ,{{k}_{p}}\} $ строим p + 1 многочленов ${{f}_{{{{K}_{i}}}}}$ с коэффициентами ${{a}_{{{{k}_{i}}}}}, \ldots ,{{a}_{{{{k}_{{i + 1}}}}}}$, $i = 0, \ldots ,p$, причем ${{k}_{0}} = 0,$ ${{k}_{{p + 1}}} = n$;

2. для каждого ${{f}_{{{{K}_{i}}}}},\;i = 1, \ldots ,p$, находим дискриминат, используя встроенную функцию $discrim$;

3. находим приведение полученных дискриминатов и домножаем его на $a_{{{{k}_{1}}}}^{2} \cdots a_{{{{k}_{p}}}}^{2}$ согласно формуле (3.2);

4. если множество координатных граней $facets2$ непустое, то определенные в нем коэффициенты приравниваем к нолю; возвращаем факторизованную срезку на координатные грани.

Алгоритм был реализован в среде Maple 18. Полный код программы доступен по ссылке https://github.com/lyapinap/LM2022. Вычисления производились на машине Intel(R) Core(TM) i5-1135G7 CPU 2.40 GHz, 64bit, ОЗУ 8.00 Гб под управлением Windows 10.

В таблице 1 приведно сравнительное время вычисления срезок многочлена по определению и по теореме 2 с использованием команды $CPUTime$ из пакета $CodeTools$.

5. ПРИМЕР

Команда

для многочлена пятой степени и его дискриминанта $\Delta = 3125a_{0}^{4}a_{5}^{4} - $ $2500a_{0}^{3}{{a}_{1}}{{a}_{4}}a_{5}^{3}$ – – $3750a_{0}^{3}{{a}_{2}}{{a}_{3}}a_{5}^{3}$ + $2000a_{0}^{3}{{a}_{2}}a_{4}^{2}a_{5}^{2}$ + $2250a_{0}^{3}a_{3}^{2}{{a}_{4}}a_{5}^{2}$ –‒ $1600a_{0}^{3}{{a}_{3}}a_{4}^{3}{{a}_{5}}$ + $256a_{0}^{3}a_{4}^{5} + $ $2000a_{0}^{2}a_{1}^{2}{{a}_{3}}a_{5}^{3}$ – ‒  $50a_{0}^{2}a_{1}^{2}a_{4}^{2}a_{5}^{2}$ + $2250a_{0}^{2}{{a}_{1}}a_{2}^{2}a_{5}^{3} - $ $2050a_{0}^{2}{{a}_{1}}{{a}_{2}}{{a}_{3}}{{a}_{4}}a_{5}^{2}$ + + $160a_{0}^{2}{{a}_{1}}{{a}_{2}}a_{4}^{3}{{a}_{5}} - $ $900a_{0}^{2}{{a}_{1}}a_{3}^{3}a_{5}^{2}$ + $1020a_{0}^{2}{{a}_{1}}a_{3}^{2}a_{4}^{2}{{a}_{5}}$ – ‒ $192a_{0}^{2}{{a}_{1}}{{a}_{3}}a_{4}^{4}$ – $900a_{0}^{2}a_{2}^{3}{{a}_{4}}a_{5}^{2}$ + $825a_{0}^{2}a_{2}^{2}a_{3}^{2}a_{5}^{2} + $ + $560a_{0}^{2}a_{2}^{2}{{a}_{3}}a_{4}^{2}{{a}_{5}}$ – $128a_{0}^{2}a_{2}^{2}a_{4}^{4}$ – $630a_{0}^{2}{{a}_{2}}a_{3}^{3}{{a}_{4}}{{a}_{5}}$ + + $144a_{0}^{2}{{a}_{2}}a_{3}^{2}a_{4}^{3}$ + $108a_{0}^{2}a_{3}^{5}{{a}_{5}}$ – $27a_{0}^{2}a_{3}^{4}a_{4}^{2}$ – $1600{{a}_{0}}a_{1}^{3}{{a}_{2}}a_{5}^{3}$ + + $160{{a}_{0}}a_{1}^{3}{{a}_{3}}{{a}_{4}}a_{5}^{2}$ – $36{{a}_{0}}a_{1}^{3}a_{4}^{3}{{a}_{5}}$ + $1020{{a}_{0}}a_{1}^{2}a_{2}^{2}{{a}_{4}}a_{5}^{2}$ + + $560{{a}_{0}}a_{1}^{2}{{a}_{2}}a_{3}^{2}a_{5}^{2}$ – $746{{a}_{0}}a_{1}^{2}{{a}_{2}}{{a}_{3}}a_{4}^{2}{{a}_{5}}$ + $144{{a}_{0}}a_{1}^{2}{{a}_{2}}a_{4}^{4} + $ + $24{{a}_{0}}a_{1}^{2}a_{3}^{3}{{a}_{4}}{{a}_{5}}$ – $6{{a}_{0}}a_{1}^{2}a_{3}^{2}a_{4}^{3}$ – $630{{a}_{0}}{{a}_{1}}a_{2}^{3}{{a}_{3}}a_{5}^{2}$ + + $24{{a}_{0}}{{a}_{1}}a_{2}^{3}a_{4}^{2}{{a}_{5}} + $ $356{{a}_{0}}{{a}_{1}}a_{2}^{2}a_{3}^{2}{{a}_{4}}{{a}_{5}}$ – $80{{a}_{0}}{{a}_{1}}a_{2}^{2}{{a}_{3}}a_{4}^{3}$ – ‒ $72{{a}_{0}}{{a}_{1}}{{a}_{2}}a_{3}^{4}{{a}_{5}}$ + $18{{a}_{0}}{{a}_{1}}{{a}_{2}}a_{3}^{3}a_{4}^{2} + $ $108{{a}_{0}}a_{2}^{5}a_{5}^{2}$ – ‒ $72{{a}_{0}}a_{2}^{4}{{a}_{3}}{{a}_{4}}{{a}_{5}}$ + $16{{a}_{0}}a_{2}^{4}a_{4}^{3} + $ $16{{a}_{0}}a_{2}^{3}a_{3}^{3}{{a}_{5}}$ – $4{{a}_{0}}a_{2}^{3}a_{3}^{2}a_{4}^{2}$ + + $256a_{1}^{5}a_{5}^{3} - $ $192a_{1}^{4}{{a}_{2}}{{a}_{4}}a_{5}^{2}$ – $128a_{1}^{4}a_{3}^{2}a_{5}^{2} + $ $144a_{1}^{4}{{a}_{3}}a_{4}^{2}{{a}_{5}} - $ – $27a_{1}^{4}a_{4}^{4} + $ $144a_{1}^{3}a_{2}^{2}{{a}_{3}}a_{5}^{2} - $ $6a_{1}^{3}a_{2}^{2}a_{4}^{2}{{a}_{5}} - $ $80a_{1}^{3}{{a}_{2}}a_{3}^{2}{{a}_{4}}{{a}_{5}} + $ + $18a_{1}^{3}{{a}_{2}}{{a}_{3}}a_{4}^{3} + $ $16a_{1}^{3}a_{3}^{4}{{a}_{5}} - $ $4a_{1}^{3}a_{3}^{3}a_{4}^{2} - $ $27a_{1}^{2}a_{2}^{4}a_{5}^{2}$ + + $18a_{1}^{2}a_{2}^{3}{{a}_{3}}{{a}_{4}}{{a}_{5}} - $ $4a_{1}^{2}a_{2}^{3}a_{4}^{3} - $ $4a_{1}^{2}a_{2}^{2}a_{3}^{3}{{a}_{5}} + $ $a_{1}^{2}a_{2}^{2}a_{3}^{2}a_{4}^{2}$, выдает срезку на некоординатную гипергрань h₂ многогранника $\mathcal{N}(\Delta )$:

$\Delta {{{\text{|}}}_{{{{h}_{2}}}}}$ = $108{{a}_{0}}a_{2}^{5}a_{5}^{2}\, - \,72{{a}_{0}}a_{2}^{4}{{a}_{3}}{{a}_{4}}{{a}_{5}}$ + $16{{a}_{0}}a_{2}^{4}a_{4}^{3}$ + + $16{{a}_{0}}a_{2}^{3}a_{3}^{3}{{a}_{5}}$ – $4{{a}_{0}}a_{2}^{3}a_{3}^{2}a_{4}^{2} - 27a_{1}^{2}a_{2}^{4}a_{5}^{2} + $ $18a_{1}^{2}a_{2}^{3}{{a}_{3}}{{a}_{4}}{{a}_{5}}$ – – $4a_{1}^{2}a_{2}^{3}a_{4}^{3}$ – $4a_{1}^{2}a_{2}^{2}a_{3}^{3}{{a}_{5}} + a_{1}^{2}a_{2}^{2}a_{3}^{2}a_{4}^{2}$,

которая в свою очередь, согласно Теореме 2, факторизуется в произведение дискриминантов двух многочленов степеней два и три:

$a_{2}^{2}(27a_{2}^{2}a_{5}^{2}\, - \,18{{a}_{2}}{{a}_{3}}{{a}_{4}}{{a}_{5}}$ + $4{{a}_{2}}a_{4}^{3}\, + \,4a_{3}^{3}{{a}_{5}}\, - $ $a_{3}^{2}a_{4}^{2})(4{{a}_{0}}{{a}_{2}}$ – – $a_{1}^{2}) = a_{2}^{2}{{\Delta }_{2}}({{a}_{0}} + $ ${{a}_{1}}y + {{a}_{2}}{{y}^{2}}){{\Delta }_{3}}({{a}_{2}}$ + a₃y + ${{a}_{4}}{{y}^{2}} + {{a}_{5}}{{y}^{3}}).$

Команда

находит факторизацию срезки рассматриваемого дискриминанта на грань многогранника $\mathcal{N}(\Delta )$, полученную пересечением некоординатной гиперграни h₂ с координатной $h_{3}^{0}$:

Время счета для приведенного примера составило менее 0.1 секунды.