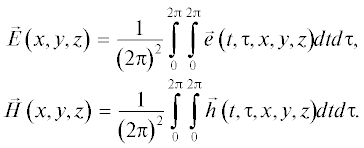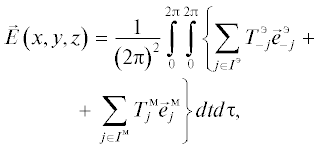Радиотехника и электроника, 2019, T. 64, № 11, стр. 1096-1102

ВВЕДЕНИЕ

Директорные антенные решетки, образованные идеально проводящими излучателями, нашли широкое применение в антенной технике. Анализу излучения таких антенн посвящены работы [1–6]. Решение внешней задачи теории антенных решеток состоит в определении характеристик направленности антенной системы при известном амплитудно-фазовом распределении токов по элементам решетки. Распределение токов в элементах решетки определяется с учетом взаимного влияния излучающих элементов друг на друга. Для расчета характеристик антенной решетки важным элементом является вычисление парциальной диаграммы направленности решетки, возникающей при возбуждении одного элемента при пассивных остальных элементах. Расчет парциальной диаграммы можно проводить для модели бесконечной периодической решетки, что позволяет использовать такие диаграммы для решения задач синтеза возбуждения антенной решетки. В данной статье рассмотрена математическая модель локального возбуждения плоской антенной решетки. Задача локального возбуждения сводится к решению задачи в “канале Флоке”.

1. ПОСТАНОВКА ЗАДАЧИ ИЗЛУЧЕНИЯ

Рассмотрим в пространстве периодически расположенную систему идеально проводящих тел ${{D}_{i}}$ с поверхностью ${{S}_{i}}.$ Все тела одинаковы и расположены симметрично друг другу. Будем считать, что тела образуют плоскую прямоугольную решетку. На поверхности тел могут быть заданы сторонние электродвижущие силы (ЭДС). Нас интересует парциальная диаграмма системы, поэтому будем считать, что сторонняя ЭДС приложена к телу, расположенному в ячейке с номером ${{i}_{0}}\left( {{{n}_{0}},{{m}_{0}}} \right),$ а на поверхности всех остальных тел в решетке касательное поле $\left[ {\vec {n},\,\vec {E}} \right] = 0.$

Задача дифракции состоит в определении решения однородной системы уравнений Максвелла

с условиями излучения и граничными условиями на поверхностях ${{S}_{i}}.$

где $P \in {{S}_{i}}.$

Функция $\vec {B}\left( P \right)$ определена лишь в точках поверхности ${{S}_{{{{i}_{0}}}}}.$ Продолжим $\vec {B}\left( P \right)$ с поверхности ${{S}_{{{{i}_{0}}}}}$нулем на все пространство и рассмотрим функцию

Очевидно, что функция $\vec {\varepsilon }\;\left( {t,\tau ,P} \right)$ определена на любой поверхности ${{S}_{i}}$ и

Координаты точек поверхности ${{S}_{i}}$ обозначены через $\left( {{{x}_{p}},{{y}_{p}},{{z}_{p}}} \right).$

Введя функцию $\vec {\varepsilon }\left( {t,\tau ,P} \right),$ мы свели задачу возбуждения системы излучателей к задаче излучения с поверхности одного тела, расположенного в условном прямоугольном волноводе с условиями Флоке на боковой поверхности.

Для решения поставленной задачи можно применить метод типа Галеркина, однако специфика этой задачи состоит в том, что среда, окружающая тело ${{S}_{i}}$, однородна, а поверхность идеально проводящая. Для решения такой задачи можно использовать метод интегральных уравнений. Для скалярной задачи дифракции интегральные уравнения получены и исследованы в работе [7]. Применим процедуру получения системы интегральных уравнений, использующую интегральные представления решения, аналогичные представлениям Стрэттона–Чу [8].

Итак, обозначим решение задачи об излучении в условном прямоугольном волноводе через $\vec {e}\left( {t,\tau ,M} \right),$ $\vec {h}\left( {t,\tau ,M} \right).$ На поверхности ${{S}_{0}}$ поле $\vec {e}$ удовлетворяет условию

где $P \in {{S}_{0}}.$

Интегральное преобразование (2) подробно рассмотрено в работах [9, 10]. Оно определено для любой функции, интегрируемой с квадратом в плоскости $\left( {x,y} \right){\text{:}}$

Найдя $\vec {e}\left( {t,\tau ,x,y,z} \right)$ и $\vec {h}\left( {t,\tau ,x,y,z} \right)$ во всем трехмерном пространстве, определим с помощью обратного преобразования основные характеристики рассеянного поля.

2. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ЗАДАЧИ

Определим внутри условного прямоугольного волновода систему фундаментальных решений $\left\{ {{{{\vec {H}}}^{{\alpha }}}\left( {M,{{M}_{0}}} \right),\,\,{{{\vec {E}}}^{{\alpha }}}\left( {M,{{M}_{0}}} \right)} \right\}$

удовлетворяющих условиям Флоке на боковой поверхности волновода Здесь ${{\vec {I}}_{{\alpha }}}$ – единичный вектор, направленный по любой координатной оси, а ${{l}_{{\alpha }}}$ – направляющие косинусы единичного вектора в произвольном направлении $\vec {l}.$ Поле ${{\vec {H}}^{{\alpha }}}$ удовлетворяет векторному уравнению Применим к функциям $\left\{ {\vec {e},\,\,\vec {h}} \right\}$ и $\left\{ {{{{\vec {H}}}^{{{{{\alpha }}^{ - }}}}},\,\,{{{\vec {E}}}^{{{{{\alpha }}^{ - }}}}}} \right\}$ векторную формулу Грина в области V, ограниченной боковой поверхностью волновода и поверхностью тела ${{S}_{0}}$

Интеграл по боковой поверхности волновода уничтожился в силу условий Флоке (5). Минус в обозначениях ${{\vec {H}}^{{{{{\alpha }}^{ - }}}}}$ и ${{\vec {E}}^{{{{{\alpha }}^{ - }}}}}$показывает, что решение (4) соответствует значениям $\left( { - t} \right)$ и $\left( { - \tau } \right)$ в условиях (5).

Вектор ${{\vec {H}}^{{{{{\alpha }}^{ - }}}}}\left( {M,{{M}_{0}}} \right)$ допускает следующее представление:

где ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\vec {H}} }^{{{{{\alpha }}^{ - }}}}}\left( {M,{{M}_{0}}} \right)$ не имеет особенности при совпадении аргументов. Определив ток на поверхности ${{S}_{0}}$ как вектор $\vec {j} = \left[ {\,\vec {n},\vec {h}} \right]$ и учитывая, что получим

Преобразуем первое слагаемое (8)

где $\vec {A}_{{\beta }}^{{\alpha }} = \int_{{{S}_{0}}} {\left[ {\vec {j},\nabla H_{{\beta }}^{{{{{\alpha }}^{ - }}}}} \right]} d{{\sigma }_{p}}.$ Так как $H_{{\beta }}^{{{{{\alpha }}^{ - }}}} = H_{{\alpha }}^{{{{{\beta }}^{ - }}}}$ то окончательно получаем выражение для первого слагаемого в (8)

Используя представление (7) и предельное свойство потенциала двойного слоя [8], имеем

Опуская точку $M$ на поверхность ${{S}_{0}},$ получим

Переходя к пределу при $M \to {{P}_{0}}$ в соотношении (8), получим следующее основное интегральное уравнение Фредгольма второго рода относительно тока на поверхности ${{S}_{0}}{\text{:}}$

В том случае, когда рассматривается дифракция на теле в свободном пространстве, уравнение (9) переходит в известное уравнение Фока [11], при этом

В силу разрешимости исходной краевой задачи, полученное уравнение разрешимо при любом способе возбуждения. К уравнению (9) применима вся теория интегральных уравнений Фредгольма. В частности, из единственности решения сопряженной задачи следует единственность полученного интегрального уравнения. Обоснование вопросов разрешимости уравнения (9) и его единственности проводится по аналогии с задачами дифракции в свободном пространстве [8].

3. УРАВНЕНИЕ ЛИНЕЙНОГО ВИБРАТОРА

Уравнение (9) представляет собой систему векторных уравнений по поверхности ${{S}_{0}},$ и его численное решение в общем случае весьма громоздко. Рассмотрим поэтому случай, когда тело ${{D}_{0}}$ представляет собой криволинейный вибратор. Характеризовать поверхность вибратора удобно в обобщенной цилиндрической системе координат. Внутри вибратора проведем плавную кривую $C,$ заданную в естественной системе координат $\vec {r} = {{\vec {R}}_{0}}\left( s \right).$ Пусть ${{r}_{0}}\left( {\varphi ,s} \right)$ – уравнение контура поперечного сечения поверхности вибратора ${{S}_{0}}$ плоскостью, нормальной к кривой $C$ в точке $0$ с координатой $s.$ При этом положение любой точки в данной плоскости однозначно определяется координатами $\left( {{\rho ,}\varphi } \right),$ введенными на данной плоскости. Полярную ось будем направлять по главной нормали к кривой $C$ в точке 0. Связь декартовых координат с координатами $\left( {{\rho ,}\varphi ,s} \right)$ легко установить, используя равенство

Здесь ${{\vec {R}}_{0}}\left( s \right)$ – нормальное уравнение кривой $C$; $\vec {n}\left( s \right),$ $\vec {b}\left( s \right)$ – векторы главной нормали и бинормали к кривой $C$ в точке $s.$ Параметрическое представление поверхности ${{S}_{0}}$ в точке $\left( {{\rho ,}\varphi ,s} \right)$ таково:

Система координат $\left( {\rho ,\varphi ,s} \right)$ не является ортогональной. Поэтому для дальнейшего удобно ввести ковариантные координаты векторов

Вектор нормали к поверхности ${{S}_{0}}$ параллелен вектору ${{\vec {a}}^{1}}.$ Поэтому для тока $\vec {j}$ на поверхности ${{S}_{0}}$ имеет место следующее разложение:

Тогда векторное уравнение (9) может быть записано как следующая система уравнений относительно компонент ${{j}_{{\varphi }}}$ и ${{j}_{s}}{\text{:}}$

где а $H_{{\alpha }}^{{{{{\alpha }}^{ - }}}}$ зависят лишь от координат точек $P\left( {s,{\varphi }} \right)$ и ${{P}_{0}}\left( {{{s}_{0}},{{{\varphi }}_{0}}} \right).$ Отсюда следует, что где $K_{{ij}}^{{\left( m \right)}}\left( {s,s_{0}^{{}}} \right)$ не зависит от ${{{\varphi }}_{0}}$ при условии, что ось вибратора прямая линия, а ${{r}_{0}}\left( {{\varphi },s} \right)$ не зависит от ${\varphi }.$ В том случае, когда эти условия нарушаются, $K_{{ij}}^{{\left( m \right)}}\left( {s,s_{0}^{{}}} \right)$ слабо зависят от ${{{\varphi }}_{0}}$ и соотношение (10) следует рассматривать как приближенное выражение для ядер. Точность такого приближения легко оценить для любого контура ${{r}_{0}}.$

Записав разложение в ряд Фурье для компонент тока, легко получить интегральное уравнение для гармоник тока

Ядра уравнений (11) имеют лишь логарифмическую особенность при совпадении точек. Это позволяет применить для решения системы (11) стандартные методы решения интегральных уравнений второго рода с использованием квадратурных формул.

Отметим, что в том случае, когда $f_{{\varphi }}^{{\left( m \right)}} \equiv 0$ и $a = \mathop {\max }\limits_{s \in C} \left| {{{r}_{0}}\left( s \right)} \right|$ достаточно мал, составляющая тока ${{j}_{{\varphi }}}$ много меньше составляющей ${{j}_{s}},$ и для уравнений (11) можно применить метод последовательных приближений, состоящий в том, что определяется нулевое приближение системы (11) из соотношений

а следующие приближения вычисляются с помощью квадратур

Для тонких вибраторов обычно достаточно исследовать нулевое приближение.

Отметим, что функции $H_{{\alpha }}^{{\alpha }}\left( {M,{{M}_{0}}} \right)$ имеют весьма простой вид

где или, представляя $H_{{\alpha }}^{{\alpha }}$ рядами по пространственным гармоникам, будем иметь

Используя интегральные представления (6) и выражение (13) для функции $H_{{\alpha }}^{{\alpha }},$ легко получить выражения для коэффициентов распространяющихся пространственных гармоник и выражения для диаграмм излучения.

При численном решении системы (11) или уравнения (12) удобно пользоваться методом Крылова–Боголюбова, а интеграл от ядра, имеющего логарифмическую особенность, вычислять аналитически, так же как в плоском случае.

4. ДИАГРАММА ИЗЛУЧЕНИЯ

Введем спектральное преобразование исходной краевой задачи по переменным $x$ и $y$

Функции $\vec {e}\left( {t,\tau ,x,y,z} \right)$ и $\vec {h}\left( {t,\tau ,x,y,z} \right)$ удовлеворяют условиям Флоке (5) по каждой переменной $x$ и $y.$ Для определения полей $\vec {E}$ и $\vec {H}$ во всем пространстве достаточно определить функции $\vec {e}$ и $\vec {h}$ внутри бесконечного прямоугольного волновода ${{D}_{1}}\left\{ {0 \leqslant x \leqslant a,\,\,0 \leqslant y \leqslant b,\,\, - \infty < z < \infty } \right\}$ и воспользоваться формулами обращения [9].

Задача определения образов полей $\vec {e}$ и $\vec {h}$ в условном волноводе сводится к определению решений уравнений Максвелла, удовлетворяющих условиям Флоке (5) на боковой поверхности условного волновода, условиям непрерывности касательных составляющих электрического и магнитного полей на поверхностях тел, образующих периодическую структуру, –

и условиям излучения. Рассматривая соответствующую краевую задачу, легко установить, что в тех случаях, когда $\operatorname{Im} {{\varepsilon }_{0}}$ = $\operatorname{Im} {{\mu }_{0}} = 0,$ существует дискретный спектр частот, при которых однородная задача имеет нетривиальные решения.

Рассмотрим систему векторных собственных функций оператора Максвелла в области ${{D}_{1}}$ с однородным заполнением $\left( {{{\varepsilon }_{0}},{{\mu }_{0}}} \right).$ Введем систему собственных функций оператора Лапласа в прямоугольнике $\left\{ {0 \leqslant x \leqslant a,\,\,0 \leqslant y \leqslant b} \right\},$ удовлетворяющих условиям Флоке

Собственной функцией, удовлетворяющей условиям (16), является

при каждом собственном значении ${{\lambda }_{j}}$ (14). Далее будем считать, что собственные значения $\lambda $ занумерованы в некотором порядке. Собственные значения будем обозначать через ${{\lambda }_{j}},$ а собственные функции через ${{\psi }_{j}},$ имея в виду, что каждому $j$ соответствует определенная пара $n$ и $m.$ Хорошо известно, что система уравнений Максвелла в однородном пространстве допускает две совокупности решений в виде $E$ и $H$ волн [12]. Для уравнений Максвелла (1) построим следующую систему решений в области ${{D}_{1}}$ по схеме работы [12]

где для полей E-волн: а для полей H-волн: где ${{\gamma }_{j}} = \sqrt {{{\omega }^{2}}{{\varepsilon }_{0}}{{\mu }_{0}} - {{\lambda }_{j}}} ,$ $\operatorname{Re} {{\gamma }_{j}} > 0.$

Нормировка функции ${{\psi }_{j}}$ выбрана таким образом, что

Система функций (17) обладает всеми свойствами системы нормальных волн в регулярных волноводах с металлизированными стенками. В частности, следуя работе [12], легко доказать полноту системы E- и H-волн в области ${{D}_{1}},$ а также получить явные формулы для компонент тензора Грина. Таким образом, любое решение системы уравнений Максвелла в области ${{D}_{1}},$ удовлетворяющее условиям Флоке (5), представимо в виде суперпозиции полей E- и H-волн.

Область ${{D}_{1}}\left\{ {0 \leqslant x \leqslant a,\,\,0 \leqslant y \leqslant b,\,\, - \infty < z < \infty } \right\}$ разделяется сечениями $z = {{z}_{{\min }}}$ и $z = {{z}_{{\max }}}$ на три области: ${{V}_{{\text{I}}}}\left( {z \leqslant {{z}_{{\min }}}} \right);$ ${{V}_{{{\text{II}}}}}\left( {{{z}_{{\min }}} \leqslant z \leqslant {{z}_{{\max }}}} \right);$ ${{V}_{{{\text{III}}}}}\left( {z \geqslant {{z}_{{\max }}}} \right).$ В силу полноты функций (17) решение задачи $\vec {e}$ и $\vec {h}$ в областях ${{V}_{{\text{I}}}}$ и ${{V}_{{{\text{III}}}}}$ допускает следующие представления:

где $\left( {x,y,z} \right) \in {{V}_{{\text{I}}}},$где $\left( {x,y,z} \right) \in {{V}_{{{\text{III}}}}}.$

Здесь ${{\vec {e}}_{{ - jt}}} = \mp {{\vec {e}}_{{jt}}},$ ${{\vec {h}}_{{ - jt}}} = \mp {{\vec {h}}_{{jt}}},\,\,\,\,\left( {j > 0} \right)$ (верхний знак (–) соответствует электрическим, а нижний (+) – магнитным волнам); ${{T}_{{ - j}}}$ и ${{R}_{j}}$ – неизвестные амплитудные коэффициенты нормальных волн.

Представление поля (18) и (19) позволяют сформулировать следующие “парциальные” условия излучения на границе области ${{V}_{{{\text{II}}}}}$

где S₀ – прямоугольник $\left\{ {0 \leqslant x \leqslant a,\,\,\,\,0 \leqslant y \leqslant b} \right\},$ ${{B}_{j}}\left( {t,\tau ,z} \right) = {{R}_{j}}\exp \left( {i{{\gamma }_{j}}z} \right),$ а ${{\beta }_{j}}$ – нормировка собственных функций

Как и в плоской задаче, коэффициенты ${{T}_{{ - j}}}$ и ${{R}_{j}}$ определяют диаграмму направленности дифрагированного поля в областях $z \leqslant {{x}_{{\min }}}$ и $z \geqslant {{x}_{{\max }}}$ соответственно. Рассмотрим представление поля в дальней зоне в области $z \leqslant {{x}_{{\min }}}.$ Согласно [9] поля $\vec {E}$ и $\vec {H}$ восстанавливаются по образам $\vec {e}$ и $\vec {h}$ по формулам (3).

Преобразуем выражение (3), используя разложение (18)

где ${{I}^{{\text{э}}}}$ обозначает множество электрических волн, а ${{I}^{{\text{м}}}}$ – магнитных. Изменяя порядок суммирования и интегрирования и вводя новые переменные интегрирования: $t{\text{'}} = t + 2\pi n\left( j \right),$ $\tau {\text{'}} = \tau + 2\pi n\left( j \right),$ получим

Рассмотрим первое слагаемое в формуле (20). Объединяя интегралы по прямоугольникам

в один интеграл, получим

Переменные $\nu ,\mu $ в каждом прямоугольнике вводятся соотношениями

a функция $T\left( {\nu ,\mu } \right)$ в каждом прямоугольнике принимает следующее значение:

Вводя сферическую систему координат в области $z \leqslant {{x}_{{\min }}}$

(${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} < \theta < \pi $) и исследуя поведение интеграла (21) при $R \to \infty $ с помощью метода стационарной фазы [13], получим следующее асимптотическое представление для интеграла (21) при $R \to \infty {\text{:}}$где ${{\nu }_{0}} = k\cos \varphi \sin \theta ,$ ${{\mu }_{0}} = k\sin \varphi \sin \theta ,$ $\gamma \left( {{{\nu }_{0}},{{\mu }_{0}}} \right) = $ $ = - k\cos \theta ,$ ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2} < \theta < \pi .$

Для функции $\vec {E}$ в дальней зоне имеем следующее выражение:

В силу того что в сферической системе координат поперечные операторы имеют следующие представления:

получим выражение для диаграмм направленности поля

Функции $\vec {N}\left( {\theta ,\varphi } \right)$ определяются лишь распространяющимися пространственными гармониками. При фиксированных значениях $ka$ и $kb$ число пространственных гармоник определяется величинами ${{N}_{x}} = \left[ {{{ka} \mathord{\left/ {\vphantom {{ka} {2\pi }}} \right. \kern-0em} {2\pi }}} \right]$ и ${{N}_{y}} = \left[ {{{kb} \mathord{\left/ {\vphantom {{kb} {2\pi }}} \right. \kern-0em} {2\pi }}} \right].$ При каждом значении углов $\theta ,\varphi $ определяются целые числа ${{n}_{0}}\left( {\theta ,\varphi } \right) = \left[ {{{{{\nu }_{0}}a} \mathord{\left/ {\vphantom {{{{\nu }_{0}}a} {2\pi }}} \right. \kern-0em} {2\pi }}} \right]$ и ${{m}_{0}}\left( {\theta ,\varphi } \right) = \left[ {{{{{\mu }_{0}}b} \mathord{\left/ {\vphantom {{{{\mu }_{0}}b} {2\pi }}} \right. \kern-0em} {2\pi }}} \right]$ и значения ${{t}_{0}}\left( {\theta ,\varphi } \right)$ = ${{\nu }_{0}}a - 2\pi {{n}_{0}}$ и ${{\tau }_{0}}\left( {\theta ,\varphi } \right)$ = ${{\mu }_{0}}b - 2\pi {{m}_{0}}.$Числа ${{n}_{0}},{{m}_{0}}$ определяют номера коэффициентов $T_{{nm}}^{{\text{э}}}$ и $T_{{nm}}^{{\text{м}}},$ по которым вычисляется диаграмма в данной точке, а значения ${{t}_{0}}\left( {\theta ,\varphi } \right)$ и ${{\tau }_{0}}\left( {\theta ,\varphi } \right)$ – это значения параметров преобразования (15) при данных значениях углов $\theta ,\varphi .$ Диаграмма направленности определяется через значения коэффициентов $T_{{nm}}^{{\text{э}}}\left( {t,\tau } \right)$ и $T_{{nm}}^{{\text{м}}}\left( {t,\tau } \right)$ следующим образом:

При фиксированных значениях $ka$ и $kb$ число распространяющихся волн всегда конечно и номера распространяющихся волн принимают последовательно все целые значения $ - {{N}_{x}} - 1 \leqslant $ $ \leqslant {{n}_{0}} \leqslant {{N}_{x}},$ $ - {{N}_{y}} - 1 \leqslant {{m}_{0}} \leqslant {{N}_{y}}.$

Отметим тот факт, что волны электрического типа определяют составляющую диграммы по координате ${{\vec {i}}_{{\theta }}},$ а магнитные волны – по координате ${{\vec {i}}_{{\varphi }}}.$ В формуле (22) выписаны члены, имеющие порядок ${1 \mathord{\left/ {\vphantom {1 R}} \right. \kern-0em} R}$ при $R \to \infty .$ Аналогичная форма справедлива и для поля $\vec {H}$ в дальней зоне.