Радиотехника и электроника, 2019, T. 64, № 12, стр. 1177-1180

ВВЕДЕНИЕ

Проблема взаимодействия электромагнитных волн со средой, относительная диэлектрическая ${{\varepsilon }_{r}}$ и относительная магнитная ${{\mu }_{r}}$ проницаемости которой одновременно являются отрицательными величинами (${{\varepsilon }_{r}} < 0$ и ${{\mu }_{r}} < 0$), – одна из наиболее обсуждаемых в научной среде за последние двадцать лет. В значительной мере внимание к этой проблеме связано с различными попытками теоретического описания эффектов, сопровождающих “отрицательную” рефракцию и впервые отмеченных Веселаго еще в 1967 г. [1]. Мы имеем в виду указанное Веселаго свойство плоского безграничного слоя среды с ${{\varepsilon }_{r}} = - 1$ и ${{\mu }_{r}} = - 1$ “необычно” преломлять поле плоской падающей волны, а также фокусировать поле падающей цилиндрической волны как внутри такого слоя, так и за ним. В современной литературе слой такой среды принято называть линзой Веселаго. Согласно утверждению, сделанному в работе [2], эффект фокусировки линзой Веселаго наблюдался экспериментально в 2000 г. В этой же работе был впервые введен термин “метаматериал” для обозначения сред с ${{\varepsilon }_{r}} < 0$ и ${{\mu }_{r}} < 0.$

После публикации [2] число работ, в которых предпринимались попытки теоретического анализа эффекта фокусировки линзы Веселаго, увеличивалось с каждым годом. При этом большинство из них основывалось на различных асимптотических методах – методе геометрической оптики, методе приближения Кирхгофа или их модификации [3]. Кроме того, практически во всех публикациях полагалось, что толщина линзы значительно превышает длину волны и тем самым выполняются условия применимости метода геометрической оптики.

Начиная с 2006 г. стали появляться работы, в которых использовались строгие методы описания взаимодействия электромагнитных волн с конечным или бесконечным [4–17] слоем метаматериала (линзой Веселаго). При этом было показано, что линза Веселаго (или ее модификация) не обладает свойством сверхразрешения (сверхфокусировки), а для распределения поля на гранях линзы характерно наличие осцилляций. При этом амплитуда таких осцилляций может значительно превышать амплитуду поля в области фокуса. Более того, было показано, что в строгой электродинамической постановке задача взаимодействия электромагнитных волн с линзой Веселаго, для которой выполняются условия ${{\varepsilon }_{r}} = - 1$ и ${{\mu }_{r}} = - 1,$ вообще не имеет решения [7].

В данной работе, основываясь на численном решении строгой задачи дифракции цилиндрической волны на конечном слое метаматериала малой электрической толщины, покажем, что особенности структуры ближнего поля вблизи границы пластины из метаматериала определяются не только существованием поля поверхностных волн, но и их резонансами.

1. ФОРМУЛИРОВКА ЗАДАЧИ

Рассмотрим двумерную задачу рассеяния цилиндрической поляризованной TM-волны

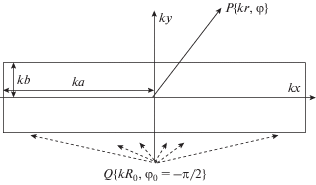
диэлектрическим цилиндром, контур поперечного сечения $\rho (\varphi )$ которого в цилиндрической (полярной) системе координат описывается уравнением

В выражения (1), (2) входят следующие величины: $r,\varphi $ – пространственные координаты точки наблюдения $P$ в цилиндрической системе координат (см. рис. 1); ${{R}_{0}},{{\varphi }_{0}}$ – пространственные координаты точки расположения источника $Q$ волны в цилиндрической системе координат (см. рис. 1); $k$ – волновое число свободного пространства; $a,b$ – определяют геометрию пластины (размеры ее сторон). Геометрия задачи представлена на рис. 1.

Пусть среда пластины (2) имеет относительную диэлектрическую проницаемость ${{\varepsilon }_{r}} < 0$ и относительную магнитную проницаемость ${{\mu }_{r}} < 0,$ т.е. представляет собой метаматериал с отрицательным показателем преломления

где $\nu $ характеризует потери среды.

Нетрудно видеть, что описание контура поперечного сечения пластины на основе формулы (2) позволяет получить форму контура $\rho (\varphi ),$ практически совпадающей с прямоугольной при значении параметра $m \gg 1$ (например, при $m \geqslant 20$) и $a \gg b.$

Представим полное поле $U(r,\varphi )$ вне цилиндрической структуры (2) в виде суперпозиции поля падающей волны (1) и рассеянного поля:

а поле внутри цилиндра (2) из метаматериала обозначим ${{U}_{2}}(r,\varphi ).$

Как известно, поля $U(r,\varphi ),$ ${{U}_{2}}(r,\varphi )$ должны удовлетворять соответствующим уравнениям Гельмгольца вне и внутри цилиндрической структуры, соответствующим граничным условиям на контуре $\rho (\varphi ),$ а также условию излучения на бесконечности (условию Зоммерфельда), т.е. являться решением граничной задачи. Для численного решения такой граничной задачи воспользуемся модифицированным методом дискретных источников (ММДИ) [18, 19], который позволяет получить решение с контролируемой точностью. При этом выбор вспомогательных контуров будем осуществлять в соответствии с результатами работ [18, 19]. Используемое в этом методе представление для полей ${{U}_{1}}(r,\varphi )$ и ${{U}_{2}}(r,\varphi )$ в виде суперпозиции полей вспомогательных источников цилиндрических волн, расположенных на вспомогательных контурах, заведомо удовлетворяет уравнениям Гельмгольца и условию Зоммерфельда [3].

Амплитудные коэффициенты для полей вспомогательных источников цилиндрических волн в методе ММДИ находятся из условия выполнения граничных условий в точках $N$ каждого контура.

Точность решения задачи контролируется путем вычисления невязки граничных условий в точках, которые расположены в середине между точками, где граничные условия выполняются точно (в таких точках граничные условия выполняются наихудшим образом [19]).

Поскольку метод ММДИ и техника его применение к ряду задач с аналогичной конфигурацией контура рассеивающего тела описаны достаточно подробно в работе [18], то не будем обсуждать особенности применения этого метода в рассматриваемом случае, а лишь укажем, что приведенные ниже результаты имеют максимальную невязку граничных условий, не превышающую величины $\Delta < {{10}^{{ - 3}}}$ для любой точки контура $\rho (\varphi ).$

2. ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Рассмотрим сначала случай, когда относительные диэлектрическая и магнитная проницаемости метаматериала полагались равными ${{\varepsilon }_{r}} = - 1.00013,$ ${{\mu }_{r}} = - 0.99027$ (${{n}_{r}} = - 0.995 \approx - 1$), потери среды $\nu = {{10}^{{ - 6}}},$ а электрические размеры пластины – ka = 10; kb = 1.00775. Источник цилиндрической волны $Q$ имел координаты $k{{R}_{0}} = kb + 1;$ ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}$ (как будет показано ниже, значения этих параметров задачи соответствуют случаю резонанса ближнего полного поля).

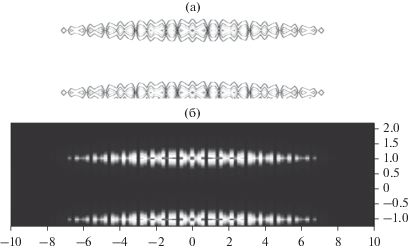
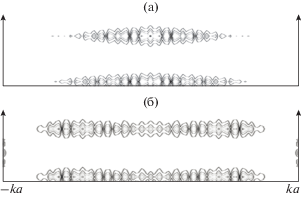
На рис. 2а и 2б представлены результаты расчетов пространственного распределения линий равной амплитуды полного поля и пространственного распределения модуля амплитуды полного поля $U = \left| {U(kx,ky)} \right|.$ Из них следует, что поле сосредоточено вблизи верхней ($ - ka \leqslant kx \leqslant ka,$ $ky = kb$) и нижней ($ - ka \leqslant kx \leqslant ka,$ $ky = - kb$) граней пластины. При этом для пространственного распределения поля характерно наличие периодических колебаний – стоячих поверхностных волн, максимальная амплитуда которых монотонно уменьшается в направлении узких торцов пластины.

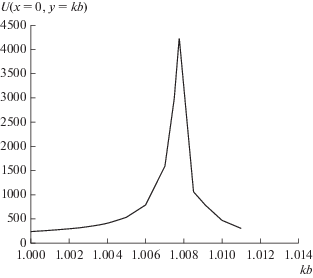
Частотная зависимость модуля амплитуды полного поля $U = \left| {U(kb)} \right|$ в точке $kx = 0;$ $ky = kb$ (т.е. в центре верхней широкой грани пластины, где амплитуда поля максимальна) представлена на рис. 3. Рассчитанные точки интерполировались отрезками прямых линий. Отметим, что расстояние от нижней широкой грани пластины до источника цилиндрической волны Q оставалось постоянным и равным $k{{R}_{0}} = kb + 1,$ ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2},$ а параметры среды совпадали с рассмотренным выше случаем. Особенностью графика частотной зависимости $\left| {U(kb)} \right|$ на рис. 2 является то, что он имеет ярко выраженный резонансный характер, причем добротность резонанса оценивается величиной порядка нескольких тысяч.

Таким образом, данные рис. 2 и 3 свидетельствуют о том, что структура ближнего поля пластины из метаматериала определяется наличием поверхностных стоячих волн, которые обладают выраженными резонансными свойствами.

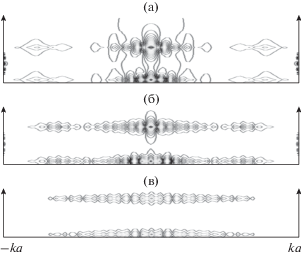
Рассмотрим теперь влияние потерь метаматериала на характер пространственного распределения ближнего поля пластины. На рис. 4 изображены рассчитанные пространственные распределения линий равных амплитуд полного поля вблизи пластины для трех значений потерь: ν = 10^–2 (а), 10^–3 (б), 10^–4 (в). Геометрия задачи характеризовалась следующими значениями: $ka = 10;$ $kb = 1.00775;$ $k{{R}_{0}} = kb + 1.0;$ ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2},$ что соответствовало случаю резонанса поля. Параметры среды метаматериала были следующие: ${{\varepsilon }_{r}} = - 1.00013,$ ${{\mu }_{r}} = - 0.99027.$ Из анализа рис. 4 следует, что потери среды могут существенно изменить структуру распределения ближнего поля (поля поверхностных волн) при его резонансе – сменить монотонно убывающий к торцам пластины характер изменения максимальной амплитуды поверхностных волн на немонотонный, характерный для интерференции двух стоячих поверхностных волн.

Было рассмотрено также влияние положения источника цилиндрической волны на структуру ближнего поля поверхностных волн пластины. На рис. 5 представлены результаты расчетов пространственного распределения линий равных амплитуд полного поля для двух положений источника Q цилиндрической волны – $k{{R}_{0}} = 2.0;$ ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}$ (а) и $k{{R}_{0}} = 3.0;$ ${{\varphi }_{0}} = {{ - \pi } \mathord{\left/ {\vphantom {{ - \pi } 2}} \right. \kern-0em} 2}$ (б); параметры, характеризующие пластину: ${{\varepsilon }_{r}} = - 1.00013;$ ${{\mu }_{r}} = - 0.99027;$ $\nu = {{10}^{{ - 6}}};$ $ka = 10;$ $kb = 1.0.$ Из рис. 5 видно, что и в этом случае наблюдаются стоячие волны ближнего поля на гранях пластины, а удаление источника Q от нижней широкой границы пластины приводит к существенным изменениям в распределении поля поверхностных стоячих волн вдоль широких границ пластины – монотонное спадание максимальной амплитуды (присущее для одной стоячей волны) в направлении узких торцов пластины сменяется на немонотонное изменение (характерное для двух стоячих волн).

ЗАКЛЮЧЕНИЕ

Сформулируем основные результаты работы:

– обнаружены как простые, так и сложные резонансы ближнего поля (плазмонов) конечной пластины из метаматериала;

– показано, что особенности поведения ближнего поля пластины из метаматериала связаны с образованием поверхностных стоячих волн (плазмонов), структура которых зависит от потерь среды и расстояния от пластины до источника;

– обнаружено, что структура резонансного поля чрезвычайно чувствительна к изменению параметров среды метаматериала, что открывает перспективы для создания устройств микроволнового диапазона, управляемых внешним полем.